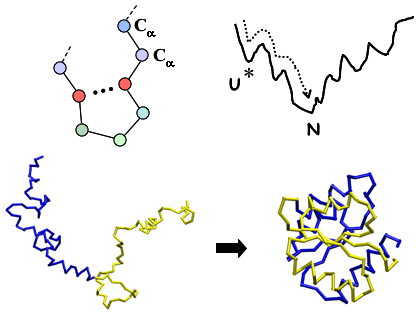
Insights from Coarse-Grained Gō Models for Protein Folding and Dynamics
Abstract
:1. Introduction
2. Role of Native Contacts in Folding
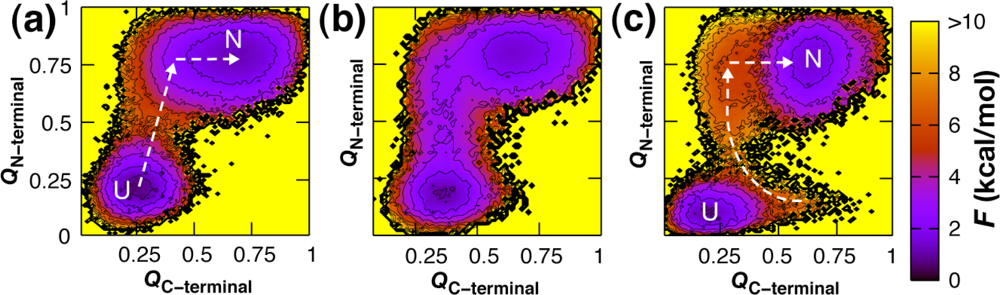
3. Sequence Dependence of Folding
4. Conclusions and Outlook
Acknowledgments
References and Notes
- Clementi, C; Nymeyer, H; Onuchic, JN. Topological and energetic factors: What determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol 2000, 298, 937–953. [Google Scholar]
- Karanicolas, J; Brooks, CL, III. The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci 2002, 11, 2351–2361. [Google Scholar]
- Koga, N; Takada, S. Roles of native topology and chain-length scaling in protein folding: A simulation study with a Go-like model. J. Mol. Biol 2001, 313, 171–180. [Google Scholar]
- Paci, E; Vendruscolo, M; Karplus, M. Validity of Go models: Comparison with a solvent-shielded empirical energy decomposition. Biophys. J 2002, 83, 3032–3038. [Google Scholar]
- Prieto, L; de Sancho, D; Rey, A. Thermodynamics of Go-type models for protein folding. J. Chem. Phys 2005, 123, 154903. [Google Scholar]
- Prieto, L; Rey, A. Influence of the chain stiffness on the thermodynamics of a Go-type model for protein folding. J. Chem. Phys 2007, 126, 166103. [Google Scholar]
- Rhee, YM; Pande, VS. On the role of chemical detail in simulating protein folding kinetics. Chem. Phys 2006, 323, 66–77. [Google Scholar]
- Shea, JE; Onuchic, JN; Brooks, CL, III. Exploring the origins of topological frustration: Design of a minimally frustrated model of fragment B of protein A. Proc. Natl. Acad. Sci. USA 1999, 96, 12512–12517. [Google Scholar]
- Dokholyan, NV; Buldyrev, SV; Stanley, HE; Shakhnovich, EI. Discrete molecular dynamics studies of the folding of a protein-like model. Fold. Des 1998, 3, 577–587. [Google Scholar]
- Cheung, MS; Finke, JM; Callahan, B; Onuchic, JN. Exploring the interplay between topology and secondary structural formation in the protein folding problem. J. Phys. Chem. B 2003, 107, 11193–11200. [Google Scholar]
- Lam, AR; Borreguero, JM; Ding, F; Dokholyan, NV; Buldyrev, SV; Stanley, HE; Shakhnovich, E. Parallel foldng pathways in the SH3 domain protein. J. Mol. Biol 2007, 373, 1348–1360. [Google Scholar]
- Sulkowska, JI; Cieplak, M. Selection of optimal variants of Go-like models of proteins through studies of stretching. Biophys. J 2008, 95, 3174–3191. [Google Scholar]
- Ding, F; Dokholyan, NV; Buldyrev, SV; Stanley, HE; Shakhnovich, EI. Molecular dynamics simulation of the SH3 domain aggregation suggests a generic amyloidogenesis mechanism. J. Mol. Biol 2002, 324, 851–857. [Google Scholar]
- Barton, S; Jacak, R; Khare, SD; Ding, F; Dokholyan, NV. The length dependence of the PolyQ-mediated protein aggregation. J. Biol. Chem 2007, 282, 25487–25492. [Google Scholar]
- Kwiecinska, JI; Cieplak, M. Chirality and protein folding. J. Phys.-Condes. Matter 2005, 17, S1565–S1580. [Google Scholar]
- Yue, K; Fiebig, KM; Thomas, PD; Chan, HS; Shakhnovich, EI; Dill, KA. A test of lattice protein folding algorithms. Proc. Natl. Acad. Sci. USA 1995, 92, 325–329. [Google Scholar]
- Han, W; Wan, CK; Wu, YD. Toward a coarse-grained protein model coupled with a coarse-grained solvent model: Solvation free energies of amino acid side chains. J. Chem. Theory Comput 2008, 4, 1891–1901. [Google Scholar]
- Han, W; Wu, YD. Coarse-grained protein model coupled with a coarse-grained water model: Molecular dynamics study of polyalanine-based peptides. J. Chem. Theory Comput 2007, 3, 2146–2161. [Google Scholar]
- Sherwood, P; Brooks, BR; Sansom, MSP. Multiscale methods for macromolecular simulations. Curr. Opin. Struct. Biol 2008, 18, 630–640. [Google Scholar]
- Tozzini, V. Coarse-grained models for proteins. Curr. Opin. Struct. Biol 2005, 15, 144–150. [Google Scholar]
- Bond, PJ; Sansom, MSP. Insertion and assembly of membrane proteins via simulation. J. Am. Chem. Soc 2006, 128, 2697–2704. [Google Scholar]
- Monticelli, L; Kandasamy, SK; Periole, X; Larson, RG; Tieleman, DP; Marrink, SJ. The MARTINI coarse-grained force field: Extension to proteins. J. Chem. Theory Comput 2008, 4, 819–834. [Google Scholar]
- Shih, AY; Arkhipov, A; Freddolino, PL; Schulten, K. Coarse grained protein-lipid model with application to lipoprotein particles. J. Phys. Chem. B 2006, 110, 3674–3684. [Google Scholar]
- Yap, EH; Fawzi, NL; Head-Gordon, T. A coarse-grained alpha-carbon protein model with anisotropic hydrogen-bonding. Proteins 2008, 70, 626–638. [Google Scholar]
- Thorpe, IF; Zhou, J; Voth, GA. Peptide folding using multiscale coarse-grained models. J. Phys. Chem. B 2008, 112, 13079–13090. [Google Scholar]
- Makowski, M; Sobolewski, E; Czaplewski, C; Oldziej, S; Liwo, A; Scheraga, HA. Simple physics-based analytical formulas for the potentials of mean force for the interaction of amino acid side chains in water. IV. Pairs of different hydrophobic side chains. J. Phys. Chem. B 2008, 112, 11385–11395. [Google Scholar]
- da Silveira, CH; Pires, DEV; Minardi, RC; Ribeiro, C; Veloso, CJM; Lopes, JCD; Meira, W; Neshich, G; Ramos, CHI; Habesch, R; Santoro, MM. Protein cutoff scanning: A comparative analysis of cutoff dependent and cutoff free methods for prospecting contacts in proteins. Proteins 2009, 74, 727–743. [Google Scholar]
- Taketomi, H; Ueda, Y; Go, N. Studies on protein folding, unfolding and fluctuations by computer simulation. 1. Effect of specific amino acid sequence represented by specific inter-unit interactions. Int. J. Pept. Protein Res 1975, 7, 445–459. [Google Scholar]
- Go, N; Scheraga, HA. On the use of classical statistical mechanics in the treatment of polymer chain conformations. Macromolecules 1976, 9, 535–542. [Google Scholar]
- Ueda, Y; Go, N. Theory of large-amplitude conformational fluctuations in native globular proteins: Independent fluctuating site model. Int. J. Pept. Protein Res 1976, 8, 551–558. [Google Scholar]
- Go, N; Taketomi, H. Respective roles of short-range and long-range interactions in protein folding. Proc. Natl. Acad. Sci. USA 1978, 75, 559–563. [Google Scholar]
- Ueda, Y; Taketomi, H; Go, N. Studies on protein folding, unfolding and fluctuations by computer simulation. 2. A three-dimensional lattice model of lysozyme. Biopolymers 1978, 17, 1531–1548. [Google Scholar]
- Go, N; Taketomi, H. Studies on protein folding, unfolding and fluctuations by computer simulation. 3. Effect of short-range interactions. Int. J. Pept. Protein Res 1979, 13, 235–252. [Google Scholar]
- Go, N; Taketomi, H. Studies on protein folding, unfolding and fluctuations by computer simulation. 4. Hydrophobic interactions. Int. J. Pept. Protein Res 1979, 13, 447–461. [Google Scholar]
- Go, N. Theoretical studies of protein folding. Annu. Rev. Biophys. Bioeng 1983, 12, 183–210. [Google Scholar]
- Taketomi, H; Kano, F; Go, N. The effect of amino acid substitution on protein folding and protein unfolding transition studied by computer simulation. Biopolymers 1988, 27, 527–559. [Google Scholar]
- Brooks, CL, III; Onuchic, JN; Wales, DJ. Statistical thermodynamics: Taking a walk on a landscape. Science 2001, 293, 612–613. [Google Scholar]
- Dill, KA; Ozkan, SB; Shell, MS; Weikl, TR. The protein folding problem. Ann. Rev. Biophys 2008, 37, 289–316. [Google Scholar]
- Onuchic, JN; Wolynes, PG. Theory of protein folding. Curr. Opin. Struct. Biol 2004, 14, 70–75. [Google Scholar]
- Ozkan, SB; Wu, GA; Chodera, JD; Dill, KA. Protein folding by zipping and assembly. Proc. Natl. Acad. Sci. USA 2007, 104, 11987–11992. [Google Scholar]
- Prieto, L; Rey, A. Influence of the native topology on the folding barrier for small proteins. J. Chem. Phys 2007, 127, 175101. [Google Scholar]
- Hills, RD, Jr; Brooks, CL, III. Subdomain competition, cooperativity, and topological frustration in the folding of CheY. J. Mol. Biol 2008, 382, 485–495. [Google Scholar]
- Fersht, AR; Sato, S. Phi-Value analysis and the nature of protein-folding transition states. Proc. Natl. Acad. Sci. USA 2004, 101, 7976–7981. [Google Scholar]
- Chavez, LL; Gosavi, S; Jennings, PA; Onuchic, JN. Multiple routes lead to the native state in the energy landscape of the beta-trefoil family. Proc. Natl. Acad. Sci. USA 2006, 103, 10254–10258. [Google Scholar]
- Dokholyan, NV; Buldyrev, SV; Stanley, HE; Shakhnovich, EI. Identifying the protein folding nucleus using molecular dynamics. J. Mol. Biol 2000, 296, 1183–1188. [Google Scholar]
- Ferreiro, DU; Cho, SS; Komives, EA; Wolynes, PG. The energy landscape of modular repeat proteins: Topology determines folding mechanism in the ankyrin family. J. Mol. Biol 2005, 354, 679–692. [Google Scholar]
- Gosavi, S; Chavez, LL; Jennings, PA; Onuchic, JN. Topological frustration and the folding of interleukin-1 beta. J. Mol. Biol 2006, 357, 986–996. [Google Scholar]
- Hubner, IA; Oliveberg, M; Shakhnovich, EI. Simulation, experiment, and evolution: Understanding nucleation in protein S6 folding. Proc. Natl. Acad. Sci. USA 2004, 101, 8354–8359. [Google Scholar]
- Karanicolas, J; Brooks, CL, III. Improved Go-like models demonstrate the robustness of protein folding mechanisms towards non-native interactions. J. Mol. Biol 2003, 334, 309–325. [Google Scholar]
- Levy, Y; Cho, SS; Onuchic, JN; Wolynes, PG. A survey of flexible protein binding mechanisms and their transition states using native topology based energy landscapes. J. Mol. Biol 2005, 346, 1121–1145. [Google Scholar]
- Levy, Y; Wolynes, PG; Onuchic, JN. Protein topology determines binding mechanism. Proc. Natl. Acad. Sci. USA 2004, 101, 511–516. [Google Scholar]
- Roy, M; Chavez, LL; Finke, JM; Heidary, DK; Onuchic, JN; Jennings, PA. The native energy landscape for interleukin-1 beta. Modulation of the population ensemble through native-state topology. J. Mol. Biol 2005, 348, 335–347. [Google Scholar]
- Settanni, G; Hoang, TX; Micheletti, C; Maritan, A. Folding pathways of prion and doppel. Biophys. J 2002, 83, 3533–3541. [Google Scholar]
- Zuo, GH; Wang, J; Wang, W. Folding with downhill behavior and low cooperativity of proteins. Proteins 2006, 63, 165–173. [Google Scholar]
- Kouza, M; Li, MS; O’Brien, EP; Hu, CK; Thirumalai, D. Effect of finite size on cooperativity and rates of protein folding. J. Phys. Chem. A 2006, 110, 671–676. [Google Scholar]
- Clementi, C; Plotkin, SS. The effects of nonnative interactions on protein folding rates: Theory and simulation. Protein Sci 2004, 13, 1750–1766. [Google Scholar]
- Das, P; Matysiak, S; Clementi, C. Balancing energy and entropy: A minimalist model for the characterization of protein folding landscapes. Proc. Natl. Acad. Sci. USA 2005, 102, 10141–10146. [Google Scholar]
- Gu, Z; Rao, MK; Forsyth, WR; Finke, JM; Matthews, CR. Structural analysis of kinetic folding intermediates for a TIM barrel protein, indole-3-glycerol phosphate synthase, by hydrogen exchange mass spectrometry and Go model simulation. J. Mol. Biol 2007, 374, 528–546. [Google Scholar]
- Paci, E; Vendruscolo, M; Karplus, M. Native and non-native interactions along protein folding and unfolding pathways. Proteins 2002, 47, 379–392. [Google Scholar]
- Zarrine-Afsart, A; Wallin, S; Neculai, AM; Neudecker, P; Howell, PL; Davidson, AR; Chan, HS. Theoretical and experimental demonstration of the importance of specific nonnative interactions in protein folding. Proc. Natl. Acad. Sci. USA 2008, 105, 9999–10004. [Google Scholar]
- Zhang, Z; Chan, HS. Native topology of the designed protein Top7 is not conducive to cooperative folding. Biophys. J 2009, 96, L25–L27. [Google Scholar]
- Griffin, MA; Friedel, M; Shea, JE. Effects of frustration, confinement, and surface interactions on the dimerization of an off-lattice beta-barrel protein. J. Chem. Phys 2005, 123, 174707. [Google Scholar]
- Zhou, YQ; Karplus, M. Folding thermodynamics of a model three-helix-bundle protein. Proc. Natl. Acad. Sci. USA 1997, 94, 14429–14432. [Google Scholar]
- Matysiak, S; Clementi, C. Optimal combination of theory and experiment for the characterization of the protein folding landscape of S6: How far can a minimalist model go? J. Mol. Biol 2004, 343, 235–248. [Google Scholar]
- Du, R; Pande, VS; Grosberg, AY; Tanaka, T; Shakhnovich, E. On the role of conformational geometry in protein folding. J. Chem. Phys 1999, 111, 10375–10380. [Google Scholar]
- Ivankov, DN; Garbuzynskiy, SO; Alm, E; Plaxco, KW; Baker, D; Finkelstein, AV. Contact order revisited: Influence of protein size on the folding rate. Protein Sci 2003, 12, 2057–2062. [Google Scholar]
- Plaxco, KW; Simons, KT; Baker, D. Contact order, transition state placement and the refolding rates of single domain proteins. J. Mol. Biol 1998, 277, 985–994. [Google Scholar]
- Dyson, HJ; Wright, PE. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol 2005, 6, 197–208. [Google Scholar]
- Thirumalai, D; Klimov, DK; Dima, RI. Emerging ideas on the molecular basis of protein and peptide aggregation. Curr. Opin. Struct. Biol 2003, 13, 146–159. [Google Scholar]
- Sutto, L; Tiana, G; Broglia, RA. Sequence of events in folding mechanism: Beyond the Go model. Protein Sci 2006, 15, 1638–1652. [Google Scholar]
- Khare, SD; Ding, F; Dokholyan, NV. Folding of Cu, Zn superoxide dismutase and familial amyotrophic lateral sclerosis. J. Mol. Biol 2003, 334, 515–525. [Google Scholar]
- Miyazawa, S; Jernigan, RL. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol 1996, 256, 623–644. [Google Scholar]
- Rao, MK; Chapman, TR; Finke, JM. Crystallographic B-factors highlight energetic frustration in aldolase folding. J. Phys. Chem. B 2008, 112, 10417–10431. [Google Scholar]
- Dixon, RDS; Chen, YW; Feng, D; Khare, SD; Prutzman, KC; Schaller, MD; Campbell, SL; Dokholyan, NV. New insights into FAK signaling and localization based on detection of a FAT domain folding intermediate. Structure 2004, 12, 2161–2171. [Google Scholar]
- Clementi, C; Garcia, AE; Onuchic, JN. Interplay among tertiary contacts, secondary structure formation and side-chain packing in the protein folding mechanism: All-atom representation study of protein L. J. Mol. Biol 2003, 326, 933–954. [Google Scholar]
- Kleiner, A; Shakhnovich, E. The mechanical unfolding of ubiquitin through all-atom Monte Carlo simulation with a Go-type potential. Biophys. J 2007, 92, 2054–2061. [Google Scholar]
- Linhananta, A; Boer, J; MacKay, I. The equilibrium properties and folding kinetics of an all-atom Go model of the Trp-cage. J. Chem. Phys 2005, 122, 114901. [Google Scholar]
- Linhananta, A; Zhou, YQ. The role of sidechain packing and native contact interactions in folding: Discontinuous molecular dynamics folding simulations of an all-atom Go model of fragment B of Staphylococcal protein A. J. Chem. Phys 2002, 117, 8983–8995. [Google Scholar]
- Meinke, JH; Hansmann, UHE. Protein simulations combining an all-atom force field with a Go term. J. Phys.-Condes. Matter 2007, 19, 285215. [Google Scholar]
- Shimada, J; Kussell, EL; Shakhnovich, EI. The folding thermodynamics and kinetics of crambin using an all-atom Monte Carlo simulation. J. Mol. Biol 2001, 308, 79–95. [Google Scholar]
- Shimada, J; Shakhnovich, EI. The ensemble folding kinetics of protein G from an all-atom Monte Carlo simulation. Proc. Natl. Acad. Sci. USA 2002, 99, 11175–11180. [Google Scholar]
- Zhou, YQ; Linhananta, A. Thermodynamics of an all-atom off-lattice model of the fragment B of Staphylococcal protein A: Implication for the origin of the cooperativity of protein folding. J. Phys. Chem. B 2002, 106, 1481–1485. [Google Scholar]
- Luo, ZL; Ding, JD; Zhou, YQ. Temperature-dependent folding pathways of pin1 WW domain: An all-atom molecular dynamics simulation of a Go model. Biophys. J 2007, 93, 2152–2161. [Google Scholar]
- Luo, ZL; Ding, JD; Zhou, YQ. Folding mechanisms of individual beta-hairpins in a Go model of Pin1 WW domain by all-atom molecular dynamics simulations. J. Chem. Phys 2008, 128, 225103. [Google Scholar]
- Whitford, PC; Noel, JK; Gosavi, S; Schug, A; Sanbonmatsu, KY; Onuchic, JN. An all-atom structure-based potential for proteins: Bridging minimal models with all-atom empirical forcefields. Proteins In press. 2009. [Google Scholar]
- Hills, RD, Jr; Brooks, CL, III. Coevolution of function and the folding landscape: Correlation with density of native contacts. Biophys. J 2008, 95, L57–L59. [Google Scholar]
- Hills, RD, Jr; Kathuria, SV; Wallace, LA; Matthews, CR; Brooks, CL, III. Functional diversity and shifting cores of stability modulate the folding mechanisms of flavodoxin fold proteins. In J Mol Biol; 2009; Pending publication. [Google Scholar]
- Kathuria, SV; Day, IJ; Wallace, LA; Matthews, CR. Kinetic traps in the folding of beta alpha-repeat proteins: CheY initially misfolds before accessing the native conformation. J. Mol. Biol 2008, 382, 467–484. [Google Scholar]
- LopezHernandez, E; Serrano, L. Structure of the transition state for folding of the 129 aa protein CheY resembles that of a smaller protein, CI-2. Fold. Des 1996, 1, 43–55. [Google Scholar]
- Du, R; Pande, VS; Grosberg, AY; Tanaka, T; Shakhnovich, ES. On the transition coordinate for protein folding. J. Chem. Phys 1998, 108, 334–350. [Google Scholar]
- Snow, CD; Rhee, YM; Pande, VS. Kinetic definition of protein folding transition state ensembles and reaction coordinates. Biophys. J 2006, 91, 14–24. [Google Scholar]
- Cho, SS; Levy, Y; Wolynes, PG. P versus Q: Structural reaction coordinates capture protein folding on smooth landscapes. Proc. Natl. Acad. Sci. USA 2006, 103, 586–591. [Google Scholar]
- Piana, S; Laio, A. Advillin folding takes place on a hypersurface of small dimensionality. Phys. Rev. Lett 2008, 101, 208101. [Google Scholar]
- Juraszek, J; Bolhuis, PG. Rate constant and reaction coordinate of Trp-cage folding in explicit water. Biophys. J 2008, 95, 4246–4257. [Google Scholar]
- Shakhnovich, E. Protein folding thermodynamics and dynamics: Where physics, chemistry, and biology meet. Chem. Rev 2006, 106, 1559–1588. [Google Scholar]
- Shakhnovich, E; Farztdinov, G; Gutin, AM; Karplus, M. Protein folding bottlenecks: A lattice Monte-Carlo simulation. Phys. Rev. Lett 1991, 67, 1665–1668. [Google Scholar]
- Faccioli, P. Characterization of protein folding by dominant reaction pathways. J. Phys. Chem. B 2008, 112, 13756–13764. [Google Scholar]
- Sola, M; Lopez-Hernandez, E; Cronet, P; Lacroix, E; Serrano, L; Coll, M; Parraga, A. Towards understanding a molecular switch mechanism: Thermodynamic and crystallographic studies of the signal transduction protein CheY. J. Mol. Biol 2000, 303, 213–225. [Google Scholar]
- Stock, AM; Guhaniyogi, J. A new perspective on response regulator activation. J. Bacteriol 2006, 188, 7328–7330. [Google Scholar]
- Varughese, KI; Tsigelny, I; Zhao, HY. The crystal structure of beryllofluoride Spo0F in complex with the phosphotransferase Spo0B represents a phosphotransfer pretransition state. J. Bacteriol 2006, 188, 4970–4977. [Google Scholar]
- Volkman, BF; Lipson, D; Wemmer, DE; Kern, D. Two-state allosteric behavior in a single-domain signaling protein. Science 2001, 291, 2429–2433. [Google Scholar]
- Cellitti, J; Bernstein, R; Marqusee, S. Exploring subdomain cooperativity in T4 lysozyme II: Uncovering the C-terminal subdomain as a hidden intermediate in the kinetic folding pathway. Protein Sci 2007, 16, 852–862. [Google Scholar]
- Cho, SS; Levy, Y; Wolynes, PG. Quantitative criteria for native energetic heterogeneity influences in the prediction of protein folding kinetics. Proc. Natl. Acad. Sci. USA 2009, 106, 434–439. [Google Scholar]
- Halle, B. Flexibility and packing in proteins. Proc. Natl. Acad. Sci. USA 2002, 99, 1274–1279. [Google Scholar]
- Hills, RD, Jr; Brooks, CL, III. Hydrophobic cooperativity as a mechanism for amyloid nucleation. J. Mol. Biol 2007, 368, 894–901. [Google Scholar]
- Aftabuddin, M; Kundu, S. Hydrophobic, hydrophilic, and charged amino acid networks within protein. Biophys. J 2007, 93, 225–231. [Google Scholar]
- Atilgan, AR; Akan, P; Baysal, C. Small-world communication of residues and significance for protein dynamics. Biophys. J 2004, 86, 85–91. [Google Scholar]
- Bode, C; Kovacs, IA; Szalay, MS; Palotai, R; Korcsmaros, T; Csermely, P. Network analysis of protein dynamics. FEBS Lett 2007, 581, 2776–2782. [Google Scholar]
- Dokholyan, NV; Li, L; Ding, F; Shakhnovich, EI. Topological determinants of protein folding. Proc. Natl. Acad. Sci. USA 2002, 99, 8637–8641. [Google Scholar]
- Greene, LH; Higman, VA. Uncovering network systems within protein structures. J. Mol. Biol 2003, 334, 781–791. [Google Scholar]
- Higman, VA; Greene, LH. Elucidation of conserved long-range interaction networks in proteins and their significance in determining protein topology. Physica A 2006, 368, 595–606. [Google Scholar]
- Vendruscolo, M; Dokholyan, NV; Paci, E; Karplus, M. Small-world view of the amino acids that play a key role in protein folding. Phys Rev E 2002, 65. 061910-1-4. [Google Scholar]
- Kathuria, SV; Matthews, CR. Clusters of isoleucine, leucine and valine side chains define cores of stability in globular proteins: Sequence determinants of structure, stability and folding. 2009; Pending publication. [Google Scholar]
- Wu, Y; Vadrevu, R; Kathuria, S; Yang, XY; Matthews, CR. A tightly packed hydrophobic cluster directs the formation of an off-pathway sub-millisecond folding intermediate in the alpha subunit of tryptophan synthase, a TIM barrel protein. J. Mol. Biol 2007, 366, 1624–1638. [Google Scholar]
- Hilser, VJ; Freire, E. Structure-based calculation of the equilibrium folding pathway of proteins. Correlation with hydrogen exchange protection factors. J. Mol. Biol 1996, 262, 756–772. [Google Scholar]
- Alm, E; Baker, D. Prediction of protein-folding mechanisms from free-energy landscapes derived from native structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11305–11310. [Google Scholar]
- Galzitskaya, OV; Finkelstein, AV. A theoretical search for folding/unfolding nuclei in three-dimensional protein structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11299–11304. [Google Scholar]
- Karanicolas, J; Brooks, CL, III. The importance of explicit chain representation in protein folding models: An examination of Ising-like models. Proteins 2003, 53, 740–747. [Google Scholar]
- Munoz, V; Eaton, WA. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11311–11316. [Google Scholar]
- Takada, S. Go-ing for the prediction of protein folding mechanisms. Proc. Natl. Acad. Sci. USA 1999, 96, 11698–11700. [Google Scholar]
- Doruker, P; Jernigan, RL; Bahar, I. Dynamics of large proteins through hierarchical levels of coarse-grained structures. J. Comput. Chem 2002, 23, 119–127. [Google Scholar]
- Tama, F; Sanejouand, YH. Conformational change of proteins arising from normal mode calculations. Protein Eng 2001, 14, 1–6. [Google Scholar]
- Petrone, P; Pande, VS. Can conformational change be described by only a few normal modes? Biophys. J 2006, 90, 1583–1593. [Google Scholar]
- Tama, F; Brooks, CL, III. Symmetry, form, and shape: Guiding principles for robustness in macromolecular machines. Annu. Rev. Biophys. Biomolec. Struct 2006, 35, 115–133. [Google Scholar]
- Yang, L; Song, G; Jernigan, RL. How well can we understand large-scale protein motions using normal modes of elastic network models? Biophys. J 2007, 93, 920–929. [Google Scholar]
- Bagci, Z; Jernigan, RL; Bahar, I. Residue packing in proteins: Uniform distribution on a coarse-grained scale. J. Chem. Phys 2002, 116, 2269–2276. [Google Scholar]
- Keskin, O; Jernigan, RL; Bahar, I. Proteins with similar architecture exhibit similar large-scale dynamic behavior. Biophys. J 2000, 78, 2093–2106. [Google Scholar]
- Lu, MY; Ma, JP. The role of shape in determining molecular motions. Biophys. J 2005, 89, 2395–2401. [Google Scholar]
- Maragakis, P; Karplus, M. Large amplitude conformational change in proteins explored with a plastic network model: Adenylate kinase. J. Mol. Biol 2005, 352, 807–822. [Google Scholar]
- Chu, JW; Voth, GA. Coarse-grained free energy functions for studying protein conformational changes: A double-well network model. Biophys. J 2007, 93, 3860–3871. [Google Scholar]
- Best, RB; Chen, YG; Hummer, G. Slow protein conformational dynamics from multiple experimental structures: The helix/sheet transition of arc repressor. Structure 2005, 13, 1755–1763. [Google Scholar]
- Koga, N; Takada, S. Folding-based molecular simulations reveal mechanisms of the rotary motor F-1-ATPase. Proc. Natl. Acad. Sci. USA 2006, 103, 5367–5372. [Google Scholar]
- Takagi, F; Kikuchi, M. Structural change and nucleotide dissociation of myosin motor domain: Dual Go model simulation. Biophys. J 2007, 93, 3820–3827. [Google Scholar]
- Cieplak, M; Hoang, TX. Universality classes in folding times of proteins. Biophys. J 2003, 84, 475–488. [Google Scholar]
- Kaya, H; Chan, HS. Solvation effects and driving forces for protein thermodynamic and kinetic cooperativity: How adequate is native-centric topological modeling? J. Mol. Biol 2003, 326, 911–931. [Google Scholar]
- Kaya, H; Liu, ZR; Chan, HS. Chevron Behavior and isostable enthalpic barriers in protein folding: Successes and limitations of simple Go-like modeling. Biophys. J 2005, 89, 520–535. [Google Scholar]
- Prieto, L; Rey, A. Simulations of the protein folding process using topology-based models depend on the experimental structure. J. Chem. Phys 2008, 129, 115101. [Google Scholar]
- Rey-Stolle, MF; Enciso, M; Rey, A. Topology-based models and NMR structures in protein folding simulations. J Comp Chem In press. 2009. [Google Scholar]
- Settanni, G; Cattaneo, A; Maritan, A. Role of native-state topology in the stabilization of intracellular antibodies. Biophys. J 2001, 81, 2935–2945. [Google Scholar]
- Cheung, MS; Garcia, AE; Onuchic, JN. Protein folding mediated by solvation: Water expulsion and formation of the hydrophobic core occur after the structural collapse. Proc. Natl. Acad. Sci. USA 2002, 99, 685–690. [Google Scholar]
- Bellesia, G; Shea, JE. Self-assembly of beta-sheet forming peptides into chiral fibrillar aggregates. J. Chem. Phys 2007, 126, 245104. [Google Scholar]
- Fawzi, NL; Kohlstedt, KL; Okabe, Y; Head-Gordon, T. Protofibril assemblies of the arctic, dutch, and flemish mutants of the Alzheimer’s A beta(1–40) peptide. Biophys. J 2008, 94, 2007–2016. [Google Scholar]
- Nguyen, HD; Hall, CK. Spontaneous fibril formation by polyalanines; Discontinuous molecular dynamics simulations. J. Am. Chem. Soc 2006, 128, 1890–1901. [Google Scholar]
- Nguyen, HD; Reddy, VS; Brooks, CL, III. Deciphering the kinetic mechanism of spontaneous self-assembly of icosahedral capsids. Nano Lett 2007, 7, 338–344. [Google Scholar]
- Cieplak, M; Filipek, S; Janovjak, H; Krzysko, KA. Pulling single bacteriorhodopsin out of a membrane: Comparison of simulation and experiment. Biochim. Biophys. Acta-Biomembr 2006, 1758, 537–544. [Google Scholar]
- Cieplak, M; Hoang, TX; Robbins, MO. Folding and stretching in a Go-like model of titin. Proteins 2002, 49, 114–124. [Google Scholar]
- Sulkowska, JI; Sulkowski, P; Szymczak, P; Cieplak, M. Stabilizing effect of knots on proteins. Proc. Natl. Acad. Sci. USA 2008, 105, 19714–19719. [Google Scholar]
- Sulkowska, JI; Kloczkowski, A; Sen, TZ; Cieplak, M; Jernigan, RL. Predicting the order in which contacts are broken during single molecule protein stretching experiments. Proteins 2008, 71, 45–60. [Google Scholar]
- Li, MS; Kouza, M; Hu, CK. Refolding upon force quench and pathways of mechanical and thermal unfolding of ubiquitin. Biophys. J 2007, 92, 547–561. [Google Scholar]
- Sulkowska, JI; Cieplak, M. Mechanical stretching of proteins: A theoretical survey of the Protein Data Bank. J. Phys.-Condes. Matter 2007, 19, 283201. [Google Scholar]
- Neri, M; Anselmi, C; Carnevale, V; Vargiu, AV; Carloni, P. Molecular dynamics simulations of outer-membrane protease T from E-coli based on a hybrid coarse-grained/atomistic potential. J. Phys.-Condes. Matter 2006, 18, S347–S355. [Google Scholar]
- Neri, M; Anselmi, C; Cascella, M; Maritan, A; Carloni, P. Coarse-grained model of proteins incorporating atomistic detail of the active site. Phys. Rev. Lett 2005, 95, 218102. [Google Scholar]
- Neri, M; Baaden, M; Carnevale, V; Anselmi, C; Maritan, A; Carloni, P. Microseconds dynamics simulations of the outer-membrane protease T. Biophys. J 2008, 94, 71–78. [Google Scholar]
- Yang, SC; Levine, H; Onuchic, JN. Protein oligomerization through domain swapping: Role of inter-molecular interactions and protein concentration. J. Mol. Biol 2005, 352, 202–211. [Google Scholar]
- Homouz, D; Perham, M; Samiotakis, A; Cheung, MS; Wittung-Stafshede, P. Crowded, cell-like environment induces shape changes in aspherical protein. Proc. Natl. Acad. Sci. USA 2008, 105, 11754–11759. [Google Scholar]
- Pincus, DL; Thirumalai, D. Crowding effects on the mechanical stability and unfolding pathways of ubiquitin. J. Phys. Chem. B 2009, 113, 359–368. [Google Scholar]
- Levy, Y; Onuchic, JN; Wolynes, PG. Fly-casting in protein-DNA binding: Frustration between protein folding and electrostatics facilitates target recognition. J. Am. Chem. Soc 2007, 129, 738–739. [Google Scholar]
- Ferreiro, DU; Hegler, JA; Komives, EA; Wolynes, PG. Localizing frustration in native proteins and protein assemblies. Proc. Natl. Acad. Sci. USA 2007, 104, 19819–19824. [Google Scholar]
- Gosavi, S; Whitford, PC; Jennings, PA; Onuchic, JN. Extracting function from a beta-trefoil folding motif. Proc. Natl. Acad. Sci. USA 2008, 105, 10384–10389. [Google Scholar]
- Jager, M; Zhang, Y; Bieschke, J; Nguyen, H; Dendle, M; Bowman, ME; Noel, JP; Gruebele, M; Kelly, JW. Structure-function-folding relationship in a WW domain. Proc. Natl. Acad. Sci. USA 2006, 103, 10648–10653. [Google Scholar]
- Miyashita, O; Onuchic, JN; Wolynes, PG. Nonlinear elasticity, proteinquakes, and the energy landscapes of functional transitions in proteins. Proc. Natl. Acad. Sci. USA 2003, 100, 12570–12575. [Google Scholar]
- Miyashita, O; Wolynes, PG; Onuchic, JN. Simple energy landscape model for the kinetics of functional transitions in proteins. J. Phys. Chem. B 2005, 109, 1959–1969. [Google Scholar]
- Whitford, PC; Miyashita, O; Levy, Y; Onuchic, JN. Conformational transitions of adenylate kinase: Switching by cracking. J. Mol. Biol 2007, 366, 1661–1671. [Google Scholar]
- Karanicolas, J; Brooks, CL, III. Integrating folding kinetics and protein function: Biphasic kinetics and dual binding specificity in a WW domain. Proc. Natl. Acad. Sci. USA 2004, 101, 3432–3437. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hills, R.D., Jr.; Brooks, C.L., III. Insights from Coarse-Grained Gō Models for Protein Folding and Dynamics. Int. J. Mol. Sci. 2009, 10, 889-905. https://doi.org/10.3390/ijms10030889
Hills RD Jr., Brooks CL III. Insights from Coarse-Grained Gō Models for Protein Folding and Dynamics. International Journal of Molecular Sciences. 2009; 10(3):889-905. https://doi.org/10.3390/ijms10030889
Chicago/Turabian StyleHills, Ronald D., Jr., and Charles L. Brooks, III. 2009. "Insights from Coarse-Grained Gō Models for Protein Folding and Dynamics" International Journal of Molecular Sciences 10, no. 3: 889-905. https://doi.org/10.3390/ijms10030889