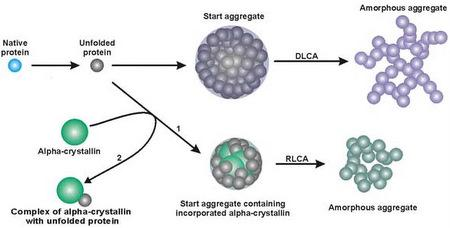
Mechanism of Suppression of Protein Aggregation by α-Crystallin
Abstract
:1. Introduction
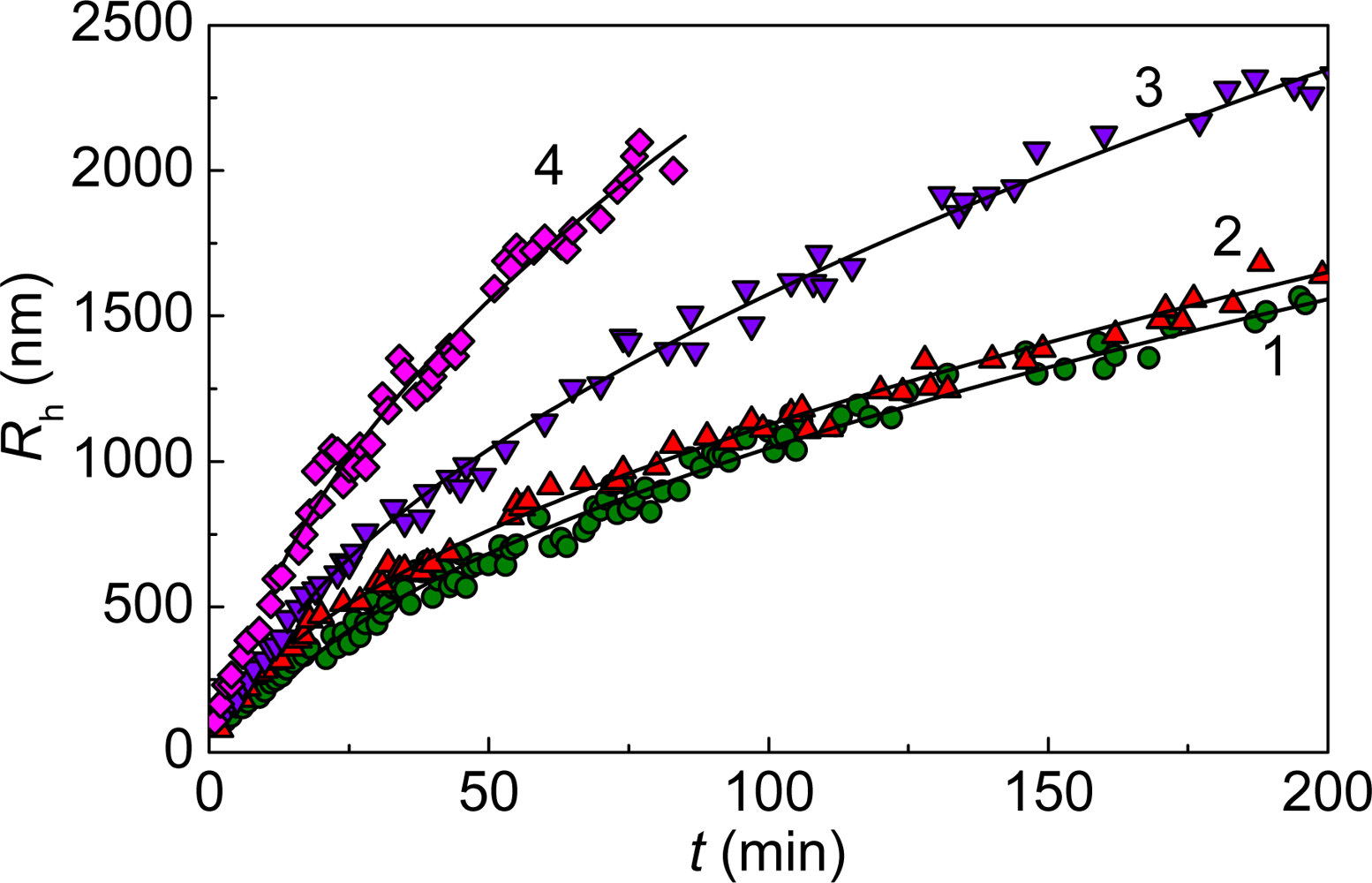
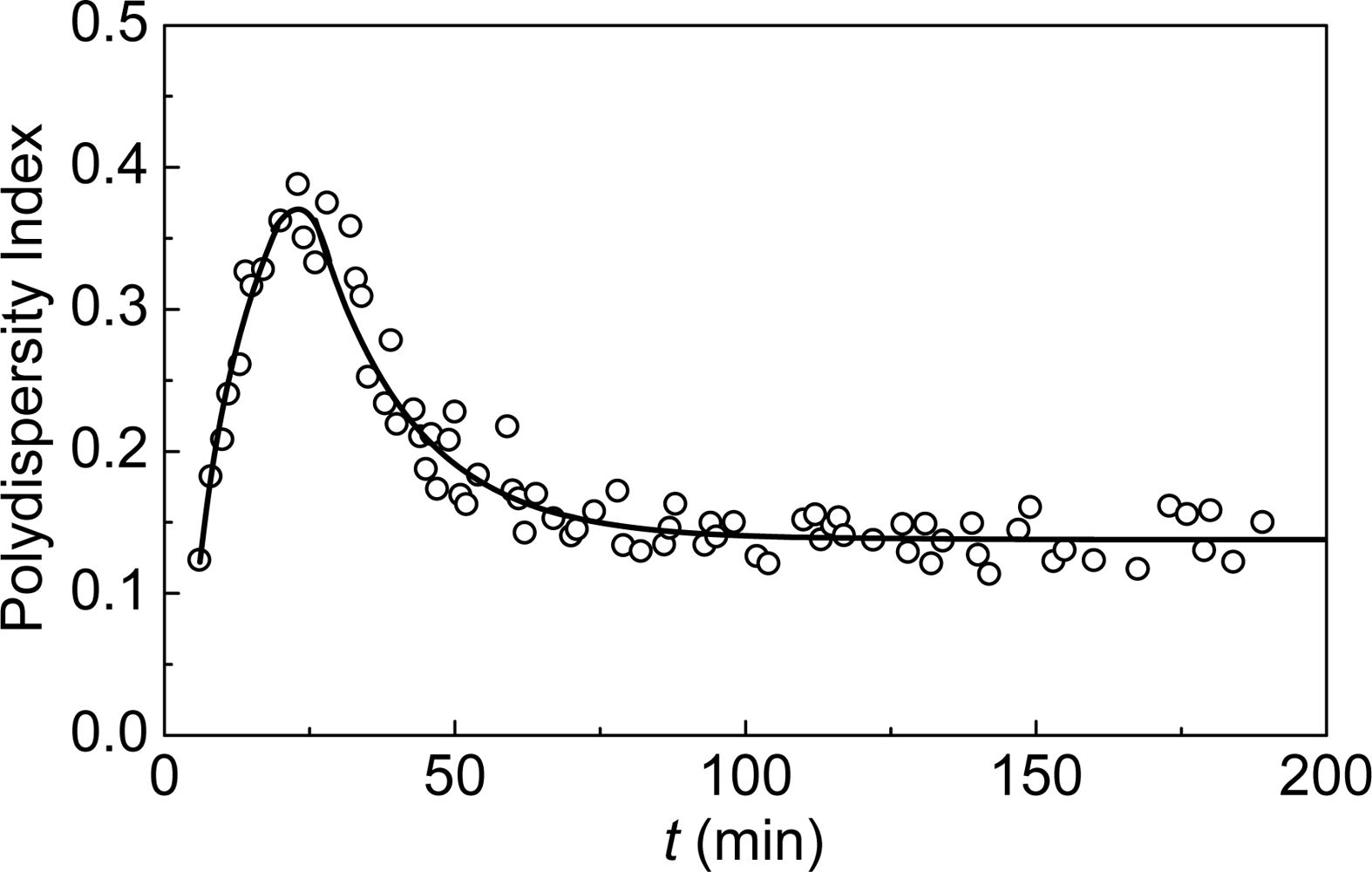
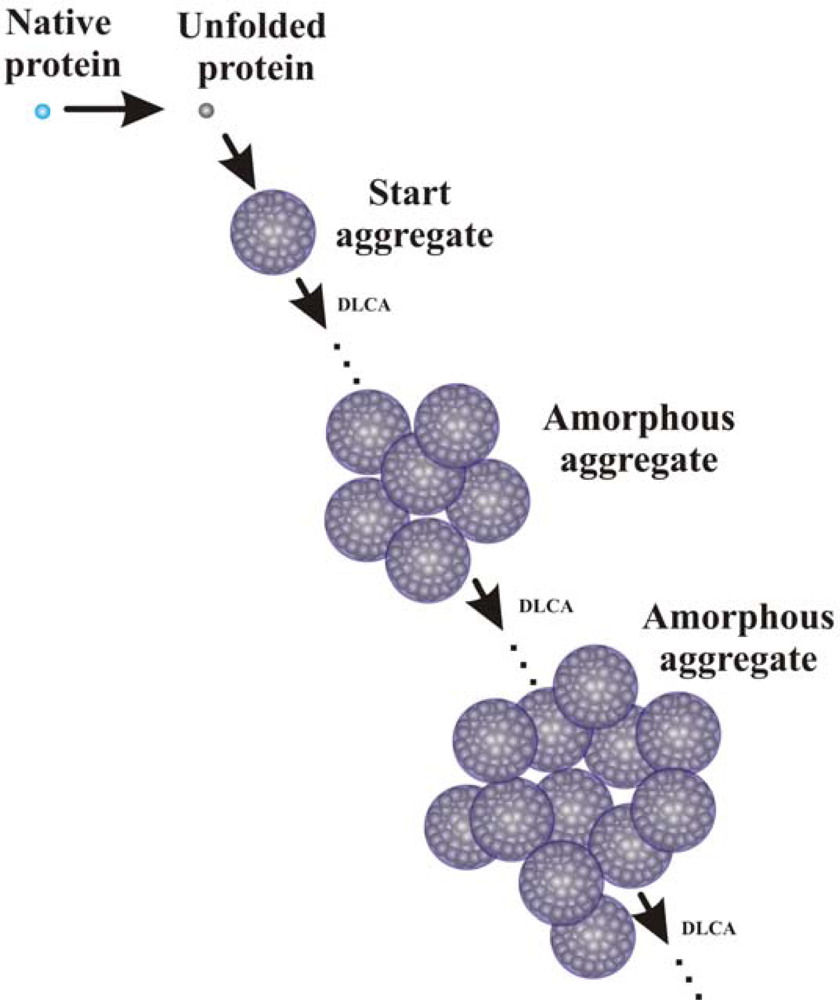
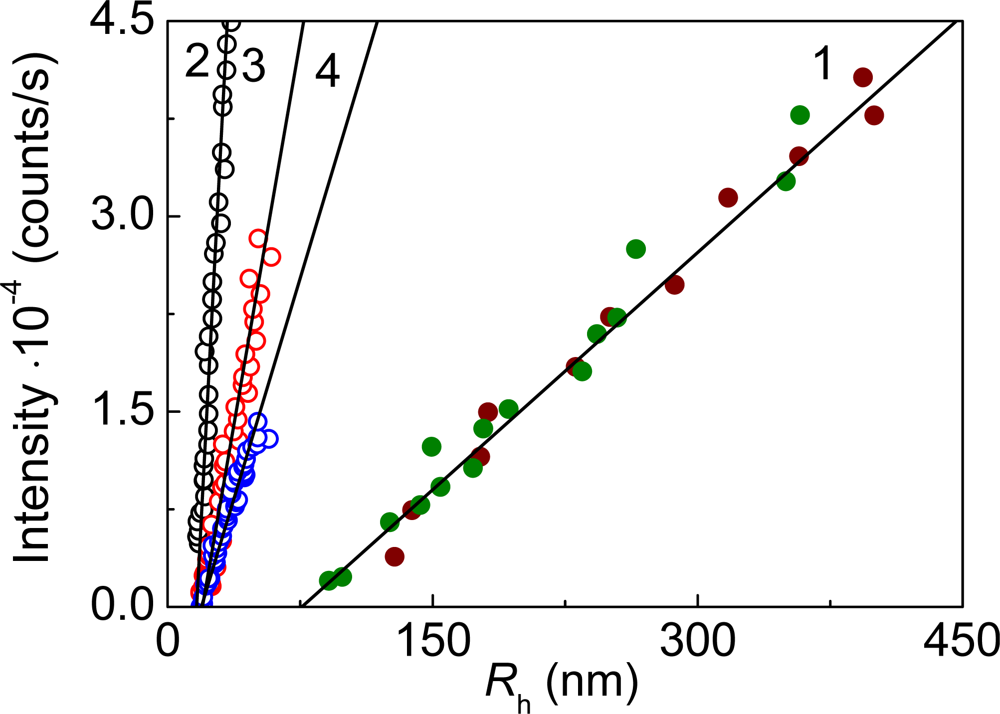
2. Mechanisms of Protein Aggregation
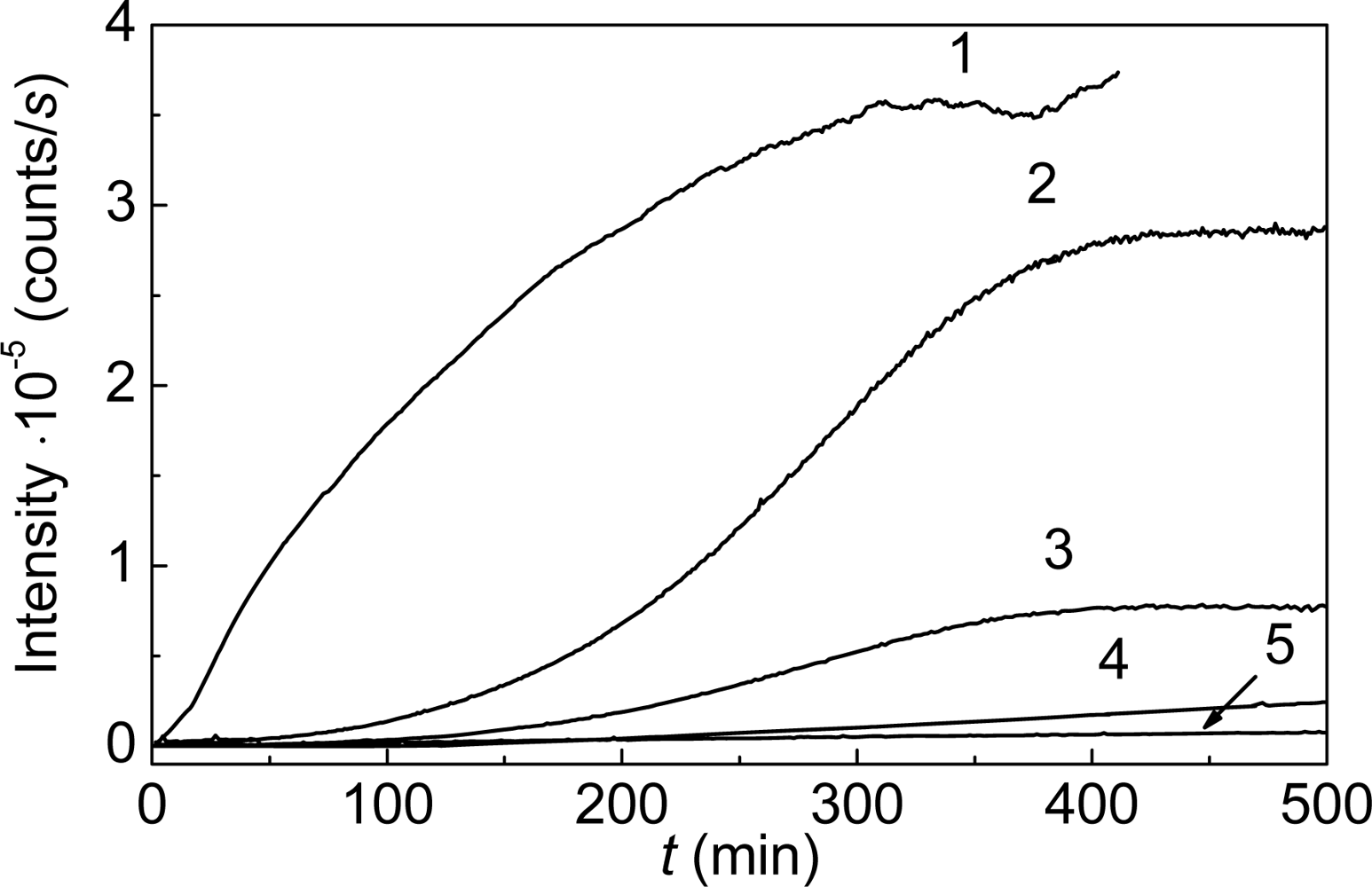
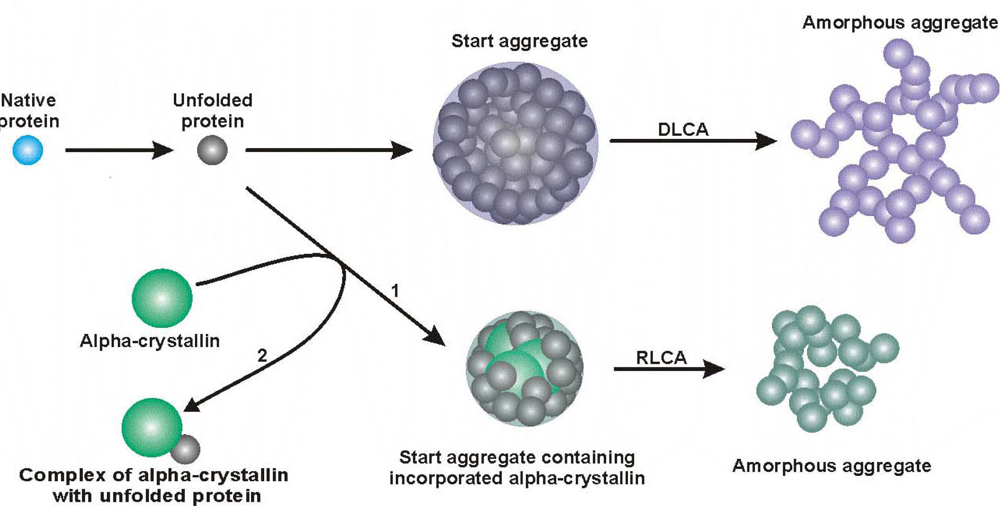
3. Mechanism of Protein Aggregation in the Presence of α-crystallin
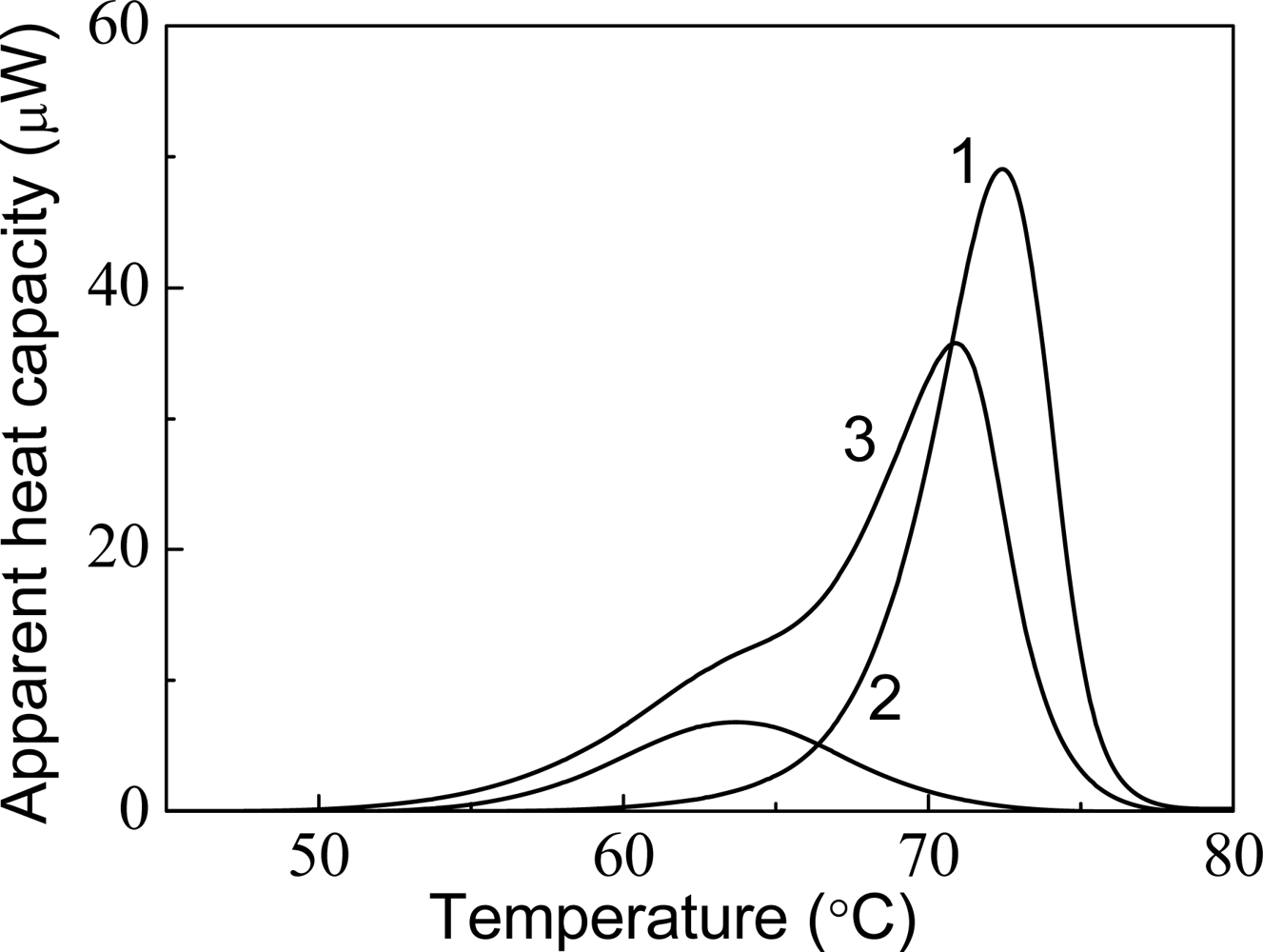
4. Effect of α-Crystallin on Thermal Stability of Proteins
5. Conclusions
Acknowledgments
References
- Horwitz, J. Alpha-crystallin. Exp. Eye Res 2003, 76, 145–153. [Google Scholar]
- Horwitz, J. Alpha-crystallin can function as a molecular chaperone. Proc. Natl. Acad. Sci. USA 1992, 89, 10449–10453. [Google Scholar]
- Carver, JA; Aquilina, JA; Cooper, PG; Williams, GA; Truscott, RJ. Alpha-crystallin: molecular chaperone and protein surfactant. Biochim. Biophys. Acta 1994, 1204, 195–206. [Google Scholar]
- Boyle, D; Takemoto, L. Characterization of the alpha-gamma and alpha-beta complex: evidence for an in vivo functional role of alpha-crystallin as a molecular chaperone. Exp. Eye Res 1994, 58, 9–15. [Google Scholar]
- Bloemendal, H; de Jong, W; Jaenicke, R; Lubsen, NH; Slingsby, C; Tardieu, A. Ageing and vision: structure, stability and function of lens crystallins. Prog. Biophys. Mol. Biol 2004, 86, 407–485. [Google Scholar]
- Evans, P; Slingsby, C; Wallace, BA. Association of partially folded lens betaB2-crystallins with the alpha-crystallin molecular chaperone. Biochem. J 2008, 409, 691–699. [Google Scholar]
- Iwaki, T; Kume-Iwaki, A; Goldman, JE. Cellular distribution of alpha B-crystallin in non-lenticular tissues. J. Histochem. Cytochem 1990, 38, 31–39. [Google Scholar]
- Kato, K; Shinohara, H; Kurobe, N; Inaguma, Y; Shimizu, K; Ohshima, K. Tissue distribution and developmental profiles of immunoreactive alpha B crystallin in the rat determined with a sensitive immunoassay system. Biochim. Biophys. Acta 1991, 1074, 201–208. [Google Scholar]
- Srinivasan, AN; Nagineni, CN; Bhat, SP. alpha A-crystallin is expressed in non-ocular tissues. J. Biol Chem 1992, 267, 23337–23341. [Google Scholar]
- Horwitz, J. The function of alpha-crystallin in vision. Semin. Cell Dev. Biol 2000, 11, 53–60. [Google Scholar]
- Wang, K; Spector, A. The chaperone activity of bovine alpha crystallin. Interaction with other lens crystallins in native and denatured states. J. Biol Chem 1994, 269, 13601–13608. [Google Scholar]
- Van Montfort, R; Slingsby, C; Vierling, E. Structure and function of the small heat shock protein/alpha-crystallin family of molecular chaperones. Adv. Protein Chem 2001, 59, 105–156. [Google Scholar]
- Carver, JA; Lindner, RA; Lyon, C; Canet, D; Hernandez, H; Dobson, CM; Redfield, C. The interaction of the molecular chaperone alpha-crystallin with unfolding alpha-lactalbumin: a structural and kinetic spectroscopic study. J. Mol Biol 2002, 318, 815–827. [Google Scholar]
- Markossian, KA; Kurganov, BI; Levitsky, DI; Khanova, HA; Chebotareva, NA; Samoilov, AM; Eronina, TB; Fedurkina, NV; Mitskevich, LG; Merem’yanin, AV; Kleymenov, SY; Makeeva, VF; Muronets, VI; Naletova, IN; Shalova, IN; Asryants, RA; Schmalhausen, EV; Saso, L; Panyukov, YV; Dobrov, EN; Yudin, IK; Timofeeva, AC; Muranov, KO; Ostrovsky, MA. Mechanisms of chaperone-like activity. In Protein Folding: New Research; Obalinsky, TR, Ed.; Nova Science Publishers Inc: New York, 2006; pp. 89–171. [Google Scholar]
- Rekas, A; Jankova, L; Thorn, DC; Cappai, R; Carver, JA. Monitoring the prevention of amyloid fibril formation by alpha-crystallin. Temperature dependence and the nature of the aggregating species. FEBS J 2007, 274, 6290–6304. [Google Scholar]
- Ecroyd, H; Carver, JA. Crystallin proteins and amyloid fibrils. Cell. Mol. Life Sci 2009, 66, 62–81. [Google Scholar]
- Pullara, F; Emanuele, A. Early stages of beta2-microglobulin aggregation and the inhibiting action of alphaB-crystallin. Proteins 2008, 73, 1037–1046. [Google Scholar]
- Siezen, RJ; Bindels, JG; Hoenders, HJ. The quaternary structure of bovine alpha-crystallin. Effects of variation in alkaline pH, ionic strength, temperature and calcium ion concentration. Eur. J. Biochem 1980, 111, 435–444. [Google Scholar]
- Koretz, JF; Augusteyn, RC. Electron microscopy of native and reconstituted alpha crystallin aggregates. Curr. Eye Res 1988, 7, 25–30. [Google Scholar]
- van den Oetelaar, PJ; van Someren, PF; Thomson, JA; Siezen, RJ; Hoenders, HJ. A dynamic quaternary structure of bovine alpha-crystallin as indicated from intermolecular exchange of subunits. Biochemistry 1990, 29, 3488–3493. [Google Scholar]
- Bova, MP; Ding, LL; Horwitz, J; Fung, BK. Subunit exchange of alphaA-crystallin. J. Biol Chem 1997, 272, 29511–29517. [Google Scholar]
- Vanhoudt, J; Aerts, T; Abgar, S; Clauwaert, J. Quaternary structure of bovine alpha-crystallin: influence of temperature. Int. J. Biol Macromol 1998, 22, 229–237. [Google Scholar]
- Aquilina, JA; Benesch, JL; Bateman, OA; Slingsby, C; Robinson, CV. Polydispersity of a mammalian chaperone: mass spectrometry reveals the population of oligomers in alpha B-crystallin. Proc. Natl. Acad. Sci. USA 2003, 100, 10611–10612. [Google Scholar]
- Thomson, JA; Augusteyn, RC. αm-Crystallin: the native form of the protein? Exp. Eye Res 1983, 37, 367–377. [Google Scholar]
- Wang, XW; Bettelheim, FA. Second virial coefficient of alpha-crystallin. Proteins 1989, 5, 166–169. [Google Scholar]
- Vanhoudt, J; Abgar, S; Aerts, T; Clauwaert, J. Native quaternary structure of bovine alpha-crystallin. Biochemistry 2000, 39, 4483–4492. [Google Scholar]
- Abgar, S; Backmann, J; Aerts, T; Vanhoudt, J; Clauwaert, J. The structural differences between bovine lens alphaA- and alphaB-crystallin. Eur. J. Biochem 2000, 267, 5916–5925. [Google Scholar]
- Putilina, T; Skouri-Panet, F; Prat, K; Lubsen, NH; Tardieu, A. Subunit exchange demonstrates a differential chaperone activity of calf alpha-crystallin toward beta LOW- and individual gamma-crystallins. J. Biol. Chem 2003, 278, 13747–56. [Google Scholar]
- Raman, B; Rao, CM. Chaperone-like activity and quaternary structure of alpha-crystallin. J. Biol. Chem 1994, 269, 27264–27268. [Google Scholar]
- Das, BK; Liang, JJ; Chakrabarti, B. Heat-induced conformational change and increased chaperone activity of lens alpha-crystallin. Curr. Eye Res 1997, 16, 303–309. [Google Scholar]
- Aquilina, JA; Benesch, JL; Ding, LL; Yaron, O; Horwitz, J; Robinson, CV. Subunit exchange of polydisperse proteins: mass spectrometry reveals consequences of alphaA-crystallin truncation. J. Biol. Chem 2005, 280, 14485–14491. [Google Scholar]
- Meehan, S; Berry, Y; Luisi, B; Dobson, CM; Carver, JA; MacPhee, CE. Amyloid fibril formation by lens crystallin proteins and its implications for cataract formation. J. Biol. Chem 2004, 279, 3413–3419. [Google Scholar]
- Meehan, S; Knowles, TP; Baldwin, AJ; Smith, JF; Squires, AM; Clements, P; Treweek, TM; Ecroyd, H; Tartaglia, GG; Vendruscolo, M; Macphee, CE; Dobson, CM; Carver, JA. Characterisation of amyloid fibril formation by small heat-shock chaperone proteins human alphaA-, alphaB- and R120G alphaB-crystallins. J. Mol. Biol 2007, 372, 470–484. [Google Scholar]
- Raman, B; Rao, CM. Chaperone-like activity and temperature-induced structural changes of alpha-crystallin. J. Biol. Chem 1997, 272, 23559–23564. [Google Scholar]
- Reddy, GB; Das, KP; Petrash, JM; Surewicz, WK. Temperature-dependent chaperone activity and structural properties of human alphaA- and alphaB-crystallins. J. Biol. Chem 2000, 275, 4565–4570. [Google Scholar]
- Devlin, GL; Carver, JA; Bottomley, SP. The selective inhibition of serpin aggregation by the molecular chaperone, alpha-crystallin, indicates a nucleation-dependent specificity. J. Biol. Chem 2003, 278, 48644–48650. [Google Scholar]
- Sharma, KK; Kaur, H; Kumar, GS; Kester, K. Interaction of 1,1′-bi(4-anilino)naphthalene-5,5′-disulfonic acid with alpha-crystallin. J. Biol. Chem 1998, 273, 8965–8970. [Google Scholar]
- Kumar, MS; Kapoor, M; Sinha, S; Reddy, GB. Insights into hydrophobicity and the chaperone-like function of alphaA- and alphaB-crystallins: an isothermal titration calorimetric study. J. Biol. Chem 2005, 280, 21726–21730. [Google Scholar]
- Lindner, RA; Treweek, TM; Carver, JA. The molecular chaperone alpha-crystallin is in kinetic competition with aggregation to stabilize a monomeric molten-globule form of alpha-lactalbumin. Biochem. J 2001, 354, 79–87. [Google Scholar]
- Abgar, S; Vanhoudt, J; Aerts, T; Clauwaert, J. Study of the chaperoning mechanism of bovine lens alpha-crystallin, a member of the alpha-small heat shock superfamily. Biophys. J 2001, 80, 1986–1995. [Google Scholar]
- Stege, GJ; Renkawek, K; Overkamp, PS; Verschuure, P; van Rijk, AF; Reijnen-Aalbers, A; Boelens, WC; Bosman, GJ; de Jong, WW. The molecular chaperone alphaB-crystallin enhances amyloid beta neurotoxicity. Biochem. Biophys. Res. Commun 1999, 262, 152–156. [Google Scholar]
- Hatters, DM; Lindner, RA; Carver, JA; Howlett, GJ. The molecular chaperone, alpha-crystallin, inhibits amyloid formation by apolipoprotein C-II. J. Biol. Chem 2001, 276, 33755–33761. [Google Scholar]
- Raman, B; Ban, T; Sakai, M; Pasta, SY; Ramakrishna, T; Naiki, H; Goto, Y; Rao, CM. AlphaB-crystallin, a small heat-shock protein, prevents the amyloid fibril growth of an amyloid beta-peptide and beta2-microglobulin. Biochem. J 2005, 392, 573–581. [Google Scholar]
- London, J; Skrzynia, C; Goldberg, ME. Renaturation of Escherichia coli tryptophanase after exposure to 8 M urea. Evidence for the existence of nucleation centers. Eur. J. Biochem 1974, 47, 409–415. [Google Scholar]
- Fink, AL. Protein aggregation: folding aggregates, inclusion bodies and amyloid. Fold. Des 1998, 3, R9–23. [Google Scholar]
- Dobson, CM. Protein misfolding, evolution and disease. Trends Biochem. Sci 1999, 24, 329–332. [Google Scholar]
- Wetzel, R. Mutations and off-pathway aggregation of proteins. Trends Biotechnol 1994, 12, 193–198. [Google Scholar]
- Jaenicke, R. Folding and association versus misfolding and aggregation of proteins. Philos. Trans. R. Soc. Lond. B Biol. Sci 1995, 348, 97–105. [Google Scholar]
- Kopito, RR. Aggresomes, inclusion bodies and protein aggregation. Trends Cell Biol 2000, 10, 524–530. [Google Scholar]
- Chiti, F; Stefani, M; Taddei, N; Ramponi, G; Dobson, CM. Rationalization of the effects of mutations on peptide and protein aggregation rates. Nature 2003, 424, 805–808. [Google Scholar]
- Alexandrescu, AT. Amyloid accomplices and enforcers. Protein Sci 2005, 14, 1–12. [Google Scholar]
- Murphy, RM; Lee, CC. Laser light scattering as an indispensable tool for probing protein aggregation. In Misbehaving Proteins: Protein (mis)Folding, Aggregation, and Stability; Murphy, RM, Tsai, AM, Eds.; Springer: New York, USA, 2006; Volume VIII, pp. 147–165. [Google Scholar]
- Wetzel, R. Amyloid fibrils-common threads in the natural history of proteins. Acc. Chem. Res 2006, 39, 567. [Google Scholar]
- Stefani, M. Protein folding and misfolding on surfaces. Int. J. Mol. Sci 2008, 9, 2515–2542. [Google Scholar]
- Perutz, MF. Amyloid fibrils. Mutations make enzyme polymerize. Nature 1997, 385, 773–775. [Google Scholar]
- Georgiou, G; Valax, P. Expression of correctly folded proteins in Escherichia coli. Curr. Opin. Biotechnol 1996, 7, 190–197. [Google Scholar]
- Villaverde, A; Carrio, MM. Protein aggregation in recombinant bacteria: biological role of inclusion bodies. Biotechnol. Lett 2003, 25, 1385–1395. [Google Scholar]
- Markossian, KA; Kurganov, BI. Protein folding, misfolding, and aggregation. Formation of inclusion bodies and aggresomes. Biochemistry (Mosc) 2004, 69, 971–84. [Google Scholar]
- Serio, TR; Cashikar, AG; Kowal, AS; Sawicki, GJ; Moslehi, JJ; Serpell, L; Arnsdorf, MF; Lindquist, SL. Nucleated conformational conversion and the replication of conformational information by a prion determinant. Science 2000, 289, 1317–1321. [Google Scholar]
- Guo, J; Hall, CK; Xu, Y; Wetzel, R. Modeling protein aggregate assembly and structure. In Biological and Medical Physics, Biomedical Engineering; Xu, Y, Xu, D, Liang, J, Eds.; Springer Science+Business Media, LLC: New York, USA, 2007; Volume 1, pp. 279–317. [Google Scholar]
- Oosawa, F; Kasai, M. A theory of linear and helical aggregations of macromolecules. J. Mol. Biol 1962, 4, 10–21. [Google Scholar]
- Speed, MA; King, J; Wang, DI. Polymerization mechanism of polypeptide chain aggregation. Biotechnol. Bioeng 1997, 54, 333–343. [Google Scholar]
- Kurganov, BI; Rafikova, ER; Dobrov, EN. Kinetics of thermal aggregation of tobacco mosaic virus coat protein. Biochemistry (Mosc) 2002, 67, 525–533. [Google Scholar]
- Kurganov, BI. Estimation of the activity of molecular chaperones in test-systems based on suppression of protein aggregation. Usp Biol Khim (Mosc) 2002, 42, 89–138. [Google Scholar]
- Kurganov, BI. Kinetics of protein aggregation. Quantitative estimation of the chaperone-like activity in test-systems based on suppression of protein aggregation. Biochemistry (Mosc) 2002, 67, 409–422. [Google Scholar]
- Wang, K; Kurganov, BI. Kinetics of heat- and acidification-induced aggregation of firefly luciferase. Biophys. Chem 2003, 106, 97–109. [Google Scholar]
- Kodaka, M. Requirements for generating sigmoidal time-course aggregation in nucleation-dependent polymerization model. Biophys. Chem 2004, 107, 243–253. [Google Scholar]
- Kodaka, M. Interpretation of concentration-dependence in aggregation kinetics. Biophys. Chem 2004, 109, 325–332. [Google Scholar]
- Kurganov, BI. Protein aggregation kinetics. In Chemical and Biological Kinetics; Burlakova, EB, Varfolomeev, SD, Eds.; Koninklijke Brill NV: The Netherlands, Leiden, Holand, 2005; Volume 2, pp. 251–279. [Google Scholar]
- Ben-Zvi, AP; Goloubinoff, P. Proteinaceous infectious behavior in non-pathogenic proteins is controlled by molecular chaperones. J. Biol. Chem 2002, 277, 49422–49427. [Google Scholar]
- Jarrett, JT; Lansbury, PT, Jr. Amyloid fibril formation requires a chemically discriminating nucleation event: studies of an amyloidogenic sequence from the bacterial protein OsmB. Biochemistry 1992, 31, 12345–12352. [Google Scholar]
- Shen, CL; Scott, GL; Merchant, F; Murphy, RM. Light scattering analysis of fibril growth from the amino-terminal fragment beta(1–28) of beta-amyloid peptide. Biophys. J 1993, 65, 2383–2395. [Google Scholar]
- Nielsen, L; Khurana, R; Coats, A; Frokjaer, S; Brange, J; Vyas, S; Uversky, VN; Fink, AL. Effect of environmental factors on the kinetics of insulin fibril formation: elucidation of the molecular mechanism. Biochemistry 2001, 40, 6036–6046. [Google Scholar]
- Fezoui, Y; Teplow, DB. Kinetic studies of amyloid beta-protein fibril assembly. Differential effects of alpha-helix stabilization. J. Biol. Chem 2002, 277, 36948–36954. [Google Scholar]
- Kentsis, A; Borden, KL. Physical mechanisms and biological significance of supramolecular protein self-assembly. Curr. Protein Pept. Sci 2004, 5, 125–134. [Google Scholar]
- Roberts, CJ. Non-native protein aggregation kinetics. Biotechnol. Bioeng 2007, 98, 927–938. [Google Scholar]
- Morris, AM; Watzky, MA; Finke, RG. Protein aggregation kinetics, mechanism, and curve-fitting: A review of the literature. Biochim. Biophys. Acta 2009, 1794, 375–397. [Google Scholar]
- Khurana, R; Gillespie, JR; Talapatra, A; Minert, LJ; Ionescu-Zanetti, C; Millett, I; Fink, AL. Partially folded intermediates as critical precursors of light chain amyloid fibrils and amorphous aggregates. Biochemistry 2001, 40, 3525–3535. [Google Scholar]
- Qin, Z; Hu, D; Zhu, M; Fink, AL. Structural characterization of the partially folded intermediates of an immunoglobulin light chain leading to amyloid fibrillation and amorphous aggregation. Biochemistry 2007, 46, 3521–3531. [Google Scholar]
- Kumar, S; Mohanty, SK; Udgaonkar, JB. Mechanism of formation of amyloid protofibrils of barstar from soluble oligomers: evidence for multiple steps and lateral association coupled to conformational conversion. J. Mol. Biol 2007, 367, 1186–11204. [Google Scholar]
- Khodarahmi, R; Beyrami, M; Soori, H. Appraisal of casein's inhibitory effects on aggregation accompanying carbonic anhydrase refolding and heat-induced ovalbumin fibrillogenesis. Arch. Biochem. Biophys 2008, 477, 67–76. [Google Scholar]
- Andreasi Bassi, F; Arcovito, G; De Spirito, M; Mordente, A; Martorana, GE. Self-similarity properties of alpha-crystallin supramolecular aggregates. Biophys. J 1995, 69, 2720–2727. [Google Scholar]
- Bettelheim, FA; Ansari, R; Cheng, QF; Zigler, JS, Jr. The mode of chaperoning of dithiothreitol-denatured alpha-lactalbumin by alpha-crystallin. Biochem. Biophys. Res. Commun 1999, 261, 292–297. [Google Scholar]
- Schuler, J; Frank, J; Saenger, W; Georgalis, Y. Thermally induced aggregation of human transferrin receptor studied by light-scattering techniques. Biophys. J 1999, 77, 1117–1125. [Google Scholar]
- Modler, AJ; Gast, K; Lutsch, G; Damaschun, G. Assembly of amyloid protofibrils via critical oligomers-a novel pathway of amyloid formation. J. Mol. Biol 2003, 325, 135–148. [Google Scholar]
- Baussay, K; Bon, CL; Nicolai, T; Durand, D; Busnel, JP. Influence of the ionic strength on the heat-induced aggregation of the globular protein beta-lactoglobulin at pH 7. Int. J. Biol. Macromol 2004, 34, 21–28. [Google Scholar]
- Follmer, C; Pereira, FV; Da Silveira, NP; Carlini, CR. Jack bean urease (EC 3.5.1.5) aggregation monitored by dynamic and static light scattering. Biophys. Chem 2004, 111, 79–87. [Google Scholar]
- Militello, V; Casarino, C; Emanuele, A; Giostra, A; Pullara, F; Leone, M. Aggregation kinetics of bovine serum albumin studied by FTIR spectroscopy and light scattering. Biophys. Chem 2004, 107, 175–187. [Google Scholar]
- Marchetti, S; Sbrana, F; Raccis, R; Lanzi, L; Gambi, CM; Vassalli, M; Tiribilli, B; Pacini, A; Toscano, A. Dynamic light scattering and atomic force microscopy imaging on fragments of beta-connectin from human cardiac muscle. Phys Rev E Stat Nonlin Soft Matter Phys 2008, 77, 021910:1–021910:11. [Google Scholar]
- Chu, B. Laser Light Scattering Basic Principles and Practice; Dover Publications, Inc: Mineola, New York, USA, 2007. [Google Scholar]
- Schärtl, W. Light Scattering from Polymer Solutions and Nanoparticle Dispersions; Springer-Verlag: Berlin, Germany, 2007. [Google Scholar]
- International standard ISO 22412:2008(E); Particle size analysis-Dynamic light scattering (DLS); International Organization for Standartization, 2008.
- Yudin, IK; Nikolaenko, GL; Kosov, VI; Agayan, VA; Anisimov, MA; Sengers, JV. Simple photon-correlation spectrometer for research and education. Int. J. Thermophys 1997, 18, 1237–1248. [Google Scholar]
- Markossian, KA; Khanova, HA; Kleimenov, SY; Levitsky, DI; Chebotareva, NA; Asryants, RA; Muronetz, VI; Saso, L; Yudin, IK; Kurganov, BI. Mechanism of thermal aggregation of rabbit muscle glyceraldehyde-3-phosphate dehydrogenase. Biochemistry 2006, 45, 13375–13384. [Google Scholar]
- Khanova, HA; Markossian, KA; Kurganov, BI; Samoilov, AM; Kleimenov, SY; Levitsky, DI; Yudin, IK; Timofeeva, AC; Muranov, KO; Ostrovsky, MA. Mechanism of chaperone-like activity. Suppression of thermal aggregation of betaL-crystallin by alpha-crystallin. Biochemistry 2005, 44, 15480–15487. [Google Scholar]
- Panyukov, Y; Yudin, I; Drachev, V; Dobrov, E; Kurganov, B. The study of amorphous aggregation of tobacco mosaic virus coat protein by dynamic light scattering. Biophys. Chem 2007, 127, 9–18. [Google Scholar]
- Meremyanin, AV; Eronina, TB; Chebotareva, NA; Kurganov, BI. Kinetics of thermal aggregation of glycogen phosphorylase b from rabbit skeletal muscle. Mechanism of protective action of alpha-crystallin. Biopolymers 2008, 89, 124–134. [Google Scholar]
- Weitz, DA; Huang, JS; Lin, MY; Sung, J. Limits of the fractal dimension for irreversible kinetic aggregation of gold colloids. Phys. Rev. Lett 1985, 54, 1416–1419. [Google Scholar]
- Weitz, DA; Lin, MY. Dynamic scaling of cluster-mass distributions in kinetic colloid aggregation. Phys. Rev. Lett 1986, 57, 2037–2040. [Google Scholar]
- Lin, MY; Lindsay, HM; Weitz, DA; Ball, RC; Klein, R; Meakin, P. Universality in colloid aggregation. Nature 1989, 939, 360–362. [Google Scholar]
- Lin, MY; Lindsay, HM; Weitz, DA; Ball, RC; Klein, R; Meakin, P. Universal reaction-limited colloid aggregation. Phys. Rev. A 1990, 41, 2005–2020. [Google Scholar]
- Lu, PJ; Zaccarelli, E; Ciulla, F; Schofield, AB; Sciortino, F; Weitz, DA. Gelation of particles with short-range attraction. Nature 2008, 453, 499–503. [Google Scholar]
- Lin, MY; Lindsay, HM; Weitz, DA; Ball, RC; Klein, R; Meakin, P. Universality of fractal aggregates as probed by light scattering. Proc. R. Soc. Lond. A 1989, 423, 71–87. [Google Scholar]
- Creighton, TE. Proteins Structures and Molecular Properties; Freeman; W.H. and Co.: New York, USA, 1993. [Google Scholar]
- Keresztes-Nagy, S; Klapper, MH; Lazer, L; Klotz, IM. Hybridization experiments: evidence of dissociation equilibrium in hemerythrin. Science 1965, 150, 357–359. [Google Scholar]
- Winklmair, D. A simple approach to the theory of cooperative aggregation of biological macromolecules. Arch. Biochem. Biophys 1971, 147, 509–514. [Google Scholar]
- Chebotareva, NA; Meremyanin, AV; Makeeva, VF; Livanova, NB; Kurganov, BI. Cooperative self-association of phosphorylase kinase from rabbit skeletal muscle. Biophys. Chem 2008, 133, 45–53. [Google Scholar]
- Berka, M; Rice, JA. Relation between aggregation kinetics and the structure of kaolinite aggregates. Langmuir 2005, 21, 1223–1229. [Google Scholar]
- Golub, NV; Markossian, KA; Sholukh, MV; Muranov, KO; Kurganov, BI. Study of kinetics of thermal aggregation of mitochondrial aspartate aminotransferase by dynamic light scattering: protective effect of alpha-crystallin. Eur Biophys J 2009. doi:10.1007/s00249-009-0403-7. [Google Scholar]
- Golub, NV; Markossian, KA; Kasilovich, NV; Sholukh, MV; Orlov, VN; Kurganov, BI. Thermal inactivation, denaturation and aggregation of mitochondrial aspartate aminotransferase. Biophys. Chem 2008, 135, 125–131. [Google Scholar]
- Eronina, TB; Chebotareva, NA; Bazhina, SG; Makeeva, VF; Kleymenov, SY; Kurganov, BI. Effect of proline on thermal inactivation, denaturation and aggregation of glycogen phosphorylase b from rabbit skeletal muscle. Biophys. Chem 2009, 141, 66–74. [Google Scholar]
- Meremyanin, AV; Eronina, TB; Chebotareva, NA; Kleimenov, SY; Yudin, IK; Muranov, KO; Ostrovsky, MA; Kurganov, BI. Effect of alpha-crystallin on thermal aggregation of glycogen phosphorylase b from rabbit skeletal muscle. Biochemistry (Mosc) 2007, 72, 518–528. [Google Scholar]
- Golub, N; Meremyanin, A; Markossian, K; Eronina, T; Chebotareva, N; Asryants, R; Muronets, V; Kurganov, B. Evidence for the formation of start aggregates as an initial stage of protein aggregation. FEBS Lett 2007, 581, 4223–4227. [Google Scholar]
- Sluzky, V; Tamada, JA; Klibanov, AM; Langer, R. Kinetics of insulin aggregation in aqueous solutions upon agitation in the presence of hydrophobic surfaces. Proc. Natl. Acad. Sci. USA 1991, 88, 9377–9381. [Google Scholar]
- Pouzot, M; Nicolai, T; Durand, D; Benyahia, L. Structure factor and elasticity of a heat-set globular protein gel. Macromolecules 2004, 37, 614–620. [Google Scholar]
- Mehalebi, S; Nicolai, T; Durand, D. Light scattering study of heat-denatured globular protein aggregates. Int. J. Biol. Macromol 2008, 43, 129–135. [Google Scholar]
- de la Fuente, MA; Singh, H; Hemar, Y. Recent advances in the characterization of heat-induced aggregates and intermediates of whey proteins. Trends Food Sci. Technol 2002, 13, 262–274. [Google Scholar]
- Durand, D; Gimel, JC; Nicolai, T. Aggregation, gelation and phase separation of heat denatured globular proteins. Physica A 2002, 304, 253–265. [Google Scholar]
- Turoverov, KK; Biktashev, AG; Khaitlina, SY; Kuznetsova, IM. The structure and dynamics of partially folded actin. Biochemistry 1999, 38, 6261–6269. [Google Scholar]
- Ball, RC; Weitz, DA; Witten, TA; Leyvraz, F. Universal kinetics in reaction-limited aggregation. Phys. Rev. Lett 1987, 58, 274–277. [Google Scholar]
- Khanova, HA; Markossian, KA; Kleimenov, SY; Levitsky, DI; Chebotareva, NA; Golub, NV; Asryants, RA; Muronetz, VI; Saso, L; Yudin, IK; Muranov, KO; Ostrovsky, MA; Kurganov, BI. Effect of alpha-crystallin on thermal denaturation and aggregation of rabbit muscle glyceraldehyde-3-phosphate dehydrogenase. Biophys. Chem 2007, 125, 521–531. [Google Scholar]
- Rajaraman, K; Raman, B; Ramakrishna, T; Rao, CM. Interaction of human recombinant alphaA- and alphaB-crystallins with early and late unfolding intermediates of citrate synthase on its thermal denaturation. FEBS Lett 2001, 497, 118–123. [Google Scholar]
- Hook, DW; Harding, JJ. Molecular chaperones protect catalase against thermal stress. Eur. J. Biochem 1997, 247, 380–385. [Google Scholar]
- Marini, I; Moschini, R; Del Corso, A; Mura, U. Complete protection by alpha-crystallin of lens sorbitol dehydrogenase undergoing thermal stress. J. Biol. Chem 2000, 275, 32559–32565. [Google Scholar]
- Hess, JF; FitzGerald, PG. Protection of a restriction enzyme from heat inactivation by [alpha]-crystallin. Mol. Vis 1998, 4, 29. [Google Scholar]
- Zhang, Y; Liu, X; Liu, J. Recombinant human alphaA-crystallin can protect the enzymatic activity of CpUDG against thermal inactivation. FEBS Lett 2005, 579, 2897–2900. [Google Scholar]
- Markossian, KA; Golub, NV; Kleymenov, SY; Muranov, KO; Sholukh, MV; Kurganov, BI. Effect of α-crystallin on thermostability of mitochondrial aspartate aminotransferase. Int J Biol Macromol 2009, in press. [Google Scholar]
- Markossian, KA; Golub, NV; Khanova, HA; Levitsky, DI; Poliansky, NB; Muranov, KO; Kurganov, BI. Mechanism of thermal aggregation of yeast alcohol dehydrogenase I. Role of intramolecular chaperone. Biochim. Biophys. Acta 2008, 1784, 1286–1293. [Google Scholar]










© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Markossian, K.A.; Yudin, I.K.; Kurganov, B.I. Mechanism of Suppression of Protein Aggregation by α-Crystallin. Int. J. Mol. Sci. 2009, 10, 1314-1345. https://doi.org/10.3390/ijms10031314
Markossian KA, Yudin IK, Kurganov BI. Mechanism of Suppression of Protein Aggregation by α-Crystallin. International Journal of Molecular Sciences. 2009; 10(3):1314-1345. https://doi.org/10.3390/ijms10031314
Chicago/Turabian StyleMarkossian, Kira A., Igor K. Yudin, and Boris I. Kurganov. 2009. "Mechanism of Suppression of Protein Aggregation by α-Crystallin" International Journal of Molecular Sciences 10, no. 3: 1314-1345. https://doi.org/10.3390/ijms10031314
APA StyleMarkossian, K. A., Yudin, I. K., & Kurganov, B. I. (2009). Mechanism of Suppression of Protein Aggregation by α-Crystallin. International Journal of Molecular Sciences, 10(3), 1314-1345. https://doi.org/10.3390/ijms10031314