Dielectric Properties of Binary Solvent Mixtures of Dimethyl Sulfoxide with Water
Abstract
:1. Introduction
2. Interaction Potentials and Simulation Details
3. Results and Discussion
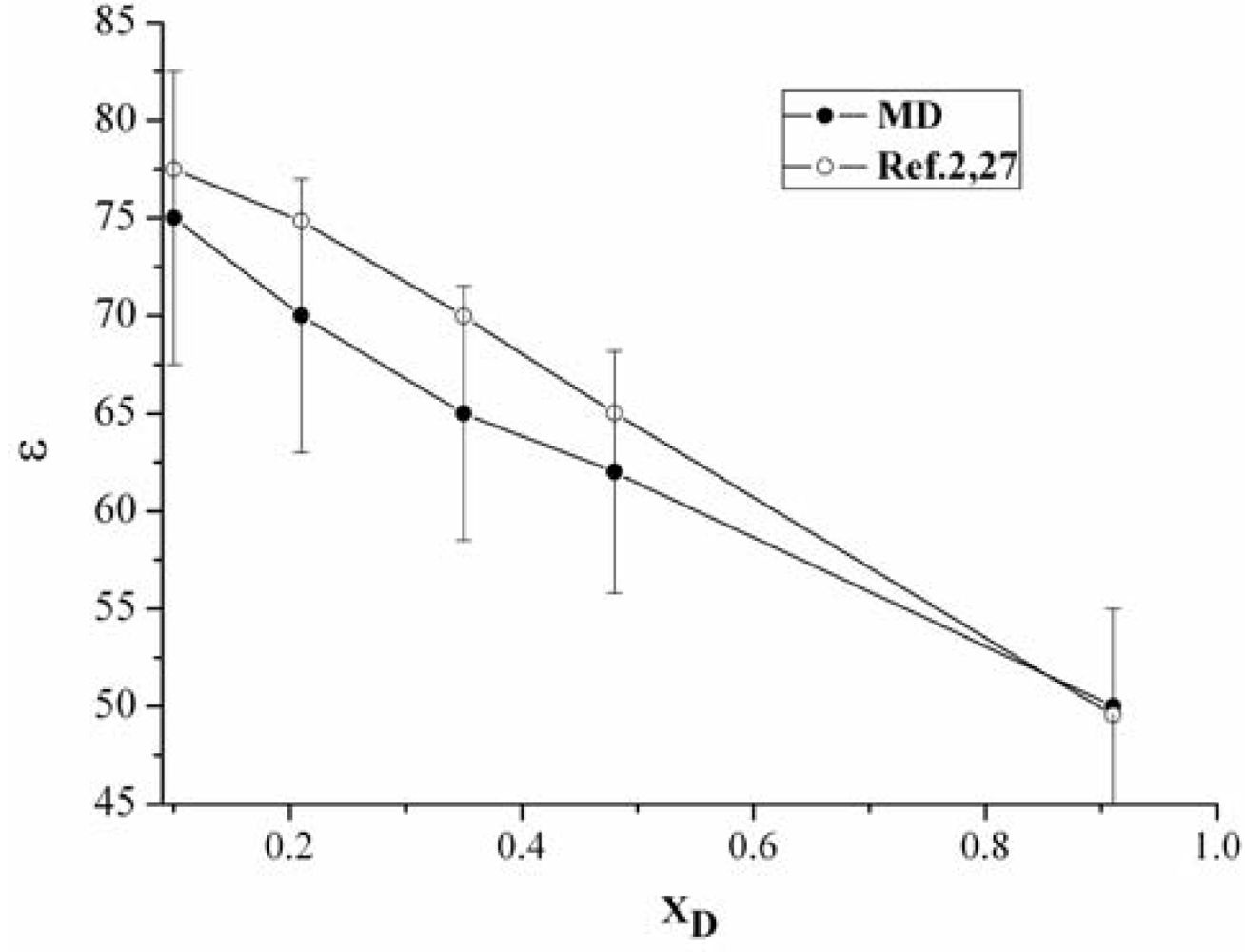
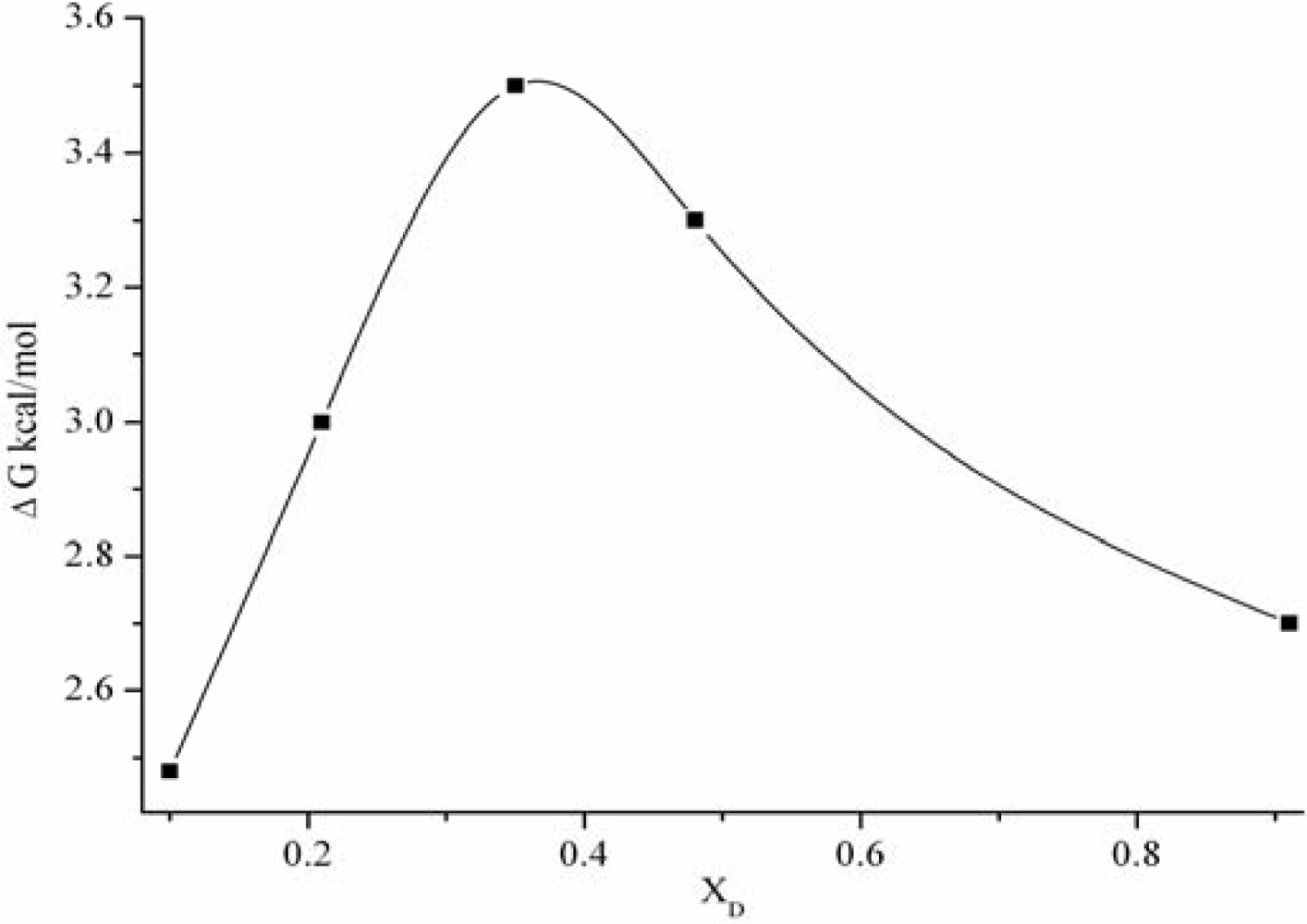
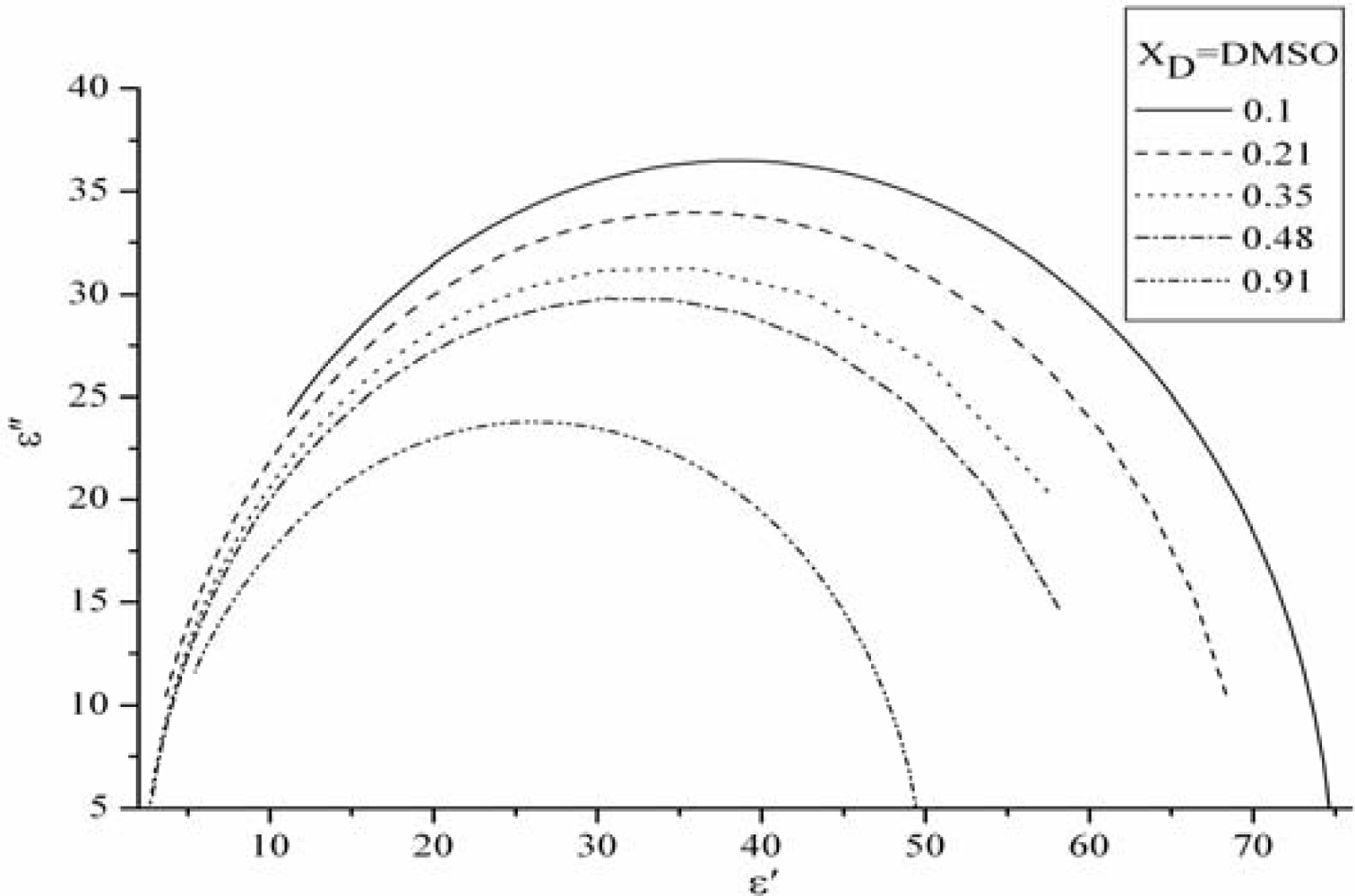
3.1. The static dielectric constant
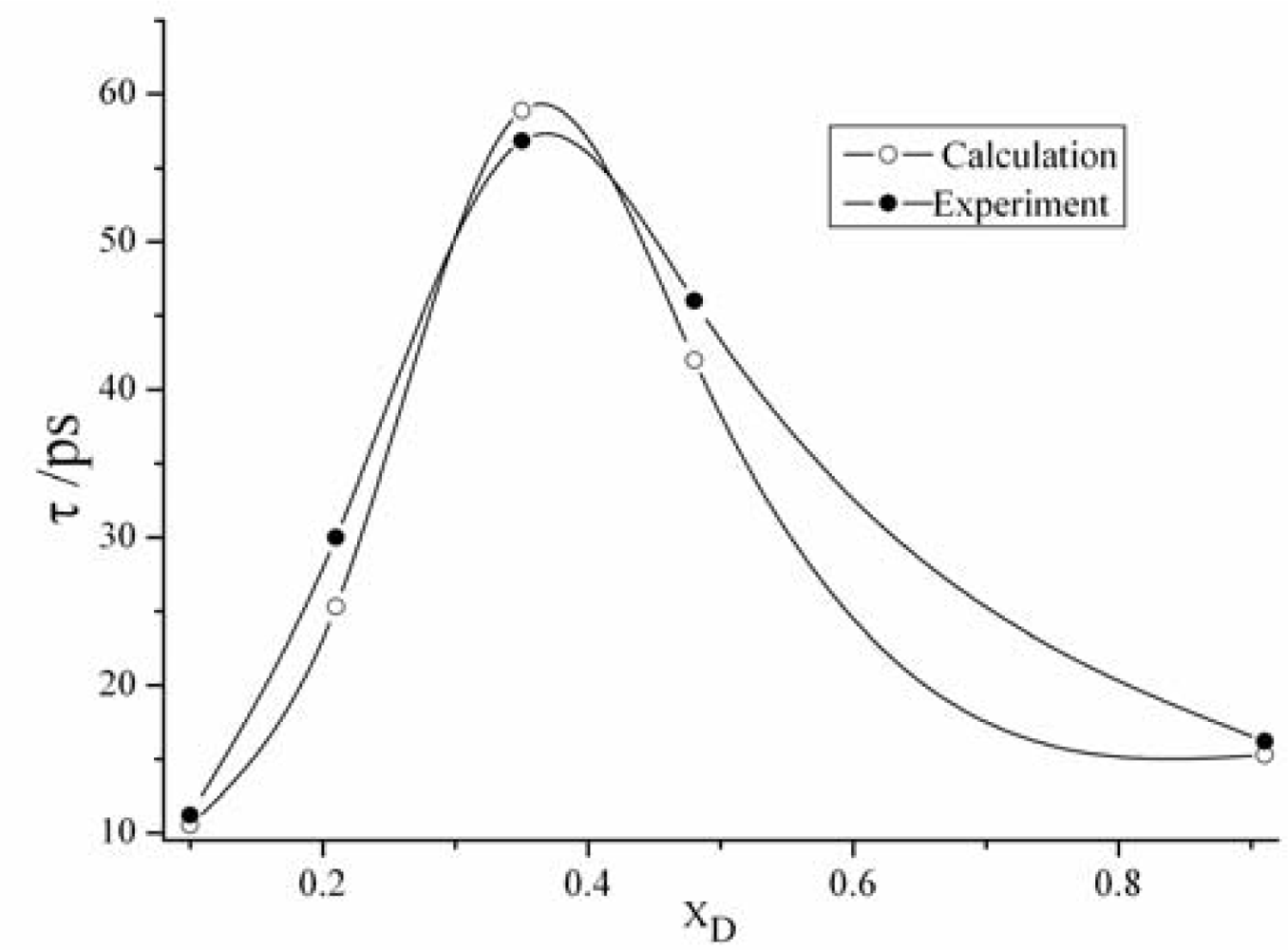
3.2. The relaxation time
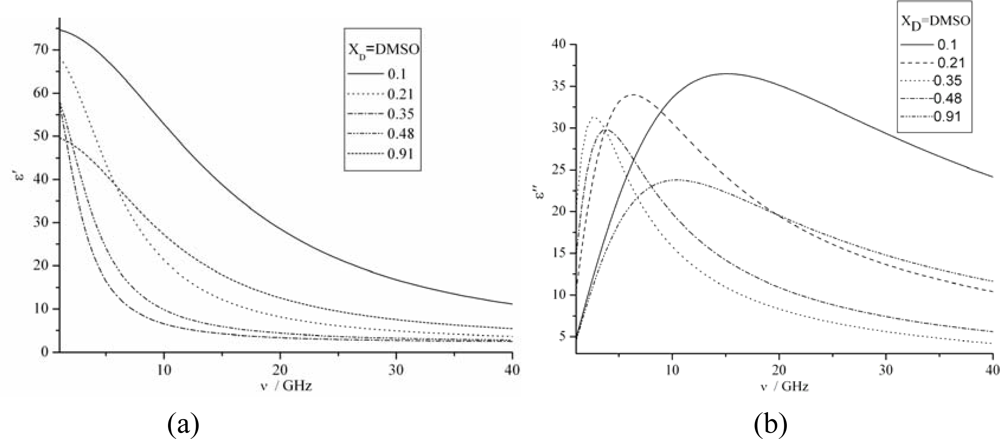
3.3. The permittivities vs. Frequency
4. Conclusions
Acknowledgments
References and Notes
- Leadbeater, N. Making microwaves. Chem. World 2004, 1, 38–41. [Google Scholar]
- Adam, D. Microwave chemistry: Out of the kitchen. Nature 2003, 421, 571–572. [Google Scholar]
- Jin, QH; Dai, SS; Huang, KM. Microwave Chemistry; Science Press: Beijing, China, 1999. [Google Scholar]
- Vechi, SM; Skaf, MS. Molecular-dynamics simulations of dimethylsulfoxide- methanol mixtures. J. Chem. Phys 2005, 123, 154507–154514. [Google Scholar]
- Cowie, JMG; Toporowski, PM. Association in binary liquid system dimethyl sulphoxide–water. Can. J. Chem 1961, 39, 2240–2243. [Google Scholar]
- Fox, MF; Whittingham, KP. Component interactions in aqueous dimethyl sulphoxide. J Chem Soc, Faraday Trans 1 1975, 71, 1407–1412. [Google Scholar]
- Clever, HL; Pigott, SP. Enthalpies of mixing of dimethylsulfoxide with water and with several ketones at 298.15 K. J. Chem. Thermodyn 1971, 3, 221–225. [Google Scholar]
- Packer, KJ; Tomlinson, DJ. Nuclear spin relaxation and self-diffusion in the binary system, dimethylsulphoxide (DMSO) + water. Trans. Faraday Soc 1971, 67, 1302– 1314. [Google Scholar]
- Gordalla, BC; Zeidler, MD. Molecular dynamics in the system water- dimethylsulphoxide: A N.M.R. relaxation study. Mol. Phys 1986, 59, 817–828. [Google Scholar]
- Baker, ES; Jonas, J. Transport and relaxation properties of dimethylsulfoxide-water mixtures at high pressure. J Phys Chem 1985, 89(9), 1730–1735. [Google Scholar]
- Kaatze, U; Pottel, R; Schäfer, M. Dielectric spectrum of dimethylsulfoxide/water mixtures as a function of composition. J Phys Chem 1989, 93(14), 5623–5627. [Google Scholar]
- Luzar, A. Dielectric behavior of DMSO-water mixtures: a hydrogenbonding model. J. Mol. Liq 1990, 46, 221–238. [Google Scholar]
- Murthy, SSN. Phase behavior of the supercooled aqueous solutions of dimethylSulfoxide, ethylene glycol, and methanol as seen by dielectric spectroscopy. J Phys Chem B 1997, 101(31), 6043–6049. [Google Scholar]
- Murthy, SSN. Some insight into the physical basis of the cryoprotective action of dimethyl sulfoxide and ethylene glycol. Cryobiology 1998, 36, 84–96. [Google Scholar]
- Rasmussen, DH; Mackenzie, AP. Phase diagram for the system water–dimethyl sulphoxide. Nature 1968, 220, 1315–1317. [Google Scholar]
- Zhang, Q; Zhang, X; Zhao, DX. Polarizable force field for water–dimethyl sulfoxide systems: I parameterization and gas phase test. J. Mol. Liq 2009, 145, 58–66. [Google Scholar]
- Zhang, Q; Zhang, X; Zhao, DX. Polarizable force field for water-dimethyl sulfoxide systems: II properties of mixtures by molecular dynamics simulations. J Mol Liq 2009, 145, 67–81. [Google Scholar]
- Catalan, J; Diaz, C; Garcia-Blanco, F. Characterization of binary solvent mixtures of DMSO with water and other cosolvents. J. Org. Chem 2001, 66, 5846–5852. [Google Scholar]
- Muller, MG; Hardy, EH; Vogt, PS; Bratschi, C; Kirchner, B; Huber, H; Searles, DJ. Calculation of the deuteron quadrupole relaxation rate in a mixture of water and dimethyl sulfoxide. J. Am. Chem. Soc 2004, 126, 4704–4710. [Google Scholar]
- Suresh, SJ. Detailed molecular model for dielectric constant of multicomponent, associating liquids. J. Phys. Chem. B 2004, 108, 715–720. [Google Scholar]
- Benjamin, I. Structure, thermodynamics, and dynamics of the liquid/vapor interface of water/dimethylsulfoxide mixtures. J. Chem. Phys 1999, 110, 8070–8079. [Google Scholar]
- De Leeuw, SW; Perram, JM; Smith, ER. Computer simulation of the static dielectric constant of systems with permanent electric dipoles. Annu. Rev. Phys. Chem 1986, 37, 245–270. [Google Scholar]
- Ryckaert, JP; Ciccotti, G; Berendsen, HJC. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J Comput Phys 1977, 23, 327–341. [Google Scholar]
- Hockney, RW. The potential calculation and some applications. Meth. Comput. Phys 1970, 9, 136–210. [Google Scholar]
- Cowie, JMG; Toporowski, PM. Association in the binary liquid system dimethylsulphoxide– water. Can. J. Chem 1961, 39, 2240–2243. [Google Scholar]
- LeBel, RG; Goring, DAI. Density, viscosity, refractive index, and hygroscopicity of mixtures of water and dimethyl sulfoxide. J. Chem. Eng. Data 1962, 7, 100–101. [Google Scholar]
- Doucet, Y; Calmes-Perrault, F; Durand, MT. Dielectric constants of pure dimethyl sulfoxide and of its aqueous solutions. Compt. Rend 1965, 260, 1878–1881. [Google Scholar]
- Zwanzig, RW. High-temperature equation of state by a perturbation method. I. nonpolar gases. J. Chem. Phys 1954, 22, 1420–1426. [Google Scholar]
- Beveridge, DL; DiCapua, FM. Free Energy via Molecular Simulation: Applications to Chemical and Biomolecular Systems. Ann. Rev. Biophys. Biophys. Chem 1989, 18, 431–492. [Google Scholar]
- Wallqvist, A; Berne, BJ. Molecular dynamics study of the dependence of water solvation free energy on solute curvature and surface area. J. Phys. Chem 1995, 99, 2885–2892. [Google Scholar]
- Glasstone, S; Laidle, KJ; Eyring, H. The theory of rate processes; McGraw-Hill: New York, USA, 1941. [Google Scholar]
- Cole, KS; Cole, RH. Dispersion and absorption in dielectrics I. alternating current characteristics. J. Chem. Phys 1941, 9, 341–351. [Google Scholar]
- Davidson, DW; Cole, RH. Dielectric relaxation in glycerol. J. Chem. Phys 1950, 18, 1417. [Google Scholar]
- Debye, P. Polar Molecules; Chemical Catalog. Co.: New York, USA, 1929. [Google Scholar]
- Puranik, SM; Kumbharkhane, AC; Mehrotra, SC. Dielectric study of dimethyl sulfoxide–water mixtures using the time-domain technique. J. Chem. Soc. Faraday Trans 1992, 88, 433–435. [Google Scholar]
| ɛ/(kJmol−1) | σ/(nm) | q/(a.u.) | |
|---|---|---|---|
| O(water) | 0.65 | 0.3165 | −0.82 |
| H(water) | 0.0 | 0.0 | 0.41 |
| O(DMSO) | 0.30 | 0.28 | −0.459 |
| S | 1.00 | 0.34 | 0.139 |
| CH3 | 1.23 | 0.38 | 0.16 |
| Composition | x1 | x2 | n1 | n2 | L (Å) | ρa (g/cm3) | Refractive index ( nD) |
|---|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.9 | 100 | 900 | 34.05 | 1.0105b | 1.3458b |
| 2 | 0.21 | 0.79 | 210 | 790 | 36.76 | 1.0242b | 1.3600b |
| 3 | 0.35 | 0.65 | 350 | 650 | 39.0 | 1.0927 | 1.4385 |
| 4 | 0.48 | 0.52 | 480 | 520 | 41.38 | 1.0983 | 1.4525 |
| 5 | 0.91 | 0.09 | 910 | 90 | 47.93 | 1.0965 | 1.4741 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yang, L.-J.; Yang, X.-Q.; Huang, K.-M.; Jia, G.-Z.; Shang, H. Dielectric Properties of Binary Solvent Mixtures of Dimethyl Sulfoxide with Water. Int. J. Mol. Sci. 2009, 10, 1261-1270. https://doi.org/10.3390/ijms10031261
Yang L-J, Yang X-Q, Huang K-M, Jia G-Z, Shang H. Dielectric Properties of Binary Solvent Mixtures of Dimethyl Sulfoxide with Water. International Journal of Molecular Sciences. 2009; 10(3):1261-1270. https://doi.org/10.3390/ijms10031261
Chicago/Turabian StyleYang, Li-Jun, Xiao-Qing Yang, Ka-Ma Huang, Guo-Zhu Jia, and Hui Shang. 2009. "Dielectric Properties of Binary Solvent Mixtures of Dimethyl Sulfoxide with Water" International Journal of Molecular Sciences 10, no. 3: 1261-1270. https://doi.org/10.3390/ijms10031261




