A Review of Computational Methods in Materials Science: Examples from Shock-Wave and Polymer Physics
Abstract
:1. Introduction
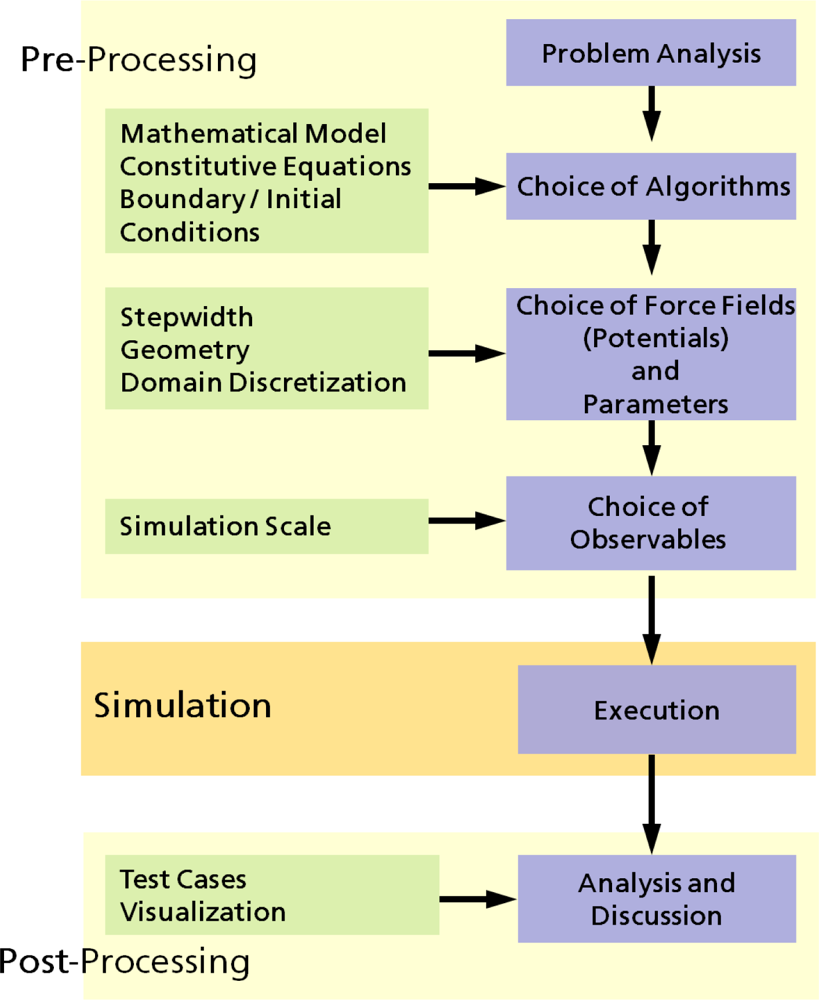
2. Physical and Numerical Modeling
2.1. Computer Simulations as a Research Tool
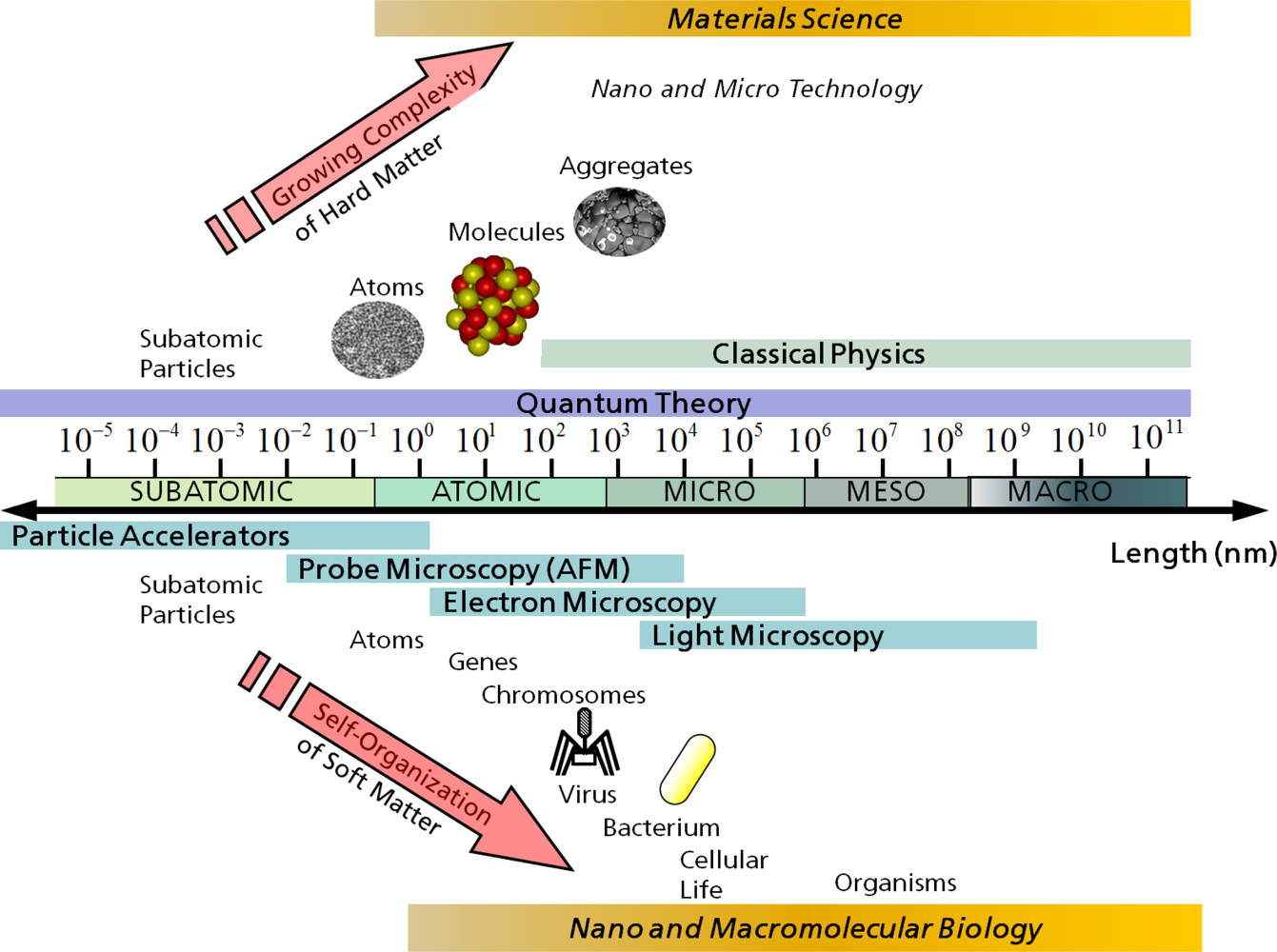
3. Simulation Methods for Different Length and Time Scales
- static equilibrium properties, e.g., the radial distribution function of a liquid, the potential energy of a system averaged over many timesteps, the static structure function of a complex molecule, or the binding energy of an enzyme attached to a biological lipid membrane.
- dynamic or non-equilibrium properties, such as diffusion processes in biomembranes, the viscosity of a liquid, or the dynamics of the propagation of cracks and defects in crystalline materials.
3.1. Electronic/Atomistic Scale
The Born-Oppenheimer Approximation
Car-Parinello MD
3.2. Atomistic/Microscopic Scale
3.3. Microscopic/Mesoscopic Scale
3.4. Mesoscopic/Macroscopic Scale
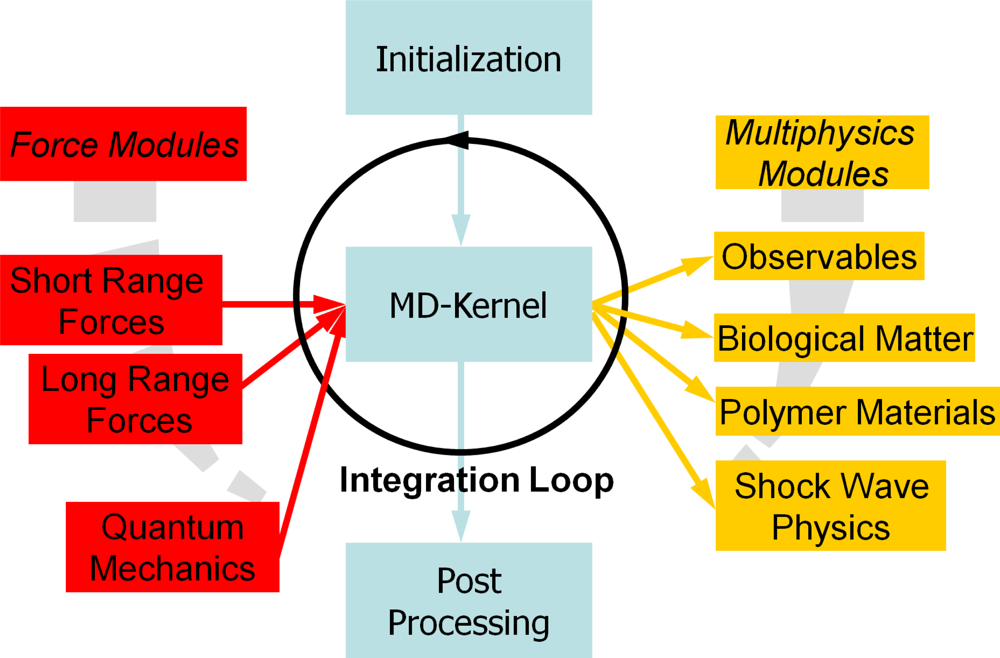
4. The Key Ingredients of Molecular Dynamics Simulations
- The knowledge of one single structure, even if it is the structure of the global energy minimum, is not sufficient. It is always necessary to generate a representative ensemble at a given temperature, in order to compute macroscopic properties.
- The atomic details of structure and motion obtained in molecular simulations, is often not relevant for macroscopic properties. This opens the route for simplifications in the description of interactions and averaging over irrelevant details. Statistical mechanics provides the theoretical framework for such simplifications.
4.1. Limitations of MD
- Artificial boundary conditionsThe system size that can be simulated with MD is very small compared to real molecular systems. Hence, a system of particles will have many unwanted artificial boundaries (surfaces). In order to avoid real boundaries one introduces periodic boundary conditions (see Section 4.3.) which can introduce artificial spatial correlations in too small systems. Therefore, one should always check the influence of system size on results.
- Cut off of long-range interactionsUsually, all non-bonded interactions are cut-off at a certain distance in order to keep the cost of force computation (and the search effort for interacting particles) as small as possible. Due to the minimum image convention (see Section 4.4.) the cutoff range may not exceed half the box size. While this is large enough for most systems in practice, problems are only to be expected with systems containing charged particles. Here, simulations can go wrong badly and, e.g., lead to an accumulation of the charged particles in one corner of the box. Here, one has to use special algorithms such as the particle-mesh Ewald method [115,116].
- The simulations are classicalUsing Newton’s equations of motion implies the use of classical mechanics for the description of the atomic motion. All those material properties connected with the fast electronic degrees of freedom are not correctly described. For example, atomic oscillations (e.g., covalent C-C-bond oscillations in polyethylene molecules, or hydrogen-bonded motion in biopolymers such as DNA, proteins or biomembranes) are typically of the order 1014 Hz. The specific heat is another example which is not correctly described in a classical model as here, at room temperature, all degrees of freedom are excited, whereas quantum mechanically, the high-frequency bonding oscillations are not excited, thus leading to a smaller (correct) value of the specific heat than in the classical picture. A general solution to this problem is to treat the bond distances and bond angles as constraints in the equations of motion. Thus, the highest frequencies in the molecular motion are removed and one can use a much higher timestep in the integration [117].
- The electrons are in the ground stateUsing conservative force fields in MD implies that the potential is a function of the atomic positions only. No electronic motions are considered, thus the electrons remain in their ground state and are considered to follow the core movements instantaneously. This means that electronically excited states, electronic transfer processes and chemical reactions cannot be treated.
- Approximative force fieldsForce fields are not really an integral part of the simulation method but are determined from experiments or from a parameterization using ab initio methods. Also, most often, force fields are pair-additive (except for the long-range Coulomb force) and hence cannot incorporate polarizabilities of molecules. However, such force fields exist and there is continuous effort to generate such kind of force fields [118,119]. In most practical applications however, e.g., for biomacromolecules in aqueous solution, pair potentials are quite accurate mostly because of error cancellation. This does not always work, for example ab initio predictions of small proteins still yields mixed results and when the proteins fail to fold, it is often unclear whether the failure is due to a deficiency in the underlying force fields or simply a lack of sufficient simulation time [120,121].
- Force fields are pair additiveAll non-bonded forces result from the sum of non-bonded pair interactions. Non pair-additive interactions such as the polarizability of molecules and atoms, are represented by averaged effective pair potentials. Hence, the pair interactions are not valid for situations that differ considerably from the test systems on which the models were parameterized. The omission of polarizability in the potential implies that the electrons do not provide a dielectric constant with the consequence that the long-range electrostatic interaction between charges is not reduced (as it should be) and thus overestimated in simulations.
4.2. Molecular Interactions
Non-bonded Interactions
Bonded Interactions
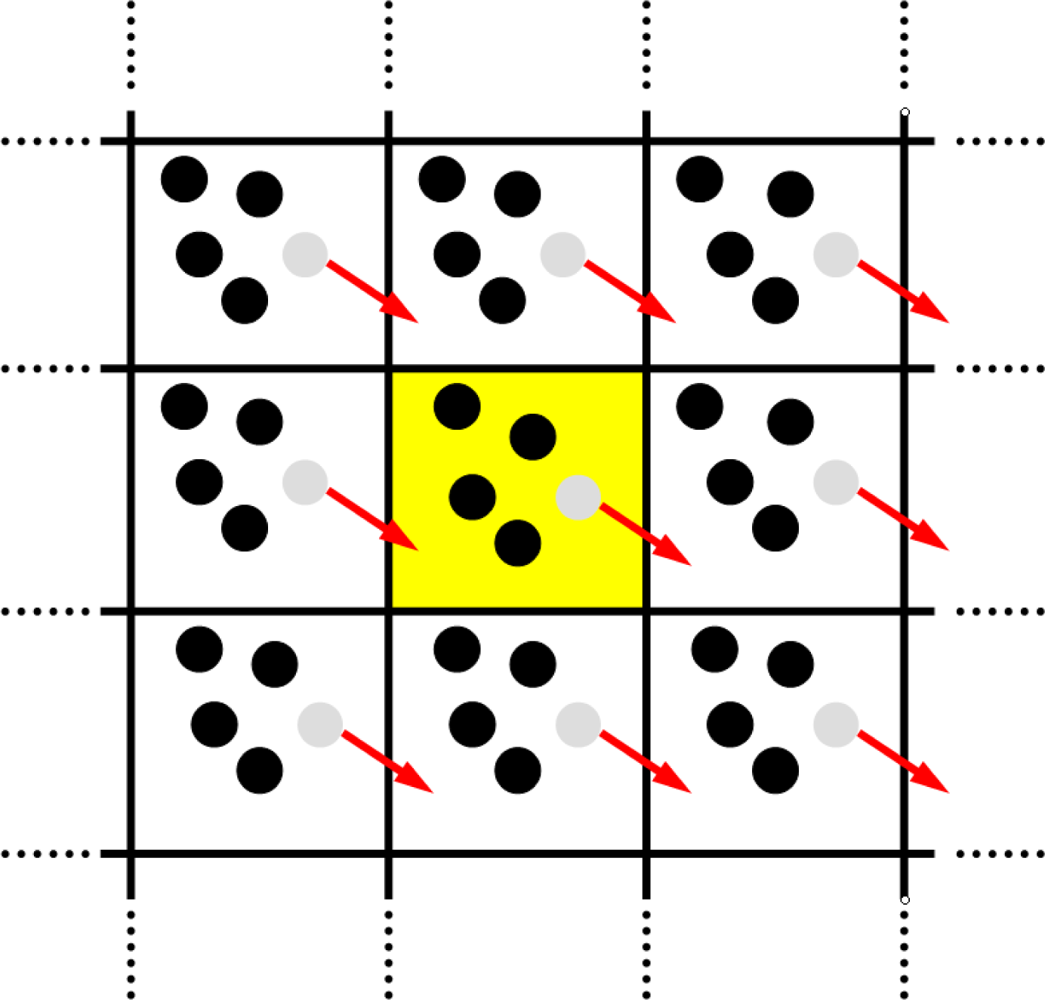
4.3. Periodic Boundary Conditions
4.4. Minimum Image Convention
4.5. Force Calculation
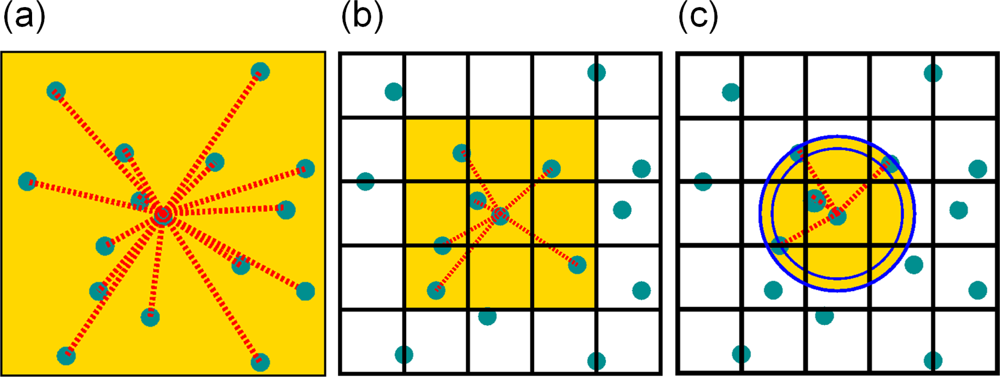
Linked-Cell Algorithm
Linked-Cell Algorithm With Neighbor-Lists
Ghostparticles
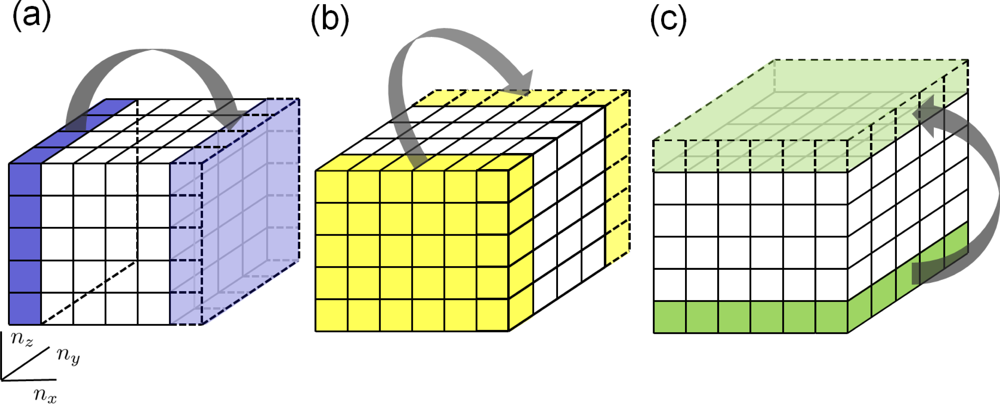
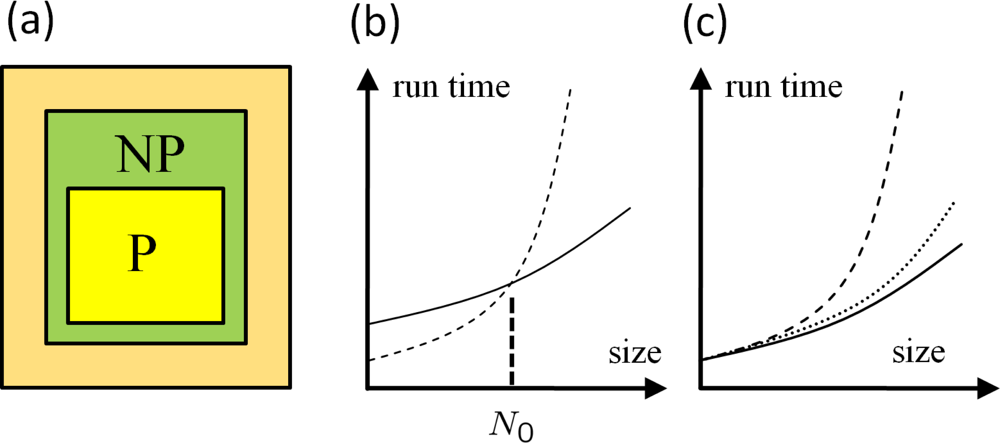
4.6. Efficiency of the MD Method
- Testing an if-condition,
- Assigning a value, i.e., changing the contents of a memory,
- Executing one of the elementary operations (+, −, ×, DIV, MOD),
- Initializing a loop variable.
- START
- for i := 1 TO N - 1 DO
- for j := 1 TO N DO
- if a[i] > a[j] then h = a[i]; a[i] = a[j]; a[j] = h
- END
Amdahl’s Law
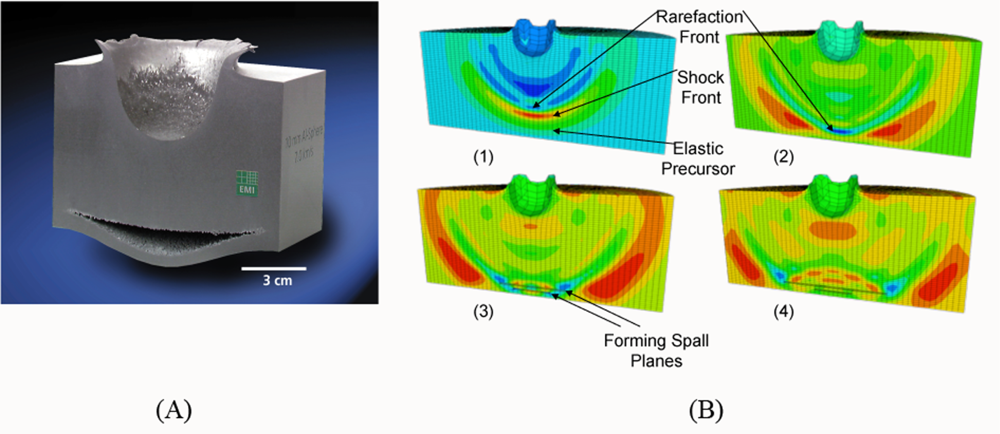
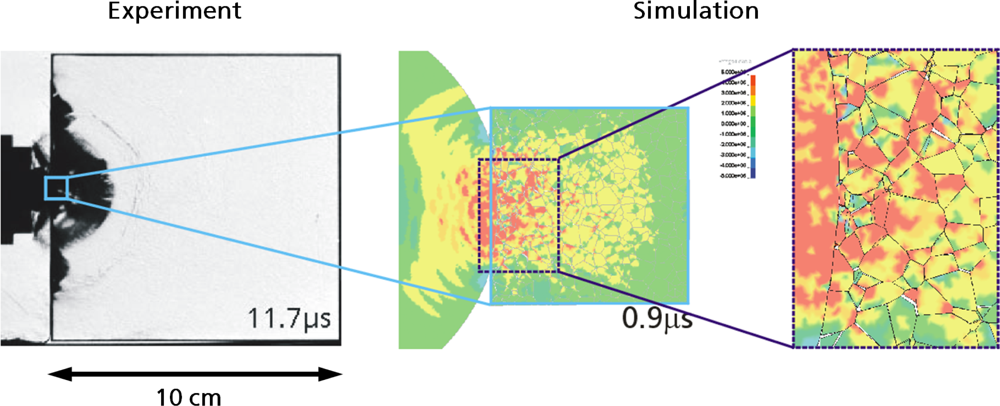
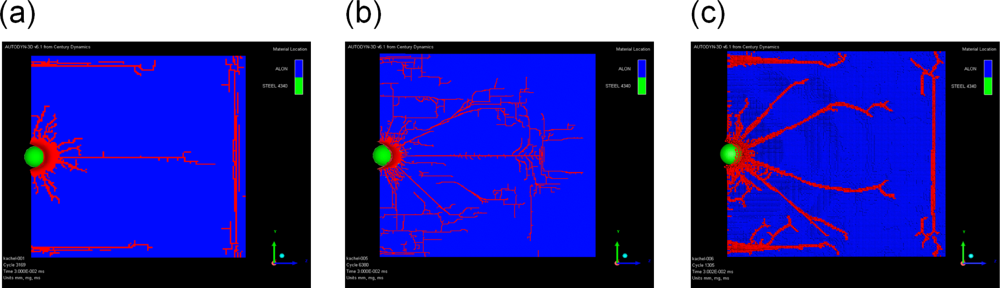
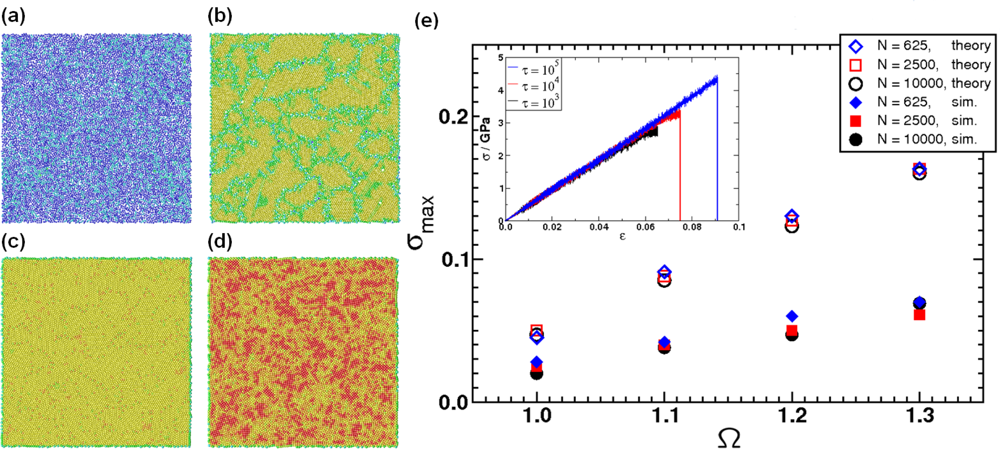
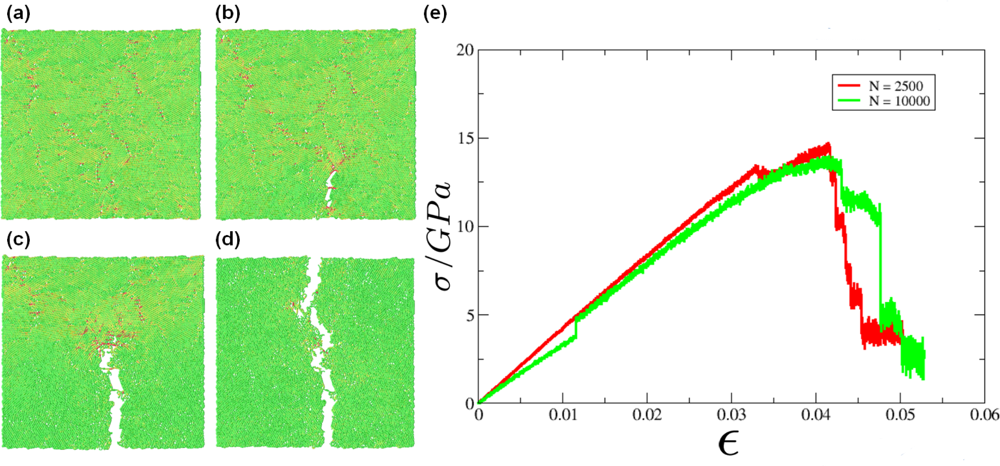
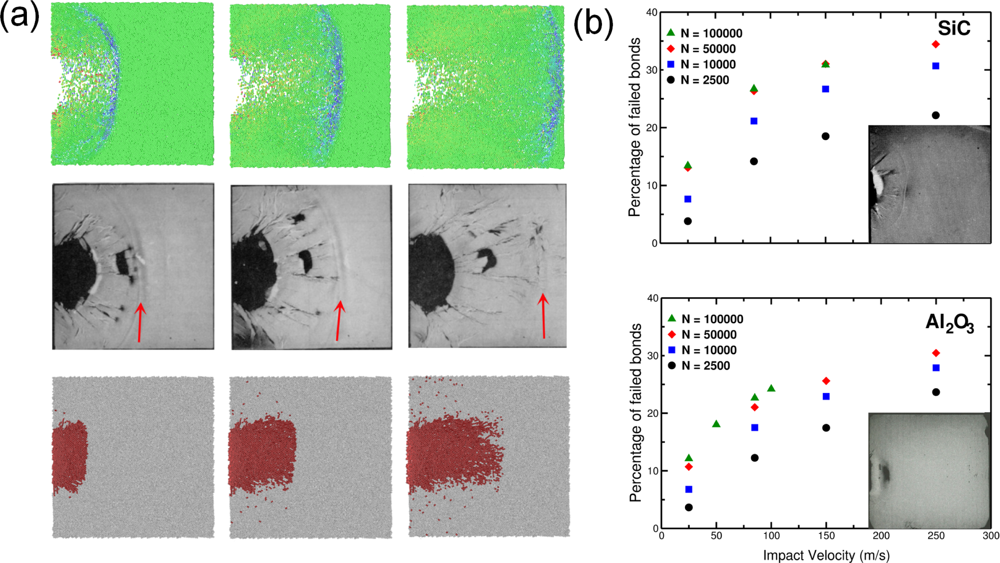
5. Application: Simulating the Effect of Shock Waves in Polycrystalline Solid States
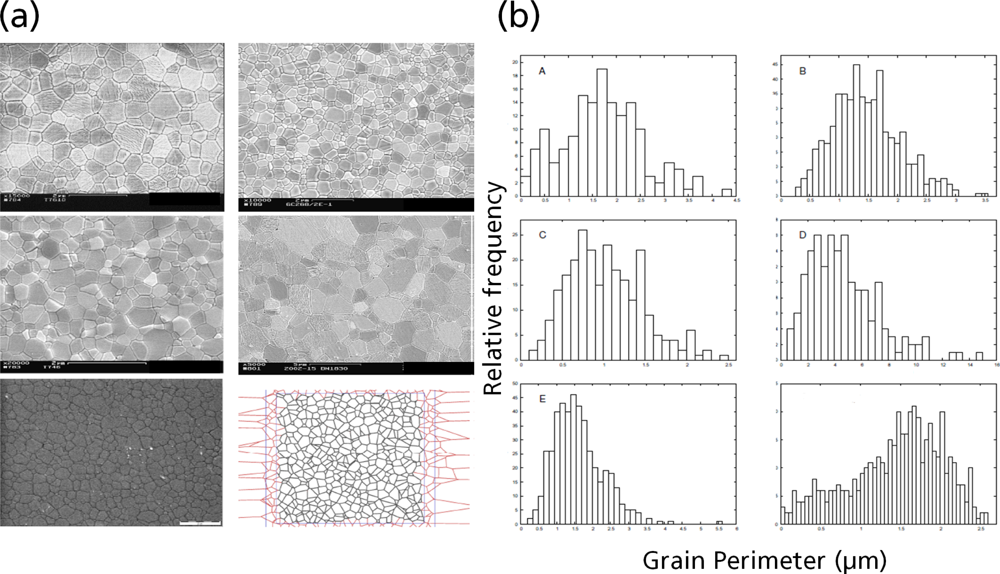
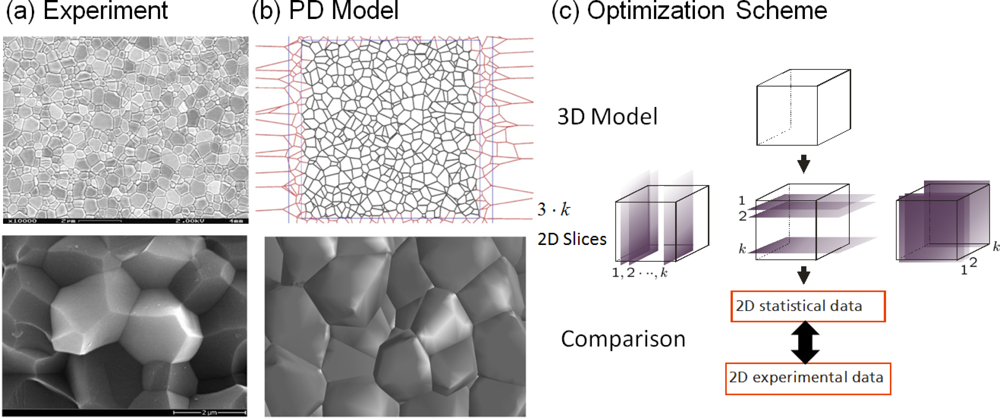
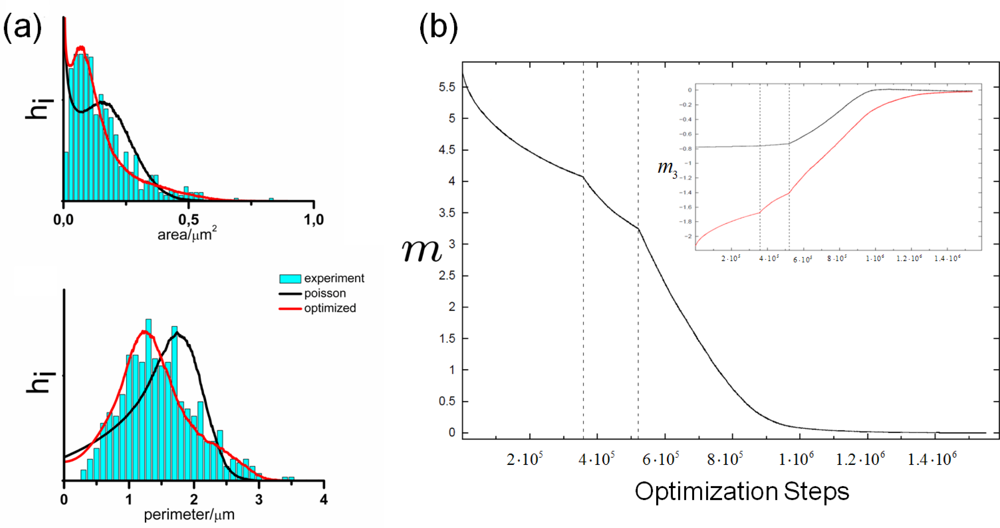
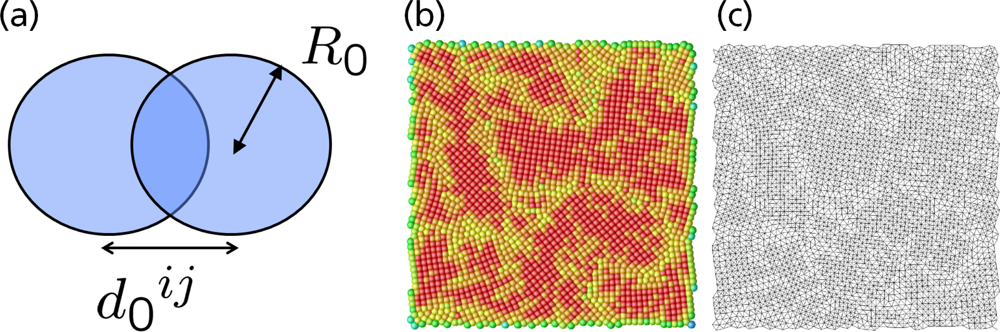
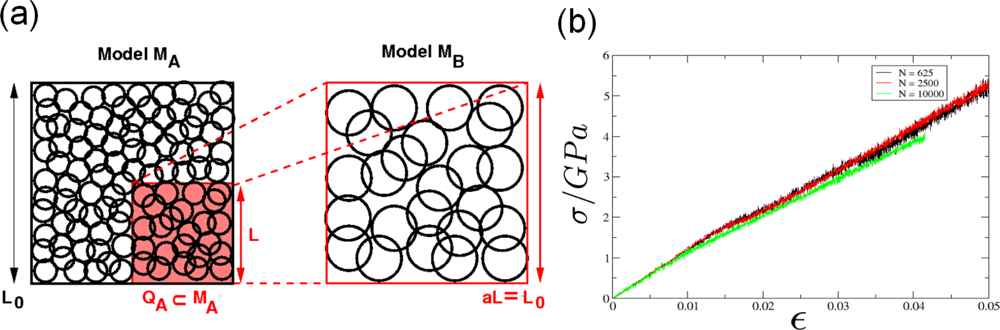
5.1. Modeling Polycrystalline Solids Using Power Diagrams
5.2. A Particle Model for Simulating Shock Wave Failure in Solids
Model Potentials
Strain, Shear and Impact Load
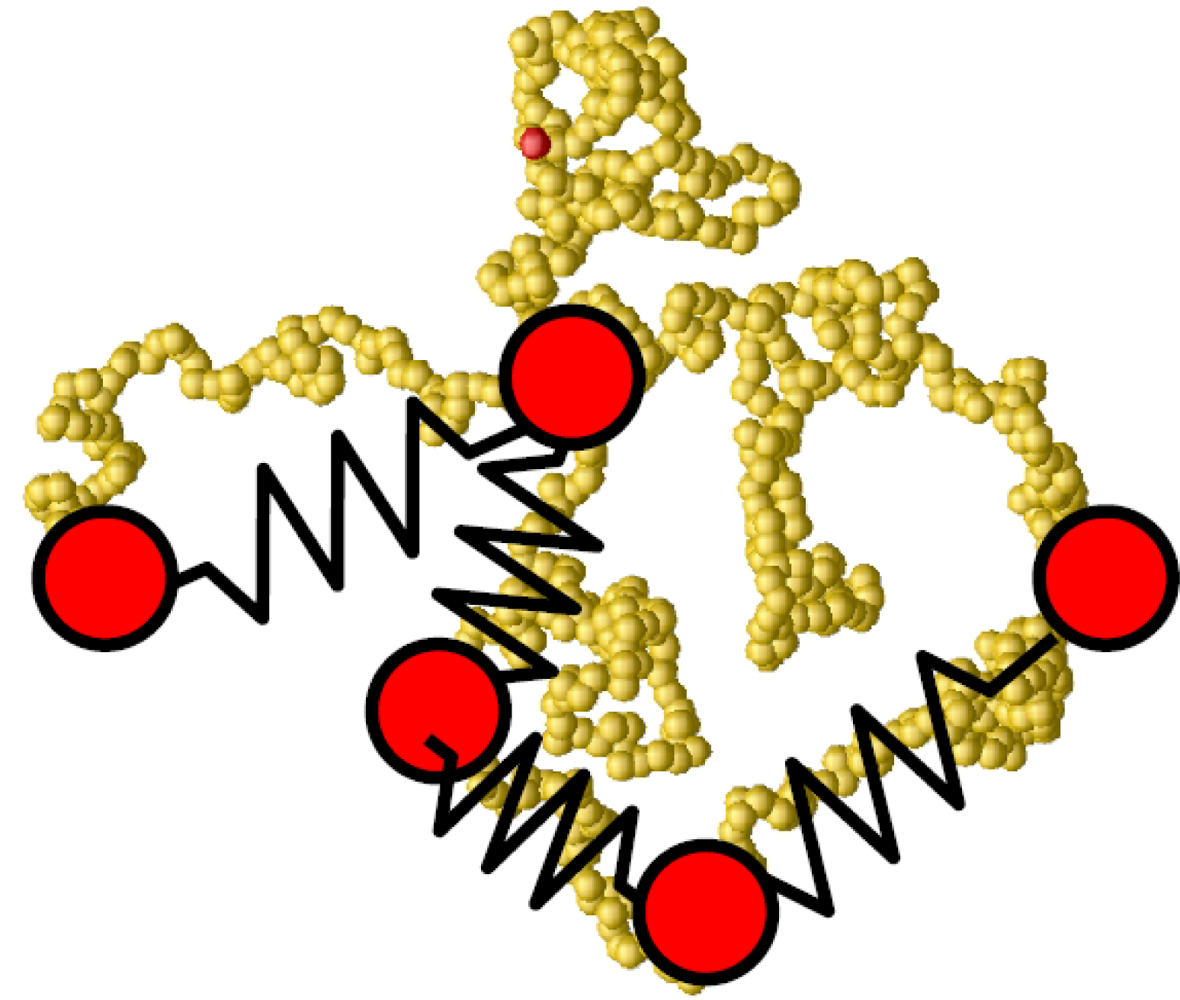
6. Coarse-Grained MD Simulations of Soft Matter: Polymers and Biomacromolecules
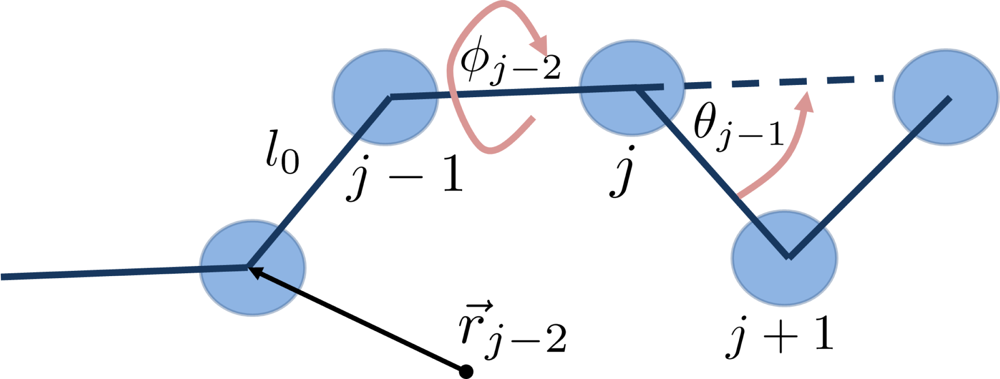
6.1. Coarse-Grained Polymers
- The connectivity of monomers in a chain.
- The topological constraints, e.g., the impenetrability of chain bonds.
- The Flexibility or stiffness of monomer segments.
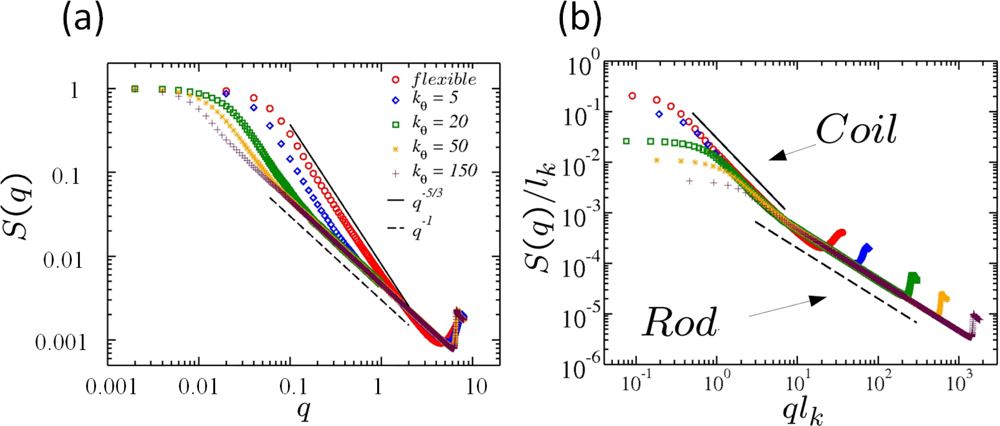
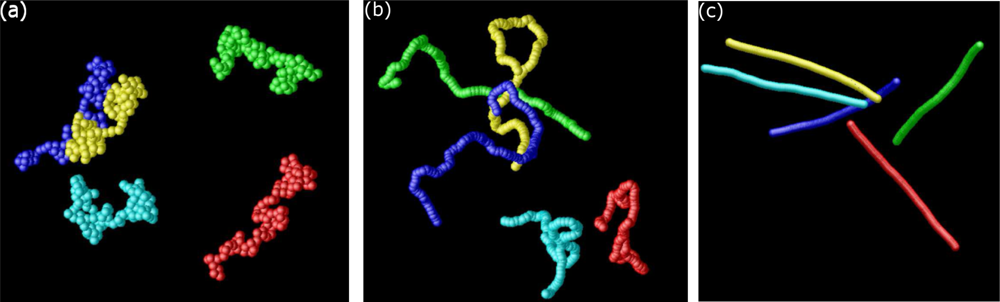
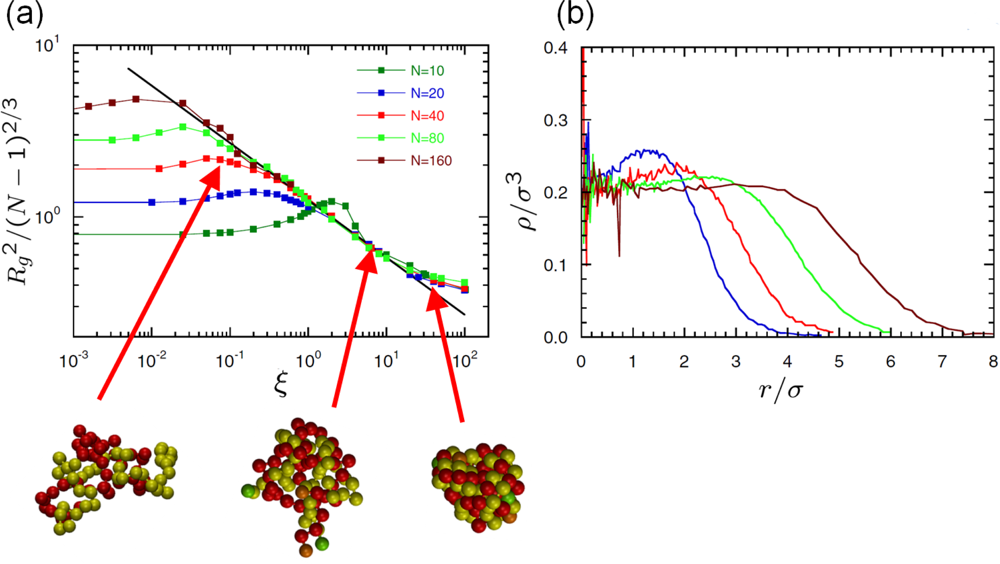
6.2. Scaling of Linear, Branched and Semiflexible Macromolecules
6.3. Polyelectrolytes
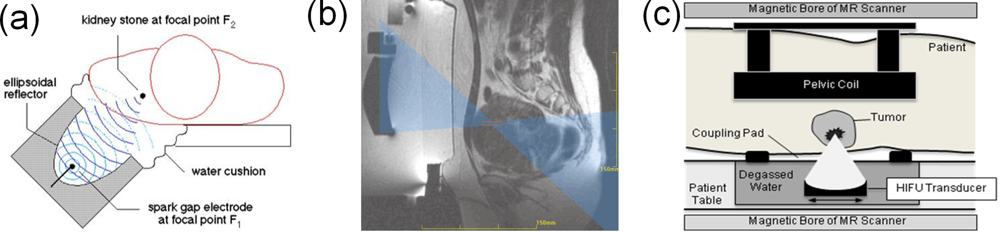
7. Emerging Computational Applications in Biophysics and Medical Tumor Treatment
8. Concluding Remarks
Acknowledgments
References
- Phillips, R. Crystals, Defects and Microstructures—Modeling Across Scales; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Yip, S (Ed.) Handbook of Materials Modeling; Springer: Berlin, Germany, 2005.
- Steinhauser, MO. Computational Multiscale Modeling of Solids and Fluids—Theory and Applications; Springer: Berlin/Heidelberg/New York, Germany/USA, 2008. [Google Scholar]
- Hockney, R; Eastwood, J. Computer Simulation Using Particles; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Ciccotti, G; Frenkel, G; McDonald, I. Simulation of Liquids and Solids; North-Holland: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Hockney, R. The Potential Calculation and Some Applications. Methods Comp. Phys 1970, 9, 136–211. [Google Scholar]
- Allen, M; Tildesly, D. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Liu, GR; Liu, MB. Smoothed Particle Hydrodynamics A Meshfree Particle Method; World Scientific Co. Pte. Ltd: Singapore, 2003. [Google Scholar]
- Gates, T; Odegard, G; Frankland, S; Clancy, T. Computational Materials: Multi-Scale Modeling and Simulation of Nanostructured Materials. Compos. Sci. Technol 2005, 65, 2416–2434. [Google Scholar]
- Steinhauser, M; Kühn, M. Numerical Simulation of Fracture and Failure Dynamics in Brittle Solids. In Anisotropy, Texture, Dislocations, Multiscale Modeling in Finite Plasticity and Viscoplasticity and Metal Forming; Khan, A, Kohei, S, Amir, R, Eds.; Neat Press: Fulton, Maryland, USA, 2006; pp. 634–636. [Google Scholar]
- Finnis, M; Sinclair, J. A Simple Empirical N-Body Potential for Transition Metals. Phil. Mag. A 1984, 50, 45. [Google Scholar]
- Kohn, W; Sham, L. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev 1965, 140, 1133–1138. [Google Scholar]
- Car, R; Parinello, M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett 1985, 55, 2471. [Google Scholar]
- Courant, R. Variational Methods for the Solution of Problems of Equilibrium and Vibrations. Bull. Amer. Math. Soc 1943, 49, 1–23. [Google Scholar]
- Bishop, J; Hill, R. A Theoretical Derivation of the Plastic Properties of a Polycrystalline Face-Centered Material. Philos. Mag 1951, 42, 414–427. [Google Scholar]
- Markenscoff, X; Gupta, A (Eds.) Collected Works of J.D. Eshelby; Springer: New York, NY, USA, 2006.
- Smith, C. Structural Hierarchy in Inorganic Systems; American Elsevier: New York, NY, USA, 1969. [Google Scholar]
- Steinhauser, MO; Grass, K; Thoma, K; Blumen, A. A Nonequilibrium Molecular Dynamics Study on Shock Waves. Europhys. Lett 2006, 73, 62. [Google Scholar]
- Eastman, J; Siegel, R. Nanophase Synthesis Assembles Materials from Atomic Clusters. Res. Develop 1989, 31, 56–60. [Google Scholar]
- Siegel, R; Hahn, H. Nanophase Materials; World Scientific: Singapore, 1987. [Google Scholar]
- Hahn, H; Averback, R. The Production of Nanocrystalline Powders by Magnetron Sputtering. J. Appl. Phys 1990, 67, 1113–1115. [Google Scholar]
- Sawaguchi, A; Toda, K; Nihara, K. Mechanical and Electrical Properties of Silicon Nitride Silicon Carbide Nanocomposite Material. J. Am. Ceram. Soc 1991, 74, 1142–1144. [Google Scholar]
- Krell, A; Blank, P; Ma, H; Hutzler, T. Processing for High-Density Submicrometer Al2O3 for New Applications. J. Am. Ceram. Soc 2003, 86, 546–553. [Google Scholar]
- Buehler, M; Abraham, F; Gao, H. Hyperelasticity Governs Dynamic Fracture at a Critical Length. Nature 2003, 426, 141–146. [Google Scholar]
- Hashin, Z; Shtrickman, S. A Variational Approach to the Theory of the Elastic Behavior of Multiphase Materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar]
- Christensen, R. Mechanics of Composite Materials; John Wiley: New York, NY, USA, 1979. [Google Scholar]
- Ahmed, S; Jones, F. A Review of Particulate Reinforcement Theories for Polymer Composites. J. Mater. Sci 1990, 25, 4933–4942. [Google Scholar]
- Gibson, L; Ashby, M. Cellular Solids; Pergamon Press: Oxford, UK, 1988. [Google Scholar]
- Kadler, K; Holmes, D; Chapman, J. Collagen Fibril Formation. Biochem. J 1996, 316, 1–11. [Google Scholar]
- Gautieri, A; Buehler, MJ; Redaelli, A. Deformation Rate Controls Elasticity and Unfolding Pathway of Single Tropocollagen Molecules. J. Mech. Behav. Biomed. Mater 2009, 2, 130–137. [Google Scholar]
- Wu, DY; Meure, S; Solomon, D. Self-Healing Polymeric Materials: A Review of Recent Developments. Porog. Polym. Sci 2008, 33, 479–522. [Google Scholar]
- Bazant, M; Kaxiras, E. Modeling of Covalent Bonding in Solids by Inversion of Cohesive Energy Curves. Phys. Rev. Lett 1996, 77, 4370–4373. [Google Scholar]
- Abraham, F; Brodbeck, D; Rafey, RA; Rudge, W. Instability Dynamics of Fracture. A Computer Simulation Investigation. Phys. Rev. Lett 1994, 72, 272–275. [Google Scholar]
- Abraham, FF; Brodbeck, D; Rudge, WE; Broughton, JQ; Schneider, D; Land, B; Lifka, D; Gerner, J; Rosenkranz, M; Skovira, J; Gao, H. Ab Initio Dynamics of Rapid Fracture. Model. Simul. Mater. Sci. Eng 1998, 6, 639. [Google Scholar]
- Abraham, F; Broughton, J; Bernstein, N; Kaxiras, E. Spanning the Length Scales in Dynamic Simulation. Comput. Phys 1998, 12, 538. [Google Scholar]
- Cabibbo, N; Iwasaki, Y; Schilling, K. High Performance Computing in Lattice QCD. Parallel Comput 1999, 25, 1197–1198. [Google Scholar]
- Evertz, H. The Loop Algorithm. Adv. Phys 2003, 52, 1–66. [Google Scholar]
- Holm, E; Bateille, C. The Computer Simulation of Microstructural Evolution. JOM-J. Min. Met. Mat. Soc 2001, 53, 20–23. [Google Scholar]
- Sundman, K. Memoire Sur Le Probleme Des Trois Corps. Acta Math 1913, 36, 105–179. [Google Scholar]
- Saari, D. A Visit to the Newtonian N-Body Problem via Elementary Complex Variables. Am. Math. Monthly 1990, 89, 105–119. [Google Scholar]
- Ahrens, J; Brislawn, K; Martin, K; Geveci, B; Law, C; Papka, M. Computer Grafics and Applications. IEEE Comp. Sci. Press 2001, 21, 34–41. [Google Scholar]
- Metropolis, N; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc 1949, 44, 335–341. [Google Scholar]
- Potts, R. Some Generalized Order-Disorder Transformations. Proc. Cambidge Phil. Soc 1952, 48, 106–109. [Google Scholar]
- Metropolis, N; Rosenbluth, A; Rosenblut, M; Teller, A; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys 1953, 21, 1087–1092. [Google Scholar]
- Alder, B; Wainwright, T. Phase Transition for a Hard Sphere System. J. Chem. Phys 1957, 27, 1208–1029. [Google Scholar]
- Alder, B; Wainwright, T. Molecular Dynamics by Electronic Computers. Proceedings of the International Symposium on Transport Processes in Statistical Mechanics, Brussels, Belgium, August 27–31, 1958; Prigogine, I, Ed.; Interscience Publishers, Inc: New York, NY, USA, 1960; pp. 97–131. [Google Scholar]
- Alder, B; Wainwright, T. Phase Transition in Elastic Disks. Phys. Rev 1962, 127, 359–361. [Google Scholar]
- Metropolis, N. The Beginning of the Monte Carlo Method. Los Alamos Science Special Issue 1987, 12, 125–130. [Google Scholar]
- Binder, K. Monte Carlo and Molecular Dynamics Simulations in Polymer Science; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Dünweg, B; Steinhauser, MO; Reith, D; Kremer, K. Corrections to Scaling in the Hydrodynamics of Dilute Polymer Solutions. J. Chem. Phys 2002, 117, 914–924. [Google Scholar]
- Steinhauser, MO. A Molecular Dynamics Study on Universal Properties of Polymer Chains in Different Solvent Qualities. Part I: A Review of Linear Chain Properties. J. Chem. Phys 2005, 122, 094901. [Google Scholar]
- De Gennes, PG. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, London, UK, 1979. [Google Scholar]
- Hartree, D. The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Proc. Cambridge Phil. Soc 1928, 24, 89–132. [Google Scholar]
- Fock, V. Näherungsmethoden zur Lösung des quantenmechanischen Mehrkörperproblems. Z. Physik 1932, 61, 126–148. [Google Scholar]
- Hohenberg, P; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev 1964, 36, 864–871. [Google Scholar]
- Kohn, W. Density Functional and Density Matrix Method Scaling Linearly with the Number of Atoms. Phys. Rev. Lett 1996, 76, 3168–3171. [Google Scholar]
- Slater, J; Koster, G. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev 1954, 94, 1498–1524. [Google Scholar]
- Hammond, M; Lester, W; Reynolds, P (Eds.) Monte Carlo Methods in Ab Initio Quantum Chemistry; World Scientific: Singapore, 1994.
- Nightingale, M; Umrigar, C (Eds.) Quantum Monte Carlo Methods in Physics and Chemistry; Springer: New York, NY, USA, 1999.
- Ballone, P; Andreoni, W. Equilibrium Structures and Finite Temperature Properties of Silicon Microclusters from ab initio Molecular-Dynamics Calculations. Phys. Rev. Lett 1988, 60, 271–274. [Google Scholar]
- Binder, K; Heermann, D. Monte Carlo Simulations in Statistical Physics; Springer Verlag Berlin: Heidelberg/New York/Tokyo, Germany/USA/Japan, 1988. [Google Scholar]
- Binder, K. Applications of Monte Carlo Methods to Statistical Physics. Rep. Progr. Phys 1997, 60, 487. [Google Scholar]
- Steinhauser, M. Computational Methods in Polymer Physics. Recent Res. Devel. Physics 2006, 7, 59–97. [Google Scholar]
- Daw, M; baskes, M. Embedded-Atom Method: Derivation and Application to Impurities, Surfaces, and Other Defects in Metals. Phys. Rev. B 1983, 29, 6443. [Google Scholar]
- Foiles, S; baskes, M; Daw, M. Embedded-Atom-Method Functions for the Fcc Metals Cu, Ag, Au, Ni, Pd, Pt, and Their Alloys. Phys. Rev. B 1986, 33, 7983–7991. [Google Scholar]
- Daw, MS. Model of Metallic Cohesion: The Embedded-Atom Method. Phys. Rev. B 1988, 39, 7441–7452. [Google Scholar]
- Harlow, F. A Machine Calculation Method for Hydrodynamic Problems. . Technical report, Los Alamos Scientific Laboratory: New Mexico, USA, 1955. [Google Scholar]
- Dawson, J. Particle Simulation of Plasmas. Rev. Mod. Phys 1983, 55, 403. [Google Scholar]
- Hoogerbrugge, P; Koelman, J. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys. Lett 1992, 19, 155–160. [Google Scholar]
- Chan, J; Hilliard, J. Free Energy of a Non-Uniform System I: Interfacial Energy. J. Chem. Phys 1958, 28, 258–266. [Google Scholar]
- Wolfram, S. Undecidability and Intractability in Theoretical Physics. Phys. Rev. Lett 1985, 54, 735–738. [Google Scholar]
- Hugh, PM; Asaro, R; Shih, C. Computational Modeling of Metal Matrix Composite Materials-I. Isothermal Deformation Patterns in Ideal Microstructures. Acta Metall. Mater 1993, 41, 1461–1476. [Google Scholar]
- Hugh, PM; Asaro, R; Shih, C. Computational Modeling of Metal Matrix Composite Materials-II. Isothermal Stress-Strain Behavior. Acta Metall. Mater 1993, 41, 1489–1499. [Google Scholar]
- Hugh, PM; Asaro, R; Shih, C. Computational Modeling of Metal Matrix Composite Materials-III. Comparisons with Phenomenological Models. Acta Metall. Mater 1993, 41, 1489–1499. [Google Scholar]
- Hugh, PM; Asaro, R; Shih, C. Computational Modeling of Metal Matrix Composite Materials-IV. Thermal Deformations. Acta Metall. Mater 1993, 41, 1501–1510. [Google Scholar]
- Lucy, L. A Numerical Approach to the Testing of the Fission Hypothesis. Astron. J 1977, 82, 1013. [Google Scholar]
- Gingold, R; Monaghan, J. Kernel Estimates as a Basis for General Particle Method in Hydrodynamics. J. Comp. Phys 1982, 46, 429–453. [Google Scholar]
- Ladd, A. Short-Time Motion of Colloidal Particles—Numerical Simulation via Fluctuating Lattice-Boltzmann Equation. Phys. Rev. Lett 1993, 70, 1339. [Google Scholar]
- Devincre, B. Three Dimensional Stress field Expressions for Straight Dislocation Segments. Solid State Commun 1993, 93, 875–878. [Google Scholar]
- Zhou, S; Preston, D; Lomdahl, P; Beazley, D. Large-Scale Molecular Dynamics Simulations of Dilocation Intersection in Copper. Science 1998, 279, 1525–1527. [Google Scholar]
- Yang, W; Cai, J; Ing, YS; Mach, CC. Transient Dislocation Emission from a Crack Tip. J. Mech. Phys. Solids 2001, 49, 2431–2453. [Google Scholar]
- Cai, W; Arsenlis, A; Weinberger, CR; Bulatov, VV. A Non-Singular Continuum Theory of Dislocations. J. Mech. Phys. Solids 2006, 54, 561–587. [Google Scholar]
- Cundall, P; Strack, O. A Discrete Numerical Model for Granular Assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar]
- Guyon, E; Hulin, JP; Petit, L; Mitescu, CD. Physical Hydrodynamics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Griebel, M. Numerical Simulation in Fluid Dynamics; ; SIAM Monographs on mathematical modeling and computation. Society for Industrial and Applied Mathematics: Philadelphia, USA, 1997. [Google Scholar]
- Chorin, A; Marsden, J. A Mathematical Introduction to Fluid Dynamics; Springer: New York, NY, USA, 1979. [Google Scholar]
- Crank, J; Nicholson, P. A Practical Method for the Numerical Evaluation of Solutions of Partial Differential Equations of the Heat-Conduction Type. Proc. Cambridge Philos. Soc 1947, 43, 50–67. [Google Scholar]
- Bathe, K. Finite Element Procedures in Engineering Analysis; Prentice Hall: Cambridge, Country, 1982. [Google Scholar]
- Benson, D. Computational Methods in Lagrangian and Eulerian Hydrocodes. Comput. Meth. Appl. Meth. Engng 1992, 99, 235. [Google Scholar]
- Belytschko, T; Hughes, T. Computational Methods for Transient Analysis; Elsevier Science Limited: New York, NY, USA, 1983. [Google Scholar]
- Liu, W; Hao, S; Belytschko, T; Li, S; Chang, C. Multiple Scale Meshfree Methods for Damage Fracture and Localization. Comp. Mat. Sci 1999, 16, 1997–2005. [Google Scholar]
- Hiermaier, S. Structures Under Crash and Impact; Springer: New York, NY, USA, 2008. [Google Scholar]
- Cohen, A. Numerical Analysis; McGraw-Hill: London, UK, 1962. [Google Scholar]
- Abramovitz, M; Segun, I. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1964. [Google Scholar]
- Carter, EA. Challenges in Modelling Materials Properties Without Experimental Input. Science 2008, 321, 800–803. [Google Scholar]
- Rambasubramaniam, A; Carter, EA. Coupled Quantum-Atomistic and Quantum-Continuum Mechanics Methods in Materials Research. MRS Bull 2007, 32, 913–918. [Google Scholar]
- Peng, Q; Zhang, X; Hung, L; Carter, EA; Lu, G. Quantum Simulation of Materials at Micron Scales and Beyond. Phys. Rev. B 2008, 78, 054118. [Google Scholar]
- Parinello, M; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys 1981, 52, 7182. [Google Scholar]
- Born, M. Quantenmechanik der Stossvorgänge. Z. Physik 1926, 38, 803–827. [Google Scholar]
- Scherz, U. Quantenmechanik: Eine Einführung mit Anwendungen auf Atome, Moleküle und Festkörper; Teubner: Stuttgart, Leipzig, Germany, 1999. [Google Scholar]
- Kosloff, R. Time-Dependent Quantum-Mechanical Methods For Molecular Dynamics. J. Chem. Phys 1988, 92, 2087–2100. [Google Scholar]
- Laasonen, K; Sprik, M; Parinello, M. “Ab Initio” Liquid Water. J.Chem. Phys 1993, 99, 9080. [Google Scholar]
- Rahman, A. Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev 1964, 136, 405–411. [Google Scholar]
- Marsh, C; Warren, P. Kinetic Thoery For Dissipative Particle Dynamics: The Importance of Collisions. Europhys. Lett 1999, 48, 1–7. [Google Scholar]
- Kschischo, M; Kern, R; Gieger, C; Steinhauser, M; Tolle, R. Automatic Scoring and SNP Quality Assessment Using Accuracy Bounds for FP-TDI SNP Genotyping Data. Applied Bioinformatics 2005, 2, 75–84. [Google Scholar]
- Cleri, F; Yip, S; Wolf, D; Phillpot, S. Atomic-Scale Mechanism of Crack-Tip Plasticity: Dislocation Nucleation and Crack-Tip Shielding. Phys. Rev. Lett 1997, 79, 1309–1312. [Google Scholar]
- Komanduri, R; Chandrasekaran, N; Raff, LM. Molecular Dynamic Simulations of Uniaxial Tension at Nanoscale of Semiconductor Materials for Micro-Electro-Mechanical Systems (MEMS) Applications. Mater. Sci. Eng., A 2003, 340, 58–67. [Google Scholar]
- Li, S; Liu, WK. Meshfree and Particle Methods and Their Applications. Appl. Mech. Rev 2002, 55, 1–34. [Google Scholar]
- Hrennikoff, H. Solutions of Problems in Elasticity by the Framework Method. J. Appl. Mech. A 1941, 8, 169–175. [Google Scholar]
- Monaghan, J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys 1992, 30, 543–574. [Google Scholar]
- Liberski, L; Petschek, A; Carney, T; Hipp, J. High Strain Lagrangian Hydrodynamics. J. Comput. Phys 1993, 109, 67–75. [Google Scholar]
- Liberski, LD; Petschek, A. Smoothed Particle Hydrodynamics with Strength of Materials. In The Next Language Conference; Springer: New York, NY, USA, 1991; pp. 248–257. [Google Scholar]
- Kadau, K; Germann, T; Lomdahl, P. Large-Scale Molecular Dynamics Simulation of 19 Billion Particles. J. Modern. Phys. C 2004, 15, 193–201. [Google Scholar]
- Voter, A; Montelenti, F; Germann, T. Extending the Time Scale in Atomistic Simulations of Materials. Annu. Rev. Mater. Res 2002, 32, 321–346. [Google Scholar]
- Darden, T; York, D; Pedersen, L. Particle Mesh Ewald: An N-log N Method for Sums in Large Systems. J. Chem. Phys 1993, 103, 8577–8592. [Google Scholar]
- Essmann, U; Perera, L; Berkowitz, M; Darden, T; Lee, H; Pedersen, L. A Smooth Paritcle Mesh Ewald Potential. J. Chem. Phys 1995, 103, 8577–8592. [Google Scholar]
- van Gunsteren, W; Berendsen, H. Algorithms for Brownian Dynamics. Molec. Phys 1982, 45, 637. [Google Scholar]
- Schutz, C; Warshel, A. What are the Dielectric Constants of Proteins and How to Validate Electrostatic Models? Proteins 2001, 44, 400–417. [Google Scholar]
- Warshel, A; Sharma, P; Kato, M; Parson, W. Modeling Electrostatic Effects in Proteins. Biochim. Biophys. Acta Mater 2006, 1764, 1647–1676. [Google Scholar]
- Freddolino, PL; Liu, F; Gruebele, M; Schulten, K. Ten-Microsecond Molecular Dynamics Simulation of a Fast-Folding WW Domain. Biophys. J 2008, 94, L75–L77. [Google Scholar]
- Freddolino, PL; Park, S; Roux, B; Schulten, K. Force Filed Bias in Protein Folding Simulations. Biophys. J 2009, 96, 3772–3780. [Google Scholar]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev 1967, 159, 1098–1003. [Google Scholar]
- Verlet, L. Computer Experiments on Classical Fluids. II. Equilibrium Correlation Functions. Phys. Rev 1968, 159, 201. [Google Scholar]
- Weeks, J; Chandler, D; Andersen, H. Role of Repulsive Forces in Forming the Equilibrium Structure of Simple Liquids. J. Chem. Phys 1971, 54, 5237–5247. [Google Scholar]
- Rahman, A; Stillinger, F. Molecular Dynamics Study of Liquid Water. Phys. Rev 1971, 55, 3336. [Google Scholar]
- Parinello, M; Rahman, A. Crystal Structure and Pair Potentials: A Molecular-Dynamics Study. Phys. Rev. Lett 1980, 45, 1196–1199. [Google Scholar]
- Hoover, W. Molecular Dynamics; Springer Verlag: Berlin/New York, Germany/USA, 1986. [Google Scholar]
- Maitland, G; Rigby, M; Smith, E; Wakeham, W. Intermolecular Forces - Their Origin and Determination; Clarendon Press: Oxford, UK, 1981. [Google Scholar]
- Hobza, P; Zahradnik, R. Weak Intermolecular Interactions in Chemistry and Biology; Academia: Prague, Czechoslovakia, 1980. [Google Scholar]
- Jackson, JD. Classical Electrodynamics; John Wiley & Sons, Inc: New York, NY, USA, 1975. [Google Scholar]
- Daune, M. Moleckulare Biophysik; Vieweg Verlag: Braunschweig, Wiesbaden, Germany, 1997. [Google Scholar]
- Haberland, R; Fritsche, S; Peinel, G; Heinzinger, K. Molekulardynamik—Grundlagen und Anwendungen; Friedrich VIeweg & Sohn Verlagsgesellschaft mbH: Braunschweig, Wiesbaden, Germany, 1995. [Google Scholar]
- Buckingham, R. The Classical Equation of State of Gaseous Helium, Neon and Argon. Proc. Roy. Soc 1938, A106, 264. [Google Scholar]
- Shih, AY; Arkhipov, A; Freddolino, PL; Schulten, K. Coarse Grained Protein-Lipid Model with Application to Lipoprotein Particles. J. Phys. Chem. B 2006, 110, 3674–3684. [Google Scholar]
- Schlenkrich, M; Brinckmann, J; MacKerell, A; Karplus, M. Empirical Potential Energy Function for Phospholipids: Criteria for Parameter Optimization and Applications; Birkhäuser: Boston, MA, USA, 1996. [Google Scholar]
- Feller, S. An Improved Empirical Potential Energy Function for Molecular Simulations of Phospholipids. J. Phys. Chem. B 2000, 104, 7510–7515. [Google Scholar]
- Siu, SWI; Vácha, R; Jungwirth, P; Böckmann, RA. Biomolecular Simulations of Membranes: Physical Properties from Different Force Fields. J. Chem. Phys 2008, 125, 125103. [Google Scholar]
- Horowitz, E; Sahni, S; Rajasekaran, S. Computer Algorithms; Computer Science Press: New York, NY, USA, 1998. [Google Scholar]
- Axilrod, B; Teller, E. Interaction of the van der Waals Type between Three Atoms. J. Chem. Phys 1943, 11, 299. [Google Scholar]
- Amdahl, G. Validity of the Single Processor Approach to Achieve Large Scale Computing Capabilities. AFIPS Spring Computer Conference, Atlantic City, NJ, USA, April 18–20, 1967; 30, pp. 483–485.
- Riemann, B. Über die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen 1860, 8, 43–65. [Google Scholar]
- von Neumann, J. A Method for the Numerical Calculation of Hydrodynamic Shocks. J. Appl. Phys 1950, 21, 232–237. [Google Scholar]
- Godunov, S. A Difference Method for Numerical Calculation of Discontinuous Solutions of the Equations of Hydrodynamics. Math. Sb 1959, 47, 271–306. [Google Scholar]
- Rankine, W. On the Thermodynamic Theory of Waves of Finite Longitudinal Disturbances. Phil Trans 1870, 160 II, 277–288. [Google Scholar]
- Hugoniot, P. Sur la propagation du mouvement dans les corps et plus specialement dans les gaz parfaits - i. Journal de l’Ecole Polytechnique 1887, 57, 3–97. [Google Scholar]
- Hugoniot, P. Sur la propagation du mouvement dans les corps et plus specialement dans les gaz parfaits - ii. Journal de l’Ecole Polytechnique 1889, 58, 1–125. [Google Scholar]
- Asay, JR; Kerley, G. The Response of Materials to Dynamic Loading. Int. J. Imp. Eng 1987, 5, 69. [Google Scholar]
- Davison, L; Graham, R. Shock Compression of Solids. Phys. Rep 1979, 55, 257. [Google Scholar]
- Knudson, M. Shock Wave Science and Technology Reference Library; Solids I; Springer: New York, NY, USA, 2007. [Google Scholar]
- Bethe, H. Classic Papers in Shock Compression Science; Springer: New York, NY, USA, 1942. [Google Scholar]
- Chen, M; McCauley, J; Hemker, K. Shock-Induced Localized Amorphization in Boron Carbide. Science 2003, 299, 1563–1566. [Google Scholar]
- Steinhauser, MO; Grass, K. Failure and Plasticity Models of Ceramics—A Numerical Study. The 11th Int. Symposium on Plasticity and Current Applications, (PLASTICITY 2005), Kauai, Hawaii, January 03–08, 2005, In Dislocations, Plasticity, Damage and Metal Forming: Materials Response and Multiscale Modeling; Khan, A, Kohei, S, Amir, R, Eds.; Neat Press: Fulton, MD, USA, 2005; pp. 370–373. [Google Scholar]
- Krell, A; Blank, P; Ma, H; Hutzler, T; van Bruggen, MP; Apetz, R. Transparent Sintered Corundum with High Hardness and Strength. J. Am. Ceram. Soc 2003, 1, 12–18. [Google Scholar]
- Bringa, EM; Caro, A; Wang, Y; Victoria, M; McNaney, JM; Remington, BA; Smith, RF; Torrala, BR; Swygenhoven, HV. Ultrahigh Strength in Nanocrastalline Materials under Shock Loading. Science 2005, 309, 1838–1841. [Google Scholar]
- Lauridsen, E. Approaches for 3D Materials Characterization. JOM 2006, 58, 12. [Google Scholar]
- Lewis, A; Suh, S; Stukowski, M; Geltmacher, A; Spanos, G; Rajan, K. Quantitative Analysis and Feature Recognition in 3D Microstructural Data Sets. JOM 2006, 12, 51. [Google Scholar]
- Descartes, R. Principia Philosophiae; Ludovicus Elzevirus: Amsterdam, The Netherlands, 1644. [Google Scholar]
- Dirichlet, G. Über die Reduktion der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen. J. Reine und Angew. Math 1850, 40, 209–227. [Google Scholar]
- Voronoi, G. Nouvelles applications des paramétres continus à la théorie des formes quadratiques. deuxième Mèmoire: Recherches sur les parallélloèdres primitifs. J. Reine und Angew. Math 1908, 134, 198–287. [Google Scholar]
- Delaunay, B. Sur la sphére vide. A la memoire de Georges Voronoi. Izv. Akad. Nauk SSSP, Otdelenie Mathematicheskih i Estestvennyh Nauk 1934, 7, 793–800. [Google Scholar]
- Stoyan, D; Kendall, WS; Mecke, J. Stochastic Geometry and its Applications; Wiley: Chichester, UK, 1987. [Google Scholar]
- Gosh, S; Yunshan, L. Voronoi Cell Finite Element Model Based on Micropolar Theory of Thermoelasticity for Heterogeneous Materials. Int. J. Num. Meth. Eng 1995, 38, 1361–1368. [Google Scholar]
- Espinosa, H; Lee, S. Modeling of Ceramic Microstructures: Dynamic Damage Initiation and Evolution. In CP505, Shock Compression of Condensed Matter; Furnish, MD, Chhabildas, LC, Hixson, RS, Eds.; American Institute of Physics: Melville, NY, USA, 1999. [Google Scholar]
- Shamos, M; Hoey, D. Closest-Point Problems. In Proc 16th Annu IEEE Sympos Found Comput Sci; IEEE Computer Society Press: Los Angelos, 1975; pp. 151–162. [Google Scholar]
- Okabe, A; Boots, B; Sugihara, K. Spatial Tesselations - Concepts and Applications of Voronoi Diagrams; John Wiley & Sons: Chichester, West Sussex, England, 1992. [Google Scholar]
- Aurenhammer, F. Power Diagrams: Properties, Algorithms and Applications. SIAM J. Comput 1987, 16, 78–96. [Google Scholar]
- Zhang, KS; Wu, MS; Feng, R. Simulation of Microplasticity-Induced Deformation in Uniaxially Strained Ceramics by 3-D Voronoi Polycrystal Modeling. Int. J. Plasticity 2005, 21, 801–834. [Google Scholar]
- Kühn, M; Steinhauser, MO. Modelling and Simulation of Microstrucutres Using Power Diagrams: Proof of the Concept. Appl. Phys. Lett 2008, 93, 1–3. [Google Scholar]
- Steinhauser, MO; Kühn, M. Anisotropy, Texture, Dislocations, Multiscale Modeling in Finite Plasticity and Viscoplasticity and Metal Forming; Neat Press: Maryland, USA, 2006; ; chapter Numerical Simulation of Fracture and Failure Dynamics in Brittle Solids, pp. 634–636. [Google Scholar]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech 1951, 18, 293–297. [Google Scholar]
- Zavattieri, PD; Espinoza, HD. An Examination if the Competition between Bulk Behavior and Interfacial Behavior of Ceramics Subjected to Dynamics Pressure-Shear Loading. J. Mech. Phys. Solids 2003, 51, 607. [Google Scholar]
- Steinhauser, M; Kühn, M. Modeling of Shock-Wave Failure in Brittle Materials. 3rd Intl Conference on Multiscale Materials Modeling (MMM), Freiburg, Germany, September 18–22, 2006, In MMM Multiscale Materials Modeling; Gumbsch, P, Ed.; Fraunhofer IRB Verlag: Stuttgart, Germany, 2006; pp. 380–382. [Google Scholar]
- Xu, XP; Needleman, A. Numerical Simulations of Dynamics Interfacial Crack Growth Allowing for Crack Growth away from the Bond Line. Int. J. Fracture 1995, 74, 253. [Google Scholar]
- D’Addetta, GA; Kun, F; Ramm, E. On the Application of a Discrete Model to the Fracture Process of Cohesive Granular Materials. Granul. Matter 2002, 4, 77. [Google Scholar]
- Zhou, SJ; Beazley, DM; Lomdahl, PS; Holian, BL. Large-Scale Molecular Dynamics Simulations of Three-Dimensional Ductile Fracture. Phys. Rev. Lett 1997, 78, 479. [Google Scholar]
- Fineberg, J; Gross, SP; Marder, M; Swinney, HL. Instability in the Propagation of Fast Cracks. Phys. Rev. B 1992, 45, 5146–5154. [Google Scholar]
- Marder, M. New Dynamical Equation for Cracks. Phys. Rev. Lett 1991, 66, 2484–2487. [Google Scholar]
- Abraham, FF. Unstable Crack Mtion is Predictable. J. Mech. Phys. Solids 2004, 53, 1071–1078. [Google Scholar]
- Abraham, FF; Gao, H. How Fast Can Cracks Propagate? Phys. Rev. Lett 2000, 84, 3113. [Google Scholar]
- Buehler, MJ; Gao, H. Dynamical Fracture instabilities Due to Local Hyperelasticity at Crack Tips. Nature 2006, 439, 307–310. [Google Scholar]
- Holland, D; Marder, M. Cracks and Atoms. Adv. Mater 1999, 11, 793–806. [Google Scholar]
- Bulatov, V; Abraham, F; Kubin, L; Devrince, B; Yip, S. Connecting Atomistic and Mesoscale Simulations of Crystal Plasticity. Nature 1998, 391, 669–672. [Google Scholar]
- Bulatov, VV; Hsiung, LL; Tang, M; Arsenlis, A; Bartelt, MC; Cai, W; Florando, JN; Hirtani, M; Rhee, M; Hommes, G; Pierce, TG; de la Rubia, T. Dilocation Multi-Junctions and Strain Hardening. Nature 2006, 440, 1174–1178. [Google Scholar]
- Sharon, E; Fineberg, J. Conifrming the Continuum Theory of Dynamic Brittle Fracture for Fast Cracks. Natrue 1998, 397, 333–335. [Google Scholar]
- Abraham, FF. The Atomic Dynamics of Fracture. J. Mech. Phys. Solids 2001, 49, 2095–2111. [Google Scholar]
- Abraham, FF. Dynamics of Brittle Fracture With Variable Elasticity. Phys. Rev. Lett 1996, 77, 869–872. [Google Scholar]
- Abraham, FF. Spanning the Continuum to Quantum Length Scales in a Dynamic Simulation of Brittle Fracture. Europhys. Lett 1998, 44, 783–787. [Google Scholar]
- Gross, SP; Fineberg, J; Marder, M; McCormick, WD; Swinney, HL. Acoustic Emissions from Rapidly Moving Cracks. Phys. Rev. Lett 1993, 71, 3162. [Google Scholar]
- Holian, B; Lomdahl, P. Plasticity Induced by Shock-Waves in Nonequilibrium Molecular-Dynamics Simulations. Science 1998, 280, 2085. [Google Scholar]
- Holian, B. Molecular Dynamics Comes of Age for Shock Wave Research. Shock Waves 2004, 13, 489–495. [Google Scholar]
- van Swygenhoven, H; Derlet, P; Feichtinger, D; Hasnaoui, A; Samaras, M. Atomistic Simulations in Nanocrystalline Materials. . Technical report, EPFL Supercomputing Review, Ecole Polytechnique Fédéral Lausanne: Lausanne, Switzerland, 2002. [Google Scholar]
- Abraham, FF; Walkup, R; Gao, H; Duchaineau, M; Rubia, TDDL; Seager, M. Simulating Materials Failure by Using up to One Billion Atoms and the World’s Fastest Computer: Brittle Fracture. Proc. Natl. Acad. Sci. USA 2002, 99, 5777–5782. [Google Scholar]
- Gao, H; Huang, Y; Abraham, F. Continuum and Atomistic Studies of Intersonic Crack Propagation. J. Mech. Phys. Solids 2001, 49, 2113–2132. [Google Scholar]
- Buehler, M; Hartmaier, A; Gao, H; Duchaineau, M; Abraham, F. Atomic Plasticity: Description and Analysis of a One-Billion Atom Simulation of Ductile Materials Failure. Comput. Methods Appl. Engrg 2004, 193, 5257–5282. [Google Scholar]
- Steinhauser, MO; Grass, K; Strassburger, E; Blumen, A. Impact Failure of Granular Materials—Non-Equilibrium Multiscale Simulations and High-Speed Experiments. Int. J. Plasticity 2009, 25, 161–182. [Google Scholar]
- Walton, OR; Braun, RL. Viscosity, Granular-Temperature, and Stress Calculation for Shearing Assemblies of Inelastic, Frictional Disks. J. Rheol 1986, 39, 949. [Google Scholar]
- Gröger, T; Tüzün, U; Heyes, DM. Modeling and Measuring of Cohesion in Wet Granular Materials. Powder Technol 2003, 133, 203. [Google Scholar]
- Leszczynski, JS. A Discrete Model of a Two-Particle Contact Applied to Cohesive Granular Materials. Granul. Matter 2003, 5, 91. [Google Scholar]
- Kadau, K. Molekulardynamik-Simulationen von strukturellen Phasenumwandlungen in Festkörpern, Nanopartikeln und ultradünnen Filmen, . PhD thesis, Gerhard-Mercator-University: Duisburg, Germany, 2001.
- Kadau, K; Bartels, G; Brendel, L; Wolf, DE. Contact Dynamics Simulations of Compacting Cohesive Granular Systems. Comp. Phys. Comm 2002, 147, 190. [Google Scholar]
- Sadd, MH. Contact Law Effects on Wave-Propagation in Particulate Materials Using Discrete Element Modelling. J. Non-Linear Mech 1993, 28, 251. [Google Scholar]
- Arias, I; Knap, J; Pandolfi, A; Ortiz, M. Massively Parallel Simulations of Dynamic Fracture and Fragmentation of Brittle Solids. XXI ICTAM, Warsaw, Poland, 15–21 August 2004; 2004. [Google Scholar]
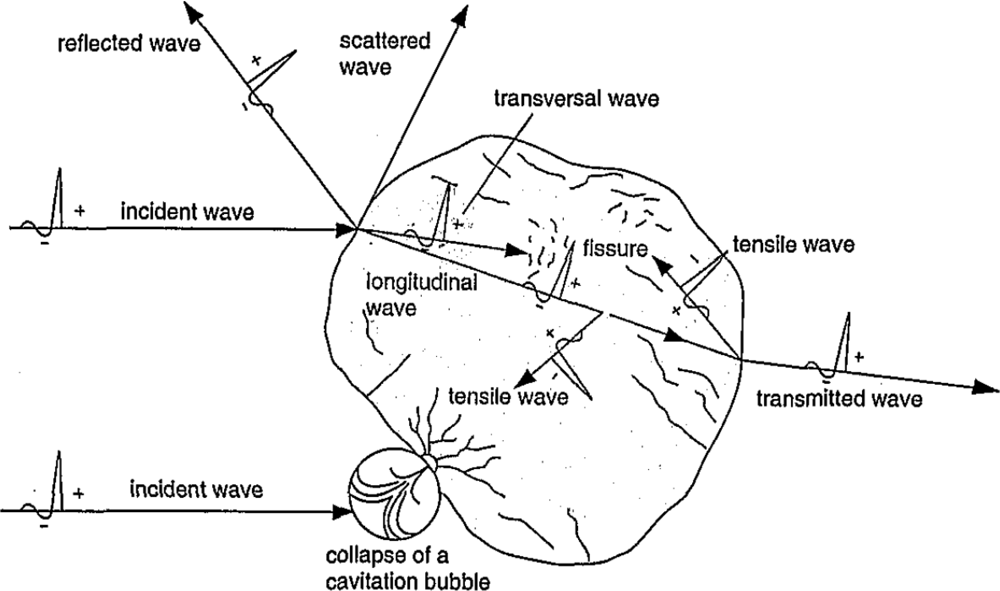
- Brendel, W. Shock Waves: A New Physical Principle in Medicine. Eur. surg. Res 1986, 18, 177–180. [Google Scholar]
- Wang, CJ. An Overview of Shock-Wave Therapy in Musculoskeletal Disorders. Med. J 2003, 26, 220–230. [Google Scholar]
- Rubinstein, M; Colby, RH. Polymer Physics; Oxford University Press: Oxford, NY, USA, 2003. [Google Scholar]
- Phillips, R; Lax, P. Scattering Theory; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Chu, B; Xu, R; Zuo, J. Transition of Polystyrene in Cyclohexane from Theta to the Collapsed State. Macromolecules 1988, 21, 273–274. [Google Scholar]
- Steinhauser, MO; Schneider, J; Blumen, A. Simulating Dynamic Crossover Behavior of Semiflexible Linear Polymers in Solution and in the Melt. J. Chem. Phys 2009, 130, 164902. [Google Scholar]
- Binder, K. Monte Carlo Methods in Condensed Matter Physics; Springer: Berlin, Germany, 1992; ; Topics Applied Physics. [Google Scholar]
- Prince, E; Rouse, J. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys 1953, 21, 1281–1286. [Google Scholar]
- Zimm, BH. Dynamics of Polymer Molecules in Dilute Solution: Viscoelasticity, Flow Birefringence and Dielectric Loss. J. Chem. Phys 1956, 24, 269–278. [Google Scholar]
- Doi, M; Edwards, S. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Bustamante, C; Marko, J; Siggia, E; Smith, S. Entropic Elasticity of Lambda-Phage DNA. Science 1994, 265, 1599–1600. [Google Scholar]
- Ober, CK. Shape Persistence of Synthetic Polymers. Science 2000, 288, 448–449. [Google Scholar]
- Manning, G. Limiting Laws and Counterion Condensation in Polyelectrolyte Solutions I. Colligative Properties. J. Chem. Phys 1969, 51, 924–933. [Google Scholar]
- Ramirez, ER. Purification of Industrial Waste Waters by Flotation. US Patent No. 3975269 1976. [Google Scholar]
- Flory, P. Statistical Mechanics of Chain Molecules; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Debye, P; Hückel, E. The Theory of Electrolytes. I. Lowering of Freezing Point and Related Phenomena. Physikalische Zeitschrift 1923, 24, 185–206. [Google Scholar]
- Barrat, JL; Joanny, F. Theory of Polyelectrolyte Solutions. Adv. Chem. Phys 2007, 94, 1–66. [Google Scholar]
- Khoklov, AR; Khalatur, PG. Solution Properties of Charged Hydrophobic/Hydrophilic Copolymers. Curr. Opin. Colloid Interface Sci 2005, 10, 22–29. [Google Scholar]
- Holm, C; Joanny, JP; Kremer, K; Netz, R; Reineker, P; Seidel, C; Vilgis, TA; Winkler, RG. Polyelectrolyte Theory. Adv. Polym. Sci 2004, 166, 67–111. [Google Scholar]
- Steinauser, MO. Molekulardynamik-Simulationen von Polyelectrolyten unterschiedlicher Ladungsdichte: Polyelektrolyt-Komplexbildung. . Master’s thesis. University of Ulm: Ulm, Germany, 1998. [Google Scholar]
- Winkler, RG; Steinhauser, MO; Reineker, P. Complex Formation in Systems of Oppositely Charged Polyelectrolytes: A Molecular Dyamics Simulation Study. Phys. Rev. E 2002, 66, 021802. [Google Scholar]
- Yamasaki, Y; Teramoto, Y; Yoshikawa, K. Disappearance of the Negative Charge in Giant DNA with a Folding Transition. Biophys. J 2001, 80, 2823–2832. [Google Scholar]
- Gössl, I; Shu, L; Schlüter, A; Rabe, J. Complexes of DNA and Positively Charged Dendronized Polymers. J. Am. Chem. Soc 2002, 124, 6860. [Google Scholar]
- Srivastava, D; Muthukumar, M. Interpenetration of Interacting Polyelectrolytes. Macromolecules 1994, 27, 1461–1465. [Google Scholar]
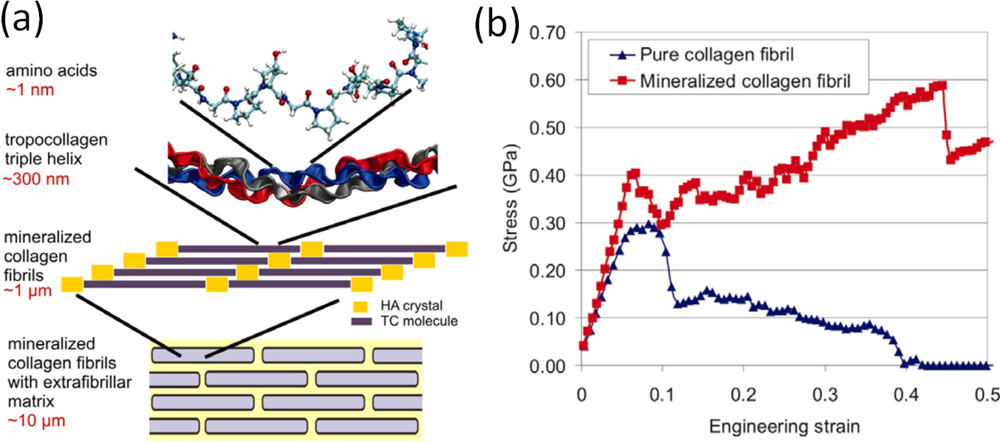
- Buehler, MJ. Molecular Nanomechanics of Nascent Bone: Fibrillar Toughening by Mineralization. Nanotechnology 2007, 18, 295102. [Google Scholar]
- Stolarska, MA; Kim, Y; Othmer, HG. Multi-Scale Models of Cell and Tissue Dynamics. Phil. Trans. R. Soc. A 2009, 367, 3525–3553. [Google Scholar]
- Cowin, SC; Gailani, G; Benalla, M. Hierarchical Proelasticity: Movement of Interstitial Fluid between Porosity Levels in Bones. Phil. Trans. R. Soc. A 2009, 367, 3401–3444. [Google Scholar]
- Hindley, J; Gedyc, WM; Regan, L; Steward, E; Hynnen, K; Macdanold, N; Inbar, Y; Itzchak, Y; Rabinovici, J; Kim, K; Geschwind, JF; Hesley, G; Gostout, B; Ehrenstein, T; Hengst, S; Sklair-Levy, M; Shushan, A; Jolesz, F. MRI Guidance of Focused Ultrasound Therapy of Uterine Fibrosis: Early Results. AJR 2004, 183, 1713–1719. [Google Scholar]
- Tempany, CMC; Steward, EA; McDannold, N; QUade, BJ; Jolesz, FA; Hynynen, K. MR Imaging—Guided Focused Ultrasound Surgery of Uterine Leiomyomas: A Feasibility Study. Radiology 2002, 226, 897–905. [Google Scholar]
- Brendel, W; Chaussy, C; Forssmann, B; Schmiedt, E. A New Method of Non-Invasive Destruction of Renal Calculi by Shock Waves. Br. J. Surg 1979, 66, 12. [Google Scholar]
- Gerdesmeyer, L; Wagenpfeil, S; Haake, M. Extracoporeal Shock Wave Therapy For The Treatment of Chronic Calcifying Lendonitis of the Rotator Cuff: A Randomized Controlled Trial. JAMA 2003, 290, 2573–2580. [Google Scholar]
- Gerdesmeyer, L; von Eiff, C; Horn, C; Henne, M. Antibacterial Effects of Extracorporeal Shock Waves. Ultrasound Med. Biol 2005, 31, 115–119. [Google Scholar]
- Thiel, M. Application of Shock Waves in Medicine. Clin. Orthop. Related Res 2001, 387, 18–21. [Google Scholar]
- Krause, H. Extrakorporale Stosswellentherapie; Chapman & Hall GmbH: Weinheim, Germany, 1997; pp. 15–34. [Google Scholar]
- .












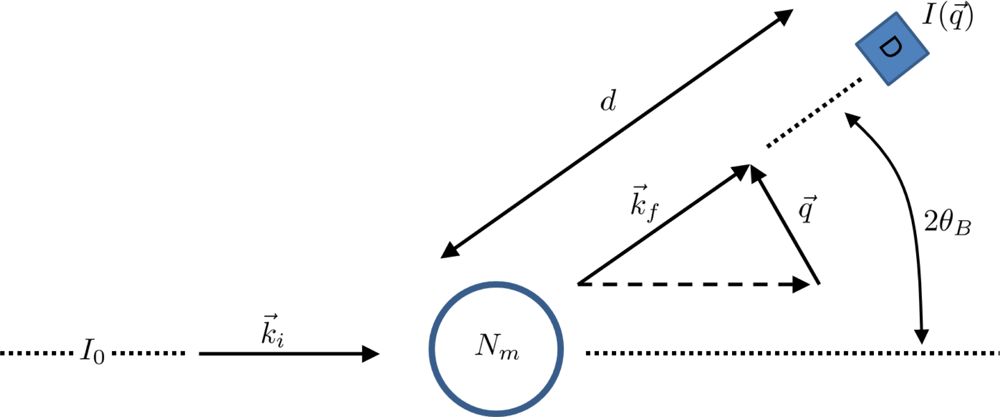
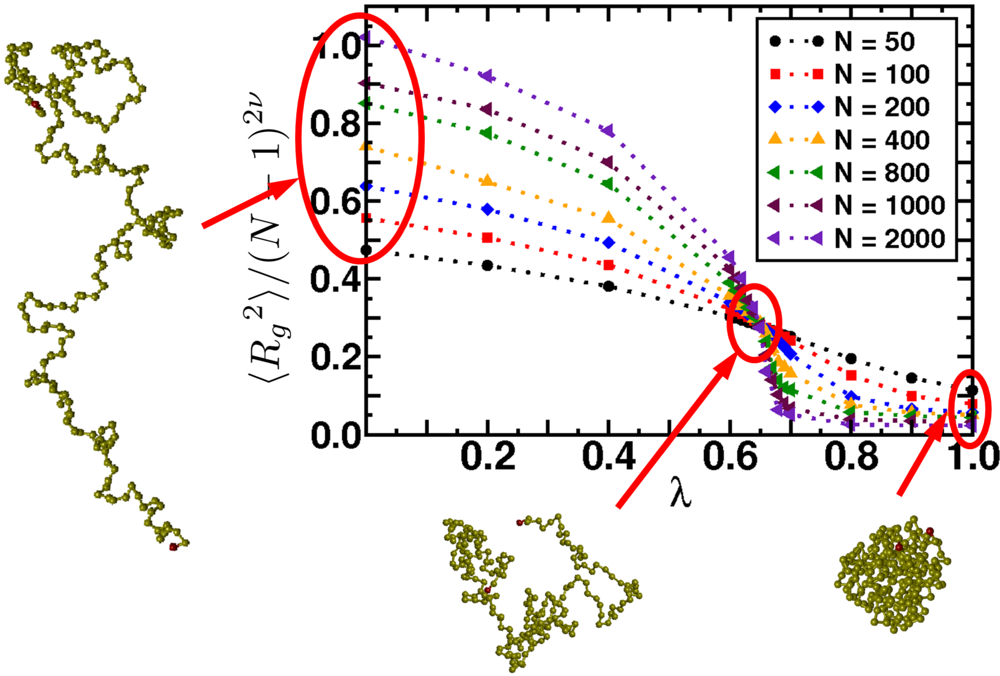
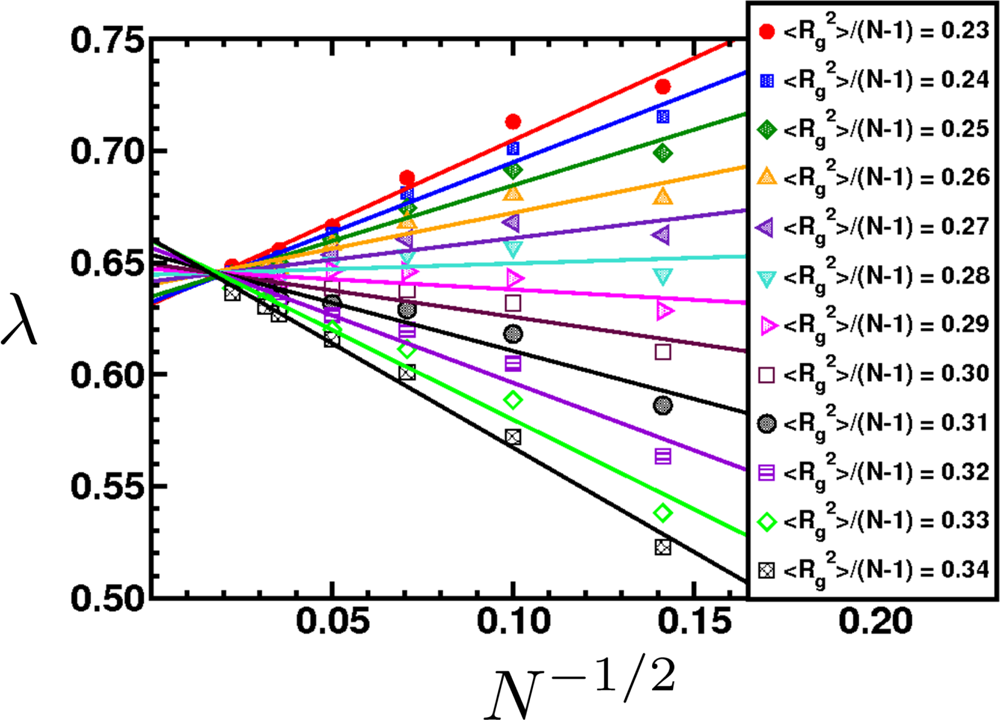

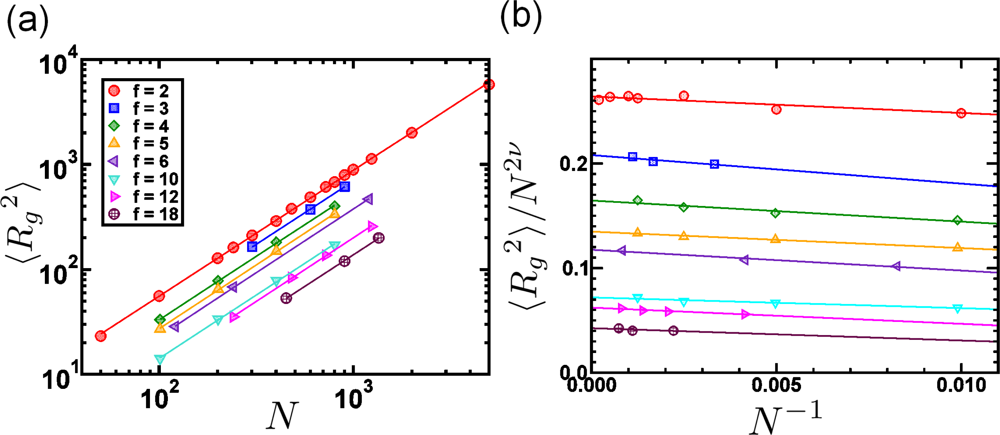

| Scale (m) | Typical Simulation Methods | Typical Applications |
|---|---|---|
| Electronic/Atomistic | ||
| ∼ 10−12 – 10−9 | Self-Consistent Hartree-Fock (SC-HF) [53,54] | crystal ground states, NMR, IR, UV spectra, molecular geometry, electronic properties, chemical reactions |
| ∼ 10−12 – 10−9 | Self-Consistent DFT [12,55,56] | |
| ∼ 10−12 – 10−9 | Car-Parinello (ab initio) Molecular Dynamics [13] | |
| ∼ 10−12 – 10−9 | Tight-Binding [57] | |
| ∼ 10−12 – 10−9 | Quantum Monte Carlo (QMC) [58–60] | |
| Atomistic/Microscopic | ||
| ∼ 10−9 – 10−6 | Molecular Dynamics [45,46] | equations of state, Ising model, DNA polymers, rheology, transport properties, phase equilibrium, |
| ∼ 10−9 – 10−6 | Monte Carlo using classical force fields [42,44] | |
| ∼ 10−9 – 10−6 | Hybrid MD/MC [61–63] | |
| ∼ 10−9 – 10−6 | Embedded Atom Method [64–66] | |
| ∼ 10−9 – 10−6 | Particle in Cell [67,68] | |
| Microscopic/Mesoscopic | ||
| ∼ 10−8 – 10−1 | MD and MC using effective force fields [51] | complex fluids, soft matter, granular matter, fracture mechanics, grain growth, phase transformations, polycrystal elasticity, polycrystal plasticity, diffusion, interface motion, dislocations, grain boundaries |
| ∼ 10−9 – 10−3 | Dissipative Particle Dynamics [69] | |
| ∼ 10−9 – 10−3 | Phase Field Models [70] | |
| ∼ 10−9 – 10−3 | Cellular Automata [71] | |
| ∼ 10−9 – 10−4 | Mean Field Theory | |
| ∼ 10−6 – 102 | Finite Element Methods including microstructural features [72–75] | |
| ∼ 10−6 – 102 | Smooth Particle Hydrodynamics [76,77] | |
| ∼ 10−9 – 10−4 | Lattice-Boltzmann [78] | |
| ∼ 10−9 – 10−4 | Dislocation Dynamics [79–82] | |
| ∼ 10−6 – 100 | Discrete Element Method [83] | |
| Mesoscopic/Macroscopic | ||
| ∼ 10−3 – 102 | Hydrodynamics [84] | macroscopic flow, macroscopic elasticity, macroscopic plasticity, fracture mechanics, aging of materials, fatigue and wear |
| ∼ 10−3 – 102 | Computational Fluid Dynamics [85–87] | |
| ∼ 10−6 – 102 | Finite Element Methods [88–90] | |
| ∼ 10−6 – 102 | Smooth Particle Hydrodynamics [8,91,92] | |
| ∼ 10−6 – 102 | Finite Difference Methods [93,94] | |
| ∼ 10−6 – 100 | Cluster & Percolation Models | |
| Algorithm | run time | N = 10 | N = 20 | N = 50 | N = 100 |
|---|---|---|---|---|---|
| 10 ES | 10 ES | 10 ES | 10 ES | ||
| A1 | N | 10−8 s | 2 × 10−8 s | 5 × 10−8 s | 10−7 s |
| 100 ES | 400 ES | 2.5 × 103 ES | 105 ES | ||
| A2 | N2 | 10−7 s | 4 × 10−7 s | 2.5 × 10−6 s | 10−5 s |
| 1000 ES | 8 × 103 ES | 105 ES | 106 ES | ||
| A3 | N3 | 10−6 s | 8 × 10−6 s | 10−4 s | 0.001 s |
| 1024 ES | 105 ES | 1015 ES | 1030 ES | ||
| A4 | 2N | 10−6 s | 10−3 s | 13 days | ~ 1013 years |
| ~ 106 ES | ~ 1018 ES | ~ 1064ES | 10158 ES | ||
| A5 | N! | 3 × 10−3 s | 77 years | 1048 years | ~ 10141 years |
| Algorithm | run time | efficiency | CPU speedup factor 10 | CPU speedup factor 100 |
|---|---|---|---|---|
| A1 | N | E1 | 10 × N1 | 100 × N1 |
| A2 | N2 | E2 | ||
| A3 | N3 | E3 | ||
| A4 | 2N | E4 | log2(10 × N4) = N4 + 3.3 | log2(100 × N4) = N4 + 6.6 |
| A5 | N! | E5 | ≈ N5 + 1 | ≈ N5 + 2 |
| f | 2 | 3 | 4 | 5 | 6 | 10 | 12 | 18 |
| ν | 0.5989 | 0.601 | 0.603 | 0.614 | 0.617 | 0.603 | 0.599 | 0.601 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Steinhauser, M.O.; Hiermaier, S. A Review of Computational Methods in Materials Science: Examples from Shock-Wave and Polymer Physics. Int. J. Mol. Sci. 2009, 10, 5135-5216. https://doi.org/10.3390/ijms10125135
Steinhauser MO, Hiermaier S. A Review of Computational Methods in Materials Science: Examples from Shock-Wave and Polymer Physics. International Journal of Molecular Sciences. 2009; 10(12):5135-5216. https://doi.org/10.3390/ijms10125135
Chicago/Turabian StyleSteinhauser, Martin O., and Stefan Hiermaier. 2009. "A Review of Computational Methods in Materials Science: Examples from Shock-Wave and Polymer Physics" International Journal of Molecular Sciences 10, no. 12: 5135-5216. https://doi.org/10.3390/ijms10125135






