Robustness in Regulatory Interaction Networks. A Generic Approach with Applications at Different Levels: Physiologic, Metabolic and Genetic
Abstract
:“In nova fert animus mutatas dicere formas corpora... Unus erat toto naturae vultus in orbe, Quem dixere chaos: rudis indigestaque moles, Nec quidquam, nisi pondus iners, congestaque eodem non bene junctarum discordia semina rerum…”. I want to speak about bodies changed into new forms... Nature appeared the same throughout the whole world, What we call chaos: a raw confused mass, Nothing but inert matter, badly combined discordant atoms of things, confused in the one place...(Ovide, Metamorphoses, 1st Book, 10 A.D.).
1. Introduction
2. Preliminary: Notations and Definitions
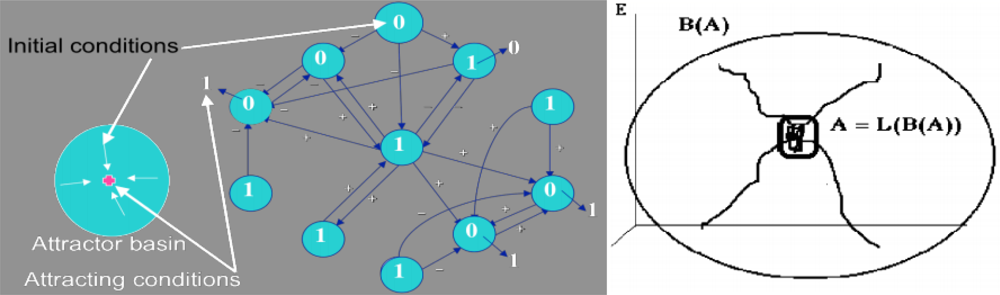
2.1. Definition of an Attractor and of Its Basin
- A is a fixed set for the composed set operator LoB: A = L(B(A)),
- there is no set C ⊃ Ā, C ≠ Ā, verifying i),
- there is no D ⊂ A, D ≠ A, verifying (i) and (ii).
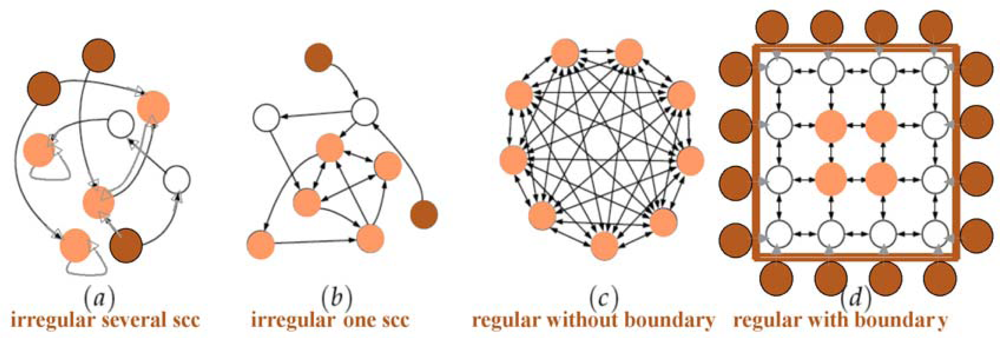
2.2. Degree, Connectivity and Connectedness
2.2.1. Undirected Graph
2.2.2. Regular Graph
2.2.3. Weighted and Signed Graph
2.2.4. Directed Graph
2.2.5. Indegree and Outdegree
2.2.6. Connectedness and Connectivity in Graphs
2.3. Kauffman Boolean Networks
2.4. Threshold Boolean Automata Networks
2.5. Attractors in Kauffman Boolean Networks and Threshold Boolean Automata Networks
3. Notions of Boundary, Core, Critical Node and Critical Edge of a Regulatory Interaction Network
3.1. Boundary and Core
3.2. Critical Node and Critical Edge
4. Theoretical Complements
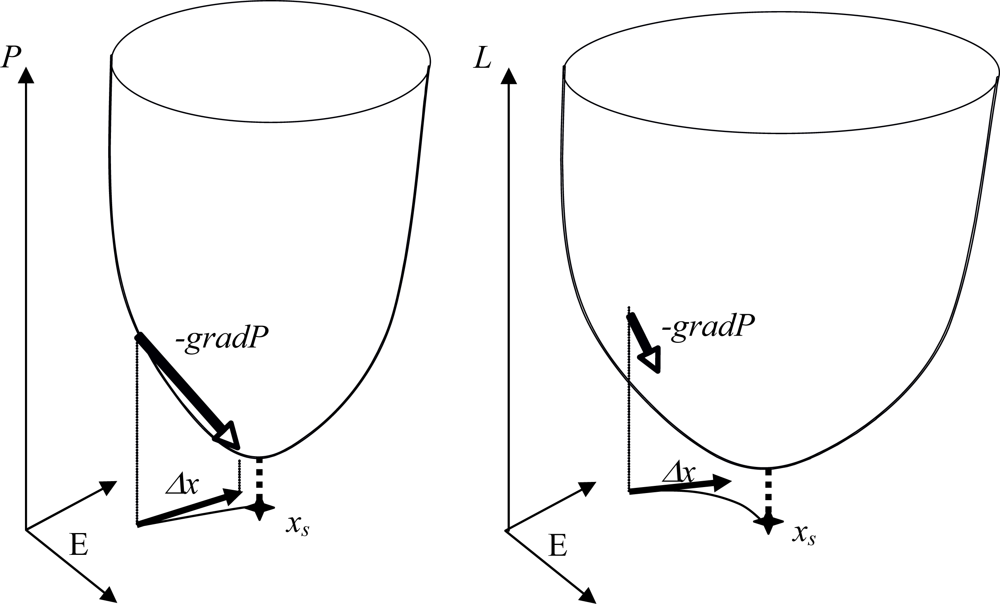
4.1. Potential Regulatory Networks
4.2. Hamiltonian Networks
4.3. Relationships between Kauffman Boolean and Threshold Boolean Automata Networks
4.4. Relationships between Undirected and Directed Graphs
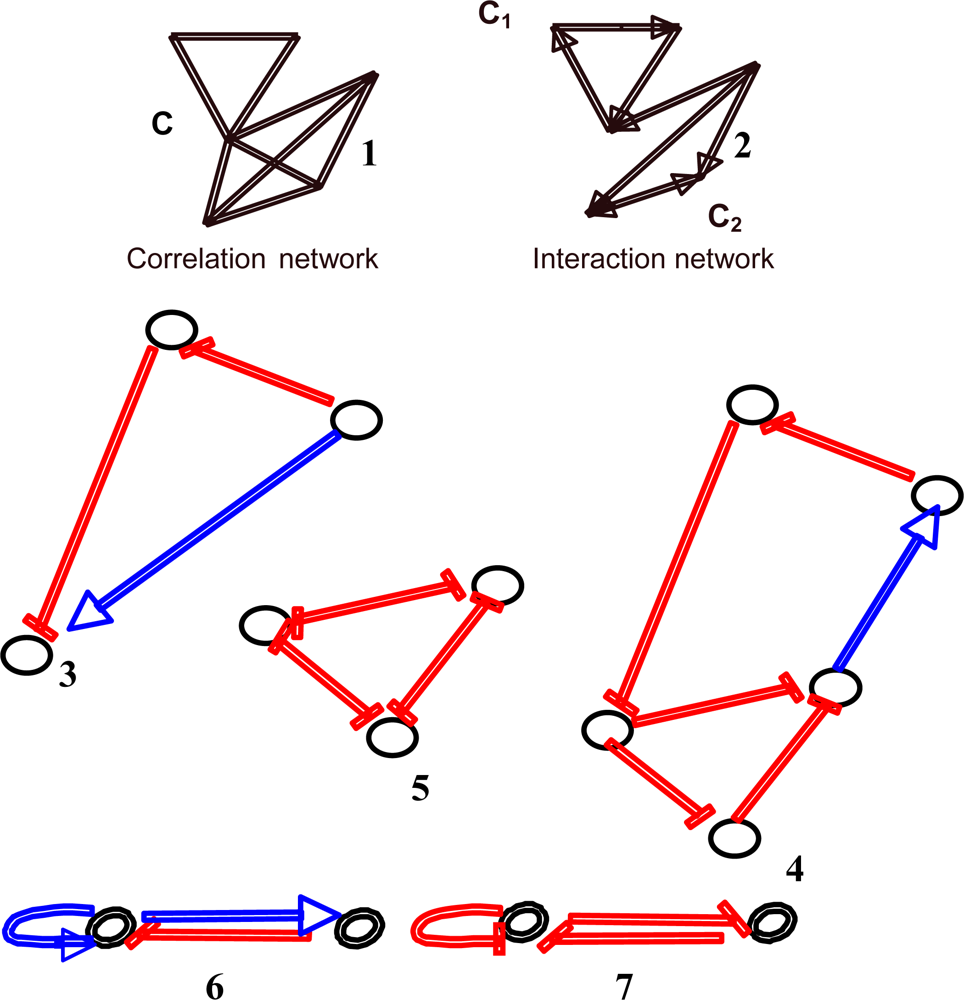
4.5. Circuits
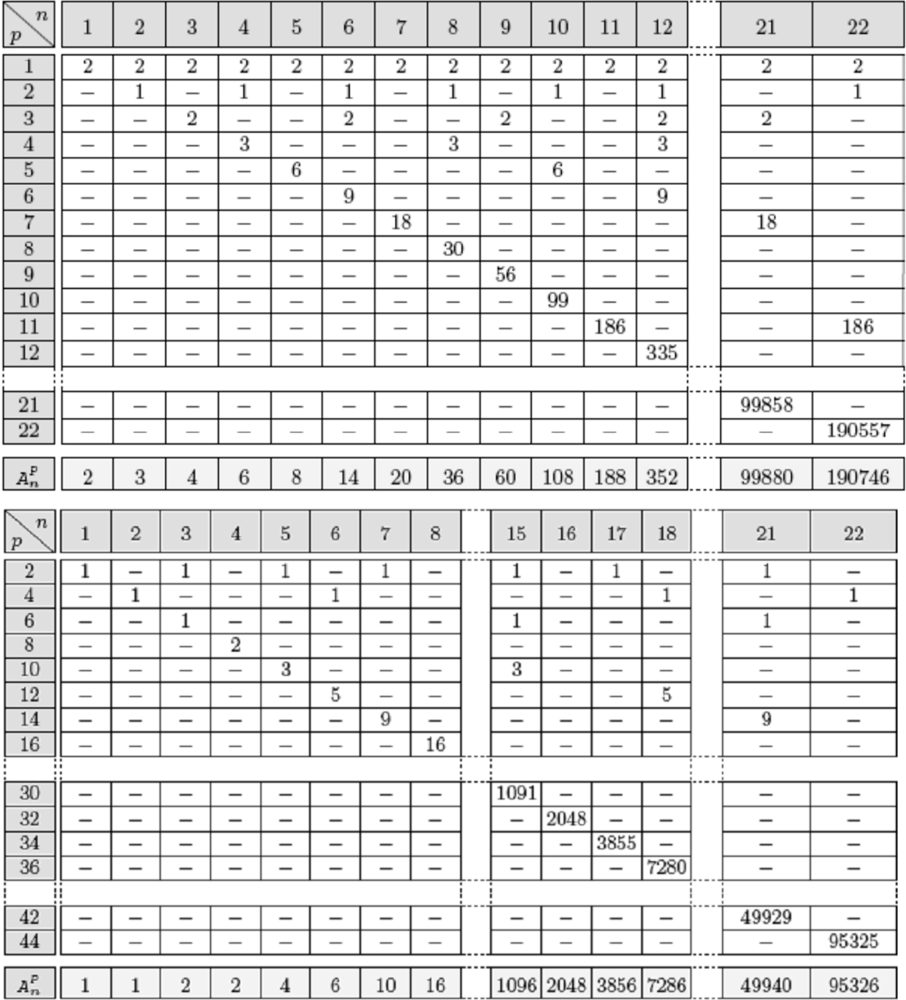
4.6. Attractors Counting in Real Regulatory Networks
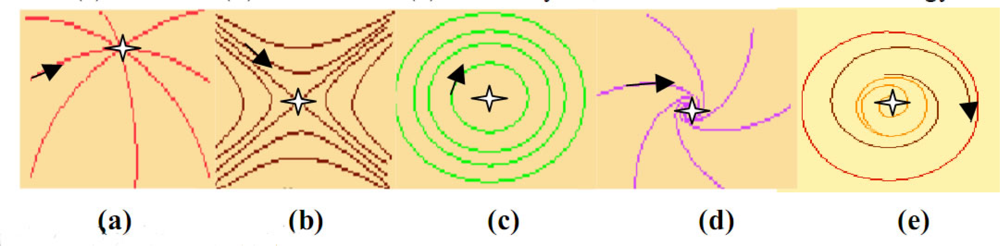
5. Robustness
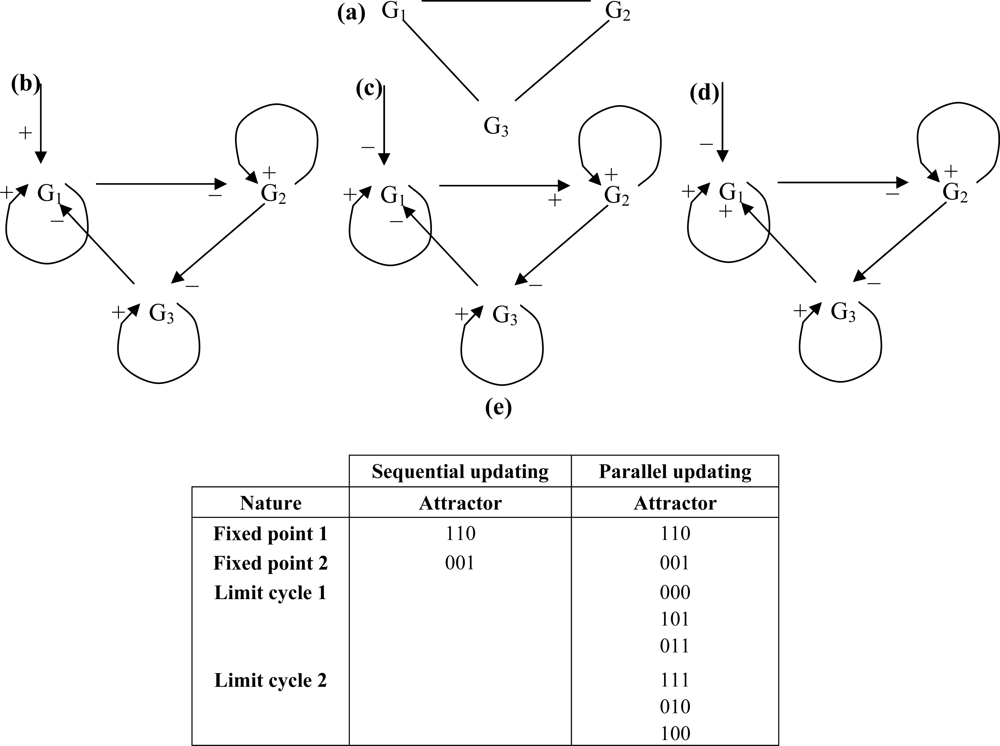
- - if the nodes are sequentially visited by the updating process, the system has 6 fixed configurations, with state 1 (resp. 0) at one node and state 0 (resp. 1) at the others. Such a system having only fixed configurations is potential in the sense of the Section 4.1. [64], because the discrete velocity of the dynamics is equal to the gradient of a Lyapunov function (it is for example more generally the case in a n-switch when the interaction weights are symmetrical),
- - if the nodes are synchronously updated, we have one limit-cycle of order 2 (made of the full 0 and full 1 configurations) and 6 fixed configurations (corresponding to those of the sequential updating). Such a discrete system is Hamiltonian in the sense of Section 4.2.,
- - in the intermediary case, called block-sequential, in which we update first a node, and then synchronously the two others, we have the same attractors as in the sequential case.
- - those for which the cycles disappear when we are going down in the hierarchy from the synchronous to the sequential modes (behaviour “Down”),
- - those for which the cycles disappear when we are going up in the hierarchy from the sequential modes to the synchronous one (behaviour “Up”),
- - those not corresponding to any previous behaviour, for which the cycles occur and disappear inside the hierarchy without clear rule (behaviour “None”).
6. Examples of Robust and Non-Robust Networks
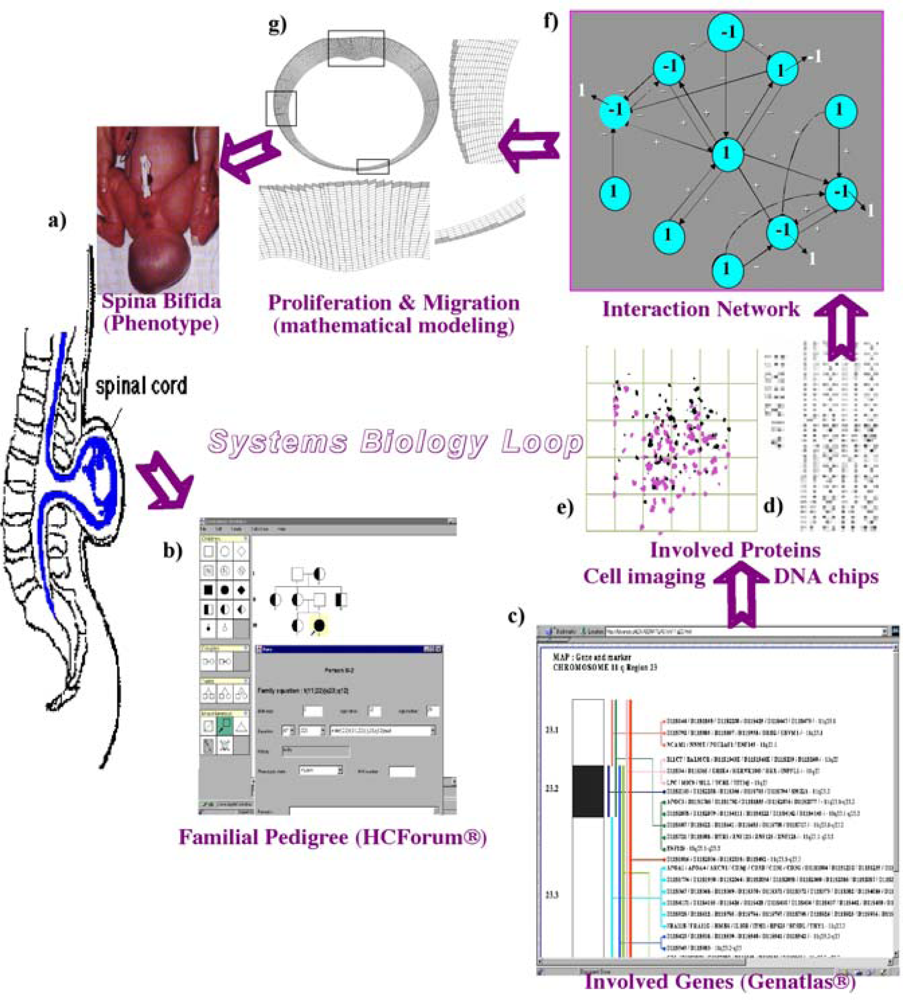
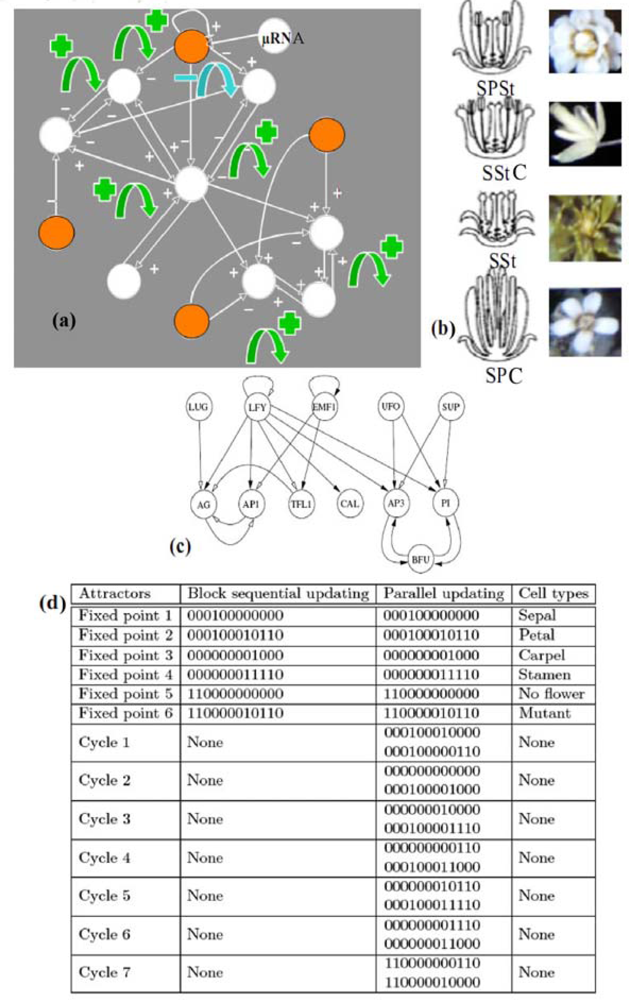
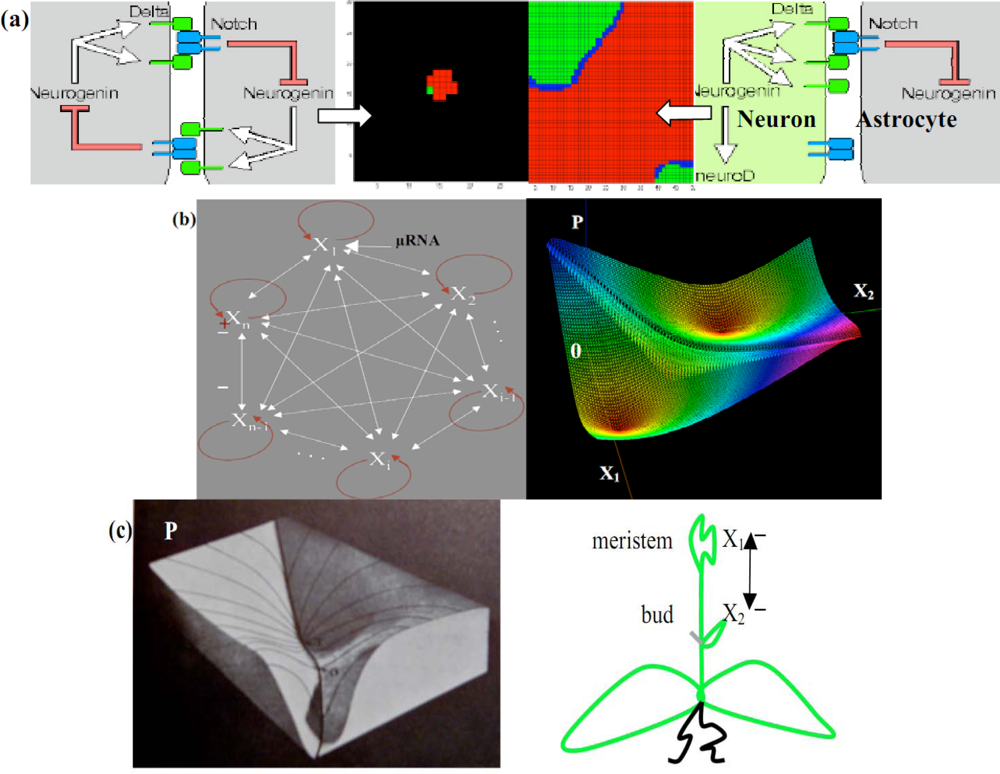
6.1. Neuron and Plant Morphogenesis
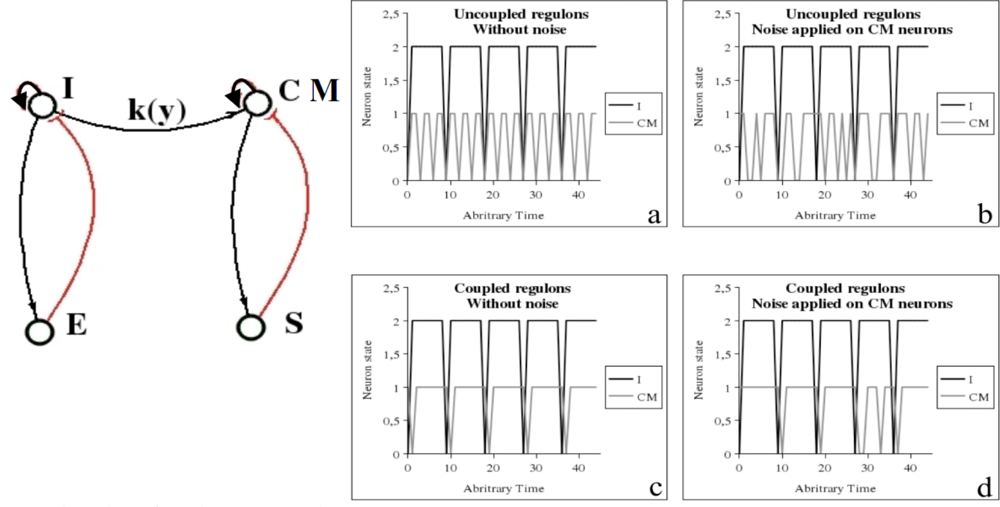
6.2. Cardio-Respiratory Physiologic Regulation
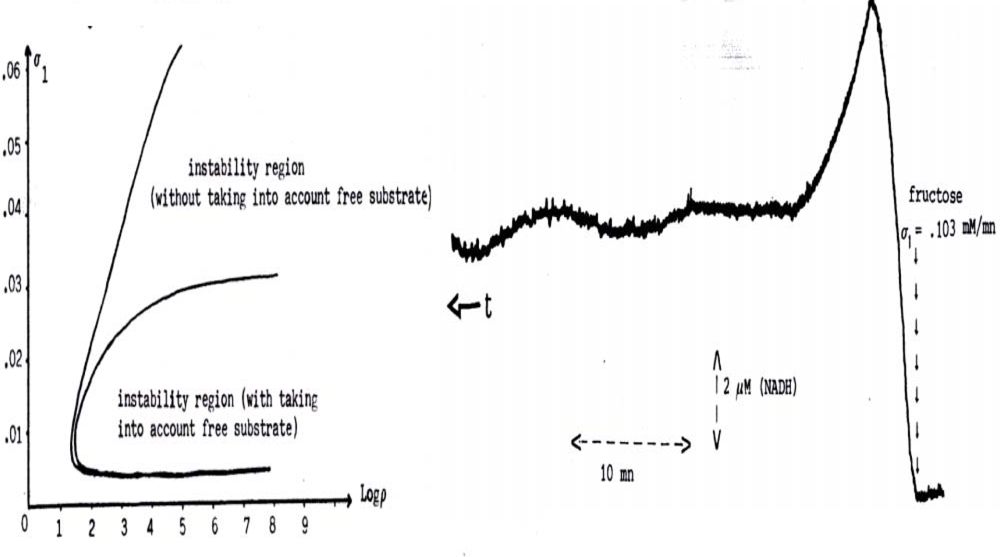
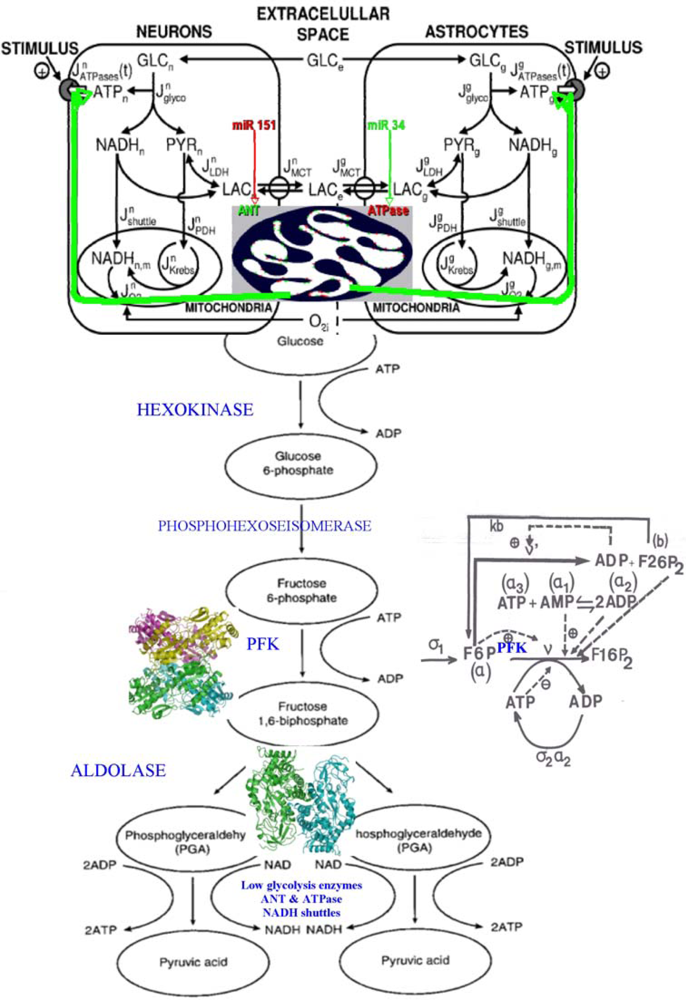
6.3. Glycolytic/Oxidative Coupling
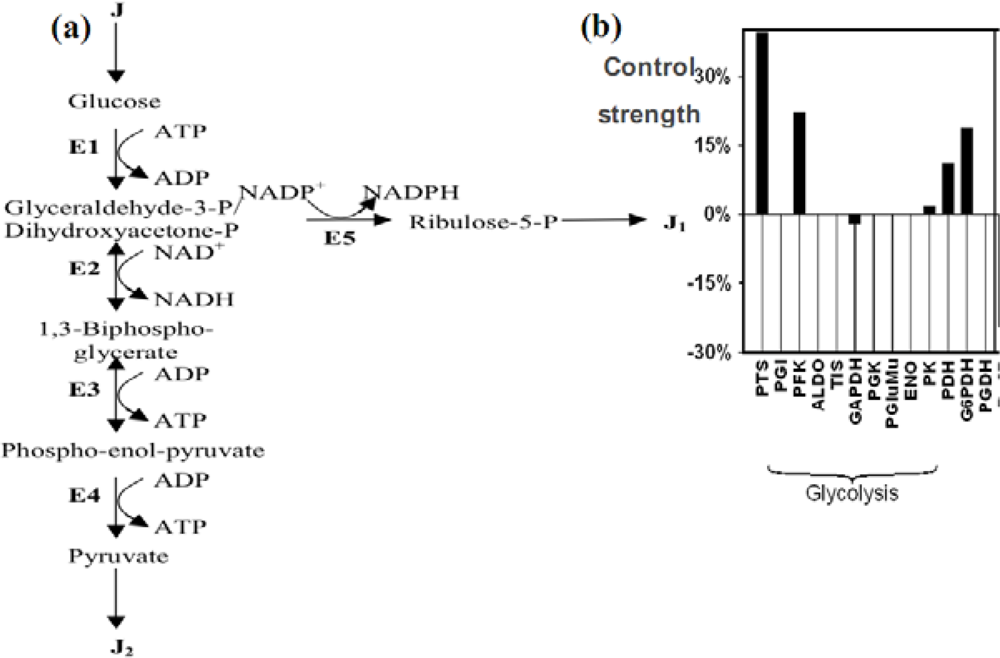
6.3.1. The Glycolysis
6.3.2. Control Strength
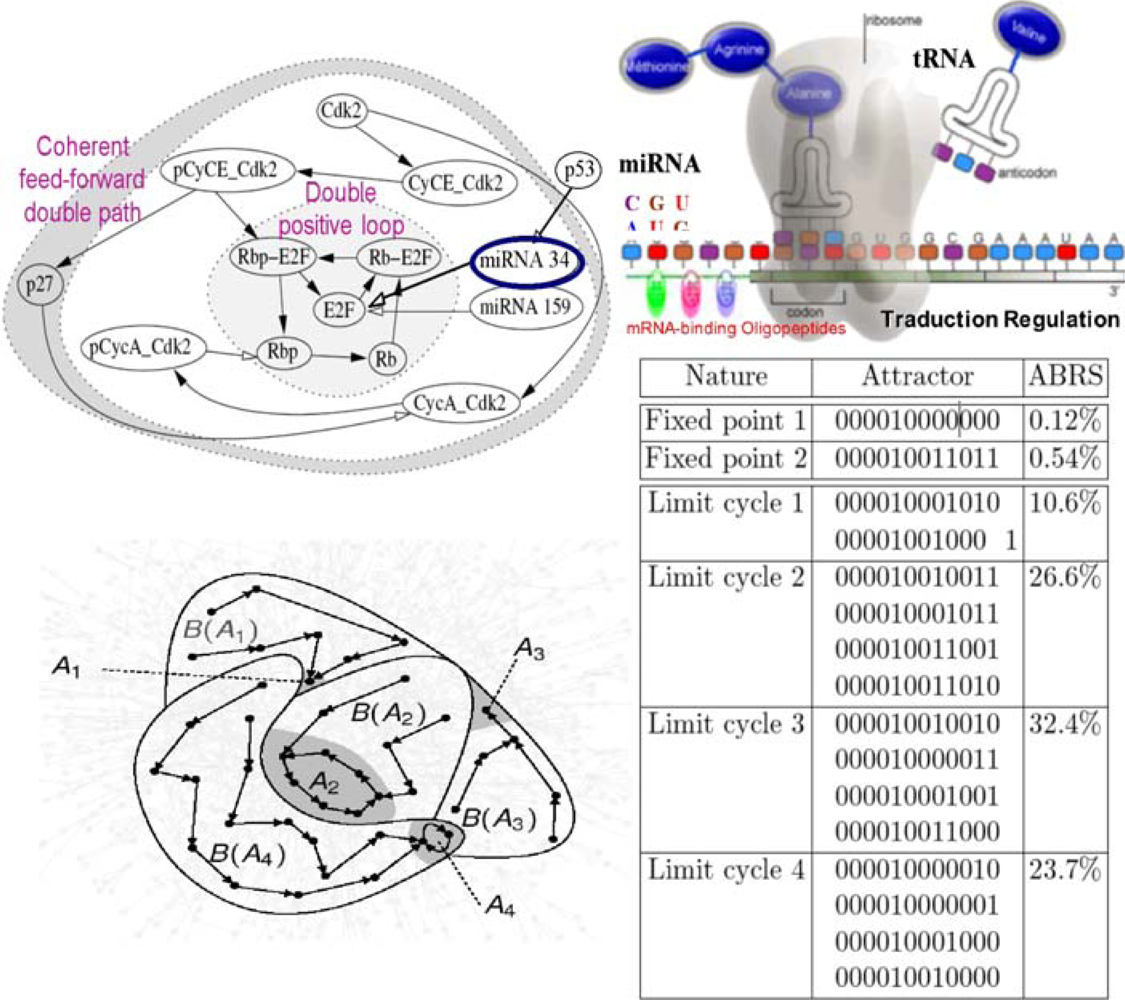
6.4. Cell Cycle Control
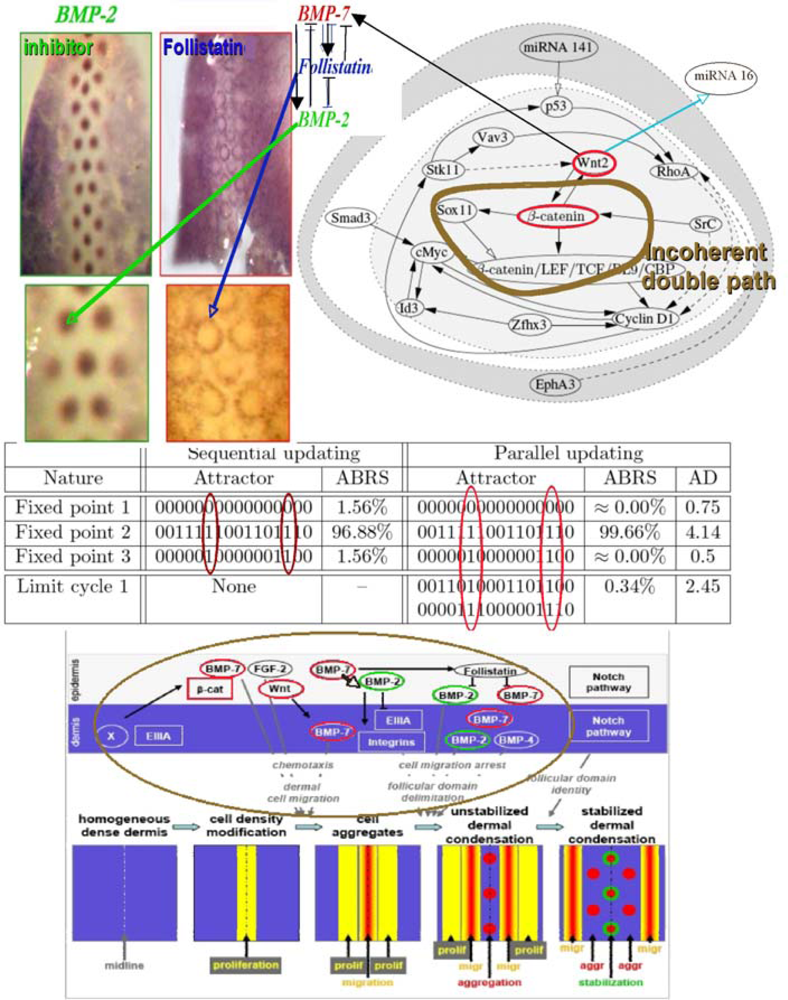
6.5. Feather Morphogenesis
7. Perspectives and Conclusions
Acknowledgments
References
- Fell, DA; Wagner, A. The small world of metabolism. Nat. Biotechnol 2000, 18, 1121–1122. [Google Scholar]
- van Noort, V; Snel, B; Huynen, MA. The yeast coexpression network has a small-world, scale free architecture and can be explained by a simple model. EMBO Rep 2004, 5, 280–284. [Google Scholar]
- Henri, V. Lois Générales de l’Action des Diastases; Hermann: Paris, France, 1903. [Google Scholar]
- Hill, AV. The possible effects of the aggregation of the molecules of hemoglobin on its dissociation curves. J. Physiol. (London) 1910, 40, 4–7. [Google Scholar]
- Michaelis, L; Menten, M. Die Kinetik der Invertinwirkung. Biochem. Z 1913, 49, 333–369. [Google Scholar]
- Monod, J. Recherches Sur La Croissance Des Cultures bactériennes; Hermann: Paris, France, 1941. [Google Scholar]
- Delbrück, M. Unités Biologiques Douées De Continuité génétique; Éditions du CNRS: Paris, France, 1949; pp. 33–34. [Google Scholar]
- von Neumann, J; Burks, AW. Theory of Self-Reproducing Automata; University of Illinois Press: Urbana, IL, USA, 1966. [Google Scholar]
- Monod, J; Wyman, J; Changeux, JP. On the nature of the allosteric transitions. J. Mol. Biol 1965, 12, 88–118. [Google Scholar]
- Changeux, JP; Thiery, J; Tung, Y; Kittel, C. On the cooperativity of biological membranes. Proc. Natl Acad. Sci 1967, 57, 335–341. [Google Scholar]
- Thomas, R. Boolean formalization of genetic control circuits. J. Theor. Biol 1973, 42, 563–585. [Google Scholar]
- Demongeot, J. A stochastic model for the cellular metabolism. In Recent Developments in Statistics; Barra, JR, Brodeau, F, Romier, G, Eds.; North Holland: Amsterdam, The Netherlands, 1977; pp. 655–662. [Google Scholar]
- Goss, PEJ; Peccoud, J. Quantitative modeling of stochastic systems in molecular biology by using stochastic Petri nets. Proc. Natl. Acad. Sci. USA 1998, 95, 6750–6755. [Google Scholar]
- Poincaré, H. Note sur les propriétés des fonctions définies par les équations différentielles. Journal de l’Ecole Polytechnique 1875, 45, 13–26. [Google Scholar]
- Poincaré, H. Sur un théorème de M. Liapounoff relatif à l’équilibre d’une masse fluide en rotation. Comptes Rendus Hebdomadaires de l’Académie des Sciences 1887, 104, 622–625. [Google Scholar]
- Poincaré, H. Sur les solutions périodiques et le principe de moindre action. Comptes rendus hebdomadaires de l’Académie des sciences 1896, 123, 915–918. [Google Scholar]
- Poincaré, H. Les fondements de la géométrie. Journal des Savants 1902, 238, 252–271. [Google Scholar]
- Lyapunov, AM. Problème général de la stabilité des mouvements. Annales de la Faculté des Sciences de Toulouse 1907, 9, 203–274. [Google Scholar]
- Birkhoff, GD. Proof of Poincaré’s geometric theorem. Trans. Am. Soc 1913, 14, 14–22. [Google Scholar]
- Thom, R. Stabilité Structurelle et Morphogenèse; Benjamin: New York, NY, USA, 1972. [Google Scholar]
- Aracena, J; Ben Lamine, S; Mermet, MA; Cohen, O; Demongeot, J. Mathematical modelling in genetic networks: Relationships between the genetic expression and both chromosomic breakage and positive circuits. IEEE Trans. Syst. Man Cybern 2003, 33, 825–834. [Google Scholar]
- Aracena, J; Demongeot, J. Mathematical methods for inferring regulatory networks interactions: Application to genetic regulation. Acta Biotheor 2004, 52, 391–400. [Google Scholar]
- Alvarez-Buylla, ER; Mariana Benítez, M; Balleza Dávila, E; Chaos, A; Espinosa-Soto, C; Padilla-Longoria, P. Gene regulatory network models for plant development. Curr. Opin. Plant Biol 2007, 10, 83–91. [Google Scholar]
- Alon, U. Network motifs: Theory and experimental approaches. Nat. Rev. Genet 2007, 8, 450–461. [Google Scholar]
- Elena, A; Ben Amor, H; Glade, N; Demongeot, J. Motifs in regulatory networks and their structural robustness. IEEE BIBE’ 08; IEEE Proceedings, Piscataway, NJ, USA, 2008; pp. 234–242.
- Elena, A; Demongeot, J. Interaction motifs in regulatory networks and structural robustness. IEEE ARES-CISIS’08 & IIBM’08; IEEE Proceedings, Piscataway, NJ, USA, 2008; pp. 682–686.
- Elena, A. Robustesse des réseaux d’automates booléens à seuil aux modes d’itération; Ph.D. ThesisUniversity Joseph Fourier: Grenoble, France, 2009. [Google Scholar]
- Cosnard, M; Demongeot, J. On the definitions of attractors. Lect. Notes Math 1985, 1163, 23–31. [Google Scholar]
- Cosnard, MJ; Demongeot, J; Lausberg, K; Lott, K. Attractors, confiners & fractal dimensions. Applications in neuromodelling. In 1st Eur Conf Maths in Biol & Med Grenoble 1991; Mathematical Biology Wuerz: Winnipeg, MB, Canada, 1993; pp. 69–94. [Google Scholar]
- Bowen, R. Limit sets for axiom A diffeomorphisms. J. Diff. Equa 1975, 18, 333–339. [Google Scholar]
- Thomas, R. On the relation between the logical structure of systems and their ability to generate multiple steady states or sustained oscillations. Springer Series in Synergetics 1981, 9, 180–193. [Google Scholar]
- Snoussi, EH. Necessary conditions for multistationnarity and stable periodicity. J. Biol. Syst 1999, 6, 3–9. [Google Scholar]
- Gouzé, JL. Necessary conditions for multistationnarity and stable periodicity. J. Biol. Syst 1999, 6, 11–15. [Google Scholar]
- Demongeot, J. Multi-stationarity and cell differentiation. J. Biol. Syst 1999, 6, 1–2. [Google Scholar]
- Cinquin, O; Demongeot, J. Positive and negative feedback: Mending the ways of sloppy systems. C.R. Biol 2002, 325, 1085–1095. [Google Scholar]
- Soulé, C. Graphic requirements for multistationarity. Complexus 2003, 1, 123–133. [Google Scholar]
- Soulé, C; Kaufmann, M; Thomas, R. A new necessary condition on interaction graphs for multistationarity. J. Theor. Biol 2007, 248, 675–685. [Google Scholar]
- Aracena, J; Demongeot, J; Goles, E. Fixed points and maximal independent sets on AND-OR networks. Discr. Appl. Maths 2004, 138, 277–288. [Google Scholar]
- Remy, E; Ruet, EP; Thieffry, D. Graphic requirement for multistability and attractive cycles in a Boolean dynamical framework. Adv. Appl. Maths 2008, 41, 335–350. [Google Scholar]
- Richard, A; Comet, JP. Necessary conditions for multistationarity in discrete dynamical systems. Discrete Appl. Math 2007, 155, 2403–2413. [Google Scholar] [Green Version]
- Kauffman, SA. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol 1969, 22, 437–467. [Google Scholar]
- Kauffman, SA. The large scale structure and dynamics of genetic control circuits: An ensemble approach. J. Theor. Biol 1974, 44, 167–190. [Google Scholar]
- Kauffman, SA. The Origins of Order; Oxford Un. Press: Oxford, UK, 1993. [Google Scholar]
- Kauffman, SA; Peterson, C; Samuelsson, B; Troein, C. Random Boolean network models and the yeast transcriptional network. Proc. Natl. Acad. Sci. USA 2003, 100, 14796–14799. [Google Scholar]
- Samuelsson, B; Troein, C. Superpolynomial growth in the number of attractors in Kauffman networks. Phys. Rev. Lett 2003, 90, 088701. [Google Scholar]
- Shmulevich, I; Kauffman, SA. Activities and sensitivities in Boolean network models. Phys. Rev. Lett 2004, 93, 048701. [Google Scholar]
- Chaves, M; Albert, R; Sontag, ED. Robustness and fragility of Boolean models for genetic regulatory networks. J. Theor. Biol 2005, 235, 431–449. [Google Scholar]
- Zhang, SQ; Hayashida, M; Akutsu, T; Ching, WK; Ng, MK. Algorithms for finding small attractors in boolean networks. EURASIP J. Bioinform. Syst. Biol 2007, 2, 20180. [Google Scholar]
- Ribeiro, AS; Kauffman, SA; Lloyd-Price, J; Samuelsson, B; Socolar, JES. Mutual information in random Boolean models of regulatory networks. Phys. Rev. E 2008, 77, 011901. [Google Scholar]
- Fox, JJ; Hill, CC. From topology to dynamics in biochemical networks. Chaos 2001, 11, 809–815. [Google Scholar]
- Aldana, M; Cluzel, P. A natural class of robust networks. Proc. Natl. Acad. Sci. USA 2003, 100, 8710–8714. [Google Scholar]
- Hopfield, JJ. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar]
- Aracena, J; Demongeot, J; Goles, E. Mathematical modelling in genetic networks. IEEE Trans. Neural Networks 2004, 15, 77–83. [Google Scholar]
- Aracena, J; Demongeot, J; Goles, E. On limit cycles of monotone functions with symmetric connection graphs. Theoret. Comp. Sci 2004, 322, 237–244. [Google Scholar]
- Cooper, C; Frieze, A; Reed, B. Random regular graphs of non-constant degree: Connectivity and hamiltonicity. Comb. Probab. Comput 2002, 11, 249–261. [Google Scholar]
- Bonchev, D; Rouvray, DH. Complexity in Chemistry, Biology, and Ecology; Springer Verlag: Berlin, Germany, 2005. [Google Scholar]
- Somorjai, RL; Goswami, DN. Relationship between stability and connectedness of non-linear systems. Nature 1972, 236, 466–466. [Google Scholar]
- Gardner, MR; Ashby, WR. Connectivity of large, dynamical (cybernetic) systems: Critical values for stability. Nature 1970, 228, 784–784. [Google Scholar]
- Mendoza, L; Alvarez-Buylla, ER. Dynamics of the genetic reglatory network for Arabidopsis thaliana flower morphogenesis. J. Theor. Biol 1998, 193, 307–319. [Google Scholar]
- Goles, E; Olivos, J. Comportement périodique des fonctions seuils binaires et applications. Discrete Appl. Math 1981, 3, 93–105. [Google Scholar]
- Demongeot, J; Goles, E; Sené, S. Loss of linearity and symmetrisation in regulatory networks. AINA’ 09 & BLSMC’ 09; IEEE Proceedings, Piscataway, NJ, USA; 2009; pp. 908–913. [Google Scholar]
- Ben Amor, H; Demongeot, J; Sené, S. Structural sensitivity of neural and genetic networks. LNCS 2008, 5317, 973–986. [Google Scholar]
- Demongeot, J; Morvan, M; Sené, S. Robustness of dynamical systems attraction basins against state perturbations: Theoretical protocol and application in systems biology, IEEE ARES-CISIS’ 08 & IIBM’ 08; IEEE Proceedings, Piscataway, NJ, USA; 2008; pp. 675–681.
- Demongeot, J; Elena, A; Weil, G. Potential-Hamiltonian decomposition of cellular automata. Application to degeneracy of genetic code and cyclic codes III. Comptes Rendus Biologies 2006, 329, 953–962. [Google Scholar]
- Needham, J. Order and Life; Yale University Press: Yale, CT, USA, 1936. [Google Scholar]
- Gonzalez, O. Time integration and discrete Hamiltonian systems. J. Nonlinear Sci 1996, 6, 449–467. [Google Scholar]
- Demongeot, J; Noual, M; Sené, S. On the number of attractors of positive and negative Boolean automata circuits. AINA’ 10 & BLSMC’ 10, IEEE Proceedings, Piscataway, NJ, USA.
- Bollobas, R. Random Graphs; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Wormald, NC. The asymptotic distribution of short cycles in random regular graphs. J. Combin. Theory Ser. B 1981, 31, 168–182. [Google Scholar]
- McKay, BD; Wormald, NC; Wysocka, B. Short cycles in random regular graphs. Electronic J Combinatorics 2004, 11. [Google Scholar]
- Socolar, JES; Kauffman, SA. Scaling in ordered and critical random Boolean metworks. Phys. Rev. Lett 2003, 90, 068702. [Google Scholar]
- Kauffman, S; Peterson, C; Samuelsson, B; Troein, C. Genetic networks with canalyzing Boolean rules are always stable. Proc. Natl Acad. Sci. USA 2004, 101, 17102–17107. [Google Scholar]
- Drossel, B; Mihaljev, T; Greil, F. Number and length of attractors in critical Kauffman model with connectivity one. Phys Rev Lett 2005, 94. [Google Scholar]
- Drossel, B. On the number of attractors in random Boolean networks. Phys Rev E 2005, 72, 016110.1–5. [Google Scholar]
- Hawick, K; James, H; Scogings, C. Structural circuits and attractors in Kauffman networks. LNAI 2007, 4828, 189–200. [Google Scholar]
- Drossel, B. Random Boolean networks. In Reviews of Nonlinear Dynamics and Complexity; Schuster, HG, Ed.; J. Wiley: New York, NY, USA, 2008; Volume 1, pp. 69–110. [Google Scholar]
- Berdahl, A; Shreim, A; Sood, V; Paczuski, M; Davidsen, J. Random sampling versus exact enumeration of attractors in random Boolean networks. New J Phys 2009, 11. [Google Scholar]
- Tamura, T; Akutsu, T. Detecting a singleton attractor in a boolean network utilizing SAT algorithms. IEICE-Tran. Fund. Elec., Comm. & Comp. Sci 2009, 92, 493–501. [Google Scholar]
- Bentwich, I; Avniel, A; Karov, Y; Aharonov, R; Gilad, S; Barad, O; Barzilai, A; Einat, P; Einav, U; Meiri, E; Sharon, E; Spector, Y; Bentwich, Z. Identification of hundreds of conserved and nonconserved human microRNAs. Nat. Genet 2005, 37, 766–770. [Google Scholar]
- John, B; Enright, AJ; Aravin, A; Tuschl, T; Sander, C; Marks, DS. Human microRNA targets. PLoS Biol 2004, 2, 1862–1879. [Google Scholar]
- Palka, ZJ; Cohen, JE. Isolated vertices of random niche overlap graphs. Ars Combinatoria 1994, 37, 65–74. [Google Scholar]
- Lentz, TL. Cell Fine Structure: An Atlas of Drawings of Whole-Cell Structure; Saunders: Philadelphia, PA, USA, 1971. [Google Scholar]
- Vickaryous, MK; Hall, BK. Human cell type diversity, evolution, development, and classification with special reference to cells derived from the neural crest. Biol. Rev 2006, 81, 425–455. [Google Scholar]
- Kohn, KW. Molecular interaction map of the mammalian cell cycle control and DNA repair systems. Mol. Biol. Cell 1999, 10, 2703–2734. [Google Scholar]
- Appel, N; Bartenschlager, R. A novel function for a miR: Negative regulators can do positive for the hepatitis C virus. Hepatology 2006, 43, 612–615. [Google Scholar]
- Kepes, F. Periodic transcriptional organization of E. coli genome. J. Mol. Biol 2004, 340, 957–964. [Google Scholar]
- Cinquin, O; Demongeot, J. High-dimensional switches and the modeling of cellular differentiation. J. Theor. Biol 2005, 233, 391–411. [Google Scholar]
- Demongeot, J; Thomas, R; Thellier, M. A mathematical model for storage and recall functions in plants. C.R. Acad. Sci. Sciences de la Vie 2000, 323, 93–97. [Google Scholar]
- Jolliot, A; Prochiantz, A. Transduction peptides: From technology to physiology. Nat. Cell Biol 2004, 6, 189–196. [Google Scholar]
- Demongeot, J; Fouquet, Y; Tayyab, M; Vuillerme, N. Understanding physiological & degenerative natural vision mechanisms to define robust contrast and segmentation operators. PLoS ONE 2009, 4, 1–17. [Google Scholar]
- Edlund, T; Jessell, TM. Progression from extrinsic to intrinsic signaling in cell fate specification: A view from the nervous system. Cell 1999, 96, 211–224. [Google Scholar]
- Wilson, PA; Hemmati-Brivanlou, A. Vertebrate neural induction: Inducers, inhibitors, and a new synthesis. Neuron 1997, 18, 699–710. [Google Scholar]
- Pham Dinh, T; Demongeot, J; Baconnier, P; Benchetrit, G. Simulation of a biological oscillator: The respiratory rhythm. J. Theor. Biol 1983, 103, 113–132. [Google Scholar]
- Demongeot, J; Virone, G; Duchêne, F; Benchetrit, G; Hervé, T; Noury, N; Rialle, V. Multi-sensors acquisition, data fusion, knowledge mining and alarm triggering in health smart homes for elderly people. C.R. Biol 2002, 325, 673–682. [Google Scholar]
- Thomas, R. On the relation between the logical structure of systems and their ability to generate multiple steady states or sustained oscillations. Springer Ser. Synerget 1981, 9, 180–193. [Google Scholar]
- Boiteux, A; Goldbeter, A; Hess, B. Control of oscillating glycolysis of yeast by stochastic, periodic, and steady source of substrate: A model and experimental study. Proc. Natl. Acad. Sci. USA 1975, 72, 3829–3833. [Google Scholar]
- Demongeot, J; Seydoux, F. Oscillations glycolytiques: Modélisation d’un système minimum à partir des données physiologiques et moléculaires. In Elaboration et Justification de Modèles; Delattre, P, Thellier, M, Eds.; Maloine: Paris, French, 1979; pp. 519–536. [Google Scholar]
- Hervagault, JF; Duban, MC; Kernevez, JP; Thomas, D. Multiple steady states and oscillatory behaviour of a compartmentalized phosphofructokinase system. Proc. Natl. Acad. Sci. USA 1983, 80, 5455–5459. [Google Scholar]
- Demongeot, J; Kellershohn, N. Glycolytic oscillations: An attempt to an “in vitro” reconstitution of the higher part of glycolysis. Lect. Notes Biomath 1983, 49, 17–31. [Google Scholar]
- Demongeot, J; Doncescu, A. Modelling the glycolysis: An inverse problem approach. IEEE AINA’ 09 & BLSMC’ 09, IEEE Proceedings, Piscataway, NJ, USA; 2009; pp. 930–935. [Google Scholar]
- Aubert, A; Costalat, R; Magistretti, PJ. Brain lactate kinetics: Modeling evidence for neuronal lactate uptake upon activation. Proc. Natl. Acad. Sci. USA 2005, 102, 16448–16453. [Google Scholar]
- Aubert, A; Pellerin, L; Magistretti, P J; Costalat, R. A coherent neurobiological framework for functional neuroimaging provided by a model integrating compartmentalized energy metabolism. Proc. Natl. Acad. Sci. USA 2007, 104, 4188–4193. [Google Scholar]
- Demongeot, J; Glade, N; Hansen, O; Moreira, A. An open issue: The inner mitochondrial membrane (IMM) as a free boundary problem. Biochimie 2007, 89, 1049–1057. [Google Scholar]
- Ovadi, J. Old pathway-new concept: Control of glycolysis by metabolite-modulated dynamic enzyme associations. Trends Biochem. Sci 1988, 13, 486–490. [Google Scholar]
- Reder, C. Metabolic control theory: A structural approach. J. Theor. Biol 1988, 135, 175–201. [Google Scholar]
- Ritter, JB; Genzela, Y; Reichl, U. Simultaneous extraction of several metabolites of energy metabolism and related substances in mammalian cells: Optimization using experimental design. Anal. Biochem 2008, 373, 349–369. [Google Scholar]
- Thellier, M; Legent, G; Amar, P; Norris, V; Ripoll, C. Steady-state kinetic behaviour of functioning-dependent structures. FEBS J 2006, 273, 4287–4299. [Google Scholar]
- Demongeot, J; Laurent, M. Sigmoidicity in allosteric models. Math. Biosci 1983, 67, 1–17. [Google Scholar]
- Demongeot, J; Glade, N; Forest, L. Liénard systems and potential-Hamiltonian decomposition. I Methodology. Comptes Rendus Mathématique 2007, 344, 121–126. [Google Scholar]
- Krasnosel’ski, MA. The Operator of Translation along Trajectories of Ordinary Differential Equations; Mir: Moskow, Russia, 1966. [Google Scholar]
- Kaczer, H; Burns, JA. The control of flux. Symp. Soc. Exp. Bot 1973, 28, 65–104. [Google Scholar]
- Wolf, J; Heinrich, R. Effect of cellular interaction on glycolytic oscillations in yeast: A theoretical investigation. Biochem. J 2000, 345, 321–334. [Google Scholar]
- Bier, M; Teusink, B; Kholodenk, BN; Westerhoff, HV. Control analysis of glycolytic oscillations. Biophys. Chem 1996, 62, 15–24. [Google Scholar]
- Baconnier, P; Pachot, P; Demongeot, J. An attempt to generalize the control coefficient concept. J. Biol. Systems 1993, 1, 335–347. [Google Scholar]
- Li, M; Chen, L; Lee, DHS; Yu, LC; Zhang, Y. The role of intracellular amyloid beta in Alzheimer disease. Prog. Neurobiol 2007, 83, 131–139. [Google Scholar]
- Zhang, Y; McLaughlin, R; Goodyer, C; LeBlanc, A. Selective cytotoxicity of intracellular amyloid beta peptide 1–42 through p53 and Bax in cultured primary human neurons. J. Cell Biol 2002, 156, 519–529. [Google Scholar]
- Jouanneau, J; Larsen, CJ. Les microARN: Un « bras armé » du suppresseur de tumeur p53. Bull. Cancer 2007, 94, 634–635. [Google Scholar]
- Forest, L; San Martin, J; Padilla, F; Chassat, F; Giroud, F; Demongeot, J. Morphogenetic processes: Application to cambial growth dynamics. Acta Biotheoretica 2004, 52, 415–438. [Google Scholar]
- Forest, L; Demongeot, J. Cellular modelling of secondary radial growth in conifer trees: Application to Pinus radiata. Bull. Math. Biol 2006, 68, 753–784. [Google Scholar]
- Forest, L; Martinez, S; Padilla, F; Demongeot, J; San Martin, J. Modelling of auxin transport affected by gravity and differential radial growth. J. Theor. Biol 2006, 241, 241–251. [Google Scholar]
- Forest, L; Michon, F; Cadau, S; Demongeot, J; Dhouailly, D. What is the biological basis of pattern formation of skin lesions? Viewpoint 4. Skin Patterns belong to three main types, determined at three steps of development. Exp. Dermatol 2006, 12, 559–564. [Google Scholar]
- Michon, F; Forest, L; Collomb, E; Demongeot, J; Dhouailly, D. BMP-2 and BMP-7 play antagonistic roles in feather induction. Development 2008, 135, 2797–2805. [Google Scholar]
- Garg, A; Di Cara, A; Xenarios, I; Mendoza, L; De Micheli, G. Synchronous versus asynchronous modeling of gene regulatory networks. Bioinformatics 2008, 24, 1917–1925. [Google Scholar]
- Ben Amor, H; Cadau, S; Elena, A; Dhouailly, D; Demongeot, J. Regulatory networks analysis: Robustness in biological regulatory networks. AINA’ 09 & BLSMC’ 09; IEEE Proceedings, Piscataway, NJ, USA; 2009; pp. 224–229. [Google Scholar]
- Forest, L; Demongeot, J. A general formalism for tissue morphogenesis based on cellular dynamics and control system interactions. Acta Biotheoretica 2008, 56, 51–74. [Google Scholar]
- Ross, R. Report on the Prevention of Malaria in Mauritius; University of Liverpool: Liverpool, UK, 1908. [Google Scholar]
- Volterra, V. Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Mem. Acad. Lincei III 1926, 6, 31–113. [Google Scholar]
- Demongeot, J; Elena, A; Sené, S. Robustness in regulatory networks: A multi-disciplinary approach. Acta Biotheor 2008, 56, 27–49. [Google Scholar]
- Demongeot, J; Jezequel, C; Sené, S. Boundary conditions and phase transitions in neural networks. Theoretical results. Neural Networks 2008, 21, 971–979. [Google Scholar]
- Demongeot, J; Sené, S. Boundary conditions and phase transitions in neural networks. Simulation results. Neural Networks 2008, 21, 962–970. [Google Scholar]
- Demongeot, J; Glade, N; Moreira, A; Vial, L. RNA relics and origin of life. Int. J. Mol. Sci 2009, 10, 3420–3441. [Google Scholar]
- Makarenkov, L; Leclerc, B. On some relations between 2-trees and tree metrics. Discrete Math 1998, 192, 223–249. [Google Scholar]
- Makarenkov, V; Leclerc, B. An algorithm for the fitting of a tree metric according to weighted least-squares criterion. J. Classif 1999, 16, 3–26. [Google Scholar]
- Makarenkov, L; Leclerc, B. Comparison of additive trees using circular orders. J. Comput. Biol 2000, 7, 731–744. [Google Scholar]
- Makarenkov, L. T-REX: Reconstructing and visualizing phylogenetic trees and reticulation networks. Bioinformatics 2001, 17, 664–668. [Google Scholar]
- Demetrius, L. Boltzmann, Darwin and directionality theory. Quart. Rev. Biophysics, submitted.
- Duchon, A; Hanusse, N; Lebhar, E; Schabanel, N. Could any graph be turned into a small-world. Theor. Comp. Sci 2006, 355, 96–103. [Google Scholar]
- Karonski, M. On the number of k-trees in a random graph. Probability and Math. Statistics 1982, 2, 197–205. [Google Scholar]
- R.W. Robinson, RW; Wormald, NC. Almost all regular graphs are Hamiltonian. Random Structures and Algorithms 1994, 5, 363–374. [Google Scholar]
- Raynaud, H. Sur les graphes aléatoires. Annales de l’institut Henri Poincaré (B) Probabilités et Statistiques 1968, 4, 255–329. [Google Scholar]
- Bollobas, B. Extremal Graph Theory with Emphasis on Probabilistic Methods; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Gao, Y. The degree distribution of random k-trees. Theor. Comp. Sci 2009, 410, 688–695. [Google Scholar]
- Guelzim, N; Bottani, S; Bourgine, P; Kepes, F. Topological and causal structure of the yeast transcriptional regulatory network. Nat. Genet 2002, 31, 60–63. [Google Scholar]
- Briche, J. Adaptation d’un algorithme génétique pour la reconstruction de réseaux de régulation génétique: COGARE; PhD ThesisUniversité du Sud: Toulon, 2009. [Google Scholar]
- Pécou, E; Maass, A; Remenik, D; Briche, J; Gonzales, M. A mathematical model for copper homeostasis in Enterococcus hirae. Math. Biosci 2006, 203, 222–239. [Google Scholar]


| Down | None | Up | Total |
|---|---|---|---|
| 21,729 | 13,110 | 108 | 34,947 |
| 62.18% | 37.51% | 0.31% | 100% |
| Down | None | Up | Total | |
|---|---|---|---|---|
| 2 | 86.19% | 70.53% | 37.04% | 80.16% |
| 3 | 8.28% | 20.93% | 62.96% | 13.20% |
| 4 | 4.59% | 6.71% | 0.00% | 5.37% |
| 5 | 0.70% | 1.83% | 0.00% | 1.12% |
| 6 | 0.24% | 0.00% | 0.00% | 0.15% |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Demongeot, J.; Ben Amor, H.; Elena, A.; Gillois, P.; Noual, M.; Sené, S. Robustness in Regulatory Interaction Networks. A Generic Approach with Applications at Different Levels: Physiologic, Metabolic and Genetic. Int. J. Mol. Sci. 2009, 10, 4437-4473. https://doi.org/10.3390/ijms10104437
Demongeot J, Ben Amor H, Elena A, Gillois P, Noual M, Sené S. Robustness in Regulatory Interaction Networks. A Generic Approach with Applications at Different Levels: Physiologic, Metabolic and Genetic. International Journal of Molecular Sciences. 2009; 10(10):4437-4473. https://doi.org/10.3390/ijms10104437
Chicago/Turabian StyleDemongeot, Jacques, Hedi Ben Amor, Adrien Elena, Pierre Gillois, Mathilde Noual, and Sylvain Sené. 2009. "Robustness in Regulatory Interaction Networks. A Generic Approach with Applications at Different Levels: Physiologic, Metabolic and Genetic" International Journal of Molecular Sciences 10, no. 10: 4437-4473. https://doi.org/10.3390/ijms10104437




