The Capabilities of Chaos and Complexity
Abstract
:1. Introduction
- Modern-day human applications of non linear dynamical systems theory.
- Investigator involvement (artificial selection) in chaos, catastrophe, and complexity experimental designs.
- Information defined in terms of the reduced uncertainty of subjective “observers” and “knowers”, who did not exist for 99.9% of life’s history.
- Prescriptive Information (PI) [1–3]? PI refers not just to intuitive or semantic information, but specifically to linear digital instructions using a symbol system (e.g., 0’s and 1’s, letter selections from an alphabet, A, G, T, or C from a phase space of four nucleotides). PI can also consist of purposefully programmed configurable switch-settings that provide cybernetic controls.
- Bona fide Formal Organization [4]? By “formal” we mean function-oriented, computationally halting, integrated-circuit producing, algorithmically optimized, and choice-contingent at true decision nodes (not just combinatorial bifurcation points).
Molecular substrates can be viewed as computational devices that process physical or chemical ‘inputs’ to generate ‘outputs’ based on a set of logical operators. By recognizing this conceptual crossover between chemistry and computation, it can be argued that the success of life itself is founded on a much longer-term revolution in information handling when compared with the modern semiconductor computing industry. Many of the simpler logic operations can be identified within chemical reactions and phenomena, as well as being produced in specifically designed systems. Some degree of integration can also be arranged, leading, in some instances, to arithmetic processing. These molecular logic systems can also lend themselves to convenient reconfiguring. Their clearest application area is in the life sciences, where their small size is a distinct advantage over conventional semiconductor counterparts. Molecular logic designs aid chemical (especially intracellular) sensing, small object recognition and intelligent diagnostics [181].
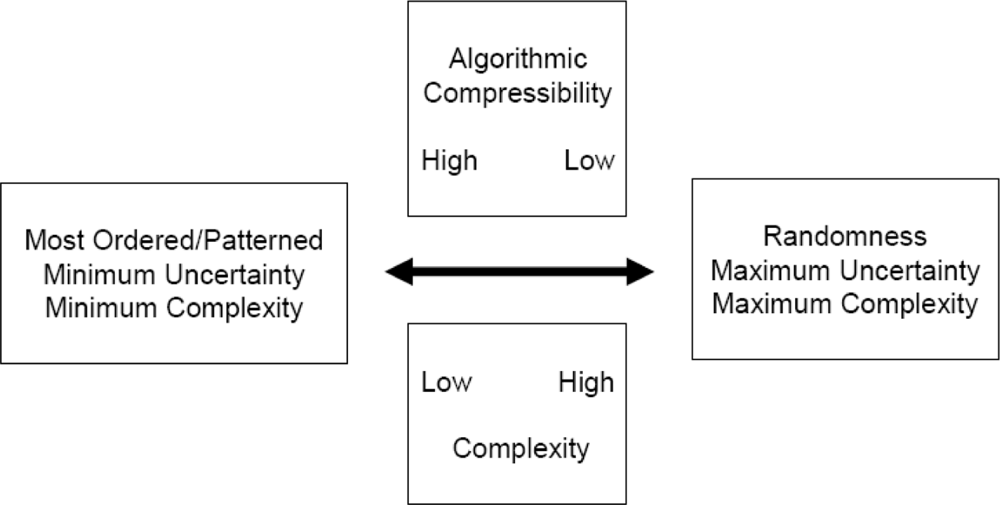
2. What exactly is complexity?
3. Order, structure and pattern
| Adenine | 0.46 (– log2 0.46) | = 0.515 |
| Uracil | 0.40 (– log2 0.40) | = 0.529 |
| Guanine | 0.12 (– log2 0.12) | = 0.367 |
| Cytosine
| 0.02 (– log2 0.02)
| = 0.113
|
| 1.00 | 1.524 bits |
4. Autopoesis
If living systems are machines, that they are physical autopoietic machines is trivially obvious: they transform matter into themselves in a manner such that the product of their operation is their own organization. However, we deem the converse as also true: A physical system if autopoietic is living. In other words, we claim that the notion of autopoiesis is necessary and sufficient to characterize the organization of living systems.
5. Complex adaptive systems (CAS)
6. The big three: Chance, necessity and selection
- Natural selection is a very special case indeed. Differential survival and reproduction of the fittest already-computed, already-living small populations of organisms is very indirect. Selection is not intended; it just happens secondarily. No purpose guides selection events. No true decision nodes are involved because evolution has no goal. In this sense, selection “pressure” is a misnomer. Differential survival is more happenstantial than pushed, more after-the-fact than pursued.
- Artificial selection is the essence of formalism. Despite decades of concentrated research on consciousness and artificial intelligence, choice contingency remains elusive when approached from the direction of physicality. The mind/body problem is alive and well in the philosophy of science.
7. Do symbol systems exist outside of human minds?
8. Symbolic dynamics analysis
9. Two kinds of contingency
- Chance contingency is exampled by heat agitation and Brownian movement of molecules in gas and fluid phases. We refer to chance contingency as “randomness.” Chance contingency is statistically describable and predictable. Relative degrees of determinism and chance contingency can co-exist. Weighted means can be calculated for situations with seeming incomplete determinism. Some argue that all physical behavior is ultimately caused, and that chance contingency is only an illusion. Combinations of forces and their effects can be extremely complex. Yet-to-be-discovered forces and relationships may also be at work [199]. But functionally, on the macroscopic level especially, distinct advantages obtain from regarding chance contingency as real and for quantifying possible outcomes statistically.
- Choice contingency obtains at true decision nodes. Decision nodes are much more than mere bifurcation points. Bifurcation points can be traversed by chance contingency. Any attempt to reduce decision nodes to mere bifurcation points results in rapid deterioration of any potential non trivial formal function. The existence of bifurcation points does not account for computational success. Organization and formal utility are achieved through the controlled opening and closing of logic gates. The latter requires bona fide choices made with steering and programming intent.
10. Configurable switches
11. Two kinds of selection
‘Chemical evolution’ should not be confused with Darwinian evolution with its requirements for reproduction, mutation and natural selection. These did not occur before the development of the first living organism, and so chemical evolution and Darwinian evolution are quite different processes.
12. What optimizes genetic algorithms?
13. Order vs. Organization
14. What exactly is chaos?
- highly ordered,
- monotonous,
- predictable,
- regular (vortices, sand piles)
- low informational
- strings of momentary states
15. The Edge of Chaos
16. Systems theory
- Calculus.
- Algorithm.
- Program that achieves computational halting.
- Organizer of formal function.
- A bona fide system.
17. Formalism vs. Physicality
18. The Cybernetic Cut
19. Conclusions
Acknowledgments
References
- Abel, DL; Trevors, JT. Three subsets of sequence complexity and their relevance to biopolymeric information. Theoret. Biol. Med. Model 2005, 2. [Google Scholar]
- Abel, DL; Trevors, JT. More than metaphor: Genomes are objective sign systems. J. BioSemiotics 2006, 1, 253–267. [Google Scholar]
- Abel, DL. The BioSemiosis of Prescriptive Information. Semiotica, 2009; In Press. [Google Scholar]
- Abel, DL; Trevors, JT. Self-Organization vs. Self-Ordering events in life-origin models. Phys. Life Rev 2006, 3, 211–228. [Google Scholar]
- Abel, DL. To what degree can we reduce “life” without “loss of life”? In Workshop on Life: A satellite meeting before the Millenial World Meeting of University Professors; Palyi, G, Caglioti, L, Zucchi, C, Eds.; University of Modena: Modena, Italy, 2000; Vol. Book of Abstracts; p. 4. [Google Scholar]
- Abel, DL. Is Life Reducible to Complexity? In Fundamentals of Life; Palyi, G, Zucchi, C, Caglioti, L, Eds.; Elsevier: Paris, 2002; pp. 57–72. [Google Scholar]
- Abel, DL. Life origin: The role of complexity at the edge of chaos. In Washington Science 2006; Headquarters of the National Science Foundation: Arlington, VA, 2006. [Google Scholar]
- Abel, DL. Complexity, self-organization, and emergence at the edge of chaos in life-origin models. J. Wash. Acad. Sci 2007, 93, 1–20. [Google Scholar]
- Abel, DL. The ‘Cybernetic Cut’: Progressing from description to prescription in systems theory. Open Cybernet. Systemat. J. 2008, 2, 234–244. [Google Scholar]
- Abel, DL. The GS (Genetic Selection) Principle. Front. Biosci 2009, 14, 2959–2969. [Google Scholar]
- Abel, DL. The capabilities of chaos and complexity. In Society for Chaos Theory: Society for Complexity in Psychology and the Life Sciences; Virginia Commonwealth University: Richmond, VA, Aug; pp. 8–10. 2008. [Google Scholar]
- Abel, DL; Trevors, JT. More than metaphor: Genomes are objective sign systems. In BioSemiotic Research Trends; Barbieri, M, Ed.; Nova Science Publishers, Inc: New York, 2007; pp. 1–15. [Google Scholar]
- Trevors, JT; Abel, DL. Chance and necessity do not explain the origin of life. Cell Biol. Internat 2004, 28, 729–739. [Google Scholar]
- Aristotle. Metaphysics, , Book 8.6.1045a:8–10.
- Lewes, GH. Problems of Life and Mind (First Series); Trübner: London, 1875; Volume 2. [Google Scholar]
- Lovejoy, AO. The meanings of ‘emergence’ and its modes, with an introduction by Alicia Juarrero and Carl A. Rubino. E:CO 2008, 10, 62–78. [Google Scholar]
- Chalmers, DJ. Strong and Weak Emergence. In The Re-Emergence of Emergence; Clayton, P, Davies, P, Eds.; Oxford Univeristy Press: Oxford, UK, 2006. [Google Scholar]
- Steels, L. Towards a Theory of Emergent Functionality. In Animals to Animats 1; Meyer, J-A, Wilson, S, Eds.; MIT Press: Cambridge, Mass, 1991. [Google Scholar]
- Corning, PA. The Re-Emergence of “Emergence”: A Venerable Concept in Search of a Theory. Complexity 2002, 7, 18–30. [Google Scholar]
- Kauffman, SA. The Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Kauffman, S. At Home in the Universe: The Search for the Laws of Self-Organization and Complexity; Oxford University Press: New York, 1995; p. 320. [Google Scholar]
- Kauffman, SA. Investigations; Oxford University Press: New York, 2000; p. 286. [Google Scholar]
- Fromm, J. Types and Forms of Emergence. arXiv:nlin. 2005; 0506028v1 [nlin.AO]. [Google Scholar]
- Bedau, MA. Weak emergence. In Philosophical Perspectives: Mind, Causation, and World; Tomberlin, J, Ed.; Blackwell Publishers: Hoboken, N.J. USA, 1997; Volume 11, pp. 375–399. [Google Scholar]
- Eigen, M. Self-organization of matter and the evolution of biological macromolecules. Naturwissenchaften (In German) 1971, 58, 465–523. [Google Scholar]
- Eigen, M. Molecular self-organization and the early stages of evolution. Experientia 1971, 27, 149–212. [Google Scholar]
- Eigen, M. Life from the test tube? MMW Munch Med. Wochenschr 1983, (Suppl 1), S125–135. [Google Scholar]
- Eigen, M. New concepts for dealing with the evolution of nucleic acids. Cold Spring Harb. Symp. Quant. Biol 1987, 52, 307–320. [Google Scholar]
- Eigen, M. The origin of genetic information: viruses as models. Gene 1993, 135, 37–47. [Google Scholar]
- Eigen, M. Selection and the origin of information. Int. Rev. Neurobiol 1994, 37, 35–46. [Google Scholar]
- Eigen, M; Biebricher, CK; Gebinoga, M; Gardiner, WC. The hypercycle. Coupling of RNA and protein biosynthesis in the infection cycle of an RNA bacteriophage. Biochemistry 1991, 30, 11005–11018. [Google Scholar]
- Eigen, M; de Maeyer, L. Chemical means of information storage and readout in biological systems. Naturwissenchaften 1966, 53, 50–57. [Google Scholar]
- Eigen, M; Winkler-Oswatitsch, R. Transfer-RNA: The early adaptor. Naturwissenchaften 1981, 68, 217–228. [Google Scholar]
- Eigen, M; Winkler-Oswatitsch, R. Transfer-RNA, an early gene? Naturwissenchaften 1981, 68, 282–292. [Google Scholar]
- Eigen, M; Winkler-Oswatitsch, R. Statistical geometry on sequence space. Methods Enzymol 1990, 183, 505–530. [Google Scholar]
- Eigen, M; Winkler-Oswatitsch, R; Dress, A. Statistical geometry in sequence space: A method of quantitative comparative sequence analysis. Proc. Natl. Acad. Sci. USA 1988, 85, 5913–5917. [Google Scholar]
- Gánti, T. Organization of chemical reactions into dividing and metabolizing units: the chemotons. Biosystems 1975, 7, 15–21. [Google Scholar]
- Gánti, T. On the organizational basis of the evolution. Acta Biol 1980, 31, 449–459. [Google Scholar]
- Gánti, T. Biogenesis itself. J. Theor. Biol 1997, 187, 583–593. [Google Scholar]
- Gánti, T. On the early evolutionary origin of biological periodicity. Cell Biol. Int 2002, 26, 729–735. [Google Scholar]
- Gánti, T. The Principles of Life; Oxford University Press: Oxford, UK, 2003; p. 200. [Google Scholar]
- Eigen, M; Gardiner, W; Schuster, P; Winkler-Oswatitsch, R. The origin of genetic information. Sci. Am 1981, 244, 88–92. [Google Scholar]
- Eigen, M; Gardiner, W; Schuster, P; Winkler-Oswatitsch, R. The origin of genetic information, laws governing natural selection of prebiotic molecules have been inferred and tested, making it possible to discover how early RA genes interacted with proteins and how the genetic code developed. Sci. Am 1981, 244, 88–118. [Google Scholar]
- Eigen, M; Gardiner, WC, Jr; Schuster, P. Hypercycles and compartments. Compartments assists—but do not replace—hypercyclic organization of early genetic information. J. Theor. Biol 1980, 85, 407–411. [Google Scholar]
- Eigen, M; Schuster, P. The hypercycle. A principle of natural self-organization. Part A: Emergence of the hypercycle. Naturwissenchaften 1977, 64, 541–565. [Google Scholar]
- Eigen, M; Schuster, P. The Hypercycle: A Principle of Natural Self Organization; Springer Verlag: Berlin, 1979. [Google Scholar]
- Eigen, M; Schuster, P. Comments on “growth of a hypercycle” by King (1981). Biosystems 1981, 13, 235. [Google Scholar]
- Eigen, M; Schuster, P. Stages of emerging life—five principles of early organization. J. Mol. Evol 1982, 19, 47–61. [Google Scholar]
- Eigen, M; Schuster, P; Sigmund, K; Wolff, R. Elementary step dynamics of catalytic hypercycles. Biosystems 1980, 13, 1–22. [Google Scholar]
- Waldrop, MM. Complexity; Simon and Schuster: New York, 1992. [Google Scholar]
- Kauffman, SA; Johnsen, S. Coevolution to the edge of chaos: Coupled fitness landscapes, poised states, and coevolutionary avalanches. J. Theor. Biol 1991, 149, 467–505. [Google Scholar]
- Bratman, RL. Edge of chaos. J. R. Soc. Med 2002, 95, 165. [Google Scholar]
- Ito, K; Gunji, YP. Self-organisation of living systems towards criticality at the edge of chaos. Biosystems 1994, 33, 17–24. [Google Scholar]
- Munday, D. Edge of chaos. J. R. Soc. Med 2002, 95, 165. [Google Scholar]
- Forrest, S. Creativity on the edge of chaos. Semin. Nurse Manag 1999, 7, 136–140. [Google Scholar]
- Innes, AD; Campion, PD; Griffiths, FE. Complex consultations and the ‘edge of chaos’. Br. J. Gen. Pract 2005, 55, 47–52. [Google Scholar]
- Mitchell, M; Hraber, PT; Crutchfield, JT. Dynamics, computation, and “the edge of chaos:” A re-examination. In Complexity: Metaphors, Models, and Reality; Cowan, GPD, Melzner, D, Eds.; Addison-Wesley: Reading, MA, 1994; pp. 1–16. [Google Scholar]
- Kauffman, S. Behavior of randomly constructed genetic nets. In Towards a Theoretical Biology Vol. 3; Waddington, CH, Ed.; Aldine Publishing Co.: Chicago, 1970; Volume 3, p. 18. [Google Scholar]
- Kauffman, S. Beyond Reductionism: Reinventing the Sacred. Zygon 2007, 42, 903–914. [Google Scholar]
- Kauffman, SA. Prolegomenon to a general biology. Ann. N.Y. Acad. Sci 2001, 935, 18–36. [Google Scholar]
- Dawkins, R. The Selfish Gene, 2nd Ed ed; Oxford Univerisy Press: Oxford, UK, 1989. [Google Scholar]
- Dawkins, R. The Blind Watchmaker; W. W. Norton and Co.: New York, 1986. [Google Scholar]
- Dawkins, R. Climbing Mount Impossible; W. W. Norton and Co.: New York, 1996. [Google Scholar]
- Gell-Mann, M. What is complexity? Complexity 1995, 1, 16–19. [Google Scholar]
- Ricard, J. What do we mean by biological complexity? C.R. Biol 2003, 326, 133–140. [Google Scholar]
- van de Vijver, G; van Speybroeck, L; Vandevyvere, W. Reflecting on complexity of biological systems: Kant and beyond? Acta Biotheor 2003, 51, 101–109. [Google Scholar]
- Edelman, GM; Gally, JA. Degeneracy and complexity in biological systems. Proc. Natl. Acad. Sci. USA 2001, 98, 13763–13768. [Google Scholar]
- Simon, HA. The architecture of complexity. Proc. Am. Philos. Soc 1962, 106, 467–482. [Google Scholar]
- Nicolis, G; Prigogine, I. Exploring Complexity; Freeman: New York, 1989. [Google Scholar]
- Badii, R; Politi, A. Complexity: Hierarchical Structures and Scaling in Physics; Cambridge University Press: New York, 1997; p. 318. [Google Scholar]
- Yockey, HP. Information Theory and Molecular Biology; Cambridge University Press: Cambridge, 1992; p. 408. [Google Scholar]
- Yockey, HP. Information Theory, Evolution, and the Origin of Life, 2nd Ed ed; Cambridge University Press: Cambridge, 2005. [Google Scholar]
- Lenski, RE; Ofria, C; Collier, TC; Adami, C. Genome complexity, robustness and genetic interactions in digital organisms. Nature 1999, 400, 661–664. [Google Scholar]
- Lempel, A; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inform. Theory 1976, 22, 75. [Google Scholar]
- Konopka, AK; Owens, J. Complexity charts can be used to map functional domains in DNA. Genet. Anal. Tech. Appl 1990, 7, 35–38. [Google Scholar]
- Adami, C; Cerf, NJ. Physical complexity of symbolic sequences. Physica D 2000, 137, 62–69. [Google Scholar]
- Durston, KK; Chiu, DK; Abel, DL; Trevors, JT. Measuring the functional sequence complexity of proteins. Theor. Biol. Med. Model 2007, 4. [Google Scholar]
- Ebeling, W; Jimenez-Montano, MA. On grammars, complexity, and information measures of biological macromolecules. Math. Biosci 1980, 52, 53–71. [Google Scholar]
- Gell-Mann, M; Lloyd, S. Information measures, effective complexity, and total information. Complexity 1996, 2, 44–52. [Google Scholar]
- Zurek, WH. Complexity, Entropy, and the Physics of Information; Addison-Wesley: Redwood City, CA, 1990. [Google Scholar]
- Farre, GL; Oksala, T. Emergence, Complexity, Hierarchy, Organization; Selected and Edited Papers from ECHO III; Acta Polytechnia Scandinavica; Espoo: Helsinki, 1998. [Google Scholar]
- Rosen, R. On information and complexity. In Complexity, Language, and Life: Mathematical Approaches; Casti, JL, Karlqvist, A, Eds.; Springer: Berlin, 1985. [Google Scholar]
- Zvonkin, AK; Levin, LA. The complexity of finite objects and the development of the concepts of information and randomness by means of the theory of algorithms. Russ. Math. Surv 1970, 256, 83–124. [Google Scholar]
- Konopka, AK. Is the information content of DNA evolutionarily significant? J. Theor. Biol 1984, 107, 697–704. [Google Scholar]
- Konopka, AK. Theory of degenerate coding and informational parameters of protein coding genes. Biochimie 1985, 67, 455–468. [Google Scholar]
- Konopka, AK. Sequences and Codes: Fundamentals of Biomolecular Cryptology. In Biocomputing: Informatics and Genome Projects; Smith, D, Ed.; Academic Press: San Diego, 1994; pp. 119–174. [Google Scholar]
- Konopka, AK. Systems biology: Aspects related to genomics. In Nature Encyclopidia of the Human Genome; Cooper, DN, Ed.; Nature Publishing Group Reference: London, 2003; Volume 5, pp. 459–465. [Google Scholar]
- Konopka, AK. Information theories in molecular biology and genomics. In Nature Encyclopedia of teh Human Genome; Cooper, DN, Ed.; Nature Publishing Group Reference: London, 2003; Volume 3, pp. 464–469. [Google Scholar]
- Konopka, AK. Sequence complexity and composition. In Nature Encyclopedia of the Human Genome; Volume 5, Cooper, DN, Ed.; Nature Publishing Group Reference: London, 2003; pp. 217–224. [Google Scholar]
- Koonin, EV. Evolution of genome architecture. Int. J. Biochem. Cell Biol 2009, 41, 298–306. [Google Scholar]
- Koonin, EV; Dolja, VV. Evolution of complexity in the viral world: The dawn of a new vision. Virus research 2006, 117, 1–4. [Google Scholar]
- Koonin, EV; Wolf, YI. Genomics of bacteria and archaea: The emerging dynamic view of the prokaryotic world. Nucleic Acids Res 2008, 36, 6688–6719. [Google Scholar]
- Toussaint, O; Schneider, ED. The thermodynamics and evolution of complexity in biological systems. Comp. Biochem. Physiol. A Mol. Integr. Physiol 1998, 120, 3–9. [Google Scholar]
- Barham, J. A dynamical model of the meaning of information. Biosystems 1996, 38, 235–241. [Google Scholar]
- Stonier, T. Information as a basic property of the universe. Biosystems 1996, 38, 135–140. [Google Scholar]
- Boniolo, G. Biology without information. Hist. Phil. Life Sci 2003, 25, 255–273. [Google Scholar]
- Sarkar, S. Biological information: A skeptical look at some central dogmas of molecular biology. In The Philosophy and History of Molecular Biology: New Perspectives; Sarkar, S, Ed.; Kluwer Academic Publishers: Dordrecht, 1996; pp. 187–231. [Google Scholar]
- Sarkar, S. Information in genetics and developmental biology: Comments on Maynard Smith. Philos. Sci 2000, 67, 208–213. [Google Scholar]
- Sarkar, S. Genes encode information for phenotypic traits. In Comtemporary debates in Philosophy of Science; Hitchcock, C, Ed.; Blackwell: London, 2003; pp. 259–274. [Google Scholar]
- Stent, GS. Strength and weakness of the genetic approach to the development of the nervous system. Annu. Rev. Neurosci 1981, 4, 163–194. [Google Scholar]
- Griffiths, PE. Genetic information: A metaphor in search of a theory. Philos. Sci 2001, 68, 394–412. [Google Scholar]
- Godfrey-Smith, P. Genes do not encode information for phenotypic traits. In Contemporary Debates in Philosophy of Science; Hitchcock, C, Ed.; Blackwell: London, 2003; pp. 275–289. [Google Scholar]
- Noble, D. Modeling the heart—from genes to cells to the whole organ. Science 2002, 295, 1678–1682. [Google Scholar]
- Mahner, M; Bunge, MA. Foundations of Biophilosophy; Springer Verlag: Berlin, 1997. [Google Scholar]
- Kitcher, P. Battling the undead; how (and how not) to resist genetic determinism. In Thinking About Evolution: Historical Philosophical and Political Perspectives; Singh, RS, Krimbas, CB, Paul, DB, Beattie, J, Eds.; Cambridge University Press: Cambridge, 2001; pp. 396–414. [Google Scholar]
- Chargaff, E. Essays on Nucleic Acids; Elsevier: Amsterdam, 1963. [Google Scholar]
- Jacob, F. The Logic of Living Systems—a History of Heredity; Allen Lane: London, 1974. [Google Scholar]
- Alberts, B; Bray, D; Lewis, J; Raff, M; Roberts, K; Watson, JD. Molecular Biology of the Cell; Garland Science: New York, 2002. [Google Scholar]
- Davidson, EH; Rast, JP; Oliveri, P; Ransick, A; Calestani, C; Yuh, CH; Minokawa, T; Amore, G; Hinman, V; Arenas-Mena, C; Otim, O; Brown, CT; Livi, CB; Lee, PY; Revilla, R; Rust, AG; Pan, Z; Schilstra, MJ; Clarke, PJ; Arnone, MI; Rowen, L; Cameron, RA; McClay, DR; Hood, L; Bolouri, H. A genomic regulatory network for development. Science 2002, 295, 1669–1678. [Google Scholar]
- Wolpert, L; Smith, J; Jessell, T; Lawrence, P. Principles of Development; Oxford University Press: Oxford, 2002. [Google Scholar]
- Stegmann, UE. Genetic information as instructional content. Philos. Sci 2005, 72, 425–443. [Google Scholar]
- Barbieri, M. Biology with information and meaning. Hist. Philos.Life Sci 2004, 25, 243–254. [Google Scholar]
- Deely, J. Semiotics and biosemiotics: Are sign-science and life-science coextensive? In Biosemiotics: The Semiotic Web 1991; Sebeok, TA, Umiker-Sebeok, J, Eds.; Mouton de Gruyter: Berlin/N.Y., 1992; pp. 46–75. [Google Scholar]
- Sebeok, TA; Umiker-Sebeok, J. Biosemiotics: The Semiotic Web 1991; Mouton de Gruyter: Berlin, 1992. [Google Scholar]
- Hoffmeyer, J. Biosemiotics: Towards a new synthesis in biology. Eur. J. Semiotic Stud 1997, 9, 355–376. [Google Scholar]
- Sharov, A. Biosemiotics. A functional-evolutionary approach to the analysis of the sense of evolution. In Biosemiotics: The Semiotic Web 1991; Sebeok, TA, Umiker-Sebeok, J, Eds.; Mouton de Gruyter: Berlin, 1992; pp. 345–373. [Google Scholar]
- Kull, K. Biosemiotics in the twentieth century: A view from biology. Semiotica 1999, 127, 385–414. [Google Scholar]
- Kawade, Y. Molecular biosemiotics: molecules carry out semiosis in living systmes. Semiotica 1996, 111, 195–215. [Google Scholar]
- Barbieri, M. Life is ‘artifact-making’. J. BioSemiotics 2005, 1, 113–142. [Google Scholar]
- Pattee, HH. The physics and metaphysics of Biosemiotics. J. BioSemiotics 2005, 1, 303–324. [Google Scholar]
- Salthe, SN. Meaning in nature: Placing biosemitotics within pansemiotics. J. BioSemiotics 2005, 1, 287–301. [Google Scholar]
- Kull, K. A brief history of biosemiotics. J. BioSemiotics 2005, 1, 1–36. [Google Scholar]
- Nöth, W. Semiotics for biologists. J. BioSemiotics 2005, 1, 195–211. [Google Scholar]
- Artmann, S. Biosemiotics as a structural science. J. BioSemiotics 2005, 1, 247–285. [Google Scholar]
- Barbieri, M. Is the Cell a Semiotic System? In Introduction to Biosemiotics: The New Biological Synthesis; Barbieri, M, Ed.; Springer-Verlag New York, Inc.: Secaucus, NJ, USA, 2006. [Google Scholar]
- Barbieri, M. Introduction to Biosemiotics: The New Biological Synthesis; Springer-Verlag New York, Inc.: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Barbieri, M. Has biosemiotics come of age? In Introduction to Biosemiotics: The New Biological Synthesis; Barbieri, M, Ed.; Springer: Dorcrecht, The Netherlands, 2007; pp. 101–114. [Google Scholar]
- Jämsä, T. Semiosis in evolution. In Introduction to Biosemiotics: The New Biological Synthesis; Barbieri, M, Ed.; Springer-Verlag New York, Inc.: Dordrecht, The Netherlands; Secaucus, NJ, USA, 2006. [Google Scholar]
- Hoffmeyer, J. Semiotic scaffolding of living systems. In Introduction to Biosemiotics: The New Biological Synthesis; Barbieri, M, Ed.; Springer-Verlag New York, Inc.: Dordrecht, The Netherlands, 2006; pp. 149–166. [Google Scholar]
- Kull, K. Biosemiotics and biophysics—The fundamental approaches to the study of life. In Introduction to Biosemiotics: The New Biological Synthesis; Barbieri, M, Ed.; Springer-Verlag New York, Inc.: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Barbieri, M. The Codes of Life: The Rules of Macroevolution (Biosemiotics); Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Barbieri, M. Biosemiotics: A new understanding of life. Naturwissenchaften 2008, 95, 577–599. [Google Scholar]
- Hodge, B; Caballero, L. Biology, semiotics, complexity: An experiment in interdisciplinarity. Semiotica 2005, 477–495. [Google Scholar]
- Adami, C; Ofria, C; Collier, TC. Evolution of biological complexity. P.N.A.S 2000, 97, 4463–4468. [Google Scholar]
- Goodwin, B. How the Leopard Changed Its Spots: The Evolution of Complexity; Simon and Schuster; Charles Scribner & Sons: New York, 1994. [Google Scholar]
- Mao, C. The emergence of complexity: Lessons from DNA. PLoS Biol 2004, 2, e431. [Google Scholar]
- Holland, JH. Hidden Order: How Adaptation Builds Complexity; Addison-Wesley: Redwood City, CA, 1995. [Google Scholar]
- Mikulecky, DC. The emergence of complexity: Science coming of age or science growing old? Computers Chem 2001, 25, 341–348. [Google Scholar]
- Salthe, SN. Development and Evolution: Complexity and Change in Biology; MIT Press: Cambridge, MA, 1993. [Google Scholar]
- Pattee, HH. Causation, Control, and the Evolution of Complexity. In Downward Causation: Minds, Bodies, and Matter; Andersen, PB, Emmeche, C, Finnemann, NO, Christiansen, PV, Eds.; Aarhus University Press: Aarhus, DK, 2000; pp. 63–77. [Google Scholar]
- Szathmary, E; Smith, JM. The major evolutionary transitions. Nature 1995, 374, 227–232. [Google Scholar]
- Sole, R; Goodwin, B. Signs of Life: How Complexity Pervades Biology; Basic Books: New York, 2000. [Google Scholar]
- Stano, P; Luisi, PL. Basic questions about the origins of life: proceedings of the Erice international school of complexity (fourth course). Orig. Life Evol. Biosh 2007, 37, 303–307. [Google Scholar]
- Homberger, DG. Ernst Mayr and the complexity of life. J. Biosci 2005, 30, 427–433. [Google Scholar]
- Pross, A. On the emergence of biological complexity: life as a kinetic state of matter. Orig. Life Evol. Biosph 2005, 35, 151–166. [Google Scholar]
- Bedau, MA. Artificial life: Organization, adaptation and complexity from the bottom up. Trends Cogn. Sci 2003, 7, 505–512. [Google Scholar]
- Umerez, J. Howard Pattee’s theoretical biology--a radical epistemological stance to approach life, evolution and complexity. Biosystems 2001, 60, 159–177. [Google Scholar]
- Branca, C; Faraone, A; Magazu, S; Maisano, G; Migliardo, P; Villari, V. Suspended life in biological systems. Fragility and complexity. Ann. N.Y. Acad. Sci 1999, 879, 224–227. [Google Scholar]
- Oltvai, ZN; Barabasi, AL. Systems biology. Life’s complexity pyramid. Science 2002, 298, 763–764. [Google Scholar]
- Rosen, R. Complexity and system description. In Systems, Approaches, Theories, Applications; Harnett, WE, Ed.; Reidel Co.: Boston, MA, 1977. [Google Scholar]
- Rosen, R. On Complex Systems. Euro. J. Operational Rsrch 1987, 30, 129–134. [Google Scholar]
- Behe, MJ. Darwin’s Black Box; The Free Press: New York, 1996. [Google Scholar]
- Anderson, E. Irreducible complexity reduced: An integrated Approach to the complexity space. PCID 2004, 1–29. [Google Scholar]
- Thompson, C. Fortuitous phenomena: On complexity, pragmatic randomised controlled trials, and knowledge for evidence-based practice. Worldviews Evid. Based Nurs 2004, 1, 9–17. [Google Scholar]
- Pennock, RT. Creationism and intelligent design. Annu. Rev. Genomics Hum. Genet 2003, 4, 143–163. [Google Scholar]
- Aird, WC. Hemostasis and irreducible complexity. J. Thromb. Haemost 2003, 1, 227–230. [Google Scholar]
- Keller, EF. Developmental robustness. Ann. N.Y. Acad. Sci 2002, 981, 189–201. [Google Scholar]
- von Neumann, J; Burks, AW. Theory of Self-Reproducing Automata; University of Illinois Press: Urbana, 1966; p. xix. 388 p. [Google Scholar]
- Pattee, HH. The complementarity principle in biological and social structures. J. Soc. Biol. Struct 1978, 1, 191–200. [Google Scholar]
- Pattee, HH. Complementarity vs. reduction as explanation of biological complexity. Amer. J. Physiol 1979, 236, R241–246. [Google Scholar]
- Pattee, HH. Evolving self-reference: Matter, symbols, and semantic closure. Commun. Cog 1995, 12, 9–28. [Google Scholar]
- Hoffmeyer, J. Code-duality and the epistemic cut. Ann. N.Y. Acad. Sci 2000, 901, 175–186. [Google Scholar]
- Hoffmeyer, J. Code duality revisited. SEED 2002, 2, 1–19. [Google Scholar]
- Lectures in the Sciences of Complexity; Stein, DL (Ed.) Addison-Wesley: Redwood City, CA, 1988.
- Norris, V; Cabin, A; Zemirline, A. Hypercomplexity. Acta Biotheor 2005, 53, 313–330. [Google Scholar]
- Garzon, MH; Jonoska, N; Karl, SA. The bounded complexity of DNA computing. Bio. Systems 1999, 52, 63–72. [Google Scholar]
- Levins, R. The limits of complexity. In Biological Hierarchies: Their Origin and Dynamics; Pattee, H, Ed.; Gordon and Breach: New York, 1971. [Google Scholar]
- Bennett, DH. Logical depth and physical complexity. In The Universal Turing Machine: A Half-Century Survey; Herken, R, Ed.; Oxford University Press: Oxford, 1988. [Google Scholar]
- Grandpierre, A. Complexity, information and biological organization. INDESC 2005, 3, 59–71. [Google Scholar]
- Chandler, JL. Complexity IX. Closure over the organization of a scientific truth. Ann. N.Y. Acad. Sci 2000, 901, 75–90. [Google Scholar]
- Wimsatt, WC. Complexity and organization. In SA-1972 (Boston Studies in the Philosophy of Science); Reidel: Dordrecht, 1974; Volume 20, pp. 67–86. [Google Scholar]
- Mayr, E. Introduction, pp. 1–7; Is biology an autonomous science? pp. 8–23. In Toward a New Philosophy of Biology, Part 1; Mayr, E, Ed.; Harvard University Press: Cambridge, MA, 1988. [Google Scholar]
- Mayr, E. The place of biology in the sciences and its conceptional structure. In The Growth of Biological Thought: Diversity, Evolution, and Inheritance; Mayr, E, Ed.; Harvard University Press: Cambridge, MA, 1982; pp. 21–82. [Google Scholar]
- Monod, J. Chance and Necessity; Knopf: New York, 1972. [Google Scholar]
- Mayr, E. What Evolution Is; Basic Books: New York, 2001. [Google Scholar]
- Popper, K. Conjectures and Refutations; Harper: New York, 1963. [Google Scholar]
- Popper, K. The Logic of Scientific Discovery; Hutchinson, London, 1968. [Google Scholar]
- Kuhn, TS. The Structure of Scientific Revolutions, 2nd Ed ed; The University of Chicago Press: Chicago, 1970. [Google Scholar]
- Dinger, ME; Pang, KC; Mercer, TR; Mattick, JS. Differentiating protein-coding and noncoding RNA: Challenges and ambiguities. PLoS computational biology 2008, 4, e1000176. [Google Scholar]
- Banks, E; Nabieva, E; Chazelle, B; Singh, M. Organization of Physical Interactomes as Uncovered by Network Schemas. PLoS Computational Biology 2008, 4, e1000203. [Google Scholar]
- de Silva, AP; Uchiyama, S. Molecular logic and computing. Nat. Nano 2007, 2, 399–410. [Google Scholar]
- Adami, C. What is complexity? Bioessays 2002, 24, 1085–1094. [Google Scholar]
- Li, M; Vitanyi, P. An Introduction to Kolmogorov Complexity and Its Applications, 2nd Ed ed; Springer-Verlag: New York, 1997; p. 637. [Google Scholar]
- Chaitin, GJ. Algorithmic information theory, 1st paperback Ed ed; Cambridge University Press: Cambridge, UK; New York, 2004. [Google Scholar]
- Yockey, HP. Information theory, evolution and the origin of life. Inform. Sci 2002, 141, 219–225. [Google Scholar]
- Shannon, C. Part I and II: A mathematical theory of communication. Bell Sys. Tech. J. 1948, XXVII, 379–423. [Google Scholar]
- Chaitin, GJ. Algorithmic Information Theory; Revised Second Printing Ed; Cambridge University Press: Cambridge, 1988. [Google Scholar]
- Vitányi, PMB; Li, M. Minimum Description Length Induction, Bayesianism and Kolmogorov Complexity. IEEE Trans. Inform. Theory 2000, 46, 446–464. [Google Scholar]
- Swinburne, R. Simplicity as Evidence for Truth; Marquette University Press: Milwaukee, Wisconsin, 1997. [Google Scholar]
- Barbieri, M. The Organic Codes: An Introduction to Semantic Biology; Cambridge University Press: Cambridge, 2003. [Google Scholar]
- Pattee, HH. The physical basis of coding and reliabiity in biological evolution. In Prolegomena to Theoretical Biology; Waddington, CH, Ed.; University of Edinburgh: Edinburgh, 1968. [Google Scholar]
- Pattee, HH. How does a molecule become a message? In Communication in Development; Twenty-eighth Symposium of the Society of Developmental Biology; Lang, A, Ed.; Academic Press: New York, 1969; pp. 1–16. [Google Scholar]
- Pattee, HH. Physical problems of decision-making constraints. Int. J. Neurosci 1972, 3, 99–106. [Google Scholar]
- Pattee, HH. The physics of symbols: Bridging the epistemic cut. Biosystems 2001, 60, 5–21. [Google Scholar]
- Durston, KK; Chiu, DKY. A functional entropy model for biological sequences. Dynamics of Continuous, Discrete & Impulsive Systems, Series B 2005. [Google Scholar]
- Rocha, LM. Evolution with material symbol systems. Biosystems 2001, 60, 95–121. [Google Scholar]
- Rocha, LM; Hordijk, W. Material representations: From the genetic code to the evolution of cellular automata. Artif. Life 2005, 11, 189–214. [Google Scholar]
- Mitchell, M; Hraber, PT; Crutchfield, JT. Revisiting the edge of chaos: Evolving cellular automata to perform computations. Complex Systems 1993, 7, 89–130. [Google Scholar]
- Pearle, J. Causation; Cambridge University Press: Cambridge, 2000. [Google Scholar]
- Shapiro, R. Prebiotic cytosine synthesis: A critical analysis and implications for the origin of life. Proc. Natl. Acad. Sci. USA 1999, 96, 4396–4401. [Google Scholar]
- Ferris, JP; Huang, CH; Hagan, WJ, Jr. Montmorillonite: A multifunctional mineral catalyst for the prebiological formation of phosphate esters. Orig. Life Evol. Biosph 1988, 18, 121–133. [Google Scholar]
- Ferris, JP; Ertem, G. Oligomerization of ribonucleotides on montmorillonite: reaction of the 5’-phosphorimidazolide of adenosine. Science 1992, 257, 1387–1389. [Google Scholar]
- Ferris, JP. Catalysis and prebiotic RNA synthesis. Orig. Life Evol. Biosph 1993, 23, 307–315. [Google Scholar]
- Ferris, JP; Hill, AR, Jr; Liu, R; Orgel, LE. Synthesis of long prebiotic oligomers on mineral surfaces. Nature 1996, 381, 59–61. [Google Scholar]
- Miyakawa, S; Ferris, JP. Sequence- and regioselectivity in the montmorillonite-catalyzed synthesis of RNA. J. Am. Chem. Soc 2003, 125, 8202–8208. [Google Scholar]
- Huang, W; Ferris, JP. Synthesis of 35–40 mers of RNA oligomers from unblocked monomers. A simple approach to the RNA world. Chem. Commun. (Camb) 2003, 12, 1458–1459. [Google Scholar]
- Kolmogorov, AN. Three approaches to the quantitative definition of the concept “quantity of information”. Problems Inform. Transmission 1965, 1, 1–7. [Google Scholar]
- Gilbert, W. Origin of life — the RNA World. Nature 1986, 319, 618. [Google Scholar]
- Gesteland, RF; Cech, TR; Atkins, JF. The RNA World, 2nd Ed ed; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, 1999. [Google Scholar]
- Cairns-Smith, AG. Seven Clues to the Origin of Life; Canto Ed.; Cambridge University Press: Cambridge, 1990; p. 130. [Google Scholar]
- Cairns-Smith, AG. The origin of life and the nature of the primitive gene. J. Theor. Biol 1966, 10, 53–88. [Google Scholar]
- Cairns-Smith, AG. Takeover mechanisms and early biochemical evolution. Biosystems 1977, 9, 105–109. [Google Scholar]
- Cairns-Smith, AG; Walker, GL. Primitive metabolism. Curr. Mod. Biol 1974, 5, 173–186. [Google Scholar]
- Segre, D; Ben-Eli, D; Lancet, D. Compositional genomes: prebiotic information transfer in mutually catalytic noncovalent assemblies. Proc. Natl. Acad. Sci. USA 2000, 97, 4112–4117. [Google Scholar]
- Segre, D; Lancet, D; Kedem, O; Pilpel, Y. Graded autocatalysis replication domain (GARD): Kinetic analysis of self-replication in mutually catalytic sets. Orig. Life Evol. Biosph 1998, 28, 501–514. [Google Scholar]
- Guimaraes, RC. Linguistics of biomolecules and the protein-first hypothesis for the origins of cells. J. Biol. Phys 1994, 20, 193–199. [Google Scholar]
- Shapiro, R. A replicator was not involved in the origin of life. IUBMB Life 2000, 49, 173–176. [Google Scholar]
- Freeland, SJ; Knight, RD; Landweber, LF. Do proteins predate DNA? Science 1999, 286, 690–692. [Google Scholar]
- Rode, BM. Peptides and the origin of life. Peptides 1999, 20, 773–786. [Google Scholar]
- Wong, JT. A co-evolution theory of the genetic code. Proc. Natl. Acad. Sci. USA 1975, 72, 1909–1912. [Google Scholar]
- Wong, JT. The evolution of a universal genetic code. Proc. Natl. Acad. Sci. USA 1976, 73, 2336–2340. [Google Scholar]
- Wong, JT. Coevolution theory of the genetic code at age thirty. Bioessays 2005, 27, 416–425. [Google Scholar]
- Wong, JT. Question 6: coevolution theory of the genetic code: a proven theory. Orig. Life Evol. Biosph 2007, 37, 403–408. [Google Scholar]
- Zhao, YF; Cao, P-s. Phosphoryl amino acids: Common origin for nucleic acids and protein. J. Biol. Phys 1994, 20, 283–287. [Google Scholar]
- Zhou, W; Ju, Y; Zhao, Y; Wang, Q; Luo, G. Simultaneous formation of peptides and nucleotides from N-phosphothreonine. Orig. Life Evol. Biosph 1996, 26, 547–560. [Google Scholar]
- Nashimoto, M. The rna/protein symmetry hypothesis: Experimental support for reverse translation of primitive proteins. J. Theor. Biol 2001, 209, 181–187. [Google Scholar]
- Dyson, FJ. Origins of Life, 2nd ed; Cambridge University Press: Cambridge, 1998. [Google Scholar]
- Dyson, F. Life in the Universe: Is Life Digital or Analog? NASA Goddard Space Flight Center Colloquiem: Greenbelt, MD, 1999. [Google Scholar]
- Dyson, FJ. A model for the origin of life. J. Mol. Evol 1982, 18, 344–350. [Google Scholar]
- Maturana, H; Varela, F. Autopoiesis and Cognition: The Realization of the Living; Reidel: Dordrecht, 1980. [Google Scholar]
- Maturana, HR. The organization of the living: a Theory of the Living Organization. International Journal of Human-Computer Studies 1999, 51, 149–168. [Google Scholar]
- Maturana, HR; Varela, FJ. Review of The Tree of Knowledge: The Biological Roots of Human Understanding; Rev. Ed.; Shambhala; Distributed in the U.S. by Random House: Boston New York, 1992; p. 269. [Google Scholar]
- Luisi, PL. Autopoiesis: A review and a reappraisal. Naturwissenchaften 2003, 90, 49–59. [Google Scholar]
- Boden, MA. The Philosophy of Artificial Life. Oxford Readings in Philosophy; Publisher: New York, 1996. [Google Scholar]
- Boden, MA. Autopoiesis and life. Cognitive Science Quarterly 2000, 1, 117–145. [Google Scholar]
- Boden, MA. The Creative Mind: Myths and Mechanisms; Routledge: New York, 2004. [Google Scholar]
- Holland, JH. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, 1975. [Google Scholar]
- Holland, JH. Emergence: From chaos to order; Perseus Books: Reading, MA, 1998. [Google Scholar]
- Johnson, J. The Allure of Machinic Life: Cybernetics, Artificial Life, and the New AI; MIT Press: Bradford Books: Cambridge, 2008. [Google Scholar]
- Rocha, LM; Yaeger, LS; Bedau, MA; Floreano, D; Goldstone, RL; Vespignani, A. Artificial Life X: Proceedings of the Tenth International Conference on the Simulation and Synthesis of Living Systems; MIT Press: Cambridge, MA, 2006. [Google Scholar]
- Rasmussen, S; Chen, L; Nilsson, M; Abe, S. Bridging nonliving and living matter. Artificial Life 2003, 9, 269–316. [Google Scholar]
- Bedau, MA; McCaskill, JS; Packard, NH; Rasmussen, S; Adami, C; Green, DG; Ikegami, T; Kaneko, K; Ray, TS. Open problems in artificial life. Artif. Life 2000, 6, 363–376. [Google Scholar]
- Adami, C. Introduction to Artificial Life; Springer/Telos: New York, 1998; p. 374. [Google Scholar]
- Langton, CG. Studying Artificial life with cellular automata. Physica D 1986, 22, 120–149. [Google Scholar]
- Langton, CG. Artificial life. In Artificial Life; Langton, C, Ed.; Addison-Wiley: Redwood City, CA, 1988; pp. 1–47. [Google Scholar]
- Langton, CG. Introduction. In Artificial Life II; Langton, C, Taylor, C, Farmer, JS, Rasmussen, E, Eds.; Addison-Wesley: Redwood City, California USA, 1992; pp. 1–23. [Google Scholar]
- Bateson, G. Steps to an Ecology of Mind; Chandler: New York, 1972. [Google Scholar]
- Bateson, G. Mind and Nature; Bentam Books: New York, 1979. [Google Scholar]
- Bateson, G; Bateson, MC. Angels fear: Towards an epistemology of the sacred; Hampton Press: Cresskill, New Jersey, USA, 2005. [Google Scholar]
- Carnap, R; Bar-Hillel, Y. An outline of a theory of semantic information. Technical Report #247, MIT Research Laboratory in Electronics; Also in Bar-Hillel, 1964, Language and Information, Chapter 15, 1952. [Google Scholar]
- Bar-Hillel, Y. Semantic Information and Its Measures, Transactions of the Tenth Conference on Cybernetics, New York; Josiah Macy Jr. Foundation: New York; pp. 33–48.
- Devlin, K. Logic and Information; Cambridge University Press: New York, 1991. [Google Scholar]
- Barwise, J; Perry, J. Situations and Attitudes; MIT Press: Cambridge, MA, 1983. [Google Scholar]
- Floridi, L. Information. In The Blackwell Guide to the Philosophy of Computing and Information; Floridi, L, Ed.; Blackwell: Oxford, 2003; pp. 40–62. [Google Scholar]
- Floridi, L. Open problems in the philosophy of information. Metaphilosophy 2003, 35, 554–582. [Google Scholar]
- Dretske, F. Knowledge and the Flow of Information; MIT Press: Cambridge, MA, 1981. [Google Scholar]
- Bar-Hillel, Y. Language and information: Selected essays on their theory and application; Addison-Wesley Pub. Co.: Reading, MA, 1964. [Google Scholar]
- Hintikka, J. On semantic information. In Information and Inference; Hintikka, J, Suppes, P, Eds.; D. Reidel: Dorcrecht, 1970. [Google Scholar]
- Godfrey-Smith, P. Theoretical role of “genetic coding”. Philos. Sci 2000, 67, 26–44. [Google Scholar]
- Godfrey-Smith, P. Information, arbitrariness, and selection: Comments on Maynard Smith. Philos. Sci 2000, 67, 202–207. [Google Scholar]
- Khazen, AM. [Origin and evolution of life and intellect from the point of view of information processing]. Biofizika 1992, 37, 105–122. [Google Scholar]
- Maynard Smith, J. The concept of information in biology. Philos. Sci 2000, 67, 177–194. [Google Scholar]
- Hoffmeyer, J; Emmeche, C. Code-Duality and the Semiotics of Nature, (Forward to and reprinting of, with new footnotes). J. BioSemiotics 2005, 1, 37–91. [Google Scholar]
- Jablonka, E. Information: Its interpretation, its inheritance, and its sharing. Philos. Sci 2002, 69, 578–605. [Google Scholar]
- Stegmann, UE. The arbitrariness of the genetic code. Bio. Philos 2004, 19, 205–222. [Google Scholar]
- Szathmary, E. From RNA to language. Curr. Biol 1996, 6, 764. [Google Scholar]
- Szathmary, E. The origin of the genetic code: Amino acids as cofactors in an RNA world. Trends Genet 1999, 15, 223–229. [Google Scholar]
- Szathmary, E. Biological information, kin selection, and evolutionary transitions. Theor. Popul. Biol 2001, 59, 11–14. [Google Scholar]
- Szostak, JW. Functional information: Molecular messages. Nature 2003, 423, 689. [Google Scholar]
- Hazen, RM; Griffin, PL; Carothers, JM; Szostak, JW. Functional information and the emergence of biocomplexity. Proc. Natl. Acad. Sci. USA 2007, 104, 8574–8581. [Google Scholar]
- Bowong, S; Kagou, AT. Adaptive Control for Linearizable Chaotic Systems. J. Vibrat. Cont 2006, 12, 119–137. [Google Scholar]
- Schimmel, P; Soll, D. When protein engineering confronts the tRNA world. Proc. Natl. Acad. Sci. USA 1997, 94, 10007–10009. [Google Scholar]
- Benner, SA; Allemann, RK; Ellington, AD; Ge, L; Glasfeld, A; Leanz, GF; Krauch, T; MacPherson, LJ; Moroney, S; Piccirilli, JA; et al. Natural selection, protein engineering, and the last riboorganism: rational model building in biochemistry. Cold Spring Harb. Symp. Quant. Biol 1987, 52, 53–63. [Google Scholar]
- Gewolb, J. Bioengineering: Working outside the protein-synthesis rules. Science 2002, 295, 2205–2207. [Google Scholar]
- Yeung, MKS; Tegner, J; Collins, JJ. Reverse engineering gene networks using singular value decomposition and robust regression. Proc. Natl. Acad. Sci. USA 2002, 99, 6163–6168. [Google Scholar]
- Ohuchi, S; Ikawa, Y; Shiraishi, H; Inoue, T. Modular engineering of a Group I intron ribozyme. Nucleic Acids Res. 2002, 30, 3473–3480. [Google Scholar]
- Csete, ME; Doyle, JC. Reverse engineering of biological complexity. Science 2002, 295, 1164–1169. [Google Scholar]
- Luisi, PL. Toward the engineering of minimal living cells. Anat. Rec 2002, 268, 208–214. [Google Scholar]
- McCarthy, AA. Microbia: engineering microbial network biology. Chem. Biol 2003, 10, 99–100. [Google Scholar]
- Clymer, JR. Simulation-Based Engineering Of Complex Adaptive Systems. SIMULATION 1999, 72, 250–260. [Google Scholar]
- Lewontin, RC. Evolution as engineering. In Integrative Approaches to Molecular Biology; Collado-Vides, J, Smith, T, Magasanik, B, Eds.; MIT Press: Cambridge, MA, 1996. [Google Scholar]
- Shapiro, JA. A 21st century view of evolution: genome system architecture, repetitive DNA, and natural genetic engineering. Gene 2005, 345, 91–100. [Google Scholar]
- Kaplan, M. Decision Theory as Philosophy; Cambridge Univ. Press: Cambridge, 1996; p. 227. [Google Scholar]
- Chernoff, H; Moses, LE. Elementary Decision Theory, 2nd Ed ed; Dover Publications: Mineola, N.Y., 1986. [Google Scholar]
- Resnik, MD. Choices: An Introduction to Decision Theory; University of Minnesota Press: Minneapolis, Minn, 1987. [Google Scholar]
- Bradley, D. Informatics. The genome chose its alphabet with care. Science 2002, 297, 1789–1791. [Google Scholar]
- Veening, J-W; Smits, WK; Kuipers, OP. Bistability, Epigenetics, and Bet-Hedging in Bacteria. Annu. Rev. Microbio 2008, 62, 193–210. [Google Scholar]
- Allis, DC; Jenuwein, T; Reinberg, D; Wood, R; Caparros, M-L. Epigenetics; Cold Springs Harbor Press: Woodbury, NY, 2007. [Google Scholar]
- Qiu, J. Epigenetics: unfinished symphony. Nature 2006, 441, 143–145. [Google Scholar]
- Grant-Downton, RT; Dickinson, HG. Epigenetics and its implications for plant biology. 1. The epigenetic network in plants. Ann. Bot 2005, 96, 1143–1164. [Google Scholar]
- Jablonka, E; Lamb, MJ. The changing concept of epigenetics. Ann. N.Y. Acad. Sci 2002, 981, 82–96. [Google Scholar]
- Griesemer, J. What is “epi” about epigenetics? Ann. N.Y. Acad. Sci 2002, 981, 97–110. [Google Scholar]
- Bachmair, A; Novatchkova, M; Potuschak, T; Eisenhaber, F. Ubiquitylation in plants: A post-genomic look at a post-translational modification. Trends Plant Sci 2001, 6, 463–470. [Google Scholar]
- Eisenhaber, B; Bork, P; Eisenhaber, F. Post-translational GPI lipid anchor modification of proteins in kingdoms of life: Analysis of protein sequence data from complete genomes. Protein Eng 2001, 14, 17–25. [Google Scholar]
- Vaish, NK; Dong, F; Andrews, L; Schweppe, RE; Ahn, NG; Blatt, L; Seiwert, SD. Monitoring post-translational modification of proteins with allosteric ribozymes. Nat. Biotechnol 2002, 20, 810–815. [Google Scholar]
- Mata, J; Marguerat, S; Bahler, J. Post-transcriptional control of gene expression: A genome-wide perspective. Trends Biochem. Sci 2005, 30, 506–514. [Google Scholar]
- Pattee, HH. Universal principles of measurement and language functions in evolving systems. In Complexity, Language, and Life: Mathematical Approaches; Casti, JL, Karlqvist, A, Eds.; Springer-Verlag: Berlin, 1986; pp. 579–581. [Google Scholar]
- Pattee, HH. The physics of symbols and the evolution of semiotic controls. In Proc. Workshop on Control Mechanisms for Complex Systems; Coombs, M. e. a., Ed.Addison-Wesley, 1997. [Google Scholar]
- Pattee, HH. On the origin of macromolecular sequences. Biophys. J 1961, 1, 683–710. [Google Scholar]
- Pattee, HH. The nature of hierarchichal controls in living matter. In Foundations of Mathematical Biology; Rosen, R, Ed.; Academic Press: New York, 1971; Volume 1, pp. 1–22. [Google Scholar]
- Pattee, HH. Laws and constraints, symbols and languages. In Towards a Theoretical Biology; Waddington, CH, Ed.; University of Edinburgh Press: Edinburgh, 1972; Volume 4, pp. 248–258. [Google Scholar]
- Pattee, HH. Physical problems of the origin of natural controls. In Biogenesis, Evolution, and Homeostasis; Locker, A, Ed.; Springer-Verlag: Heidelberg, 1973; pp. 41–49. [Google Scholar]
- Pattee, HH. Dynamic and linguistic modes of complex systems. Int. J. General Systems 1977, 3, 259–266. [Google Scholar]
- Rocha, LM. Selected self-organization and the semiotics of evolutionary systems. In Evolutionary Systems: Biological and Epistemological Perspectives on Selection and Self-Organization; Salthe, S, van de Vijver, G, Delpos, M, Eds.; Kluwer: The Netherlands, 1998; pp. 341–358. [Google Scholar]
- Rocha, LM. Syntactic autonomy: Or why there is no autonomy without symbols and how self-organizing systems might evolve them. Annals of the New York Academy of Science 2000, 901, 207–223. [Google Scholar]
- Morse, M; Hedlund, GA. Symbolic Dynamics. Amer. J. Math 1938, 60, 815–866. [Google Scholar]
- Kitchens, B. Symbolic dynamics. One-sided, two-sided and countable state Markov shifts; Universitext, Springer-Verlag: Berlin, 1998; p. 252. [Google Scholar]
- Lind, D; Marcus, B. An Introduction to Symbolic Dynamics and Coding; Cambridge University Press: Cambridge, 1995; p. 495. [Google Scholar]
- Jiménez-Montaño, MA; Feistel, R; Diez-Martínez, O. On the information hidden in signals and macromolecules. I. Symbolic time-series analysis. Nonlinear Dynamics Psychol. Life Sci 2004, 8, 445–478. [Google Scholar]
- Luisi, PL. Contingency and determinism. Phil. Trans. R. Soc. A 2003, 361, 1141–1147. [Google Scholar]
- Spinelli, G; Mayer-Foulkes, D. New Method to Study DNA Sequences: The Languages of Evolution. Nonlinear Dynamics Psychol. Life Sci 2008, 12, 133–151. [Google Scholar]
- Searls, DB. The language of genes. Nature 2002, 420, 211–217. [Google Scholar]
- Chang, S; DesMarais, D; Mack, R; Miller, SL; Streathearn, GE. Prebiotic organic syntheses and the origin of life. In Earth’s Earliest Biosphere: Its Origin and Evolution; Schopf, JW, Ed.; Princeton University Press: Princeton, NJ, 1983; pp. 53–92. [Google Scholar]
- Pattee, HH. Artificial Life Needs a Real Epistemology. In Advances in Artificial Life; Moran, F, Ed.; Springer: Berlin, 1995; pp. 23–38. [Google Scholar]
- Pattee, HH. Irreducible and complementary semiotic forms. Semiotica 2001, 134, 341–358. [Google Scholar]
- Albano, EV; Monetti, RA. Comment on “Life at the edge of chaos”. Phys. Rev. Lett 1995, 75, 981. [Google Scholar]
- Baym, M; Hubler, AW. Conserved quantities and adaptation to the edge of chaos. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys 2006, 73, 056210. [Google Scholar]
- Bernardes, AT; dos Santos, RM. Immune network at the edge of chaos. J. Theor. Biol 1997, 186, 173–187. [Google Scholar]
- Bertschinger, N; Natschlager, T. Real-time computation at the edge of chaos in recurrent neural networks. Neural Comput 2004, 16, 1413–1436. [Google Scholar]
- Borges, EP; Tsallis, C; Ananos, GF; de Oliveira, PM. Nonequilibrium probabilistic dynamics of the logistic map at the edge of chaos. Phys. Rev. Lett 2002, 89, 254103. [Google Scholar]
- Hiett, PJ. Characterizing critical rules at the ‘edge of chaos’. Biosystems 1999, 49, 127–142. [Google Scholar]
- Legenstein, R; Maass, W. Edge of chaos and prediction of computational performance for neural circuit models. Neural Netw 2007, 20, 323–334. [Google Scholar]
- Melby, P; Kaidel, J; Weber, N; Hubler, A. Adaptation to the edge of chaos in the self-adjusting logistic map. Phys. Rev. Lett 2000, 84, 5991–5993. [Google Scholar]
- Mycek, S. Teetering on the edge of chaos. Volunt. Leader 1999, 40, 13–16. [Google Scholar]
- Mycek, S. Teetering on the edge of chaos. Giving up control and embracing uncertainty can lead to surprising creativity. Trustee 1999, 52, 10–13. [Google Scholar]
- Neubauer, J. Beyond hierarchy: working on the edge of chaos. J. Nurs. Manag 1997, 5, 65–67. [Google Scholar]
- Schneider, TM; Eckhardt, B; Yorke, JA. Turbulence transition and the edge of chaos in pipe flow. Phys. Rev. Lett 2007, 99, 034502. [Google Scholar]
- Stokic, D; Hanel, R; Thurner, S. Inflation of the edge of chaos in a simple model of gene interaction networks. Phys. Rev. E. Stat. Nonlin. Soft Matter. Phys 2008, 77, 061917. [Google Scholar]
- Rocha, LM. The physics and evolution of symbols and codes: Reflections on the work of Howard Pattee. Biosystems 2001, 60, 1–4. [Google Scholar]
- Pattee, HH. The measurement problem in artificial world models. Biosystems 1989, 23, 281–289. [Google Scholar]
- Pattee, HH. Laws, constraints, and the modeling relation--History and interpretations. Chem. Biodivers 2007, 4, 2272–2295. [Google Scholar]
- Allweis, C. Proposal for APS-IUPS convention for diagraming physiological mechanisms. Amer. J. Physiol 1988, 254, R717–726. [Google Scholar]
- Ellington, AD; Szostak, JW. In vitro selection of RNA molecules that bind specific ligands. Nature 1990, 346, 818–822. [Google Scholar]
- Tuerk, C; Gold, L. Systematic evolution of ligands by exponential enrichment — RNA ligands to bacteriophage - T4 DNA-polymerase. Science 1990, 249, 505–510. [Google Scholar]
- Robertson, DL; Joyce, GF. Selection in vitro of an RNA enzyme that specifically cleaves single-stranded DNA. Nature 1990, 344, 467–468. [Google Scholar]



| Length (aa) | Number of Sequences | Null State (Bits) | FSC (Fits) | Average Fits/Site | |
|---|---|---|---|---|---|
| Ankyrin | 33 | 1,171 | 143 | 46 | 1.4 |
| HTH 8 | 41 | 1,610 | 177 | 76 | 1.9 |
| HTH 7 | 45 | 503 | 194 | 83 | 1.8 |
| HTH 5 | 47 | 1,317 | 203 | 80 | 1.7 |
| HTH 11 | 53 | 663 | 229 | 80 | 1.5 |
| HTH 3 | 55 | 3,319 | 238 | 80 | 1.5 |
| Insulin | 65 | 419 | 281 | 156 | 2.4 |
| Ubiquitin | 65 | 2,442 | 281 | 174 | 2.7 |
| Kringle domain | 75 | 601 | 324 | 173 | 2.3 |
| Phage Integr N-dom | 80 | 785 | 346 | 123 | 1.5 |
| VPR | 82 | 2,372 | 359 | 308 | 3.7 |
| RVP | 95 | 51 | 411 | 172 | 1.8 |
| Acyl-Coa dh N-dom | 103 | 1,684 | 445 | 174 | 1.7 |
| MMR HSR1 | 119 | 792 | 514 | 179 | 1.5 |
| Ribosomal S12 | 121 | 603 | 523 | 359 | 3.0 |
| FtsH | 133 | 456 | 575 | 216 | 1.6 |
| Ribosomal S7 | 149 | 535 | 644 | 359 | 2.4 |
| P53 DNA domain | 157 | 156 | 679 | 525 | 3.3 |
| Vif | 190 | 1,982 | 821 | 675 | 3.6 |
| SRP54 | 196 | 835 | 847 | 445 | 2.3 |
| Ribosomal S2 | 197 | 605 | 851 | 462 | 2.4 |
| Viral helicase1 | 229 | 904 | 990 | 335 | 1.5 |
| Beta-lactamase | 239 | 1,785 | 1,033 | 336 | 1.4 |
| RecA | 240 | 1,553 | 1,037 | 832 | 3.5 |
| tRNA-synt 1b | 280 | 865 | 1,210 | 438 | 1.6 |
| SecY | 342 | 469 | 1,478 | 688 | 2.0 |
| EPSP Synthase | 372 | 1,001 | 1,608 | 688 | 1.9 |
| FTHFS | 390 | 658 | 1,686 | 1,144 | 2.9 |
| DctM | 407 | 682 | 1,759 | 724 | 1.8 |
| Corona S2 | 445 | 836 | 1,923 | 1,285 | 2.9 |
| Flu PB2 | 608 | 1,692 | 2,628 | 2,416 | 4.0 |
| Usher | 724 | 316 | 3,129 | 1,296 | 1.8 |
| Paramyx RNA Pol | 887 | 389 | 3,834 | 1,886 | 2.1 |
| ACR Tran | 949 | 1,141 | 4,102 | 1,650 | 1.7 |
| Random sequences | 1000 | 500 | 4,321 | 0 | 0 |
| 50-mer polyadenosine | 50 | 1 | 0 | 0 | 0 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Abel, D.L. The Capabilities of Chaos and Complexity. Int. J. Mol. Sci. 2009, 10, 247-291. https://doi.org/10.3390/ijms10010247
Abel DL. The Capabilities of Chaos and Complexity. International Journal of Molecular Sciences. 2009; 10(1):247-291. https://doi.org/10.3390/ijms10010247
Chicago/Turabian StyleAbel, David L. 2009. "The Capabilities of Chaos and Complexity" International Journal of Molecular Sciences 10, no. 1: 247-291. https://doi.org/10.3390/ijms10010247
APA StyleAbel, D. L. (2009). The Capabilities of Chaos and Complexity. International Journal of Molecular Sciences, 10(1), 247-291. https://doi.org/10.3390/ijms10010247





