Tetrel Interactions from an Interacting Quantum Atoms Perspective
Abstract
1. Introduction
2. Theoretical Methods
3. Computational Details
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| QTAIM | Quantum theory of atoms in molecules |
| IQA | Interacting quantum atoms |
| NBO | Natural bond orbital |
| MP2 | Second-order Møller–Plesset |
| MEP | Molecular electrostatic potential |
| EDA | Energy decomposition analysis |
| DFT | Density functional theory |
| CCSD | Singles and doubles coupled cluster |
| HF | Hartree–Fock |
| FNO | Frozen natural orbital |
| BSSE | Basis set superposition error |
| EOM | Equation of motion |
| full-CI | Full interaction configuration |
| MR-CISD | Multireference singles and doubles interaction configuration |
References
- Atwood, J.L. Encyclopedia of Supramolecular Chemistry; M. Dekker: New York, NY, USA, 2004. [Google Scholar]
- DiStasio, R.A.; Gobre, V.V.; Tkatchenko, A. Many-body van der Waals interactions in molecules and condensed matter. J. Phys. Condens. Matter 2014, 26, 213202. [Google Scholar] [CrossRef] [PubMed]
- Hermann, J.; DiStasio, R.A.; Tkatchenko, A. First-Principles Models for van der Waals Interactions in Molecules and Materials: Concepts, Theory, and Applications. Chem. Rev. 2017, 117, 4714–4758. [Google Scholar] [CrossRef] [PubMed]
- Rance, G.A.; Marsh, D.H.; Bourne, S.J.; Reade, T.J.; Khlobystov, A.N. van der Waals Interactions between Nanotubes and Nanoparticles for Controlled Assembly of Composite Nanostructures. ACS Nano 2010, 4, 4920–4928. [Google Scholar] [CrossRef] [PubMed]
- Reimers, J.R.; Ford, M.J.; Marcuccio, S.M.; Ulstrup, J.; Hush, N.S. Competition of van der Waals and chemical forces on gold-sulfur surfaces and nanoparticles. Nat. Rev. Chem. 2017, 1. [Google Scholar] [CrossRef]
- Kronik, L.; Tkatchenko, A. Understanding Molecular Crystals with Dispersion-Inclusive Density Functional Theory: Pairwise Corrections and Beyond. Acc. Chem. Res. 2014, 47, 3208–3216. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, L.M.; Weatherby, J.A.; Otero-de-la Roza, A.; Johnson, E.R. Non-Covalent Interactions in Molecular Crystals: Exploring the Accuracy of the Exchange-Hole Dipole Moment Model with Local Orbitals. J. Chem. Theory Comput. 2018, 14, 5715–5724. [Google Scholar] [CrossRef] [PubMed]
- Maurer, R.J.; Ruiz, V.G.; Tkatchenko, A. Many-body dispersion effects in the binding of adsorbates on metal surfaces. J. Chem. Phys. 2015, 143, 102808. [Google Scholar] [CrossRef]
- Ruiz, V.G.; Liu, W.; Tkatchenko, A. Density-functional theory with screened van der Waals interactions applied to atomic and molecular adsorbates on close-packed and non-close-packed surfaces. Phys. Rev. B 2016, 93, 035118. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Cao, B.H.; Price, I.K.; Hein, J.E.; Johnson, E.R. Predicting the Relative Solubilities of Racemic and Enantiopure Crystals by Density-Functional Theory. Angew. Chem. Int. Ed. 2014, 53, 7879–7882. [Google Scholar] [CrossRef]
- Mohebifar, M.; Johnson, E.R.; Rowley, C.N. Evaluating Force-Field London Dispersion Coefficients Using the Exchange-Hole Dipole Moment Model. J. Chem. Theory Comput. 2017, 13, 6146–6157. [Google Scholar] [CrossRef]
- He, X.; Fusti-Molnar, L.; Cui, G.; Merz, K.M. Importance of dispersion and electron correlation in ab initio protein folding. J. Phys. Chem. B 2009, 113, 5290–5300. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. What Is the Covalency of Hydrogen Bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef] [PubMed]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the hydrogen bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
- Neaton, J.B. A direct look at halogen bonds. Science 2017, 358, 167–168. [Google Scholar] [CrossRef] [PubMed]
- Luyckx, R.; Coulon, P.; Lekkerkerker, H.N. Dispersion forces between noble gas atoms. J. Chem. Phys. 1978, 69, 2424–2427. [Google Scholar] [CrossRef]
- Legon, A.C.; Sharapa, D.; Clark, T. Dispersion and polar flattening: noble gas–halogen complexes. J. Mol. Model. 2018, 24. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef]
- Brammer, L. Halogen bonding, chalcogen bonding, pnictogen bonding, tetrel bonding: Origins, current status and discussion. Faraday Discuss. 2017, 203, 485–507. [Google Scholar] [CrossRef]
- Bürgi, H.B. Chemical reaction coordinates from crystal structure data. I. Inorg. Chem. 1973, 12, 2321–2325. [Google Scholar] [CrossRef]
- Bürgi, H.B.; Dunits, J.D.; Schefter, E. Geometrical Reaction Coordinates. II. Nucleophilic Addition to a Carbonyl Group. J. Am. Chem. Soc. 1973, 95, 5065–5067. [Google Scholar] [CrossRef]
- Bürgi, H.B.; Dunitz, J.D.; Lehn, J.M.; Wipff, G. Stereochemistry of reaction paths at carbonyl centres. Tetrahedron 1974, 30, 1563–1572. [Google Scholar] [CrossRef]
- Maccallum, P.H.; Poet, R.; Milner-White, E.J. Coulombic attractions between partially chargedmain-chain atoms stabilise the right-handed twist found in most β-strands. J. Mol. Biol. 1995, 248, 374–384. [Google Scholar] [CrossRef]
- Bartlett, G.J.; Choudhary, A.; Raines, R.T.; Woolfson, D.N. n→π⋆ interactions in proteins. J. Mol. Biol. 2010, 6, 615–620. [Google Scholar] [CrossRef] [PubMed]
- Harder, M.; Kuhn, B.; Diederich, F. Efficient Stacking on Protein Amide Fragments. ChemMedChem 2013, 8, 397–404. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.P.; Pavan, M.S.; Row, T.N.G. Experimental evidence for ‘carbon bonding’ in the solid state from charge density analysis. Chem. Commun. 2014, 50, 49–51. [Google Scholar] [CrossRef]
- Southern, S.A.; Bryce, D.L. NMR Investigations of Noncovalent Carbon Tetrel Bonds. Computational Assessment and Initial Experimental Observation. J. Phys. Chem. A 2015, 119, 11891–11899. [Google Scholar] [CrossRef]
- Scilabra, P.; Kumar, V.; Ursini, M.; Resnati, G. Close contacts involving germanium and tin in crystal structures: experimental evidence of tetrel bonds. J. Mol. Model. 2018, 24, 37. [Google Scholar] [CrossRef]
- Mitzel, N.W.; Losehand, U. β-Donor Bonds in Compounds Containing SiON Fragments. Angew. Chem. Int. Ed. 1997, 36, 2807–2809. [Google Scholar] [CrossRef]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-Bonding Interaction: Rediscovered Supramolecular Force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Influence of ring size on the strength of carbon bonding complexes between anions and perfluorocycloalkanes. Phys. Chem. Chem. Phys. 2014, 16, 19192–19197. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A.; Mooibroek, T.J. 1,1,2,2-Tetracyanocyclopropane (TCCP) as supramolecular synthon. Phys. Chem. Chem. Phys. 2016, 18, 1693–1698. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. The Bright Future of Unconventional σ/π-Hole Interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel Bonding Interactions. Chem. Rec. 2016, 16, 473–487. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Comparison of halide receptors based on H, halogen, chalcogen, pnicogen, and tetrel bonds. Faraday Discuss. 2017, 203, 213–226. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Natural bond orbitals and extensions of localized bonding concepts. Chem. Educ. Res. Pract. 2001, 2, 91–104. [Google Scholar] [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural bond orbital methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 1–42. [Google Scholar] [CrossRef]
- Bene, J.D.; Elguero, J.; Alkorta, I. Complexes of CO2 with the Azoles: Tetrel Bonds, Hydrogen Bonds and Other Secondary Interactions. Molecules 2018, 23, 906. [Google Scholar] [CrossRef]
- Bene, J.E.D.; Alkorta, I.; Elguero, J. Carbenes as Electron-Pair Donors To CO2 for C…C Tetrel Bonds and C–C Covalent Bonds. J. Phys. Chem. A 2017, 121, 4039–4047. [Google Scholar] [CrossRef]
- Mani, D.; Arunan, E. The X-C⋯Y (X = O/F, Y = O/S/F/Cl/Br/N/P) carbon bond and hydrophobic interactions. Phys. Chem. Chem. Phys. 2013, 15, 14377–14383. [Google Scholar] [CrossRef]
- Mani, D.; Arunan, E. The X-C⋯π (X = F, Cl, Br, CN) Carbon Bond. J. Phys. Chem. A 2014, 118, 10081–10089. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Grabowski, S.J. Tetrel bond—σ-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef] [PubMed]
- Sethio, D.; Oliveira, V.; Kraka, E. Quantitative Assessment of Tetrel Bonding Utilizing Vibrational Spectroscopy. Molecules 2018, 23, 2763. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Cheng, J.; Yang, X.; Liu, Z.; Bo, X.; Li, Q. Interplay between the σ-tetrel bond and σ-halogen bond in PhSiF3⋯4-iodopyridine⋯N-base. RSC Adv. 2017, 7, 21713–21720. [Google Scholar] [CrossRef]
- Esrafili, M.D.; Kiani, H.; Mohammadian-Sabet, F. Tuning of carbon bonds by substituent effects: An ab initio study. Mol. Phys. 2016, 114, 3658–3668. [Google Scholar] [CrossRef]
- Esrafili, M.; Mousavian, P. Strong Tetrel Bonds: Theoretical Aspects and Experimental Evidence. Molecules 2018, 23, 2642. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Li, Q.; Li, W.; Cheng, J. Tetrel bonds between PySiX3 and some nitrogenated bases: Hybridization, substitution, and cooperativity. J. Mol. Graph. Model. 2016, 65, 35–42. [Google Scholar] [CrossRef]
- Liu, M.; Li, Q.; Cheng, J.; Li, W.; Li, H.B. Tetrel bond of pseudohalide anions with XH3F (X = C, Si, Ge, and Sn) and its role in SN2 reaction. J. Chem. Phys. 2016, 145, 224310. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Guo, X.; Yang, X.; Li, W.; Cheng, J.; Li, H.B. A σ-hole interaction with radical species as electron donors: does single-electron tetrel bonding exist? Phys. Chem. Chem. Phys. 2014, 16, 11617–11625. [Google Scholar] [CrossRef]
- Mitzel, N.W.; Losehand, U. β-Donor Interactions of Exceptional Strength inN, N-Dimethylhydroxylaminochlorosilane, ClH2SiONMe2. J. Am. Chem. Soc. 1998, 120, 7320–7327. [Google Scholar] [CrossRef]
- Blanco, M.A.; Pendás, A.M.; Francisco, E. Interacting quantum atoms: A correlated energy decomposition scheme based on the quantum theory of atoms in molecules. J. Chem. Theory Comput. 2005, 1, 1096–1109. [Google Scholar] [CrossRef] [PubMed]
- Francisco, E.; Pendás, A.M.; Blanco, M.A. A molecular energy decomposition scheme for atoms in molecules. J. Chem. Theory Comput. 2006, 2, 90–102. [Google Scholar] [CrossRef] [PubMed]
- Pendás, A.M.; Francisco, E.; Blanco, M.A.; Gatti, C. Bond paths as privileged exchange channels. Chemistry 2007, 13, 9362–9371. [Google Scholar] [CrossRef] [PubMed]
- Pendás, A.M.; Blanco, M.A.; Francisco, E. Steric repulsions, rotation barriers, and stereoelectronic effects: A real space perspective. J. Comput. Chem. 2009, 30, 98–109. [Google Scholar] [CrossRef]
- Francisco, E.; Casals-Sainz, J.L.; Rocha-Rinza, T.; Martín Pendás, A. Partitioning the DFT exchange-correlation energy in line with the interacting quantum atoms approach. Theor. Chem. Acc. 2016, 135. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll (Version 12.06.03); TK Gristmill Software: Overland Park, KS, USA, 2012. [Google Scholar]
- Shavitt, I.; Bartlett, R.J. Many-Body Methods in Chemistry and Physics. MBPT and Coupled-Cluster Theory, 1st ed.; Cambridge Molecular Science, Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- McWeeny, R.; Sutcliffe, B.T. Methods of Molecular Quantum Mechanics; Theoretical Chemistry; A Series of Monographs; Academic Press Inc.: Cambridge, MA, USA, 1969. [Google Scholar]
- Martín Pendás, A.; Blanco, M.A.; Francisco, E. Chemical Fragments in Real Space: Definitions, Properties, and Energetic Decompositions. J. Comput. Chem. 2007, 28, 161–184. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618. [Google Scholar] [CrossRef]
- Tkatchenko, A.; DiStasio, R.A.; Head-Gordon, M.; Scheffler, M. Dispersion-corrected Møller–Plesset second-order perturbation theory. J. Chem. Phys. 2009, 131, 094106. [Google Scholar] [CrossRef]
- Holguín-Gallego, F.J.; Chávez-Calvillo, R.; García-Revilla, M.; Francisco, E.; Pendás, Á.M.; Rocha-Rinza, T. Electron correlation in the interacting quantum atoms partition via coupled-cluster lagrangian densities. J. Comput. Chem. 2016, 37, 1753–1765. [Google Scholar] [CrossRef]
- Ziegler, T.; Rauk, A. On the calculation of bonding energies by the Hartree Fock Slater method. Theor. Chim. Acta 2006, 46, 1–10. [Google Scholar] [CrossRef]
- Morokuma, K.; Kitaura, K. Energy Decomposition Analysis of Molecular Interactions. Chem. Appl. Atom. Mol. Electrostat. Potentials 2013, 215–242. [Google Scholar] [CrossRef]
- Su, P.; Li, H. Energy decomposition analysis of covalent bonds and intermolecular interactions. J. Chem. Phys. 2009, 131, 014102. [Google Scholar] [CrossRef] [PubMed]
- Martín Pendás, A.; Blanco, M.A.; Francisco, E. The nature of the hydrogen bond: a synthesis from the interacting quantum atoms picture. J. Chem. Phys. 2006, 125, 184112. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Sun, Q.; Berkelbach, T.C.; Blunt, N.S.; Booth, G.H.; Guo, S.; Li, Z.; Liu, J.; McClain, J.D.; Sayfutyarova, E.R.; Sharma, S.; et al. PySCF: The Python-based simulations of chemistry framework. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1340. [Google Scholar] [CrossRef]
- Taube, A.G.; Bartlett, R.J. Frozen natural orbital coupled-cluster theory: Forces and application to decomposition of nitroethane. J. Chem. Phys. 2008, 128, 164101. [Google Scholar] [CrossRef]
- Martín Pendás, A.; Francisco, E. Promolden. A QTAIM/IQA Code. Unpublished work.
- Martín Pendás, A.; Blanco, M.A.; Francisco, E. Two-electron integrations in the quantum theory of atoms in molecules. J. Chem. Phys. 2004, 120, 4581. [Google Scholar] [CrossRef] [PubMed]
- Martín Pendás, A.; Francisco, E.; Blanco, M.A. Two-electron integrations in the Quantum Theory of Atoms in Molecules with correlated wave functions. J. Comput. Chem. 2005, 26, 344. [Google Scholar] [CrossRef] [PubMed]
- Rafat, M.; Popelier, P.L.A. The Quantum Theory of Atoms in Molecules. From Solid State to DNA and Drug Design; WIley-VCH: Hoboken, NJ, USA, 2007; p. 121. [Google Scholar]
- Francisco, E.; Menéndez Crespo, D.; Costales, A.; Martín Pendás, A. A Multipolar Approach to the Interatomic Covalent Interaction Energy. J. Comput. Chem. 2017. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; Stephens, M.E. Spatial localization of the electronic pair and number distributions in molecules. J. Am. Chem. Soc. 1975, 97, 7391–7399. [Google Scholar] [CrossRef]
- Menéndez-Crespo, D.; Costales, A.; Francisco, E.; Martín Pendás, Á. Real-Space In Situ Bond Energies: Toward A Consistent Energetic Definition of Bond Strength. Chem. Eur. J. 2018, 24, 9101–9112. [Google Scholar] [CrossRef] [PubMed]
- Sainz, J.L.; Jara-Cortés, J.; Hernández-Trujillo, J.; Guevara-Vela, J.; Francisco, E.; Martín Pendás, A. Chemical Bonding in Excited States: Electron Localization, Delocalization and Statistics in Real Space. ChemRxiv 2019. [Google Scholar] [CrossRef]
- Fernández-Alarcón, A.; Casals-Sainz, J.; Guevara-Vela, J.M.; Costales, A.; Francisco, E.; Martín Pendás, A.; Rocha-Rinza, T. Partition of electronic excitation energies: The IQA/EOM-CCSD method. Phys. Chem. Chem. Phys. 2019. [Google Scholar] [CrossRef]
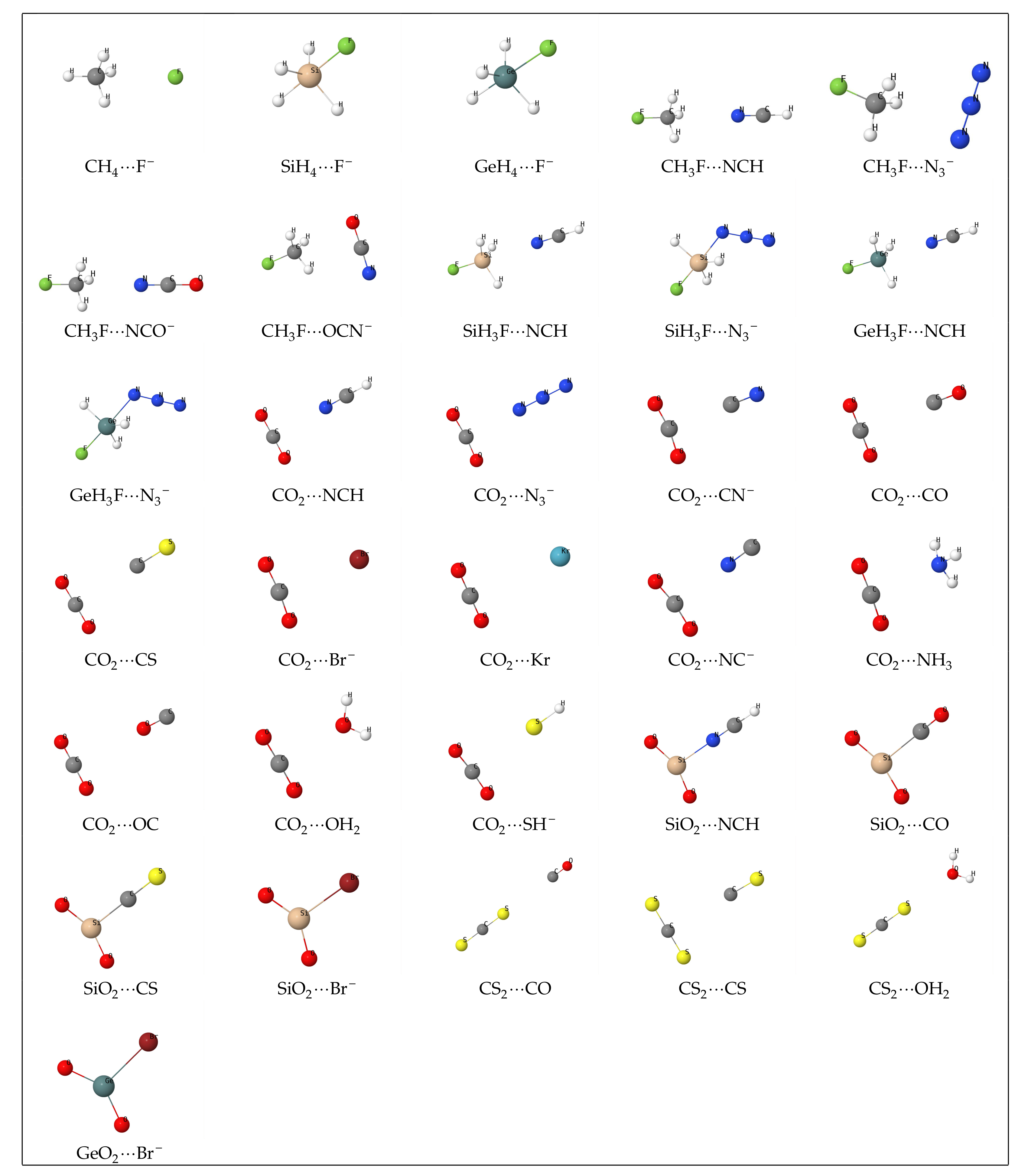

| System (A···B) | (CCSD) | (IQA) | diff | Q | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CH4···F- | −3.42 | −3.41 | 0.01 | −0.0112 | −0.9891 | −1.0003 | 8.42 | 3.77 | −6.27 | −8.46 | −9.33 | −15.60 | 3.73 |
| SiH4···F- | −60.17 | −59.87 | 0.31 | −0.0426 | −0.9579 | −1.0005 | 123.02 | 87.24 | −183.63 | −82.43 | −86.50 | −270.13 | 127.83 |
| GeH4···F- | −40.17 | −38.89 | 1.28 | −0.0830 | −0.9170 | −1.0001 | 79.50 | 46.57 | −92.28 | −69.62 | −72.69 | −164.97 | 56.46 |
| CH3F···NCH | −1.52 | −1.36 | 0.16 | −0.0033 | 0.0032 | −0.0000 | 3.37 | 3.47 | −1.94 | −5.53 | −6.25 | −8.19 | 1.31 |
| CH3F···N3− | −9.21 | −8.78 | 0.44 | −0.0200 | −0.9789 | −0.9989 | 11.18 | 5.05 | −8.47 | −14.46 | −16.54 | −25.01 | 1.77 |
| CH3F···NCO- | −9.89 | −9.69 | 0.21 | −0.0188 | −0.9809 | −0.9997 | 10.11 | 6.32 | −11.73 | −12.96 | −14.39 | −26.12 | 3.47 |
| CH3F···OCN- | −8.37 | −8.31 | 0.06 | −0.0147 | −0.9854 | −1.0001 | 10.24 | 5.51 | −9.28 | −12.97 | −14.78 | −24.06 | 2.78 |
| SiH3F···NCH | −3.06 | −3.02 | 0.04 | −0.0052 | 0.0043 | −0.0008 | 8.44 | 10.29 | −5.06 | −14.99 | −16.68 | −21.75 | 3.74 |
| SiH3F···N3− | −40.91 | −41.45 | −0.54 | −0.0678 | −0.9282 | −0.9960 | 73.85 | 70.33 | −103.27 | −77.13 | −82.36 | −185.64 | 67.05 |
| GeH3F···NCH | −3.65 | −2.99 | 0.66 | −0.0031 | 0.0041 | 0.0010 | 9.20 | 9.77 | −5.92 | −14.31 | −16.04 | −21.96 | 4.66 |
| GeH3F···N3− | −36.72 | −36.31 | 0.40 | −0.1110 | −0.8878 | −0.9988 | 46.32 | 39.64 | −53.01 | −65.10 | −69.26 | −122.27 | 20.86 |
| CO2···NCH | −1.60 | −2.08 | −0.48 | −0.0056 | 0.0059 | 0.0003 | 3.55 | 4.13 | −2.28 | −6.58 | −7.47 | −9.76 | 1.09 |
| CO2···N3− | −6.79 | −6.46 | 0.34 | −0.0236 | −0.9757 | −0.9994 | 12.43 | 8.07 | −9.87 | −15.31 | −17.09 | −26.96 | 5.20 |
| CO2···CN- | −8.25 | −8.64 | −0.39 | −0.0564 | −0.9428 | −0.9992 | 14.77 | 11.78 | −10.12 | −23.26 | −25.07 | −35.19 | 3.29 |
| CO2···CO | −0.65 | −1.14 | −0.49 | −0.0058 | 0.0058 | 0.0000 | 2.71 | 2.88 | −0.76 | −5.31 | −5.97 | −6.73 | 0.28 |
| CO2···CS | −1.29 | −1.83 | −0.54 | −0.0105 | 0.0096 | −0.0008 | 3.84 | 4.19 | −1.68 | −7.27 | −8.19 | −9.87 | 0.77 |
| CO2···Br- | −5.60 | −4.99 | 0.62 | −0.0401 | −0.9600 | −1.0001 | 9.08 | 6.79 | −4.97 | −14.01 | −15.89 | −20.86 | 1.87 |
| CO2···Kr | −0.48 | +0.03 | 0.52 | −0.0035 | 0.0028 | −0.0007 | 0.58 | 2.33 | −0.08 | −2.29 | −2.79 | −2.88 | 0.61 |
| CO2···NC- | −8.34 | −8.89 | −0.55 | −0.0333 | −0.9662 | −0.9996 | 14.29 | 10.83 | −12.70 | −19.43 | −21.31 | −34.01 | 5.69 |
| CO2···NH3 | −2.09 | −2.41 | −0.31 | −0.0158 | 0.0155 | −0.0003 | 6.63 | 7.39 | −4.12 | −11.06 | −12.32 | −16.43 | 2.97 |
| CO2···OC | −0.44 | −0.91 | −0.47 | 0.0001 | −0.0000 | 0.0001 | 1.11 | 1.40 | −0.57 | −2.39 | −2.85 | −3.42 | 0.12 |
| CO2···OH2 | −2.24 | −2.52 | −0.28 | −0.0051 | 0.0052 | 0.0000 | 5.42 | 5.87 | −3.86 | −8.86 | −9.94 | −13.81 | 2.43 |
| CO2···SH- | −3.99 | −4.32 | −0.33 | −0.0244 | −0.9758 | −1.0003 | 6.64 | 3.96 | −3.67 | −9.68 | −11.25 | −14.93 | 0.93 |
| SiO2···NCH | −22.43 | −21.00 | 1.42 | −0.0174 | 0.0185 | 0.0010 | 57.82 | 77.23 | −89.17 | −62.94 | −66.89 | −156.06 | 72.12 |
| SiO2···CO | −9.61 | −8.69 | 0.92 | −0.0112 | 0.0114 | 0.0002 | 49.33 | 69.34 | −57.46 | −66.28 | −69.91 | −127.37 | 52.39 |
| SiO2···CS | −30.17 | −28.78 | 1.39 | −0.0082 | 0.0086 | 0.0003 | 75.50 | 92.86 | −107.86 | −85.39 | −89.29 | −197.15 | 82.98 |
| SiO2···Br- | −78.06 | −76.19 | 1.87 | −0.1552 | −0.8433 | −0.9985 | 60.08 | 84.17 | −134.94 | −79.98 | −85.51 | −220.45 | 64.27 |
| CS2···CO | −0.77 | −0.86 | −0.09 | −0.0008 | 0.0010 | 0.0002 | 0.96 | 1.64 | −0.09 | −2.90 | −3.36 | −3.45 | −0.31 |
| CS2···CS | −0.95 | −0.46 | 0.49 | −0.0007 | 0.0006 | −0.0001 | 3.95 | 3.57 | −0.40 | −6.37 | −7.57 | −7.98 | 1.14 |
| CS2···OH2 | −1.48 | −1.97 | −0.40 | 0.0012 | −0.0003 | 0.0009 | 2.44 | 3.17 | −1.88 | −4.99 | −5.70 | −7.58 | 0.61 |
| GeO2···Br- | −65.37 | −65.29 | 0.08 | −0.2923 | −0.7068 | −0.9991 | 23.17 | 48.63 | −44.92 | −88.70 | −92.17 | −137.09 | −16.90 |
| A···B | CCSD | DFT | A···B | CCSD | DFT |
|---|---|---|---|---|---|
| CH4···F- | 0.0910 | 0.1281 | CO2···Br- | 0.1649 | 0.2030 |
| SiH4···F- | 0.6142 | 0.7611 | CO2···Kr | 0.0299 | 0.0357 |
| GeH4···F- | 0.5431 | 0.6878 | CO2···NC- | 0.1871 | 0.2364 |
| CH3F···NCH | 0.0602 | 0.0752 | CO2···NH3 | 0.1137 | 0.1405 |
| CH3F···N3− | 0.1564 | 0.1877 | CO2···OC | 0.0274 | 0.0338 |
| CH3F···NCO- | 0.1328 | 0.1672 | CO2···OH2 | 0.0878 | 0.1086 |
| CH3F···OCN- | 0.1378 | 0.1700 | CO2···SH- | 0.1178 | 0.1425 |
| SiH3F···NCH | 0.1526 | 0.1837 | SiO2···NCH | 0.5048 | 0.6375 |
| SiH3F···N3− | 0.6431 | 0.7535 | SiO2···CO | 0.5439 | 0.7054 |
| GeH3F···NCH | 0.1479 | 0.1770 | SiO2···CS | 0.6823 | 0.9346 |
| GeH3F···N3− | 0.5702 | 0.6671 | SiO2···Br- | 0.6868 | 0.8568 |
| CO2···NCH | 0.0694 | 0.0860 | CS2···CO | 0.0368 | 0.0431 |
| CO2···N3− | 0.1546 | 0.1919 | CS2···CS | 0.0803 | 0.0930 |
| CO2···CN- | 0.2320 | 0.2910 | CS2···OH2 | 0.0560 | 0.0677 |
| CO2···CO | 0.0596 | 0.0726 | GeO2···Br- | 0.7631 | 0.9514 |
| CO2···CS | 0.0806 | 0.0980 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casals-Sainz, J.L.; Castro, A.C.; Francisco, E.; Pendás, Á.M. Tetrel Interactions from an Interacting Quantum Atoms Perspective. Molecules 2019, 24, 2204. https://doi.org/10.3390/molecules24122204
Casals-Sainz JL, Castro AC, Francisco E, Pendás ÁM. Tetrel Interactions from an Interacting Quantum Atoms Perspective. Molecules. 2019; 24(12):2204. https://doi.org/10.3390/molecules24122204
Chicago/Turabian StyleCasals-Sainz, José Luis, Aurora Costales Castro, Evelio Francisco, and Ángel Martín Pendás. 2019. "Tetrel Interactions from an Interacting Quantum Atoms Perspective" Molecules 24, no. 12: 2204. https://doi.org/10.3390/molecules24122204
APA StyleCasals-Sainz, J. L., Castro, A. C., Francisco, E., & Pendás, Á. M. (2019). Tetrel Interactions from an Interacting Quantum Atoms Perspective. Molecules, 24(12), 2204. https://doi.org/10.3390/molecules24122204







