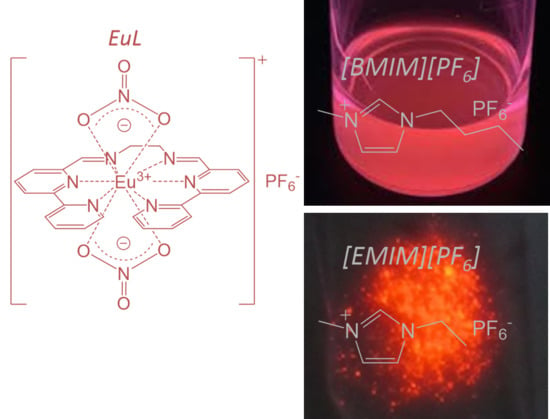
The Enhanced Intramolecular Energy Transfer and Strengthened ff Luminescence of a Stable Helical Eu Complex in Ionic Liquids
Abstract
:1. Introduction
2. Results and Discussion
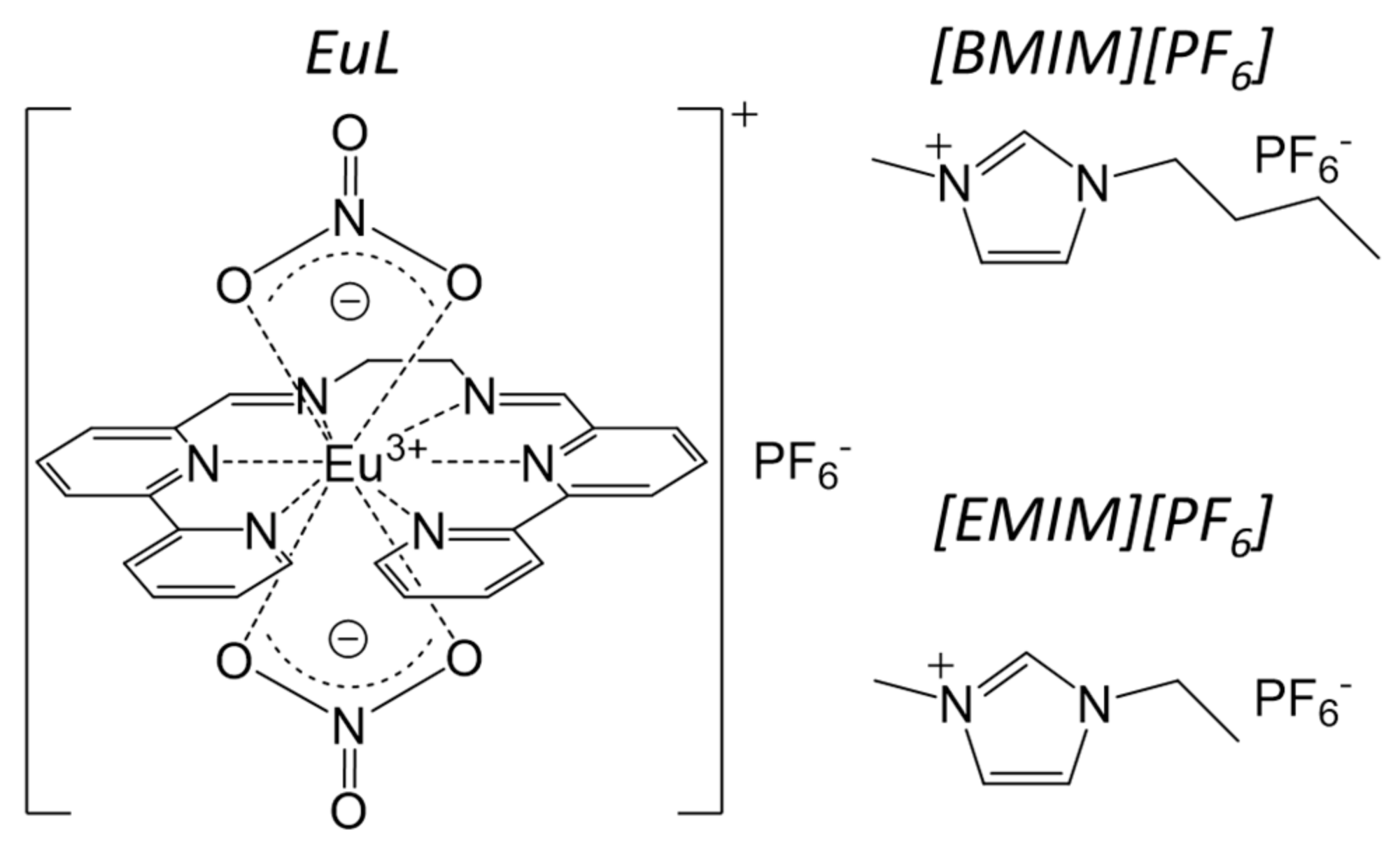
2.1. Electronic Structure of EuL in [BMIM][PF6]
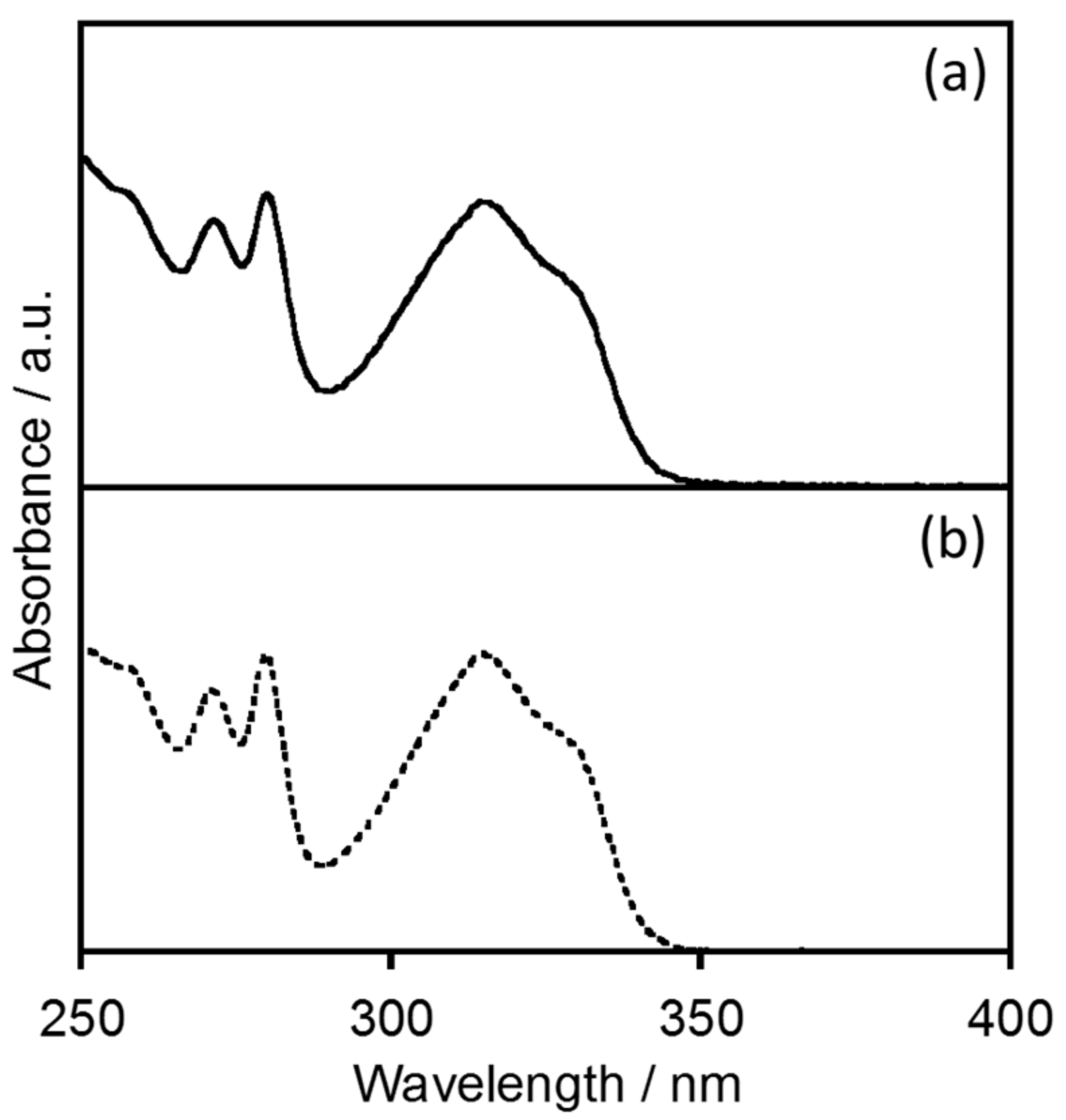
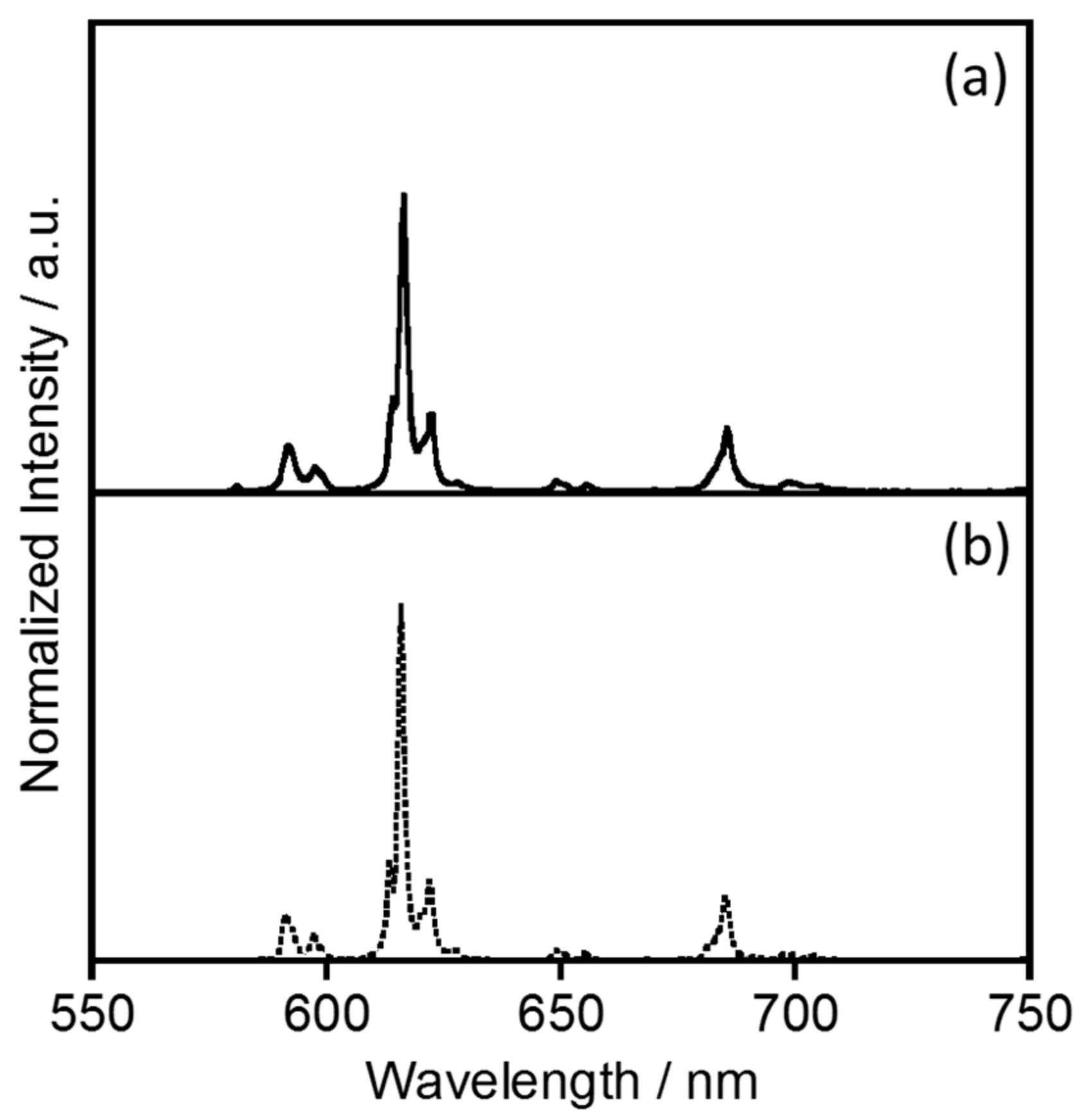
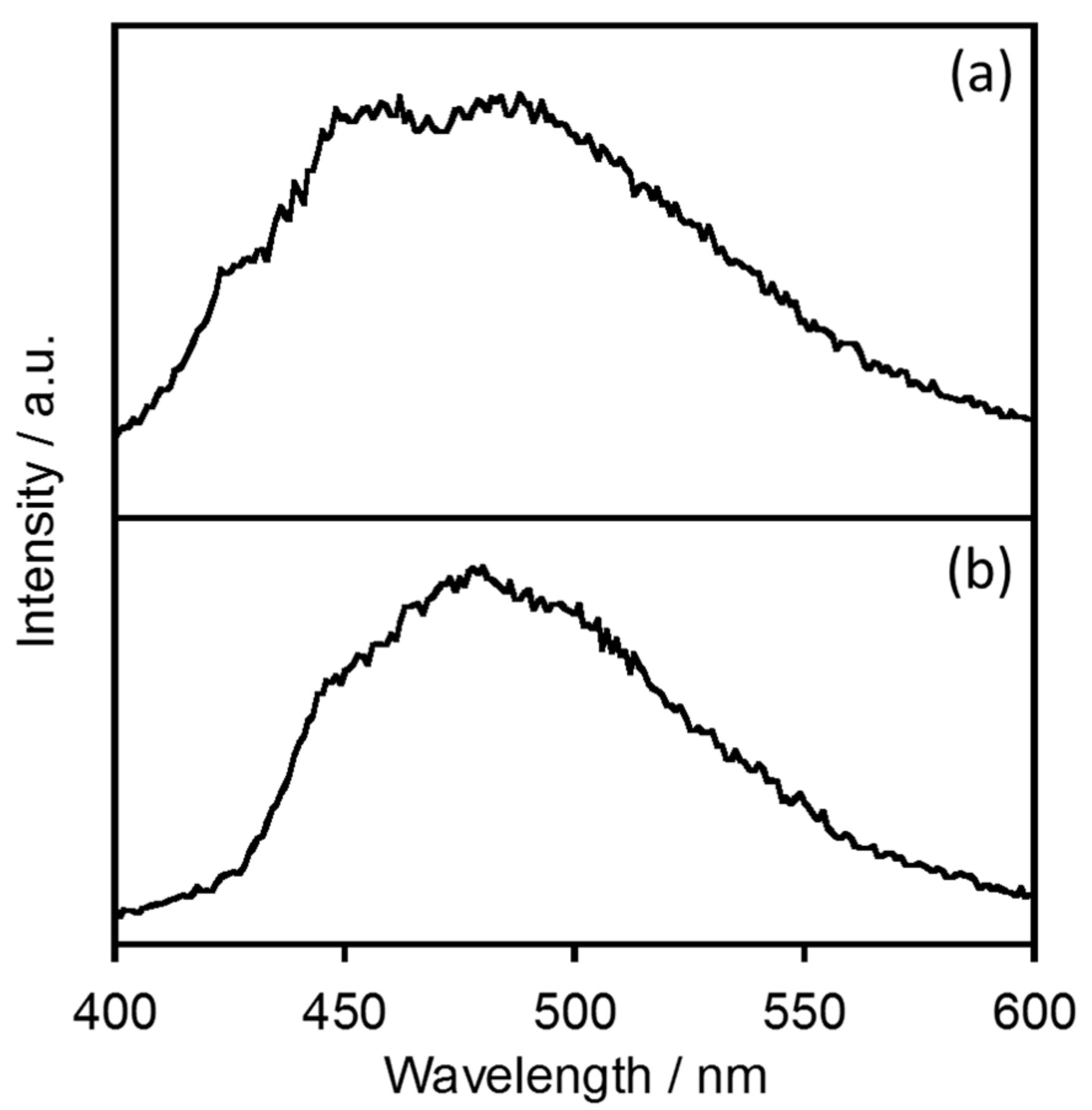
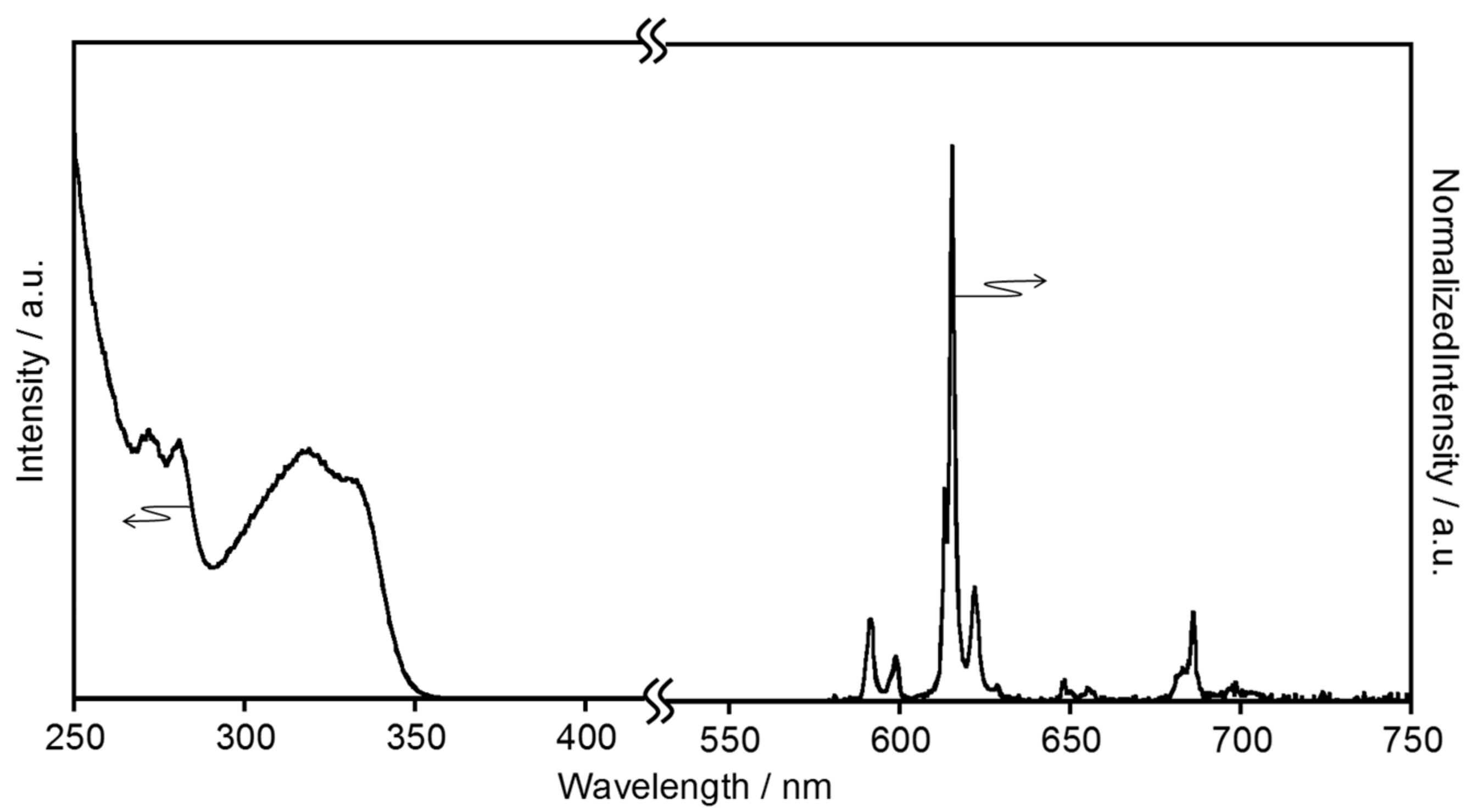
2.1.1. Electronic Absorption and Luminescence Properties
2.1.2. Energy Transfer Efficiency
2.1.3. Estimation of the Energy Donor State
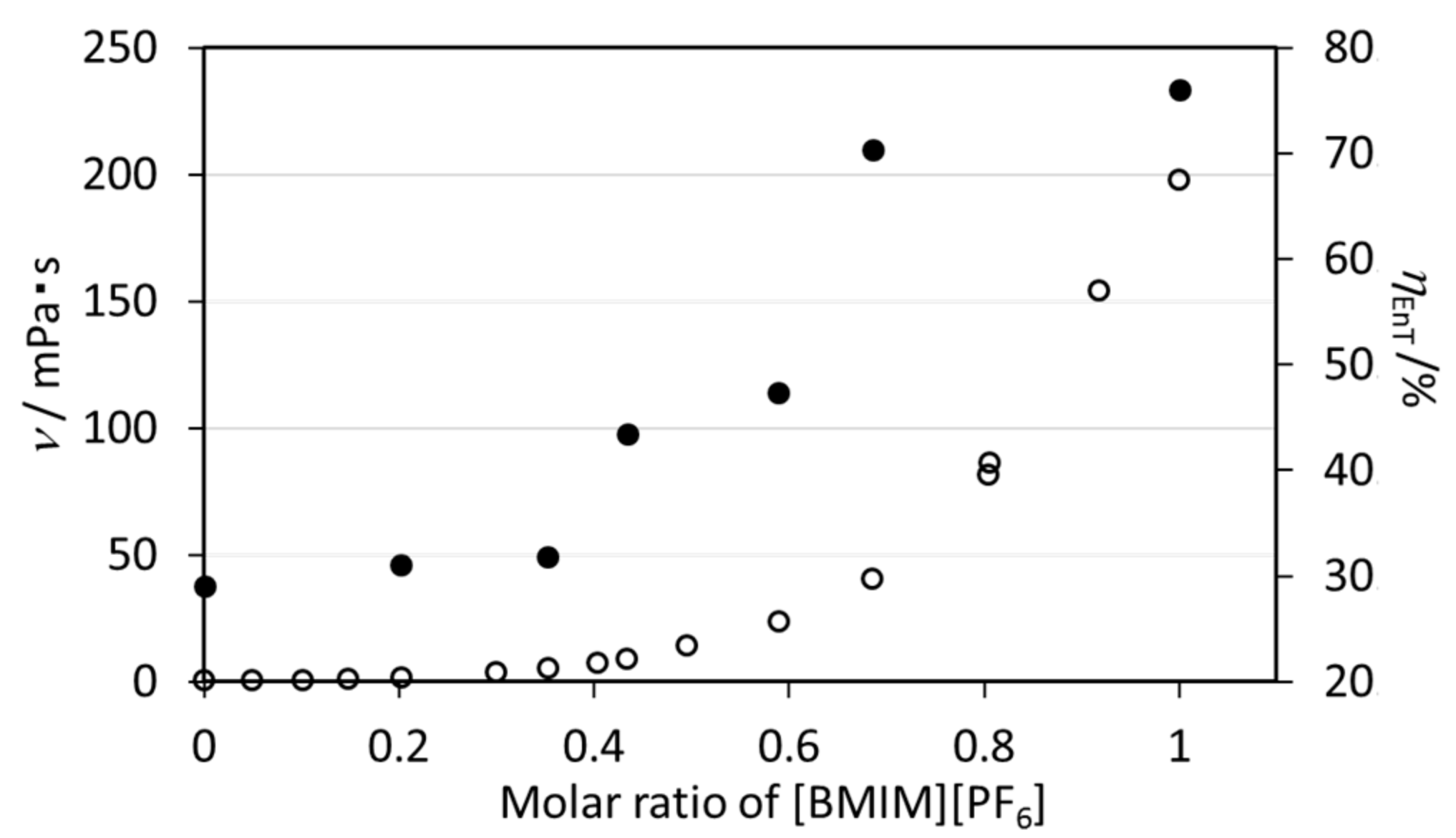
2.1.4. Effect of the Viscosity of [BMIM][PF6] on the Energy Transfer Efficiency of EuL
2.2. Temperature Dependence of the Structure and Luminescence Properties of EuL in [EMIM][PF6]
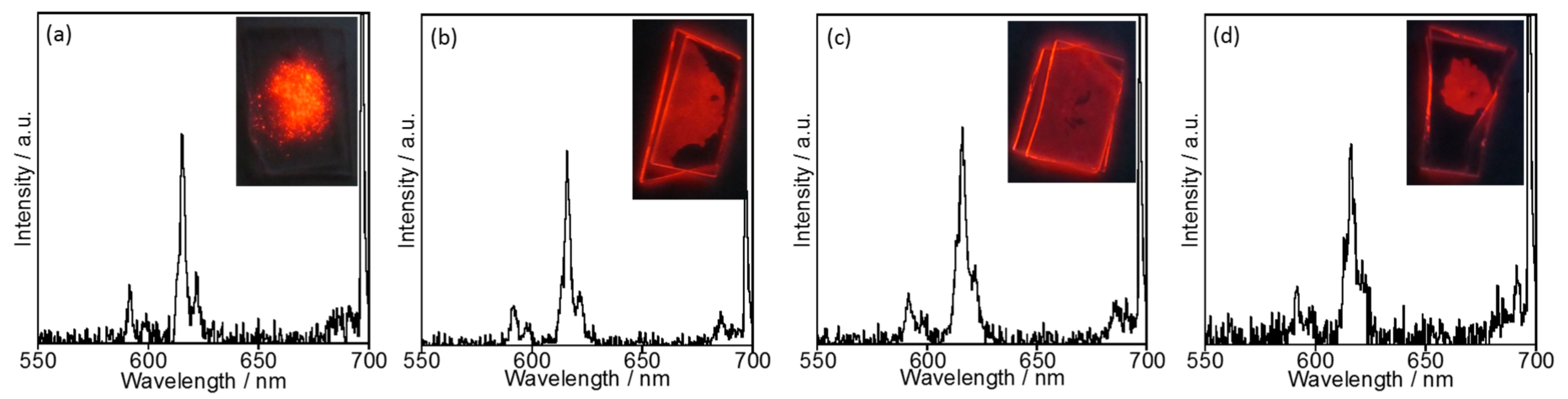
2.2.1. Luminescence Properties
2.2.2. Structural Analyses
2.2.3. Temperature Dependence of Luminescence Properties
3. Materials and Methods
3.1. Reagents and Materials
3.2. Measurements
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bünzli, J.C.G.; Comby, S.; Chauvin, A.S.; Vandevyver, C.D.B. New Opportunities for Lanthanide Luminescence. J. Rare Earths 2007, 25, 257–274. [Google Scholar] [CrossRef]
- Bünzli, J.C.G.; Eliseeva, S.V. Intriguing aspects of lanthanide luminescence. Chem. Sci. 2013, 4, 1939–1949. [Google Scholar] [CrossRef]
- Ogata, S.; Shimizu, T.; Ishibashi, T.; Ishiyone, Y.; Hanami, M.; Ito, M.; Ishii, A.; Kawaguchi, S.; Sugimoto, K.; Hasegawa, M. Water-soluble lanthanide complexes with a helical ligand modified for strong luminescence in a wide pH region. New J. Chem. 2017, 14, 6385–6394. [Google Scholar] [CrossRef]
- Hasegawa, M.; Ohtsu, H.; Kodama, D.; Kasai, T.; Sakurai, S.; Ishii, A.; Suzuki, K. Luminescence behaviour in acetonitrile and in the solid state of a series of lanthanide complexes with a single helical ligand. New J. Chem. 2014, 38, 1225–1234. [Google Scholar] [CrossRef]
- Hatanaka, M.; Osawa, A.; Wakabayashi, T.; Morokuma, K.; Hasegawa, M. Computational study on the luminescence quantum yields of terbium complexes with 2,2′-bipyridine derivative ligands. Phys. Chem. Chem. Phys. 2017. [Google Scholar] [CrossRef] [PubMed]
- Holzweber, M.; Lungwitz, R.; Doerfler, D.; Spange, S.; Koel, M.; Hutter, H.; Linert, W. Mutual Lewis Acid–Base Interactions of Cations and Anions in Ionic Liquids. Chem. Eur. J. 2013, 19, 288–293. [Google Scholar] [CrossRef] [PubMed]
- Shimomura, K.; Harami, H.; Matsubara, Y.; Nokami, T.; Katada, N.; Itoh, T. Lipase-mediated dynamic kinetic resolution (DKR) of secondary alcohols in the presence of zeolite using an ionic liquid solvent system. Catal. Today 2015, 255, 41–48. [Google Scholar] [CrossRef]
- Endo, T.; Kato, T.; Tozaki, K.; Nishikawa, K. Phase behaviors of room temperature ionic liquid linked with cation conformational changes: 1-butyl-3-methylimidazolium hexafluorophosphate. J. Phys. Chem. B 2010, 114, 407–411. [Google Scholar] [CrossRef] [PubMed]
- Fukaya, Y.; Hayashi, K.; Wada, M.; Ohno, H. Cellulose dissolution with polar ionic liquids under mild conditions: Required factors for anions. Green Chem. 2008, 10, 44–46. [Google Scholar] [CrossRef]
- Funasako, Y.; Mori, S.; Mochida, T. Reversible transformation between ionic liquids and coordination polymers by application of light and heat. Chem. Commun. 2016, 52, 6277–6279. [Google Scholar] [CrossRef] [PubMed]
- Takao, K.; Takao, S. Efficient and Versatile Anion Metathesis Reaction for Ionic Liquid Preparation by Using Conjugate Acid and Ortho Ester. Bull. Chem. Soc. Jpn. 2014, 87, 974–981. [Google Scholar] [CrossRef]
- Canales, R.I.; Brennecke, J.F. Comparison of ionic liquids to conventional organic solvents for extraction of aromatics from aliphatics. J. Chem. Eng. Data 2016, 61, 1685–1699. [Google Scholar] [CrossRef]
- Deferm, C.; de Voorde, M.V.; Luyten, J.; Oosterhof, H.; Fransaer, J.; Binnemans, K. Purification of indium by solvent extraction with undiluted ionic liquids. Green Chem. 2016, 18, 4116–4127. [Google Scholar] [CrossRef]
- Nockemann, P.; Beurer, E.; Driesen, K.; Deun, R.V.; Hecke, K.V.; Meervelt, L.V.; Binnemans, K. Photostability of a highly luminescent europium β-diketonate complex in imidazolium ionic liquids. Chem. Commun. 2005, 34, 4354–4356. [Google Scholar] [CrossRef] [PubMed]
- Driesen, K.; Lunstroot, K.; Nockemann, P.; Hecke, K.V.; Meervelt, L.V.; Gorller-Walrand, C.; Binnemans, K. Visible and near-infrared emission by samarium (III)-containing ionic liquid mixtures. Inorg. Chem. 2009, 48, 3018–3026. [Google Scholar]
- Shobukawa, H.; Tokuda, H.; Tabata, S.; Watanabe, M. Preparation and transport properties of novel lithium ionic liquids. Electrochim. Acta 2004, 50, 1–5. [Google Scholar] [CrossRef]
- Hayashi, S.; Hamaguchi, H. Discovery of a magnetic ionic liquid [bmim] FeCl4. Chem. Lett. 2004, 33, 1590–1591. [Google Scholar] [CrossRef]
- Welton, T. Room-temperature ionic liquids. Solvents for synthesis and catalysis. Chem. Rev. 1999, 99, 2071–2083. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Li, H.; Huang, X.; Chen, L. Novel room temperature molten salt electrolyte based on LiTFSI and acetamide for lithium batteries. Electrochem. Commun. 2004, 6, 28–32. [Google Scholar] [CrossRef]
- Yi, S.; Wang, J.; Chen, X. Enhanced energy transfer efficiency and stability of europium β-diketonate complex in ionic liquid-based lyotropic liquid crystals. Phys. Chem. Chem. Phys. 2015, 17, 20322–20330. [Google Scholar] [CrossRef] [PubMed]
- Kabo, G.J.; Blokhin, A.V.; Paulechka, Y.U.; Kabo, A.G.; Shymanovich, M.P. Thermodynamic properties of 1-butyl-3-methylimidazolium hexafluorophosphate in the condensed state. J. Chem. Eng. Data 2004, 49, 453–461. [Google Scholar] [CrossRef]
- Fuller, J.; Carlin, R.T.; De Long, H.C.; Haworth, D. Structure of 1-ethyl-3-methylimidazolium hexafluorophosphate: Model for room temperature molten salts. J. Chem. Soc. Chem. Commun. 1994, 3, 299–300. [Google Scholar] [CrossRef]
- Huddleston, J.G.; Visser, A.E.; Reichert, W.M.; Willauer, H.D.; Broker, G.A.; Rogers, R.D. Characterization and comparison of hydrophilic and hydrophobic room temperature ionic liquids incorporating the imidazolium cation. Green Chem. 2001, 3, 156–164. [Google Scholar] [CrossRef]
- Reichardt, C. Solvents and Solvent Effects in Organic Chemistry, 2nd ed.; VCH: New York, NY, USA, 1988; pp. 365–371. [Google Scholar]
- Carnall, W.T.; Fields, P.T.; Rajnak, K. Electronic energy levels of the trivalent lanthanide aquo ions. IV. Eu3+. J. Chem. Phys. 1968, 49, 4450–4455. [Google Scholar] [CrossRef]
- Frez, C.; Diebold, G.J.; Tran, C.D.; Yu, S. Determination of thermal diffusivities, thermal conductivities, and sound speeds of room-temperature ionic liquids by the transient grating technique. J. Chem. Eng. Data 2006, 51, 1250–1255. [Google Scholar] [CrossRef]
- Moattar, M.T.Z.; Cegincara, R.M. Viscosity, density, speed of sound, and refractive index of binary mixtures of organic solvent+ ionic liquid, 1-butyl-3-methylimidazolium hexafluorophosphate at 298.15 K. J. Chem. Eng. Data 2007, 52, 2359–2364. [Google Scholar] [CrossRef]
- Reichert, W.M.; Holbrey, J.D.; Swatloski, R.P.; Gutowski, K.E.; Visser, A.E.; Nieuwenhuyzen, M.; Seddon, K.R.; Rogers, R.D. Solid-state analysis of low-melting 1, 3-dialkylimidazolium hexafluorophosphate salts (ionic liquids) by combined X-ray crystallographic and computational analyses. Cryst. Growth Des. 2007, 7, 1106–1114. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are available from the authors. |

| ϕff (%) a | τobs (ms) b | |
|---|---|---|
| in [BMIM][PF6] | 32.3 | 1.48 |
| in acetonitrile | 12.0 | 1.55 |
| ϕT (%) a | τT(ns) b | kNR(T) (s−1) | |
|---|---|---|---|
| in [BMIM][PF6] | <0.1 | ca. 200 | 5.0 × 106 |
| in ethanol | <0.1 | ca. 5 | 2.0 × 108 |
| Molar Ratios [BMIM][PF6]: Acetonitrile | ν (mPa·s) | ϕff(%) a | τobs(ms) b | kR (s−1) | kNR (s−1) | ηEnT (%) | |
|---|---|---|---|---|---|---|---|
| 1.00 | 0.00 | 198.18 | 32.3 | 1.46 | 287.2 | 388.5 | 76.0 |
| 0.64 | 0.36 | 40.69 | 30.0 | 1.42 | 300.7 | 403.6 | 70.3 |
| 0.59 | 0.41 | 23.84 | 17.6 | 1.46 | 254.3 | 430.6 | 47.4 |
| 0.43 | 0.75 | 9.15 | 15.8 | 1.43 | 254.6 | 444.7 | 43.4 |
| 0.35 | 0.65 | 5.31 | 12.1 | 1.49 | 255.2 | 416.0 | 31.8 |
| 0.20 | 0.80 | 1.87 | 11.6 | 1.45 | 257.6 | 432.0 | 31.1 |
| 0.00 | 1.00 | 0.48 | 12.0 | 1.55 | 266.2 | 379.0 | 29.1 |
| ϕff (%) a | τobs (ms) b | ηEnT (%) |
|---|---|---|
| 52.1 | 1.37 | >99 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasegawa, Y.; Ishii, A.; Inazuka, Y.; Yajima, N.; Kawaguchi, S.; Sugimoto, K.; Hasegawa, M. The Enhanced Intramolecular Energy Transfer and Strengthened ff Luminescence of a Stable Helical Eu Complex in Ionic Liquids. Molecules 2018, 23, 55. https://doi.org/10.3390/molecules23020055
Hasegawa Y, Ishii A, Inazuka Y, Yajima N, Kawaguchi S, Sugimoto K, Hasegawa M. The Enhanced Intramolecular Energy Transfer and Strengthened ff Luminescence of a Stable Helical Eu Complex in Ionic Liquids. Molecules. 2018; 23(2):55. https://doi.org/10.3390/molecules23020055
Chicago/Turabian StyleHasegawa, Yuki, Ayumi Ishii, Yudai Inazuka, Naho Yajima, Shogo Kawaguchi, Kunihisa Sugimoto, and Miki Hasegawa. 2018. "The Enhanced Intramolecular Energy Transfer and Strengthened ff Luminescence of a Stable Helical Eu Complex in Ionic Liquids" Molecules 23, no. 2: 55. https://doi.org/10.3390/molecules23020055