Predicting the Effect of Single and Multiple Mutations on Protein Structural Stability
Abstract
1. Introduction
1.1. Related Work
1.1.1. Experimental Mutagenesis
1.1.2. Computational Approaches
1.1.3. Combinatorial, Rigidity Based Methods
1.1.4. Machine Learning Based Approaches
1.1.5. Model Ensembling
1.2. Motivations and Contributions
2. Results
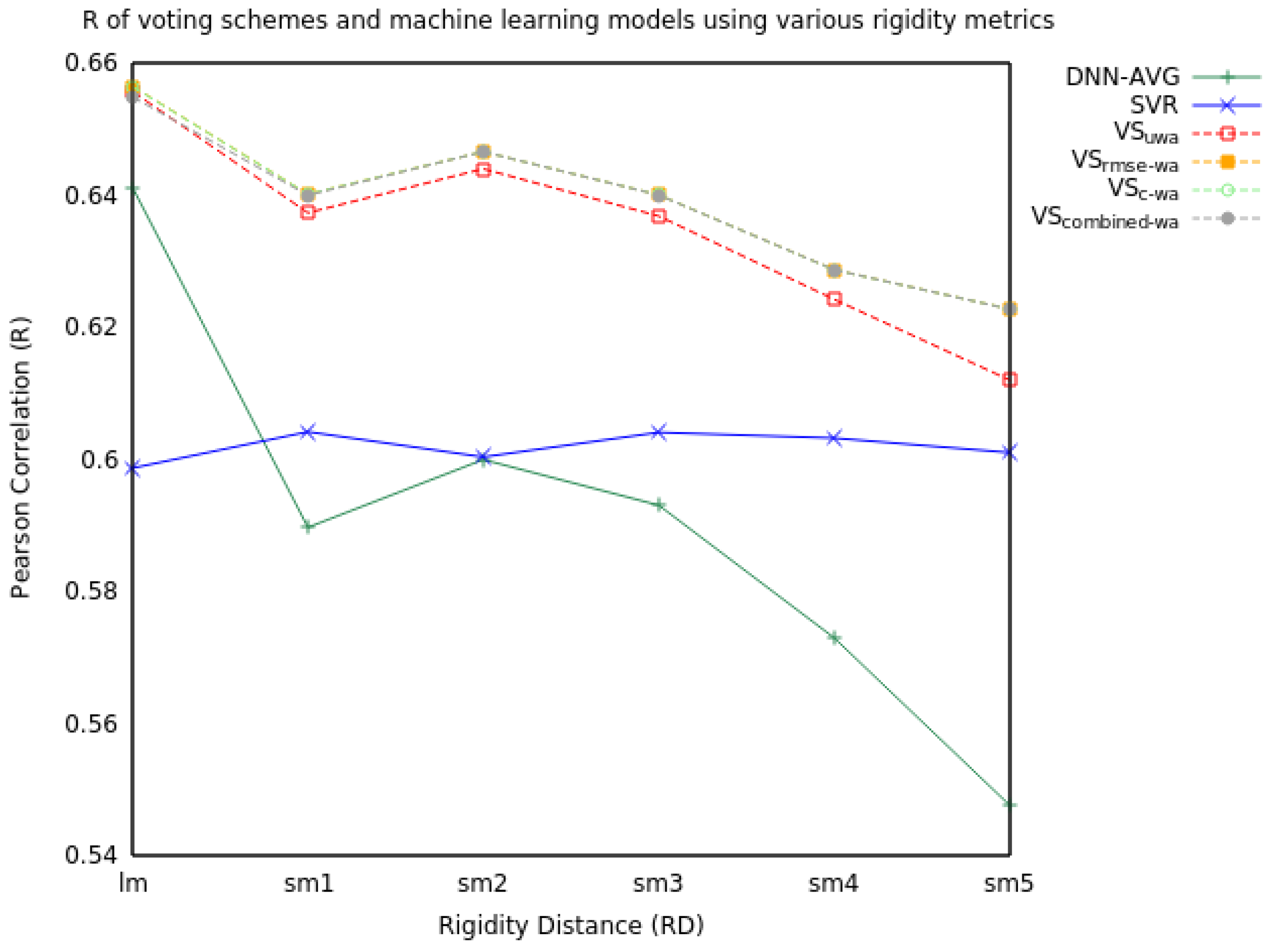
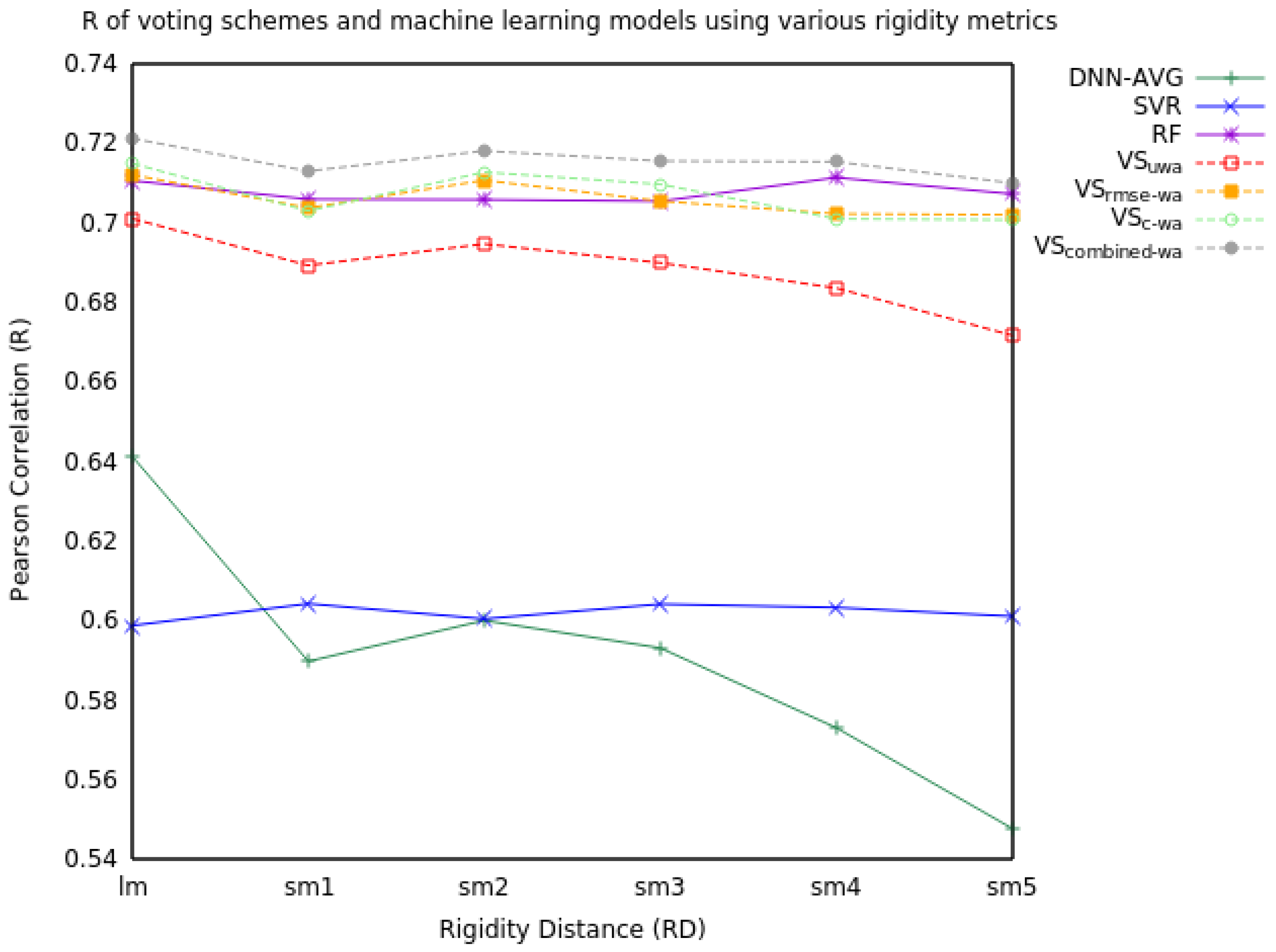
2.1. Voting
2.1.1. Two Model Voting
2.1.2. Three Model Voting
2.2. Feature Ablation Study
3. Discussion
4. Materials and Methods
4.1. Data Preparation
4.1.1. In Silico Mutants
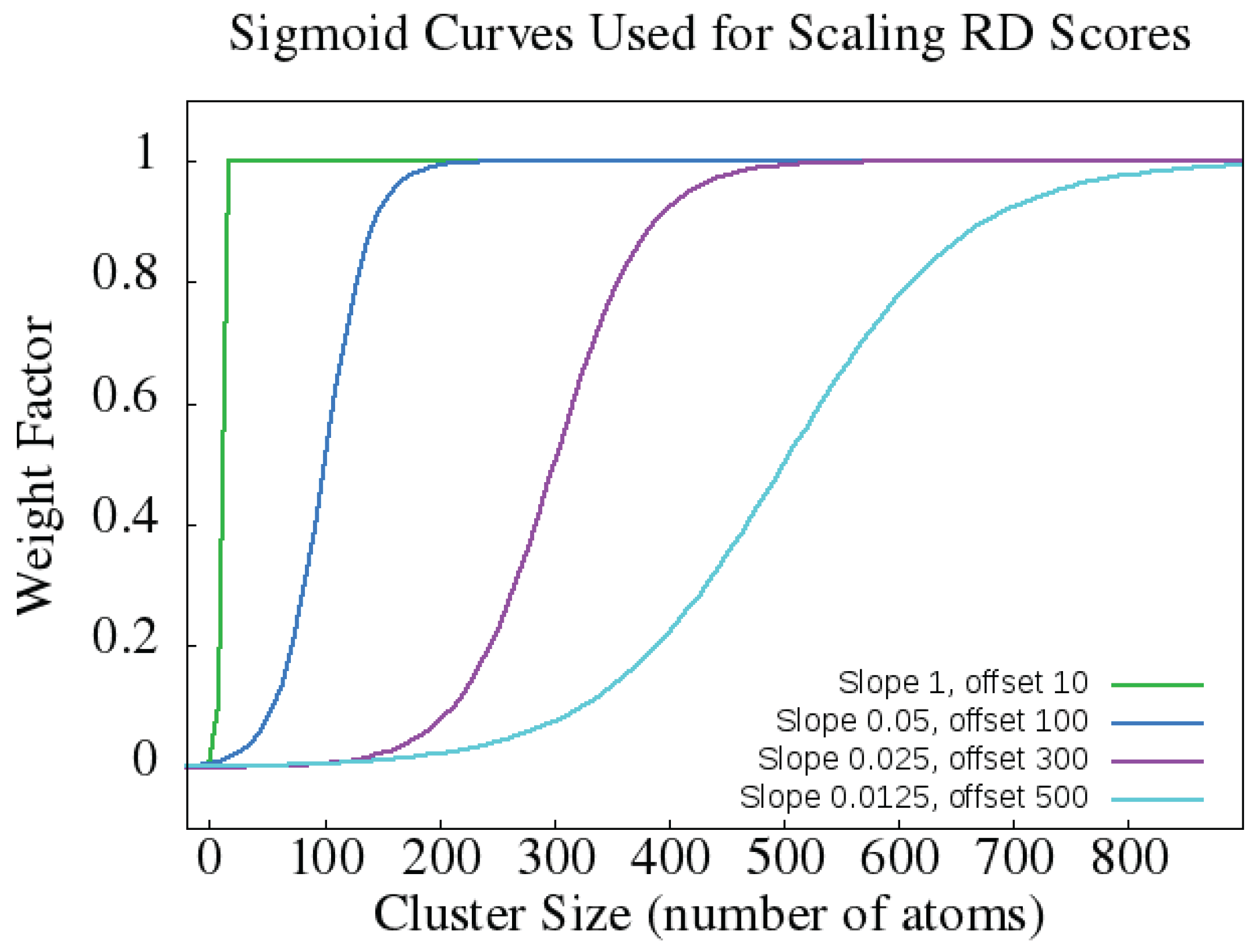
4.1.2. Rigidity Distance Scores
4.1.3. Feature Extraction
- Solvent accessible surface area (SASA): 2 real-valued features (4 in double mutations) indicating how exposed to the surface a residue is (both absolute and percentage).
- Secondary Structure: 4 binary features (8 for double mutations) indicating whether each mutation is part of a sheet, coil, turn or helix.
- Temperature and pH at which the experiment for calculating ddG was performed.
- Rigidity distances (RD): one of lm, sm1, sm2, sm3, sm4, and sm5 (see above and [37]).
- Rigid Cluster Fraction: 48 features giving the fraction of atoms in the WT and MUT that belong to rigid clusters of size 2, 3, ... , 20, 21–30, 31–50, 51–100, 101–1000, and 1001+, respectively.
- Residue type: 8 categorical features (16 in double mutants) indicating whether the mut1wt, mut1target (in double mutants also mut2wt, and mut2target) are Charged (D, E, K, R), Polar (N, Q, S, T), Aromatic (F, H, W, Y), or Hydrophobic (A, C, G, I, L, M, P, V).
4.1.4. Data Split
4.2. Machine Learning Methods
4.2.1. SVR
4.2.2. RF
4.2.3. DNN
4.3. Voting Schemes
- VSuwa: An unweighted average of all models’ predictions for a given mutation. For m models each with an output , where , our voting prediction is:
- VSc-wa: A weighted average of all models’ predictions for a given mutation, adjusting each model’s prediction based on the strength of its Pearson Correlation Coefficient, R, relative to the model with the best R. Again assume we have a set of models for but let denote the output from the best performing model, denote the R for model i and let denote R for the best performing model, then our voting prediction is:
- VSrmse-wa: A weighted average of all models’ predictions for a given mutation analogous to VSc-wa, except using RMSE instead of R. In this case, is the prediction of the best model (according to RMSE), is the RMSE for model i and is the RMSE of the best model. Then our voting prediction is:
- VScombined-wa: A weighted average of all models’ predictions for a given mutation incorporating both the R and RMSE performance. Letting and denote the best (max) , our prediction is:
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DNN | Deep Neural Network |
| SVR | Support Vector Regression |
| RF | Random Forest |
| LRC | Largest Rigid Cluster |
| RD | Rigidity Distance |
| WT | Wild Type |
References
- Garman, S.C.; Garboczi, D.N. Structural basis of Fabry disease. Mol. Genet. Metabol. 2002, 77, 3–11. [Google Scholar] [CrossRef]
- Kumar, M.; Bava, K.; Gromiha, M.; Prabakaran, P.; Kitajima, K.; Uedaira, H.; Sarai, A. Protherm and Pronit: Thermodynamic databases for proteins and protein-nucleic acid interactions. Nucleic Acids Res. 2005, 34, D204–D206. [Google Scholar] [CrossRef] [PubMed]
- Alber, T.; Sun, D.-P.; Wozniak, J.A.; Cook, S.P.; Matthews, B.W. Contributions of hydrogen bonds of Thr 157 to the thermodynamic stability of phage T4 lysozyme. Nature 1987, 330, 41–46. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.; Becktel, W.; Sauer, U.; Baase, W.; Matthews, B. Dissection of helix capping in T4 lysozyme by structural and thermodynamic analysis of six amino acid substitutions at Thr 59. Biochemistry 1992, 31, 3590–3596. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, A.; Baase, W.; Zhang, X.; Heinz, D.; Baldwin, E.; Matthews, B. Response of a protein structure to cavity-creating mutations and its relation to the hydrophobic effect. Science 1992, 255, 178–183. [Google Scholar] [CrossRef] [PubMed]
- Matsumura, M.; Becktel, W.; Matthews, B. Hydrophobic stabilization in T4 lysozyme determined directly by multiple substitutions of Ile 3. Nature 1988, 334, 406–410. [Google Scholar] [CrossRef] [PubMed]
- Mooers, B.; Baase, W.; Wray, J.; Matthews, B. Contributions of all 20 amino acids at site 96 to the stability and structure of T4 lysozyme. Protein Sci. 2009, 18, 871–880. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, H.; Soderlind, E.; Tronrud, D.; Matthews, B. Contributions of left-handed helical residues to the structure and stability of bacteriophage T4 lysozyme. J. Mol. Biol. 1989, 210, 181–193. [Google Scholar] [CrossRef]
- Dunbrack, R.J.; Karplus, M. Conformational analysis of the backbone-dependent rotamer preferences of protein sidechains. Nat. Struct. Biol. 1994, 1, 334–340. [Google Scholar] [CrossRef] [PubMed]
- Janin, J.; Wodak, S. Conformation of amino acid side-chains in proteins. J. Mol. Biol. 1978, 125, 357–386. [Google Scholar] [CrossRef]
- Ponder, J.; Richards, F. Tertiary templates for proteins: Use of packing criteria in the enumeration of allowed sequences for different structural classes. J. Mol. Biol. 1987, 193, 775–791. [Google Scholar] [CrossRef]
- Lee, C.; Levitt, M. Accurate prediction of the stability and activity effects of site-directed mutagenesis on a protein core. Nature 1991, 352, 448–451. [Google Scholar] [CrossRef] [PubMed]
- Gilis, D.; Rooman, M. Predicting protein stability changes upon mutation usings database derived potentials: Solvent accessiblity determines the importances of local versus non-local interactions along the sequence. J. Mol. Biol. 1997, 272, 276–290. [Google Scholar] [CrossRef] [PubMed]
- Prevost, M.; Wodak, S.; Tidor, B.; Karplus, M. Contribution of the hydrophobic effect to protein stability: analysis based on simulations of the Ile-96-Ala mutation in barnase. Proc. Natl. Acad. Sci. USA 1991, 88, 10880–10884. [Google Scholar] [CrossRef] [PubMed]
- Radestock, S.; Gohlke, H. Exploiting the Link between Protein Rigidity and Thermostability for Data-Driven Protein Engineering. Eng. Life Sci. 2008, 8, 507–522. [Google Scholar] [CrossRef]
- Jacobs, D.; Rader, A.; Thorpe, M.; Kuhn, L. Protein Flexibility Predictions Using Graph Theory. Proteins 2001, 44, 150–165. [Google Scholar] [CrossRef] [PubMed]
- Fox, N.; Jagodzinski, F.; Li, Y.; Streinu, I. KINARI-Web: A server for protein rigidity analysis. Nucleic Acids Res. 2011, 39, W177–W183. [Google Scholar] [CrossRef] [PubMed]
- Jagodzinski, F.; Hardy, J.; Streinu, I. Using rigidity analysis to probe mutation-induced structural changes in proteins. J. Bioinform. Comput. Biol. 2012, 10, 1242010. [Google Scholar] [CrossRef] [PubMed]
- Akbal-Delibas, B.; Jagodzinski, F.; Haspel, N. A Conservation and Rigidity Based Method for Detecting Critical Protein Residues. BMC Struct. Biol. 2013, 13 (Suppl. 1), S6. [Google Scholar] [CrossRef] [PubMed]
- Jagodzinski, F.; Akbal-Delibas, B.; Haspel, N. An Evolutionary Conservation & Rigidity Analysis Machine Learning Approach for Detecting Critical Protein Residues. CSBW (Computational Structural Bioinformatics Workshop). In Proceedings of the ACM International Conference on Bioinformatics and Computational Biology (ACM-BCB), Washington, DC, USA, 22–25 September 2013; pp. 780–786. [Google Scholar]
- Cheng, J.; Randall, A.; Baldi, P. Prediction of Protein Stability Changes for Single-Site Mutations Using Support Vector Machines. Proteins 2006, 62, 1125–1132. [Google Scholar] [CrossRef] [PubMed]
- Topham, C.; Srinivasan, N.; Blundell, T. Prediction of the stability of protein mutants based on structural environment-dependent amino acid substitutions and propensity tables. Protein Eng. 1997, 10, 7–21. [Google Scholar] [CrossRef] [PubMed]
- Worth, C.; Preissner, R.; Blundell, L. SDM—A server for predicting effects of mutations on protein stability and malfunction. Nucleic Acids Res. 2011, 39, W215–W222. [Google Scholar] [CrossRef] [PubMed]
- Brender, J.R.; Zhang, Y. Predicting the effect of mutations on protein-protein binding interactions through structure-based interface profiles. PLoS Comput. Biol. 2015, 11, e1004494. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Xing, P.; Shi, G.; Ji, Z.L.; Zou, Q. Fast prediction of protein methylation sites using a sequence-based feature selection technique. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Xing, P.; Tang, J.; Zou, Q. PhosPred-RF: A Novel Sequence-Based Predictor for Phosphorylation Sites Using Sequential Information Only. IEEE Trans. Nanobiosci. 2017, 16, 240–247. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Duan, Y.; Zou, Q. HPSLPred: An Ensemble Multi-Label Classifier for Human Protein Subcellular Location Prediction with Imbalanced Source. Proteomics 2017, 17, 1700262. [Google Scholar] [CrossRef] [PubMed]
- Jia, L.; Yarlagadda, R.; Reed, C.C. Structure Based Thermostability Prediction Models for Protein Single Point Mutations with Machine Learning Tools. PLoS ONE 2015, 10, e0138022. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Fang, J. PROTS-RF: A robust model for predicting mutation-induced protein stability changes. PLoS ONE 2012, 7, e47247. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Breiman, L. Stacked regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef]
- LeBlanc, M.; Tibshirani, R. Combining estimates in regression and classification. J. Am. Stat. Assoc. 1996, 91, 1641–1650. [Google Scholar] [CrossRef]
- Van der Laan, M.J.; Polley, E.C.; Hubbard, A.E. Super learner. Stat. Appl. Genet. Mol. Biol. 2007, 6. [Google Scholar] [CrossRef] [PubMed]
- Sapp, S.; van der Laan, M.J.; Canny, J. Subsemble: An ensemble method for combining subset-specific algorithm fits. J. Appl. Stat. 2014, 41, 1247–1259. [Google Scholar] [CrossRef] [PubMed]
- LeDell, E.; LeDell, M.E.; Java, S.; SuperLearner, S. Package ‘h2oEnsemble’. 2015. [Google Scholar]
- Schmidt, F.L.; Hunter, J.E. Methods of Meta-Analysis: Correcting Error and Bias in Research Findings; Sage Publications: Thousand Oaks, CA, USA, 2014. [Google Scholar]
- Andersson, E.; Hsieh, R.; Szeto, H.; Farhoodi, R.; Haspel, N.; Jagodzinski, F. Assessing how multiple mutations affect protein stability using rigid cluster size distributions. In Proceedings of the 2016 IEEE 6th International Conference on Computational Advances in Bio and Medical Sciences (ICCABS), Atlanta, GA, USA, 13–15 October 2016; IEEE: New York, NY, USA, 2016; pp. 1–6. [Google Scholar]
- Andersson, E.; Jagodzinski, F. ProMuteHT: A High Throughput Compute Pipeline for Generating Protein Mutants in Silico. In Proceedings of the 8th ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics (ACM-BCB’17), Boston, MA, USA, 20–23 August 2017; ACM: New York, NY, USA, 2017; pp. 655–660. [Google Scholar]
- Farhoodi, R.; Shelbourne, M.; Hsieh, R.; Haspel, N.; Hutchinson, B.; Jagodzinski, F. Predicting the Effect of Point Mutations on Protein Structural Stability. In Proceedings of the International Conference on Bioinformatics, Computational Biology and Health Informatics (ACM-BCB’17), Boston, MA, USA, 20–23 August 2017; ACM: New York, NY, USA, 2017; pp. 247–252. [Google Scholar]
- Krivov, G.G.; Shapovalov, M.V.; Dunbrack, R.L. Improved prediction of protein side-chain conformations with SCWRL4. Proteins 2009, 77, 778–795. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Basak, D.; Pal, S.; Patranabis, D.C. Support vector regression. Neural Inform. Proc.-Lett. Rev. 2007, 11, 203–224. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27:1–27:27. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015. Software available from tensorflow.org.
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
Sample Availability: Samples of the compounds are not available from the authors. |
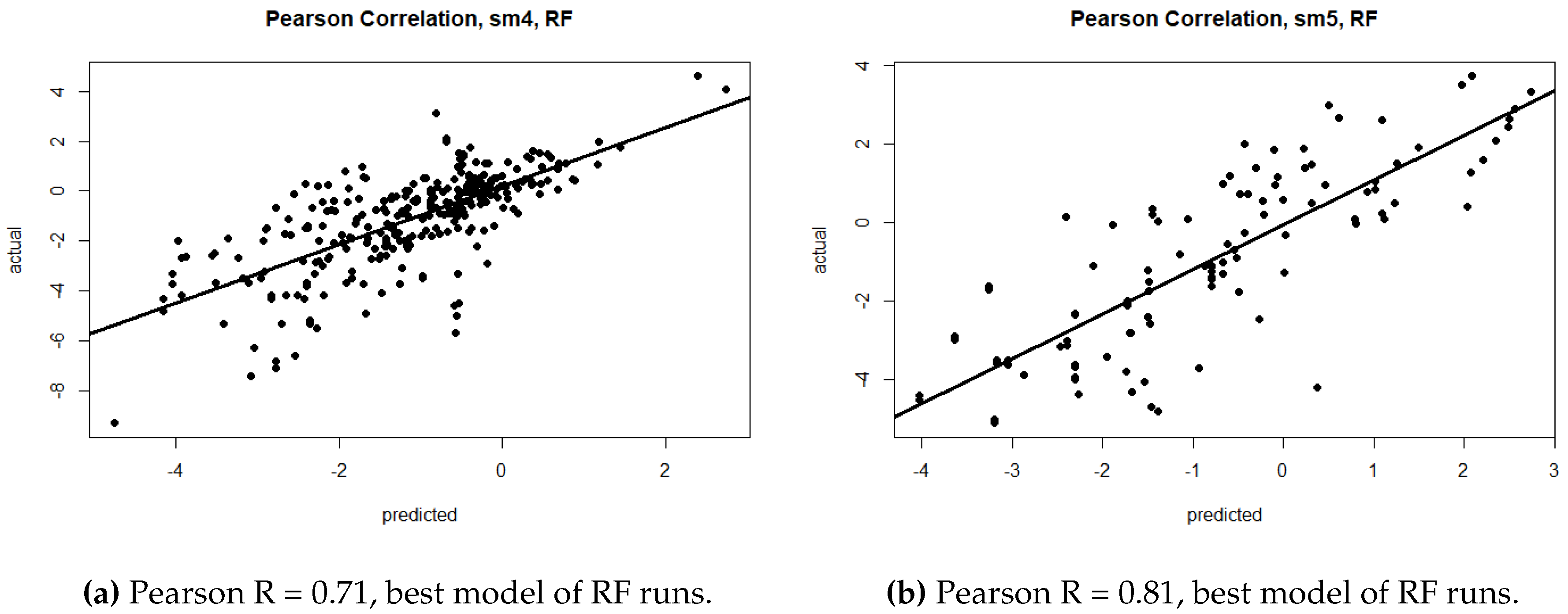
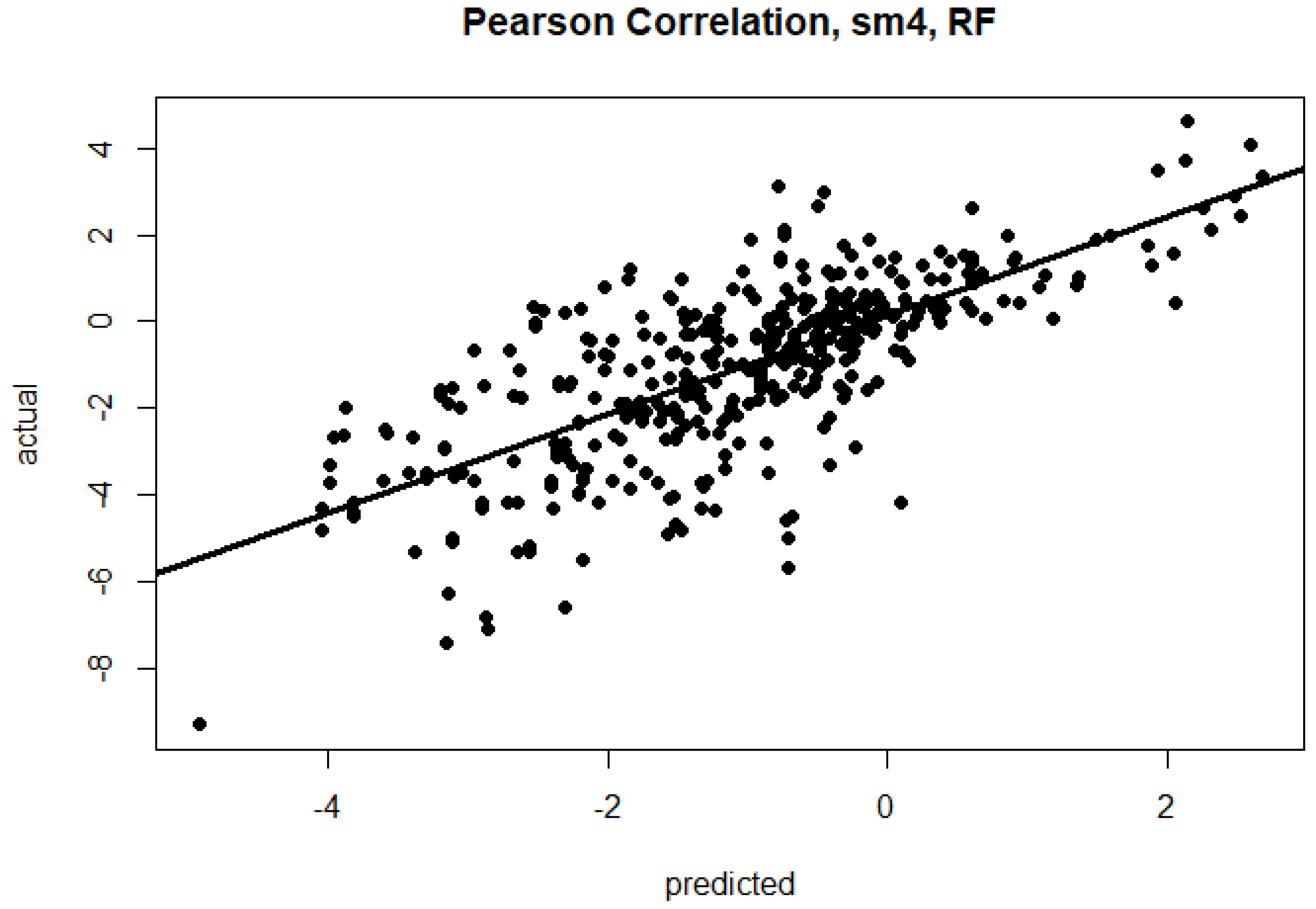
| Single Mutants | Double Mutants | Combined | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RD | Measure | SVR | RF | DNN | SVR | RF | DNN | SVR | RF | DNN |
| lm | RMSE | 1.53 | 1.34 | 1.60 | 1.61 | 1.41 | 1.74 | 1.54 | 1.39 | 1.71 |
| R | 0.60 | 0.71 | 0.58 | 0.76 | 0.79 | 0.66 | 0.65 | 0.72 | 0.52 | |
| sm1 | RMSE | 1.52 | 1.35 | 1.60 | 1.60 | 1.37 | 1.64 | 1.54 | 1.39 | 1.80 |
| R | 0.60 | 0.71 | 0.57 | 0.76 | 0.81 | 0.71 | 0.65 | 0.72 | 0.46 | |
| sm2 | RMSE | 1.53 | 1.35 | 1.71 | 1.61 | 1.36 | 1.90 | 1.54 | 1.40 | 1.87 |
| R | 0.60 | 0.71 | 0.55 | 0.76 | 0.81 | 0.60 | 0.65 | 0.72 | 0.46 | |
| sm3 | RMSE | 1.52 | 1.35 | 1.60 | 1.60 | 1.38 | 1.93 | 1.54 | 1.39 | 1.81 |
| R | 0.60 | 0.71 | 0.58 | 0.76 | 0.80 | 0.60 | 0.65 | 0.72 | 0.44 | |
| sm4 | RMSE | 1.52 | 1.34 | 1.57 | 1.56 | 1.38 | 1.83 | 1.54 | 1.38 | 1.77 |
| R | 0.60 | 0.71 | 0.57 | 0.77 | 0.80 | 0.64 | 0.66 | 0.73 | 0.55 | |
| sm5 | RMSE | 1.53 | 1.35 | 1.70 | 1.60 | 1.35 | 1.89 | 1.54 | 1.39 | 1.74 |
| R | 0.60 | 0.71 | 0.52 | 0.76 | 0.81 | 0.52 | 0.65 | 0.72 | 0.51 | |
| Avg. | RMSE | 1.53 | 1.35 | 1.63 | 1.60 | 1.38 | 1.82 | 1.54 | 1.39 | 1.78 |
| R | 0.60 | 0.71 | 0.56 | 0.76 | 0.80 | 0.62 | 0.65 | 0.72 | 0.49 | |
| Accuracy | Measure | SVR | RF | DNN |
|---|---|---|---|---|
| Single | Avg. Train RMSE | 1.08 | 0.47 | 1.04 |
| Avg. Test RMSE | 1.53 | 1.35 | 1.67 | |
| Avg. Train R | 0.79 | 0.97 | 0.79 | |
| Avg. Test R | 0.60 | 0.71 | 0.56 | |
| Double | Avg. Train RMSE | 1.08 | 0.70 | 1.20 |
| Avg. Test RMSE | 1.60 | 1.38 | 1.82 | |
| Avg. Train R | 0.83 | 0.93 | 0.69 | |
| Avg. Test R | 0.76 | 0.80 | 0.62 | |
| Combined | Avg. Train RMSE | 1.11 | 0.50 | 1.33 |
| Avg. Test RMSE | 1.52 | 1.39 | 1.78 | |
| Avg. Train R | 0.79 | 0.96 | 0.62 | |
| Avg. Test R | 0.65 | 0.72 | 0.49 |
| RD | Measure | SVR | DNN-AVG | VSuwa | VSrmse-wa | VSc-wa | VScombined-wa |
|---|---|---|---|---|---|---|---|
| lm | RMSE | 1.53 | 1.46 | 1.43 | 1.43 | 1.43 | 1.43 |
| R | 0.60 | 0.64 | 0.66 | 0.66 | 0.66 | 0.65 | |
| sm1 | RMSE | 1.52 | 1.55 | 1.46 | 1.46 | 1.46 | 1.46 |
| R | 0.60 | 0.59 | 0.64 | 0.64 | 0.64 | 0.64 | |
| sm2 | RMSE | 1.53 | 1.57 | 1.45 | 1.45 | 1.45 | 1.45 |
| R | 0.60 | 0.60 | 0.64 | 0.65 | 0.65 | 0.65 | |
| sm3 | RMSE | 1.52 | 1.57 | 1.46 | 1.46 | 1.46 | 1.46 |
| R | 0.60 | 0.59 | 0.64 | 0.64 | 0.64 | 0.64 | |
| sm4 | RMSE | 1.52 | 1.56 | 1.48 | 1.48 | 1.48 | 1.48 |
| R | 0.60 | 0.57 | 0.62 | 0.63 | 0.63 | 0.63 | |
| sm5 | RMSE | 1.53 | 1.63 | 1.50 | 1.49 | 1.49 | 1.49 |
| R | 0.60 | 0.55 | 0.61 | 0.62 | 0.62 | 0.62 |
| RD | Measure | DNN-AVG | SVR | RF | VSuwa | VSrmse-wa | VSc-wa | VScombined-wa |
|---|---|---|---|---|---|---|---|---|
| lm | RMSE | 1.46 | 1.53 | 1.34 | 1.37 | 1.35 | 1.35 | 1.33 |
| R | 0.64 | 0.60 | 0.71 | 0.70 | 0.71 | 0.71 | 0.72 | |
| sm1 | RMSE | 1.55 | 1.52 | 1.35 | 1.39 | 1.37 | 1.37 | 1.34 |
| R | 0.59 | 0.60 | 0.71 | 0.69 | 0.70 | 0.70 | 0.71 | |
| sm2 | RMSE | 1.57 | 1.53 | 1.35 | 1.37 | 1.35 | 1.35 | 1.33 |
| R | 0.60 | 0.60 | 0.71 | 0.69 | 0.71 | 0.71 | 0.72 | |
| sm3 | RMSE | 1.56 | 1.52 | 1.35 | 1.38 | 1.36 | 1.36 | 1.34 |
| R | 0.59 | 0.60 | 0.71 | 0.69 | 0.70 | 0.71 | 0.72 | |
| sm4 | RMSE | 1.56 | 1.52 | 1.34 | 1.40 | 1.37 | 1.38 | 1.34 |
| R | 0.57 | 0.60 | 0.71 | 0.68 | 0.70 | 0.70 | 0.72 | |
| sm5 | RMSE | 1.63 | 1.53 | 1.35 | 1.41 | 1.37 | 1.37 | 1.35 |
| R | 0.55 | 0.60 | 0.71 | 0.67 | 0.70 | 0.70 | 0.71 |
| Accuracy Measure | Feature 1 | Feature 2 | Feature 3 | No Ablation | |
|---|---|---|---|---|---|
| lm | SASA | temp | type | ||
| RMSE | 1.48 | 1.39 | 1.38 | 1.34 | |
| R | 0.63 | 0.68 | 0.69 | 0.71 | |
| sm1 | SASA | temp | type | ||
| RMSE | 1.50 | 1.39 | 1.38 | 1.35 | |
| R | 0.62 | 0.66 | 0.69 | 0.71 | |
| sm2 | SASA | temp | type | ||
| RMSE | 1.50 | 1.39 | 1.38 | 1.35 | |
| R | 0.62 | 0.68 | 0.69 | 0.71 | |
| sm3 | SASA | temp | type | ||
| RMSE | 1.49 | 1.38 | 1.37 | 1.36 | |
| R | 0.62 | 0.68 | 0.69 | 0.70 | |
| sm4 | SASA | temp | type | ||
| RMSE | 1.49 | 1.38 | 1.38 | 1.35 | |
| R | 0.63 | 0.69 | 0.69 | 0.71 | |
| sm5 | SASA | temp | type | ||
| RMSE | 1.50 | 1.40 | 1.38 | 1.36 | |
| R | 0.62 | 0.68 | 0.69 | 0.70 |
| Accuracy Measure | Feature 1 | Feature 2 | Feature 3 | No Ablation | |
|---|---|---|---|---|---|
| lm | mut2SASA | mutClusterFrac16 | wtClusterFrac1001 | ||
| RMSE | 1.47 | 1.41 | 1.40 | 1.39 | |
| R | 0.77 | 0.79 | 0.79 | 0.80 | |
| sm1 | mut2SASA | wtClusterFrac11 | |||
| RMSE | 1.46 | 1.39 | 1.39 | ||
| R | 0.77 | 0.80 | 0.80 | ||
| sm2 | mut2SASA | wtClusterFrac11 | mut1target_type | ||
| RMSE | 1.46 | 1.39 | 1.38 | 1.37 | |
| R | 0.77 | 0.80 | 0.80 | 0.81 | |
| sm3 | mut2SASA | ph | mutClusterFrac11 | ||
| RMSE | 1.46 | 1.40 | 1.38 | 1.37 | |
| R | 0.77 | 0.80 | 0.80 | 0.80 | |
| sm4 | mut2SASA | wtClusterFrac18 | wtClusterFrac101 | ||
| RMSE | 1.45 | 1.40 | 1.40 | 1.37 | |
| R | 0.78 | 0.79 | 0.80 | 0.80 | |
| sm5 | mut2SASA | wtClusterFrac11 | ph | ||
| RMSE | 1.47 | 1.39 | 1.39 | 1.36 | |
| R | 0.77 | 0.80 | 0.80 | 0.81 |
| Accuracy Measure | Feature 1 | Feature 2 | Feature 3 | No Ablation | |
|---|---|---|---|---|---|
| lm | mut1SASA | temp | mut1type | ||
| RMSE | 1.47 | 1.43 | 1.42 | 1.40 | |
| R | 0.68 | 0.70 | 0.70 | 0.72 | |
| sm1 | mut1SASA | temp | mut1type | ||
| RMSE | 1.48 | 1.42 | 1.41 | 1.39 | |
| R | 0.68 | 0.71 | 0.71 | 0.72 | |
| sm2 | mut1SASA | temp | mut1type | ||
| RMSE | 1.48 | 1.42 | 1.42 | 1.39 | |
| R | 0.68 | 0.70 | 0.71 | 0.72 | |
| sm3 | mut1SASA | mut1type | temp | ||
| RMSE | 1.48 | 1.42 | 1.42 | 1.39 | |
| R | 0.68 | 0.70 | 0.71 | 0.72 | |
| sm4 | mut1SASA | temp | mut1type | ||
| RMSE | 1.47 | 1.42 | 1.41 | 1.39 | |
| R | 0.69 | 0.71 | 0.71 | 0.72 | |
| sm5 | mut1SASA | temp | mut1type | ||
| RMSE | 1.48 | 1.43 | 1.41 | 1.40 | |
| R | 0.68 | 0.70 | 0.71 | 0.72 |
| Dataset | Training | Development | Test | Total |
|---|---|---|---|---|
| Single | 1488 | 331 | 320 | 2139 |
| Double | 147 | 60 | 107 | 314 |
| Combined | 1635 | 391 | 427 | 2453 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehghanpoor, R.; Ricks, E.; Hursh, K.; Gunderson, S.; Farhoodi, R.; Haspel, N.; Hutchinson, B.; Jagodzinski, F. Predicting the Effect of Single and Multiple Mutations on Protein Structural Stability. Molecules 2018, 23, 251. https://doi.org/10.3390/molecules23020251
Dehghanpoor R, Ricks E, Hursh K, Gunderson S, Farhoodi R, Haspel N, Hutchinson B, Jagodzinski F. Predicting the Effect of Single and Multiple Mutations on Protein Structural Stability. Molecules. 2018; 23(2):251. https://doi.org/10.3390/molecules23020251
Chicago/Turabian StyleDehghanpoor, Ramin, Evan Ricks, Katie Hursh, Sarah Gunderson, Roshanak Farhoodi, Nurit Haspel, Brian Hutchinson, and Filip Jagodzinski. 2018. "Predicting the Effect of Single and Multiple Mutations on Protein Structural Stability" Molecules 23, no. 2: 251. https://doi.org/10.3390/molecules23020251
APA StyleDehghanpoor, R., Ricks, E., Hursh, K., Gunderson, S., Farhoodi, R., Haspel, N., Hutchinson, B., & Jagodzinski, F. (2018). Predicting the Effect of Single and Multiple Mutations on Protein Structural Stability. Molecules, 23(2), 251. https://doi.org/10.3390/molecules23020251






