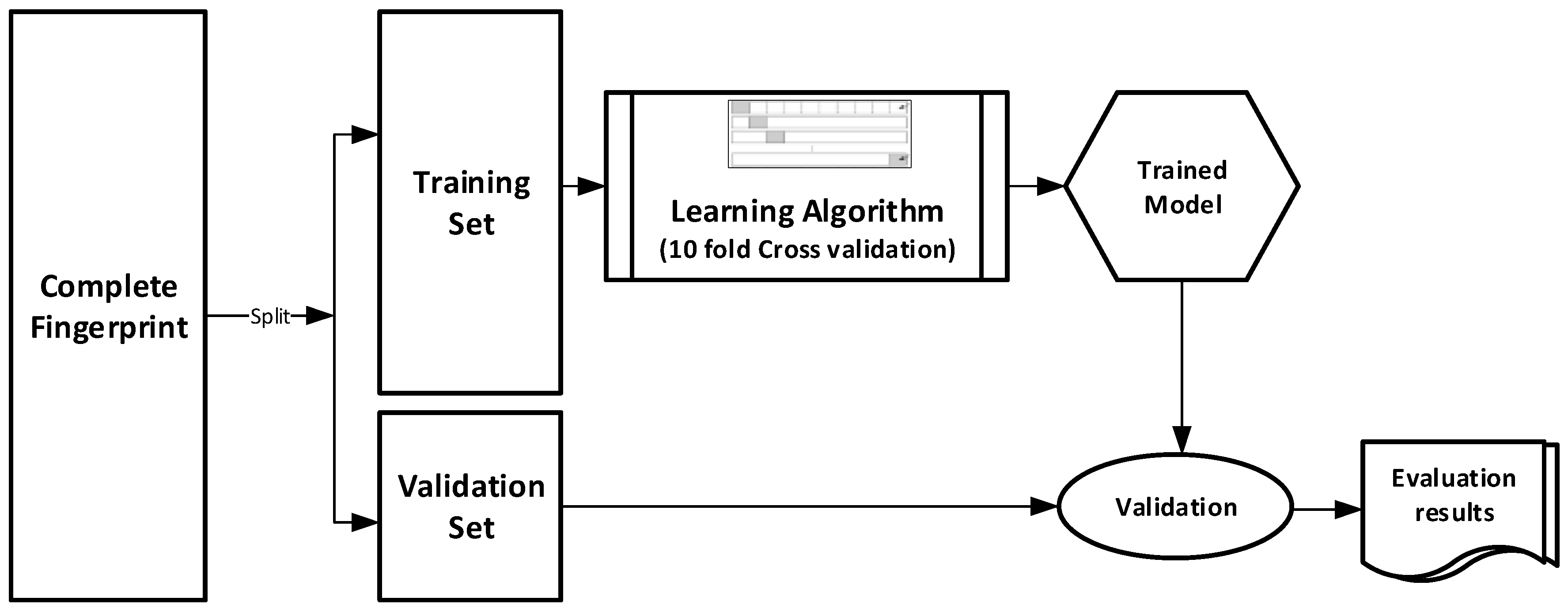
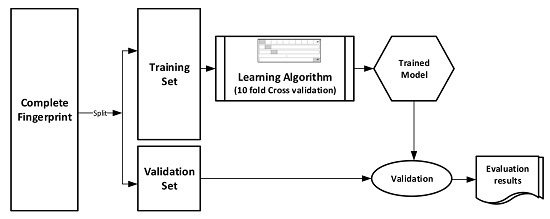
3.1. Datasets
This work was evaluated on seven carefully selected datasets that have been used to validate fingerprint based molecule classification and activity prediction in the past. A description of COX2 cyclooxygenase-2 inhibitors (COX2) (467 samples), benzodiazepine receptor (BZR) (405 samples) and estrogen receptor (ER) (393 samples) datasets [
19,
20] is shown in
Table 1. The compounds are classified as active or inactive, and divided into training (70%) and validation (30%) sets for the purpose of this work. The table shows the mean pairwise Tanimoto similarity that was calculated based on ECFC_4 across all pairs of molecules for both active and inactive molecules.
The fourth dataset utilized as a part of this study is Directory of Useful Decoys (DUD), which was presented by [
21]. Although recently compiled as a benchmark data, its use in virtual screening can be found in [
22,
23].The decoys for each target have been chosen to fulfill a number of criteria to make them relevant and as unbiased as possible. Only 12 subsets of the DUD with only 704 active compounds were considered and divided into training (70%) and validation (30%) set in this study as shown in
Table 2.
The last three datasets (MDDR1-3), selected from the MDL Drug Data Report MDDR [
24], have been previously used for LBVS [
22,
25] and activity prediction [
26]. The MDDR data sets contain well defined derivatives and biologically relevant compounds that were converted to Pipeline Pilot’s ECFC_4 fingerprints and folded to give 1024 element fingerprints. A detailed description of each dataset showing the training (70%) and validation (30%) sets, activity classes, number of molecules per class, and their average pairwise Tanimoto similarity across all pairs of molecules is given in
Table 3,
Table 4 and
Table 5. The active molecules for each dataset were used. For instance, the MDDR1 (
Table 3) contains a total of 8294 active molecules, which is a mixture of both structurally homogeneous and heterogeneous active molecules (11 classes). The MDDR2 (5083 molecules) and MDDR3 (8568 Molecules) in
Table 4 and
Table 5 respectively, contain 10 homogeneous activity classes and 10 heterogeneous ones respectively [
27].
The datasets were divided into training (70%) and validation (30%) sets for the purpose of this experiment. Ten-fold cross-validation was used for the Training set. In this cross-validation, the data set was split into 10 parts; 9 were used for training and the remaining 1 was used for testing. This process is repeated 10 times with a different 10th of the dataset used to test the remaining 9 parts during every run of the 10-fold cross validation.
Figure 1 pictorially illustrates the various stages involved in the work under study.
3.2. Xgboost and Machine Learning Algorithms Parameters
Identifying the optimal parameters for a classifier can be time consuming and tedious and Xgboost is not an exception. This is even more challenging in Xgboost due to the wide range of tuneable parameters for optimal performance; a few of which, using the R [
28] implementation of Xgboost, we have restricted our scope to in this work. Thus, by using brute force, we obtained the best performance for Xgboost when eta, gamma, minimum child weight and maximum depth were 0.2, 0.16, 5 and 16 respectively. Where; eta is the step size shrinkage meant to control the learning rate and over-fitting through scaling each tree contribution, gamma is the minimum loss reduction required to make a split, minimum child weight is the minimum sum of instance weight needed in a child and max depth is the maximum depth of a child. Other tree booster parameters like maximum delta step, subsample, column sample and the number of trees to grow per round are left at their default values of 1 respectively. For LSVM, WEKA workbench offers a way to automate the search for optimal parameters. By using grid search, a peak performance with the radial basis kernel was obtained when gamma and cost were 5.01187233627273 × 10
4 and 20 respectively. RF performed best when the maximum depth of tree was not constrained and the number of iteration set to its default value of 100. The NB classifier achieved best performance when kernel estimator parameter is used instead of normal distribution. For RBFN, we converted numeric attributes to nominal and set the minimum standard deviation to 0.1 to get the best performance.
3.3. Evaluation Metrics
The choice of performance evaluation for both model building and validation have been carefully selected from the most commonly used metrics in the literature. The selected evaluation metrics includes the accuracy, area under curve (AUC), sensitivity (SEN), specificity (SPC) and F-measure (F-Sc). The one run definition of AUC (Equation (11)) also known as balanced accuracy which is given by the average of the sum of sensitivity and specificity has been used in this work.
while sensitivity (SEN) (Equation (12)) and specificity (SPC) (Equation (13)) show the ability of the model to correctly classify true positive as positive and true negative as negative respectively, AUC simply describes the tradeoff between them.
where tp, tn, fp and fn are true positive, true negative, false positive and false negative respectively. In addition to the accuracy (Equation (14)) which is the sum of the correctly classified divided by the total number of classes, F-measure (FSc) (Equation (15)), which is the harmonic mean of precision and recall is included to serve as measure the model’s accuracy.
This work aims to introduce Xgboost for activity prediction through its performance on known datasets in drug discovery. To achieve this aim, the performance of Xgboost was compared with four state of the art machine learning algorithms used in drug discovery based on the afore-stated evaluation metrics. The prediction performances of the different machine learning algorithms on the datasets under study are tabulated in
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11 and
Table 12. The best values for each metric is shaded.
The experimental results on MDDR1-3 Validation datasets (
Table 6,
Table 7 and
Table 8) shows that Xgboost produced the best accuracy, sensitivity, specificity, AUC and F-Sc across all the activity classes compared to the other machine learning methods (RF, LSVM, RBFN and NB) despite the obvious imbalance distribution of activity classes in the most of the datasets. Hence, the Xgboost method performed well for the high diverse dataset (MDDR3), and these results are particularly interesting since the MDDR3 is made up of heterogeneous activity classes which are more challenging for most machine learning algorithms.
For DUD Validation dataset (
Table 9), Xgboost and RF produced the best accuracy (0.9471) compared to the other methods. In addition, Xgboost produced the best specificity across all DUD sub datasets. However, NB obtained the best sensitivity, AUC and F-Sc results.
For COX2, ER and BZR Validation datasets (
Table 10,
Table 11 and
Table 12), it is shown that Xgboost performed well and produced the best accuracy and AUC for COX2 and ER datasets. In addition, it obtained the best F-Sc results for COX2 dataset compared to the other state-of-art methods.
Visual inspection of the results shows that Xgboost produced the best accuracy for all used datasets (except for BZR dataset which produced the second best accuracy). While the performance of Xgboost on most activity classes in terms of accuracy and AUC remains the best, it still produces the best average performance across all evaluation metrics. In addition, the good performance of Xgboost is not only restricted to homogenous activity classes since it also performed well on the heterogeneous dataset.
Moreover, a quantitative approach using Kendall W test of concordance was used to rank the effectiveness of all used methods as shown in
Table 13. This test shows whether a set of raters make comparable judgments on the ranking of a set of objects. Hence, the XGB, RF, LSVM, RBFN and NB methods were used as the raters, and the accuracy measure (using MDDR1-3, DUD, COX2, BZR and ER datasets respectively) were used as the ranked objects. The outputs of this test are the Kendall coefficient (W) and the associated significance level (p value). In this paper, if the value is significant at a cutoff value of 0.01, then it is possible to give an overall ranking for the methods.
The results of the Kendall analysis for the seven datasets are shown in
Table 13. The columns show the evaluation measure, the value of the Kendall coefficient (W), the associated significance level (p value), and the ranking of prediction methods. The overall rankings of the four methods show that Xgboost significantly outperforms the other methods using accuracy measure across all datasets.