Thermodynamics and Kinetics of Guest-Induced Switching between “Basket Handle” Porphyrin Isomers
Abstract
:1. Introduction
2. Results and Discussion
2.1. Design

2.2. Synthesis

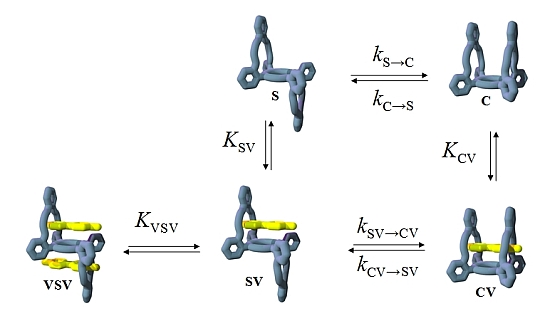
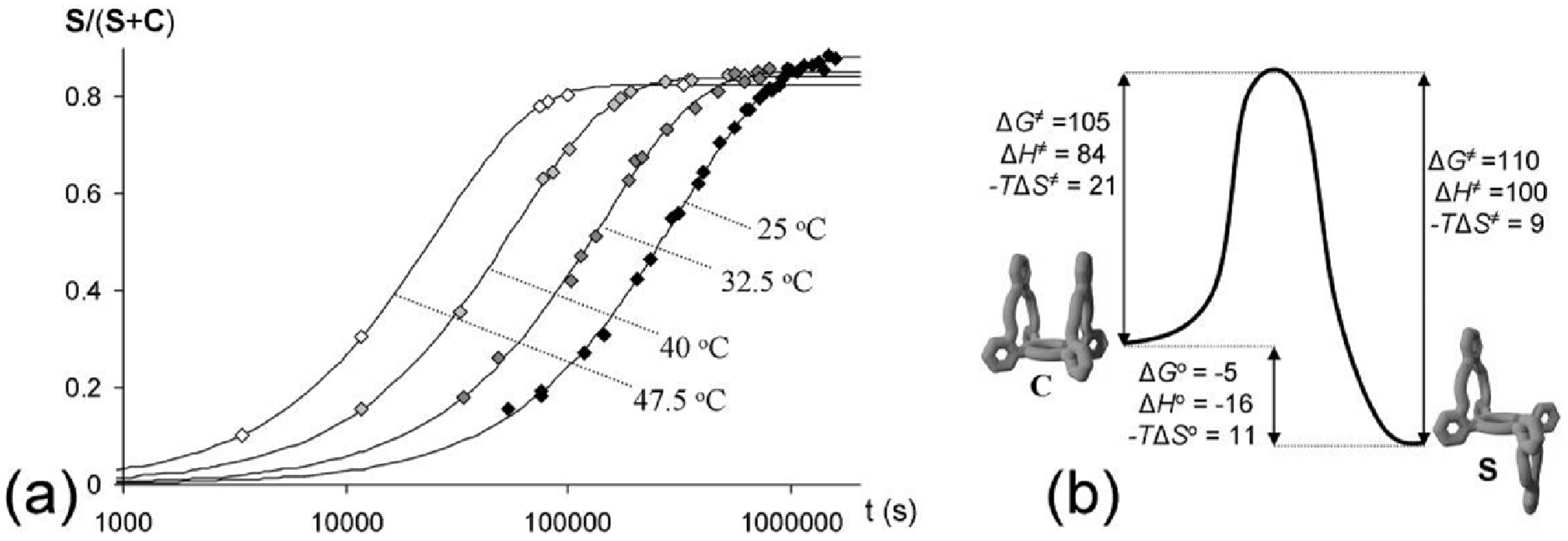
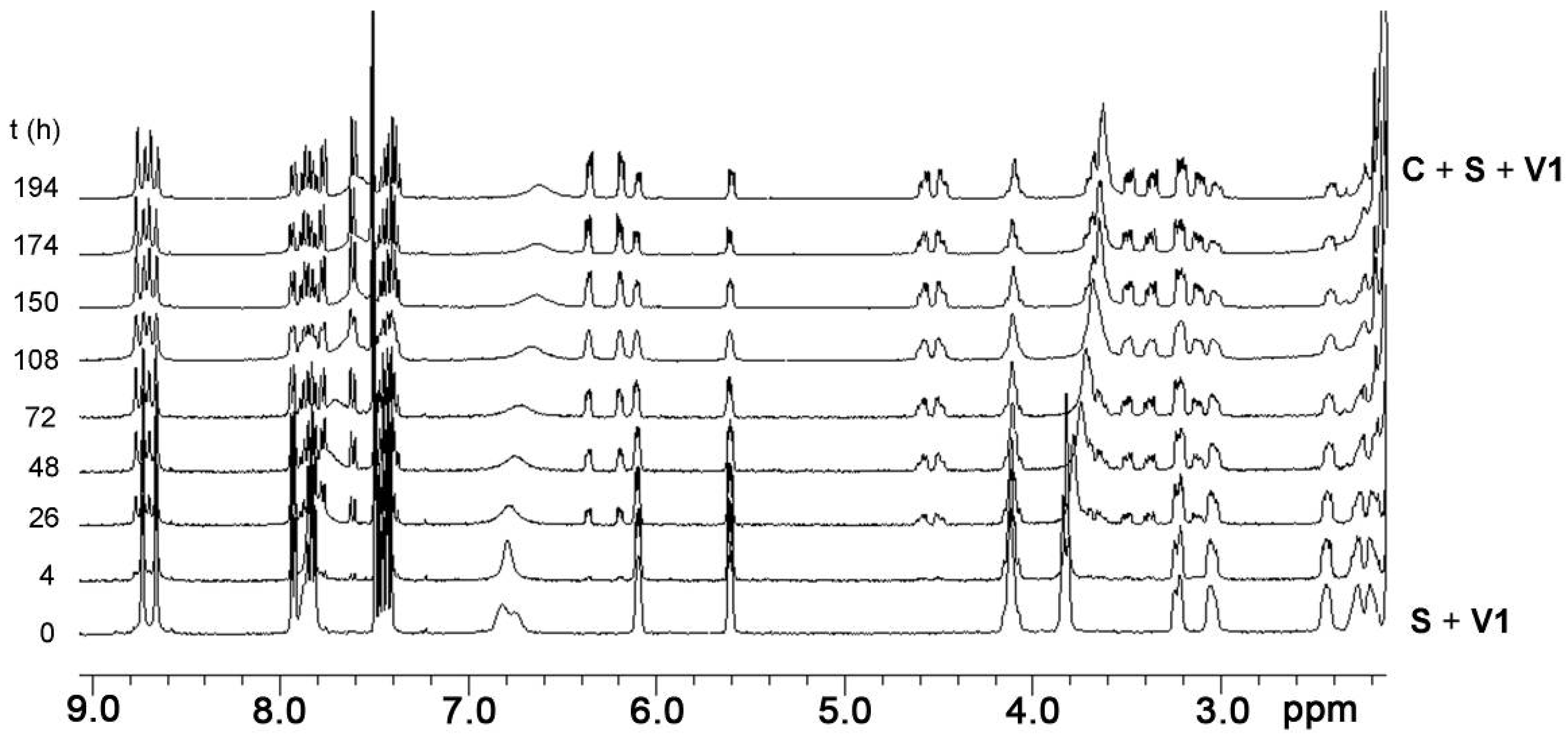
2.3. Isomerization

| T (°C) | kC→S (s−1) a | kS→C (s−1) b,c | K b |
|---|---|---|---|
| 25 | 2.8 × 10−6 | 3.7 × 10−7 | 7.6 |
| 32.5 | 6.0 × 10−6 | 1.0 × 10−6 | 5.8 |
| 40 | 1.5 × 10−5 | 2.8 × 10−6 | 5.3 |
| 47.5 | 3.2 × 10−5 | 6.8 × 10−6 | 4.7 |
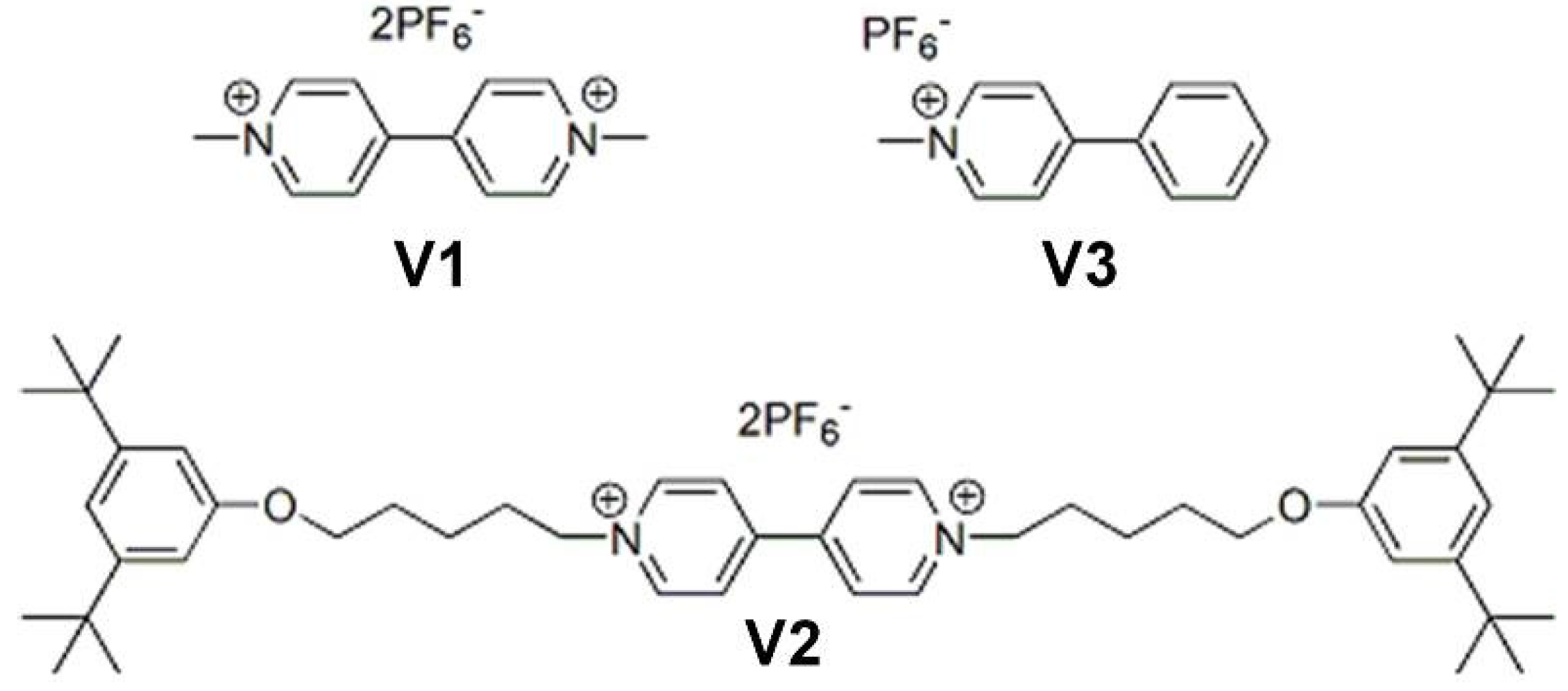
2.4. Binding of Viologen Derivatives
| Proton b | C | S | ||||
|---|---|---|---|---|---|---|
| V1 | V2 | V3 d | V1 | V2 e | V3 d | |
| H-1 | 0.00 | 0.01 | 0.01 | −0.28 | −0.06 | −0.28 |
| H-2 | −0.03 | −0.10 | −0.03 | −0.13 | −0.08 | −0.06 |
| H-3 to H-5 c | 0.42 | 0.43 | f | 0.47 | f | 0.50 |
| H-6a | 0.51 | 0.64 | f | 0.25 | f | 0.21 |
| H-6b | 0.47 | 0.29 | f | 0.21 | f | 0.17 |
| N-H | −1.04 | −0.98 | −0.51 | −1.12 | −0.33 | −0.85 |
| Receptor isomer | Guest | Kac(M−1) | Δ G°(kJ/mol) | Δ H° d(kJ/mol) | Δ S° eJ/molK |
|---|---|---|---|---|---|
| S | V1 ( KSV) | 1.3 × 104a,b | −23.6 | −31.3 | −25.9 |
| V1 ( KVSV) | 6.0 × 102a | −15.8 | |||
| C | V1 | 3.0 × 105b | −31.2 | −30.1 | +3.7 |
| V2 | 3.5 × 103a | −20.2 |
2.5. Guest-Induced Switching: Thermodynamics
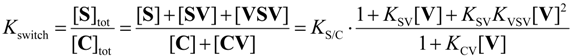
 ) and 47.5 °C (
) and 47.5 °C (  ) plotted against the concentration of V1 present in solution and the expected equilibrium ratios ([C]tot/([S]tot + [C]tot}) based on the experimentally derived individual equilibrium constants (thin lines) and the bests fits (thicker lines matching the data points) of the experimental data (37.5 °C: KS/C = 5.5, KSV = 1.5 × 104 M−1, KVSV = 2.0 × 102 M−1, KCV = 1.8 × 105 M−1. 47.5 °C: KS/C = 4.7, KSV = 7.0 × 103 M−1, KVSV = 70 M−1, KCV = 9.5 × 104 M−1). (b) Observed initial rates (kS→C-obs) for the switching of S to C in solutions with different concentrations of V1 at 37.5 °C. The framework represents the theoretical rates based on different values of the cooperativity factor (cf), assuming equilibrium constants KSV = 1.5 × 104 M−1 and KVSV = 2.0 × 102 M−1.
) plotted against the concentration of V1 present in solution and the expected equilibrium ratios ([C]tot/([S]tot + [C]tot}) based on the experimentally derived individual equilibrium constants (thin lines) and the bests fits (thicker lines matching the data points) of the experimental data (37.5 °C: KS/C = 5.5, KSV = 1.5 × 104 M−1, KVSV = 2.0 × 102 M−1, KCV = 1.8 × 105 M−1. 47.5 °C: KS/C = 4.7, KSV = 7.0 × 103 M−1, KVSV = 70 M−1, KCV = 9.5 × 104 M−1). (b) Observed initial rates (kS→C-obs) for the switching of S to C in solutions with different concentrations of V1 at 37.5 °C. The framework represents the theoretical rates based on different values of the cooperativity factor (cf), assuming equilibrium constants KSV = 1.5 × 104 M−1 and KVSV = 2.0 × 102 M−1.
 ) and 47.5 °C (
) and 47.5 °C (  ) plotted against the concentration of V1 present in solution and the expected equilibrium ratios ([C]tot/([S]tot + [C]tot}) based on the experimentally derived individual equilibrium constants (thin lines) and the bests fits (thicker lines matching the data points) of the experimental data (37.5 °C: KS/C = 5.5, KSV = 1.5 × 104 M−1, KVSV = 2.0 × 102 M−1, KCV = 1.8 × 105 M−1. 47.5 °C: KS/C = 4.7, KSV = 7.0 × 103 M−1, KVSV = 70 M−1, KCV = 9.5 × 104 M−1). (b) Observed initial rates (kS→C-obs) for the switching of S to C in solutions with different concentrations of V1 at 37.5 °C. The framework represents the theoretical rates based on different values of the cooperativity factor (cf), assuming equilibrium constants KSV = 1.5 × 104 M−1 and KVSV = 2.0 × 102 M−1.
) plotted against the concentration of V1 present in solution and the expected equilibrium ratios ([C]tot/([S]tot + [C]tot}) based on the experimentally derived individual equilibrium constants (thin lines) and the bests fits (thicker lines matching the data points) of the experimental data (37.5 °C: KS/C = 5.5, KSV = 1.5 × 104 M−1, KVSV = 2.0 × 102 M−1, KCV = 1.8 × 105 M−1. 47.5 °C: KS/C = 4.7, KSV = 7.0 × 103 M−1, KVSV = 70 M−1, KCV = 9.5 × 104 M−1). (b) Observed initial rates (kS→C-obs) for the switching of S to C in solutions with different concentrations of V1 at 37.5 °C. The framework represents the theoretical rates based on different values of the cooperativity factor (cf), assuming equilibrium constants KSV = 1.5 × 104 M−1 and KVSV = 2.0 × 102 M−1.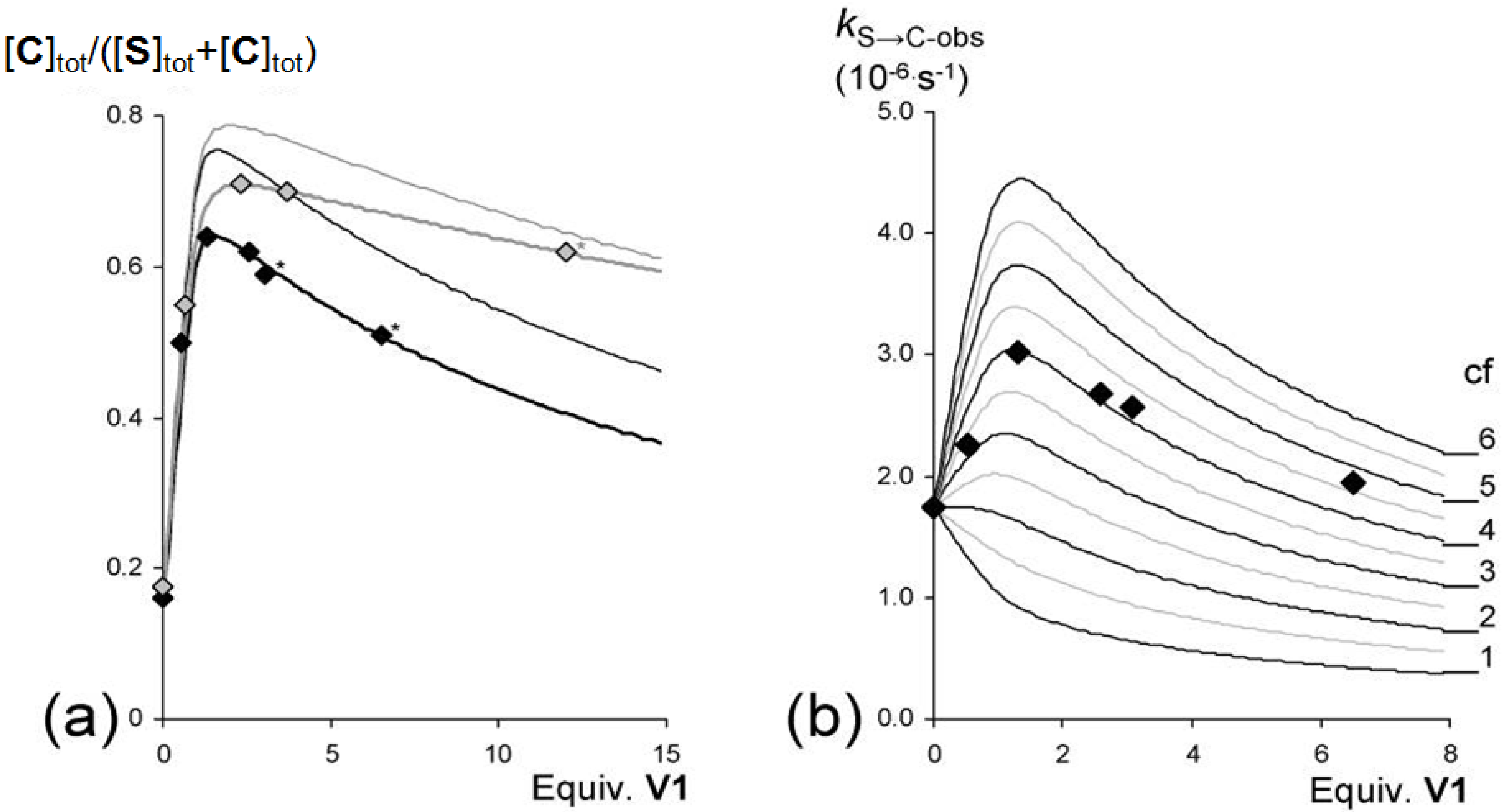
| Guest | Conc (mM) | kS→C-obsb,d (s−1) | Kswitchc,e |
|---|---|---|---|
| No | 0 | 1.8 × 10−6 | 5.5 |
| V1 | 0.5 | 2.3 × 10−6 | 1.0 |
| V1 | 1.3 | 3.0 × 10−6 | 0.6 |
| V1 | 2.6 | 2.7 × 10−6 | 0.6 |
| V1 | 3.1 | 2.6 × 10−6 | 0.7 |
| V1 | 6.5 | 1.9 × 10−6 | 1.0 |
| V2 | 3.3 | 2.4 × 10−6 | 0.9 |
| V3 | 20 | 1.1 × 10−6 | 10.0 |

 ) and in the presence of 1.3 equivalents of V1 (
) and in the presence of 1.3 equivalents of V1 (  ), 3.3 equivalents of V2 (
), 3.3 equivalents of V2 (  ) and 20 equivalents of V3 (
) and 20 equivalents of V3 (  ). The line represents the calculated curve for the switching in the presence of 1.3 equivalents of V1 assuming no induced switching effect.
). The line represents the calculated curve for the switching in the presence of 1.3 equivalents of V1 assuming no induced switching effect.
 ) and in the presence of 1.3 equivalents of V1 (
) and in the presence of 1.3 equivalents of V1 (  ), 3.3 equivalents of V2 (
), 3.3 equivalents of V2 (  ) and 20 equivalents of V3 (
) and 20 equivalents of V3 (  ). The line represents the calculated curve for the switching in the presence of 1.3 equivalents of V1 assuming no induced switching effect.
). The line represents the calculated curve for the switching in the presence of 1.3 equivalents of V1 assuming no induced switching effect.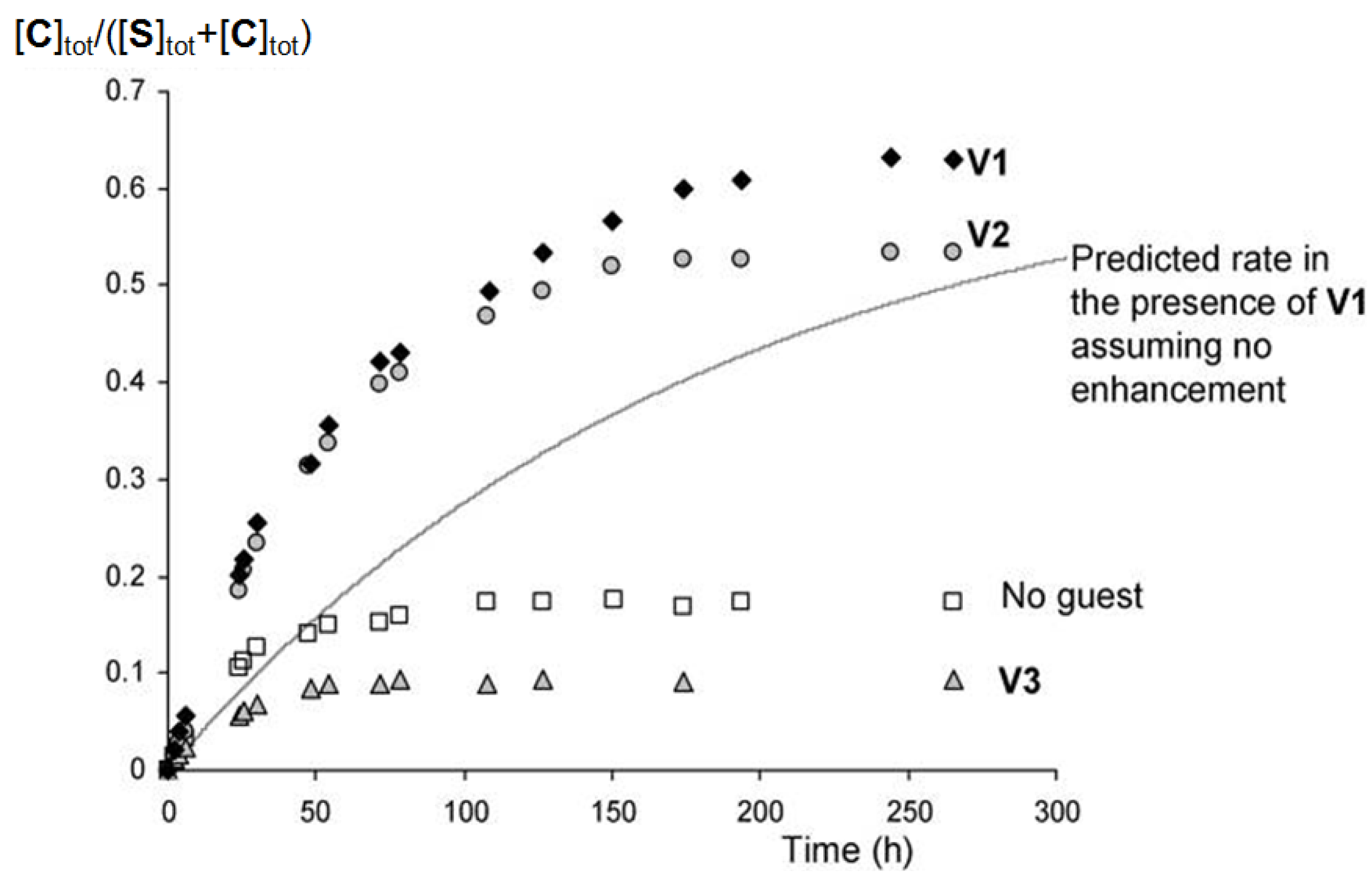
2.6. Guest-Induced Switching: Kinetics
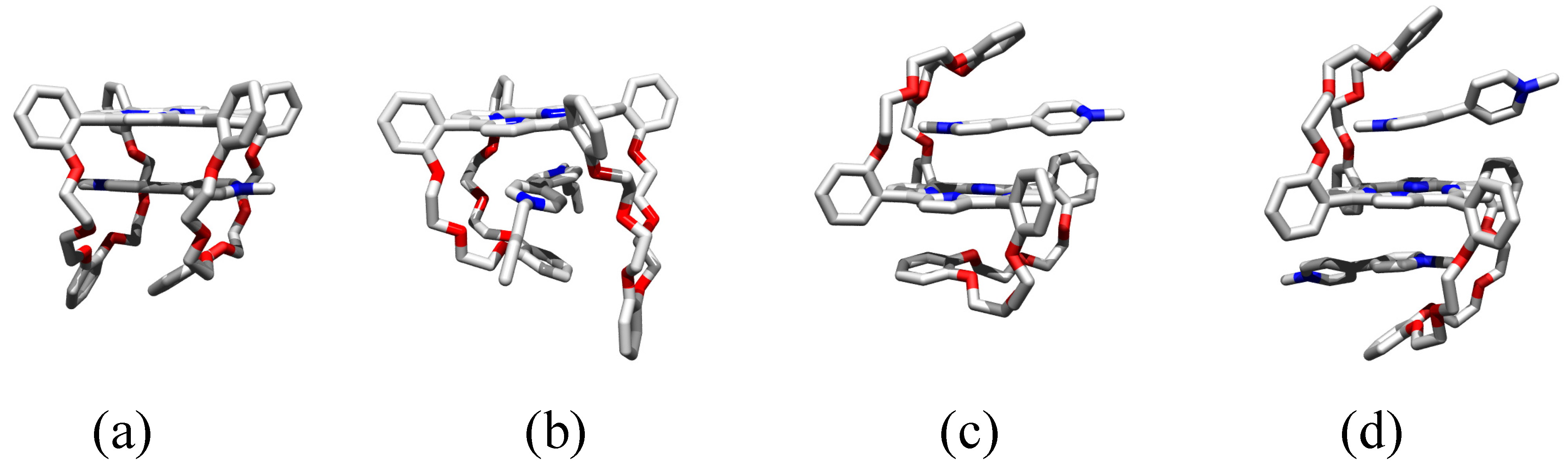
2.7. Mechanism

3. Experimental
3.1. Materials and Methods
3.2. Syntheses
3.2.1. “Basket Handle” Isomers X, S and C
3.2.2. 1-Methyl-4-phenylpyridinium hexafluorophosphate (V3)
3.3. X-ray Analysis of S
3.4. Determination of Association Constants
| Crystal Property | Value |
|---|---|
| Identification code | CLIP10 |
| Crystal colour | dark purple |
| Crystal shape | rough thick platelet |
| Crystal size | 0.21 × 0.20 × 0.05 mm |
| Empirical formula | C72 H66 N4 O12 |
| Formula weight | 1179.29 |
| Temperature | 208(2) K |
| Radiation/Wavelength | MoKα (graphite monochromated)/0.71073 Å |
| Crystal system, space group | Monoclinic, P21/a |
| Unit cell dimensions | a, alp = 12.9808(4) Å, 90° |
| 44169 reflections | b, bet = 14.6770(9) Å, 105.642(4)° |
| 1.900 < theta < 25.000 | c, gam = 16.2856(12) Å, 90° |
| Volume | 2987.8(3) Å3 |
| Z, Calculated density | 2, 1.311 Mg/m3 |
| Absorption coefficient | 0.090 mm−1 |
| Diffractometer/scan | Nonius KappaCCD with area detector φ and ω scan |
| F(000) | 1244 |
| Theta range for data collection | 1.90 to 27.50°. |
| Index ranges | −16 <= h<= 16, −18 <= k <= 18, −21 <= l <= 21 |
| Reflections collected/unique | 50597/6846 [R(int) = 0.0684] |
| Reflections observed | 4082 ([Io > 2σ(Io)]) |
| Completeness to 2theta = 25.00 | 95.7% |
| Absorption correction | SADABS multiscan correction (Sheldrick,1996) |
| Refinement method | Full-matrix least-squares on F2 |
| Computing | SHELXL-97 (Sheldrick, 1997) |
| Data/restraints/parameters | 6846/0/398 |
| Goodness-of-fit on F^2 | 1.084 |
| SHELXL-97 weight parameters | 0.033600 2.925100 |
| Final R indices [I > 2sigma(I)] | R1 = 0.0788, wR2 = 0.1286 |
| R indices (all data) | R1 = 0.1434, wR2 = 0.1485 |
| Largest diff. peak and hole | 0.871 and −0.257 e.Å−3 |
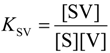
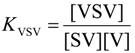
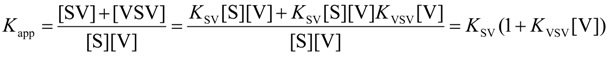
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Le Gac, S.W.; Marrot, J.; Reinaud, O.; Jabin, I. Allosterically coupled double induced fit for 1+1+1+1 self-assembly of a calix[6]trisamine, a calix[6]trisacid, and their guests. Angew. Chem. Int. Ed. 2006, 19, 3123–3126. [Google Scholar]
- Specht, A.; Bernard, P.; Goeldner, M.; Peng, L. Mutually induced formation of host-guest complexes between p-sulfonated calix[8]arene and photolabile cholinergic ligands. Angew. Chem. Int. Ed. 2002, 41, 4706–4708. [Google Scholar] [CrossRef]
- Schneider, H.-J.; Güttes, D.; Schneider, U. Host guest chemistry 16. Host guest complexes with water-soluble macrocyclic polyphenolates including induced fit and simple elements of a proton pump. J. Am. Chem. Soc. 1988, 110, 6449–6451. [Google Scholar] [CrossRef]
- Reek, J.N.H.; Engelkamp, H.; Rowan, A.E.; Elemans, J.A.A.W.; Nolte, R.J.M. Conformational behavior and binding properties of naphthalene-walled clips. Chem.-Eur. J. 1998, 4, 716–722. [Google Scholar]
- Cram, D.J.; Choi, H.-J.; Bryant, J.A.; Knobler, C.B. Host-guest complexation 62. Solvophobic and entropic driving forces for forming verlcraplexes which are 4-fold, lock-key dimers in organic media. J. Am. Chem. Soc. 1992, 114, 7748–7765. [Google Scholar]
- Liu, Y.; Chen, Y. Cooperative binding and multiple recognition by bridged bis(beta-cyclodextrin)s with functional linkers. Acc. Chem. Res. 2006, 39, 681–691. [Google Scholar] [CrossRef]
- Trabolsi, A.; Urbani, M.; Delgado, J.L.; Ajamaa, F.; Elhabari, M.; Solladié, N.; Nierengarten, J.-F.; Albrecht-Gary, A.-M. Large photoactive supramolecular ensembles prepared from C(60)-pyridine substrates and multi-Zn(II)-porphyrin receptors. New J. Chem. 2008, 32, 159–165. [Google Scholar] [CrossRef]
- Gibson, H.W.; Yamaguchi, N.; Hamilton, L.; Jones, J.W. Cooperative self-assembly of dendrimers via pseudorotaxane formation from a homotritopic guest molecule and complementary monotopic host dendrons. J. Am. Chem. Soc. 2002, 124, 4653–4665. [Google Scholar] [CrossRef]
- Jones, J.W.; Zakharov, L.N.; Gibson, H.W. Cooperative host/guest interactions via counterion assisted chelation: Pseudorotaxanes from supramolecular cryptands. J. Am. Chem. Soc. 2002, 124, 13378–13379. [Google Scholar] [CrossRef]
- Sato, H.; Tashiro, K.; Shinmori, H.; Osuka, A.; Murata, Y.; Komatsu, K.; Aida, T. Positive heterotropic cooperativity for selective guest binding via electronic communications through a fused zinc porphyrin array. J. Am. Chem. Soc. 2005, 127, 13086–13087. [Google Scholar]
- Thordarson, P.; Coumans, R.G.E.; Elemans, J.A.A.W.; Thomassen, P.J.; Visser, J.; Rowan, A.E.; Nolte, R.J.M. Allosterically driven multi-component assembly. Angew. Chem. Int. Ed. 2004, 43, 4755–4759. [Google Scholar] [CrossRef]
- Deutman, A.B.C.; Monnereau, C.; Moalin, M.; Coumans, R.G.E.; Veling, N.; Coenen, M.; Smits, J.M.M.; de Gelder, R.; Elemans, J.A.A.W.; Ercolani, G.; et al. Squaring cooperative circles. Proc. Natl. Acad. Sci. USA 2009, 106, 10471–10476. [Google Scholar]
- Koshland, D.E., Jr. Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. USA 1958, 44, 98–104. [Google Scholar]
- Steitz, T.A.; Ludwig, M.L.; Quiocho, F.A.; Lipscomb, W.N. Structure of carboxypepridase A: V. Studies of enzyme-substrate and enzyme-inhibitor complexes at 6 Å resolution. J. Biol. Chem. 1967, 242, 4662–4668. [Google Scholar]
- Bennett, W.S.; Huber, R. Structureal and functional aspects of domain motions in proteins. Crit. Rev. Biochem. 1984, 15, 291–384. [Google Scholar] [CrossRef]
- Koshland, D.E., Jr. The key-lock theory and the induced-fit theory. Angew. Chem. Int. Ed. Engl. 1994, 33, 2375–2378. [Google Scholar] [CrossRef]
- Gerstein, M.; Lesk, A.M.; Chothia, C. Structural mechanisms for domain movements in proteins. Biochemistry 1994, 33, 6739–6749. [Google Scholar] [CrossRef]
- Rebek, J., Jr.; Askew, B.; Killoran, M.; Nemeth, D.; Lin, F.-T. Convergent functional-groups. 3. A molecular cleft recognizes substrates of complementary size, shape and functionality. J. Am. Chem. Soc. 1987, 109, 2426–2431. [Google Scholar]
- Vicent, C.; Hirst, S.C.; Garcia-Tellado, F.; Hamilton, A.D. Conformational selectivity in molecular recognition—The influence of artificial receptors on the cis-trans isomerization of acylprolines. J. Am. Chem. Soc. 1991, 113, 5466–5467. [Google Scholar] [CrossRef]
- Sijbesma, R.P.; Nolte, R.J.M. A molecular clip with allosteric binding properties. J. Am. Chem. Soc. 1991, 113, 6695–6696. [Google Scholar] [CrossRef]
- Hayashi, T.; Asai, T.; Hokazono, H.; Ogoshi, H. Dynamic molecular recognition in a multifunctional porphyrin and a ubiquinone analog. J. Am. Chem. Soc. 1993, 115, 12210–12211. [Google Scholar] [CrossRef]
- Hayashi, T.; Asai, T.; Borgmeier, F.M.; Hokazono, H.; Ogoshi, H. Kinetic and thermodynamic analysis of induced-fit molecular recognition between tetraarylporphyrin and ubiquinone analogues. Chem. Eur. J. 1998, 4, 1266–1274. [Google Scholar] [CrossRef]
- Palyulin, V.A.; Emets, S.V.; Chertkov, V.A.; Kasper, C.; Schneider, H.-J. Conformational switching of 3,7-diacyl-3,7-diazabicyclo[3.3.1]nonanes by metal binding and by solvent changes. Eur. J. Org. Chem. 1999, 3479–3482. [Google Scholar]
- Weinig, H.-G.; Krauss, R.; Seydeck, M.; Bending, J.; Koert, U. Molecular signal transduction by conformational transmission: Use of tetrasubstituted perhydroanthracenes as transducers. Chem. Eur. J. 2001, 7, 2075–2088. [Google Scholar] [CrossRef]
- Chong, Y.S.; Smith, M.D.; Shimizu, K.D. A conformationally programmable ligand. J. Am. Chem. Soc. 2001, 123, 7463–7464. [Google Scholar] [CrossRef]
- Kacprzak, K.; Gawroncski, J. Bifunctional receptor triad for efficient recognition of mono- and dicarboxylic acids. Chem. Commun. 2003, 1532–1533. [Google Scholar] [CrossRef]
- Rebek, J., Jr. Binding forces, equilibria, and rates—New models for enzymatic catalysis. Acc. Chem. Res. 1984, 17, 258–264. [Google Scholar] [CrossRef]
- Takeuchi, M.; Ikeda, M.; Sugasaki, A.; Shinkai, S. Molecular design of artificial molecular and ion recognition systems with allosteric guest responses. Acc. Chem. Res. 2001, 34, 865–873. [Google Scholar] [CrossRef]
- Gawronski, J.; Kacprzak, K. Architecture and function of atropisomeric molecular triads. Chirality 2002, 14, 689–702. [Google Scholar] [CrossRef]
- Iwasawa, N.; Takahagi, H. Boronic esters as a system for crystallization-induced dynamic self-assembly equipped with an “on-off” switch for equilibration. J. Am. Chem. Soc. 2007, 129, 7754–7755. [Google Scholar] [CrossRef]
- Houk, K.N.; Leach, A.G.; Kim, S.P.; Zhang, X. Binding affinities of host-guest, protein-ligand, and protein-transition-state complexes. Angew. Chem. Int. Ed. 2003, 42, 4872–4897. [Google Scholar] [CrossRef]
- Gottwald, L.K.; Ullman, E.F. Biphenyl-type atropisomerism as a probe for coformational rigidity of alpha, beta, gamma, delta-tetraarylporphines. Tetrahedron Lett. 1969, 36, 3071–3074. [Google Scholar] [CrossRef]
- Walker, F.A. Biphenyl-type atropisomerism as a probe for conformational rigidity of α,β,γ,δ-tetraarylporphines. Tetrahedron Lett. 1971, 52, 4949–4952. [Google Scholar] [CrossRef]
- Momenteau, M.; Loock, B.; Mispelter, J.; Bisagni, E. Basket handle porphyrins and their ferrous complexes as stable oxygen carriers. Nouv. J. Chim. 1979, 3, 77–79. [Google Scholar]
- Momenteau, M.; Loock, B. Basket handle porphyrins—New synthetic iron(II) complexes for oxygen binding. J. Mol. Catal. 1980, 7, 315–320. [Google Scholar] [CrossRef]
- Jimenez, H.R.; Moratal, J.M.; Faus, J.; Momenteau, M. A solution study of the interaction of superstructured iron(II) porphyrins with catechol. New J. Chem. 1994, 18, 1247–1252. [Google Scholar]
- Landergren, M.; Baltzer, L. The effect of porphyrin ruffling on the intrinsic binding of carbon monoxide in iron(II) hybrid basket-handle porphyrins by multinuclear NMR and FT-IR spectroscopy. J. Chem. Soc. Perkin Trans. 2 1992, 2, 355–360. [Google Scholar] [CrossRef]
- Picaud, T.; le Moigne, C.; Loock, B.; Momenteau, M.; Desbois, A. Nonplanar distortions of bis-base low-spin iron(II)-porphyrinates: Absorption and resonance Raman investigations of cross-trans-linked iron(II)-basket-handle porphyrin complexes. J. Am. Chem. Soc. 2003, 125, 11616–11625. [Google Scholar]
- Rose, E.; Gallo, E.; Raoul, N.; Bouché, L.; Pille, A.; Caselli, A.; Lequin, O. Chiral “basket handle” binaphthyl porphyrins: Synthesis, catalytic epoxidation and NMR conformational studies. J. Porphyr. Phthalocyanines 2010, 14, 646–659. [Google Scholar] [CrossRef]
- Li, P.; Alenezi, K.; Ibrahim, S.K.; Wright, J.A.; Hughes, D.L.; Pickett, C.J. Towards alternatives to anodic water oxidation: Basket-handle thiolate FeIII porphyrins for electrocatalytic hydrocarbon oxidation. ChemSusChem 2012, 5, 2361–2375. [Google Scholar] [CrossRef]
- Elemans, J.A.A.W.; Claase, M.B.; Aarts, P.P.M.; Rowan, A.E.; Schenning, A.P.H.J.; Nolte, R.J.M. Porphyrin clips derived from diphenylglycoluril. Synthesis, conformational analysis and binding properties. J. Org. Chem. 1999, 64, 7009–7016. [Google Scholar]
- Elemans, J.A.A.W.; Bijsterveld, E.J.A.; Rowan, A.E.; Nolte, R.J.M. Manganese porphyrin hosts as epoxidation catalysts: Activity and stability control by axial ligand effects. Eur. J. Org. Chem. 2007, 2007, 751–757. [Google Scholar] [CrossRef]
- Simonis, U.; Walker, F.A.; Lee, P.L.; Hanquet, B.J.; Meyerhoff, D.J.; Scheidt, W.R. Synthesis, spectroscopic, and structural studies of extremely short chain basket handle porphyrins and their zinc(II) complexes. J. Am. Chem. Soc. 1987, 109, 2659–2668. [Google Scholar]
- The error obtained via measuring the integrals was significantly higher.
- Experimental uncertainties in van’t Hoff plots used to determine the ΔH° and ΔS° values may lead to accidental correlations with no statistical significance.
- Hunter, C.A.; Sanders, J.K.M. The nature of π-π interactions. J. Am. Chem. Soc. 1990, 112, 5525–5534. [Google Scholar] [CrossRef]
- Williams, A.R.; Northrop, B.H.; Chang, T.; Stoddart, J.F.; White, A.J.P.; Williams, D.J. Suitanes. Angew. Chem. Int. Ed. 2006, 45, 6665–6669. [Google Scholar] [CrossRef]
- Gunter, M.J.; Hockless, D.C.R.; Johnston, R.; Skelton, B.W.; White, A.H. Self-assembling porphyrin [2]-catenanes. J. Am. Chem. Soc. 1994, 116, 4810–4823. [Google Scholar]
- Gunter, M.J.; Jeynes, T.P.; Johnston, M.R.; Turner, P.; Chen, Z. Structural control of co-receptor binding in porphyrin-bipyridinium supramolecular assemblies. J. Chem. Soc. Perkin Trans. 1 1998, 1, 1945–1958. [Google Scholar]
- Thordarson, P.; Bijsterveld, E.J.A.; Elemans, J.A.A.W.; Kasák, P.; Nolte, R.J.M.; Rowan, A.E. Highly negative homotropic allosteric binding of viologens in a double-cavity porphyrin. J. Am. Chem. Soc. 2003, 125, 1186–1187. [Google Scholar]
- Unfortunately, the effect of temperature on the binding of the second molecule of V1 to S (KVSV) could therefore not be investigated.
- Although it could also be a result of significant 1:2 complex formation. Nevertheless, it is clear that V3 does not show significant stronger binding to C than to S.
- Crossley, M.J.; Field, L.D.; Forster, A.J.; Harding, M.M.; Sternhell, S. Kinetics of tautomerism in 2-substituted 5,10,15,20-tetraphenylporphyrins—Directionality of proton-transfer between the inner nitrogens. J. Am. Chem. Soc. 1987, 109, 341–348. [Google Scholar]
- Hatano, K.; Anzai, K.; Kubo, T.; Tamai, S. Synthesis and kinetic investigation of the atropisomerization of meso-tetra(2-cyanophenyl)porphine. Bull. Chem. Soc. Jpn. 1981, 54, 3518–3521. [Google Scholar]
- Hatano, K.; Anzai, K.; Nishino, A.; Fujii, K. A kinetic-study of thermal rotational isomerization of 5,10,15,20-tetrakis(ortho-aminophenyl)porphyrin and 5,10,15,20-tetrakis(ortho-pivaloylaminophenyl)porphyrin. Bull. Chem. Soc. Jpn. 1985, 58, 3653–3654. [Google Scholar] [CrossRef]
- Fujimoto, T.; Umekawa, H.; Nishino, N. A new picket-fence porphyrin precursor—Synthesis and atropisomerism of free base and zinc complex of meso-tetra(ortho-methoxycarbonylphenyl)porphyrin. Chem. Lett. 1992, 1992, 37–40. [Google Scholar] [CrossRef]
- Spasojevic, I.; Menzeleev, R.; White, P.S.; Fridovich, I. Rotational isomers of N-alkylpyridylporphyrins and their metal complexes. HPLC separation, H-1 NMR and X-ray structural characterization, electrochemistry, and catalysis of O-2(center dot-) disproportionation. J. Inorg. Chem. 2002, 41, 5874–5875. [Google Scholar]
- Song, R.; Robert, A.; Bernadou, J.; Meunier, B. Illustrating atropisomerism in the porphyrin series using NMR spectroscopy. Analusis 1999, 27, 464–467. [Google Scholar]
- Reginato, G.; di Bari, L.; Salvadori, P.; Guilard, R. Chiral atropisomeric metalloporphyrins in the enantioselective styrene epoxidation. Eur. J. Org. Chem. 2000, 2000, 1165–1171. [Google Scholar] [CrossRef]
- Coumans, R.G.E.; Elemans, J.A.A.W.; Nolte, R.J.E.; Rowan, A.E. Processive enzyme mimic. Kinetics and thermodynamics of the threading and sliding process. Proc. Natl. Acad. Sci. USA 2006, 103, 19647–19651. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SADABS. Program for Emperical Absorption Correction; University of Göttingen: Göttingen, Germany, 1996. [Google Scholar]
- De Gelder, R.; de Graaff, R.A.G.; Schenk, H. Automatic determination of crystal structures using Karle-Hauptman matrices. Acta Cryst. 1993, A49, 287–293. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXL-97. Program for the Refinement of Crystal Structures; University of Göttingen: Göttingen, Germany, 1997. [Google Scholar]
- These data can be obtained free of charge via http://www.ccdc.cam.ac.uk/conts/retrieving.html or from the CCDC, 12 Union Road, Cambridge CB2 1EZ, UK; Fax: +44 1223 336033; E-Mail: [email protected].
- Warshel, A. Computer Modeling of Chemical Reactions in Enzymes and Solutions; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Warshel, A. Electrostatic Origin of the Catalytic Power of Enzymes and the Role of Preorganized Active Sites. J. Biol. Chem. 1998, 273, 27035–27038. [Google Scholar] [CrossRef]
- Sample Availability: Not available.
© 2014 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Deutman, A.B.C.; Woltinge, T.; Smits, J.M.M.; De Gelder, R.; Elemans, J.A.A.W.; Nolte, R.J.M.; Rowan, A.E. Thermodynamics and Kinetics of Guest-Induced Switching between “Basket Handle” Porphyrin Isomers. Molecules 2014, 19, 5278-5300. https://doi.org/10.3390/molecules19045278
Deutman ABC, Woltinge T, Smits JMM, De Gelder R, Elemans JAAW, Nolte RJM, Rowan AE. Thermodynamics and Kinetics of Guest-Induced Switching between “Basket Handle” Porphyrin Isomers. Molecules. 2014; 19(4):5278-5300. https://doi.org/10.3390/molecules19045278
Chicago/Turabian StyleDeutman, Alexander B. C., Tim Woltinge, Jan M. M. Smits, René De Gelder, Johannes A. A. W. Elemans, Roeland J. M. Nolte, and Alan E. Rowan. 2014. "Thermodynamics and Kinetics of Guest-Induced Switching between “Basket Handle” Porphyrin Isomers" Molecules 19, no. 4: 5278-5300. https://doi.org/10.3390/molecules19045278