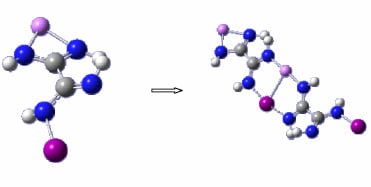
3.1. Geometries
Geometries obtained with both aug-cc-pVDZ and aug-cc-pVTZ basis sets (with corresponding aug-cc-pVDZ-PP and aug-cc-pVTZ-PP for iodine) are similar, and thus only the results with the larger basis set will be used for discussion.
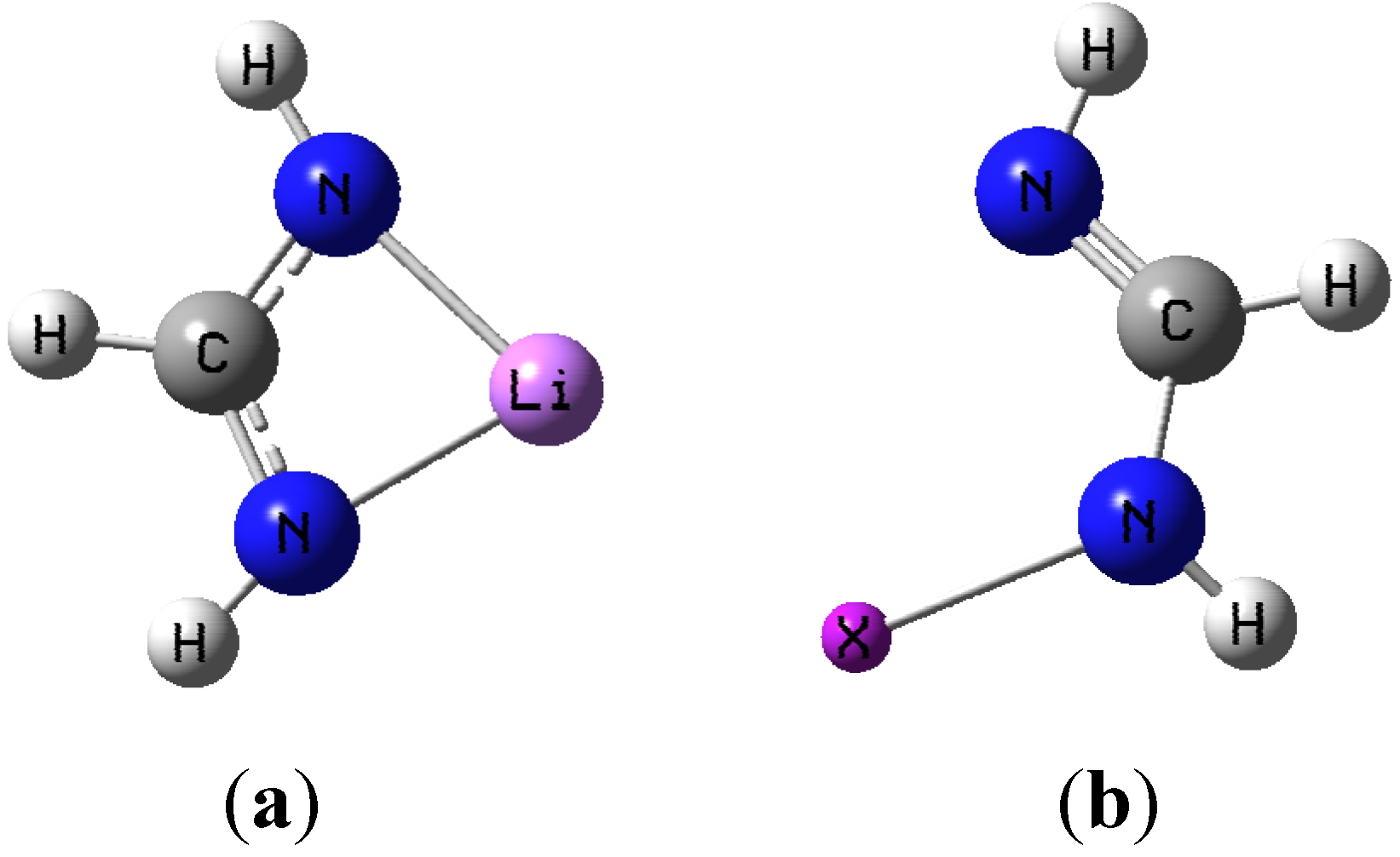
Figure 1a,b show the general shape of the two monomer structures used as basic motifs.
Figure 1.
(a) Lithium formamidinate; (b) Halogenated formamidine (X = Cl, Br, or I).
Figure 1.
(a) Lithium formamidinate; (b) Halogenated formamidine (X = Cl, Br, or I).
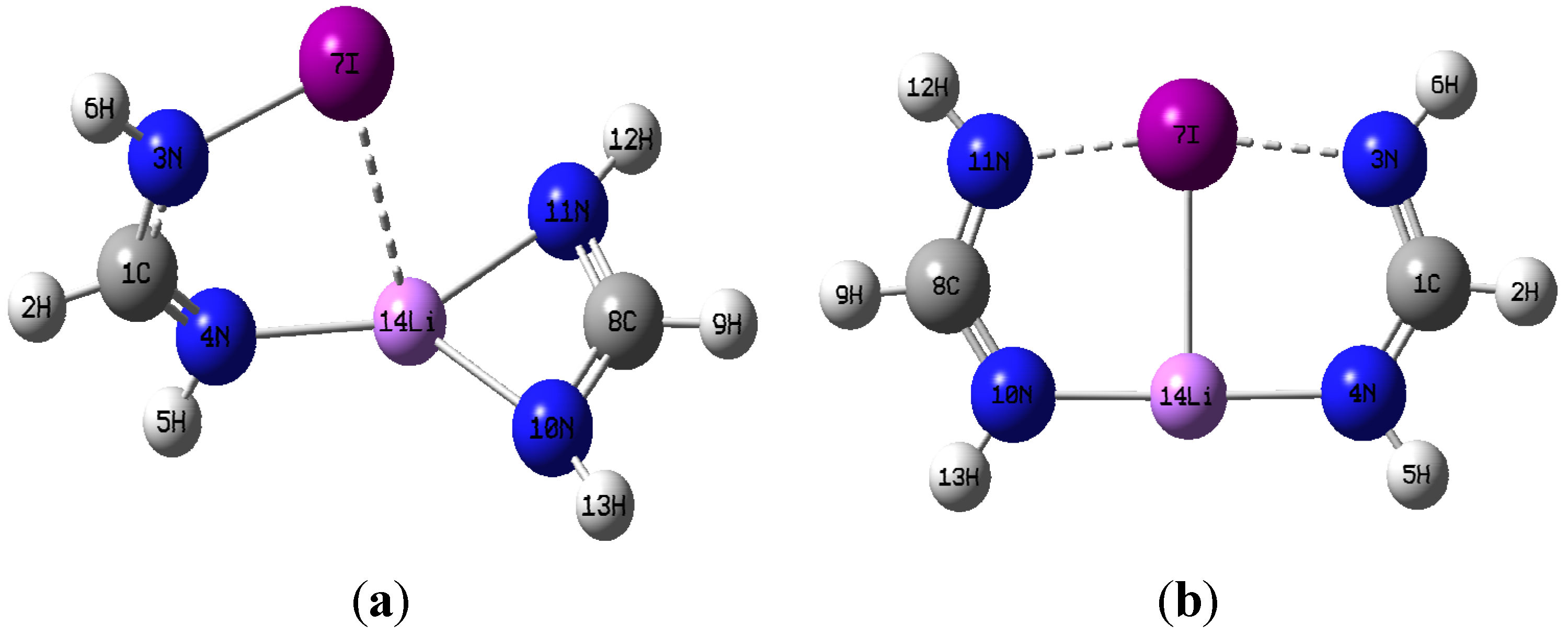
M06-2X geometry optimizations resulted in two very distinct dimer structures of C
1 and C
2v symmetry respectively, and they are illustrated in
Figure 2a,b using the I-containing dimer as an example.
Figure 2.
(a) optimized dimer geometry of C1 symmetry; (b) optimized dimer geometry of C2v.
Figure 2.
(a) optimized dimer geometry of C1 symmetry; (b) optimized dimer geometry of C2v.
Table 1 shows selected geometrical parameters obtained with the M06-2X method for the monomers and dimers using the numbering scheme given in
Figure 2a,b. With regard to the C
2v structures, it is strikingly apparent that dimer formation brings about drastic geometrical distortions in the constituent monomers. One noticeable change is the disappearance of the intramolecular N
10-Li-N
11 chelate coordination of the lithium metal in the CH(NH
2)Li monomer, and the development of quasi-linear N
10···Li···N
4 interactions in the dimer with two equal N···Li distances. Accordingly, the N
10-Li bond is elongated relative to the isolated monomer, the N
11-Li bond is actually broken completely, and a new N
4···Li bonding interaction appears upon formation of the C
2v dimer. The extent of these changes increases with increasing size of the halogen present in the dimer. For example, the percentage change of the N
10-Li bond length increases in the order: 2.9% (Cl) < 3.5% (Br) < 4.5% (I).
Table 1.
Selected geometrical parameters for HN=CHNHX and CH(NH2)Li, anddimers at the M06-2X/aug-cc-pVTZ level. Distances in Å, and angles in degrees.
Table 1.
Selected geometrical parameters for HN=CHNHX and CH(NH2)Li, anddimers at the M06-2X/aug-cc-pVTZ level. Distances in Å, and angles in degrees.
| HN=CHNHX | | CH(NH2)Li | |
|---|
| X | N4-C1 | C1-N3 | N3-X | τXN3H6C1 | | N10-C8 | C8-N11 | N10-Li | N11-Li | |
|---|
| Cl | 1.259 | 1.383 | 1.702 | 138.1 | | 1.321 | 1.321 | 1.879 | 1.879 | |
| Br | 1.260 | 1.380 | 1.848 | 140.2 | | | | | | |
| I | 1.263 | 1.373 | 2.032 | 145.5 | | | | | | |
| | Dimers of C2v symmetry |
| X | N4-C1 | C1-N3 | N3-X | N10-C8 | C8-N11 | N10-Li | N11-Li | N11∙∙∙X | N4∙∙∙Li | Li∙∙∙X |
| Cl | 1.305 | 1.318 | 1.964 | 1.305 | 1.318 | 1.933 | 2.979 | 1.933 | 1.964 | 2.323 |
| Br | 1.306 | 1.320 | 2.071 | 1.306 | 1.320 | 1.945 | 3.086 | 1.945 | 2.071 | 2.437 |
| I | 1.308 | 1.323 | 2.228 | 1.308 | 1.323 | 1.963 | 3.220 | 1.963 | 2.228 | 2.594 |
| X | ΘN3XN11 | ΘN20LiN4 | ΘXLiN10 | τXN3H6C1 | | | | | | |
| Cl | 175.2 | 175.8 | 92.1 | 180.0 | | | | | | |
| Br | 171.9 | 178.6 | 90.7 | 180.0 | | | | | | |
| I | 166.9 | 178.7 | 89.3 | 180.0 | | | | | | |
| | Dimer of C1 symmetry |
| X | N4-C1 | C1-N3 | N3-X | N10-C8 | C8-N11 | N10-Li | N11-Li | N11∙∙∙X | N4∙∙∙Li | Li∙∙∙X |
| Cl | 1.270 | 1.361 | 1.696 | 1.318 | 1.321 | 1.934 | 1.964 | 2.040 | 3.229 | 2.606 |
| Br | 1.272 | 1.356 | 1.839 | 1.318 | 1.321 | 1.934 | 1.966 | 2.036 | 3.368 | 2.769 |
| I | 1.277 | 1.347 | 2.025 | 1.318 | 1.321 | 1.940 | 1.971 | 2.033 | 3.530 | 2.961 |
| X | ΘN3XN11 | ΘN10LiN4 | ΘXLiN10 | τXN3H6C1 | | | | | | |
| Cl | 131.5 | 134.8 | 109.0 | 147.0 | | | | | | |
| Br | 124.5 | 135.2 | 107.3 | 153.1 | | | | | | |
| I | 117.0 | 134.6 | 104.7 | 172.7 | | | | | | |
Even more substantial elongations, relative to the halogenated formamidine monomers, occur for the N3-X bond upon dimerization. The extent of the elongation decreases with halogen size: 15% (Cl) > 12% (Br) > 10% (I). In all cases, the N3-X elongation enables the equal sharing of the halogen atom by two nitrogen atoms, N3···X···N11, in a quasi-linear arrangement. Another distinct change is seen in the geometry around the nitrogen in the amino NHX group which is trigonal planar in the C2v structure but pyramidal in the isolated monomers. The change in the geometry around the nitrogen in the NHX group is evinced by changes in the dihedral angle τXN3H6C1. This angle is 180° in all C2v dimers in agreement with a trigonal planar geometry, but significantly less in the monomers, consistent with a pyramidal geometry. In addition to the N···Li···N, and N···X···N interactions, a Li···X interaction takes place that appears practically orthogonal to the N···X···N and N···Li···N interactions, with X···Li···N angles close to 90°. Given the drastic geometrical changes occurred upon formation of the C2v structures, the identity of each of the individual monomers can be seen as essentially lost. It is apparent, therefore, that the general C2v structure actually represents a new compound rather than the two original monomers simply engaged in non-covalent intermolecular interactions.
With regard to the dimers of C
1 symmetry,
Table 1 shows that dimerization also brings about important geometrical changes. However these changes are not drastic enough to render the formation of a new compound. Indeed, the structures of both the halogenated formamidine and lithium formamidinate monomers are still clearly distinguishable in the dimer. As seen in
Table 1, dimerization results in a sizeable elongation of the imino N
4-C1 bond, and an equally important shortening of the amino C
1-N
3 bond, relative to the isolated halogenated formamidine. A small reduction of the N
3-X bond lengths is observed for all the dimers, in contrast to the major elongation of this bond seen in the C
2v dimers. Moreover, a reduction in the pyramidal character of the amino nitrogen is manifested in a sizeable increase in the τ
XN3H6C1dihedral angle. The two symmetrical N-Li bonds in the Li-formamidinate monomer are replaced by two somewhat longer and different N-Li bond lengths in the dimer. An additional and important Li…N
4 interaction takes place with the imino nitrogen of the X-formamidine partner. For any given dimer, the Li…X distance in the C
1 dimer is significantly longer than that in the corresponding C
2v dimer, suggesting a much weaker interaction, if any, between these two atoms in the C
1 dimer.
Table 2 shows relevant optimized geometrical parameters for the monomers and dimers at the MP2 level of theory. Very interestingly, geometry optimizations with the MP2 method resulted in the C
1 and C
2v dimer structures only for the chlorine-containing dimers. In contrast, the C
2v dimer structure was the only one found for the Br- and I-containing dimers. In fact, geometry optimizations for these dimers using the C
1 structures as initial guess geometry consistently collapsed into the corresponding C
2v structures. When compared with the MP2 results, the M06-2X method tends to underestimate bond distances in the monomers and the dimers. For example, cross examination of
Table 1 and
Table 2 reveals that the M06-2X method predicts N-Li distances for the CH(NH
2)Li monomer that are 0.038 Å shorter than those predicted by the MP2 method. Also, the hybrid functional predicts a double bond N
4-C
1 for the HN=CHNHX monomer that is 0.014 Å shorter than that predicted by the MP2 method. The N-I bond lengths are actually overestimated by the hybrid functional in both monomer and dimers. It can also be seen that the M06-2X method tends to overestimate the τ
XN3H6C1 dihedral angle for the monomers by about 3° to 4°, and for the C
1 dimer by about 6°.
3.2. Vibrational Frequency Shifts
Dimerization is expected to result in shifts in the vibrational frequencies of the individual monomers, and in the appearance of new modes of vibrations characteristic of the newly formed dimer.
Table 3 shows selected harmonic vibrational frequencies of all halogenated formamidine monomers and of their dimers with lithium formamidinate calculated with the M06-2X hybrid functional and the MP2 method using the aug-cc-pVDZ basis set (aug-cc-pVDZ-PP basis set was used for the iodine atom). For the lithium formamidinate monomer, a vibrational stretching frequency involving the chelate N-Li-N moiety, ν
(N-Li-N), is found at 575 cm
−1 with the M06-2X method, and at 550 cm
−1 with the MP2 method. This mode is still present in the dimers of C
1 symmetry although it is shifted to the blue, with the largest shift seen in the Cl-containing dimer. The calculated larger frequency for this mode is consistent with the additional interaction of the lithium atom with the imino nitrogen on formamidine. For the Cl-containing dimer, the MP2 method also predicts a blue shift of 39 cm
−1 for this mode, similar to the 33 cm
−1 shift seen with M06-2X.
Table 2.
Selected geometrical parameters for HN=CHNHX and CH(NH2)Li, and dimers at the MP2/aug-cc-pVTZ level. Distances in Å, and angles in degrees.
Table 2.
Selected geometrical parameters for HN=CHNHX and CH(NH2)Li, and dimers at the MP2/aug-cc-pVTZ level. Distances in Å, and angles in degrees.
| HN=CHNHX | | CH(NH2)Li | |
|---|
| X | N4-C1 | C1-N3 | 3-X | τXN3H6C1 | | N10-C8 | C8-N11 | N10-Li | N11-Li | |
|---|
| Cl | 1.273 | 1.386 | 1.711 | 133.8 | | 1.329 | 1.329 | 1.916 | 1.916 | |
| Br | 1.274 | 1.383 | 1.847 | 135.8 | | | | | | |
| I | 1.276 | 1.375 | 2.022 | 142.2 | | | | | | |
| Dimers of C2v symmetry |
| X | N4-C1 | C1-N3 | N3-X | N10-C8 | C8-N11 | N10-Li | N11-Li | N11∙∙∙X | N4∙∙∙Li | Li∙∙∙X |
| Cl | 1.314 | 1.324 | 1.969 | 1.314 | 1.324 | 1.957 | 3.029 | 1.969 | 1.957 | 2.374 |
| Br | 1.315 | 1.326 | 2.064 | 1.315 | 1.326 | 1.966 | 3.123 | 2.064 | 1.966 | 2.473 |
| I | 1.317 | 1.330 | 2.204 | 1.317 | 1.330 | 1.985 | 3.250 | 2.204 | 1.985 | 2.619 |
| X | ΘN3XN11 | ΘN10LiN4 | ΘXLiN10 | τXN3H6C1 | | | | | | |
| Cl | 175.8 | 178.9 | 90.6 | 180.0 | | | | | | |
| Br | 173.0 | 178.7 | 86.5 | 180.0 | | | | | | |
| I | 168.5 | 175.9 | 87.9 | 180.0 | | | | | | |
| Dimer of C1 symmetry |
| X | N4-C1 | C1-N3 | N3-X | N10-C8 | C8-N11 | N10-Li | N11-Li | N11∙∙∙X | N4∙∙∙Li | Li∙∙∙X |
| Cl | 1.282 | 1.366 | 1.705 | 1.327 | 1.330 | 1.967 | 2.000 | 3.195 | 2.081 | 2.618 |
| X | ΘN3XN11 | ΘN10LiN4 | ΘXLiN10 | τXNH6C1 | | | | | | |
| Cl | 134.8 | 136.5 | 111.0 | 140.8 | | | | | | |
Table 3.
Selected stretching (cm−1) frequencies for HN=CHNHX and their dimers with CH(NH2)Li.
Table 3.
Selected stretching (cm−1) frequencies for HN=CHNHX and their dimers with CH(NH2)Li.
| M06-2X/aug-cc-pVDZ |
|---|
| | HN=CHNHX | Dimer of C1 symmetry | Dimers of C2v symmetry |
|---|
| X | ν(N-X) | | ν(N-X) | νas(N-Li-N) | ν(N∙∙∙X∙∙∙N) | νas(N∙∙∙Li∙∙∙N) | ν(Li∙∙∙X) |
| Cl | 659 | | 688 | 608 | 236 | 663 | 294 |
| Br | 586 | | 607 | 602 | 286 | 640 | 307 |
| I | 540 | | 550 | 596 | 327 | 607 | 326 |
| MP2/aug-cc-pVDZ |
| | HN=CHNHX | Dimer of C1 symmetry | Dimers of C2v symmetry |
| X | ν(N-X) | | ν(N-X) | νas(N-Li-N) | ν(N∙∙∙X∙∙∙N) | νas(N∙∙∙Li∙∙∙N) | ν(Li∙∙∙X) |
| Cl | 637 | | 664 | 589 | 304 | 647 | 342 |
| Br | 576 | | | | 313 | 633 | 338 |
| I | 539 | | | | 337 | 604 | 356 |
As expected, the ν
(N-Li-N) mode of vibration is missing in the dimers of C
2v symmetry because the intramolecular lithium formamidinate ring is no longer present in these dimers. However, a stretching mode, ν
(N···Li···N), appears in the C
2v dimers that corresponds primarily with the linear N···Li···N bonds. Both M06-2X and MP2 predict a decrease of the ν
(N···Li···N) frequency with an increase in the size of the halogen atom. One distinctive mode of vibration in the halogenated formamidine, ν
N-X, involves stretching of the N-X bond in the amino group. This mode is shifted to the blue in the dimers of C
1 symmetry, in accord with the reduction in the corresponding bond lengths discussed in the previous section. In the C
2v dimers, however, a vibrational stretching mode encompassing the linear N···X···N interactions, ν
(N···X···N), is observed. Because of the relatively large N···X separation, the ν
(N···X···N) frequencies appear significantly shifted to the red when compared with the ν
N-X frequencies in the corresponding monomers or C
1 dimers. Lastly, a well defined mode of vibration that emerges upon formation of the C
2v structures is a halogen-metal, ν
Li···X, stretching mode which occurs at low wavenumbers for the various X-containing dimers as seen in
Table 3. This mode is clearly absent in the dimers of C
1 symmetry. It is worth noticing that the ν
(N···X···N) and ν
Li···X frequencies obtained with M06-2X occur at lower wavenumbers than the corresponding frequencies obtained with the MP2 method. The opposite is true for the calculated ν
(N···Li···N) frequencies.
3.3. Energetics
Of the two distinct dimer structures obtained with the M06-2X hybrid functional, the one with C2v symmetry is found lower in energy than that of C1 symmetry. The energy difference is very small for the Cl-containing dimer, but increases significantly with the size of the halogen. The relative energy results for a given X-containing dimer, EC1(X)-EC2v(X), using the aug-cc-pVTZ (aug-cc-pVTZ-PP for the iodine atom) follow the sequence: 0.44 kcal/mol (Cl) < 10.1 kcal/mol (Br) < 17.2 kcal/mol (I). The MP2 method favors the C2v dimer more than the M06-2X functional does. In fact at the MP2 level, only the Cl-containing dimer is found to exist as a dimer of C1 and C2v symmetry, with the latter being 4.50 kcal/mol lower in energy. For the other two halogens, Br and I, only the C2v dimer structures are predicted to exist.
The BSSE-corrected interaction energies, ΔE
int, listed in
Table 4 were obtained as the difference between the energy of the dimer and the sum of the energies of the constituent monomers, assuming they have the same geometries as in the corresponding dimers. Also listed in
Table 4 are the complexation energies, ΔE
comp, of the dimers which take into account the increase in energy of the monomers due to the geometrical deformations that each monomer goes through upon dimer formation. It is worth noticing that both M06-2X and MP2 yield similar results. With regard to the C
1 dimers,
Table 4 shows that all these dimers have interaction energies (and complexation energies) that are within 1 kcal/mol of one another, although their magnitudes tend to increase slightly with the size of the halogen. Moreover, for any given C
1 dimer, both the interaction and complexation energies are close to each other, with the largest difference (1.35 kcal/mol) seen for the I-containing dimer. The closeness of the interaction and complexation energies for the C
1 dimers is consistent with the relatively small geometric deformations that occur during dimer formation. In sharp contrast, all the C
2v dimers have interaction energies that are significantly larger than the corresponding complexation energies. The comparatively much smaller complexation energies in the C
2v dimers align with the large geometric deformations of the constituent monomers upon C
2v dimer formation. The deformation energy varies with the size of the halogen, and for the M06-2X functional the trend is: Cl (42.14 kcal/mol) > Br (38.08 kcal/mol) > I (35.28 kcal/mol), with similar results for the MP2 method. For the C
2v dimers, both the interaction and complexation energies display an important increase with the size of the halogen. When comparing the C
1 and C
2v dimer energetics, it is evident that the C
2v structures exhibit stronger interactions with the difference being more pronounced the larger the halogen atom is.
Table 4.
Interaction energies, ΔEint, and complexation energies, ΔEcomp, using the aug-cc-pVTZ basis set. Values in kcal/mol.
Table 4.
Interaction energies, ΔEint, and complexation energies, ΔEcomp, using the aug-cc-pVTZ basis set. Values in kcal/mol.
| | | | C2v-Dimers | | |
|---|
| | M06-2X | | MP2 |
|---|
| X | ΔEint | ΔEcomp | | ΔEint | ΔEcomp |
|---|
| Cl | −62.02 | −19.88 | | −62.77 | −22.17 |
| Br | −67.97 | −29.88 | | −66.84 | −30.56 |
| I | −72.76 | −37.48 | | −69.32 | −36.37 |
| | | | C1-Dimers | | |
| | M06-2X | | MP2 |
| X | ΔEint | ΔEcomp | | ΔEint | ΔEcomp |
| Cl | −20.72 | −19.57 | | −19.79 | −18.79 |
| Br | −21.03 | −19.83 | | | |
| I | −21.58 | −20.23 | | | |
3.4. AIM Analysis
Additional insight on the nature and strength of the various N···Li, N···X, and X···Li interactions is gained by analyzing relevant topological parameters of the electron densities at the corresponding critical points [
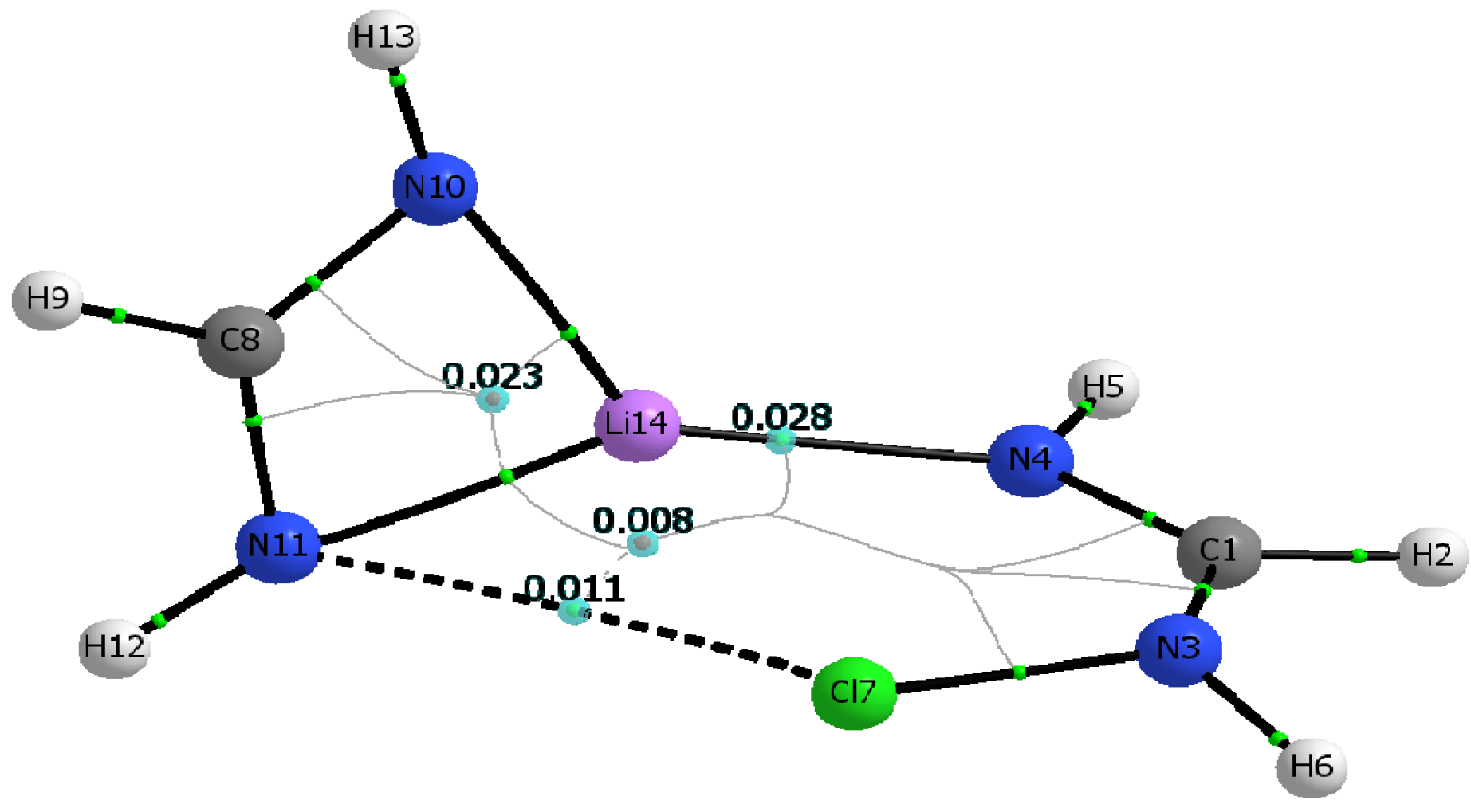
46]. The calculated molecular graphs for all C
1 dimers mirror that of the Cl-containing dimer shown in
Figure 3.
Table 5 lists the electron densities at the critical points of the intermolecular N···Li and N···X interactions, ρ
c(N
4···Li), and ρ
c(N
11···X), as well as their corresponding total electron energy densities, H
c(N
4···Li), and H
c(N
11···X), calculated for both the M06-2X and MP2 geometries. Also listed in
Table 5 are the electron densities at the two ring critical points found in the dimer. Inspection of
Figure 3 and
Table 5 makes readily apparent that the structural identity of the constituent monomers remains unaltered upon formation of the C
1 dimer. For example, the ring critical point of the Li-formamidinate unit is still present in the dimer, and the geometry around the amino nitrogen remains pyramidal. Formation of the C
1 dimer is driven mostly by the N···Li interaction and to a lesser extent by the N···X interaction. Thus, the C
1 dimers exhibit ρ
c(N···Li) values that are about three times larger than the ρ
c(N···X) values. Similarly, the electron density value of the ring critical point of the formamidinate unit is about three times larger than that of the six-membered ring resulting from formation of a C
1 dimer. The positive signs of the total energy densities, H
c(N···Li) and H
c(N···X), confirm the non-covalent nature of these interactions [
47]. The presence of a relatively weak halogen bond, N···X, as established by the existence of its bond critical point is particularly noteworthy given the unfavorable interaction angles Θ
N3-X···N11. Indeed, for any given C
1 dimer, Θ
N3‑X···N11 is severely deviated from linearity, and it gets even smaller as the halogen gets bigger: 131.5° (Cl) > 124.5° (Br) > 117.0° (I). Yet another striking feature of the C
1 dimers is the absence of a critical point linking the lithium and the halogen atom.
Figure 3.
Molecular graph of the C1 symmetry dimer of chlorinated formamidine and lithium formamidinate. Bond critical points, ring critical points, and bond paths are shown. Molecular graph obtained using B3LYP/aug-cc-pvtz wavefunction obtained from the M06-2X/aug-cc-pvtz optimized dimer.
Figure 3.
Molecular graph of the C1 symmetry dimer of chlorinated formamidine and lithium formamidinate. Bond critical points, ring critical points, and bond paths are shown. Molecular graph obtained using B3LYP/aug-cc-pvtz wavefunction obtained from the M06-2X/aug-cc-pvtz optimized dimer.
Table 5.
Intermolecular bond and ring critical point electron densities (ρ, au), and bond energy densities (H, au) in the dimers of C1 symmetry*.
Table 5.
Intermolecular bond and ring critical point electron densities (ρ, au), and bond energy densities (H, au) in the dimers of C1 symmetry*.
| M06-2X |
|---|
| ρc (N∙∙∙X) | ρc (N∙∙∙Li) | Hc (N∙∙∙X) | Hc (N∙∙∙Li) | ρrcp1 |
|---|
| 0.0107 | 0.0275 | 0.0012 | 0.0058 | 0.0228 |
| 0.0102 | 0.0278 | 0.0009 | 0.0058 | 0.0227 |
| 0.0100 | 0.0281 | 0.0007 | 0.0058 | 0.0225 |
| MP2 |
| ρc (N∙∙∙X) | ρc (N∙∙∙Li) | Hc (N∙∙∙X) | Hc (N∙∙∙Li) | ρrcp1 |
| 0.0112 | 0.0248 | 0.0012 | 0.0057 | 0.0210 |
The calculated molecular graphs for the Cl- and Br-containing dimers of C
2v symmetry look alike, and in particular the molecular graph of the former is shown in
Figure 4a. Similarly,
Figure 4b shows the molecular graph calculated for the I-containing C
2v dimer.
Figure 4a,b consistently show that all C
2v dimers have a set of parallel and quasi-linear N
4···Li···N
10, and N
11···X···N
3, interactions that are connected by orthogonal Li…X interactions. For X = I, however,
Figure 4b shows two additional curved bond paths connecting the iodine atom with the two farther nitrogen atoms, N
4 and N
10 respectively. Because of these additional interactions, the I-containing C
2v dimer has two equivalent 4-membered rings and two equivalent 3-membered rings, rather than the two symmetric 5-membered rings seen when the C
2v dimer contains either of the other two halogen atoms, Br or Cl.
Table 6 lists electron densities at the relevant intermolecular bond critical points, as well as their corresponding total electron energy densities, calculated for both the M06-2X and MP2 geometries. Also listed in
Table 6 are the electron densities at the ring critical points found in each of the C
2v dimers.
Figure 4.
Molecular graph of dimers with C2v symmetry (a) dimer of chlorinated formamidine and lithium formamidinate. (b) dimer of iodinated formamidine and lithium formamidinate. Bond critical points, ring critical points, and bond paths are sown. Molecular graphs obtained using B3LYP/aug-cc-pvtz wavefunction obtained from the M06-2X/aug-cc-pvtz optimized dimers.
Figure 4.
Molecular graph of dimers with C2v symmetry (a) dimer of chlorinated formamidine and lithium formamidinate. (b) dimer of iodinated formamidine and lithium formamidinate. Bond critical points, ring critical points, and bond paths are sown. Molecular graphs obtained using B3LYP/aug-cc-pvtz wavefunction obtained from the M06-2X/aug-cc-pvtz optimized dimers.
Inspection of
Figure 4a,b and
Table 6 demonstrates that the structural identity of each constituent monomer in the C
2v dimers is drastically altered. Particularly outstanding is the disappearance of one of the N-Li bond critical points present in the Li-formamidinate monomer, and hence the disappearance of the formamidinate ring unit as such. Instead, a well-defined Li···X bond critical point is present accompanied by two equivalent bond critical points in quasi-linear N…X…N interactions (as opposed to the severely curved N-X···N interactions seen in the C
1 dimers). Formation of the C
2v dimer appears then driven by the interplay of at least three major interactions: quasi-linear and parallel N
4···Li···N
10 and N
11···X···N
3 interactions, with orthogonal Li···X interactions.
As seen in
Table 6, the quasi-linear interactions are characterized by electron density values at their critical points that are significantly larger than the corresponding values in the C
1 dimer counterparts (see
Table 5). Another salient finding is that, for any given C
2v dimer, the N
11···X···N
3 interactions appear stronger than the adjacent and parallel N
4···Li···N
10 interactions. Indeed, ρ
c(N11···X···N3) values are larger by a factor of about 3 in the Br- and Cl-containing dimers, and by a factor of 2.5 in the I-containing dimer. The two additional N
4···I and N
10···I interactions seen in the I-containing dimer provide further stabilization and help drive the formation of the C
2v dimer. It is worth noticing that although the electron density values at the bond critical points of these additional interactions are smaller than those of their quasi-linear counterparts in the C
2v dimer, they are actually larger than that of the intermolecular N···I interaction in the C
1 dimer. As in the C
1 dimers, it is important to stress that the presence of the relatively weak and curved halogen bonds, N
4···I and N
10···I as confirmed by the existence of their bond critical point is remarkable given the unfavorable interaction angles. For example, Θ
N3···X···N4 is about 120°, just a bit larger than Θ
N3-X···N11 for the halogen bond in the C
1 dimer. Lastly, it is equally important to highlight the fact that the quasi-linear halogen bonds N
11···X···N
3 exhibit a partly covalent nature, as revealed by the negative sign of the total electronic energy densities, evaluated at the pertinent bond critical points, H
c. In contrast, the weaker N
4···I (or N
10…I) halogen bond interaction, the Li···X, and the N
4···Li···N
10 interactions all exhibit a non-covalent closed-shell interaction (all with H
c > 0) [
47,
48,
49].
Table 6.
Intermolecular bond and ring critical point electron densities (ρ, au), and bond energy densities (H, au) in the dimers of C2v symmetry *.
Table 6.
Intermolecular bond and ring critical point electron densities (ρ, au), and bond energy densities (H, au) in the dimers of C2v symmetry *.
| | M06-2x |
|---|
| X | ρc (N∙∙∙X) | ρc (N∙∙∙Li) | ρc (Li∙∙∙X) | Hc (N∙∙∙X) | Hc (N∙∙∙Li) | Hc (Li∙∙∙X) | ρrcp1 | ρrcp2 |
|---|
| Cl | 0.1222 | 0.0377 | 0.0202 | −0.0500 | 0.0054 | 0.0046 | 0.0133 | 0.0133 |
| Br | 0.1066 | 0.0351 | 0.0197 | −0.0472 | 0.0052 | 0.0036 | 0.0139 | 0.0139 |
| I | 0.0888 | 0.0355 | 0.0188 | −0.0346 | 0.0052 | 0.0026 | 0.0145 | 0.0145 |
| | 0.0150 | | | 0.0008 | | | 0.0143 | 0.0143 |
| | MP2 |
| X | ρc (N∙∙∙X) | ρc (N∙∙∙Li) | ρc (Li∙∙∙X) | Hc (N∙∙∙X) | Hc (N∙∙∙Li) | Hc (Li∙∙∙X) | ρrcp1 | ρrcp2 |
| Cl | 0.1211 | 0.0358 | 0.0177 | −0.0471 | 0.0052 | 0.0044 | 0.0123 | 0.0123 |
| Br | 0.1084 | 0.0351 | 0.0180 | −0.0460 | 0.0052 | 0.0034 | 0.0132 | 0.0132 |
| I | 0.0926 | 0.0336 | 0.0178 | −0.0346 | 0.0052 | 0.0025 | 0.0145 | 0.0145 |
| | 0.0149 | | | 0.0008 | | | 0.0139 | 0.0139 |