Entropy Characteristic on Harmonious Unifying Hybrid Preferential Networks
Abstract
:1. Introduction
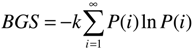

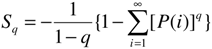
2. Basic network models: the HUHPM
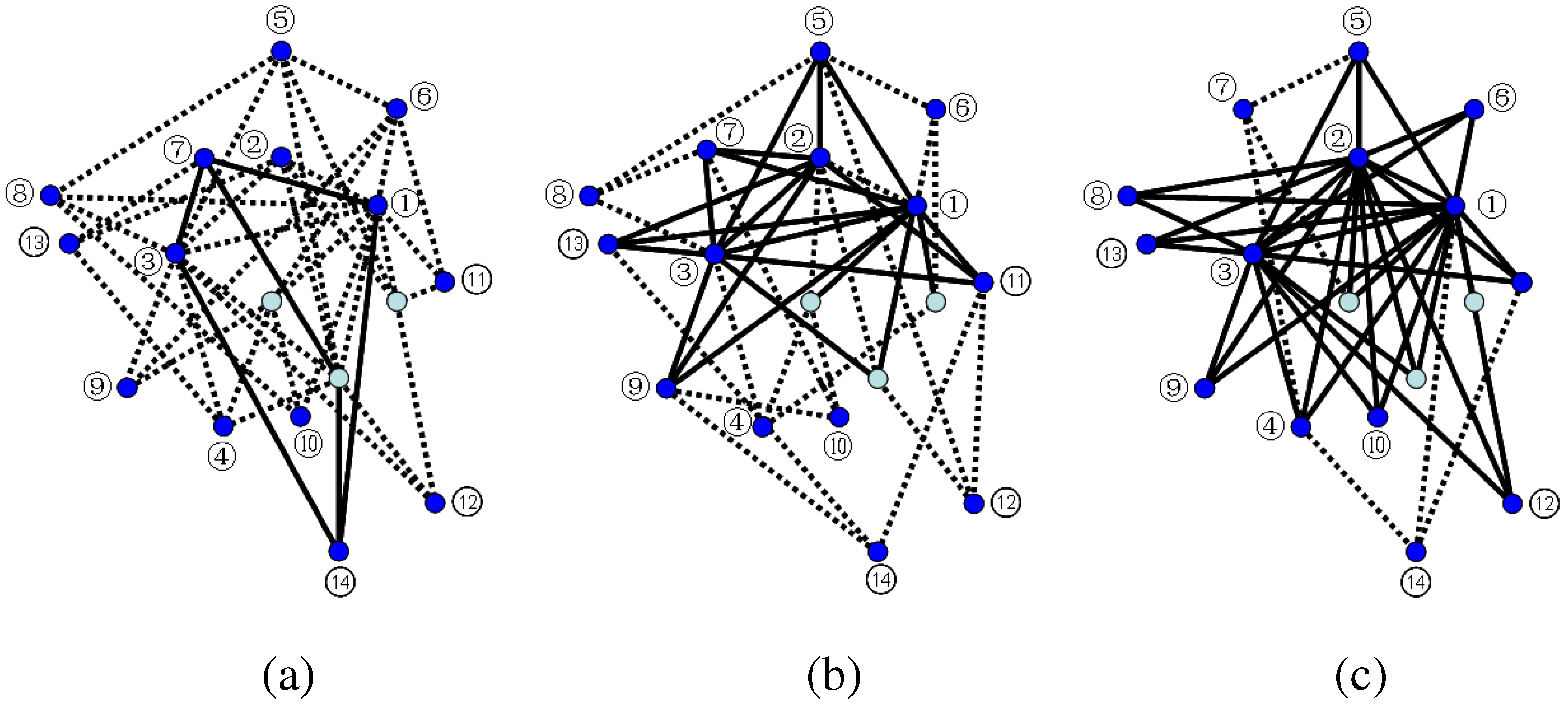
3. Entropy characteristic in the HUHPM-BA

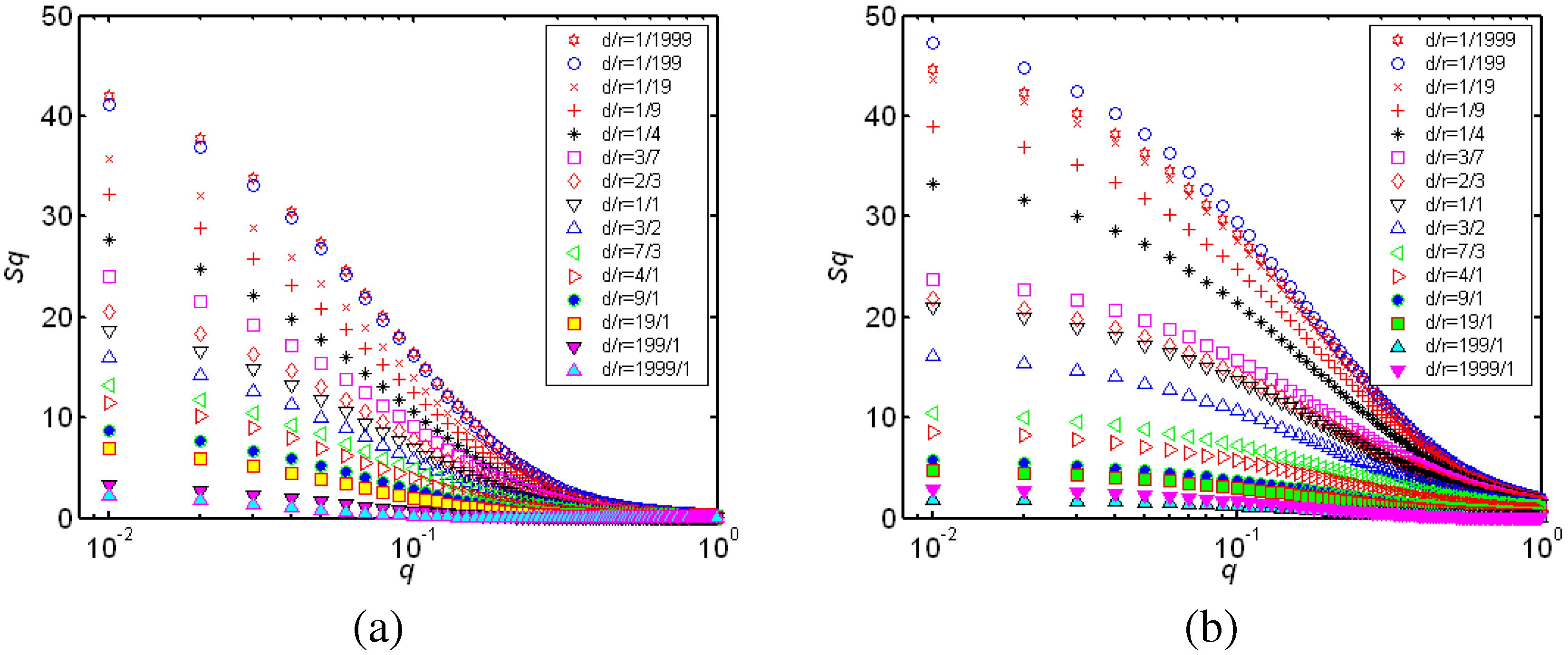
4. Entropy characteristic in the weighted HUHPM-BBV
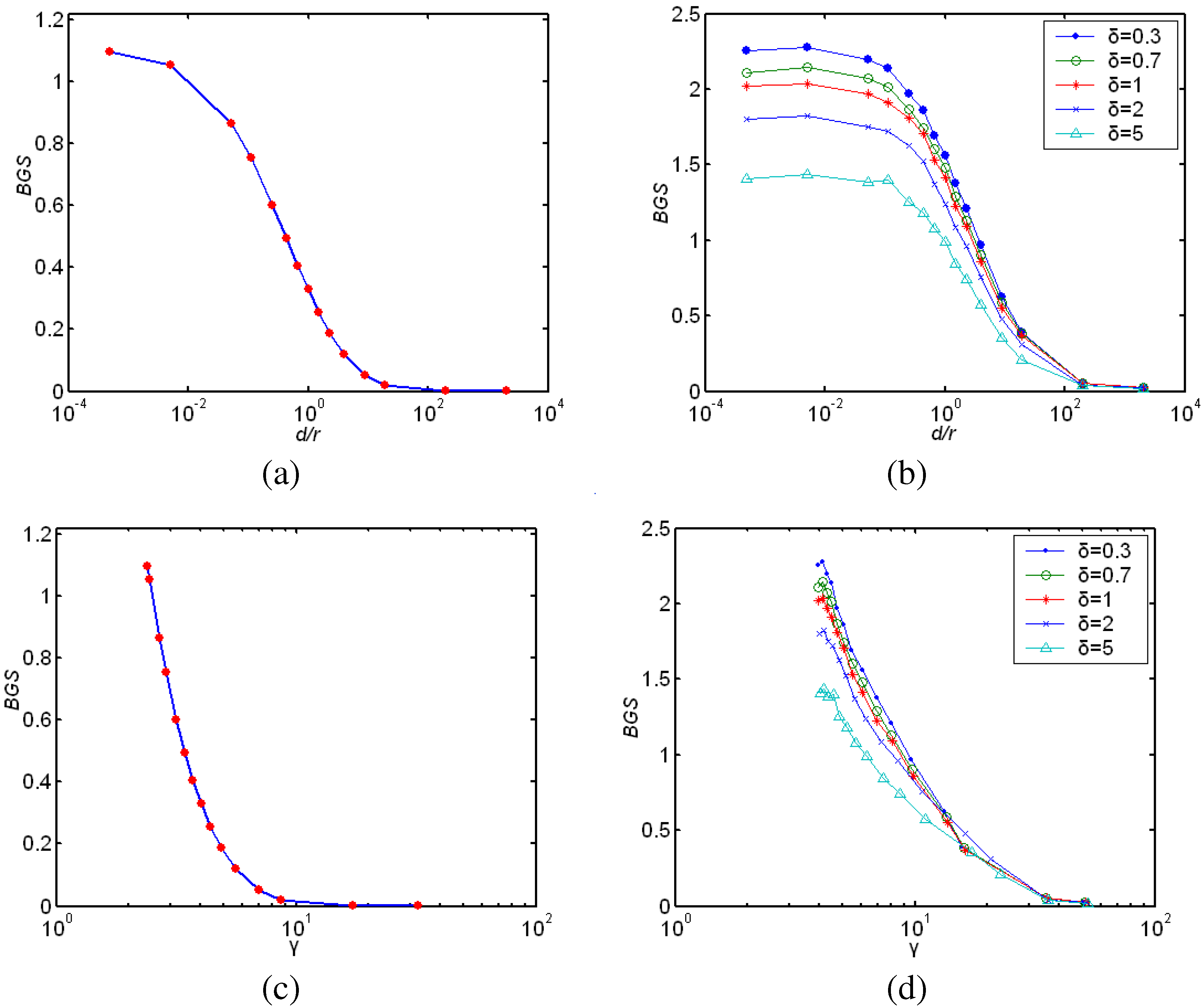

5. Conclusion and potential of application
Acknowledgements
References and Notes
- Watts, D.J.; Strogatz, S.H. Collective dynamics of 'small-world' networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Reviews of Modern Physics 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Fang, J.Q.; Liang, Y. Topological properties and transition features generated by a new hybrid preferential model. Chin. Phys. Lett. 2005, 22(10), 2719–2722. [Google Scholar]
- Barabási, A.L.; Albert, R.; Jeong, H. Mean-field theory for scale-free random networks. Physica A 1999, 272, 130–131. [Google Scholar] [CrossRef]
- Barrat, A.; Barthélemy, M.; Vespignani, A. Weighted evolving networks: coupling topology and weight dynamics. Phys. Rev. Lett. 2004, 92, 228701. [Google Scholar] [CrossRef] [PubMed]
- Barrat, A.; Barthelemy, M.; Vespignani, A. Modeling the evolution of weighted networks. Phys. Rev. E 2004, 70, 066149. [Google Scholar] [CrossRef]
- Wang, W.X.; Wang, B.H.; Hu, B.; Yan, G.; Ou, Q. General dynamics of topology and traffic on weighted technological networks. Phys. Rev. Lett. 2005, 94, 188702. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Fang, J.Q.; Liu, Q.; Liang, Y. Small world properties generated by a new algorithm under same degree of all nodes. Commun. Theor.Phys (Beijing, China) 2006, 45, 950–954. [Google Scholar]
- Fang, J.Q.; Bi, Q.; Li, Y.; Lu, X.B.; Liu, Q. A harmonious unifying hybrid preferential model and its universal properties for complex dynamical networks (in Chinese). Chinese Science 2007, 37(2), 1–20. [Google Scholar]
- Fang, J. Q.; Bi, Q.; Li, Y.; Lu, X. B.; Liu, Q. Sensitivity of exponents of three-power-laws to hybrid ratio in weighted HUHPM. Chi. Phys. Lett. 2007, 24(1), 279–282. [Google Scholar]
- Fang, J. Q. Exploring theoretical model of network science and research progresses (in Chinese). Sci. & Tech. Rev. 2006, 12, 67–72. [Google Scholar]
- Fang, J. Q. Theoretical research progress in dynamical complexity of nonlinear complex networks. Progress in Nature Science 2006. (in print). [Google Scholar]
- Fang, J. Q.; Bi, Q.; Li, Y. Advances in theoretical models of network. Frontiers of Physics in China 2007, 2(1), 109–124. [Google Scholar] [CrossRef]
- Fronczak, A.; Fronczak, P.; Hołyst, J.A. Fluctuation-dissipation relations in complex networks. Phys. Rev. E 2006, 73, 016108. [Google Scholar] [CrossRef]
- Tsallis, C.; Baldovin, F.; Cerbino, R.; Pierobon, P. Introduction to nonextensive statistical mechanics and thermodynamics. arXiv cond-mat/0309093 2003. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Nonextensive information entropy for stochastic networks. arXiv cond-mat/0212056 2003. [Google Scholar]
- Lu, X. B.; Wang, X. F.; Fang, J. Q. Topological transition features and synchronizability of a weighted hybrid preferential network. Physica A 2006, 371(2), 841–850. [Google Scholar] [CrossRef]
- Solé, R. V.; Valverde, S. Information theory of complex networks: on evolution and architectural constraints. Lect. Notes Phys. 2004, 650, 189–207. [Google Scholar]
© 2007 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Li, Y.; Fang, J.-Q.; Bi, Q.; Liu, Q. Entropy Characteristic on Harmonious Unifying Hybrid Preferential Networks. Entropy 2007, 9, 73-82. https://doi.org/10.3390/e9020073
Li Y, Fang J-Q, Bi Q, Liu Q. Entropy Characteristic on Harmonious Unifying Hybrid Preferential Networks. Entropy. 2007; 9(2):73-82. https://doi.org/10.3390/e9020073
Chicago/Turabian StyleLi, Yong, Jin-Qing Fang, Qiao Bi, and Qiang Liu. 2007. "Entropy Characteristic on Harmonious Unifying Hybrid Preferential Networks" Entropy 9, no. 2: 73-82. https://doi.org/10.3390/e9020073
APA StyleLi, Y., Fang, J.-Q., Bi, Q., & Liu, Q. (2007). Entropy Characteristic on Harmonious Unifying Hybrid Preferential Networks. Entropy, 9(2), 73-82. https://doi.org/10.3390/e9020073



