Van der Waals gas as working substance in a Curzon and Ahlborn-Novikov engine

Abstract

Using a van der Waals gas as the working substance the so called Curzon and Ahlborn- Novikov engine is studied. It is shown that some previous results found in the literature of finite time thermodynamics can be written in a more general form, means of this gas and by taking a non linear heat transfer law.

1. Introduction

In classical equilibrium thermodynamics the efficiency of a reversible thermal engine operating between two reservoirs, at temperatures T_1w > T_2w, is known to be:

(1.1)

In this description the temperatures of the working substance along the isothermal branches, T_1w, i = 1,2 , are assumed to be the same as the corresponding reservoirs; as a consequence the processes associated with the heat transfer between the engine and the reservoirs are ignored.

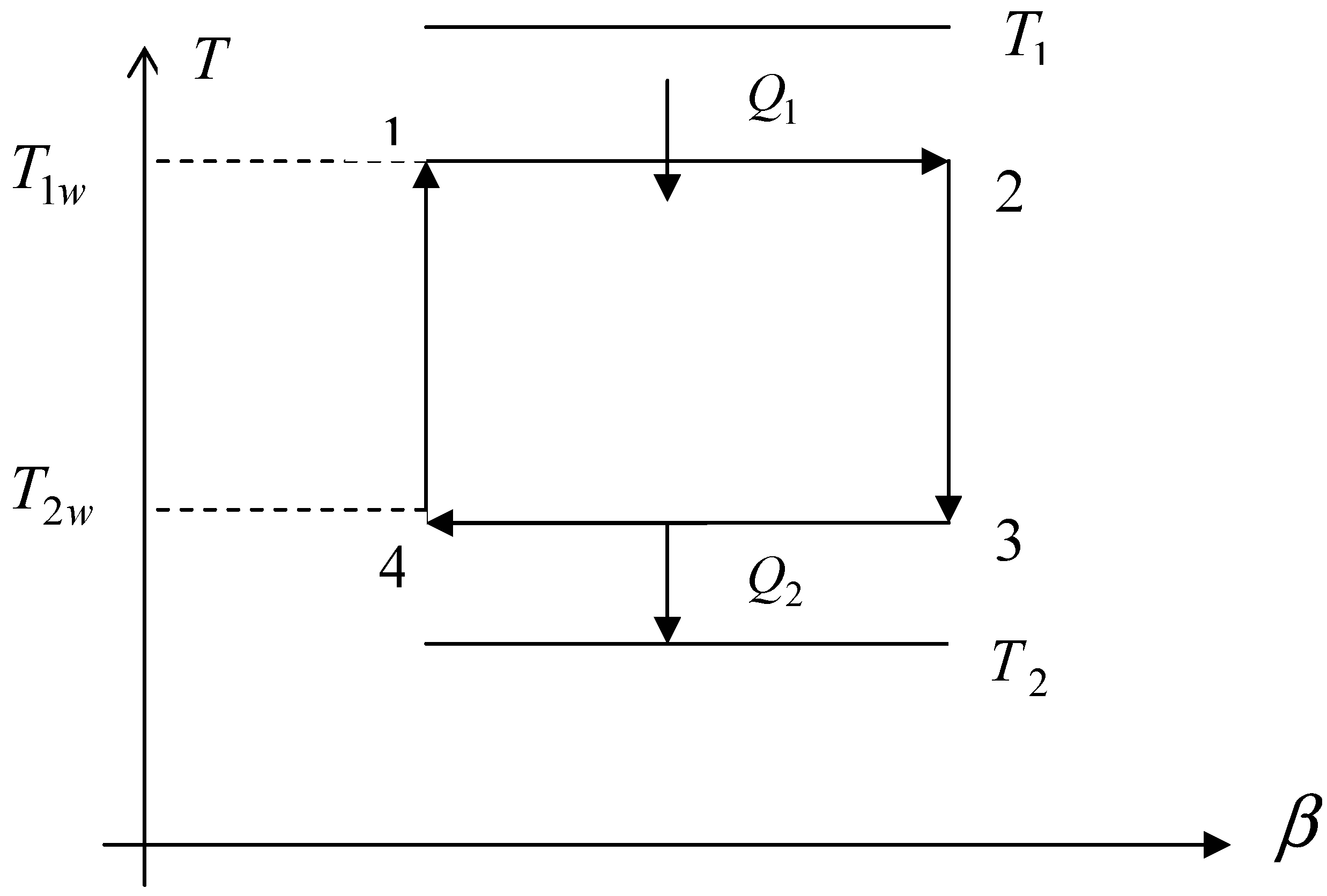
Novikov[1], Chambadal[2] and Curzon and Ahlborn[3], by independent way, took into account those processes and in doing so the temperatures of the reservoirs, T₁ > T₂ , enter the thermodynamic description together with the temperatures of the working substance in contact with the reservoirs. The relations between these temperatures in this cycle are T_1w < T₁ and T_2w > T₂, see Fig. 1. They also assumed that the heat transfer is represented by Newton's law and at the same time the Clausius equality

(1.2)

holds. Q₁ is the absorbed heat by the engine and Q₂ is the rejected heat by the engine. This last assumption is known as endoreversibility hypothesis. Upon the maximization of the power yield of the cycle obtained (Fig. 1), named Curzon and Ahlborn-Novikov cycle, they found the efficiency

(1.3)

Equation (1.3) has been obtained also by De Vos[4], Rubin[5] and Gordon[6] with different methods. As well as some authors have analized equation (1.3) and its consecuences[7,8,9,10], and they have discussed advances in the named finite time thermodynamics.

Angulo-Brown[11] has given a method to obtain the efficiency through the maximization of the so called ecological function:

E ≡ P − T₂σ,

(1.4)

where P is the cycle power output and σ is the entropy production associated to the heat transfer processes[12,13]. The efficiency obtained in this way, when it is using Newton's heat transfer law, is the following one[11,14]

(1.4)

where β is the ratio $\beta \equiv \frac{T_2}{T_1}$.

It has also been found by numerical comparison that η_E = (β) has values very near the semisum ${\eta }_s=\frac{1}{2}({\eta }_C+{\eta }_{CAN})$ for the whole span 0 ≤ β ≤ 1, where η_C and η_CAN are shown in Equations (1.1) and (1.3) respectively.

Fig. 1. Curzon and Ahlborn-Novikov cycle in the temperature T and entropy S plane. T₁ and T₂ are the temperatures of hot and cool reservoirs respectively; T_1w and T_2w are the hot and cool temperatures of the system respectively.

Fig. 1. Curzon and Ahlborn-Novikov cycle in the temperature T and entropy S plane. T₁ and T₂ are the temperatures of hot and cool reservoirs respectively; T_1w and T_2w are the hot and cool temperatures of the system respectively.

Other authors have analized some aspects related with this ecological function; thus Cheng and Chen[15] optimized the ecological performance of Carnot heat engine with heat resistance and internal irreversibilities; Chen et al.[16] presented a generalized Carnot heat engine model with heat resistance, heat lekage and internal irreversibilities, and derived the optimal ecological relation for Newton's heat transfer law between the working fluid and the heat reservoirs[17]; Zhu et al.[18] further discussed the effect of the heat transfer law on the ecological performance of the generalized irreversible Carnot heat engine (the Curzon and Ahlborn-Novikov engine), and derived the optimal performance with Dulong and Petit's heat transfer law. More recently, Chen et al.[19] provided ecological optimization results for a generalized irreversible Carnot refrigerator with heat resistance, heat lekage and internal irreversibilities, which was proposed by Chen et al.[20,21,22].

On other hand, Chen et al.[23] and Arias-Hernández et al.[24] have pointed out that the performance of an irreversible Carnot engine depends on the heat transfer law, but its properties still hold the same; so that, one can take a different heat transfer law to obtain a different form of the efficiency. In this sense the efficiency has also been calculated with Dulong and Petit's heat transfer law by Arias-Hernández and Angulo-Brown[25], and Angulo-Brown and Páez-Hernández[26], maximizing E . Those numerical results have shown that η value changes with the heat transfer law one assumes. Velasco et al.[27] have studied both the power and the ecological function optimizations, using Newton's transfer law through De Vos formalism[4].

The consequences of Dulong and Petit's heat transfer law on the performance of the heat engine have been also discussed by some others authors: O'Sullivan[28] discussed the Dulong and Petit's heat transfer law in detail, Chen et al.[29] derived the fundamental optimal relation between power output and efficiency of an endoreversible Carnot engine, Wu et al.[30] derived the optimal profit of an endoreversible Carnot engine, Zhu et al.[18] derived the optimal ecological performance.

Some of the above quoted authors do not take into account the time of the adiabatic branches explicitly. By taking into account the time explicitly for all the branches of the cycle in terms of thermodynamic properties, and with the heat transfer Newton's law, Gutkowics-Krusin et al.[31] have shown that the Curzon and Ahlborn-Novikov efficiency η_CAN is an upper bound for the efficiency as a function of both the ratio $\beta \equiv \frac{T_2}{T_1}$ and the ratio of the maximum and the minimum volume spanned by the cycle, through the quantity $\ln \frac{V_3}{V_1}$, see Fig. 1.

Ladino-Luna and de la Selva[14] also have shown that the ecological efficiency as a function of $\ln \frac{V_3}{V_1}$ and β reduces itself to Eq. (1.5) when $\frac{V_3}{V_1}\to \infty$, as well as shown in reference [31] for the case of power output for the Curzon and Ahlborn-Novikov efficiency.

On other hand, Ladino-Luna[32] has shown that the expression of power output and the efficiency of the heat engine by maximization of power output, and by using Dulong and Petit heat transfer, can be written also as a power series in the parameter λ, $\lambda ~\frac{1}{\ln V_{\max }-\ln V_{\min }}$. To arrive to the previous result it was necessary to build the power output as

(1.6)

where t_tot is the time of duration of the cycle including the time of the adiabatic branches; k is a constant parameter, with k > 1; x is the ratio of the cold temperatures, both of the engine and of the reservoir; z is the ratio of the cold and hot temperatures of the engine.

Also, Ladino-Luna[33] has shown that ecological function has the same form in [14] if it is taken as working substance a van der Waals gas as well as it is using an ideal gas as the working substance, in the case of Newton heat transfer law, by taking the change V → V − b, where b is a constant that depends on the system. Efficiency with van der Waals gas reduces to the efficiency with ideal gas when b goes to zero. It was necessary to build the entropy production in the same parameters as the power output was, as soon as

(1.7)

where , and its corresponding ecological function like

(1.8)

In the present work use is made of a non linear heat transfer law, $\frac{dQ}{dt}$ ~ (T − T₀)^k with k > 1, particularly the Dulong and Petit heat transfer law, taking into account explicitly the time for all the branches of the cycle for the Curzon and Ahlborn-Novikov engine, to find the functions P = P(V − b) and E = E(V − b) and to combine the form of them in references [31,32,33], taking a van der Waals gas as the working substance. Furthermore it is easy to look that P(V − b) and E(V − b) reduce to the ideal gas case when the new parameter ${\lambda }_{VW}~\frac{1}{\ln (V_{\max }-b)-\ln (V_{\min }-b)}$ goes to λ in references [31,32]. Thus Eqs. (1.6), (1.7) and (1.8) will be found as a limit when b → 0 and k → 1. The Dulong and Petit heat transfer law has been chosen because the main ocurring heat transfers in the system are conduction through the wall separating the working fluid from the thermal bath, and convection within the working fluid. Radiative heat transfer is of smaller magnitude. It is followed the procedure employed in [14], [31] and [32] references. The conclusions and comparison of results here obtained with the results obtained in these references are shown in the last section.

2. The van der Waals gas

The internal energy in the case of a van der Waals gas is written as [34]

(2.1)

for n moles with a change of temperature ΔT = T − T₀, at volume V, and with the characteristic constant a of the system, and the constant heat capacity C. So that taking the temporary derivative for an adiabatic process,

(2.2)

the first law of thermodynamics leads to

(2.3)

taking p as the internal pressure and p_ext as the presure of surroundings. Combining Eq. (2.2) and Eq. (2.3), in mechanical equilibrium, one obtains

(2.4)

so that, for a non linear heat transfer law

(2.5)

with the constant thermal conductance α, and the constant exponent k, k > 1, from Eq. (2.4), in an isothermal branch,

(2.6)

On other hand, the state equation for a van der Waals gas, with a constant b characteristic of the system, is

(2.7)

whose derivative respect T at p = constant leads to

(2.8)

By taking n = 1, Eq. (2.7) into Eq. (2.6) leads to

(2.9)

In the case of a Curzon and Ahlborn-Novikov cycle (Fig. 1), for the heat exchange between the engine and the reservoirs, Eq. (2.9) leads to the time of the isothermal branches by taking its integration.

Moreover in the case of an adiabatic branch $\frac{dQ}{dt}=0$, so that Eq. (2.3) reduces to

(2.10)

and by integration of Eq. (2.1) with n = 1, one obtains

C_V lnT = −Rln(V − b),

(2.11)

or as it is usually written,

(2.12)

Also, the time of duration of the adiabatic branches can be obtained by integration of (2.9). Therefore the time of duration of all branches in the cycle can be obtained from Eq. (2.9), and Eq. (2.12) leads to the relation between temperarures of the engine and the changes of volume in the adiabatic transformation.

3. Power output and ecological function

Taking into account the difference of temperatures between the engine and the reservoirs (Fig. 1), it can be written the time for all of the branches in the cycle from Eq. (2.9). It is taking n = 1 moles. For the isothermal branches, Eq. (2.9) is written as

(3.1)

and by direct integration of Eqs. (3.1) one gets

(3.2)

Analogously the time for the adiabatic branches can be obtained as

(3.3)

Now, taking into account Eq. (2.12), for the first adiabatic branch,

(3.4)

and for the second adiabatic branch,

(3.5)

and the combination of Eqs. (3.4) and (3.5) permits to have the relation

(3.6)

The main problem is to build an expression for the power output P and for the ecological function E. From the definition $p=\frac{W}{t_{tot}}$, the power output of the cycle, can be written as,

(3.7)

with W = Q₂ + Q₁ obtained by Eqs. (2.5) and (3.2), and where the total time of the cycle, t_tot = t₁ + t₂ + t₃ + t₄ , has been simplified by using Eq. (3.6). The substitutions $x=\frac{T_{1w}}{T_1}$, $z=\frac{T_{2w}}{T_{1w}}$ and $\beta =\frac{T_2}{T_1}$ permit to transform Eq. (3.7) as

(3.8)

or, by using , and the logarithm properties,

(3.9)

where . One can see that b → 0 leads to λ_VW → λ in Eq. (1.6) such as it was found in reference [32]; also one can see that b → 0 and k → 1 reduce (3.9) to expression of P in reference [31]. An expression of power in λ_VW leads to the efficiency that can be obtained following the procedure in those references. The efficiency obtained in this form also reduces to the efficiency obtained in the before cited references with the same limits.

In the case of ecological function it is necessary to build the entropy production σ, $\sigma =\frac{\Delta S}{t_{tot}}$, so that

ΔS = ΔS_1→2 + ΔS_3→4,

(3.10)

where ΔS_1→2 is the change of entropy in the first isothermal branch and ΔS_3→4 is the change of entropy at the second isothermal branch. For heat reservoirs, $\Delta S=\frac{Q}{T}$, assumed as it is only in the transfer processes between the reservoirs and the engine,

(3.11)

so that Eq. (3.10) can be written as

(3.12)

and by using Eq. (3.6) and Eq. (2.12) one can obtain Eq. (3.12) in the form

(3.13)

The entropy production takes the form

(3.14)

or by taking a factorization of production as T_1w and taking also the changes in Eq. (3.8) it is found the entropy production as

(3.15)

then, by using Eq. (1.4), Eq. (3.2) and Eq. (3.15) the ecological function can be written as

(3.16)

One can see that the estructure of Eq. (3.16) leads to (1.8) when the limit k → 1 is. It is also obtained the case of Newton heat transfer with an ideal gas as the working substance when k = 1 and b = 0 . A general form of ecological function and power output function can be obtained replacing λ_VW instead of λ, and with approximations for the cases when k > 1. z_PDP and η_PDP in reference [32] are modified with the substitution V − b instead of V. The corresponding maximization of ecological function taking Dulong-Petit's heat transfer and a van der Waals gas as the working substance can be found with the substitution λ_VW instead of λ in all of the process to build the ecological efficiency. In the case of power output with the same substitution, following the procedure in reference [32], one obtains the approximate formula for the efficiency when λ_VW goes to zero (infinite compression ratio), and a similar power series of the efficiency as a function of λ_VW

(3.17)

With the approximate function z_PDP, obtained in reference [32],

(3.18)

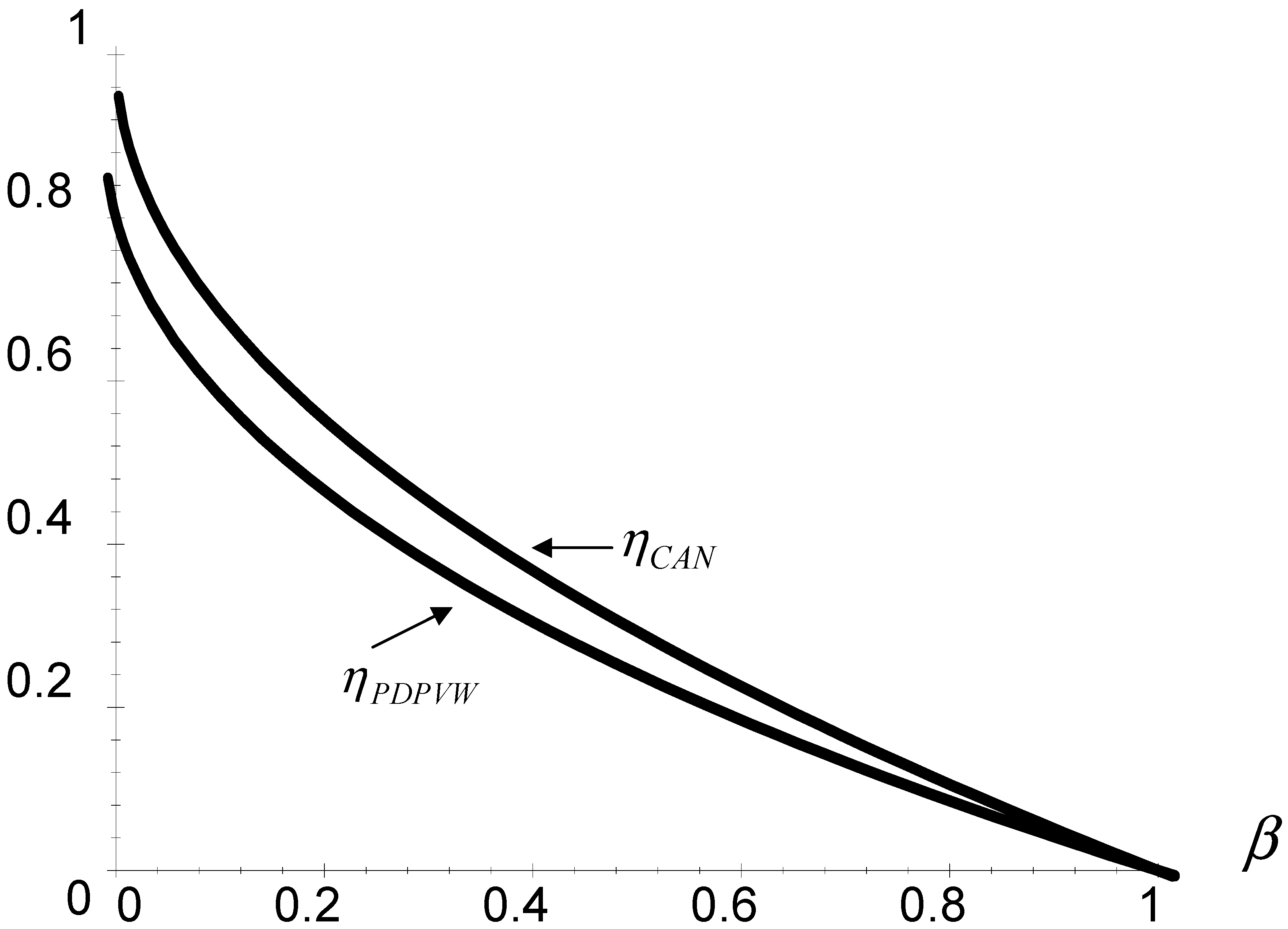
and at the limit λ_VW → 0 one obtains η_PDPVW(λ_VW = 0) = η_PDP where η_PDP is the same approximate efficiency found in reference [32]. Figure 2 shows a comparison between η_CAN and η_PDPVW at zero order in λ_VW. As one can see, η_PDPVW(λ_VW = 0) < η_CAN, so η_CAN can be consider as an upper bound for the efficiencies that taking into account the time of the adiabatic branches in the Curzon and Ahlborn-Novikov cycle.

Equation (3.18) is obtained by taking the condition $\frac{\partial P}{\partial x}=0$ in Eq. (3.9). The function x = x(λ_VW, z, β) obtained in this way is substituted in the resulting expression from the condition $\frac{\partial P}{\partial z}=0$, and it permits to get a function z = z(λ_VW, β), for a given parameter k, and by thickness approximations for the resulting exponents at the limit λ_VW → 0 one gets,

(3.19)

For the Dulong-Petit's heat transfer, $k=\frac{5}{4}$, (3.19) goes to (3.18), with values for the parameter β as 0 < β < 1.

Fig. 2. Comparison between the Curzon and Ahlborn-Novikov efficiency, η_CAN, and the efficiency η_PDPVW at zero order in λ_VW, for the Dulong and Petit's heat transfer law.

Fig. 2. Comparison between the Curzon and Ahlborn-Novikov efficiency, η_CAN, and the efficiency η_PDPVW at zero order in λ_VW, for the Dulong and Petit's heat transfer law.

4. Conclusions

A first result is emboided in Eqs. (3.9) and (3.15). It expresses the fact that the efficiency for a Curzon and Ahlborn-Novikov engine depends on both the size of the engine, which is represented by the parameter , and on the heat transfer law one uses for describing the heat exchange between the working fluid and the thermal reservoirs. The estructure of those equations shows that all calculation made to evaluate the performance of an engine with a van der Waals gas as working substance leads to the same calculation made with an ideal gas as working substance, and by using any heat transfer law of the form of Eq. (2.5). With acceptable approximation in the case $k=\frac{5}{4}$, it is possible to obtain numerical results that one can compare with other results found in the literature. Our results also conserve the dependence on the compression ratio, $\frac{V_3-b}{V_1-b}$. For a known value of b one can find that exits a leading term of the corresponding efficiency that corresponds to the exact numerical value calculated without explicitly taking into account the dependence on the compression ratio, and it is an upper bound for the value of the efficiency; in fact the larger the ratio $\frac{V_3-b}{V_1-b}$, the larger the efficiency becomes. It can also been shown that for the Dulong-Petit’s heat transfer law and the ideal gas law, the limits λ_VW → 0 and k → 1 lead to the Curzon and Ahlborn-Novikov result.