A Cellular Automata Study of Constraints (Dissolvence) in a Percolating Many-Particle System
Abstract
:Introduction
Methods
The model
The rules
Study design and cell properties monitored
| Parameter set | Joining parameter J | Breaking probability PB | C50%a) |
|---|---|---|---|
| 1 | 0.50 | 0.25 | 0.503 |
| 2 | 1.50 | 0.25 | 0.488 |
| 3 | 3.00 | 0.25 | 0.476 |
| 4 | 0.50 | 0.50 | 0.546 |
| 5 | 1.50 | 0.50 | 0.530 |
| 6 | 3.00 | 0.50 | 0.519 |
| 7 | 0.50 | 0.75 | 0.573 |
| 8 | 1.50 | 0.75 | 0.559 |
| 9 | 3.00 | 0.75 | 0.558 |
Programs
Results and Discussion
Study A: Average percent of occupied cells in each configuration (%Fi)
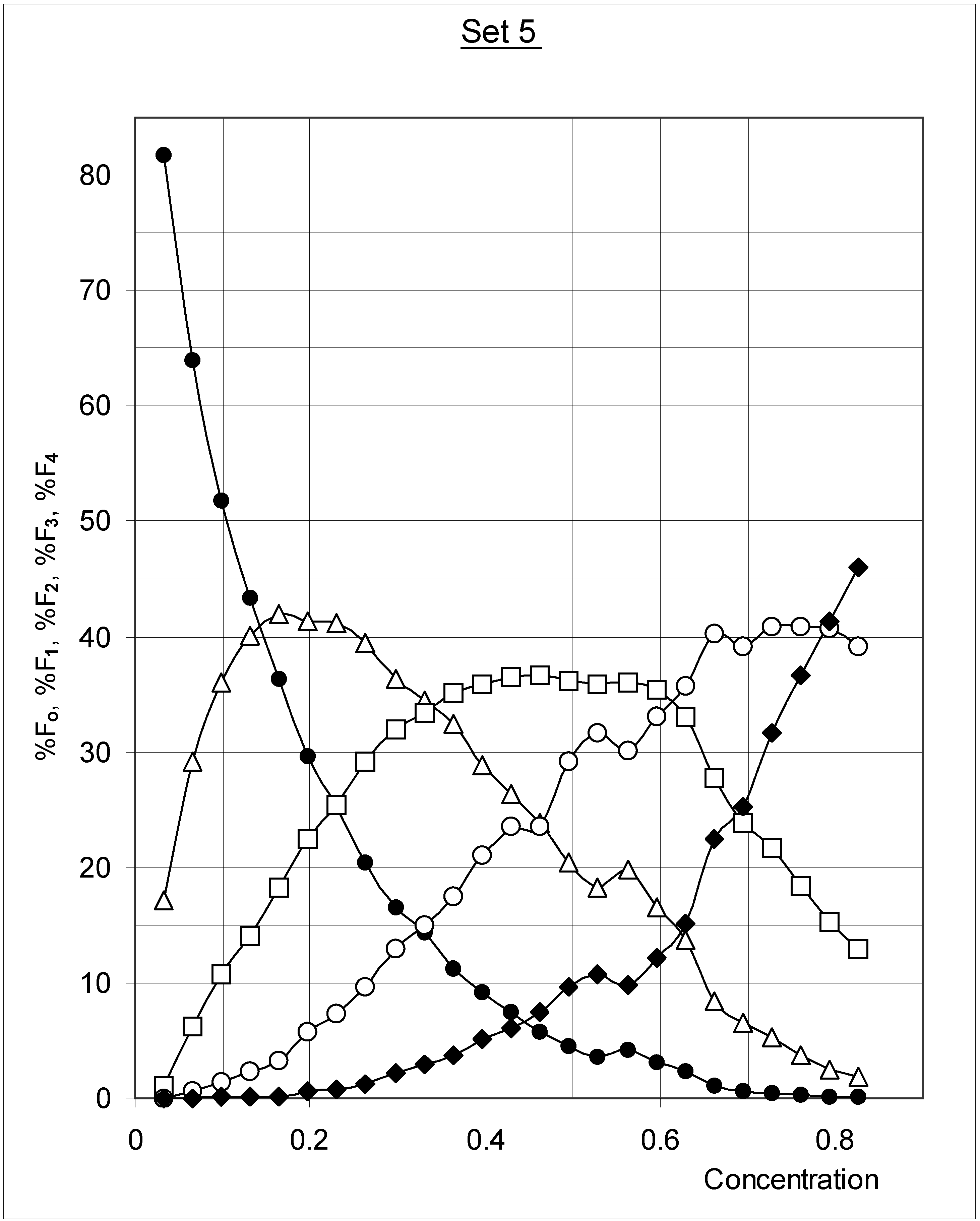
Descriptive approach
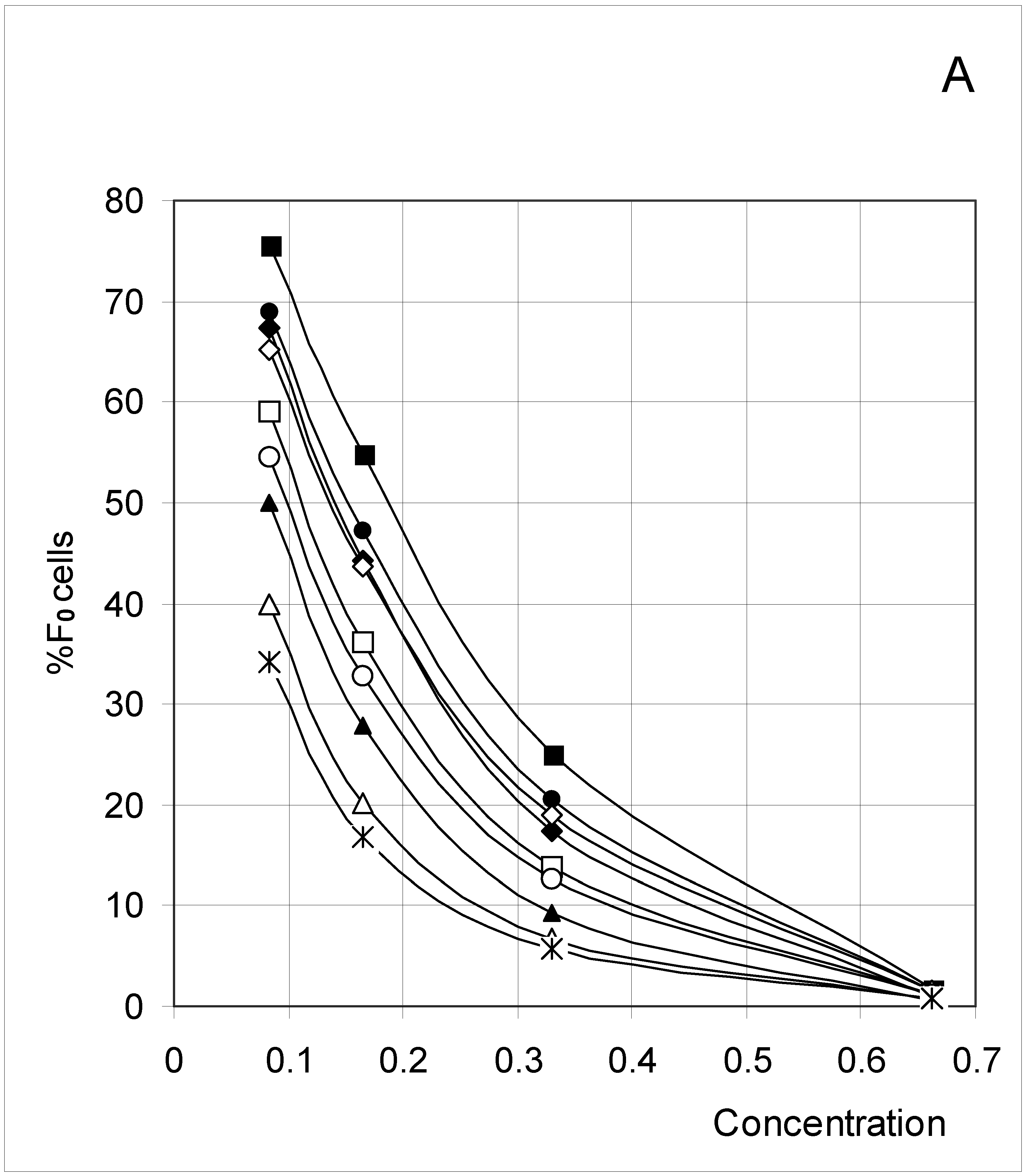
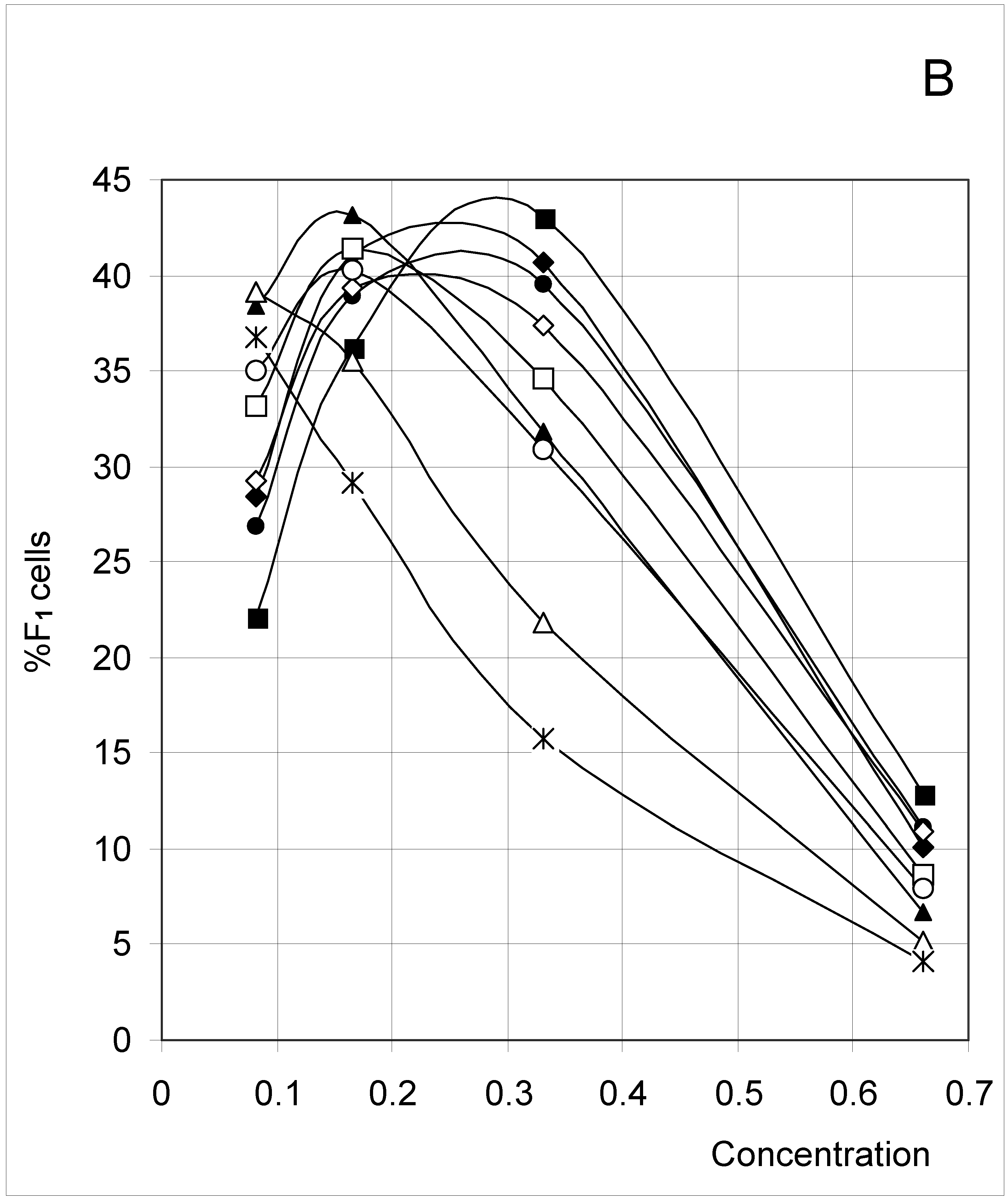
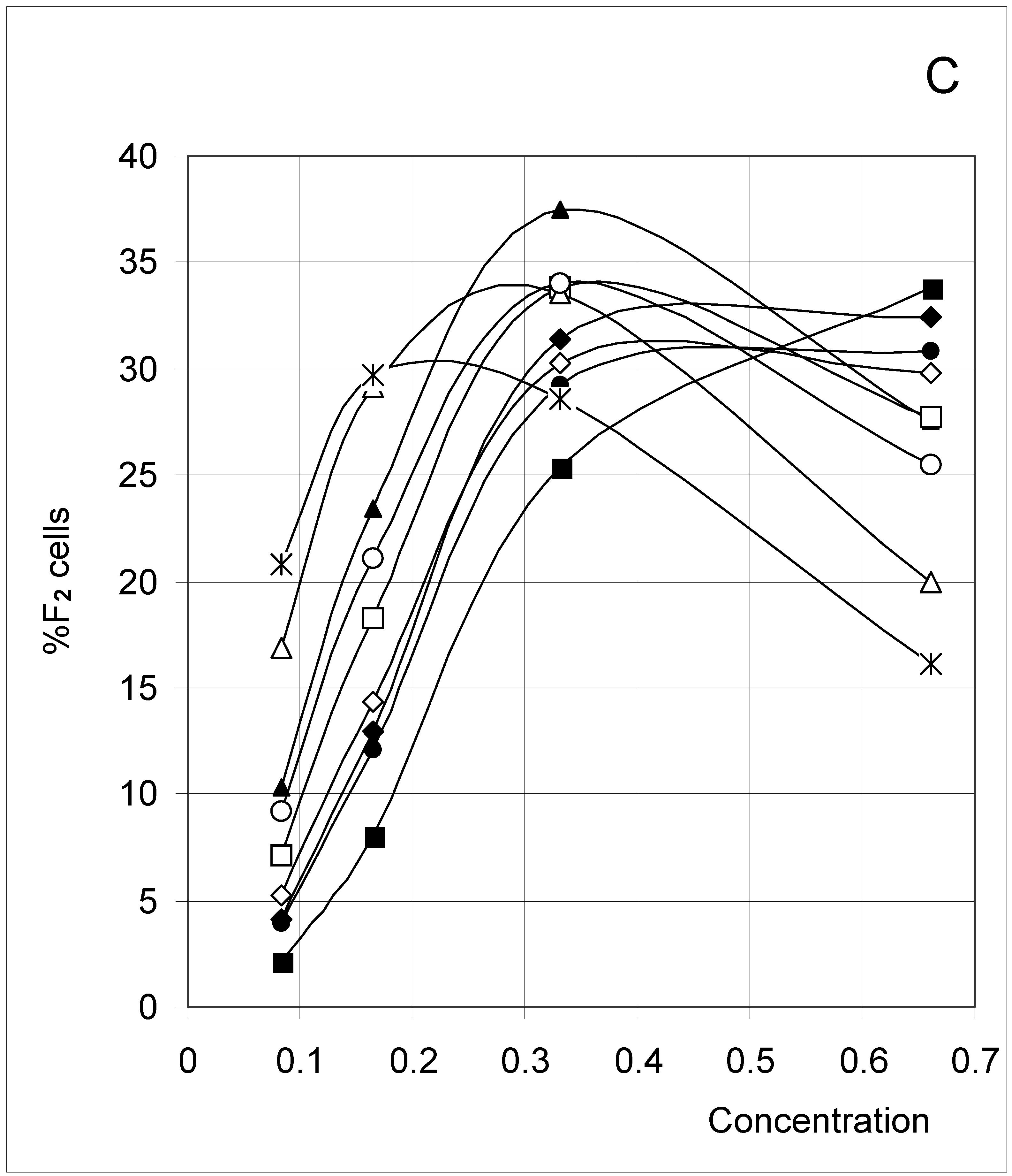
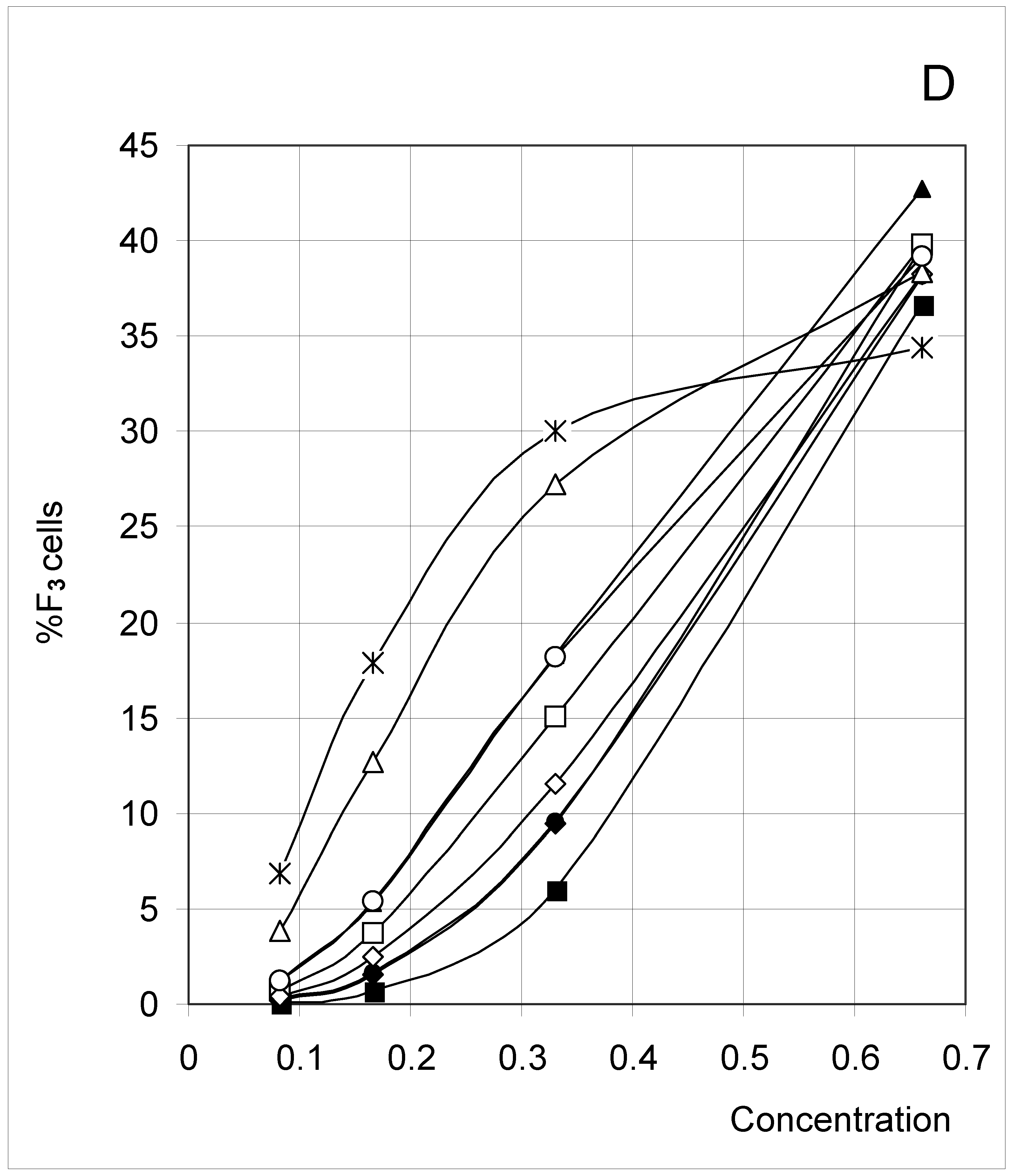
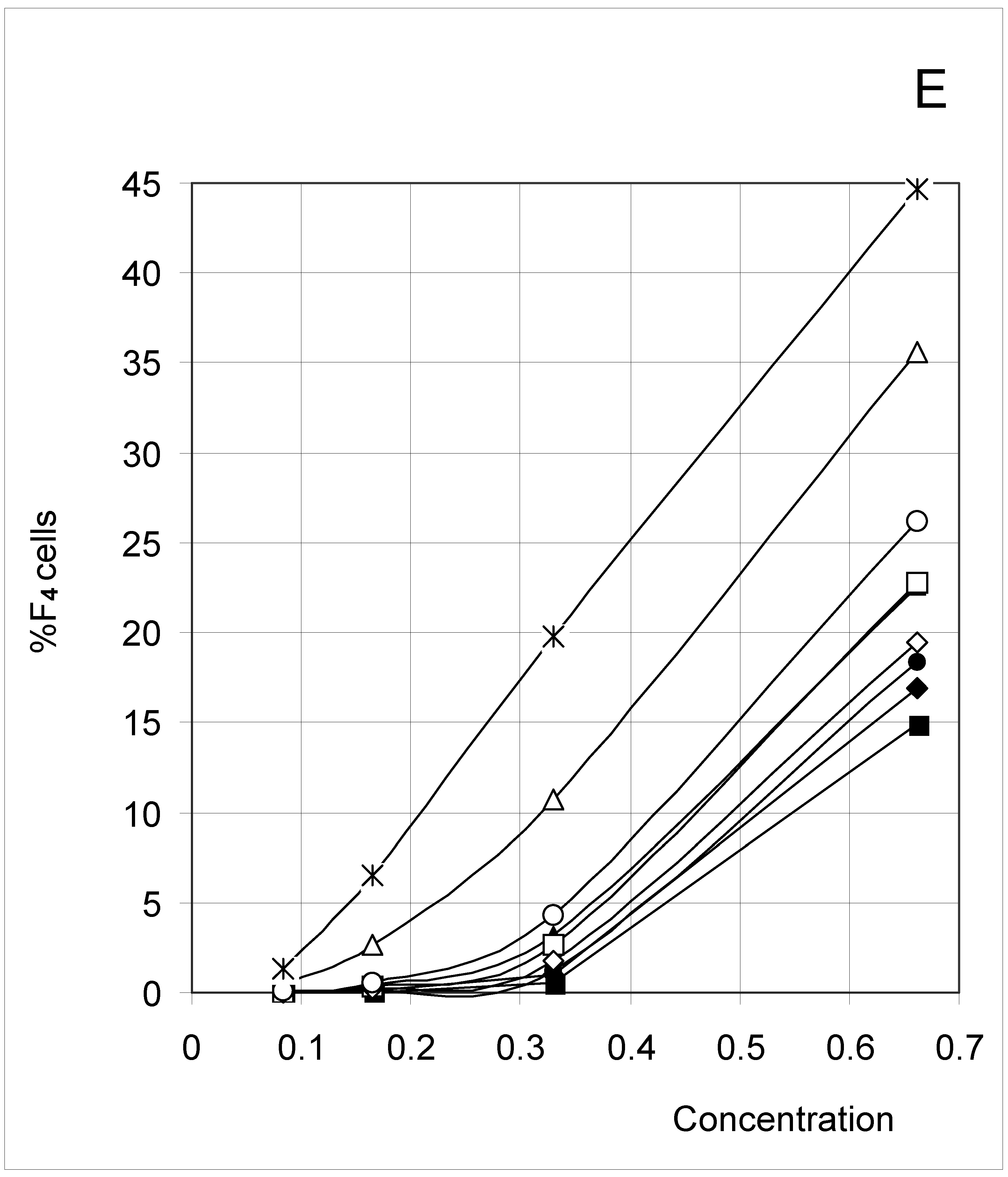
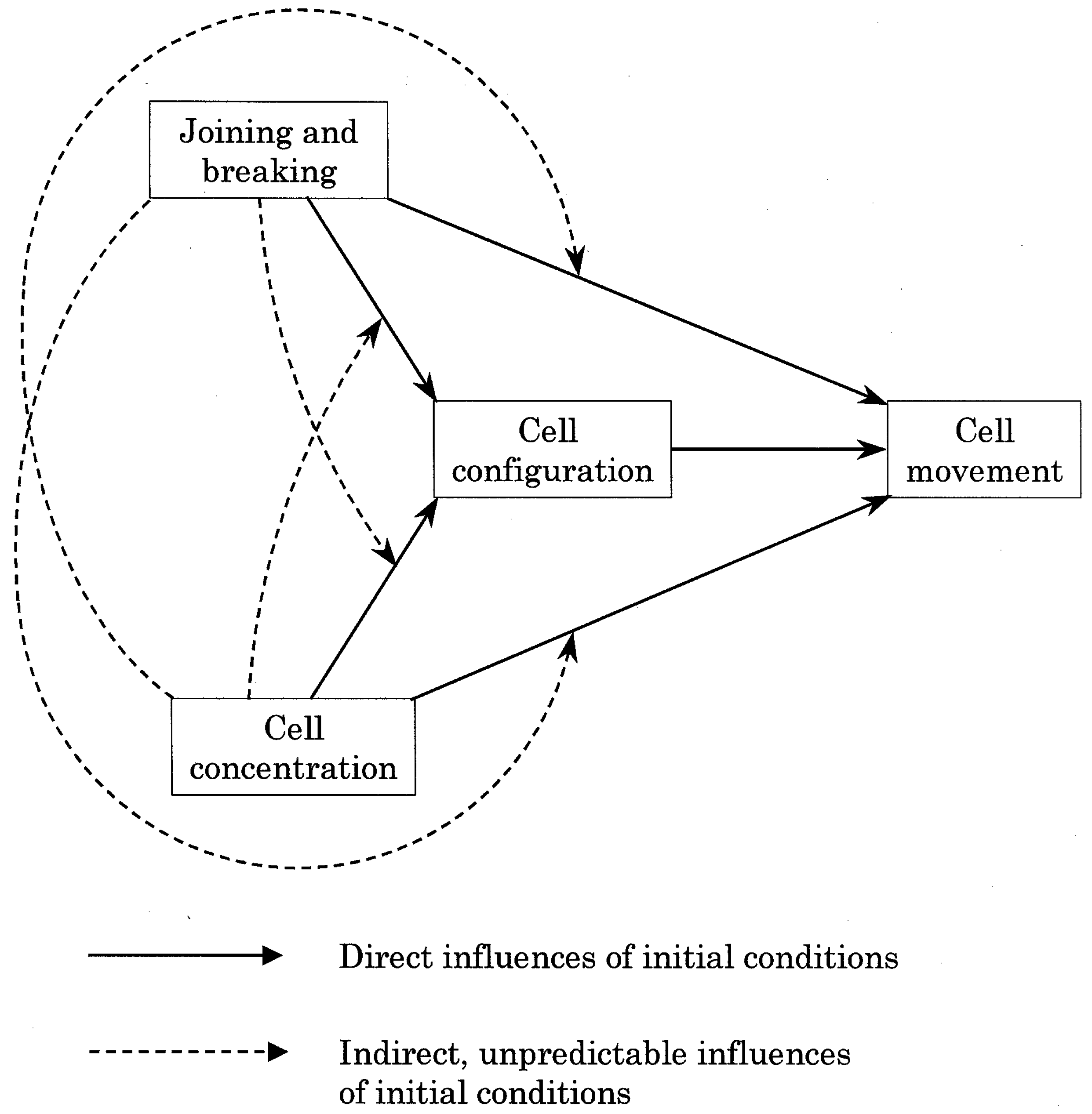
Correlations between initial conditions and configuration of occupied cells
Kinematic-like description

| Set 3 | Set 5 | Set 7 | |
|---|---|---|---|
| k0,1 | 11.07 ± 0.44 | 6.27 ± 0.11 | 4.47 ± 0.15 |
| k1,2 | 8.23 ± 0.33 | 4.86 ± 0.09 | 4.09 ± 0.16 |
| k2,3 | 5.19 ± 0.17 | 3.62 ± 0.08 | 3.10 ± 0.15 |
| k3,4 | 2.91 ± 0.09 | 2.08 ± 0.06 | 1.74 ± 0.17 |
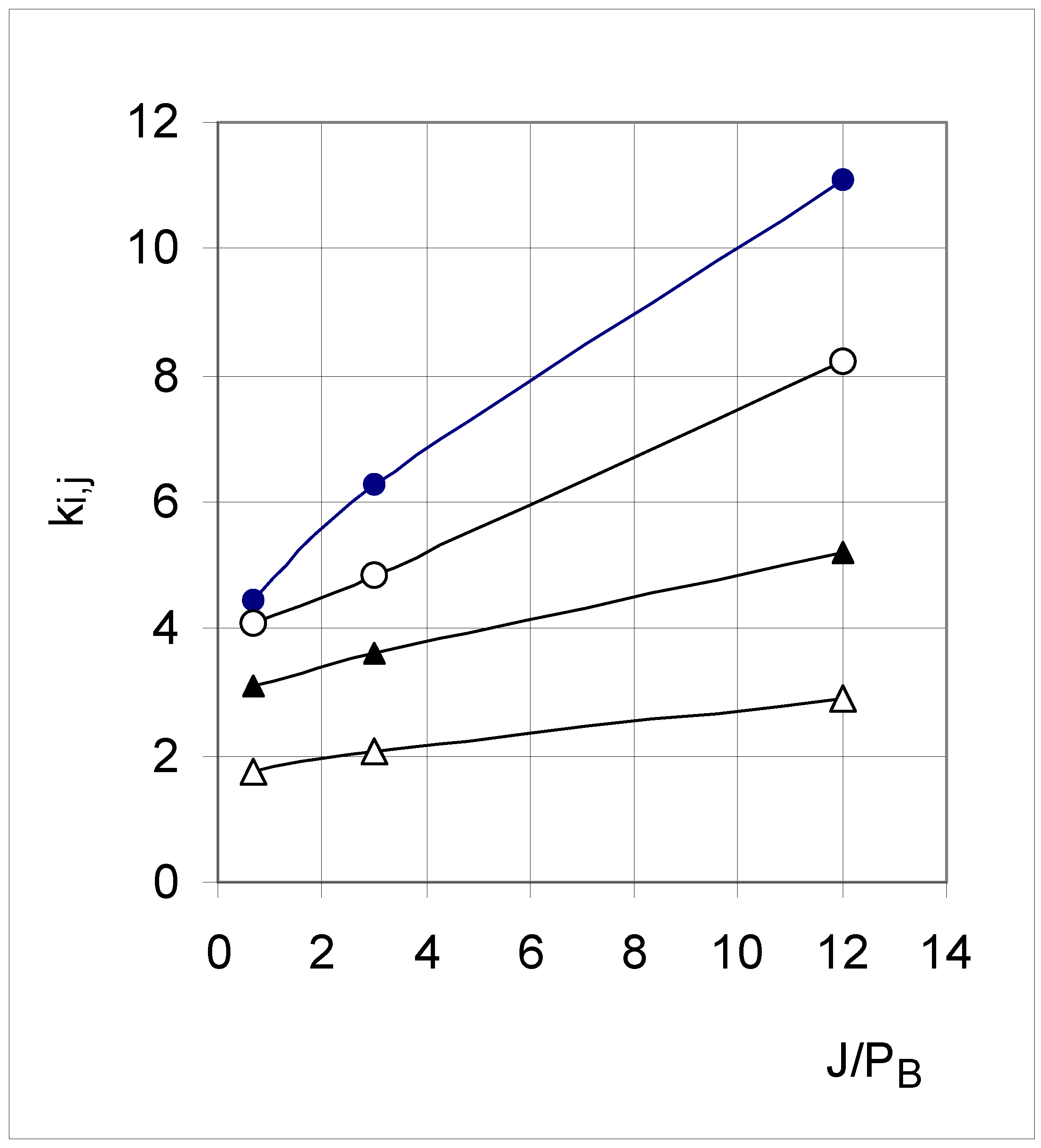
Conclusion of Study A
Study B: Probability of a single occupied cell to move (%Mi)
Descriptive approach
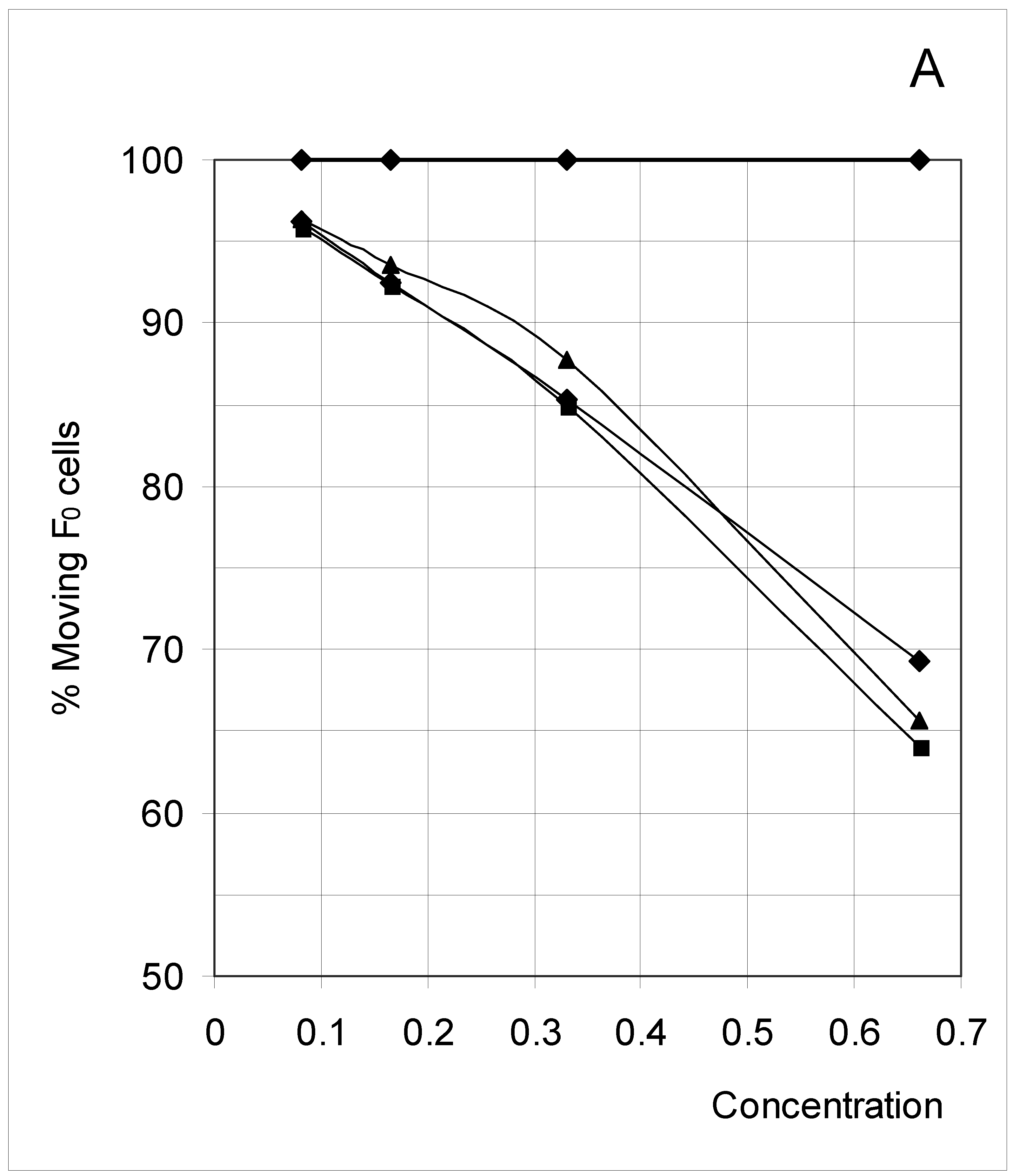
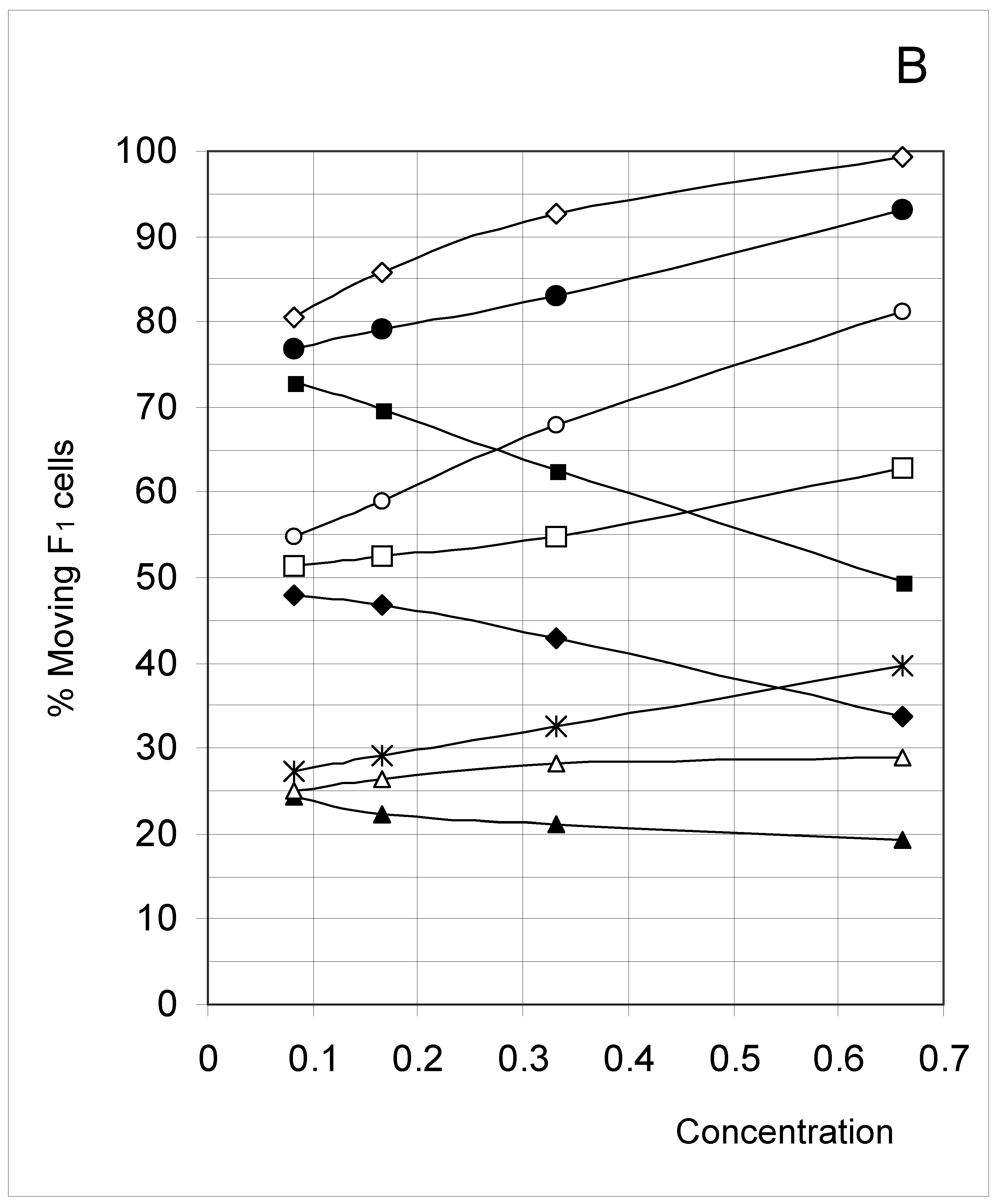

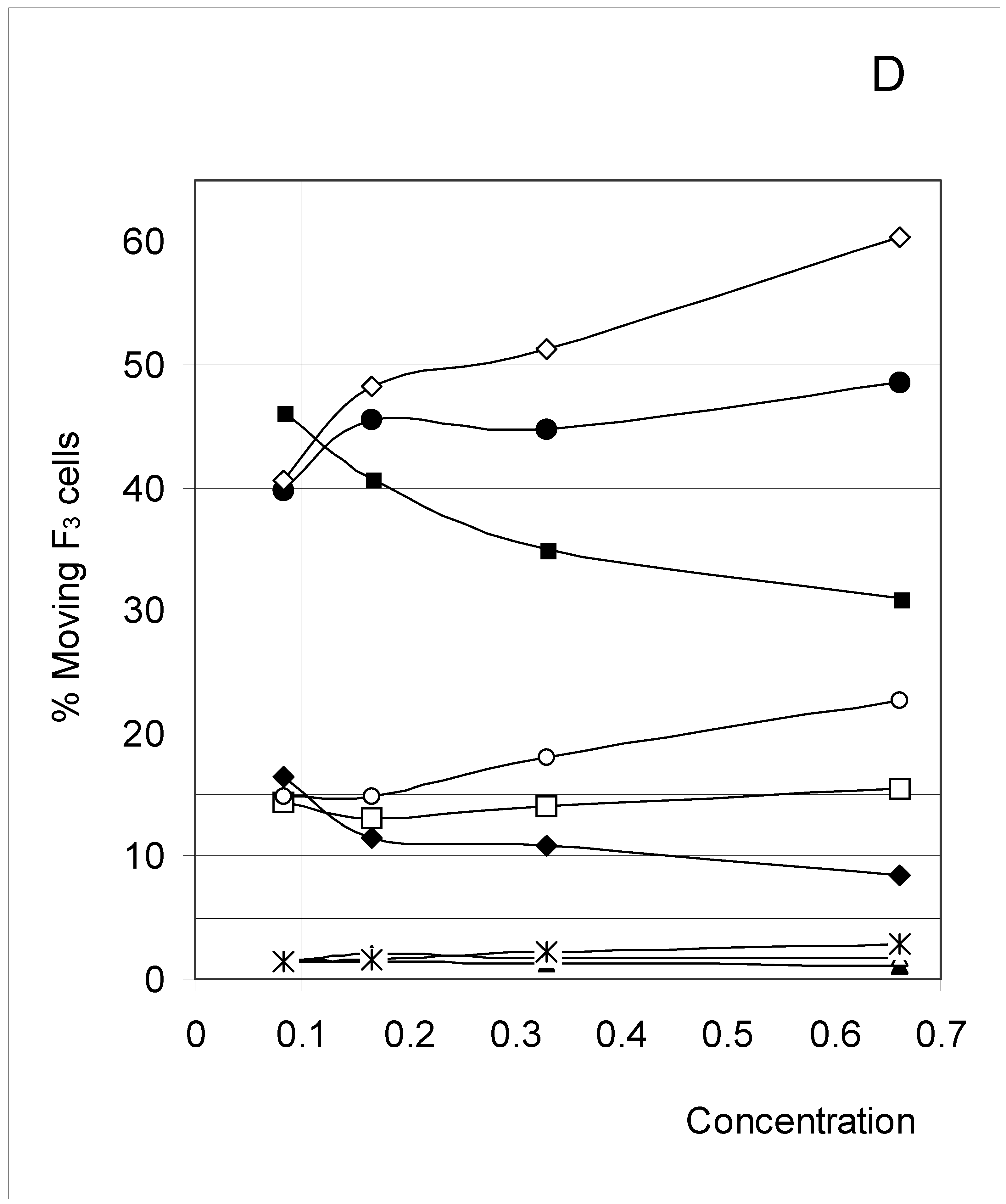
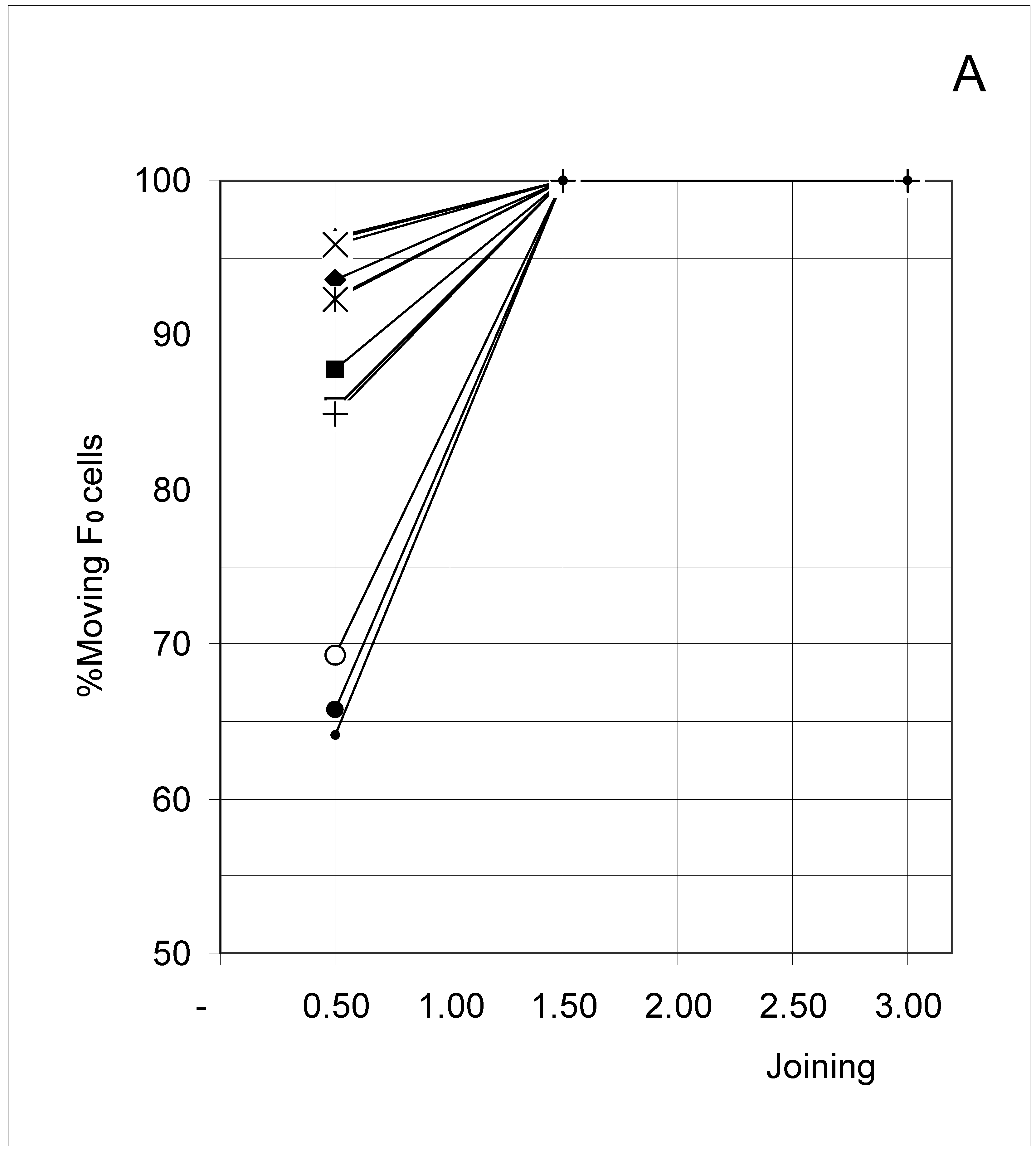

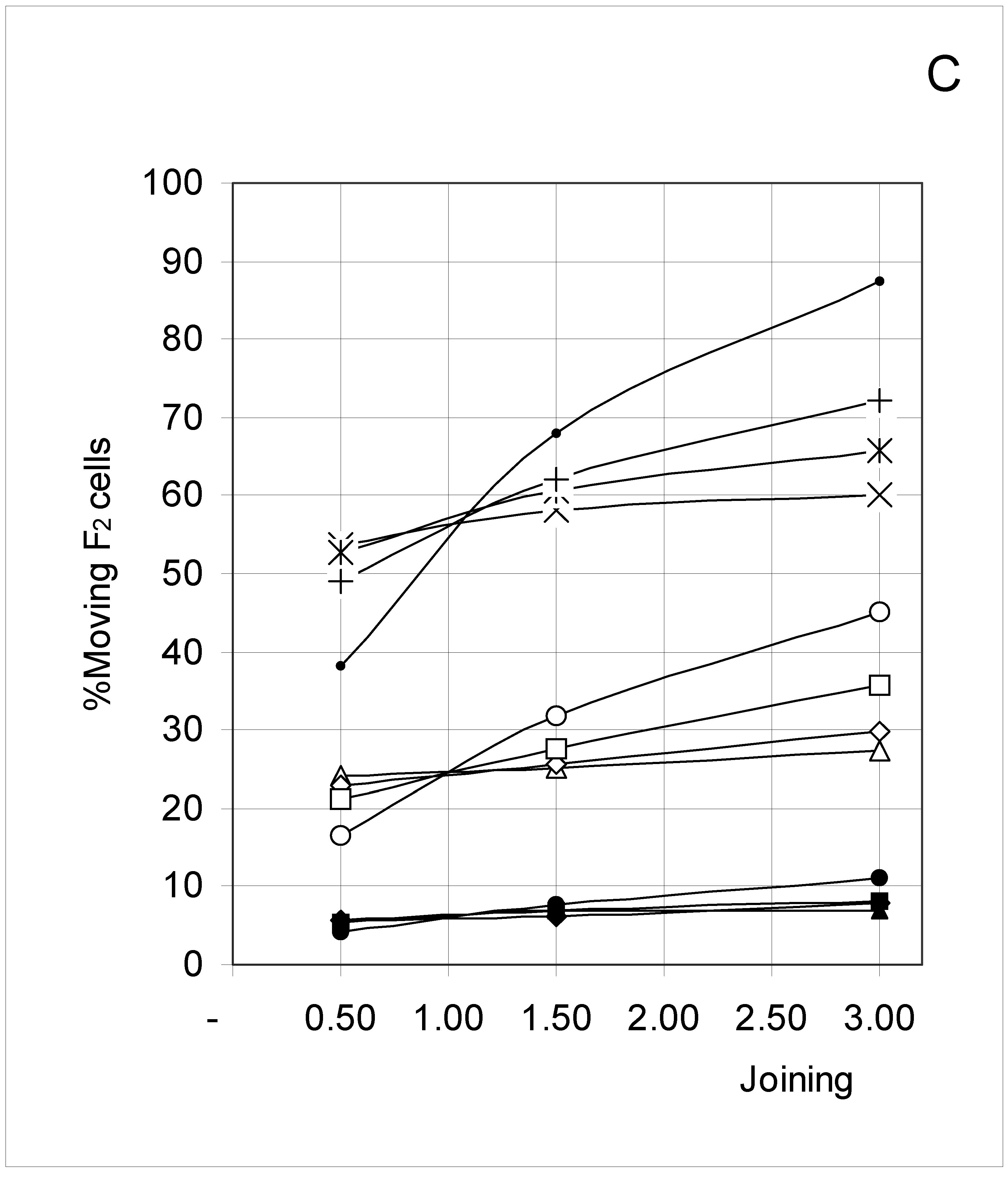
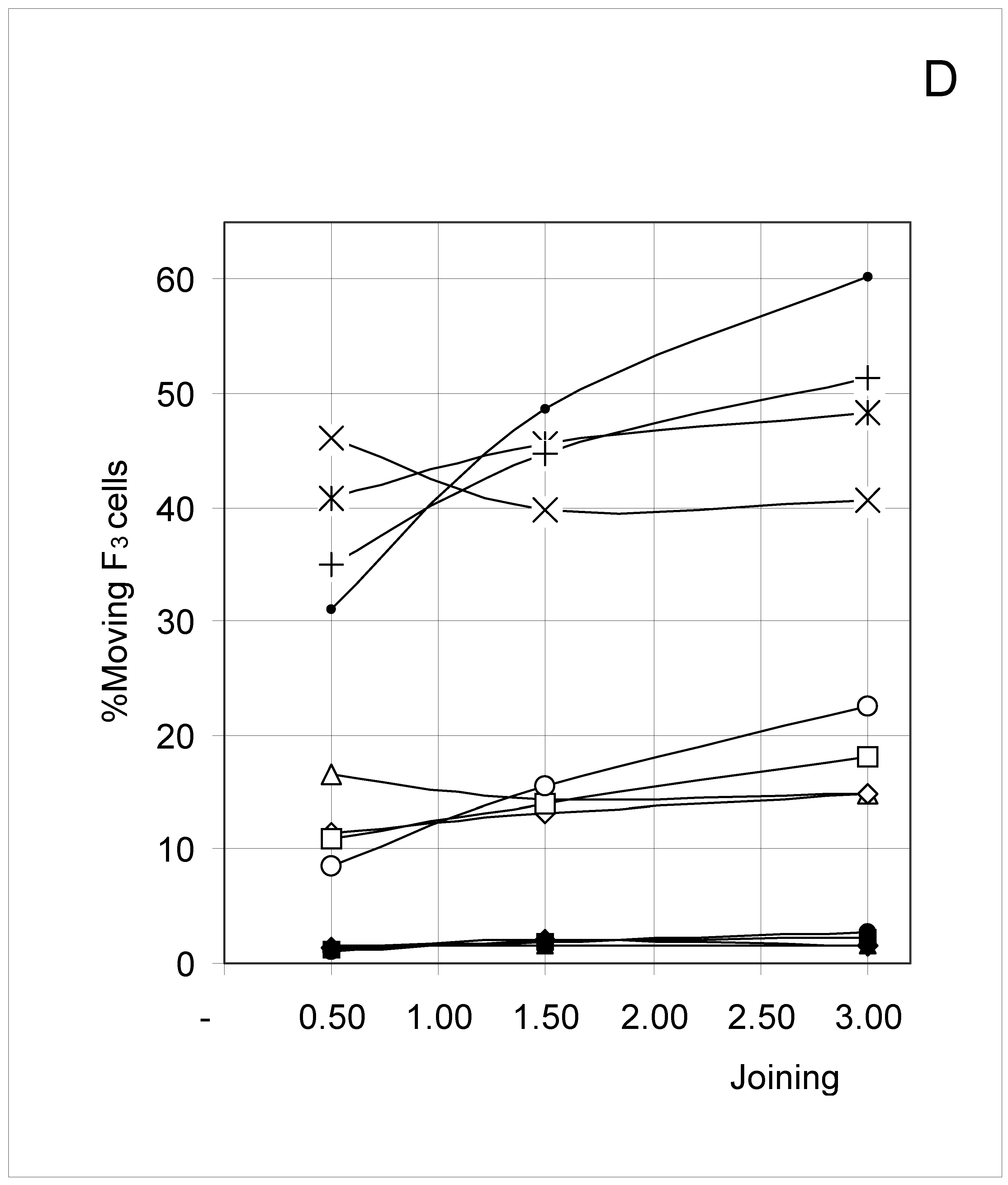
Correlations between initial conditions and movement probability
Conclusion of Study B
Relations between constraints and the emergence of percolation
Conclusions
Expected and unexpected constraints on the behavior of CA
Constraints versus emergence
Physical relevance of the present study
References
- Holland, J.H. Emergence - From Chaos to Order; Perseus Books: Reading, USA, 1999. [Google Scholar]
- Von Neumann, J. Theory of Self-Reproducing Automata. In Theory of Self-Reproducing Automata; Burks, A., Ed.; University of Illinois Press: Urbana, IL, 1966. [Google Scholar]
- Kier, L.B.; Cheng, C.-K.; Testa, B. Cellular automata models of biochemical phenomena. Fut. Generat. Comput. Syst. 1999, 16, 273–289. [Google Scholar] [CrossRef]
- Kier, L.B.; Cheng, C.-K.; Testa, B. A cellular automata model of the percolation process. J. Chem. Inf. Comput. Sci. 1999, 39, 326–332. [Google Scholar] [CrossRef]
- Stauffer, D. Introduction to Percolation Theory; Taylor and Francis: London, 1985. [Google Scholar]
- de Gennes, P.G. Dynamics of entangled polymer solutions II. Inclusion of hydrodynamic interaction. Macromolecules 1976, 9, 594–598. [Google Scholar] [CrossRef]
- Broadbent, S.R.; Hammersley, J.M. Percolation process (I). Crystals and mazes. Proc. Cambridge Phil. Soc. 1957, 53, 629–641. [Google Scholar] [CrossRef]
- Sahimi, M.; Gavalas, G.R.; Tsotsis, T.T. Statistical and continuum models of fluid-solid reactions in porus media. Chem. Eng. Sci. 1990, 45, 1443–1452. [Google Scholar] [CrossRef]
- Stauffer, D.; Sahimi, M. High dimensional simulation of simple immunological models. J. Theoret. Biol. 1994, 166, 289–297. [Google Scholar] [CrossRef] [PubMed]
- Testa, B.; Kier, L.B.; Carrupt, P.A. A systems approach to molecular structure, intermolecular recognition, and emergence-dissolvence in medicinal research. Med. Res. Rev. 1997, 17, 303–326. [Google Scholar] [CrossRef]
- Testa, B.; Kier, L.B. The concept of emergence-dissolvence in drug research. Adv. Drug Res. 1997, 30, 1–14. [Google Scholar]
- Testa, B.; Kier, L.B. Emergence and dissolvence in the self-organization of complex systems. Entropy 2000, 2, 1–25. Free access: http://natsci.net/reprints/entropy/2000/e2010001.pdf. [Google Scholar] [CrossRef]
- Campbell, D.T. Downward causation in hierarchically organised systems. In Studies in the Philosophy of Biology; Ayala, F.J., Dobzhansky, T., Eds.; Macmillan: London, 1974; pp. 179–186. [Google Scholar]
- Allen, T.F.H.; Hoekstra, T.W. Toward a Unified Ecology; Columbia University Press: New York, 1992; Chapter 1. [Google Scholar]
- Testa, B.; Raynaud, I.; Kier, L.B. What differentiates free amino acids and aminoacyl residues ? An exploration of conformational and lipophilicity spaces. Helv. Chim. Acta 1999, 82, 657–665. [Google Scholar] [CrossRef]
- Testa, B.; Bojarski, A. Molecules as complex adaptative systems. Constrained molecular properties and their biochemical significance. Eur. J. Pharm. Sci. 2000, 11 Suppl. 2, S2–S14. [Google Scholar] [CrossRef]
- Kier, L.B.; Cheng, C.-K. A cellular automata model of an aqueous solution. J. Chem. Inf. Comp. Sci. 1994, 34, 1334–1337. [Google Scholar] [CrossRef]
- Kier, L.B.; Cheng, C.-K.; Testa, B.; Carrupt, P.A. A cellular automata model of the hydrophobic effect. Pharm. Res. 1995, 12, 615–619. [Google Scholar] [CrossRef] [PubMed]
- Kier, L.B.; Cheng, C.-K.; Testa, B.; Carrupt, P.A. A cellular automata model of micelle formation. Pharm. Res. 1996, 13, 1419–1422. [Google Scholar] [CrossRef] [PubMed]
- Kier, L.B.; Cheng, C.-K.; Testa, B.; Carrupt, P.A. A cellular automata model of aqueous diffusion. J. Pharm. Sci. 1997, 87, 774–778. [Google Scholar] [CrossRef] [PubMed]
- Kier, L.B.; Cheng, C.-K.; Tute, M.; Seybold, P.G. A cellular automata model of acid dissociation. J. Chem. Inf. Comp. Sci. 1998, 38, 271–275. [Google Scholar] [CrossRef]
- Steppan, D.; Werner, J.; Yeater, B. Essential Regression and Experimental Design, version 2.218; 1998. http://www.geocities.com/SiliconValley/Network/1021/.
© 2001 by MDPI. All rights reserved.
Share and Cite
Testa, B.; Kier, L.B.; Cheng, C.-K.; Mayer, J. A Cellular Automata Study of Constraints (Dissolvence) in a Percolating Many-Particle System. Entropy 2001, 3, 27-57. https://doi.org/10.3390/e3020027
Testa B, Kier LB, Cheng C-K, Mayer J. A Cellular Automata Study of Constraints (Dissolvence) in a Percolating Many-Particle System. Entropy. 2001; 3(2):27-57. https://doi.org/10.3390/e3020027
Chicago/Turabian StyleTesta, Bernard, Lemont B. Kier, Chun-Kao Cheng, and Joachim Mayer. 2001. "A Cellular Automata Study of Constraints (Dissolvence) in a Percolating Many-Particle System" Entropy 3, no. 2: 27-57. https://doi.org/10.3390/e3020027
APA StyleTesta, B., Kier, L. B., Cheng, C.-K., & Mayer, J. (2001). A Cellular Automata Study of Constraints (Dissolvence) in a Percolating Many-Particle System. Entropy, 3(2), 27-57. https://doi.org/10.3390/e3020027




