Finite-Temperature Correlation Functions Obtained from Combined Real- and Imaginary-Time Propagation of Variational Thawed Gaussian Wavepackets
Abstract
:1. Introduction
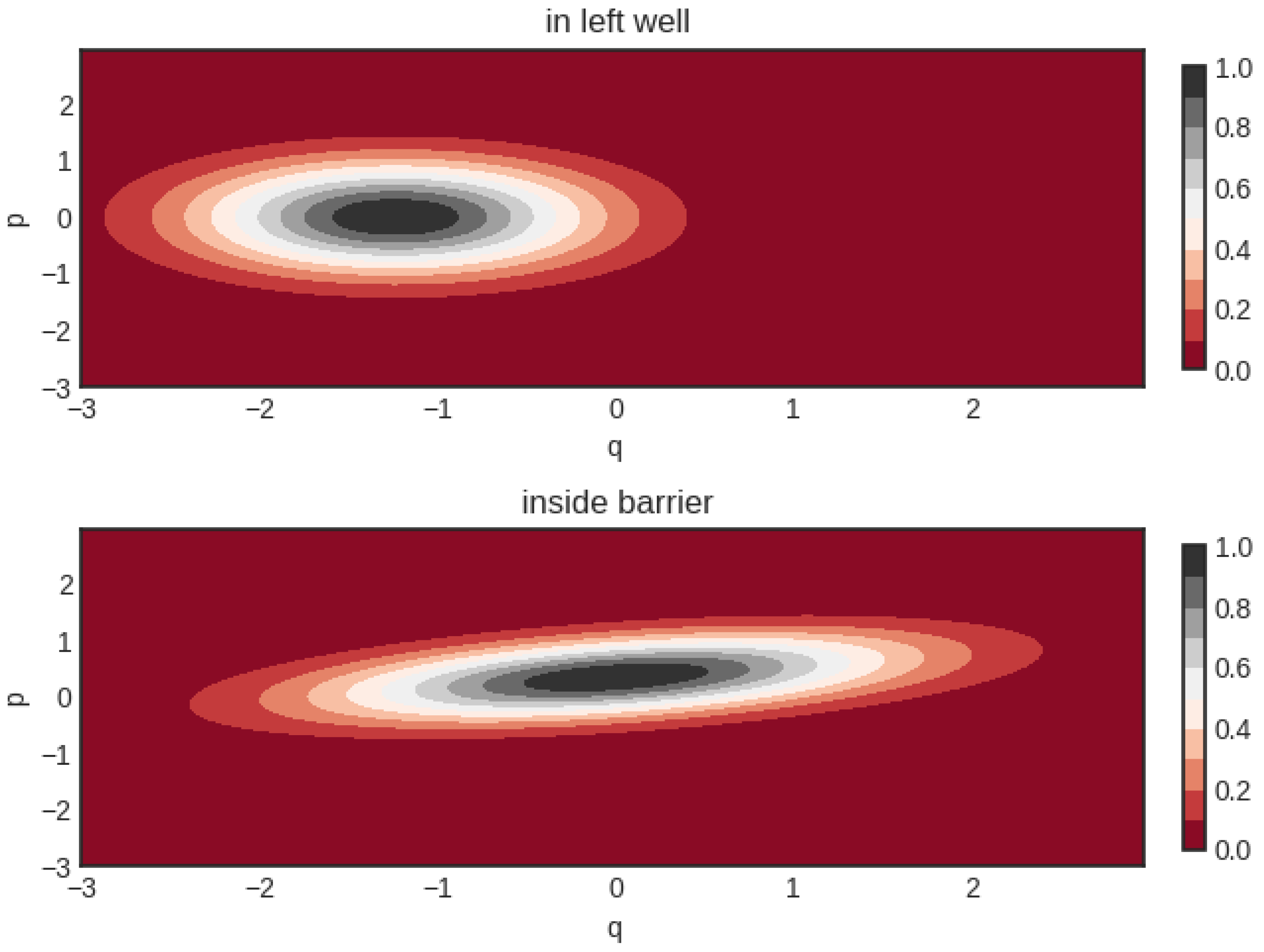
2. Methods
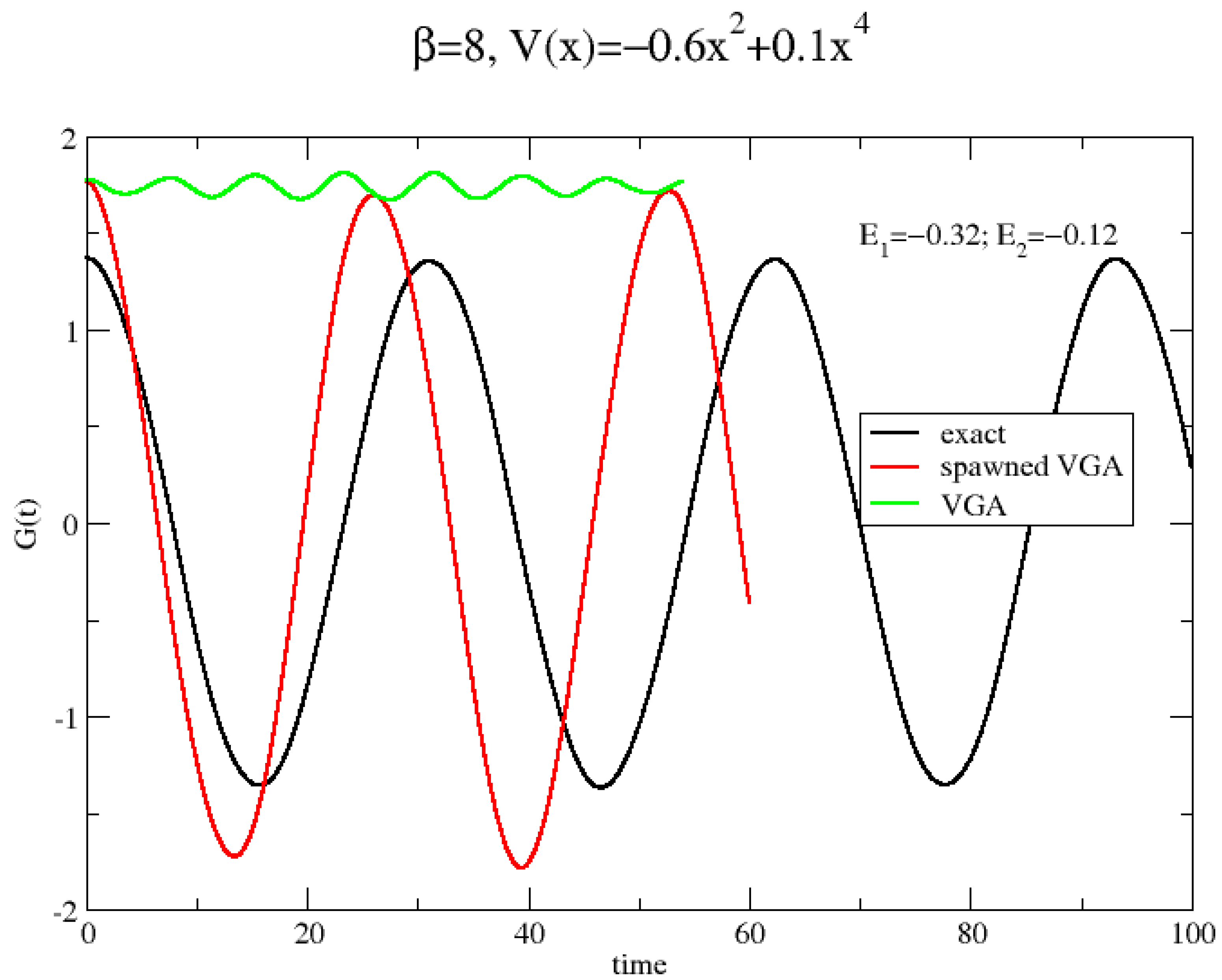
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Heller, E.J. Time-dependent approach to semiclassical dynamics. J. Chem. Phys. 1975, 62, 1544–1555. [Google Scholar] [CrossRef]
- Buch, V. Exploration of multidimensional variational Gaussian wave packets as a simulation tool. J. Chem. Phys. 2002, 117, 4738–4750. [Google Scholar] [CrossRef]
- Coalson, R.D.; Karplus, M. Multidimensional variational Gaussian wave packet dynamics with application to photodissociation spectroscopy. J. Chem. Phys. 1990, 93, 3919–3930. [Google Scholar] [CrossRef]
- Begušić, T.; Vaníček, J. On-the-fly ab initio semiclassical evaluation of vibronic spectra at finite temperature. J. Chem. Phys. 2020, 153, 024105. [Google Scholar] [CrossRef]
- Sawada, S.-I.; Heather, R.; Jackson, B.; Metiu, H. A strategy for time dependent quantum mechanical calculations using a Gaussian wave packet representation of the wave function. J. Chem. Phys. 1985, 83, 3009–3027. [Google Scholar] [CrossRef]
- Fereidan, R.M.; Vaníček, J. High-order geometric integrators for the variational Gaussian approximation. J. Chem. Phys. 2023, 159, 094114. [Google Scholar] [CrossRef] [PubMed]
- Green, J.A.; Grigolo, A.; Ronto, M.; Shalashilin, D.V. A two-layer approach to the coupled coherent states method. J. Chem. Phys. 2016, 144, 024111. [Google Scholar] [CrossRef]
- Ben-Nun, M.; Martinez, T.J. A multiple spawning approach to tunneling dynamics. J. Chem. Phys. 2000, 112, 6113–6121. [Google Scholar] [CrossRef]
- Richings, G.W.; Polyak, I.; Spinlove, K.E.; Worth, G.A.; Burghardt, I.; Lasorne, B. Quantum dynamics simulations using Gaussian wavepackets: The vMCG method. Int. Rev. Phys. Chem. 2015, 34, 269–308. [Google Scholar] [CrossRef]
- Frantsuzov, P.A.; Mandelshtam, V.A. Quantum statistical mechanics with Gaussians: Equilibrium properties of van der Waals clusters. J. Chem. Phys. 2004, 121, 9247–9256. [Google Scholar] [CrossRef]
- Liu, J.; Miller, W.H. Using the thermal Gaussian approximation for the Boltzmann operator in semiclassical initial value time correlation functions. J. Chem. Phys. 2006, 125, 224104. [Google Scholar] [CrossRef]
- Liu, J.; Miller, W.H. An approach for generating trajectory-based dynamics which conserves the canonical distribution in the phase space formulation of quantum mechanics. I. Theories. J. Chem. Phys. 2011, 134, 104101. [Google Scholar] [CrossRef]
- Cartarius, H.; Pollak, E. Imaginary time Gaussian dynamics of the Ar3 cluster. J. Chem. Phys. 2011, 134, 044107. [Google Scholar] [CrossRef] [PubMed]
- Habershon, S.; Manolopoulos, D.E.; Markland, T.E.; Miller, T.F. Ring-polymer molecular dynamics: Quantum effects in chemical dynamics from classical trajectories in an extended phase space. Annu. Rev. Phys. Chem. 2013, 64, 387–413. [Google Scholar] [CrossRef] [PubMed]
- Craig, I.R.; Manolopoulos, D.E. Quantum statistics and classical mechanics: Real time correlation functions from ring polymer molecular dynamics. J. Chem. Phys. 2003, 121, 3368–3373. [Google Scholar] [CrossRef]
- Liu, J. Path integral Liouville dynamics for thermal equilibrium systems. J. Chem. Phys. 2014, 140, 224107. [Google Scholar] [CrossRef] [PubMed]
- Liu, J. Recent advances in the linearized semiclassical initial value representation/classical Wigner model for the thermal correlation function. Int. J. Quantum Chem. 2015, 115, 657–670. [Google Scholar] [CrossRef]
- Poulsen, J.A.; Nyman, G.; Rossky, P.J. Practical evaluation of condensed phase quantum correlation functions: A Feynman–Kleinert variational linearized path integral method. J. Chem. Phys. 2003, 119, 12179–12193. [Google Scholar] [CrossRef]
- Shi, Q.; Geva, E. Semiclassical theory of vibrational energy relaxation in the condensed phase. J. Phys. Chem. A 2003, 107, 9059–9069. [Google Scholar] [CrossRef]
- Liu, J.; Miller, W.H. Linearized semiclassical initial value time correlation functions using the thermal Gaussian approximation: Applications to condensed phase systems. J. Chem. Phys. 2007, 127, 114506. [Google Scholar] [CrossRef]
- MacLachlan, A.D. A variational solution of the time-dependent Schrodinger equation. Mol. Phys. 1964, 8, 39–44. [Google Scholar] [CrossRef]
- Poulsen, J.A. A variational principle in Wigner phase-space with applications to statistical mechanics. J. Chem. Phys. 2011, 134, 034118. [Google Scholar] [CrossRef]
- Poulsen, J.A.; Svensson, S.K.-M.; Nyman, G. Dynamics of Gaussian Wigner functions derived from a time-dependent variational principle. AIP Adv. 2017, 7, 115018. [Google Scholar] [CrossRef]
- Smith, K.K.G.; Poulsen, J.; Nyman, G.; Rossky, P.J. A New Class of Ensemble Conserving Algorithms for Approximate Quantum Dynamics: Theoretical Formulation and Model Problems. J. Chem. Phys. 2015, 142, 244112. [Google Scholar] [CrossRef]
- Shalashilin, D.V.; Child, M.S. Multidimensional quantum propagation with the help of coupled coherent states. J. Chem. Phys. 2001, 115, 5367–5375. [Google Scholar] [CrossRef]
- Liu, J. Two more approaches for generating trajectory-based dynamics which conserves the canonical distribution in the phase space formulation of quantum mechanics. J. Chem. Phys. 2011, 134, 194110. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Miller, W.H. An approach for generating trajectory-based dynamics which conserves the canonical distribution in the phase space formulation of quantum mechanics. II. Thermal correlation functions. J. Chem. Phys. 2011, 134, 104102. [Google Scholar] [CrossRef]
- Poulsen, J.; Nyman, G.; Rossky, P.J. Feynman-Kleinert Linearized Path Integral (FK-LPI) Algorithms for Quantum Molecular Dynamics, with Application to Water and He(4). J. Chem. Theory Comput. 2006, 2, 1482–1491. [Google Scholar] [CrossRef]
- Markovic, N.; Poulsen, J. A linearized path integral description of the collision process between a water molecule and a graphite surface. J. Phys. Chem. A 2008, 112, 1701–1711. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poulsen, J.A.; Nyman, G. Finite-Temperature Correlation Functions Obtained from Combined Real- and Imaginary-Time Propagation of Variational Thawed Gaussian Wavepackets. Entropy 2024, 26, 412. https://doi.org/10.3390/e26050412
Poulsen JA, Nyman G. Finite-Temperature Correlation Functions Obtained from Combined Real- and Imaginary-Time Propagation of Variational Thawed Gaussian Wavepackets. Entropy. 2024; 26(5):412. https://doi.org/10.3390/e26050412
Chicago/Turabian StylePoulsen, Jens Aage, and Gunnar Nyman. 2024. "Finite-Temperature Correlation Functions Obtained from Combined Real- and Imaginary-Time Propagation of Variational Thawed Gaussian Wavepackets" Entropy 26, no. 5: 412. https://doi.org/10.3390/e26050412





