Complex Networks and Interacting Particle Systems
Abstract
:1. Introduction
2. Methods and Experiments
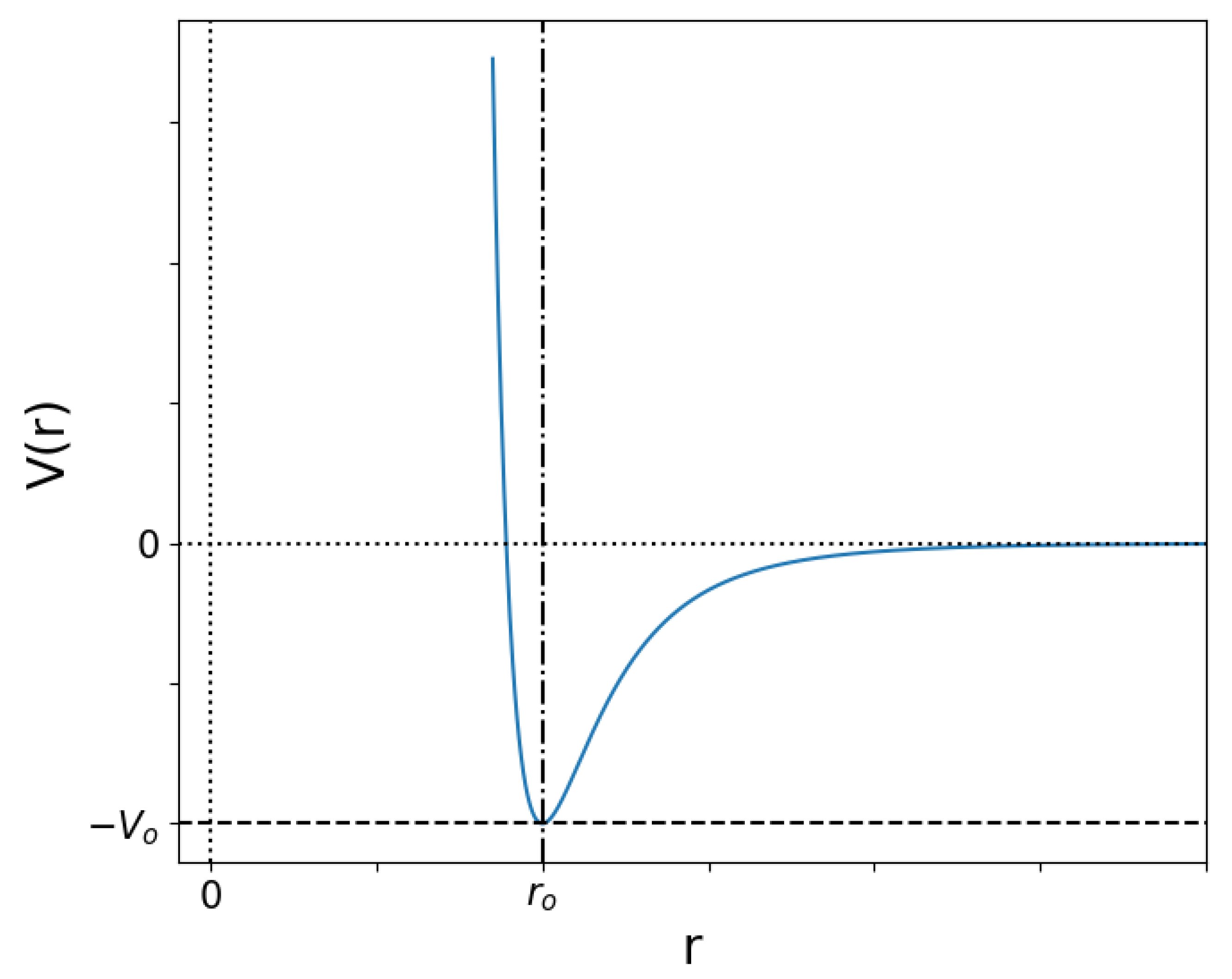
2.1. Lennard-Jones Potential
2.2. Network Construction and Stability
3. Results and Discussion
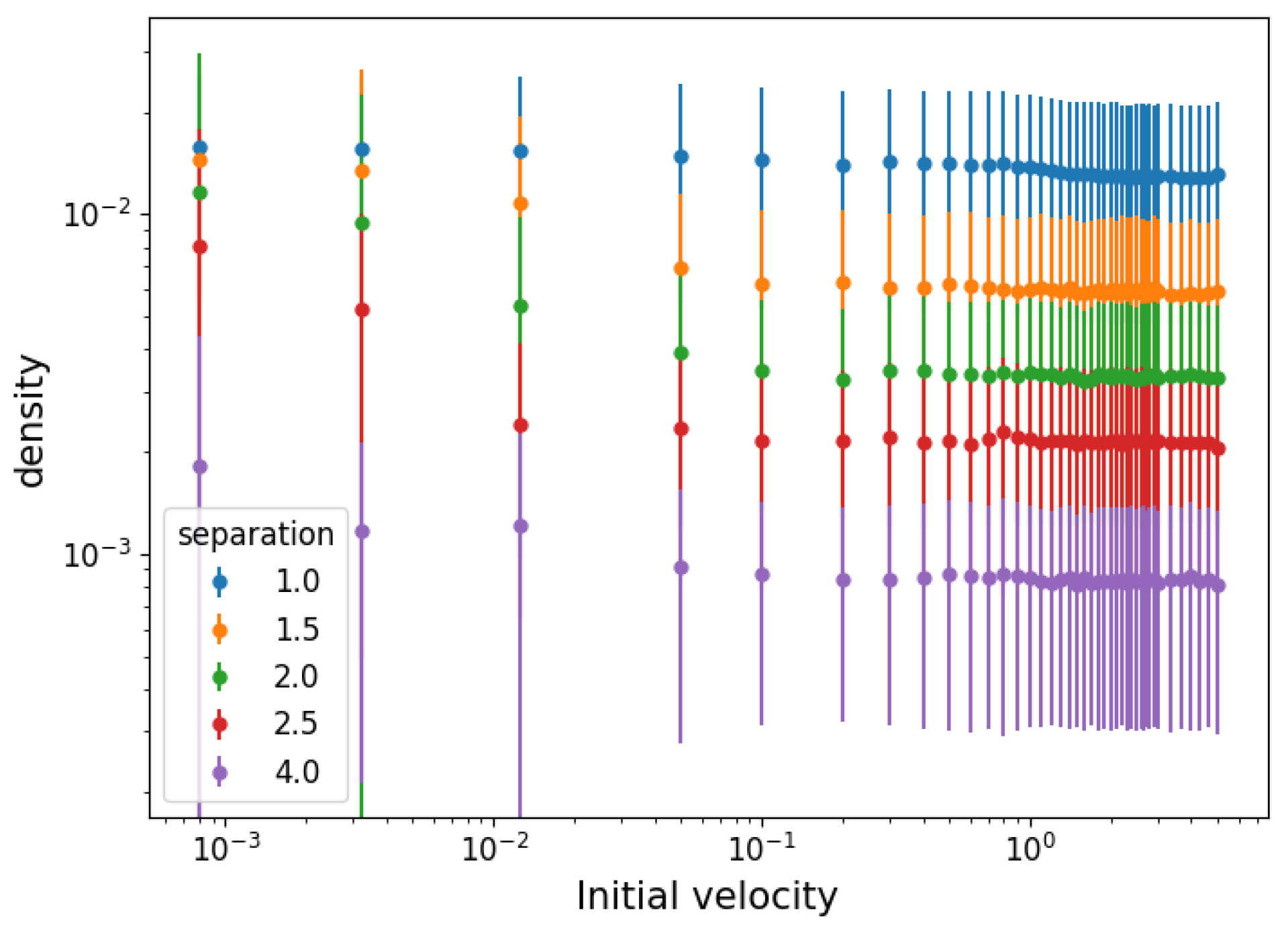
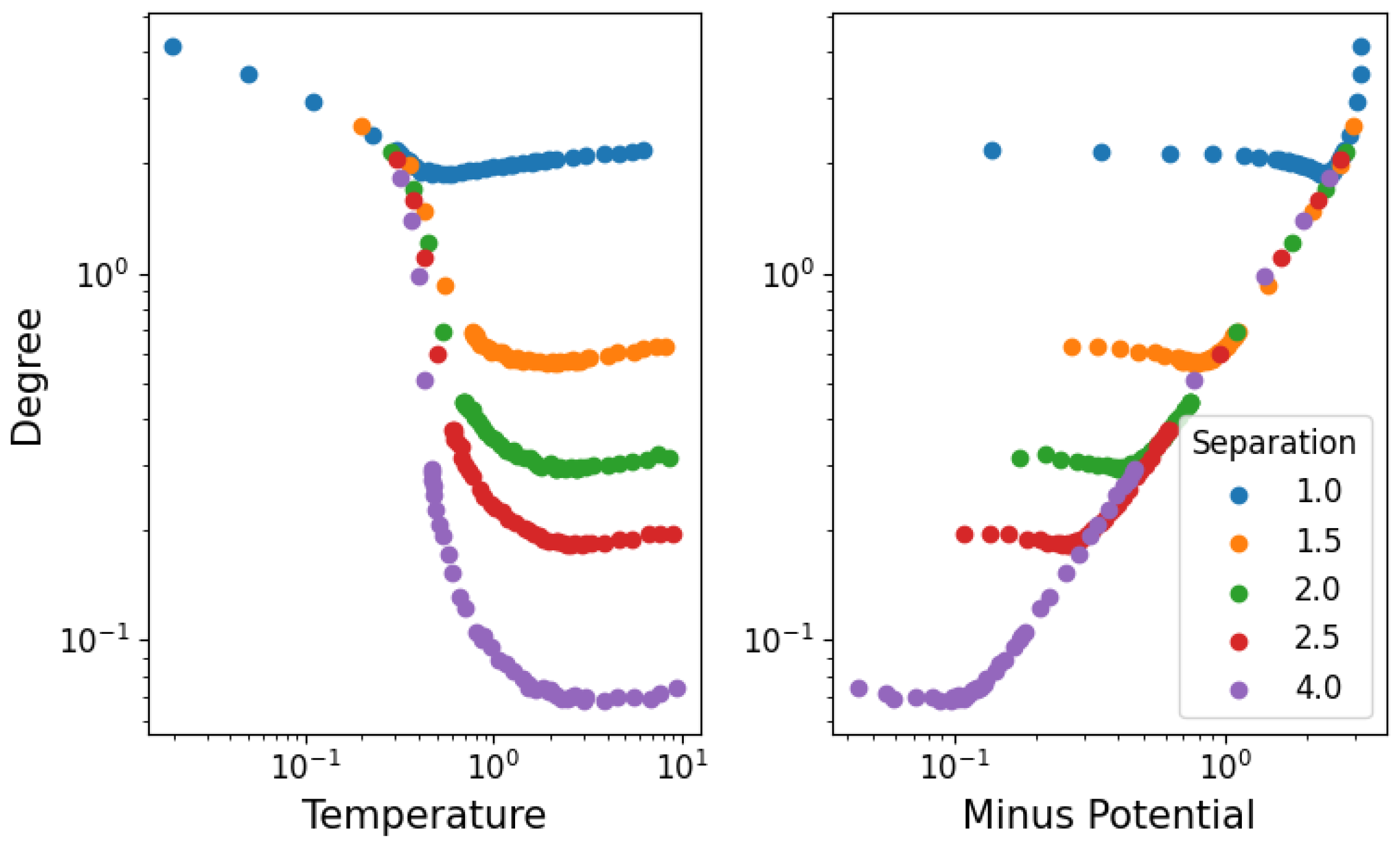
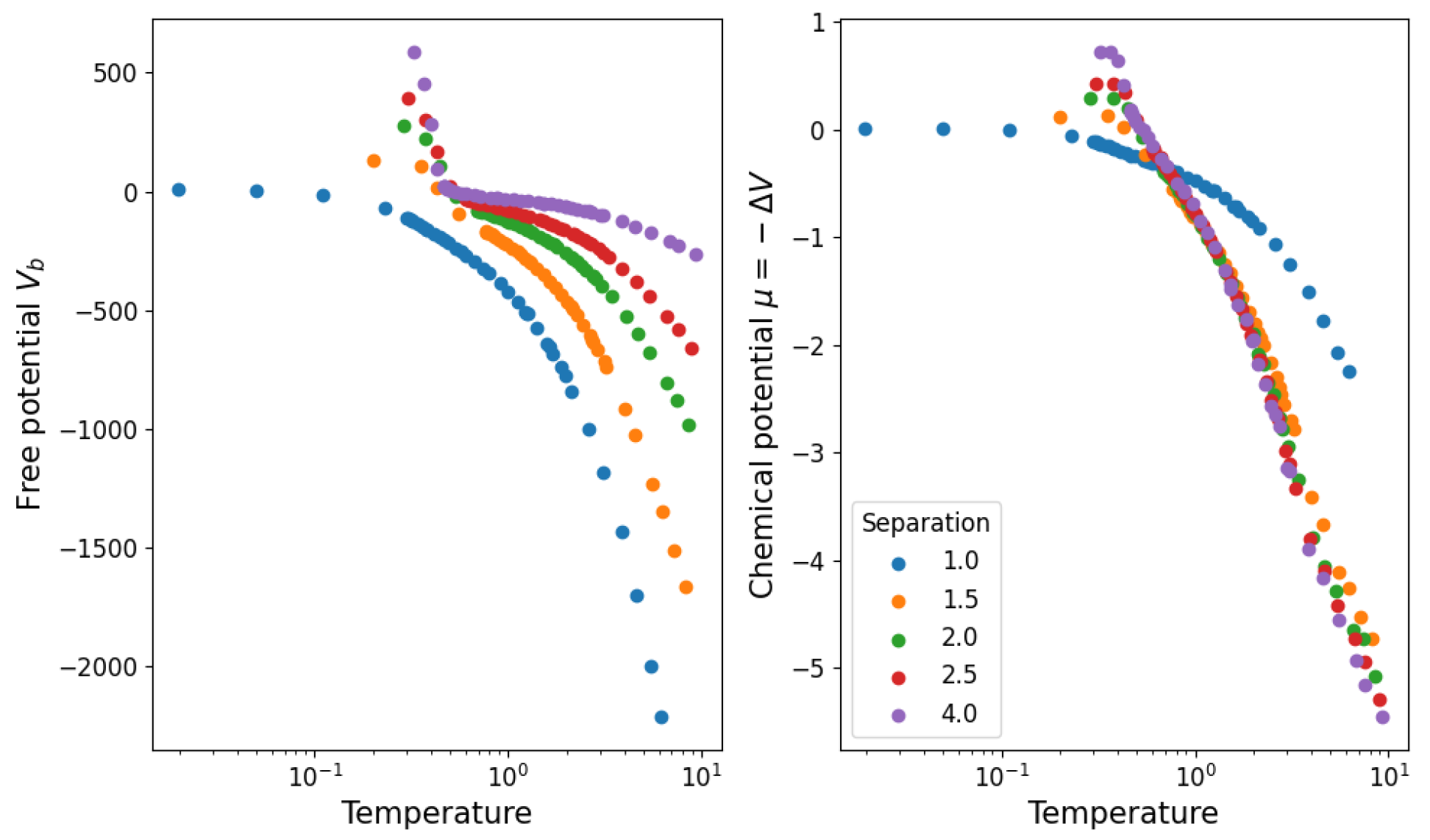
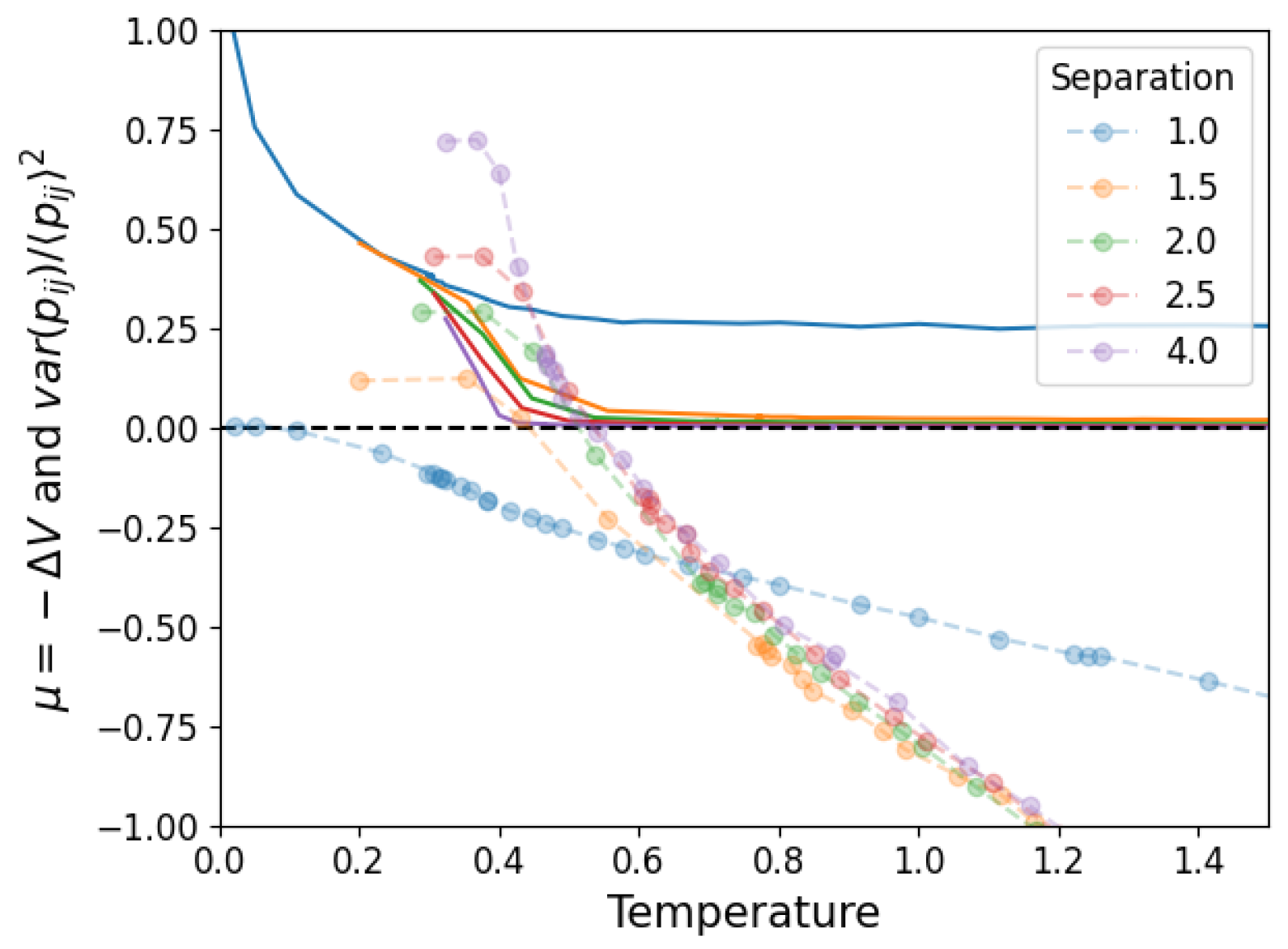
3.1. Temperature and Density
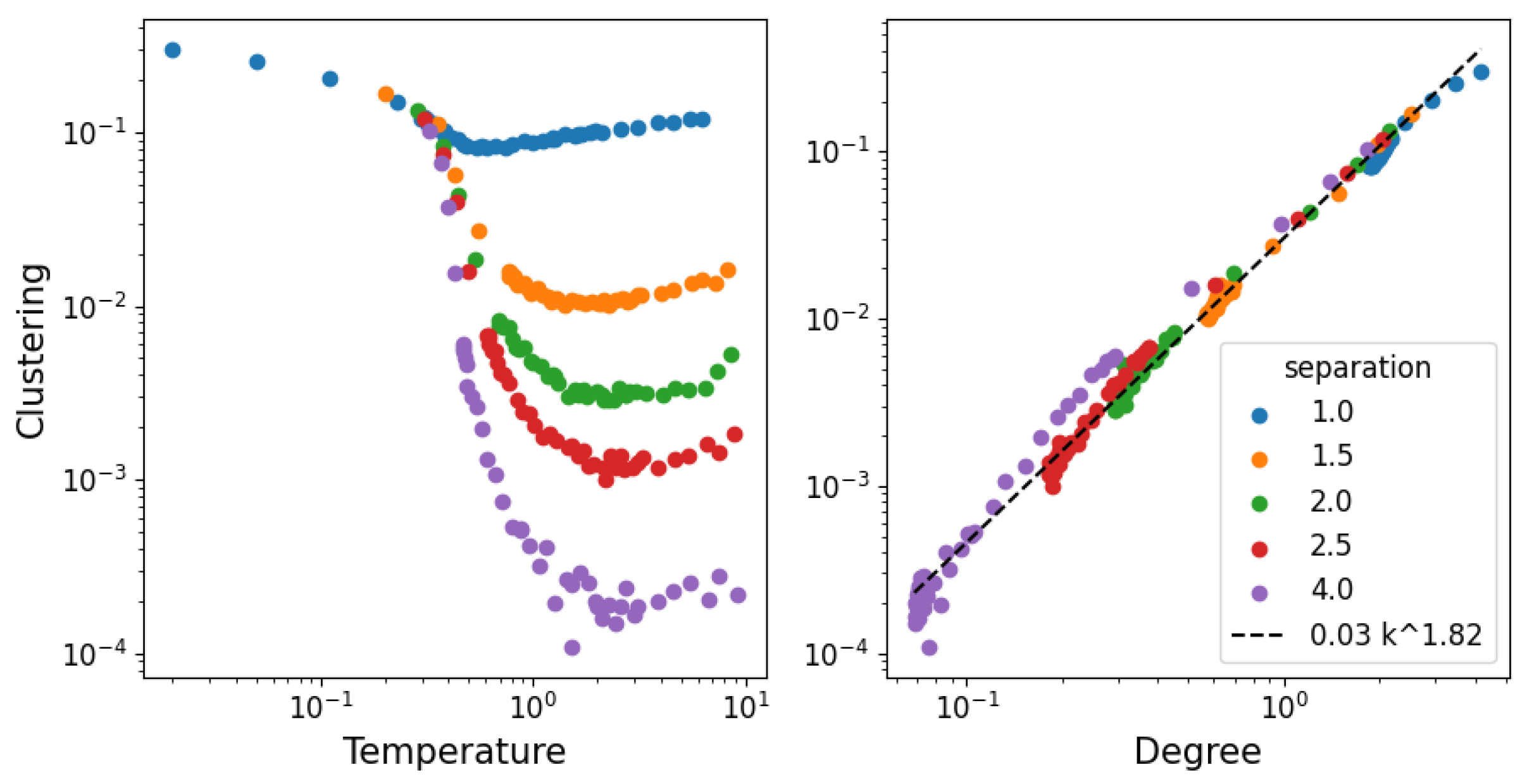
3.2. Network Properties
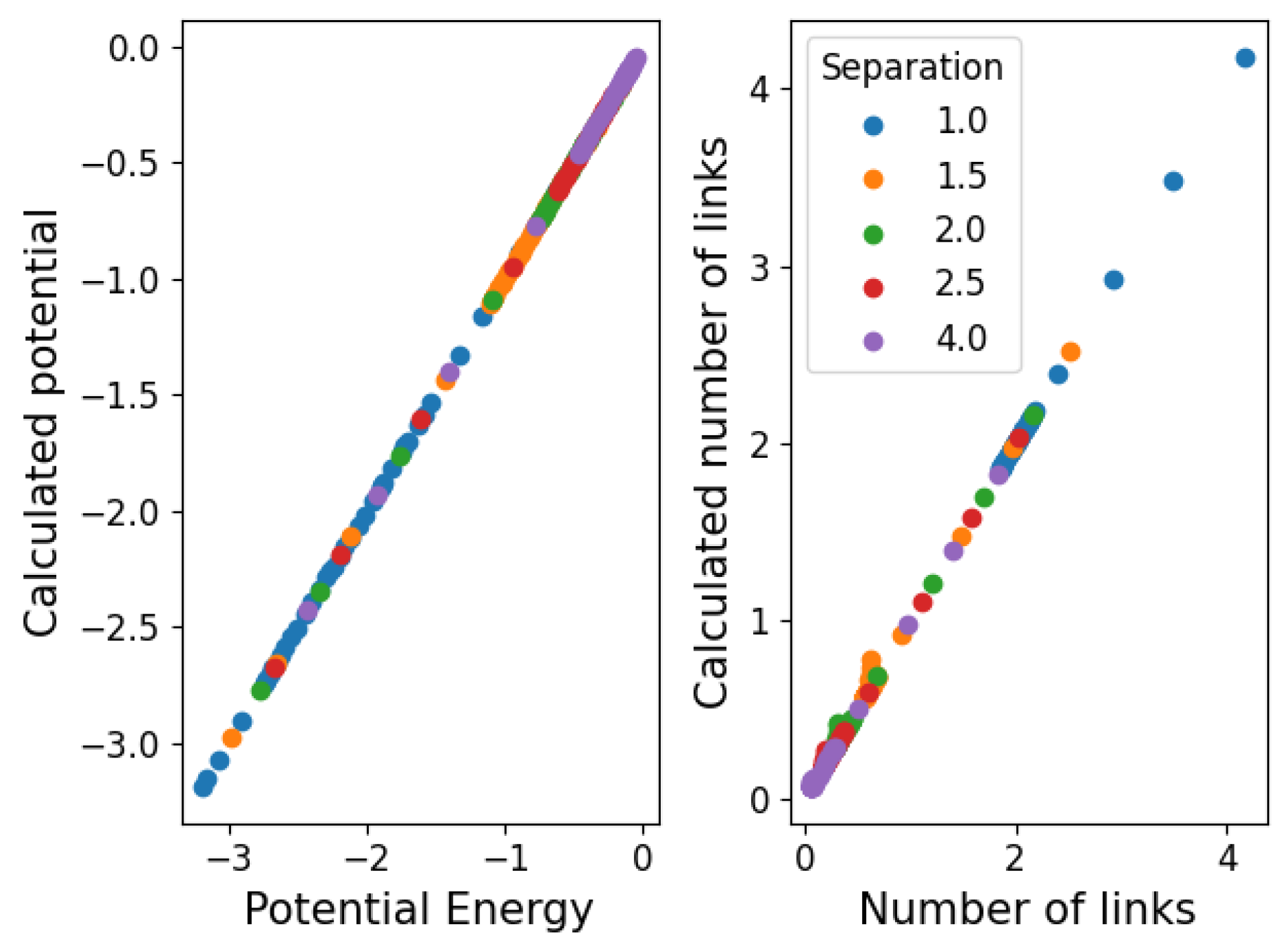
3.3. Structural Stability
4. Conclusions and Further Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. System Partition Function
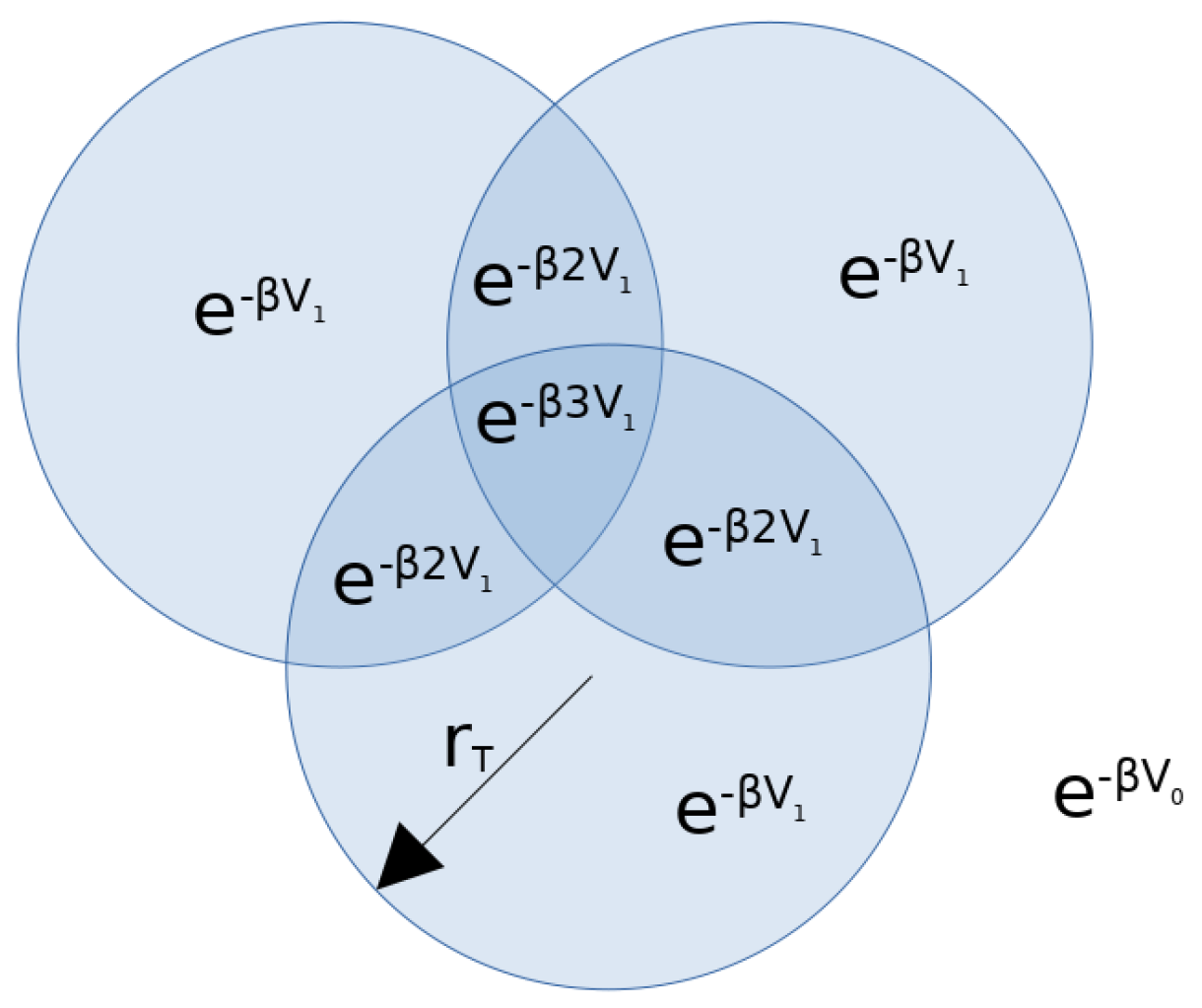
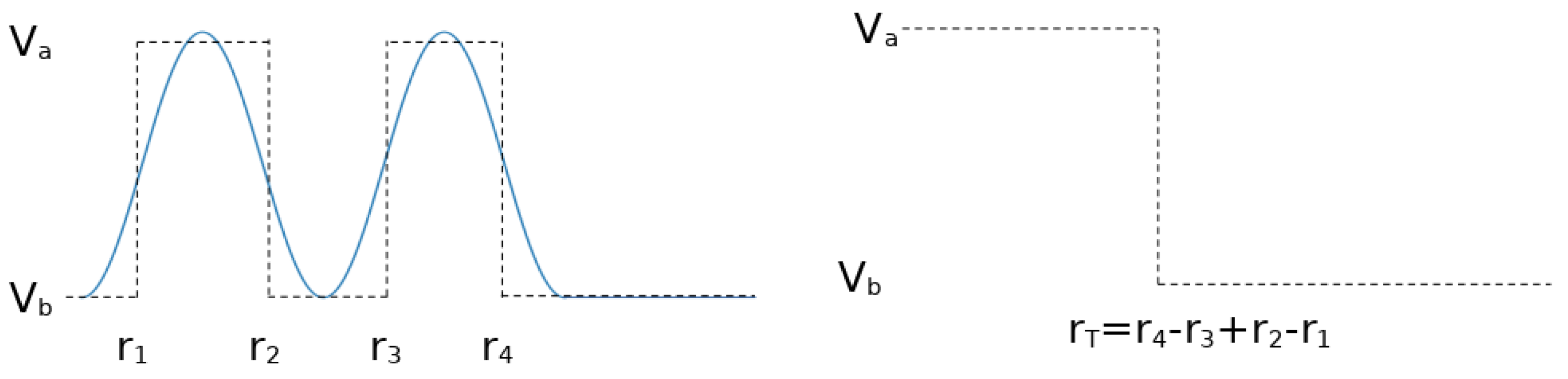
Appendix B. Beyond the Lennard-Jones Potential and Binary Networks
References
- Van Steen, M. Graph theory and complex networks. Introduction 2010, 144, 1–287. [Google Scholar]
- Reichardt, J. Introduction to complex networks. In Structure in Complex Networks. Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–11. [Google Scholar]
- Estrada, E. Introduction to complex networks: Structure and dynamics. In Evolutionary Equations with Applications in Natural Sciences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 93–131. [Google Scholar]
- Wen, T.; Cheong, K.H. The fractal dimension of complex networks: A review. Inf. Fusion 2021, 73, 87–102. [Google Scholar] [CrossRef]
- Juszczyszyn, K.; Musial, A.; Musial, K.; Bródka, P. Molecular dynamics modelling of the temporal changes in complex networks. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 553–559. [Google Scholar]
- Ozkanlar, A.; Clark, A.E. ChemNetworks: A complex network analysis tool for chemical systems. J. Comput. Chem. 2014, 35, 495–505. [Google Scholar] [CrossRef] [PubMed]
- Amamoto, Y.; Kojio, K.; Takahara, A.; Masubuchi, Y.; Ohnishi, T. Complex network representation of the structure-mechanical property relationships in elastomers with heterogeneous connectivity. Patterns 2020, 1, 100135. [Google Scholar] [CrossRef]
- García-Sánchez, M.; Jiménez-Serra, I.; Puente-Sánchez, F.; Aguirre, J. The emergence of interstellar molecular complexity explained by interacting networks. Proc. Natl. Acad. Sci. USA 2022, 119, e2119734119. [Google Scholar] [CrossRef] [PubMed]
- Hann, M.M.; Leach, A.R.; Harper, G. Molecular complexity and its impact on the probability of finding leads for drug discovery. J. Chem. Inf. Comput. Sci. 2001, 41, 856–864. [Google Scholar] [CrossRef] [PubMed]
- Goodby, J.W.; Saez, I.M.; Cowling, S.J.; Gasowska, J.S.; MacDonald, R.A.; Sia, S.; Watson, P.; Toyne, K.J.; Hird, M.; Lewis, R.A.; et al. Molecular complexity and the control of self-organising processes. Liq. Cryst. 2009, 36, 567–605. [Google Scholar] [CrossRef]
- Bertz, S.H. The first general index of molecular complexity. J. Am. Chem. Soc. 1981, 103, 3599–3601. [Google Scholar] [CrossRef]
- Böttcher, T. An additive definition of molecular complexity. J. Chem. Inf. Model. 2016, 56, 462–470. [Google Scholar] [CrossRef]
- Milano, M.; Agapito, G.; Cannataro, M. Challenges and limitations of biological network analysis. BioTech 2022, 11, 24. [Google Scholar] [CrossRef]
- Rodríguez, F.Y.; Muñuzuri, A.P. A Goodwin Model Modification and Its Interactions in Complex Networks. Entropy 2023, 25, 894. [Google Scholar] [CrossRef] [PubMed]
- Watts, A. A dynamic model of network formation. Games Econ. Behav. 2001, 34, 331–341. [Google Scholar] [CrossRef]
- Chandrasekhar, A. Econometrics of network formation. In The Oxford Handbook of the Economics of Networks; Oxford University Press: Oxford, UK, 2016; pp. 303–357. [Google Scholar]
- Barzel, B.; Barabási, A.L. Universality in network dynamics. Nat. Phys. 2013, 9, 673–681. [Google Scholar] [CrossRef]
- Cameron, M.; Vanden-Eijnden, E. Flows in complex networks: Theory, algorithms, and application to Lennard–Jones cluster rearrangement. J. Stat. Phys. 2014, 156, 427–454. [Google Scholar] [CrossRef]
- Forman, Y.; Cameron, M. Modeling aggregation processes of Lennard-Jones particles via stochastic networks. J. Stat. Phys. 2017, 168, 408–433. [Google Scholar] [CrossRef]
- Kasatkin, D.V.; Nekorkin, V.I. Transient Phase Clusters in a Two-Population Network of Kuramoto Oscillators with Heterogeneous Adaptive Interaction. Entropy 2023, 25, 913. [Google Scholar] [CrossRef] [PubMed]
- Kardar, M. Statistical Physics of Particles; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Martyushev, L.M. Maximum entropy production principle: History and current status. Phys.-Uspekhi 2021, 64, 558. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production as an inference algorithm that translates physical assumptions into macroscopic predictions: Don’t shoot the messenger. Entropy 2009, 11, 931–944. [Google Scholar] [CrossRef]
- Hut, P.; Makino, J.; McMillan, S. Building a better leapfrog. Astrophys. J. 1995, 443, L93–L96. [Google Scholar] [CrossRef]
- Park, J.; Newman, M.E. Statistical mechanics of networks. Phys. Rev. E 2004, 70, 066117. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Smil, V. Energy in Nature and Society: General Energetics of Complex Systems; MIT press: Cambridge, MA, USA, 2007. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abadi, N.; Ruzzenenti, F. Complex Networks and Interacting Particle Systems. Entropy 2023, 25, 1490. https://doi.org/10.3390/e25111490
Abadi N, Ruzzenenti F. Complex Networks and Interacting Particle Systems. Entropy. 2023; 25(11):1490. https://doi.org/10.3390/e25111490
Chicago/Turabian StyleAbadi, Noam, and Franco Ruzzenenti. 2023. "Complex Networks and Interacting Particle Systems" Entropy 25, no. 11: 1490. https://doi.org/10.3390/e25111490
APA StyleAbadi, N., & Ruzzenenti, F. (2023). Complex Networks and Interacting Particle Systems. Entropy, 25(11), 1490. https://doi.org/10.3390/e25111490





