Multi-Objective Optimization of the Basic and Regenerative ORC Integrated with Working Fluid Selection
Abstract
:1. Introduction
2. System Description
- The proposed system operates at a steady state;
- The maximum evaporation pressure is restricted below 90% of the working fluid critical pressure to ensure the safe operation of the ORC system;
- The ambient pressure and temperature are 101.3 kPa and 293.15 K, which is the reference state for the exergy analysis;
- The isentropic efficiencies of the expander and pump are assumed as 0.85;
- The heat exchangers are treated as externally adiabatic devices.
3. Mathematical Model
3.1. Thermodynamic Analysis
3.2. Thermo-Economic Analysis
3.3. Heat Exchanger Model
3.4. Working Fluid Selection and Multi-Objective Optimization with NSGA-II
3.4.1. Multi-Objective Optimization with NSGA-II
3.4.2. Decision-Making with TOPSIS
3.4.3. Working Fluid Selection Integrated with NSGA-II
4. Results and Discussion
4.1. Pareto Frontier Solutions of the BORC System
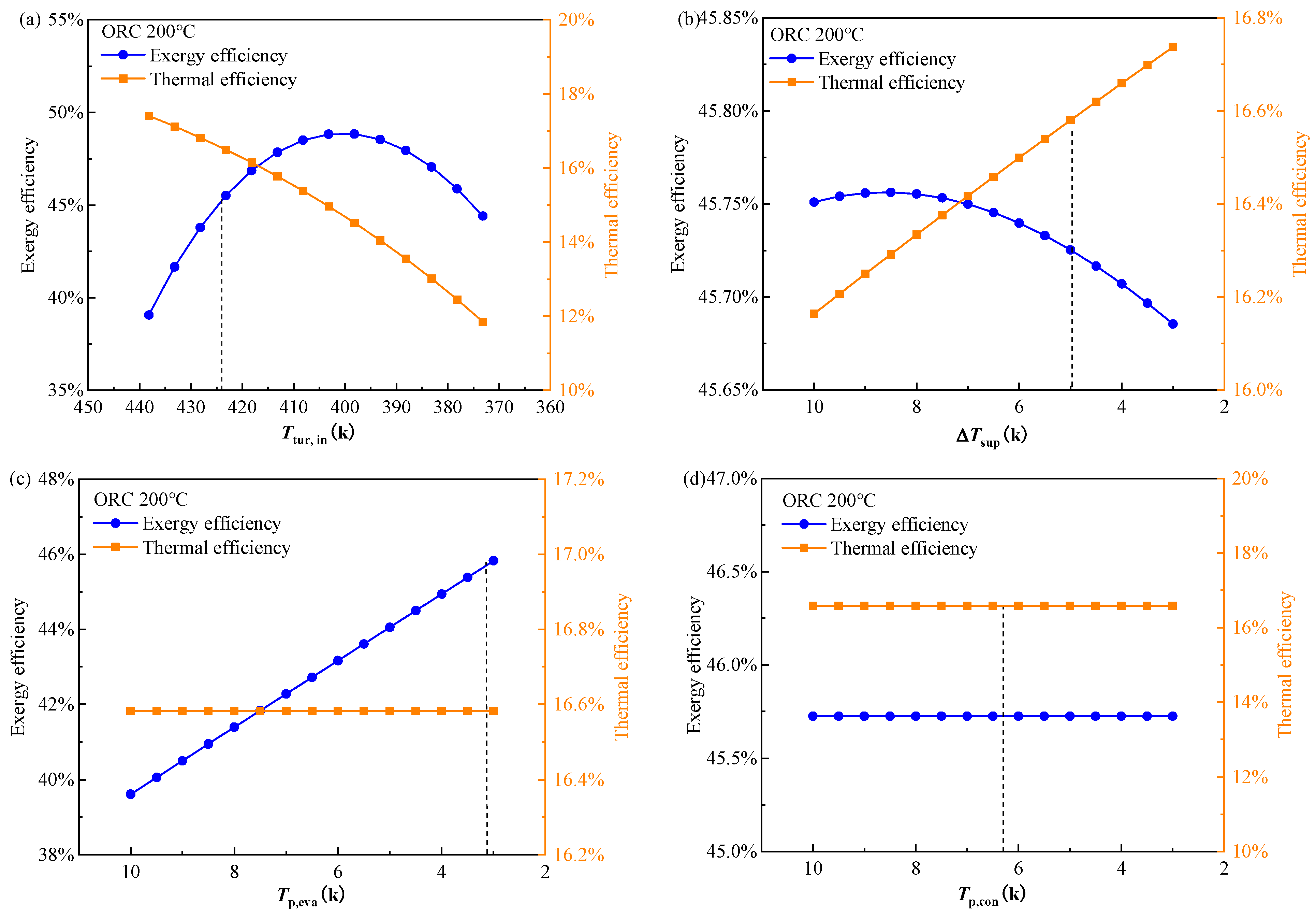
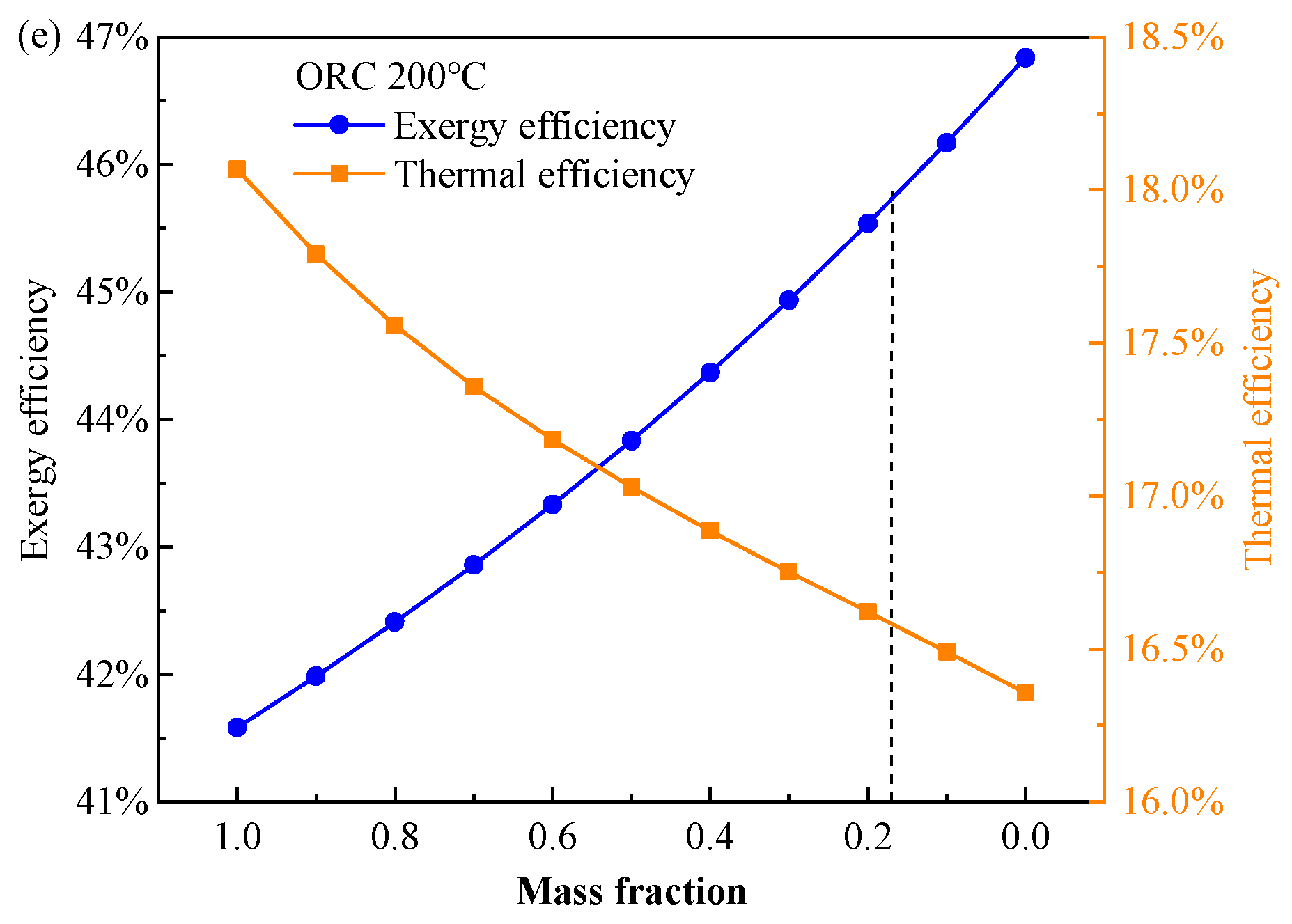
4.1.1. Pareto Frontier Solutions and Effect of Objectives on the Working Fluid Selection
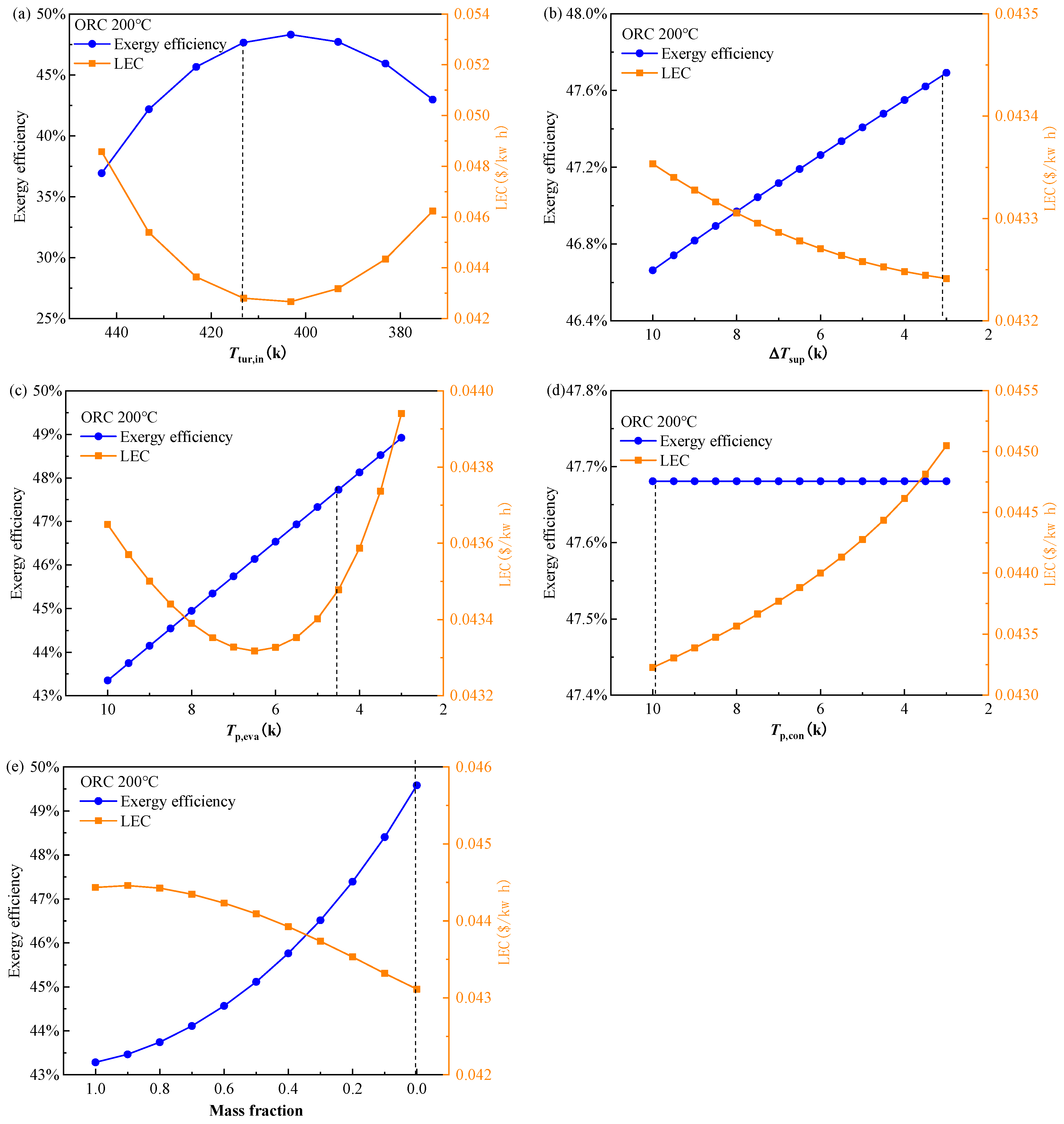
4.1.2. Parametric Analysis of the Decision Variables
4.2. Pareto Frontier Solutions of the RORC System
4.2.1. Pareto Frontier Solutions
4.2.2. Parametric Analysis of the Decision Variables
5. Conclusions
- (1)
- The selection of working fluid and multi-objective optimization of the cycle parameters could be realized simultaneously by parameterizing pure working fluids into arrays of numbers. Several types of the working fluid, pure or mixed, are presented on the Pareto frontier;
- (2)
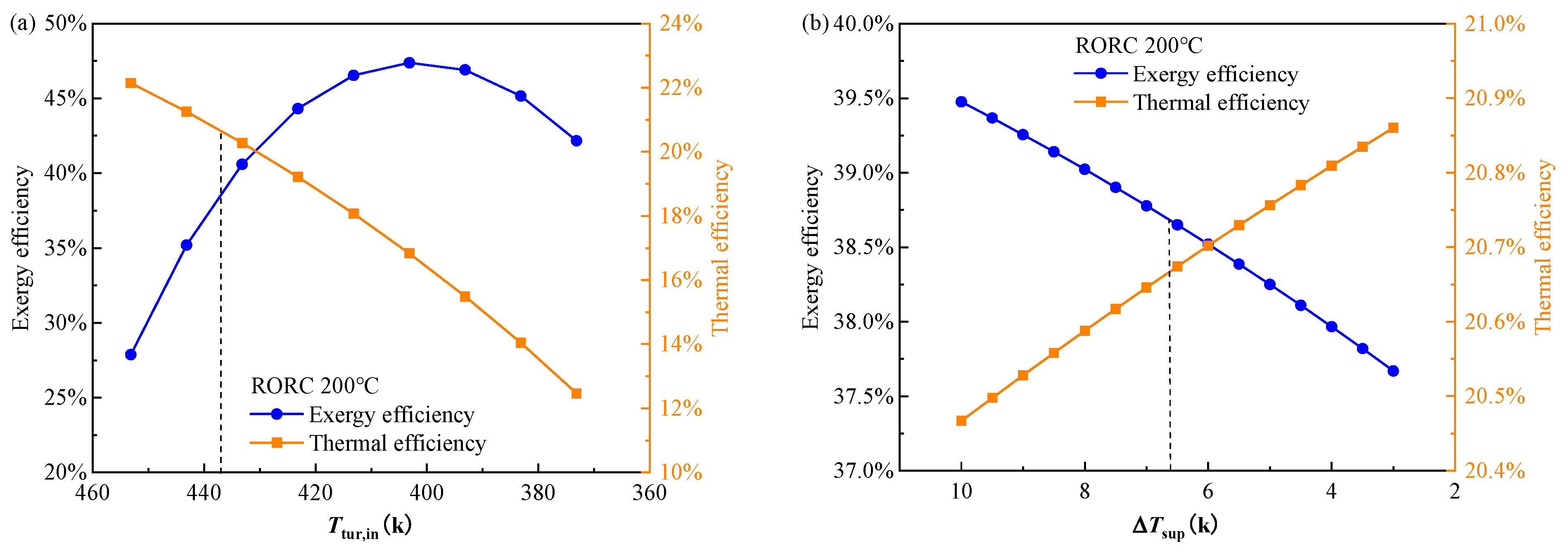
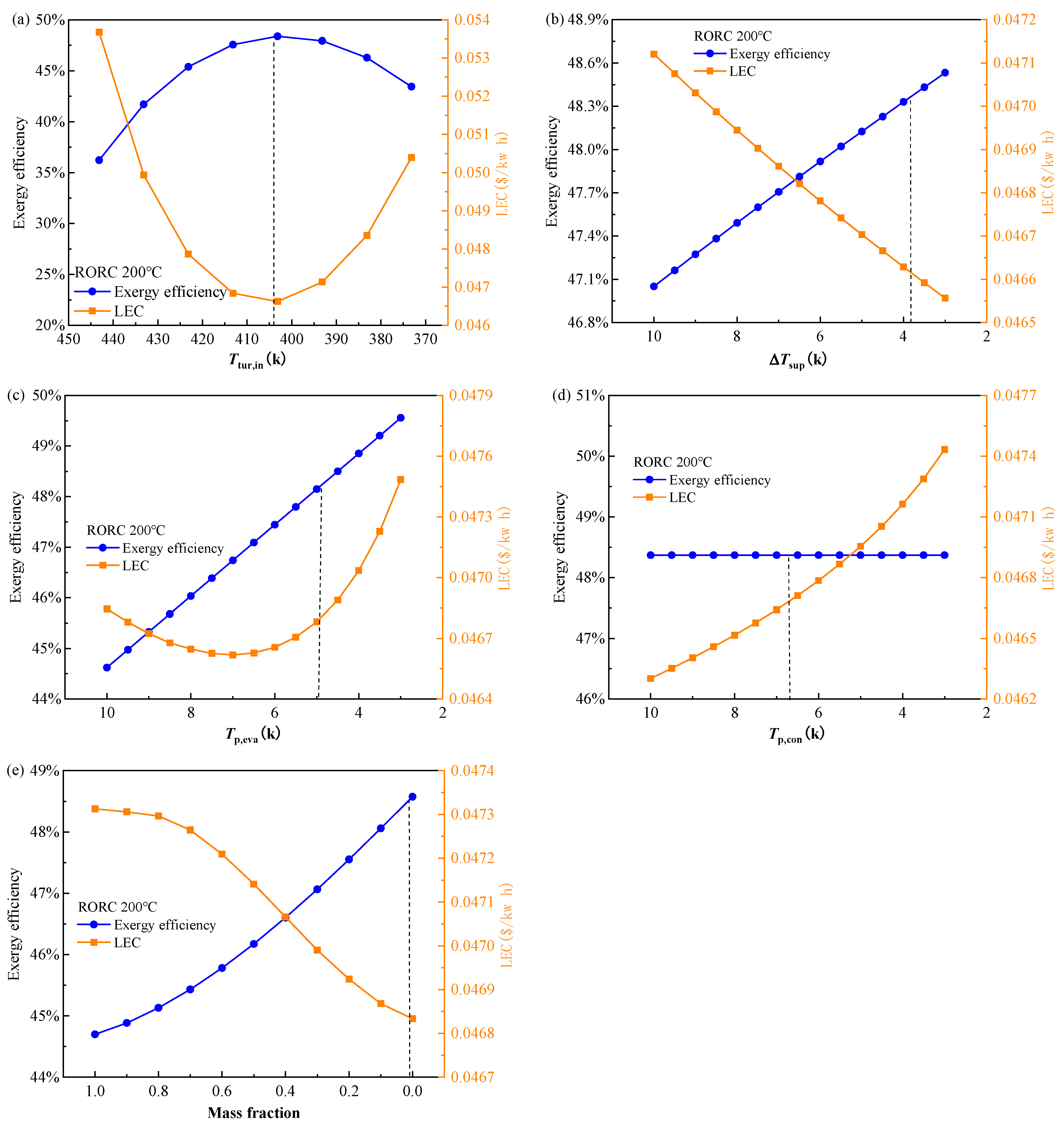
- The turbine inlet temperature is the most effective factor for both the BORC and RORC systems while the other four decision variable has quite limited influence on the objectives. The nonlinear relation between the exergy efficiency and the turbine inlet temperature is observed;
- (3)
- The decision variables mainly impose a reverse effect on the exergy efficiency and thermal efficiency while the exergy efficiency and LEC exhibit quite a weak conflict with each other. This makes the binary objective optimization tend to be a single objective optimization when the objectives are set as exergy efficiency and LEC;
- (4)
- The RORC with an IHE can provide higher thermal efficiency than ORC at the same exergy efficiency while the LEC of the RORC system also becomes higher because the bare module cost of buying one more heat exchange for the RORC is higher than the cost reduction contributed to the reduced heat transfer area;
- (5)
- The Pareto frontier solution is distributed in similar trends at different heat source temperatures. Under the heat source temperature of 423.15 K, the final obtained exergy efficiency and thermal efficiencies are 45.6% and 16.6% for BORC, and 38.6% and 20.7% for RORC, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | ) |
| boiling number | |
| cost ($) | |
| capital recovery cost | |
| diameter of the heat exchanger tube (m) | |
| exergy (kw) | |
| bare module factor | |
| material factor | |
| pressure factor | |
| h | specific enthalpy (kJ/kg) |
| K) | |
| levelized energy cost ($/kWh) | |
| mass flow rate (kg/s) | |
| Nusselt number | |
| pressure (kPa) | |
| Prandtl number | |
| energy (kW) | |
| Reynolds number | |
| specific entropy (kJ/kg K) | |
| temperature (K) | |
| operation hour (h) | |
| W | power (kW) |
| Greek Symbols | |
| K) | |
| Heat conductivity (W/m K) | |
| efficiency | |
| condensation temperature glide (K) | |
| boiling process temperature glide (K) | |
| ) | |
| Subscript | |
| 0 | environment, in equilibrium with the environment |
| con | condensation, condenser |
| eva | evaporator |
| h | heatsource |
| in | inlet |
| net | Net |
| o | outlet |
| p | pinch point temperature difference |
| pump | pump |
| reg | regenerator |
| s | isentropic |
| sup | degree of superheat |
| tur | turbine |
| v | vapor |
| wf | working fluid |
References
- Tung, T.C.; Shai, T.Y.; Wang, S.K. A review of organic Rankine cycles (ORCs) for the recovery of low-grade waste heat. Energy 1997, 22, 661–667. [Google Scholar] [CrossRef]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N.; Mirhadizadeh, S.A. Review of organic Rankine cycle for small-scale applications. Energy Convers. Manag. 2017, 134, 135–155. [Google Scholar] [CrossRef]
- Miao, Z.; Xu, J.; Yang, X.; Zou, J. Operation and performance of a low temperature organic Rankine cycle. Appl. Therm. Eng. 2015, 75, 1065–1075. [Google Scholar] [CrossRef]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar] [CrossRef]
- He, C.; Liu, C.; Gao, H.; Xie, H.; Li, Y.; Wu, S.; Xu, J. The optimal evaporation temperature and working fluids for subcritical organic Rankine cycle. Energy 2012, 38, 136–143. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Galanis, N.; Nazari, F.; Basiri Parsa, A.; Shamekhi, L. Parametric analysis and optimization of regenerative Clausius and organic Rankine cycles with two feedwater heaters using artificial bees colony and artificial neural network. Energy 2011, 36, 5728–5740. [Google Scholar] [CrossRef]
- Gholamian, E.; Habibollahzade, A.; Zare, V. Development and multi-objective optimization of geothermal-based organic Rankine cycle integrated with thermoelectric generator and proton exchange membrane electrolyzer for power and hydrogen production. Energy Convers. Manag. 2018, 174, 112–125. [Google Scholar] [CrossRef]
- Yang, S.-C.; Hung, T.-C.; Feng, Y.-Q.; Wu, C.-J.; Wong, K.-W.; Huang, K.-C. Experimental investigation on a 3 kW organic Rankine cycle for low-grade waste heat under different operation parameters. Appl. Therm. Eng. 2017, 113, 756–764. [Google Scholar] [CrossRef]
- Pei, G.; Li, J.; Li, Y.; Wang, D.; Ji, J. Construction and dynamic test of a small-scale organic Rankine cycle. Energy 2011, 36, 3215–3223. [Google Scholar] [CrossRef]
- Quoilin, S.; Lemort, V.; Lebrun, J. Experimental study and modeling of an Organic Rankine Cycle using scroll expander. Appl. Energy 2010, 87, 1260–1268. [Google Scholar] [CrossRef]
- Miao, Z.; Xu, J.; Zhang, K. Experimental and modeling investigation of an organic Rankine cycle system based on the scroll expander. Energy 2017, 134, 35–49. [Google Scholar] [CrossRef]
- Györke, G.; Deiters, U.K.; Groniewsky, A.; Lassu, I.; Imre, A.R. Novel classification of pure working fluids for Organic Rankine Cycle. Energy 2018, 145, 288–300. [Google Scholar] [CrossRef]
- Ayachi, F.; Ksayer, E.B.; Zoughaib, A.; Neveu, P. ORC optimization for medium grade heat recovery. Energy 2014, 68, 47–56. [Google Scholar] [CrossRef]
- Hærvig, J.; Sørensen, K.; Condra, T.J. Guidelines for optimal selection of working fluid for an organic Rankine cycle in relation to waste heat recovery. Energy 2016, 96, 592–602. [Google Scholar] [CrossRef]
- Vetter, C.; Wiemer, H.-J.; Kuhn, D. Comparison of sub- and supercritical Organic Rankine Cycles for power generation from low-temperature/low-enthalpy geothermal wells, considering specific net power output and efficiency. Appl. Therm. Eng. 2013, 51, 871–879. [Google Scholar] [CrossRef]
- Zhai, H.; An, Q.; Shi, L. Analysis of the quantitative correlation between the heat source temperature and the critical temperature of the optimal pure working fluid for subcritical organic Rankine cycles. Appl. Therm. Eng. 2016, 99, 383–391. [Google Scholar] [CrossRef]
- Zhao, L.; Bao, J. Thermodynamic analysis of organic Rankine cycle using zeotropic mixtures. Appl. Energy 2014, 130, 748–756. [Google Scholar] [CrossRef]
- Miao, Z.; Li, Z.; Zhang, K.; Xu, J.; Cheng, Y. Selection criteria of zeotropic mixtures for subcritical organic Rankine cycle based on thermodynamic and thermo-economic analysis. Appl. Therm. Eng. 2020, 180, 115837. [Google Scholar] [CrossRef]
- Miao, Z.; Zhang, K.; Wang, M.X.; Xu, J.L. Thermodynamic selection criteria of zeotropic mixtures for subcritical organic Rankine cycle. Energy 2019, 167, 484–497. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Li, M.; Xia, J.; Dai, Y. Multi-objective optimization design of condenser in an organic Rankine cycle for low grade waste heat recovery using evolutionary algorithm. Int. Commun. Heat Mass Transf. 2013, 45, 47–54. [Google Scholar] [CrossRef]
- Wang, L.; Bu, X.; Li, H. Multi-objective optimization and off-design evaluation of organic Rankine cycle (ORC) for low-grade waste heat recovery. Energy 2020, 203, 117809. [Google Scholar] [CrossRef]
- Martinez-Gomez, J.; Pena-Lamas, J.; Martin, M.; Ponce-Ortega, J.M. A multi-objective optimization approach for the selection of working fluids of geothermal facilities: Economic, environmental and social aspects. J. Environ. Manag. 2017, 203, 962–972. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Gao, L.; Ye, Z.; Hwang, Y.; Chen, J. Binary-objective optimization of latest low-GWP alternatives to R245fa for organic Rankine cycle application. Energy 2021, 217, 119336. [Google Scholar] [CrossRef]
- Hu, S.; Li, J.; Yang, F.; Yang, Z.; Duan, Y. Multi-objective optimization of organic Rankine cycle using hydrofluorolefins (HFOs) based on different target preferences. Energy 2020, 203, 117848. [Google Scholar] [CrossRef]
- Fergani, Z.; Morosuk, T.; Touil, D. Exergy-Based Multi-Objective Optimization of an Organic Rankine Cycle with a Zeotropic Mixture. Entropy 2021, 23, 954. [Google Scholar] [CrossRef]
- Xia, X.X.; Wang, Z.Q.; Zhou, N.J.; Hu, Y.H.; Zhang, J.P.; Chen, Y. Working fluid selection of dual-loop organic Rankine cycle using multi-objective optimization and improved grey relational analysis. Appl. Therm. Eng. 2020, 171, 115028. [Google Scholar] [CrossRef]
- Sadeghi, M.; Nemati, A.; Ghavimi, A.; Yari, M. Thermodynamic analysis and multi-objective optimization of various ORC (organic Rankine cycle) configurations using zeotropic mixtures. Energy 2016, 109, 791–802. [Google Scholar] [CrossRef]
- Groniewsky, A.; Wagner, C. Investigation of the Effect of the Regenerative Heat Exchanger on the Performance of Organic Rankine Cycles Using Perturbed Chain–Statistical Associating Fluid Theory Equation of State. Ind. Eng. Chem. Res. 2020, 59, 19643–19656. [Google Scholar] [CrossRef]
- Nondy, J.; Gogoi, T.K. Exergoeconomic investigation and multi-objective optimization of different ORC configurations for waste heat recovery: A comparative study. Energy Convers. Manag. 2021, 245, 114593. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Comparison between regenerative organic Rankine cycle (RORC) and basic organic Rankine cycle (BORC) based on thermoeconomic multi-objective optimization considering exergy efficiency and levelized energy cost (LEC). Energy Convers. Manag. 2015, 96, 58–71. [Google Scholar] [CrossRef]
- Hou, S.; Cao, S.; Yu, L.; Zhou, Y.; Wu, Y.; Zhang, F. Performance optimization of combined supercritical CO2 recompression cycle and regenerative organic Rankine cycle using zeotropic mixture fluid. Energy Convers. Manag. 2018, 166, 187–200. [Google Scholar] [CrossRef]
- Sadeghi, M.; Chitsaz, A.; Marivani, P.; Yari, M.; Mahmoudi, S.M.S. Effects of thermophysical and thermochemical recuperation on the performance of combined gas turbine and organic Rankine cycle power generation system: Thermoeconomic comparison and multi-objective optimization. Energy 2020, 210, 118551. [Google Scholar] [CrossRef]
- Safder, U.; Ifaei, P.; Yoo, C. Multi-objective optimization and flexibility analysis of a cogeneration system using thermorisk and thermoeconomic analyses. Energy Convers. Manag. 2018, 166, 602–636. [Google Scholar] [CrossRef]
- Kazemi, N.; Samadi, F. Thermodynamic, economic and thermo-economic optimization of a new proposed organic Rankine cycle for energy production from geothermal resources. Energy Convers. Manag. 2016, 121, 391–401. [Google Scholar] [CrossRef]
- Yang, M.-H. Payback period investigation of the organic Rankine cycle with mixed working fluids to recover waste heat from the exhaust gas of a large marine diesel engine. Energy Convers. Manag. 2018, 162, 189–202. [Google Scholar] [CrossRef]
- Toffolo, A.; Lazzaretto, A.; Manente, G.; Paci, M. A multi-criteria approach for the optimal selection of working fluid and design parameters in Organic Rankine Cycle systems. Appl. Energy 2014, 121, 219–232. [Google Scholar] [CrossRef]
- Turton, R.; Bailie, R.; Whiting, W. Analysis, Synthesis and Design of Chemical Processes, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Mignard, D. Correlating the chemical engineering plant cost index with macro-economic indicators. Chem. Eng. Res. Des. 2014, 92, 285–294. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Mo, X.; Qin, P.; Zhao, Z.; Ouyang, T. Multi-dimensional assessment and multi-objective optimization of electricity-cooling cogeneration system driven by marine diesel engine waste heat. J. Clean. Prod. 2022, 334, 130187. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Guo, T. Performance comparison and parametric optimization of subcritical Organic Rankine Cycle (ORC) and transcritical power cycle system for low-temperature geothermal power generation. Appl. Energy 2011, 88, 2740–2754. [Google Scholar] [CrossRef]
- Yang, M.-H.; Yeh, R.-H.; Hung, T.-C. Thermo-economic analysis of the transcritical organic Rankine cycle using R1234yf/R32 mixtures as the working fluids for lower-grade waste heat recovery. Energy 2017, 140, 818–836. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Zhao, J.; Wang, Y.; An, Q.S. Multi-objective optimization and grey relational analysis on configurations of organic Rankine cycle. Appl. Therm. Eng. 2017, 114, 1355–1363. [Google Scholar] [CrossRef]
- Kern, D. Process Heat Transfer; McGraw Hill: New York, NY, USA, 1950. [Google Scholar]
- Gnielinski, V. New equation for heat and mass transfer in tubulent pipe and channel flow. Int. Chem. Eng. 1976, 41, 8–16. [Google Scholar]
- Gungor, K.E.; Winterton, R.H.S. Simplified general correlation for saturated flow boiling and comparison with data. Chem. Eng. Res. Des. 1987, 65, 148–156. [Google Scholar]
- Thome, J.R. Prediction of the mixture effect on boiling in vertical thermosyphon reboilers. Heat Transf. Eng. 1989, 10, 29–38. [Google Scholar] [CrossRef]
- Shah, M.M. An Improved and Extended General Correlation for Heat Transfer during Condensation in Plain Tubes. HVAC&R Res. 2009, 15, 889–913. [Google Scholar] [CrossRef]
- Bell, K.J.; Ghaly, M.A. An Approximate generalized design method for multi-component/partial condensers. AICHE J. 1973, 69, 72–79. [Google Scholar]





| Coefficient | Heat Exchanger | Pump | Expander |
|---|---|---|---|
| 4.325 | 3.389 | 3.514 | |
| −0.303 | 0.054 | 0.598 | |
| 0.163 | 0.154 | 0 | |
| 1.63 | 1.89 | ||
| 1.66 | 1.35 | ||
| 0.039 | −0.394 | ||
| −0.113 | 0.396 | ||
| 0.082 | −0.002 | ||
| 1.35 | 1.55 | ||
| 1.5 |
| Fluid 1 (Number) | Critical Temperature (K) | Critical Pressure (MPa) | Fluid 2 (Number) | Critical Temperature (K) | Critical Pressure (MPa) |
|---|---|---|---|---|---|
| hexane (1) | 507 | 3.03 | propyne (1) | 402 | 5.63 |
| acetone (2) | 508 | 4.70 | isobutane (2) | 407 | 3.63 |
| cyclopentane (3) | 511 | 4.57 | isobutene (3) | 418 | 4.01 |
| heptane (4) | 540 | 2.74 | butene (4) | 419 | 4.00 |
| isooctane (5) | 544 | 2.57 | butane (5) | 425 | 3.79 |
| cyclohexane (6) | 553 | 4.08 | neopentane (6) | 433 | 3.19 |
| benzene (7) | 562 | 4.91 | isopentane (7) | 460 | 3.37 |
| octane (8) | 569 | 2.50 | Pentane (8) | 469 | 3.37 |
| nonane (9) | 594 | 2.28 | isohexane (9) | 497 | 3.04 |
| toluene (10) | 591 | 4.13 |
| Item | Symbol | Unit | Range |
|---|---|---|---|
| Inlet temperature of the turbine | K | 373–453 | |
| Superheat degree | K | 3–10 | |
| PPTD in evaporator | K | 3–10 | |
| PPTD in condenser | K | 3–10 | |
| Fluid-1 | F1 | 1–10 | |
| Fluid-2 | F2 | 1–9 | |
| Mass fraction | 0–1 |
| Selected Working Fluid | Concentration | Critical Temperature (K) | Condensation Temperature Glide (K) | |
|---|---|---|---|---|
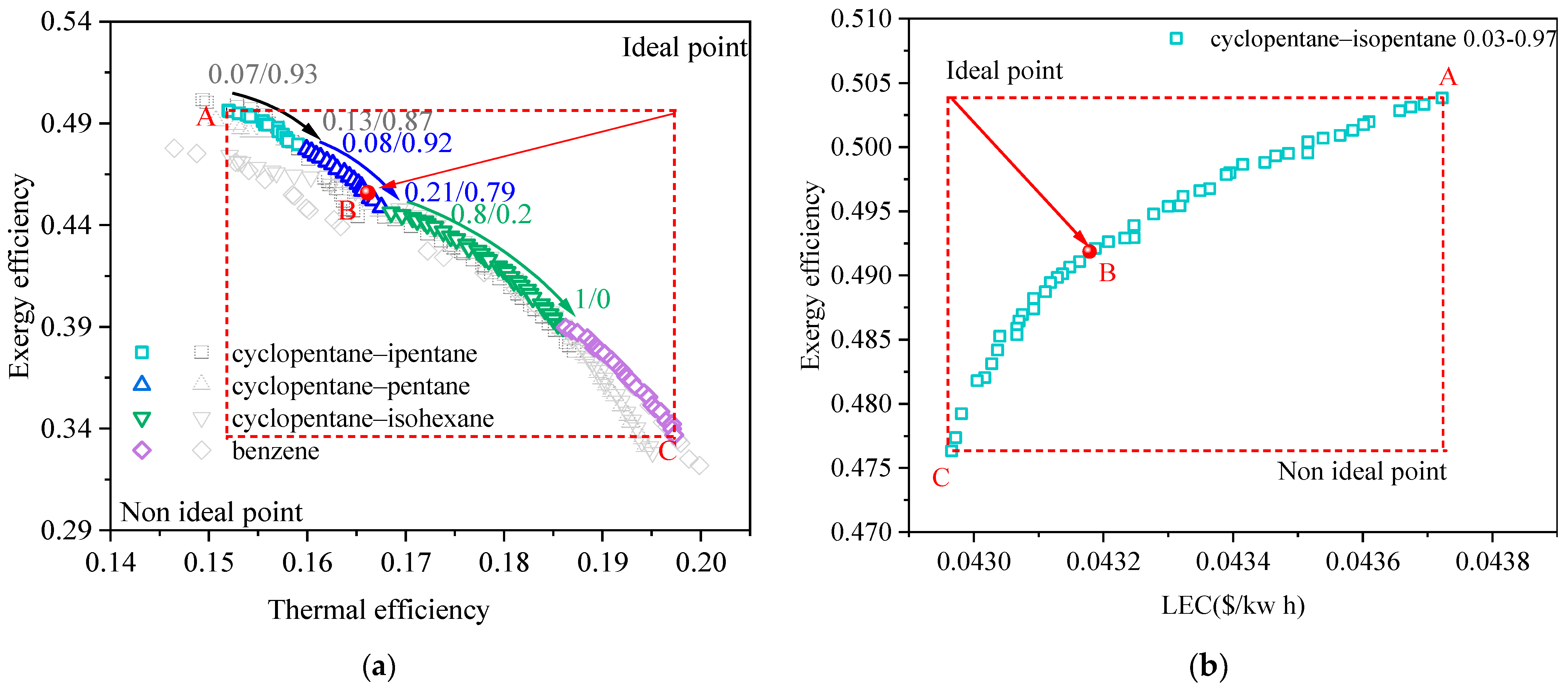
| Figure 3a: | cyclopentane/isopentane | 0.07/0.93→0.13/0.87 | 464→467 | 0.8→1.45 |
| cyclopentane/pentane | 0.08/0.92→0.21/0.79 | 473→479 | 0.25→0.69 | |
| cyclopentane/isohexane | 0.8/0.2→1/0 | 509→511 | 0.3→0 | |
| benzene | 1/0 | 562 | 0 | |
| Figure 3b: | cyclopentane/isopentane | 0.03/0.97 | 462 | 0.35 |
| Point | Exergy Efficiency | Thermal Efficiency | LEC ($/kWh) | (K) | (K) | (K) | (K) | Working Fluid | |
|---|---|---|---|---|---|---|---|---|---|
| Figure 3a: | A | 0.496 | 0.152 | 411 | 4.86 | 3.12 | 5.56 | cyclopentane/isopentane (0.07/0.93) | |
| B | 0.456 | 0.166 | 424 | 4.97 | 3.12 | 6.30 | cyclopentane/pentane (0.17/0.83) | ||
| C | 0.337 | 0.197 | 435 | 5.23 | 3.76 | 7.52 | benzene | ||
| Figure 3b: | A | 0.504 | 0.0437 | 414 | 3.08 | 3.09 | 9.75 | cyclopentane/isopentane (0.03/0.97) | |
| B | 0.492 | 0.0432 | 413 | 3.08 | 4.56 | 9.91 | cyclopentane/isopentane (0.03/0.97) | ||
| C | 0.476 | 0.0429 | 413 | 3.11 | 6.41 | 9.88 | cyclopentane/isopentane (0.03/0.97) |
| Point | Exergy Efficiency | Thermal Efficiency | LEC ($/kWh) | (K) | (K) | (K) | (K) | Working Fluid | |
|---|---|---|---|---|---|---|---|---|---|
| Figure 4a: | A | 0.406 | 0.122 | 381 | 4.21 | 3.17 | 6.58 | butane | |
| B | 0.368 | 0.131 | 381 | 4.60 | 3.04 | 7.30 | cyclopentane/isohexane (0.83/0.17) | ||
| C | 0.274 | 0.158 | 397 | 3.95 | 3.13 | 7.93 | benzene | ||
| Figure 4b: | A | 0.415 | 0.0642 | 372 | 3.33 | 3.29 | 9.68 | isobutene | |
| B | 0.399 | 0.0632 | 372 | 3.33 | 3.43 | 9.83 | isopentane | ||
| C | 0.378 | 0.0625 | 371 | 3.35 | 5.34 | 9.88 | pentane |
| Point | Exergy Efficiency | Thermal Efficiency | LEC ($/kWh) | (K) | (K) | (K) | (K) | Working Fluid | |
|---|---|---|---|---|---|---|---|---|---|
| Figure 5a: | A | 0.607 | 0.177 | 435 | 3.14 | 3.02 | 5.81 | cyclopentane/pentane (0.33/0.67) | |
| B | 0.529 | 0.207 | 458 | 3.44 | 3.04 | 5.72 | cyclopentane/pentane (0.98/0.19) | ||
| C | 0.414 | 0.225 | 470 | 3.68 | 3.77 | 5.71 | benzene | ||
| Figure 5b: | A | 0.588 | 0.0336 | 442 | 3.42 | 3.16 | 8.11 | cyclopentane/pentane (0.52/0.48) | |
| B | 0.577 | 0.0328 | 442 | 3.37 | 4.63 | 8.47 | cyclopentane/pentane (0.52/0.48) | ||
| C | 0.536 | 0.0320 | 443 | 3.44 | 7.28 | 8.92 | cyclopentane/pentane (0.66/0.34) |
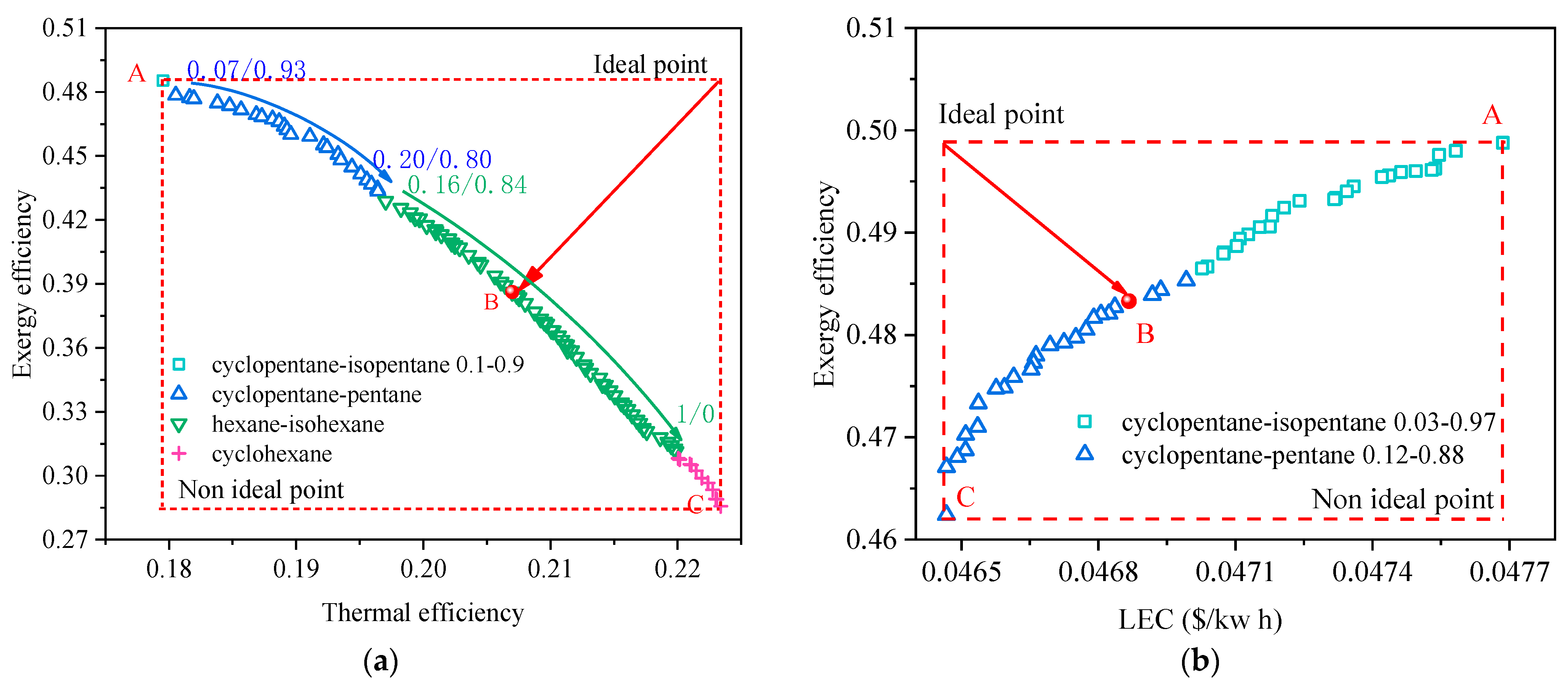
| Point | Exergy Efficiency | Thermal Efficiency | LEC ($/kWh) | (K) | (K) | (K) | (K) | Working Fluid | |
|---|---|---|---|---|---|---|---|---|---|
| Figure 8a: | A | 0.485 | 0.180 | 415 | 4.97 | 3.60 | 7.37 | cyclopentane/isopentane (0.1/0.9) | |
| B | 0.386 | 0.207 | 437 | 6.76 | 3.22 | 6.87 | hexane/isohexane (0.21/0.71) | ||
| C | 0.286 | 0.223 | 447 | 7.62 | 3.62 | 5.30 | cyclohexane | ||
| Figure 8b: | A | 0.499 | 0.0477 | 406 | 3.90 | 4.07 | 5.46 | cyclopentane/isopentane (0.03/0.97) | |
| B | 0.484 | 0.0469 | 404 | 3.82 | 4.69 | 5.63 | cyclopentane/pentane (0.04/0.96) | ||
| C | 0.462 | 0.0465 | 403 | 3.95 | 7.15 | 5.73 | cyclopentane/pentane (0.12/0.88) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Ruan, J.; Hong, G.; Miao, Z. Multi-Objective Optimization of the Basic and Regenerative ORC Integrated with Working Fluid Selection. Entropy 2022, 24, 902. https://doi.org/10.3390/e24070902
Zhou Y, Ruan J, Hong G, Miao Z. Multi-Objective Optimization of the Basic and Regenerative ORC Integrated with Working Fluid Selection. Entropy. 2022; 24(7):902. https://doi.org/10.3390/e24070902
Chicago/Turabian StyleZhou, Yuhao, Jiongming Ruan, Guotong Hong, and Zheng Miao. 2022. "Multi-Objective Optimization of the Basic and Regenerative ORC Integrated with Working Fluid Selection" Entropy 24, no. 7: 902. https://doi.org/10.3390/e24070902
APA StyleZhou, Y., Ruan, J., Hong, G., & Miao, Z. (2022). Multi-Objective Optimization of the Basic and Regenerative ORC Integrated with Working Fluid Selection. Entropy, 24(7), 902. https://doi.org/10.3390/e24070902





