1. Introduction
Graphs can be considered as the bonding of objects. To emphasis on a real problem, those objects are being bonded by some relations such as, friendship is the bonding of pupil. If the vagueness in bonding arises, then the corresponding graph can be modelled as fuzzy graph (FG) model. In twenty first century, the graph theory has been fully exploited by fuzzy theory. In a crisp graphs two vertices are either related or not related to each other, mathematically, the degree of relationship is either 0 or 1. While in FGs, the degree of relationship takes values from . The concept of FG, intuitionistic FGs and their extensions such interval valued FGs and interval valued intuitionistic FGs, and so on, have been studied deeply in over hundred papers. All these types of graphs have a common property that each edge must have a membership value less than or equal to the minimum membership of the nodes it connects. Famous Mathematician Euler described the solution of the seven bridge problem in 1736. It has become conventional to preserve the application of graph theory in different situations such as computer network, electric network, etc. In the literature, threshold graphs (TGs) as special graphs having beautiful structures and several important mathematical properties. It has a large impact in graph theory (GT) as well as in many applied areas, such as psychology, artificial intelligence, computer science, etc. These graphs can also be used to control flow of information between processors, similar to how traffic lights are used in controlling the flow of traffic.
In existing papers on TGs, all information were collected in fuzzy sense. The FTG or intuitionistic FTG model, usually demonstrate the information having fuzzy in nature. But, when description of the object or their relations or both is indeterminate and inconsistent, it cannot be handled by existing TGs models. In these scenario, the information should be taken in picture fuzzy sense. For this purpose, we proposed the concept of PFTGs based on literal indeterminacy to deal with such situations, which is more precise and more flexible than the other existing models, where vagueness and uncertainty will be characterized by picture fuzzy sets (PFSs) instead of fuzzy sets and intuitionistic fuzzy (IF) sets. However, there are are some unsolved issues in the literature:
- (1)
The TG is an advance studied topic and it was discussed in several fields except in PF field.
- (2)
The crisp TG, FTG and intuitionistic FTG models do not recognize all real life systems having an indeterminate information.
- (3)
The PFTG models are more helpful to control the flow of information than the other existing models. But, till now it was not formulate in PF environment.
The use of PFTG model in controlling several resources, which have not been addressed in the literature. In this paper, it has been shown that PFTG model can be used to control medicine resource. This study answers the following research questions:
- (1)
Is it possible to formulate a new TG model can help to solve resources allocation problems in PF surroundings?
- (2)
Is it possible to handle the systems having an indeterminate information by using PFTG models?
The FTG [
1] or intuitionistic FTG [
2] model, generally exhibit the system having fuzzy in nature. But, when its objects have more uncertainties, then these models are unable to handle the system properly. In such circumstances, PFTG models are becoming useful because of their aim of reducing the differences between the traditional numerical models used to control resource allocation problems. Considering PFSs are more suitable and powerful to deal with uncertainty and vagueness compared to fuzzy sets and IF sets, PF models can give more precision and compatibility than fuzzy models in many applications. Motivated by the above analysis, it is really significant for us to study PFTGs compared to FTGs or intuitionistic FTGs, where vagueness and uncertainty will be characterized by PFSs [
3] instead of fuzzy sets [
4] and IF sets [
5]. This study develops many novel observations in PF environment. The main Objectives of this paper are stated as follows:
- (1)
To extend the concept of FTG and intuitionistic FTG to PFTG to model systems having an indeterminate information.
- (2)
To fill the research gap, we propose TG models under PF environment.
- (3)
To compare the obtained results derived from the proposed model with the existing models.
- (4)
To control medicine resources using the proposed models.
The proposed model can be effective to control resources under PF environment. The theoretical contribution of this paper can be summarized as follows:
- (1)
We formulate PFTG along with its many interesting properties and then initiate the notions of picture fuzzy alternating 4-cycle (PFA4-C), TD and PN of PFGs.
- (2)
We introduce the relation of threshold values (TV) and vertex cardinality of a PFTG. We can decompose a PFTG in a unique way and it generates 3 distinct FTGs.
- (3)
We establish a relation between picture fuzzy TD and PN, and illustrates many important properties on decomposed FTG.
- (4)
We present the comparison of proposed TGs with the existing TGs.
- (5)
Finally, an application of PFTG is present in medicine replenishment problem. In this way, the research gap mentioned above can be filled.
The current work is novel in the sense that:
- (1)
It is capable to recognize all real life systems having an indeterminate information.
- (2)
It is more efficient and effective than in other field.
- (3)
It is based to control resources rather than in other existing TG models.
The rest of the paper is organized as follows:
Section 2, makes a literature review on TGs. In
Section 3, we describe some basic observations connected to PFTGs.
Section 4, presents the conception of PFTG along with some important properties. Also, picture fuzzy TD and PN are introduced and a relation between them is establish. Some properties of TD and PN on decomposed FTG are also illustrates.
Section 5, an application of PFTG in medicine replenishment problem is given. Before the concluding section, comparison of proposed TGs with the existing TGs are given in
Section 6. Lastly, in
Section 7, we present conclusion and future scope along with some limitations of the proposed method.
4. Picture Fuzzy Threshold Graph
Here, a new concept on PFG called PFTG is defined and exhibited few interesting properties of it.
Definition 7. A PFG is called a PFTG with threshold , where such that , and iff is a SS in . For simplicity, this PFTG is denote as .
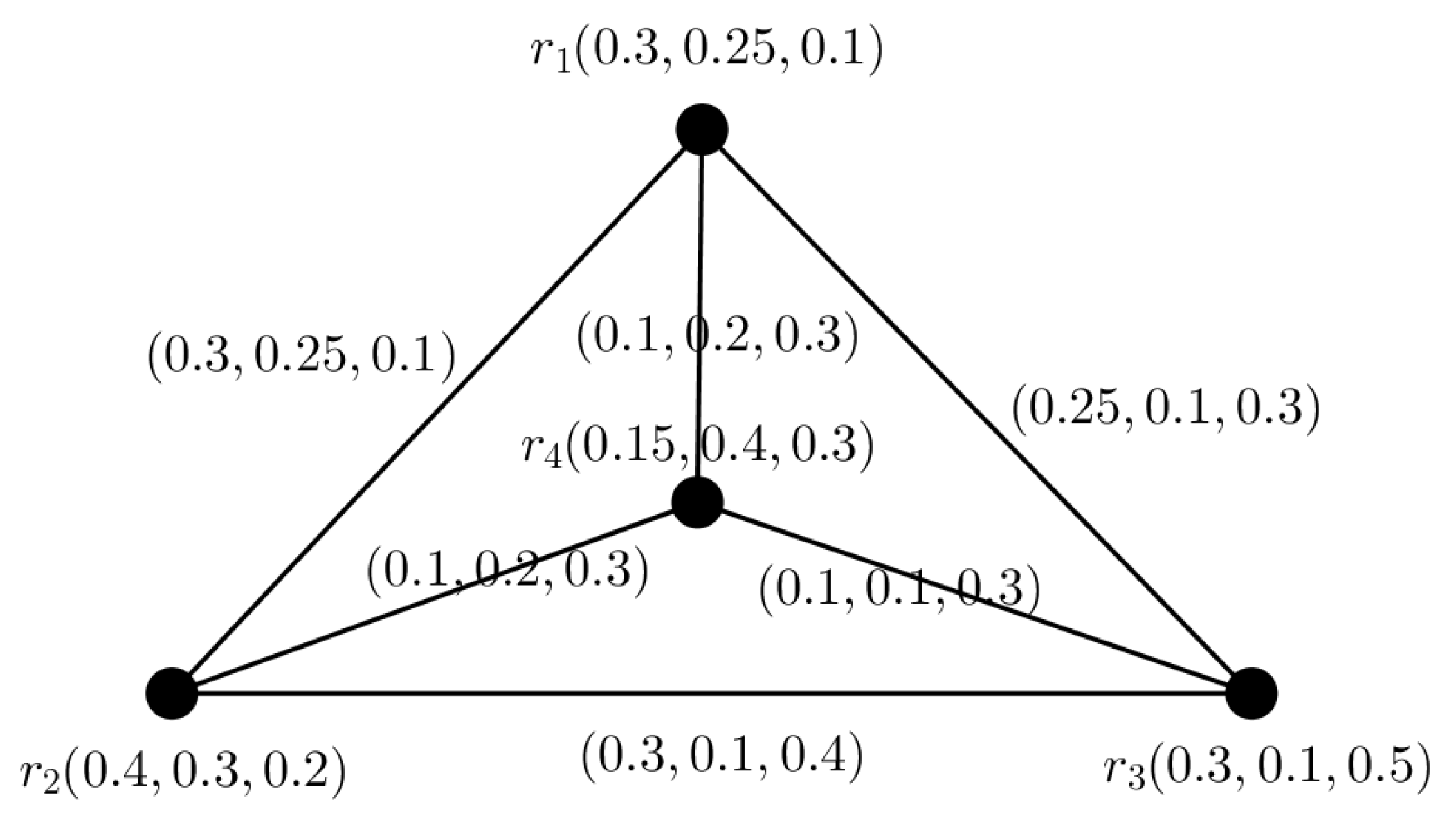
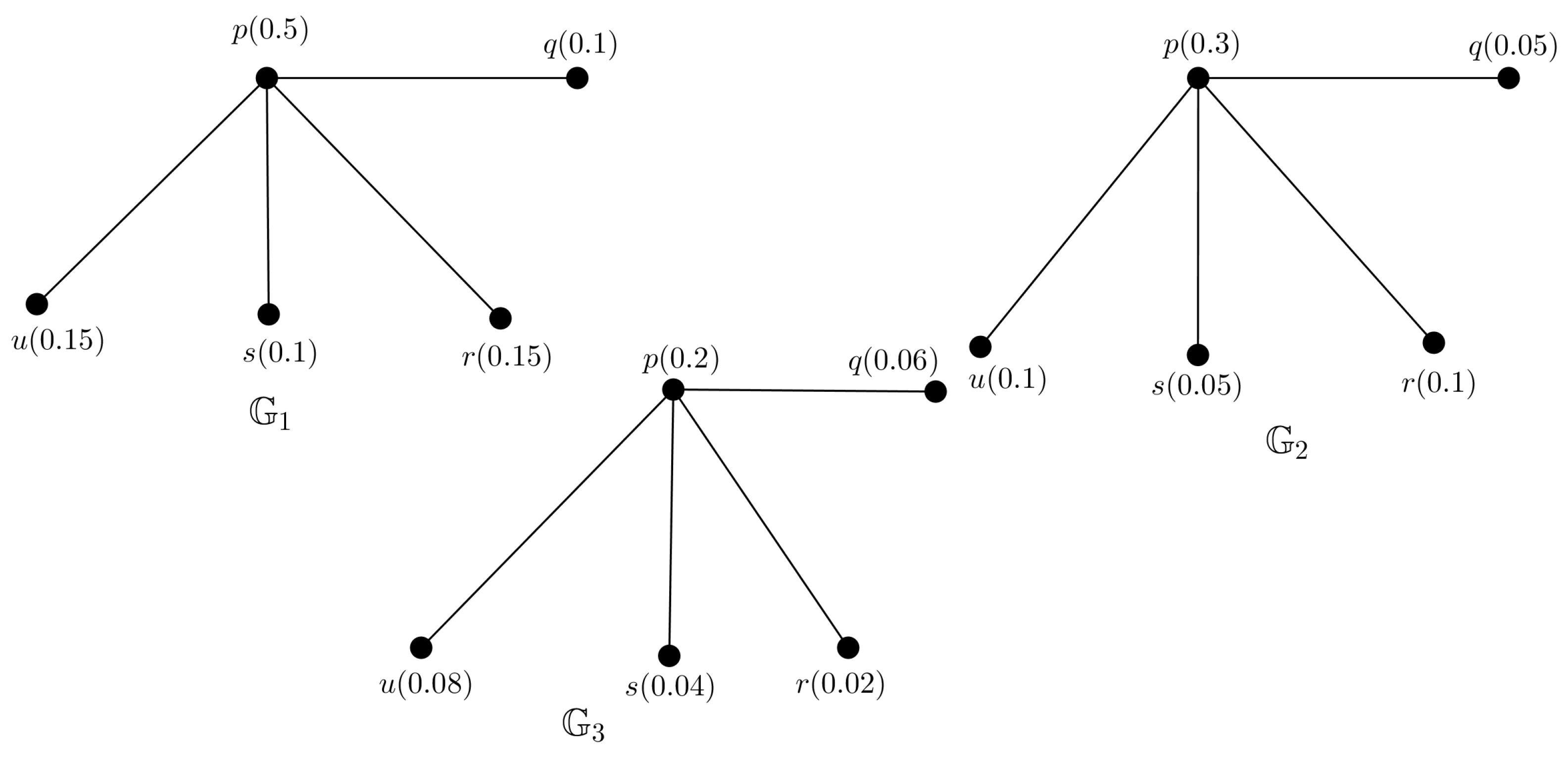
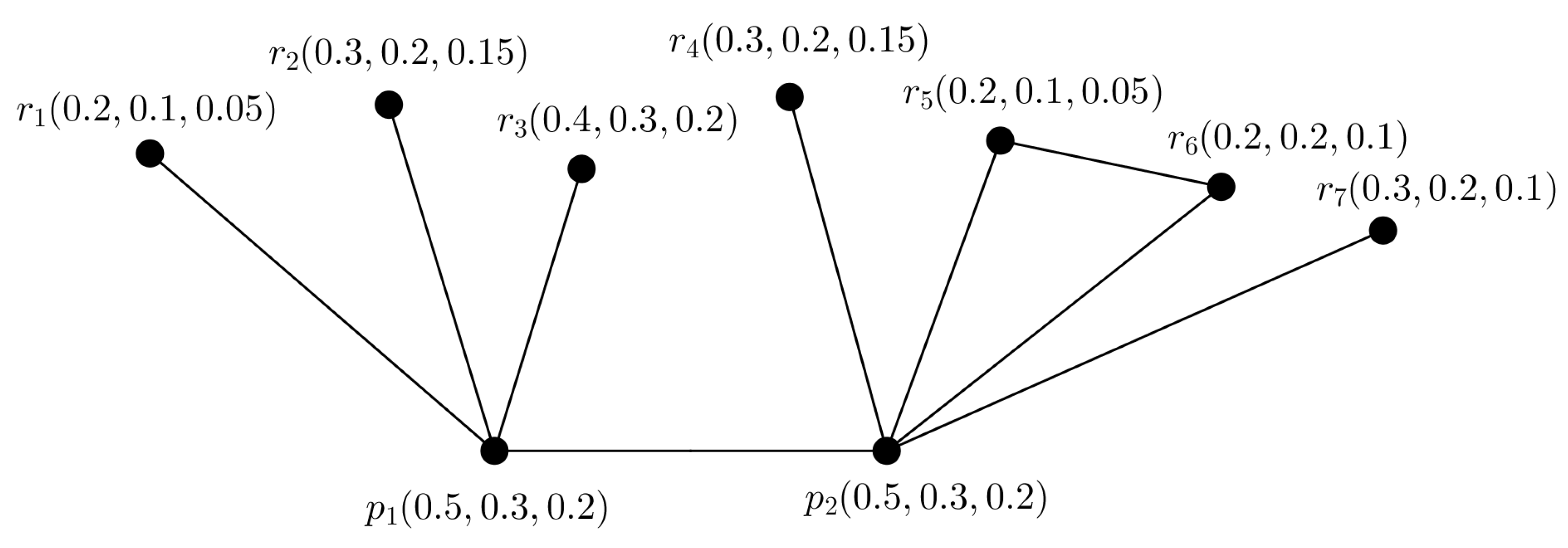
Example 2. We consider a PFG shown in Figure 2. Here one of the SS is and for the SS Ⓢ, we have .
Again, for any two non-SSs and , we have
and
.
So, the PFG shown in Figure 2 is a PFTG . Definition 8. A PFG with 4 vertices is a PF square graph if its vertices can be label such that , with .
Definition 9. A PFG with 4 vertices is a PF path graph if its vertices can be label such that , .
Definition 10. A PFG with 4 vertices is a PF matching graph if there are no PF edges adjacent to each other.
Definition 11. A configuration with 4 vertices constitute a PFA4-C if ) and , consequently and .
Based on the degree of TMS, AMS and FMS of the edges and the PFA4-C may induces 3 types of PF-subgraph:
- (1)
a PF square graph if and .
- (2)
a PF path graph if and ;
or, and .
- (3)
a PF matching graph if and .
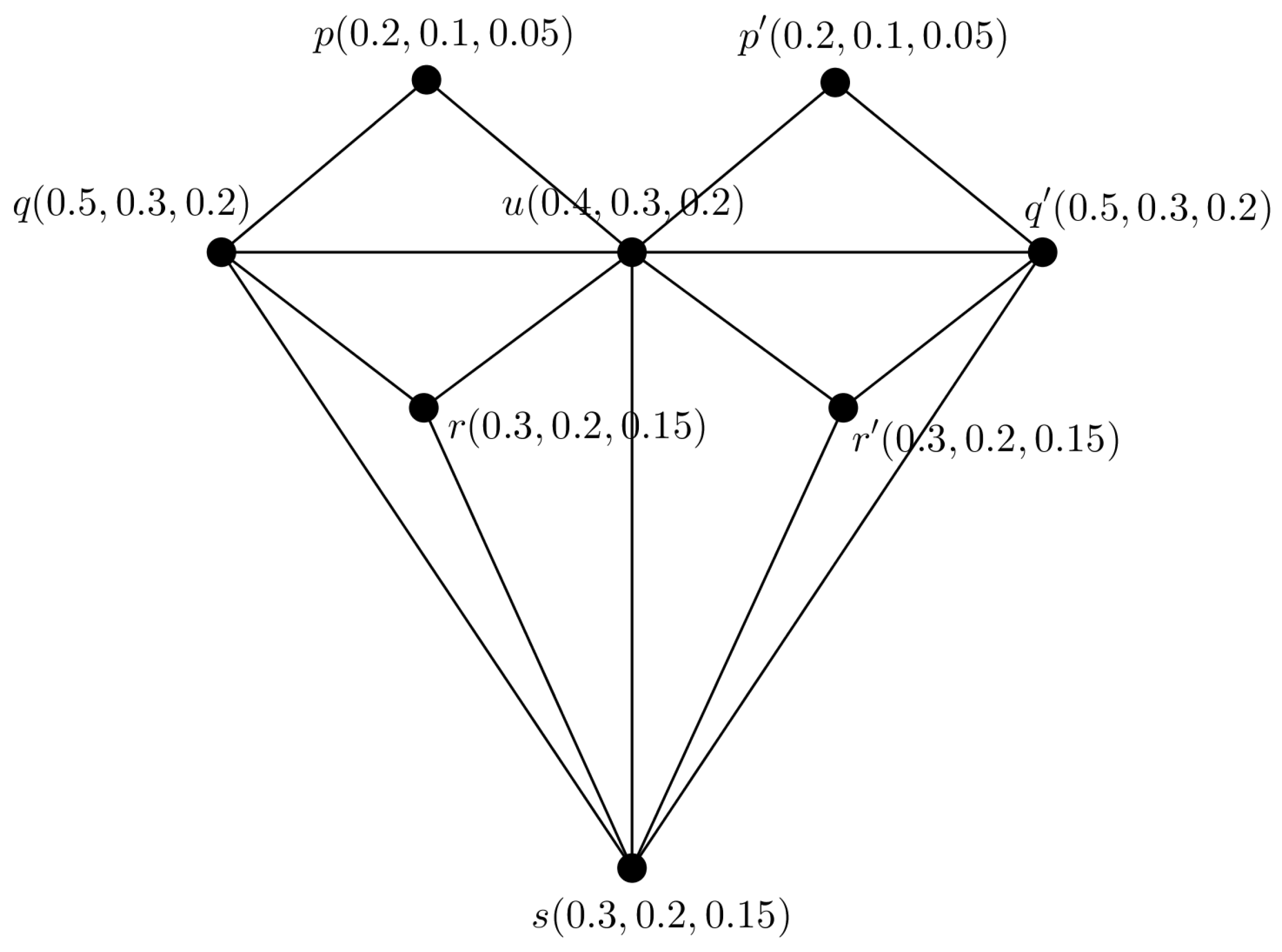
Example 3. Through an example, we depicted PFA4-C, , and shown in Figure 3. Definition 12. A strong PF alternating 4-cycle is a PF alternating 4-cycle if PF square graph can be induced from it.
Definition 13. A PFS Ⓢ is said to be a stable (independent) set if , .
Theorem 1. A FTG is a special PFTG.
Proof. Let be FTG with threshold such that iff Ⓢ is SS in . For a PFG, we know that , for all . Take (n is no. of nodes of ), then ∃, such that , and . Thus, a FTG is a PFTG. □
Theorem 2. A PFTG does not have any PFA4-C.
Proof. Let
be a PFTG. Suppose it has a PFA4-C. Then ∃
such that
,
,
and
. Since
is a PFTG, then
Adding
and
, we get
Adding
and
, we get
Obviously. Equation contradicts with Equation . Hence, a PFTG cannot have any PFA4-C. □
Definition 14. A PFG is called a picture fuzzy split graph (PFSG) if its node set can be partitioned into a PF clique and a SS.
Theorem 3. Let be a PFG with UCG . Then is SG, if is PFTG,.
Proof. Let be a PFTG. We have to show is SG, i.e., can partitioned into a clique and a SS. Assume that in , is the greatest clique. Then only leftover to prove is SS.
If is not a SS, then ∃ an arc such that . Since, is the largest clique, then ∃ distinct nodes in such that and .
This shows that creates a PFA4-C, it contradicts that is a PFTG. Hence, is a SS, and is a SG. □
Theorem 4. Let be PFG with UCG . If is PFTG, then is a TG in crisp sense.
Proof. Let be PFTG with TV , then , and iff Ⓢ is a SS in . Since, is UCG of , then Ⓢ is a SS in also. In the sense of crisp graph theory for , we set non-negative reals , for the node , we have . Then is a TG. □
Next, we can decomposed a PFTG into 3 FGs , , in such a way that FG is created by considering ith components of the membership value (MV) of vertices and arcs of , for .
Now, we present the following theorems.
Theorem 5. If be PFTG with TV . Then, its decomposed FGs , and are also FTGs with TV , and , respectively.
Proof. Let be PFTG with TV , then , and iff Ⓢ is a SS in . As, , , are the decomposed FGs of and if r be a node belongs in , and . Then, MV of r in , and are respectively , and , these are respectively the degree of TMS, AMS and FMS of .
Now, we have, , and . This proves that , and are the FTGs with TV , and , respectively. □
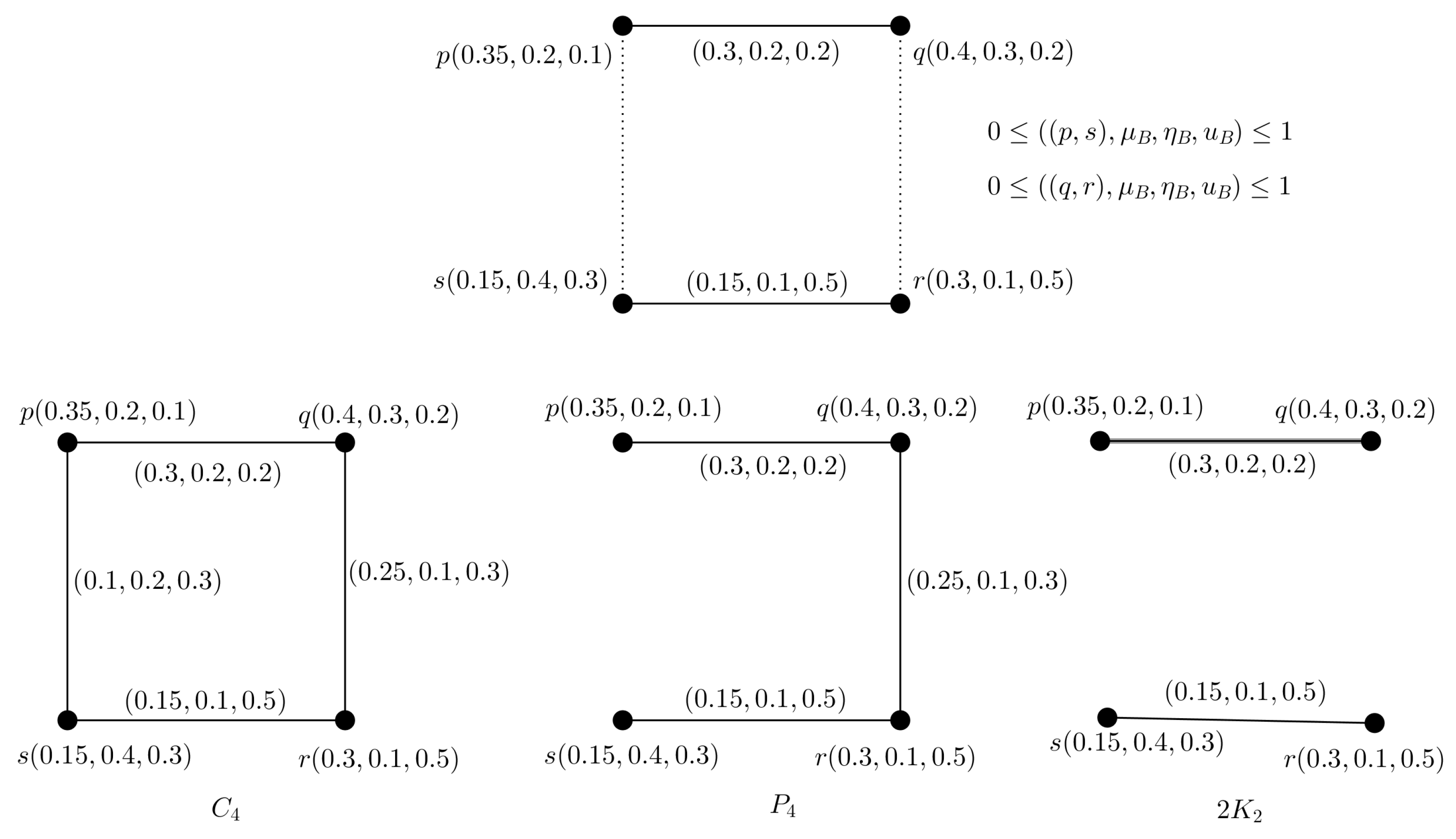
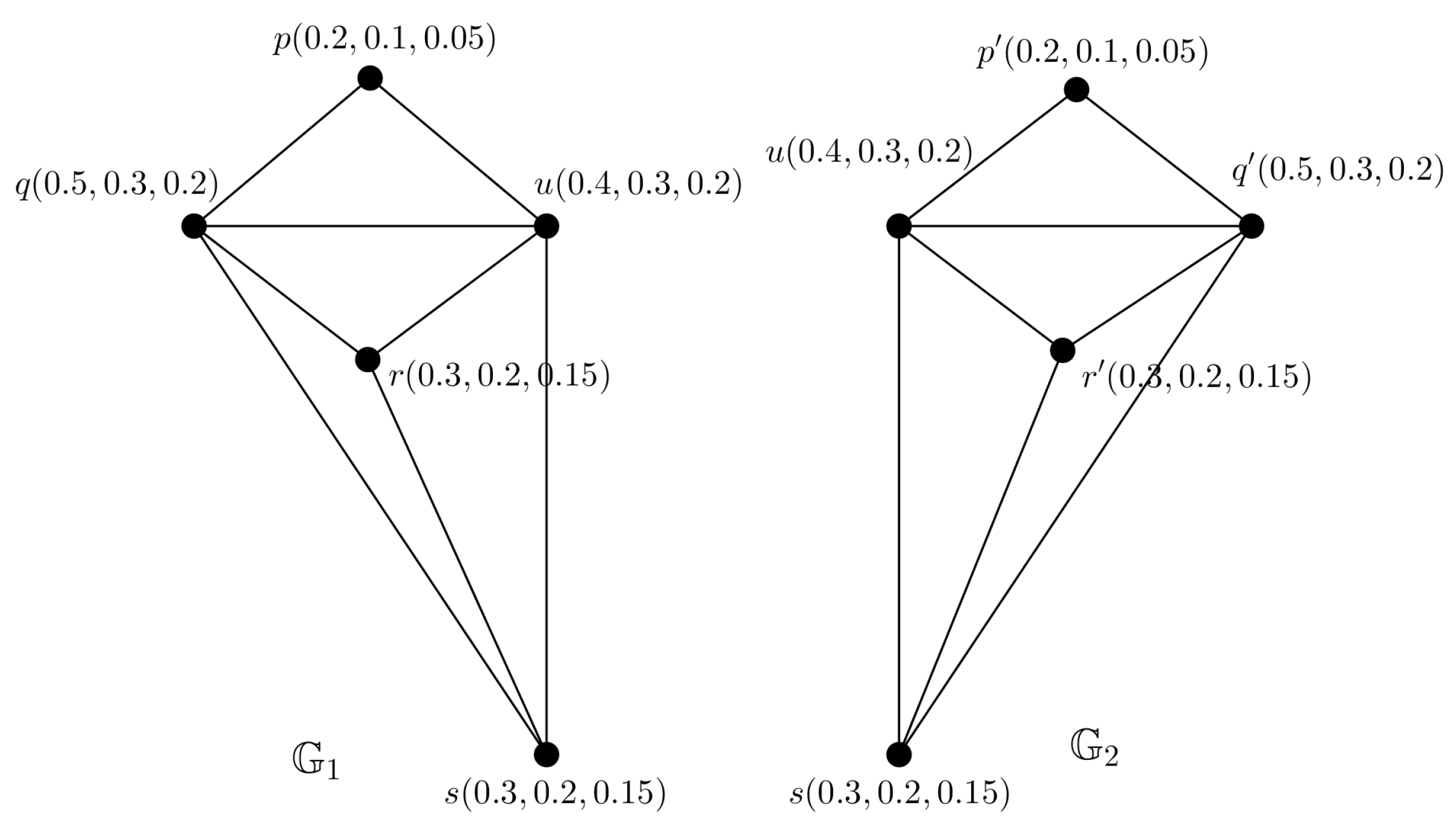
Example 4. We consider a PFTG with TV shown in Figure 4. We decomposed into 3 FGs , and shown in Figure 5, they are also FTGs with TV and , respectively. Theorem 6. If , , are 3 FTGs with TV , , , respectively and whose UCGs are isomorphic. Then their composed PFTG is also a PFTG with TV .
Proof. Since , is the FTG with TV , , we have , and , where is the SS of , . As, , the crisp graph of , are isomorphic for , (), then the SSs for each FTG remain same, say, Ⓢ and it is the SS of composed PFTG . Thus, we have , and . Therefore, is a PFTG with TV . □
Theorem 7. The TV of a complete PFG is .
Proof. Suppose be complete PFG. Then, any two nodes of it are connected. So, the SS in becomes . then, , and . Therefore, the TV of a complete PFG is . □
Theorem 8. Every PFTG is the PFSG.
Proof. Suppose be a PFTG. We have to show is PFSG, i.e., can partitioned into a clique and a SS. Assume that is the greatest clique of . Then only leftover to prove is a SS.
If is not a SS, then ∃ an arc such that . Since, is the largest clique, then ∃ distinct nodes such that and .
This shows that creates a PFA4-C, it contradicts that is a PFTG. Hence, is a SS, and is a PFSG. □
Converse part of the above theorem is given below.
Theorem 9. Every PFSG is either a PFTG or it can be converted to PFTG after modification of the TMS, AMS and FMS of nodes.
Proof. Suppose be a PFSG. Then ∃ a PF clique and a SS . If is a PFTG, then there is nothing to prove.
If PFSG is not PFTG, then changes can be made to the TMS, AMS and FMS of nodes such that for some TVs the conditions , and iff Ⓢ is a SS in , is hold good. In case, when a node is adjacent to , then the conditions are not violate. Therefore, a PFSG becomes a PFTG. □
Theorem 10. A PFTG can be made from a single node PFG by continually adding PF isolated node or a PF dominating node.
Proof. Let be a PFG with a single vertex . Theorem 9 states that each PFSG can be formed into a PFTG, it can be proved if after adding a PF isolated node or a PF dominating node the resultant graph is also an PFSG.
Since is single node PFG, it can be assumed as PFSG with PF clique and a SS . Now, a node can be added in two ways, either as a PF isolated node or a PF dominating node. If is isolated node then or is a dominating node then . The resultant graph remains a PFSG. Again, we know every PFSG is either a PFTG or it can be converted to PFTG after modification of the TMS, AMS and FMS of nodes. Hence the theorem. □
Definition 15. The TD of a PFG , is the least +ve integer m for which ∃m number of picture fuzzy threshold-subgraphs (PFTSGs) of , say, covers the edges set (ES) of . The TD of a PFTG is at least 1.
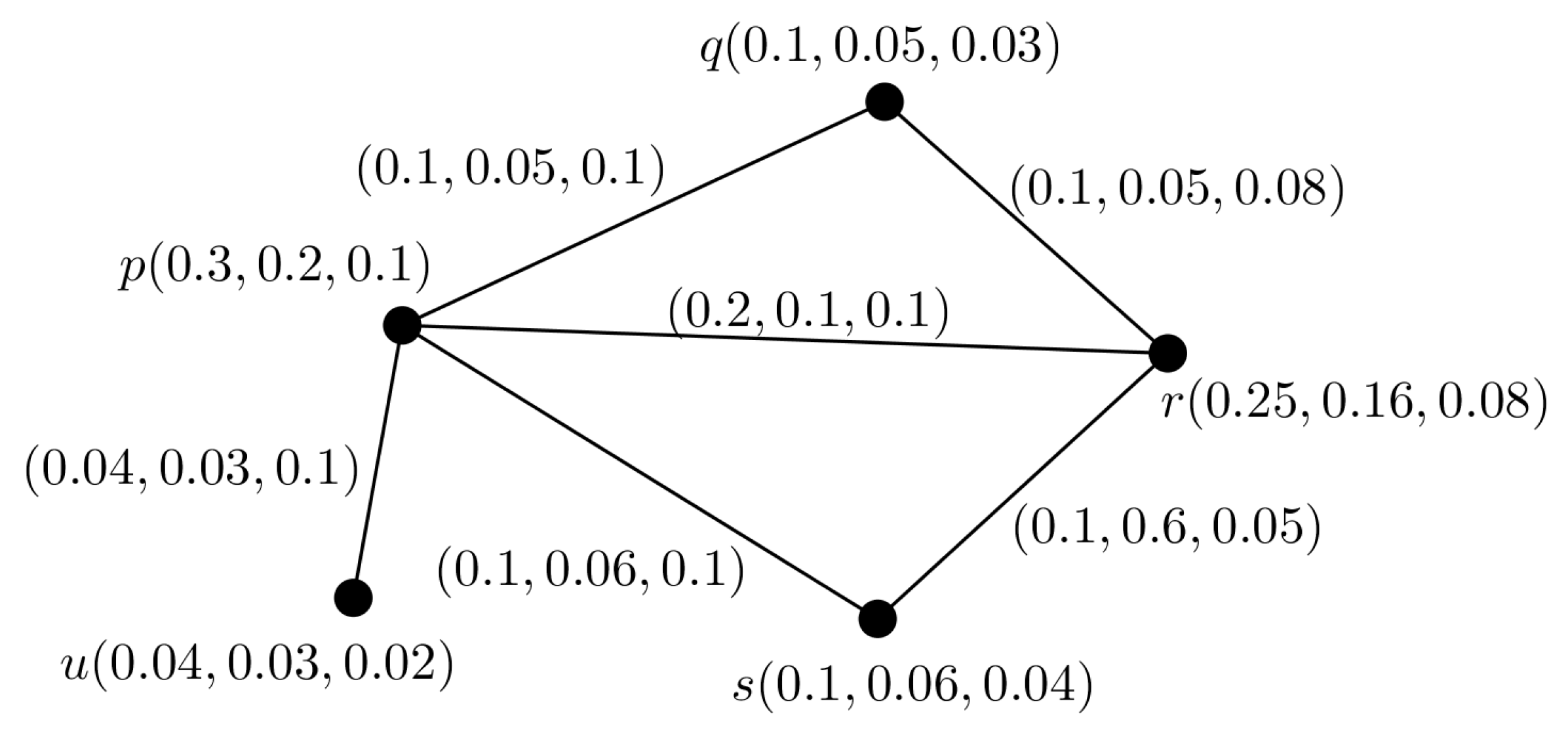
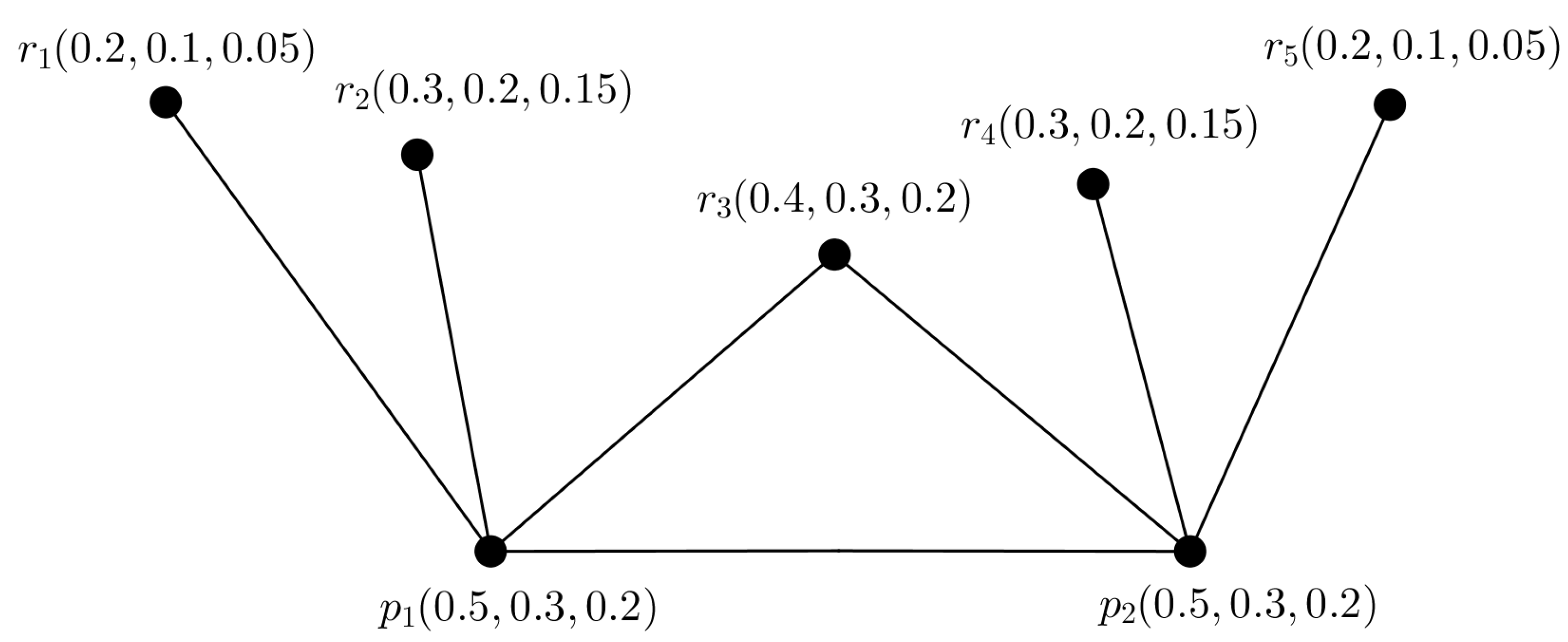
Example 5. Consider a PFG shown in Figure 6. We can construct 2 PFTSGs and with TV shown in Figure 7, they covers the ES of . Theorem 11. The TD of a PFG is at least 1.
Proof. To show, the TD of a PFG is non-zero, we have to prove, each PFG has minimum one PFTSG it can cover the ES of . If is itself a PFTG then there is nothing to prove. But, if is not a PFTG. We know, every sole node PFG can made a PFTG. Then, each PFG must have minimum one subgraph which is a PFTG and cover ES of . Thus, there always exists a TD of any PFG. □
Definition 16. The α-cut of a PFG is such that and .
Theorem 12. The α-cut of a PFTG is also a PFTG.
Proof. Let be PFTG with TV , then , and iff Ⓢ is SS in . Let be the -cut of such that and .
When in the no. of nodes remains same with but the no. of arcs may decreases. Let be the SS in . The cardinality of never decreases than Ⓢ, i.e., may contains more nodes of along with the nodes of Ⓢ. Then we have , and iff is a SS in , where we choose suitable TV for which the threshold conditions are satisfied.
When in the no. of nodes and arcs may decreases than . The cardinality of decreases than Ⓢ, i.e., may contains more nodes of along with the nodes of Ⓢ. Then , and iff is a SS in .
Therefore, becomes a PFTG in all cases. □
Theorem 13. The α-cut of a PFG has TD at least 1.
Proof. Let be a PFG with UCG . Assume that be the -cut of . We have to show ∃ minimum one PFTSG which covers the ES of .
If is a PFTG then itself fulfill the conditions. Then, has TD 1.
If is not a PFTG, we have by Theorem 10, every single vertex PFG can made a PFTG. Hence, each PFG must have minimum one subgraph which is a PFTG and cover ES of . Therefore, the -cut of a PFG has TD at least 1. □
Theorem 14. For any PFG, the TD . If is without triangle, then , where is the cardinality of the greatest SS of .
But, if , then need not be triangle free. It can discussed by an example.
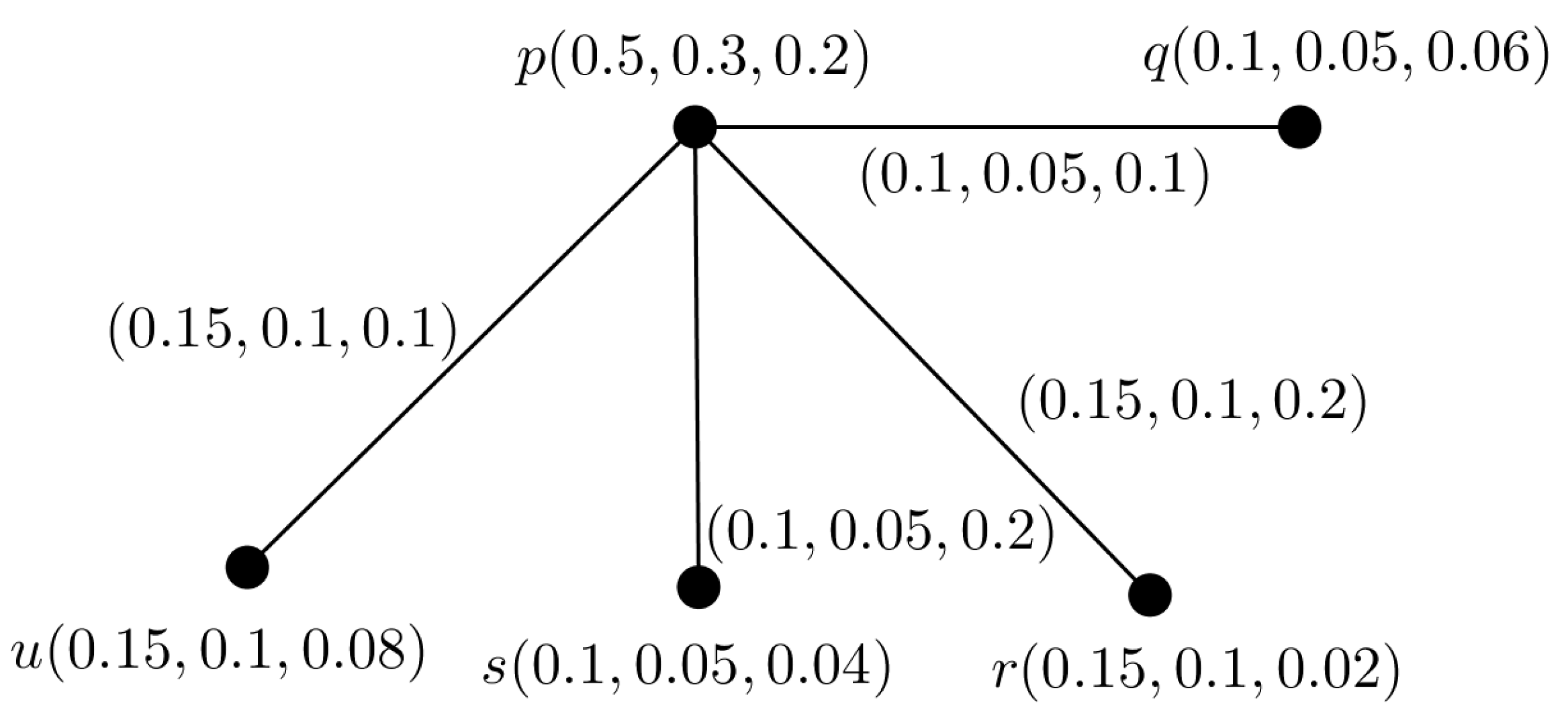
Example 6. Consider a PFTG shown in Figure 8. Here, the largest SS is . Then picture fuzzy TD of is , as minimum two PFTSGs (shown in Figure 9) are needed to cover the ES of . Thus, is satisfied. But, we see that the nodes makes a triangle in . Theorem 15. If PFG has no triangle, then .
Proof. Let be PFG without triangle. The TD of is the least no. of PFTSGs which are needed to cover ES of . If more than one PFTSGs contains a strong arc, then we eject it from all PFTSGs except one PFTSG. Then such PFTSGs cover ES of without any common arc. Hence, . □
But, if , then need not be triangle free. It can discussed by an example.
Example 7. Consider a PFTG with nine nodes shown in Figure 10. Here, we can obtain two PFTSGs without any common arcs (shown in Figure 11), those cover the ES of . Hence, . But, we see that the nodes makes a triangle in . Definition 17. The PN of a PFG , is the least +ve integer p for which ∃p no. of PFTSGs of , say, covers the ES of and they have no common edges.
Theorem 16. The TD of a PFG and its decomposed FGs are same.
Proof. Let be PFG with TV and be its decomposed FGs. Let . Then, there is m PFTSGs which cover ES of without any common arcs.
Now, the decomposed FGs , have an ES, same with the ES of . Thus, the ES of can also be covered by an equal no. of FGs. Hence, , . □
Theorem 17. The PN of a PFG and its decomposed FGs are same.
Proof. Let be PFG with TV and be its decomposed FGs. Let . Then, there is p PFTSGs which cover ES of without any common arcs.
Now, the decomposed FGs , have an ES, same as the ES of . Thus, the ES of can also be covered by an equal no. of FGs without any common arc. Hence, , . □