Vector Arithmetic in the Triangular Grid
Abstract
:1. Introduction
2. Preliminaries
2.1. Vector Additions as Translations
2.2. Coordinate Systems for the Triangular Grid
- equal to 1, then it is the midpoint of a positive trixel;
- equal to −1, then it is a midpoint of a negative trixel;
- equal to 0, then the point is on the edge of a trixel;
- positive, then the point belongs to a positive trixel;
- negative, then the point belongs to a negative trixel.
2.3. Converting Triplets to Cartesian Coordinates and Vice Versa
3. Procedure for Adding Vectors in Ω
3.1. Further Definitions and Notations
- (1)
- : The integer part of x with sign, i.e.;, whereand is the floor function, that is applied on the absolute value of x above. One may also use the rounding operation that we have already defined in Table 1.
- (2)
- {x}: The fractional part of x with sign, i.e.,
- (3)
- : The absolute-rounding-up operation that rounds a number up in absolute value, such that:
- = 1 and = −1
- {1.3} = 0.3 and {−1.3} = − 0.3
- = 2 and = −1
- (1)
- , where i, j, and k are the coordinate values of the direct-sum s.
- (2)
- The region is based on the signs of the coordinates of the direct-sum. Accordingly, the triangular grid is partitioned into six regions based on the signs of the coordinates of the triplet used in the region, as it is shown in Figure 11a,b. The region can be specified by checking the three coordinate values of s as follows. For each coordinate value, x, of the direct-sum vector, the sign is described aswhere sum is the sum of the three coordinate values of direct-sum vector, i.e., sum = i + j + k.
3.2. The Algorithm for the Computation
| Procedure to find the result-vector r |
| Input: v1 = (i1, j1, k1) and v2 = (i2, j2, k2), two vectors of Ω. Output: r = (i, j, k) = v1 + v2, the result-vector in Ω. |
| Step (1) Let: |
| (a) direct-sum s: = (i, j, k) = (i1 + i2, j1 + j2, k1 + k2) |
| (b) (c) Region: be the signs of the triplet of direct-sum. |
| Step (2) Find the type of the result-vector (r): |
|
|
| Step (3) Calculate the result-vector (r) by applying the following two steps: |
|
|
| Else If ((i + j + k) < −2) Then, let r: = (i + 1, j + 1, k + 1). |
3.3. Step 1: Finding the Direct-Sum, Rsum, and the Region
3.4. Step 2: Finding the Type of the Result-Vector
- If (adding vectors of types (A + A)) and (Rsum = −1)then the result-vector type is A.
- If (adding vectors of types (B + B)) and (Rsum = 0)then the result-vector type is B.
- If (adding vectors of types (C + C)) and (Rsum = 0)then the result-vector type is C.
3.5. Step 3: Finding Coordinate Triplet of the Result-Vector
- If the type of the result-vector is A, then its coordinate triplet is:r = (i − ({i1} + {i2}), j − ({i1} + {i2}), k − ({i1} + {i2})),
- If the type of the result-vector is B, then its coordinate triplet is:r = (i − ({j1} + {j2}), j − ({j1} + {j2}), k − ({j1} + {j2})),
- If the type of the result-vector is C, then its coordinate triplet is:r = (i − ({k1} + {k2}), j − ({k1} + {k2}), k − ({k1} + {k2})),
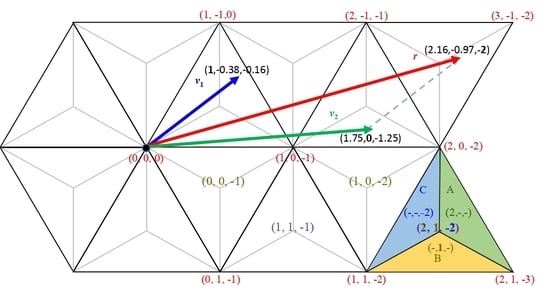
- (1)
- j = = −2.0
- (2)
- i = = + 2.85 − 2.0 = 2.582
- (3)
- k = = 2.582 − 3.464 = −0.882
4. Vector Arithmetic and its Application
4.1. Subtraction and Scalar Product
- Input: v = (i, j, k) and integer n.
- Output: r = (ir, jr, kr) the scalar product of the number n and vector v.
- Step1) If n = 0 then let r: = (0,0,0). Stop.
- Step2) If n < 0 then let n: = − n and v: = − v.
- Step3) Let r: = v.
- Step4) If n = 1 then Stop.
- Step5) For h = 2 to n do
- Step6) Let r: = r + v.
- Step7) Endfor.
- Step8) Stop.
4.2. Application: Drawing and Imaging on a Cubic Mesh
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- By our procedure, if Rsum = −1, then vector r is of Type A and since i is integer, in fact, it is r = s = (i, j, k). If Rsum = −1, then either ( and ), or ( and ). Equivalently, ( and ) or ( and ). In both cases, i + j + k = , and thus 1 ≥ i + j + k ≥ −1 holds, thus no correction is needed. As this triplet is converted exactly to r’= , this result matches, proving that our procedure gives the sum correctly in the case when the sum is also a Type A vector.To complete the proof of this subcase, we check also that the vector (i, j, k) is valid in Ω. Thus, let us prove this part by converting the Cartesian coordinates of r’ to the corresponding triplet coordinates. Let us compute the coordinate triplet r = (l, m, n) assigned to r’. From the first column of Table 1, the values of l, n and m, in this order can be determined. The first coordinate l = = = . In the given region i is always a positive integer, while j and k have non-positive values, moreover we can substitute them based on and by using the abbreviations , , and . Thus, we have l = = by taking into account the signs (both parts are nonnegative) and the meaning of the rounding bracket. We already know that , therefore l = = . Since the sum is even, maybe all of these integers are even or exactly two of them are odd. Further, since Rsum = − 1, either (2 > v ≥ 1 and 1 > u ≥ 0) or (1 > v ≥ 0 and 2 > u ≥ 1). Thus, based on these conditions there are the following eight cases:
- i is even, km is even, jm is even, v ≥ 1 > u. Then, by taking out the integers from the floor function l = . As 2 > v ≥ 1, = 1, and with these conditions, 6 > ≥ 3, which implies . Therefore, the value of l = . However, from it is clear that , and thus, . Consequently, in this case, l = i.
- i is even, km is even, jm is even, u ≥ 1 > v. l = , however, in this case, = 0. Further, 9 > ≥ 6, which implies . Thus, l = = i, as in the previous case.
- i is even, km is odd, jm is odd and v ≥ 1 > u. Then, l = . In this case and , and thus l = again.
- i is even, km is odd, jm is odd and u ≥ 1 > v. Then, l = . Again, and , and thus l .
- i is odd, km is even, jm is odd, v ≥ 1 > u. Then, by taking out the integers from the floor function, we get l = . In this case, we have and , and thus, l .
- i is odd, km is even, jm is odd, u ≥ 1 > v. Again, l = , where both and , thus l = i.
- i is odd, km is odd, jm is even, v ≥ 1 > u. l = , in this case , but 6 > ≥ 3, which implies , thus l = , that is l = i.
- i is odd, km is odd, jm is even, u ≥ 1 > v. l = , but now, and 9 > ≥ 6 implies . Thus, l = = i, as in the previous cases.
- B.
- This case consists the cases where either Rsum = 0 and {} ≤ {} or Rsum = −2 and {} ≥ {}. The two subcases are analogous, we shell show only the latter one here. The condition Rsum = −2 implies that both u = u1 + u2 > 1 and v = v1 + v2 > 1. The condition {} ≥ {} is the same as {j} ≥ {}, and in fact, since these values are negative, equivalent to u1 + u2 ≤ v1 + v2., i.e., u ≤ v. The procedure produces a Type B vector r = (i + u1 + u2, j + u1 + u2, k + u1 + u2). Remembering the notation jm = and km = and knowing that j = jm − u1 − u2, this can be written as r = (i + u1 + u2, jm, k + u1 + u2) = (i + u, jm, k + u) = (i + u, jm, km − v + u) with the integer coordinate jm. Let us check the sum of these coordinates: i + u + jm + km − v + u = i + jm + km + 2u − v = 2 + 2u − v (using i + jm + km = 2). In the studied case Rsum = −2 yielding that u, v > 1, thus it is larger than 2, we need to apply Step 3b of our procedure: by subtracting 1 from each coordinate, the procedure gives the resulted vector (i + u − 1, jm − 1, k + u −1). Now, let us check if it is correct by computing the Cartesian coordinate pair corresponding to this triplet. and = . Thus, exactly the vector r’= is obtained, the sum is correctly computed by our procedure. Now we are checking if the resulted triplet of r is a valid vector in Ω, by transforming r’ to coordinate triplet, let us say, (l, m, n) in Ω. In Area B, first coordinate m is computed (by Table 1), then l and n are determined. , by substituting y we have . Now, using the facts that and , we get the formula . Applying that , is obtained. In this case, however, 1 < u ≤ v, but none of them is larger than 2, which implies that −2 < v − 2u < 0, thus and this by the rounding operator, clearly implies that , which is exactly the same as the value that we have obtained by our procedure. Now, continuing with l = , the same value is obtained as the one our procedure gave. Further, we compute , which is also matching to the result of our procedure by proving this subcase: r = (i3, j3, k3) = (l, m, n) = (i + u − 1, j + u − 1, k + u − 1). (The other subcase with the conditions Rsum = 0 and {} ≤ {} can be proven in a similar way.)
- C.
- Finally, the last case consists of the cases in which either Rsum = 0 and {} > {} or Rsum = −2 and {} < {}. In this case, our procedure gives a vector of Type C in an analogous way as we have discussed the previous cases.
References
- Coxeter, H.S.M. Introduction to Geometry, 2nd ed.; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Klette, R.; Rosenfeld, A. Digital geometry: Geometric methods for digital picture analysis. In Morgan Kaufmann; Elsevier: San Francisco, CA, USA, 2004; Volume I–XVIII, pp. 1–656. ISBN 978-1-55860-861-0. [Google Scholar]
- Middleton, L.; Sivaswamy, J. Hexagonal Image Processing—A Practical Approach; Springer: London, UK, 2005. [Google Scholar]
- Carr, D.B.; Olsen, A.R.; White, D. Hexagon mosaic maps for display of univariate and bivariate geographical data. Cartogr. Geograph. Inform. Syst. 1992, 19, 228–236. [Google Scholar] [CrossRef]
- Sahr, K. Hexagonal discrete global grid systems for geospatial computing. Arch. Photogramm. Cartogr. Remote Sens. 2011, 22, 363–376. [Google Scholar]
- Sakai, K.I. Studies on the competition in plants. VII. Effect on competition of a varying number of competing and non-competing individuals. J. Genet. 1957, 55, 227–234. [Google Scholar] [CrossRef]
- Birch, C.P.; Oom, S.P.; Beecham, J.A. Rectangular and hexagonal grids used for observation, experiment and simulation in ecology. Ecol. Model. 2007, 206, 347–359. [Google Scholar] [CrossRef]
- Her, I. A symmetrical coordinate frame on the hexagonal grid for computer graphics and vision. J. Mech. Asme 1993, 115, 447–449. [Google Scholar] [CrossRef]
- Her, I. Geometric Transformations on the Hexagonal Grid. IEEE Trans. Image Proc. 1995, 4, 1213–1222. [Google Scholar] [CrossRef] [PubMed]
- Almansa, A. Sampling, Interpolation and Detection. Applications in Satellite Imaging. Ph.D. Thesis, École Normale Supérieure de Cachan-ENS Cachan, Cachan, France, 2002. [Google Scholar]
- Pluta, K.; Romon, P.; Kenmochi, Y.; Passat, N. Honeycomb geometry: Rigid motions on the hexagonal grid. In Proceedings of the International Conference on Discrete Geometry for Computer Imagery, Vienna, Austria, 19 September 2017; LNCS. Springer: Cham, Switzerland, 2017; Volume 10502, pp. 33–45. [Google Scholar]
- Stojmenović, I. Honeycomb networks. In MFCS 1995: Mathematical Foundations of Computer Science; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1995; Volume 969, pp. 267–276. [Google Scholar]
- Stojmenović, I. Honeycomb Networks: Topological Properties and Communication Algorithms. IEEE Trans. Parallel Distrib. Syst. 1997, 8, 1036–1042. [Google Scholar] [CrossRef] [Green Version]
- Nagy, B. Finding shortest path with neighbourhood sequences in triangular grids. In Proceedings of the 2nd International Symposium, in Image and Signal Processing and Analysis, Pula, Croatia, 19–21 June 2001; pp. 55–60. [Google Scholar]
- Nagy, B.; Abuhmaidan, K. A Continuous Coordinate System for the Plane by Triangular Symmetry. Symmetry 2019, 11, 191. [Google Scholar] [CrossRef] [Green Version]
- Abuhmaidan, K.; Nagy, B. Bijective, Non-Bijective and Semi-Bijective Translations on the Triangular Plane. Mathematics 2020, 8, 29. [Google Scholar] [CrossRef] [Green Version]
- Shao, Z.; Wu, P.; Zhu, E.; Chen, L. On Metric Dimension in Some Hex Derived Networks. Sensors 2019, 19, 94. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leoni, F.; Shokef, Y. Attraction Controls the Entropy of Fluctuations in Isosceles Triangular Networks. Entropy 2018, 20, 122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gelincik, S.; Rekaya-Ben Othman, G. Degrees-Of-Freedom in Multi-Cloud Based Sectored Cellular Networks. Entropy 2020, 22, 668. [Google Scholar] [CrossRef]
- Zhao, J.; Li, H.; Fang, Z.C.; Liu, Y. A mixed finite volume element method for time-fractional reaction-diffusion equations on triangular grids. Mathematics 2019, 7, 600. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Fang, Z.; Li, H.; Liu, Y. A Crank—Nicolson Finite Volume Element Method for Time Fractional Sobolev Equations on Triangular Grids. Mathematics 2020, 8, 1591. [Google Scholar] [CrossRef]
- Mejia-Parra, D.; Ruiz-Salguero, O.; Cadavid, C.; Moreno, A.; Posada, J. Level Sets of Weak-Morse Functions for Triangular Mesh Slicing. Mathematics 2020, 8, 1624. [Google Scholar] [CrossRef]
- Segarra-Martí, J.; Roca-Sanjuán, D.; Merchán, M. Can the Hexagonal Ice-like Model Render the Spectroscopic Fingerprints of Structured Water? Feedback from Quantum-Chemical Computations. Entropy 2014, 16, 4101–4120. [Google Scholar] [CrossRef] [Green Version]
- Sharafullin, I.F.; Diep, H.T. Skyrmions and Spin Waves in Magneto−Ferroelectric Superlattices. Entropy 2020, 22, 862. [Google Scholar] [CrossRef] [PubMed]
- Grishina, V.; Vikhrenko, V.; Ciach, A. Structural and Thermodynamic Peculiarities of Core-Shell Particles at Fluid Interfaces from Triangular Lattice Models. Entropy 2020, 22, 1215. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Lin, Z.; Yi, S. Method for 3D City Building Continuous Transformation Based on an Improved LOD Topological Data Structure. Isprs Int. J. Geo-Inf. 2019, 8, 504. [Google Scholar] [CrossRef] [Green Version]
- Deutsch, E.S. Thinning Algorithms on Rectangular, Hexagonal, and Triangular Arrays. Commun. Acm 1972, 15, 827–837. [Google Scholar] [CrossRef] [Green Version]
- Kardos, P.; Palágyi, K. Topology preservation on the triangular grid. Ann. Math. Artif. Intell. 2015, 75, 53–68. [Google Scholar] [CrossRef]
- Nagy, B.; Moisi, E.V. Memetic algorithms for reconstruction of binary images on triangular grids with 3 and 6 projections. Appl. Soft Comput. 2017, 52, 549–565. [Google Scholar] [CrossRef]
- Mir-Mohammad-Sadeghi, H.; Nagy, B. On the chamfer polygons on the triangular grid. In International Workshop on Combinatorial Image Analysis; IWCIA 2017, Lecture Notes in Computer Science, LNCS; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10256, pp. 53–65. [Google Scholar]
- Martínez-García, M.; Gordon, T. A new model of human steering using far-point error perception and multiplicative control. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC 2018), Miyazaki, Japan, 7–10 October 2018; pp. 1245–1250. [Google Scholar] [CrossRef]
- Martinez-Garcia, M.; Zhang, Y.; Gordon, T. Memory Pattern Identification for Feedback Tracking Control in Human—Machine Systems. Hum. Factors 2021, 63, 210–226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pluta, K.; Romon, P.; Kenmochi, Y.; Passat, N. Bijective rigid motions of the 2D Cartesian grid. In DGCI 2016: Discrete Geometry for Computer Imagery; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9647, pp. 359–371. [Google Scholar]
- Nouvel, B.; Rémila, E. Configurations induced by discrete rotations: Periodicity and quasi-periodicity properties. Discret. Appl. Math. 2005, 147, 325–343. [Google Scholar] [CrossRef] [Green Version]
- Pluta, K.; Romon, P.; Kenmochi, Y.; Passat, N. Bijective Digitized Rigid Motions on Subsets of the Plane. J. Math. Imaging Vis. 2017, 59, 84–105. [Google Scholar] [CrossRef]
- Nagy, B. Transformations of the triangular grid. In Proceedings of the GRAFGEO: Third Hungarian Conference on Computer Graphics and Geometry, Budapest, Hungary, 17–18 November 2005; pp. 155–162. [Google Scholar]
- Nagy, B. Isometric transformations of the dual of the hexagonal lattice. In Proceedings of the 6th International Symposium on Image and Signal Processing and Analysis, Salzburg, Austria, 16–18 September 2009; pp. 432–437. [Google Scholar]
- Nagy, B. Generalized triangular grids in digital geometry. Acta Math. Acad. Paedagog. Nyházi 2004, 20, 63–78. [Google Scholar]
- Skala, V. Barycentric coordinates computation in homogeneous coordinates. Comput. Graph. 2008, 32, 120–127. [Google Scholar] [CrossRef]
- Avkan, A.; Nagy, B.; Saadetoglu, M. Digitized Rotations of 12 Neighbors on the Triangular Grid. Ann. Math. Artif. Intell. 2020, 88, 833–857. [Google Scholar] [CrossRef]














| Area A | Area B | Area C | |
|---|---|---|---|
| i | |||
| j | |||
| k |
| Sample (a) | Sample (b) | Sample (c) | Sample (d) | Sample (e) | |
|---|---|---|---|---|---|
| Vector1 | (1.0,−0.6,−0.1) | (1.0,−0.6,−0.3) | (1.0,−0.6, −0.1) | (1.0,−0.9,−0.4) | (1.0,−0.9,−0.4) |
| Vector2 | (1.0,−0.9,−0.7) | (1.0,−0.9,−0.7) | (1.0,−0.2,−0.7) | (1.9,−1.0,−0.9) | (1.9,−1.0,−0.5) |
| direct-sum | (2.0,−1.5,−0.8) | (2.0,−1.4,−1.09) | (2.0,−0.8,−0.8) | (2.9,−1.9,−1.3) | (2.9,−1.9,−0.9) |
| 2, −2, −1 | 2, −2, −2 | 2, −1, −1 | 3, −2, −2 | 3, −2, −1 | |
| Rsum | −1 | −2 | 0 | −1 | 0 |
| Region | (+, −, −) | (+, −, −) | (+, −, −) | (+, −, −) | (+, −, −) |
| Regions | Vectors of Type (A + A) |
| (−, −, + ) (−, +, −) (+, −, + ) (+, +, −) | IF (Rsum = 0) THEN result-vector type is A |
| IF (Rsum = 1) & ({}≤{}) THEN result-vector type is B ELSE C | |
| IF (Rsum = −1) & ({}≥{}) THEN result-vector type is B ELSE C | |
| (−, +, + ) | IF (Rsum = 1) THEN result-vector type is A |
| IF (Rsum = 0) & ({}≥{}) THEN result-vector type is B ELSE C | |
| IF (Rsum = 2) & ({}≤{}) THEN result-vector type is B ELSE C | |
| (+, −, −) | IF (Rsum = −1) THEN result-vector type is A |
| IF (Rsum = 0) & ({}≤{}) THEN result-vector type is B ELSE C | |
| IF (Rsum = −2) & ({}≥{}) THEN result-vector type is B ELSE C | |
| Regions | Vectors of type (B + B) |
| (−, +, + ) (−, −, + ) (+, −, −) (+, +, −) | IF (Rsum = 0) THEN result-vector type is B |
| IF (Rsum = 1) & ({}≤{}) THEN result-vector type is A ELSE C | |
| IF (Rsum = −1) & ({}≥{}) THEN result-vector type is A ELSE C | |
| (+, −, + ) | IF (Rsum = 1) THEN result-vector type is B |
| IF (Rsum = 0) & ({}≥{}) THEN result-vector type is A ELSE C | |
| IF (Rsum = 2) & ({}≤{}) THEN result-vector type is A ELSE C | |
| (−, +, −) | IF (Rsum = −1) THEN result-vector type is B |
| IF (Rsum = 0) & ({}≤{}) THEN result-vector type is A ELSE C | |
| IF (Rsum = 2) & ({}≥{}) THEN result-vector type is A ELSE C | |
| Regions | Vectors of type (C + C) |
| (−, +, + ) (+, −, + ) (+, −, −) (−, +, −) | IF (Rsum = 0) THEN result-vector is of type C |
| IF (Rsum = 1) & ({}≤{}) THEN result-vector is of type A ELSE B | |
| IF (Rsum = −1) & ({}≥{}) THEN result-vector is of type A ELSE B | |
| (−, −, + ) | IF (Rsum = −1) THEN result-vector is of type C |
| IF (Rsum = 0) & ({}≤{}) THEN result-vector is of type A ELSE B | |
| IF (Rsum = −2) & ({}≥{}) THEN result-vector is of type A ELSE B | |
| (+, +, −) | IF (Rsum = 1) THEN result-vector is of type C |
| IF (Rsum = 0) & ({}≥{}) THEN result-vector is of type A ELSE B | |
| IF (Rsum = 2) & ({}≤{}) THEN result-vector is of type A ELSE B | |
| Regions | Vectors of type (A + B) or (A + C) or (B + C) |
| (−, −, + ) (−, +, −) (+, −, −) | IF (Rsum = 0) THEN Min({},{},{}) is the result-vector type * IF (Rsum = −1) THEN Max({},{},{}) is the result-vector type * |
| (+, −, + ) (+, +, −) (−, +, + ) | IF (Rsum = 0) THEN Max({},{},{}) is the result-vector type * IF (Rsum = 1) THEN Min({},{},{})is the result-vector type * |
| Sample (a) | Sample (b) | Sample (c) | |
|---|---|---|---|
| v1 = (i1, j1, k1) | (1.577, −2.0, 0.423) | (1.155, −1.423, 0.0) | (1.0, −0.735, −0.270) |
| v2 = (i2, j2, k2) | (1.005, 0.0, −1.305) | (0.808, 0.0, −0.808) | (1.0, −0.966, −0.732) |
| Step 1 | |||
| direct-sum | (2.582, −2.0, −0.882) | (1.963, −1.423, −0.808) | (2.0, −1.701, −1.002) |
| Rsum | 3 + (−2) + (−1) = 0 | 2 + (−2) + (−1) = −1 | 2 + (−2) + (−2) = −2 |
| Region | (+, −, −) | (+, −, −) | (+, −, −) |
| Step 2 | |||
| Rule 1 and 2 | If (Rsum = 0) Then B | If (Rsum = −1) Then Max({},{},{}) | If (Rsum = −2) & ({} ≥ {}) Then B else C |
| Apply Rule 1 and 2 | − | Max ((0.963−1), −0.423, −0.808) = −0.037 = {} | (−0.701) (−0.002) |
| Type of Result-vector | B | A | C |
| Step 3 | |||
| a) s = | (i − ({j1} + {j2}, j − ({j1} + {j2}), k − ({j1} + {j2}) ) | (i − ({i1} + {i2}), j − ({i1} + {i2}), k − ({i1} + {i2}) ) | (i − ({k1} + {k2}), j − ({k1 } + {k2}), k − ({k1} + {k2}) ) |
| Apply a) s = | (2.582,−2.0,−0.882) | (1.0, −2.386, −1.771) | (3.002, −0.699, 0.0) |
| b) Sum = | Sum = −0.3, then no need for addition or subtraction of 1 | Sum = −3.157 < −2, then add 1 to each coordinate value | Sum = 2.303 > 2, then Subtract 1 from each coordinate value |
| Result-vector | (2.582, −2.0, −0.882) | (2.0, −1.386, −0.771) | (2.002, −1.699, −1.0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abuhmaidan, K.; Aldwairi, M.; Nagy, B. Vector Arithmetic in the Triangular Grid. Entropy 2021, 23, 373. https://doi.org/10.3390/e23030373
Abuhmaidan K, Aldwairi M, Nagy B. Vector Arithmetic in the Triangular Grid. Entropy. 2021; 23(3):373. https://doi.org/10.3390/e23030373
Chicago/Turabian StyleAbuhmaidan, Khaled, Monther Aldwairi, and Benedek Nagy. 2021. "Vector Arithmetic in the Triangular Grid" Entropy 23, no. 3: 373. https://doi.org/10.3390/e23030373
APA StyleAbuhmaidan, K., Aldwairi, M., & Nagy, B. (2021). Vector Arithmetic in the Triangular Grid. Entropy, 23(3), 373. https://doi.org/10.3390/e23030373