Quantifying Athermality and Quantum Induced Deviations from Classical Fluctuation Relations
Abstract
1. Introduction
2. Background
2.1. Classical Fluctuation Relations
2.2. Fully Quantum Fluctuation Relations
3. Results
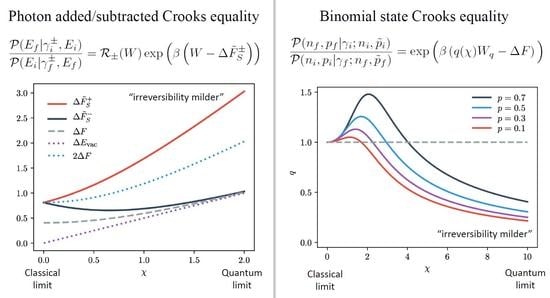
3.1. Photon Added and Subtracted Thermal States
3.2. Binomial States
- Forwards: The battery B is prepared in the state and measured in
- Reverse: The battery B is prepared in the state and measured in .
- Forwards: The battery B is prepared in the state and measured in .
- Reverse: The battery B is prepared in the state and measured in .
3.3. Energy Translation Invariance, Jarzynski Relations and Stochastic Entropy Production
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Photon Added and Subtracted Crooks Equality
Appendix B. Derivation of Binomial State Properties
Appendix B.1. The Quantum Distortion Factor for Binomial States
Appendix B.2. The Harmonic Limit
References
- Guggenheim, E.A. The Thermodynamics of Magnetization. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1936, 155, 70–101. [Google Scholar] [CrossRef]
- Alloul, H. Thermodynamics of Superconductors; Springer: Berlin/Heidelberg, Germany, 2011; pp. 175–199. [Google Scholar] [CrossRef]
- Page, D.N. Hawking radiation and black hole thermodynamics. New J. Phys. 2005, 7, 203. [Google Scholar] [CrossRef]
- Schrödinger, E.; Penrose, R. What is Life?: With Mind and Matter and Autobiographical Sketches; Canto, Cambridge University Press: Cambridge, UK, 1992. [Google Scholar] [CrossRef]
- Haynie, D. Biological Thermodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Ott, J.; Boerio-Goates, J. Chemical Thermodynamics: Principles and Applications: Principles and Applications; Elsevier Science: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Callen, H.; Callen, H.; Sons, W. Thermodynamics and an Introduction to Thermostatistics; Wiley: Hoboken, NJ, USA, 1985. [Google Scholar]
- Jarzynski, C. Equalities and Inequalities: Irreversibility and the Second Law of Thermodynamics at the Nanoscale. Annu. Rev. Condens. Matter Phys. 2011, 2, 329–351. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar] [CrossRef]
- Talkner, P.; Hänggi, P. The Tasaki–Crooks quantum fluctuation theorem. J. Phys. Math. Theor. 2007, 40, F569. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J. Equilibrium microstates which generate second law violating steady states. Phys. Rev. E 1994, 50, 1645–1648. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Tasaki, H. Jarzynski Relations for Quantum Systems and Some Applications. arXiv 2000, arXiv:cond-mat/0009244. [Google Scholar]
- Kurchan, J. A Quantum Fluctuation Theorem. arXiv 2000, arXiv:cond-mat/0007360. [Google Scholar]
- Hänggi, P.; Talkner, P. The other QFT. Nat. Phys. 2015, 11, 108. [Google Scholar] [CrossRef]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771–791. [Google Scholar] [CrossRef]
- Albash, T.; Lidar, D.A.; Marvian, M.; Zanardi, P. Fluctuation theorems for quantum processes. Phys. Rev. E 2013, 88, 032146. [Google Scholar] [CrossRef]
- Manzano, G.; Horowitz, J.M.; Parrondo, J.M.R. Nonequilibrium potential and fluctuation theorems for quantum maps. Phys. Rev. E 2015, 92, 032129. [Google Scholar] [CrossRef]
- Rastegin, A.E. Non-equilibrium equalities with unital quantum channels. J. Stat. Mech. Theory Exp. 2013, 2013, P06016. [Google Scholar] [CrossRef]
- Campisi, M.; Talkner, P.; Hänggi, P. Fluctuation Theorem for Arbitrary Open Quantum Systems. Phys. Rev. Lett. 2009, 102, 210401. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium work theorem for a system strongly coupled to a thermal environment. J. Stat. Mech. Theory Exp. 2004, 2004, P09005. [Google Scholar] [CrossRef]
- Solinas, P.; Miller, H.J.D.; Anders, J. Measurement-dependent corrections to work distributions arising from quantum coherences. Phys. Rev. A 2017, 96, 052115. [Google Scholar] [CrossRef]
- Allahverdyan, A.E. Nonequilibrium quantum fluctuations of work. Phys. Rev. E 2014, 90, 032137. [Google Scholar] [CrossRef] [PubMed]
- Miller, H.J.D.; Anders, J. Time-reversal symmetric work distributions for closed quantum dynamics in the histories framework. New J. Phys. 2017, 19, 062001. [Google Scholar] [CrossRef]
- Elouard, C.; Mohammady, M.H. Work, Heat and Entropy Production Along Quantum Trajectories. In Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions; Binder, F., Correa, L.A., Gogolin, C., Anders, J., Adesso, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 363–393. [Google Scholar] [CrossRef]
- Horowitz, J.M. Quantum-trajectory approach to the stochastic thermodynamics of a forced harmonic oscillator. Phys. Rev. E 2012, 85, 31110. [Google Scholar] [CrossRef] [PubMed]
- Elouard, C.; Herrera-Martí, D.A.; Clusel, M.; Auffèves, A. The role of quantum measurement in stochastic thermodynamics. npj Quantum Inf. 2017, 3, 9. [Google Scholar] [CrossRef]
- Åberg, J. Fully Quantum Fluctuation Theorems. Phys. Rev. X 2018, 8, 11019. [Google Scholar] [CrossRef]
- Alhambra, A.M.; Masanes, L.; Oppenheim, J.; Perry, C. Fluctuating Work: From Quantum Thermodynamical Identities to a Second Law Equality. Phys. Rev. X 2016, 6, 041017. [Google Scholar] [CrossRef]
- Kwon, H.; Kim, M.S. Fluctuation Theorems for a Quantum Channel. Phys. Rev. X 2019, 9, 031029. [Google Scholar] [CrossRef]
- Holmes, Z. The Coherent Crooks Equality. In Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions; Binder, F., Correa, L.A., Gogolin, C., Anders, J., Adesso, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 301–316. [Google Scholar] [CrossRef]
- Horodecki, M.; Oppenheim, J. Fundamental limitations for quantum and nanoscale thermodynamics. Nat. Commun. 2013, 4, 2059. [Google Scholar] [CrossRef]
- Brandão, F.; Horodecki, M.; Ng, N.; Oppenheim, J.; Wehner, S. The second laws of quantum thermodynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 3275–3279. [Google Scholar] [CrossRef]
- Åberg, J. Truly work-like work extraction via a single-shot analysis. Nat. Commun. 2013, 4, 1925. [Google Scholar] [CrossRef]
- Gour, G.; Jennings, D.; Buscemi, F.; Duan, R.; Marvian, I. Quantum majorization and a complete set of entropic conditions for quantum thermodynamics. Nat. Commun. 2018, 9, 5352. [Google Scholar] [CrossRef]
- Lostaglio, M.; Jennings, D.; Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 2015, 6, 6383. [Google Scholar] [CrossRef]
- Åberg, J. Catalytic Coherence. Phys. Rev. Lett. 2014, 113, 150402. [Google Scholar] [CrossRef] [PubMed]
- Korzekwa, K.; Lostaglio, M.; Oppenheim, J.; Jennings, D. The extraction of work from quantum coherence. New J. Phys. 2016, 18, 023045. [Google Scholar] [CrossRef]
- Holmes, Z.; Weidt, S.; Jennings, D.; Anders, J.; Mintert, F. Coherent fluctuation relations: From the abstract to the concrete. Quantum 2019, 3, 124. [Google Scholar] [CrossRef]
- Mingo, E.H.; Jennings, D. Decomposable coherence and quantum fluctuation relations. Quantum 2019, 3, 202. [Google Scholar] [CrossRef]
- Zavatta, A.; Parigi, V.; Kim, M.S.; Bellini, M. Subtracting photons from arbitrary light fields: Experimental test of coherent state invariance by single-photon annihilation. New J. Phys. 2008, 10, 123006. [Google Scholar] [CrossRef]
- Ueda, M.; Imoto, N.; Ogawa, T. Quantum theory for continuous photodetection processes. Phys. Rev. A 1990, 41, 3891–3904. [Google Scholar] [CrossRef]
- Barnett, S.M.; Ferenczi, G.; Gilson, C.R.; Speirits, F.C. Statistics of photon-subtracted and photon-added states. Phys. Rev. A 2018, 98, 013809. [Google Scholar] [CrossRef]
- Zavatta, A.; Parigi, V.; Bellini, M. Experimental nonclassicality of single-photon-added thermal light states. Phys. Rev. A 2007, 75, 052106. [Google Scholar] [CrossRef]
- Hlousek, J.; Jezek, M.; Filip, R. Work and information from thermal states after subtraction of energy quanta. Sci. Rep. 2017, 7, 13046. [Google Scholar] [CrossRef]
- Vidrighin, M.D.; Dahlsten, O.; Barbieri, M.; Kim, M.S.; Vedral, V.; Walmsley, I.A. Photonic Maxwell’s Demon. Phys. Rev. Lett. 2016, 116, 050401. [Google Scholar] [CrossRef]
- Quantum communication with photon-added coherent states. Quantum Inf. Process. 2013, 12, 537–547. [CrossRef]
- Braun, D.; Jian, P.; Pinel, O.; Treps, N. Precision measurements with photon-subtracted or photon-added Gaussian states. Phys. Rev. A 2014, 90, 013821. [Google Scholar] [CrossRef]
- Mari, A.; Eisert, J. Positive Wigner Functions Render Classical Simulation of Quantum Computation Efficient. Phys. Rev. Lett. 2012, 109, 230503. [Google Scholar] [CrossRef]
- Walschaers, M.; Fabre, C.; Parigi, V.; Treps, N. Entanglement and Wigner Function Negativity of Multimode Non-Gaussian States. Phys. Rev. Lett. 2017, 119, 183601. [Google Scholar] [CrossRef] [PubMed]
- Perelomov, A. Generalized Coherent States and Their Applications; Theoretical and Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Arecchi, F.T.; Courtens, E.; Gilmore, R.; Thomas, H. Atomic Coherent States in Quantum Optics. Phys. Rev. A 1972, 6, 2211–2237. [Google Scholar] [CrossRef]
- Stoler, D.; Saleh, B.; Teich, M. Binomial States of the Quantized Radiation Field. Opt. Acta Int. J. Opt. 1985, 32, 345–355. [Google Scholar] [CrossRef]
- Vidiella-Barranco, A.; Roversi, J.A. Statistical and phase properties of the binomial states of the electromagnetic field. Phys. Rev. A 1994, 50, 5233–5241. [Google Scholar] [CrossRef]
- Maleki, Y.; Maleki, A. Entangled multimode spin coherent states of trapped ions. J. Opt. Soc. Am. B 2018, 35, 1211–1217. [Google Scholar] [CrossRef]
- Miry, S.R.; Tavassoly, M.K.; Roknizadeh, R. On the generation of number states, their single- and two-mode superpositions, and two-mode binomial state in a cavity. J. Opt. Soc. Am. B 2014, 31, 270–276. [Google Scholar] [CrossRef]
- Garling, D.J.H. Inequalities: A Journey into Linear Analysis; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Baştuğ, T.; Kuyucak, S. Application of Jarzynski’s equality in simple versus complex systems. Chem. Phys. Lett. 2007, 436, 383–387. [Google Scholar] [CrossRef]
- West, D.K.; Olmsted, P.D.; Paci, E. Free energy for protein folding from nonequilibrium simulations using the Jarzynski equality. J. Chem. Phys. 2006, 125, 204910. [Google Scholar] [CrossRef] [PubMed]
- Gittes, F. Two famous results of Einstein derived from the Jarzynski equality. Am. J. Phys. 2018, 86, 31–35. [Google Scholar] [CrossRef]
- Deffner, S.; Jarzynski, C. Information Processing and the Second Law of Thermodynamics: An Inclusive, Hamiltonian Approach. Phys. Rev. X 2013, 3, 041003. [Google Scholar] [CrossRef]
- Ballentine, L. Quantum Mechanics: A Modern Development; World Scientific: Singapore, 1998. [Google Scholar]
- Crooks, G.E. Quantum operation time reversal. Phys. Rev. A 2008, 77, 034101. [Google Scholar] [CrossRef]
- Jones, G.N.; Haight, J.; Lee, C.T. Nonclassical effects in the photon-added thermal state. Quantum Semiclassical Opt. J. Eur. Soc. Part B 1997, 9, 411–418. [Google Scholar] [CrossRef]
- Usha Devi, A.R.; Prabhu, R.; Uma, M.S. Non-classicality of photon added coherent and thermal radiations. Eur. Phys. J. D 2006, 40, 133–138. [Google Scholar] [CrossRef]
- Hu, L.-Y.; Fan, H.-Y. Wigner function and density operator of the photon-subtracted squeezed thermal state. Chin. Phys. B 2009, 18, 4657–4661. [Google Scholar] [CrossRef]
- Bogdanov, Y.I.; Katamadze, K.G.; Avosopiants, G.V.; Belinsky, L.V.; Bogdanova, N.A.; Kalinkin, A.A.; Kulik, S.P. Multiphoton subtracted thermal states: Description, preparation, and reconstruction. Phys. Rev. A 2017, 96, 063803. [Google Scholar] [CrossRef]
- Li, J.; Gröblacher, S.; Zhu, S.Y.; Agarwal, G.S. Generation and detection of non-Gaussian phonon-added coherent states in optomechanical systems. Phys. Rev. A 2018, 98, 011801. [Google Scholar] [CrossRef]
- Fu, H.C.; Sasaki, R. Negative binomial and multinomial states: Probability distributions and coherent states. J. Math. Phys. 1997, 38, 3968–3987. [Google Scholar] [CrossRef]
- Lee Loh, Y.; Kim, M. Visualizing spin states using the spin coherent state representation. Am. J. Phys. 2015, 83, 30–35. [Google Scholar] [CrossRef]
- Sperling, J.; Walmsley, I.A. Quasiprobability representation of quantum coherence. Phys. Rev. A 2018, 97, 062327. [Google Scholar] [CrossRef]
- Atkins, P.W.; Dobson, J.C.; Coulson, C.A. Angular momentum coherent states. Proc. R. Soc. London. Math. Physical Sci. 1971, 321, 321–340. [Google Scholar] [CrossRef]
- Zelaya, K.D.; Rosas-Ortiz, O. Optimized Binomial Quantum States of Complex Oscillators with Real Spectrum. J. Phys. Conf. Ser. 2016, 698, 12026. [Google Scholar] [CrossRef]
- Skotiniotis, M.; Gour, G. Alignment of reference frames and an operational interpretation for theG-asymmetry. New J. Phys. 2012, 14, 073022. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef]
- Kieferová, M.; Scherer, A.; Berry, D.W. Simulating the dynamics of time-dependent Hamiltonians with a truncated Dyson series. Phys. Rev. A 2019, 99, 042314. [Google Scholar] [CrossRef]
- Lukacs, E. Characteristic Functions; Griffin Books of Cognate Interest; Hafner Publishing Company: New York, NY, USA, 1970. [Google Scholar]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holmes, Z.; Hinds Mingo, E.; Chen, C.Y.-R.; Mintert, F. Quantifying Athermality and Quantum Induced Deviations from Classical Fluctuation Relations. Entropy 2020, 22, 111. https://doi.org/10.3390/e22010111
Holmes Z, Hinds Mingo E, Chen CY-R, Mintert F. Quantifying Athermality and Quantum Induced Deviations from Classical Fluctuation Relations. Entropy. 2020; 22(1):111. https://doi.org/10.3390/e22010111
Chicago/Turabian StyleHolmes, Zoë, Erick Hinds Mingo, Calvin Y.-R. Chen, and Florian Mintert. 2020. "Quantifying Athermality and Quantum Induced Deviations from Classical Fluctuation Relations" Entropy 22, no. 1: 111. https://doi.org/10.3390/e22010111
APA StyleHolmes, Z., Hinds Mingo, E., Chen, C. Y.-R., & Mintert, F. (2020). Quantifying Athermality and Quantum Induced Deviations from Classical Fluctuation Relations. Entropy, 22(1), 111. https://doi.org/10.3390/e22010111