Crystallisation in Melts of Short, Semi-Flexible Hard-Sphere Polymer Chains: The Role of the Non-Bonded Interaction Range
Abstract
:1. Introduction
2. Materials and Methods
3. Results
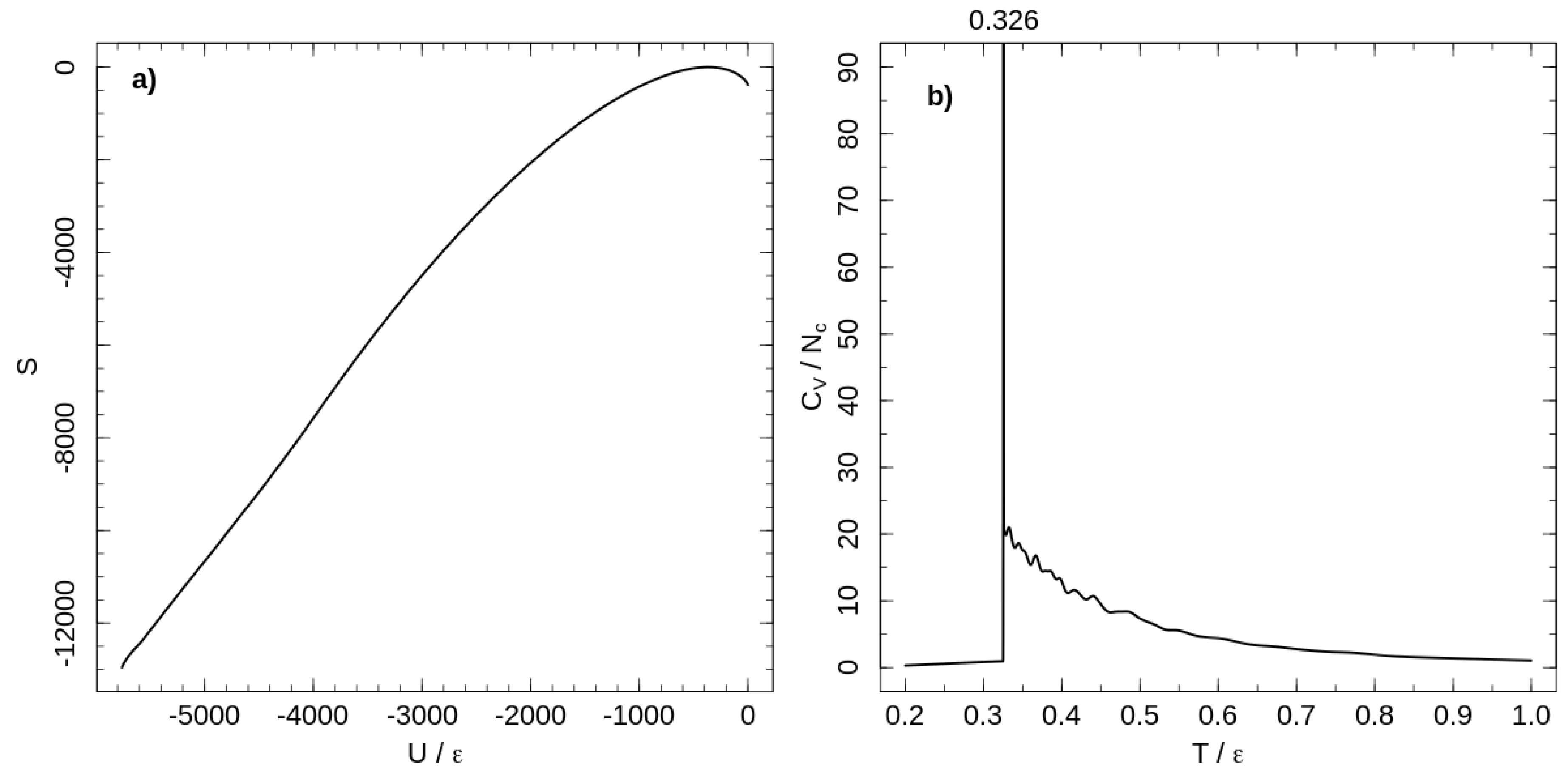
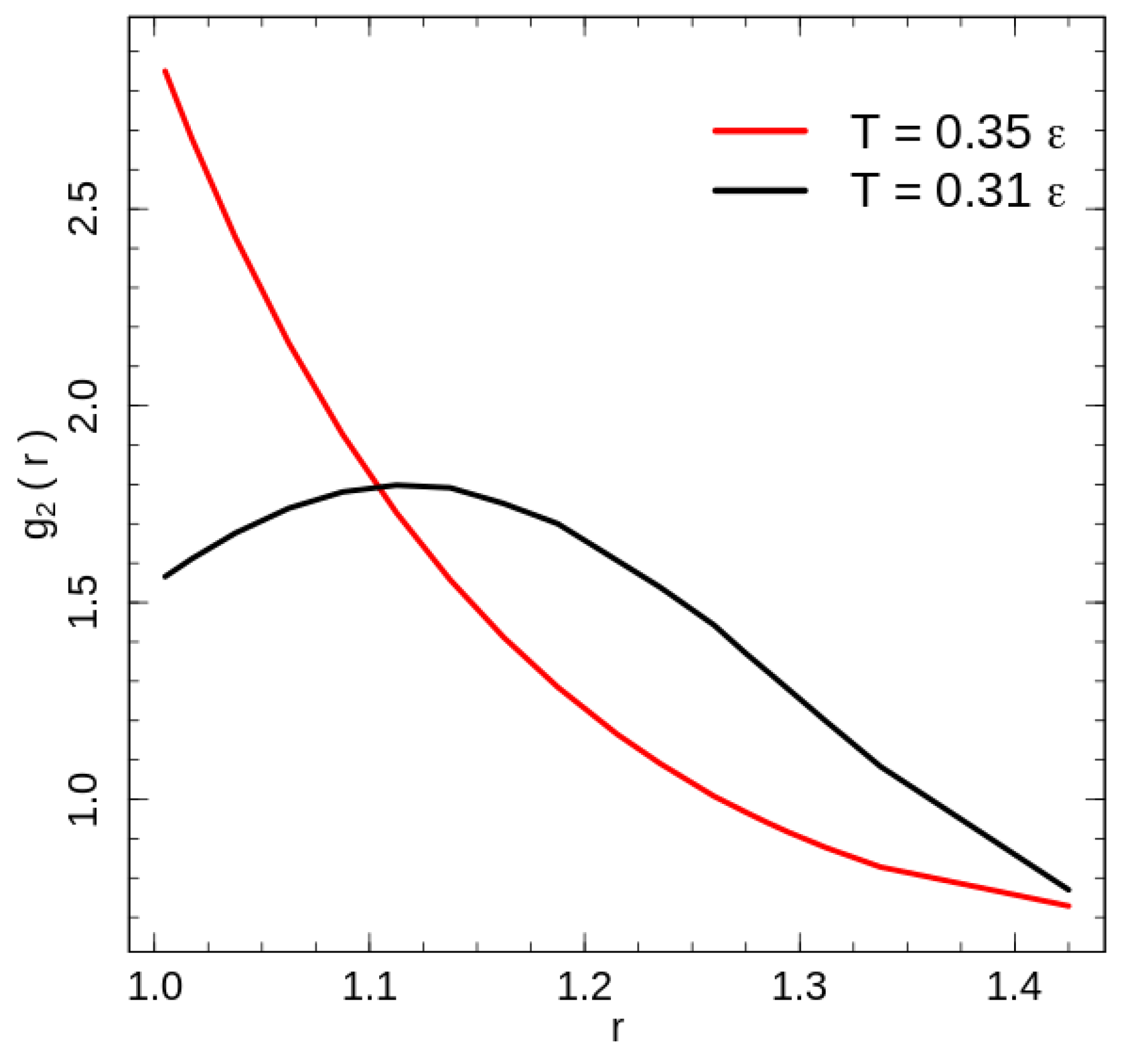
3.1. Structural Properties of the Non-Perturbed System
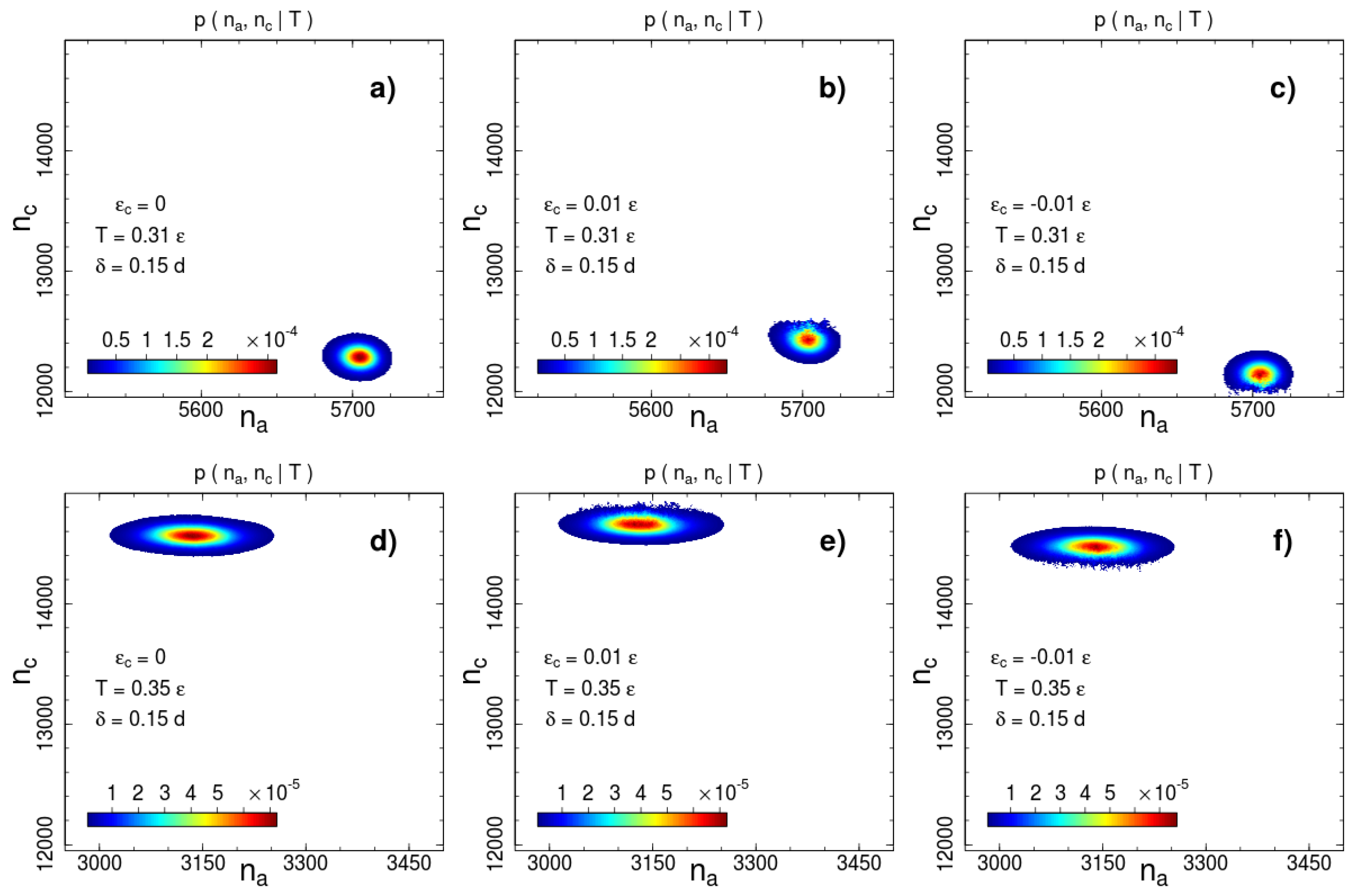
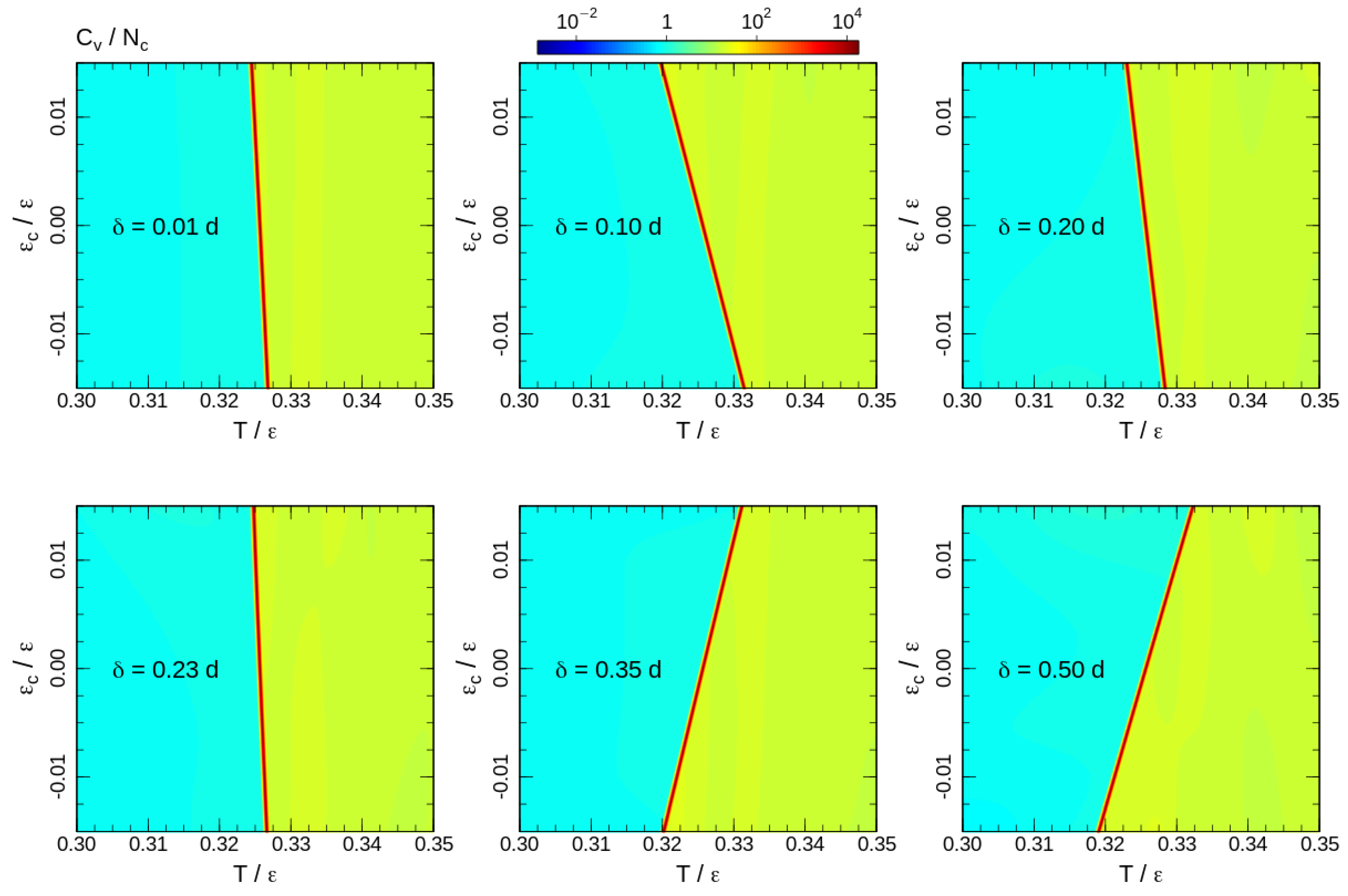
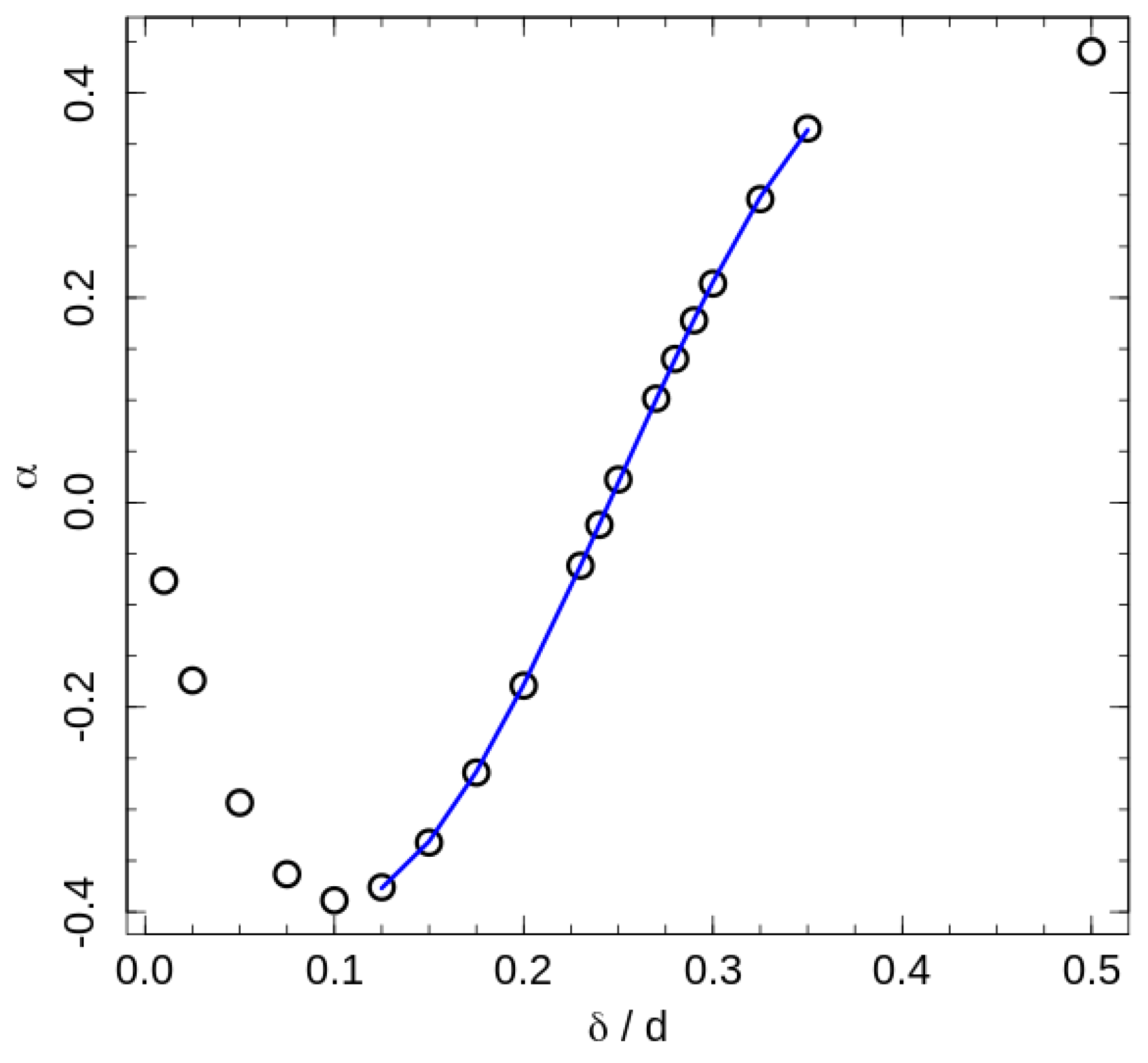
3.2. The Role of Non-Bonded Interactions
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FCC | Face-centred cubic |
| HCP | Hexagonal close packed |
| BCC | Body-centred cubic |
| DOS | Density of states |
| SAMC | stochastic approximation Monte Carlo |
| 1D | one-dimensional |
| 2D | two-dimensional |
References
- Karayiannis, N.C.; Laso, M. Dense and nearly jammed random packings of freely jointed chains of tangent hard spheres. Phys. Rev. Lett. 2008, 100, 050602. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-driven crystallisation in dense systems of athermal chain molecules. Phys. Rev. Lett. 2009, 103, 045703. [Google Scholar] [CrossRef] [PubMed]
- Engel, M.; Anderson, J.A.; Glotzer, S.C.; Isobe, M.; Bernard, E.P.; Krauth, W. Hard-disk equation of state: First-order liquid-hexatic transition in two dimensions with three simulation methods. Phys. Rev. E 2013, 87, 042134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, M.P. Collapse transition for isolated square-well chain molecules: The exact density of states for short chains. J. Chem. Phys. 2003, 118, 883–891. [Google Scholar] [CrossRef]
- Taylor, M.P.; Paul, W.; Binder, K. All-or-none proteinlike folding transition of a flexible homopolymer chain. Phys. Rev. E 2009, 79, 050801. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.P.; Paul, W.; Binder, K. Phase transitions of a single polymer chain: A Wang–Landau simulation study. J. Chem. Phys. 2009, 131, 114907. [Google Scholar] [CrossRef] [PubMed]
- Shakirov, T.; Paul, W. Folded alkane chains and the emergence of the lamellar crystal. J. Chem. Phys. 2019, 150, 084903. [Google Scholar] [CrossRef] [PubMed]
- Khokhlov, A.R.; Semenov, A.N. On the theory of liquid-crystalline ordering of polymer chains with limited flexibility. J. Stat. Phys. 1985, 38, 161–182. [Google Scholar] [CrossRef]
- Anwar, M.; Turci, F.; Schilling, T. Crystallisation mechanism in melts of short n-alkane chains. J. Chem. Phys. 2013, 139, 214904. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Smith, T.B.; Hoy, R.S.; Karayiannis, N.C. Effect of chain stiffness on the competition between crystallization and glass-formation in model unentangled polymers. J. Chem. Phys. 2015, 143, 144901. [Google Scholar] [CrossRef]
- Rochette, C.N.; Rosefeldt, S.; Henzler, K.; Polzer, F.; Ballauf, M.; Tong, Q.; Mecking, S.; Drechsler, M.; Narayanan, T.; Harnau, L. Annealing of Single Lamella Nanoparticles of Polyethylene. Macromolecules 2011, 44, 4845–4851. [Google Scholar] [CrossRef] [Green Version]
- Osichov, A.; Rabe, C.; Vogtt, K.; Narayanan, T.; Harnau, L.; Drechsler, M.; Ballauf, M.; Mecking, S. Ideal polyethylene nanocrystals. J. Am. Chem. Soc. 2013, 135, 11645–11650. [Google Scholar] [CrossRef] [PubMed]
- Bu, H.; Pang, Y.; Song, D.; Yu, T.; Voll, T.M.; Czronyj, G.; Wunderlich, B. Single-molecule single crystals. J. Polym Sci. B, Polym. Phys. 1991, 29, 139–152. [Google Scholar] [CrossRef]
- Werlich, B.; Taylor, M.; Shakirov, T.; Paul, W. On the Pseudo Phase Diagram of Single Semi-Flexible Polymer Chains: A Flat-Histogram Monte Carlo Study. Polymers 2017, 9, 38. [Google Scholar] [CrossRef] [PubMed]
- Liang, F.; Liu, C.; Carroll, R.J. Stochastic approximation in Monte Carlo computation. J. Am. Stat. Assoc. 2007, 102, 305–320. [Google Scholar] [CrossRef]
- Liang, F.; Liu, C.; Carroll, R.J. Stochastic Approximation Monte Carlo. In Advanced Markov Chain Monte Carlo Methods: Learning from Past Samples; John Wiley & Sons: Chichester, UK, 2011; pp. 207–218. [Google Scholar]
- Shakirov, T. Convergence estimation of flat-histogram algorithms based on simulation results. Comput. Phys. Commun. 2018, 228, 38–43. [Google Scholar] [CrossRef]
- Shakirov, T.; Paul, W. Crystallisation in melts of short, semiflexible hard polymer chains: An interplay of entropies and dimensions. Phys. Rev. E 2018, 97, 042501. [Google Scholar] [CrossRef]
- Sirota, E.B.; King, H.E., Jr.; Singer, D.M.; Shao, H.H. Rotator phases of the normal alkanes: An X-ray scattering study. J. Chem. Phys. 1993, 98, 5809–5824. [Google Scholar] [CrossRef]
- Sirota, E.B.; Singer, D.M. Phase transitions among the rotator phases of the normal alkanes. J. Chem. Phys. 1994, 101, 10873–10882. [Google Scholar] [CrossRef]
- Wentzel, N.; Milner, S.T. Crystal and rotator phases of n-alkanes: A molecular dynamics study. J. Chem. Phys. 2010, 132, 044901. [Google Scholar] [CrossRef]
- Milner, S.T.; Wentzel, N. Twist solitons in ordered phases of n-alkanes. Soft Matter 2011, 7, 7477–7492. [Google Scholar] [CrossRef]
- Zablotskiy, S.V.; Ivanov, V.A.; Paul, W. Multidimensional stochastic approximation Monte Carlo. Phys. Rev. E 2016, 93, 063303. [Google Scholar] [CrossRef] [PubMed]
- Maltseva, D.; Zablotskiy, S.V.; Martemyanova, J.; Ivanov, V.A.; Shakirov, T.; Paul, W. Diagrams of States of Single Flexible-Semiflexible Multi-Block Copolymer Chains: A Flat-Histogram Monte Carlo Study. Polymers 2019, 11, 757. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.R.; Zhang, R.F. AACSD: An atomistic analyzer for crystal structure and defects. Comput. Phys. Commun. 2018, 222, 229–239. [Google Scholar] [CrossRef]
- Gil-Villegas, A.; del Río, F.; Vega, C. Thermodynamics of fluids obtained by mapping the collision properties. Phys. Rev. E 1996, 53, 2326. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakirov, T. Crystallisation in Melts of Short, Semi-Flexible Hard-Sphere Polymer Chains: The Role of the Non-Bonded Interaction Range. Entropy 2019, 21, 856. https://doi.org/10.3390/e21090856
Shakirov T. Crystallisation in Melts of Short, Semi-Flexible Hard-Sphere Polymer Chains: The Role of the Non-Bonded Interaction Range. Entropy. 2019; 21(9):856. https://doi.org/10.3390/e21090856
Chicago/Turabian StyleShakirov, Timur. 2019. "Crystallisation in Melts of Short, Semi-Flexible Hard-Sphere Polymer Chains: The Role of the Non-Bonded Interaction Range" Entropy 21, no. 9: 856. https://doi.org/10.3390/e21090856




