An Expression for Velocity Lag in Sediment-Laden Open-Channel Flows Based on Tsallis Entropy Together with the Principle of Maximum Entropy
Abstract
:1. Introduction
2. Tsallis Entropy for Velocity Lag
2.1. Definition of the Tsallis Entropy
2.2. Constraint Equations
2.3. Maximization of Entropy
2.4. Determination of Lagrange Multipliers
2.5. Hypothesis for the Cumulative Distribution Function of Velocity Lag
2.6. Derivation of Velocity Lag
2.7. Reparameterization
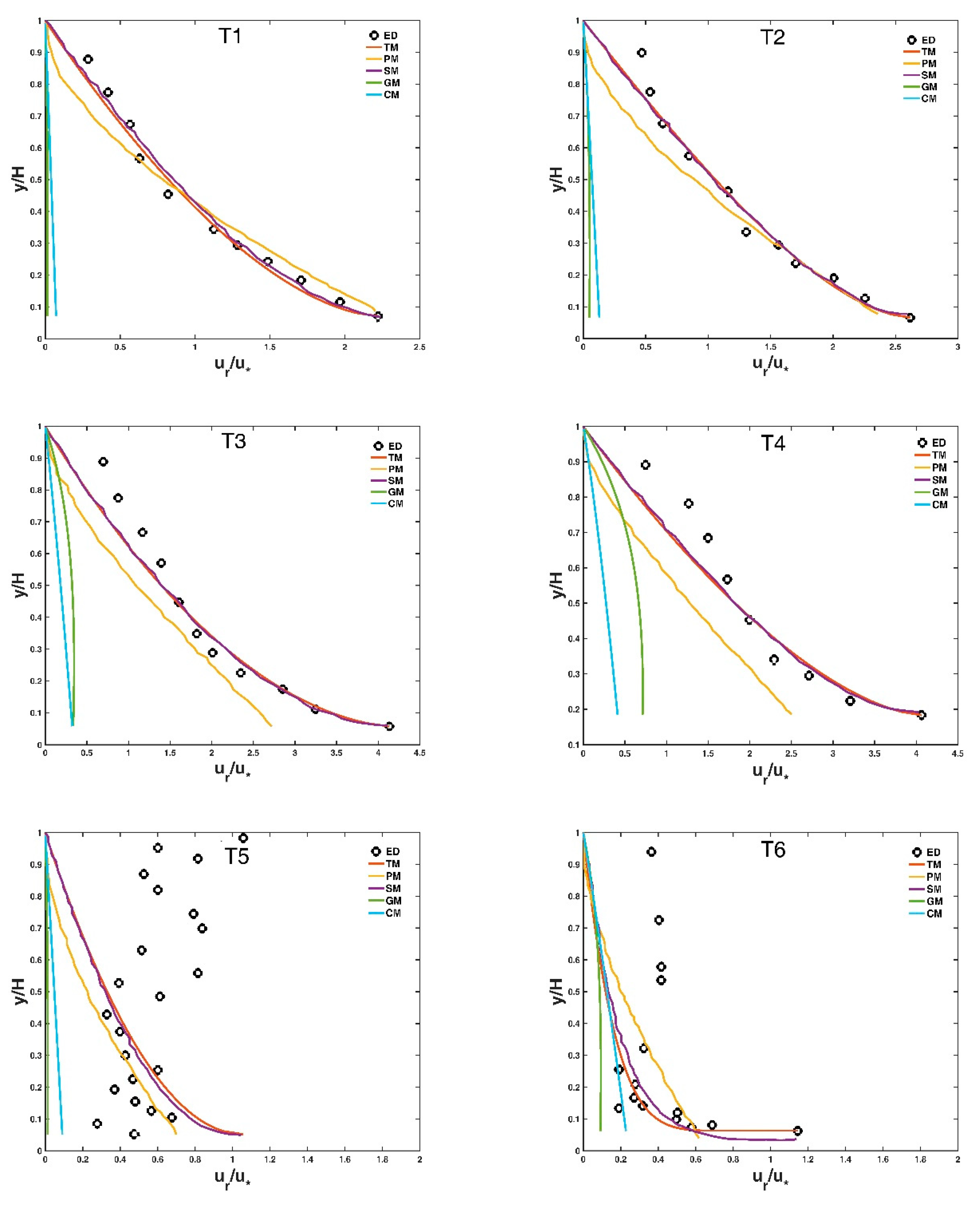
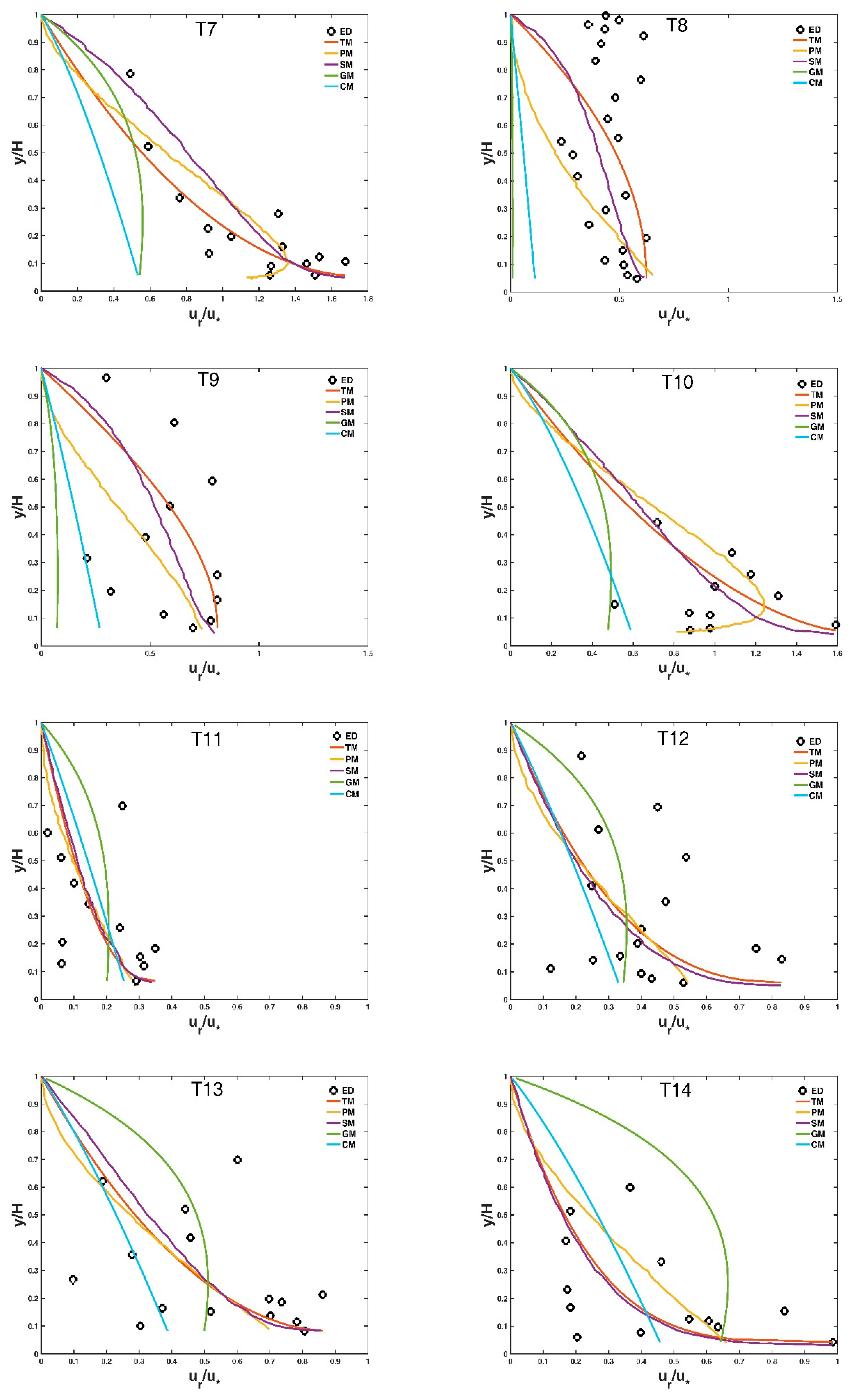
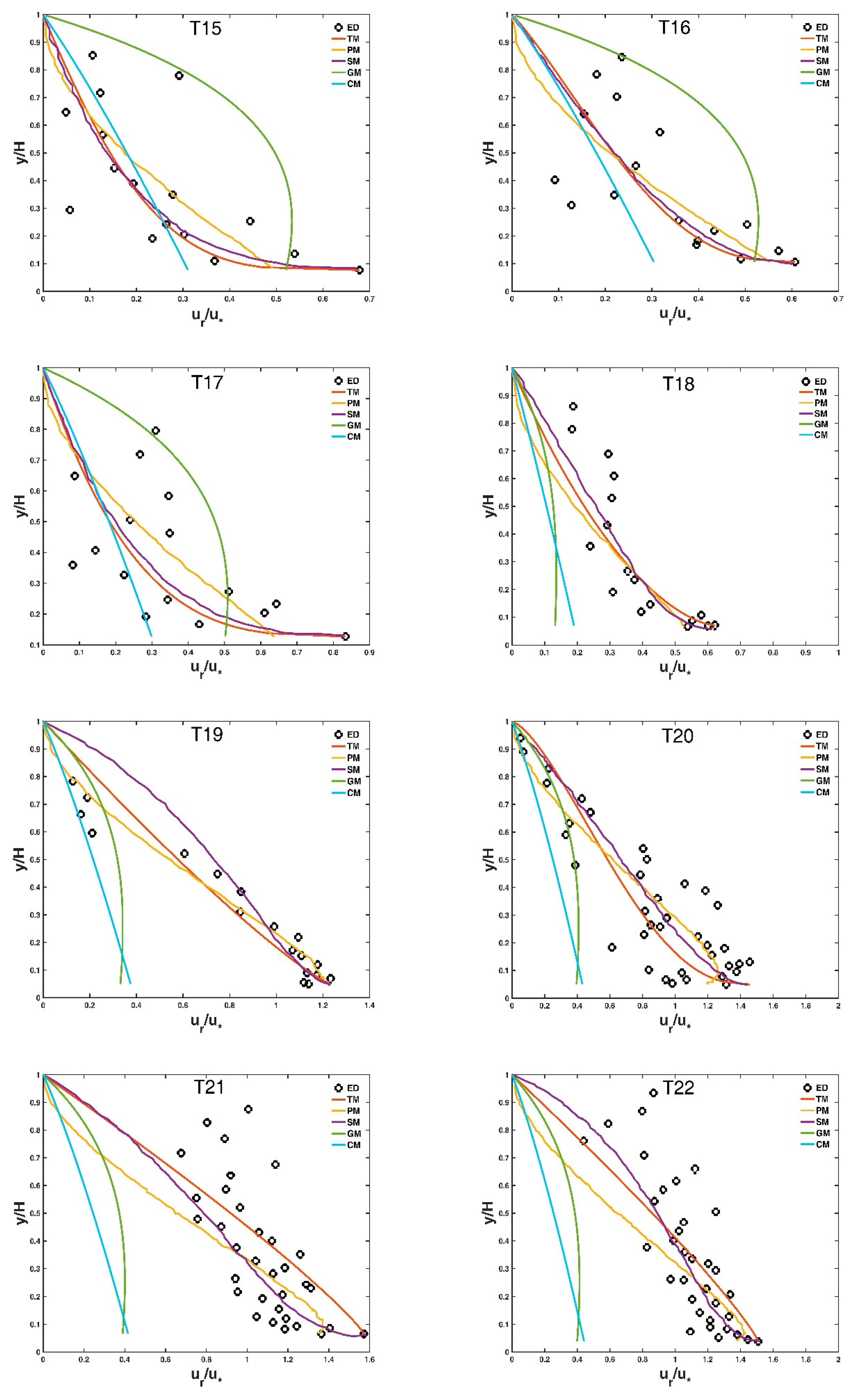
3. Comparison with Experimental Data and Other Models and Discussion
3.1. Selected Experimental Data
3.2. Some Deterministic Models
3.3. Comparison with Experimental Data and Other Models
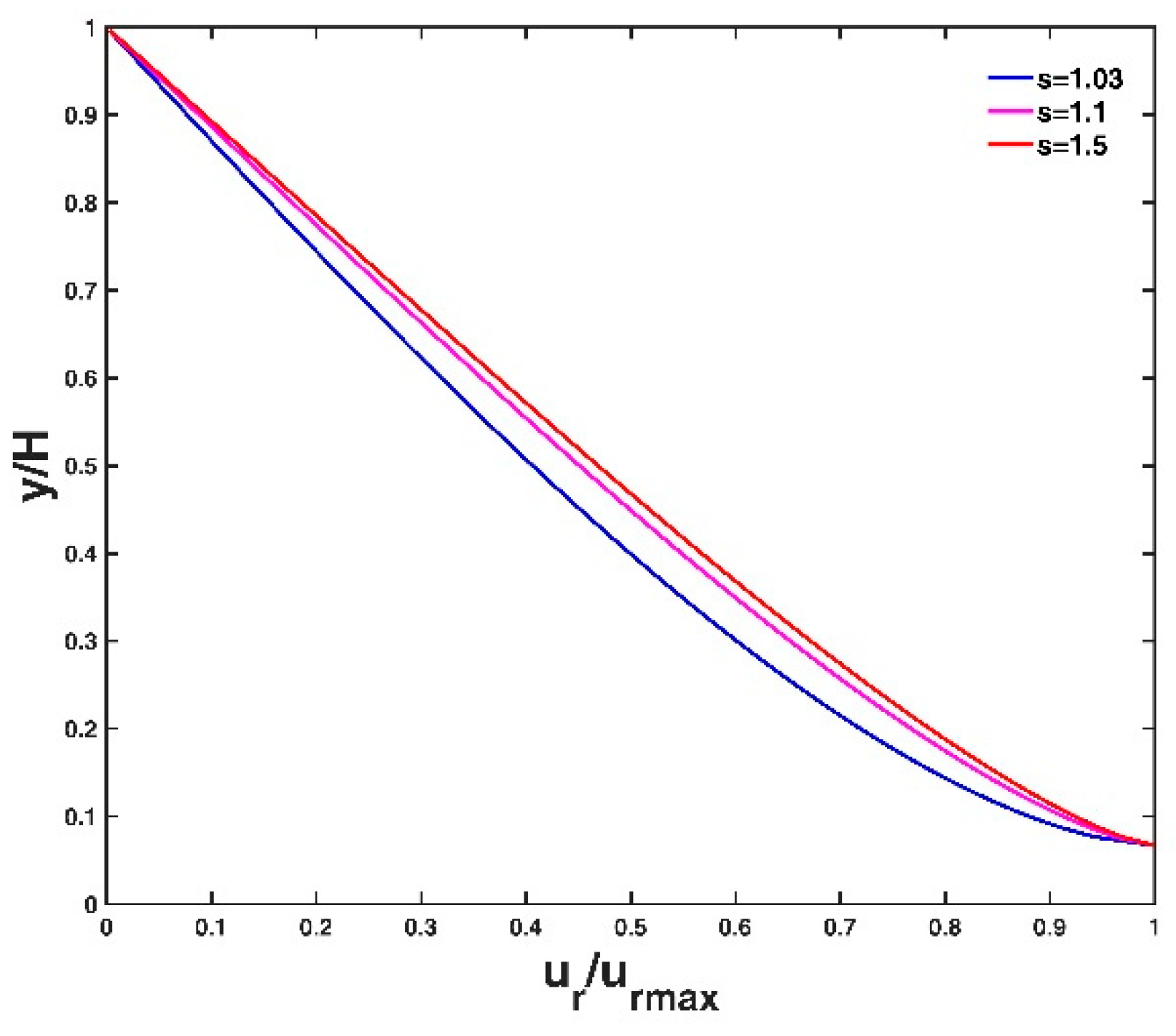
3.4. Physical Explanation
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cheng, N.S. Analysis of velocity lag in sediment-laden open channel flows. J. Hydraul. Eng. 2004, 130, 657–666. [Google Scholar] [CrossRef]
- Chien, N.; Wan, Z. Sediment transport mechanics; Science Press: Beijing, China, 1983. [Google Scholar]
- Bagnold, R.A. The nature of saltation and bedload transport in water. Proc. Royal Soc. Lond. Ser. A 1973, 332, 473–504. [Google Scholar] [CrossRef]
- Aziz, N.M. Error estimate in Einstein’s suspended sediment load method. J. Hydraul. Eng. 1996, 122, 282–285. [Google Scholar] [CrossRef]
- Muste, M.; Patel, V.C. Velocity profiles for particles and liquid in open-channel flow with suspended sediment. J. Hydraul. Eng. 1997, 123, 742–751. [Google Scholar] [CrossRef]
- Best, J.; Bennett, S.; Bridge, J.; Leeder, M. Turbulence modulation and particle velocities over flat sand beds at low transport rates. J. Hydraul. Eng. 1997, 123, 1118–1129. [Google Scholar] [CrossRef]
- Rashidi, M.; Hetsroni, G.; Banerjee, S. Particle-turbulence interaction in a boundary layer. Int. J. Multiph. Flow 1990, 16, 935–949. [Google Scholar] [CrossRef]
- Taniere, A.; Oesterle, B.; Monnier, J.C. On the behavior of solid particles in a horizontal boundary layer with turbulence and saltation effects. Exp. Fluids 1997, 23, 463–471. [Google Scholar]
- Kiger, K.T.; Pan, C. Suspension and turbulence modification effects of solid particulates on a horizontal turbulent channel flow. J. Turbul. 2002. [Google Scholar] [CrossRef]
- Chauchat, J.; Guillou, S. On turbulence closures for two-phase sediment-laden flow models. J. Geophys. Res. Oceans 2008. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Jha, S.K. Hierarchical modeling of the dilute transport of suspended sediment in open channels. Environ. Fluid Mech. 2009, 9, 207–235. [Google Scholar] [CrossRef]
- Greimann, B.P.; Muste, M.; Holly, F.M. Two-phase formulation of suspended sediment transport. J. Hydraul. Res. 1999, 37, 479–500. [Google Scholar] [CrossRef]
- Jiang, J.S.; Law, A.W.K.; Cheng, N.S. Two-phase modeling of suspended sediment distribution in open channel flows. J. Hydraul. Res. 2004, 42, 273–281. [Google Scholar] [CrossRef]
- Pal, D.; Jha, S.K.; Ghoshal, K. Velocity lag between particle and liquid in sediment-laden open channel turbulent flow. Eur. J. Mech. B Fluids 2016, 56, 130–142. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Kundu, S.; Ghoshal, K.; Singh, V.P. Entropy-based modeling of velocity lag in sediment-laden open channel turbulent flow. Entropy 2016, 18, 318. [Google Scholar] [CrossRef]
- Singh, V.P.; Sivakumar, B.; Cui, H.J. Tsallis entropy theory for modelling in water engineering: A review. Entropy 2017, 19, 641. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. One dimensional velocity distribution in open channels using Tsallis entropy. J. Hydrol. Eng. 2014, 19, 290–298. [Google Scholar] [CrossRef]
- Luo, H.; Singh, V.P.; Schmidt, A. Comparative study of 1D entropy-based and conventional deterministic velocity distribution equations for open channel flows. J. Hydrol. 2018, 563, 679–693. [Google Scholar] [CrossRef]
- Luo, H.; Singh, V.P. Entropy theory for two-dimensional velocity distribution. J. Hydrol. Eng. 2011, 16, 303–315. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Two-dimensional velocity distribution in open channels using the Tsallis entropy. J. Hydrol. Eng. 2013, 18, 331–339. [Google Scholar] [CrossRef]
- Singh, V.P. Tsallis entropy theory for derivation of infiltration equations. Trans. ASABE 2010, 53, 447–463. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy theory for derivation of infiltration equations. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy theory for movement of moisture in soils. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Chiu, C.L.; Jin, W.; Chen, Y.C. Mathematical models of distribution of sediment concentration. J. Hydraul. Eng. 2000, 1, 16–23. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Suspended sediment concentration in open channels using Tsallis entropy. J. Hydrol. Eng. 2013, 19, 966–977. [Google Scholar] [CrossRef]
- Singh, V.P.; Byrd, A.; Cui, H. Flow duration curve using entropy theory. J. Hydrol. Eng. 2014, 19, 1340–1348. [Google Scholar] [CrossRef]
- Singh, V.P.; Cui, H.J. Modelling sediment concentration in debris flow by Tsallis entropy. Phys. A 2015, 420, 49–58. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, H.; Pang, B.; Dou, J.; Peng, D. Comparison of conventional deterministic and entropy-based methods for predicting sediment concentration in debris flow. Water 2019, 11, 439. [Google Scholar] [CrossRef]
- Zhu, Z.; Yu, J. Estimating the bed-load layer thickness in open channels by Tsallis entropy. Entropy 2019, 21, 123. [Google Scholar] [CrossRef]
- Righetti, M.; Romano, G.P. Particle-fluid interactions in a plane near-wall turbulent flow. J. Fluid Mech. 2004, 505, 93–121. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics I. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the rationale of maximum entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Zhu, Z.; Peng, D. Using Shannon entropy to model turbulence-induced flocculation of cohesive sediment in water. Environ. Sci. Pollut. Res. 2018, 11, 959–974. [Google Scholar] [CrossRef] [PubMed]
- Kaftori, D.; Hetsroni, G.; Banerjee, S. Particle behavior in the turbulent boundary layer velocity and distribution profiles. Phys. Fluids 1995, 7, 1107–1121. [Google Scholar] [CrossRef]
- Muste, M.; Yu, K.; Fujita, I.; Ettema, R. Two-phase versus mixed-flow perspective on suspended sediment transport in turbulent channel flows. Water Resour. Res. 2005, 41, W10402. [Google Scholar] [CrossRef]
- Cheng, N.S. Simplified settling velocity formula for sediment particle. J. Hydraul. Eng. 1997, 123, 149–152. [Google Scholar] [CrossRef]
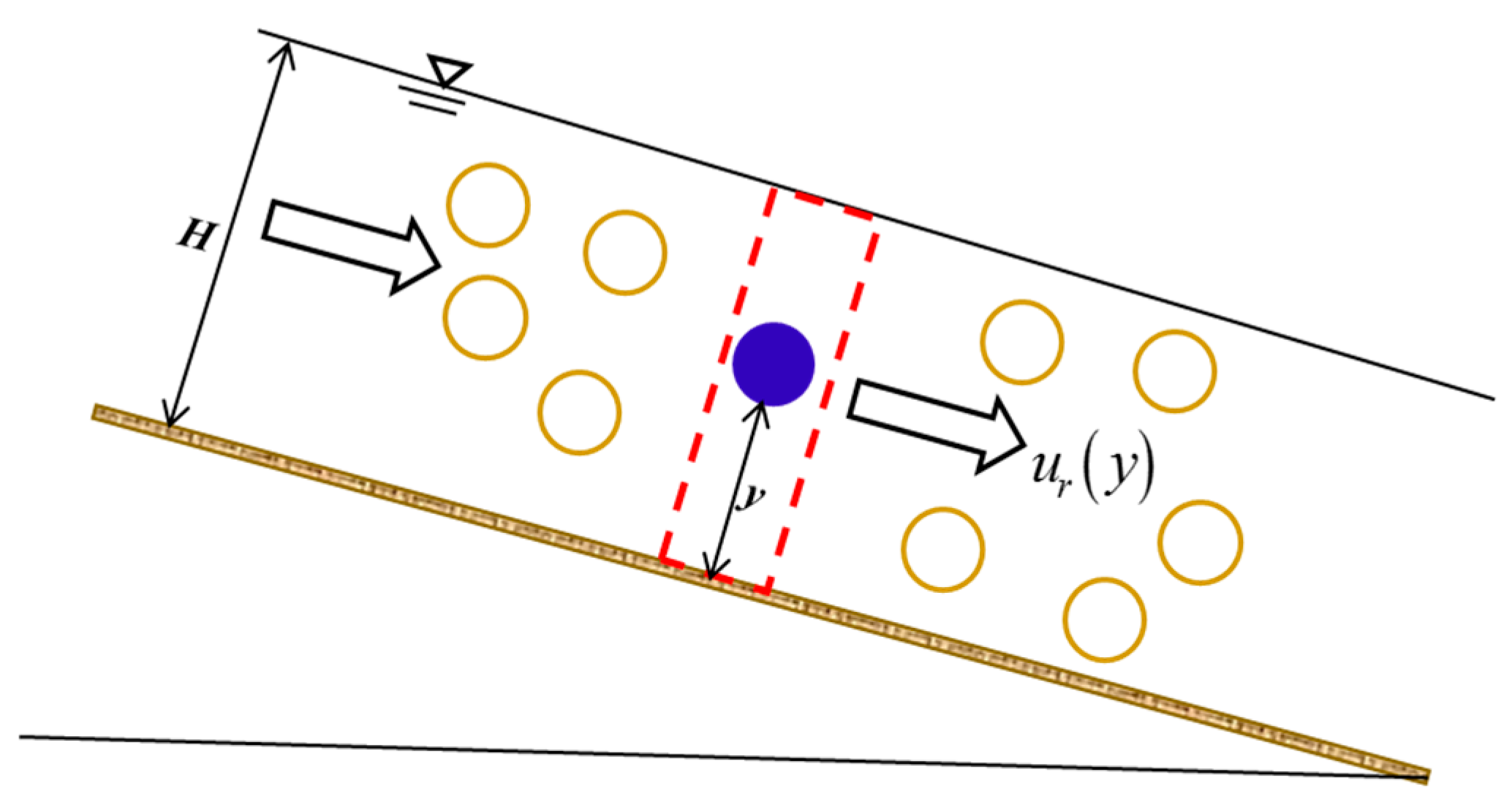



| Test Number | Reference | Particle Material | (mm) | (cm) | ||||
|---|---|---|---|---|---|---|---|---|
| T1 | Rashidi et al. [7] | Polystyrene | 0.12 | 1.03 | 0.9 | 2.75 | 0.0084 | 1.286 |
| T2 | 0.22 | 1.03 | 0.9 | 2.75 | 0.0084 | 2.357 | ||
| T3 | 0.65 | 1.03 | 0.9 | 2.75 | 0.0084 | 6.964 | ||
| T4 | 1.10 | 1.03 | 0.9 | 2.75 | 0.0084 | 11.786 | ||
| T5 | Kaftori et al. [36] | Polystyrene | 0.1 | 1.05 | 1.28 | 3.25 | 0.008 | 1.600 |
| T6 | 0.275 | 1.05 | 1.29 | 3.27 | 0.0079 | 4.491 | ||
| T7 | 0.9 | 1.05 | 1.34 | 3.27 | 0.0081 | 14.889 | ||
| T8 | 0.1 | 1.05 | 1.6 | 3.52 | 0.0081 | 1.975 | ||
| T9 | 0.275 | 1.05 | 1.6 | 3.51 | 0.008 | 5.500 | ||
| T10 | 0.9 | 1.05 | 1.55 | 3.77 | 0.0078 | 17.885 | ||
| T11 | Best et al. [6] | Glass | 0.125 | 2.6 | 3.4 | 5.75 | 0.0083 | 5.120 |
| T12 | 0.175 | 2.6 | 3.4 | 5.75 | 0.0083 | 7.169 | ||
| T13 | 0.225 | 2.6 | 3.4 | 5.75 | 0.0083 | 9.217 | ||
| T14 | 0.275 | 2.6 | 3.4 | 5.75 | 0.0083 | 11.265 | ||
| T15 | Muste and Patel [5] | Natural sand | 0.23 | 2.65 | 3.02 | 12.9 | 0.0103 | 6.744 |
| T16 | 0.23 | 2.65 | 3.05 | 12.9 | 0.0103 | 6.811 | ||
| T17 | 0.23 | 2.65 | 3.13 | 12.9 | 0.0105 | 6.856 | ||
| T18 | Righetti and Romano [30] | Glass | 0.1 | 2.6 | 3.29 | 2.3 | 0.009 | 3.656 |
| T19 | 0.2 | 2.6 | 3.97 | 2 | 0.0094 | 8.447 | ||
| T20 | Muste et al. [37] | Natural sand | 0.23 | 2.65 | 4.2 | 2.1 | 0.0093 | 10.387 |
| T21 | 0.23 | 2.65 | 4.2 | 2.1 | 0.0096 | 10.063 | ||
| T22 | 0.23 | 2.65 | 4.2 | 2.1 | 0.0091 | 10.615 |
| Test Number | Value | ||||
|---|---|---|---|---|---|
| Tsallis Entropy-Based Model | Greimann et al. [12] Model | Cheng [1] Model | Pal et al. [14] Model | Shannon Entropy-Based Model [15] | |
| T1 | 8.38 *** | 98.48 | 95.79 | 21.65 | 8.69 |
| T2 | 9.85 *** | 96.16 | 94.04 | 22.88 | 9.98 |
| T3 | 15.03 *** | 82.86 | 89.46 | 32.68 | 15.51 |
| T4 | 17.60 *** | 69.98 | 87.53 | 42.75 | 17.96 |
| T5 | 63.44 | 97.81 | 89.16 | 57.24 *** | 59.55 |
| T6 | 41.52 *** | 75.94 | 53.04 | 59.21 | 44.08 |
| T7 | 18.28 *** | 49.08 | 59.15 | 18.43 | 18.52 |
| T8 | 47.92 | 98.23 | 87.37 | 54.29 | 42.39 *** |
| T9 | 56.02 | 87.02 | 63.59 | 52.88 | 50.36 *** |
| T10 | 36.91 | 47.88 | 44.83 | 44.42 | 33.70 *** |
| T11 | 90.82 *** | 147.92 | 115.36 | 94.38 | 97.19 |
| T12 | 68.09 | 38.92 *** | 48.46 | 58.20 | 60.81 |
| T13 | 61.13 *** | 65.69 | 61.79 | 61.96 | 62.07 |
| T14 | 54.16 *** | 117.68 | 57.86 | 69.26 | 55.78 |
| T15 | 46.69 *** | 193.70 | 56.01 | 67.96 | 50.00 |
| T16 | 38.45 *** | 90.44 | 47.19 | 50.31 | 40.94 |
| T17 | 50.96 *** | 104.97 | 51.73 | 71.01 | 55.60 |
| T18 | 25.17 | 65.54 | 64.08 | 30.31 | 21.68 *** |
| T19 | 28.52 | 61.72 | 57.65 | 15.71 *** | 49.53 |
| T20 | 30.85 | 52.87 | 59.14 | 26.30 *** | 26.64 |
| T21 | 22.45 | 65.27 | 72.40 | 26.31 | 18.60 *** |
| T22 | 19.80 | 65.23 | 72.08 | 27.08 | 12.23 *** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Yu, J.; Dou, J.; Peng, D. An Expression for Velocity Lag in Sediment-Laden Open-Channel Flows Based on Tsallis Entropy Together with the Principle of Maximum Entropy. Entropy 2019, 21, 522. https://doi.org/10.3390/e21050522
Zhu Z, Yu J, Dou J, Peng D. An Expression for Velocity Lag in Sediment-Laden Open-Channel Flows Based on Tsallis Entropy Together with the Principle of Maximum Entropy. Entropy. 2019; 21(5):522. https://doi.org/10.3390/e21050522
Chicago/Turabian StyleZhu, Zhongfan, Jingshan Yu, Jie Dou, and Dingzhi Peng. 2019. "An Expression for Velocity Lag in Sediment-Laden Open-Channel Flows Based on Tsallis Entropy Together with the Principle of Maximum Entropy" Entropy 21, no. 5: 522. https://doi.org/10.3390/e21050522





