Thermodynamics of Superdiffusion Generated by Lévy–Wiener Fluctuating Forces
Abstract
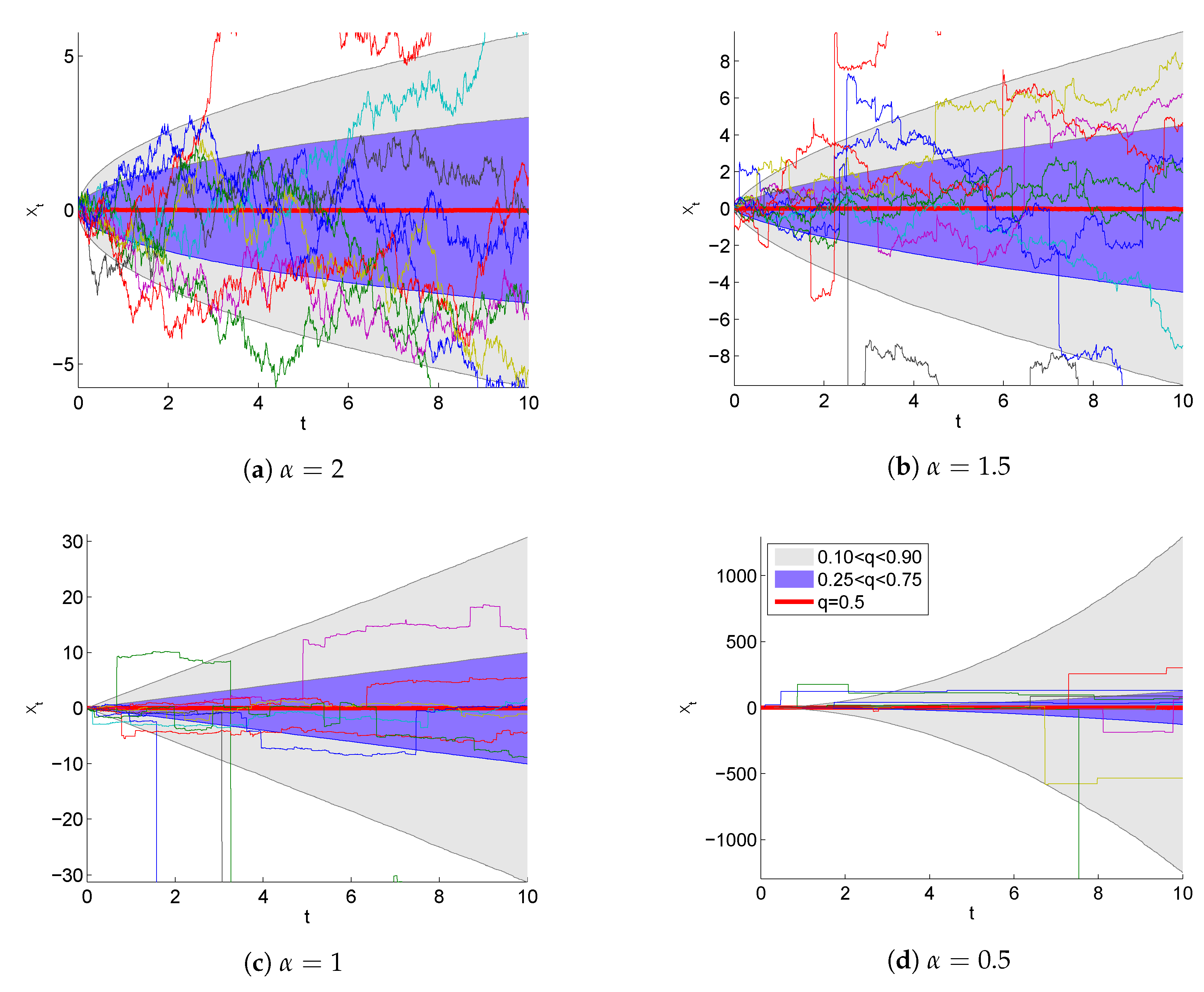
:1. Introduction: Lévy Stable Distributions and Lévy Stable Processes
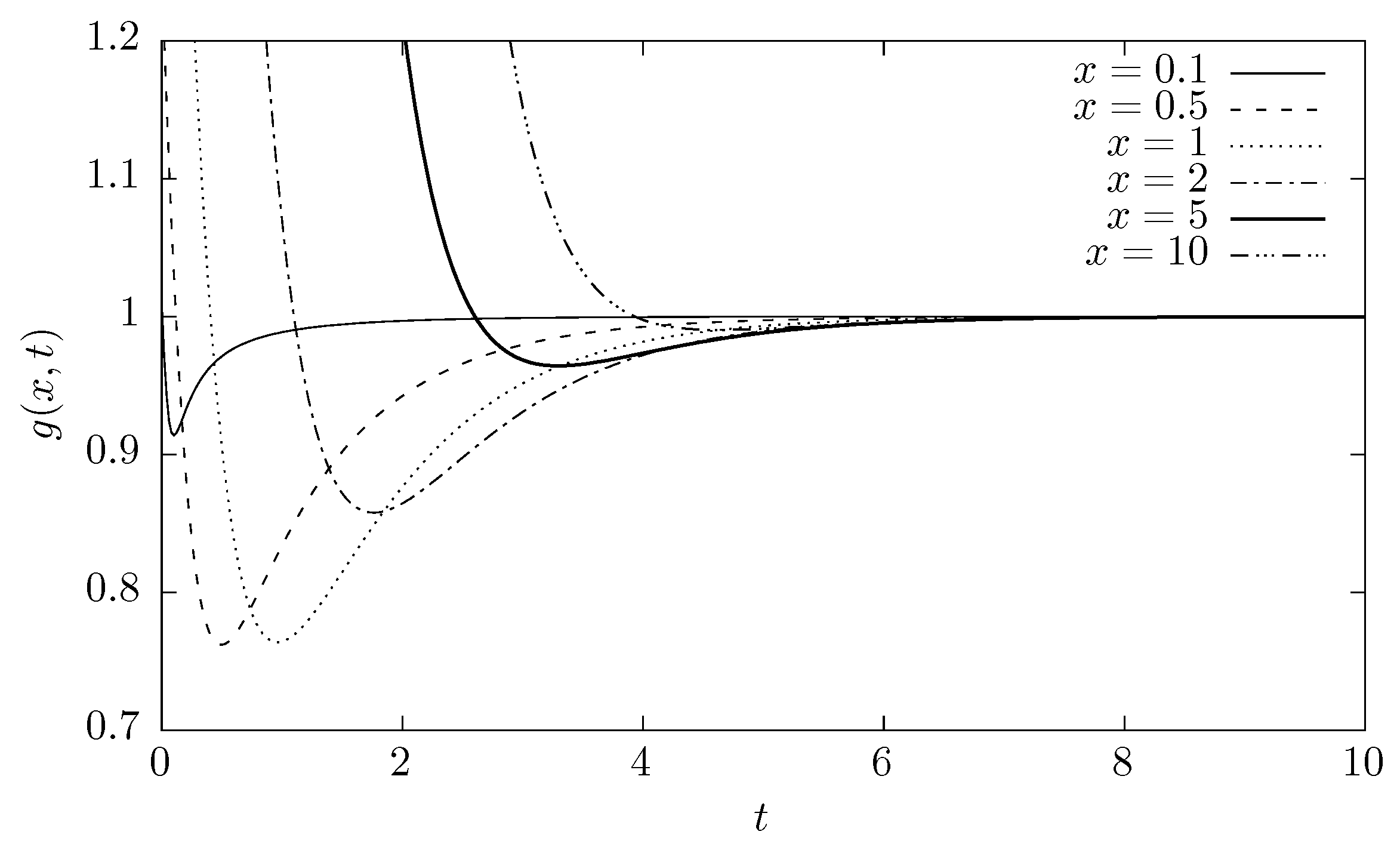
2. Lévy Flights and Detailed Balance
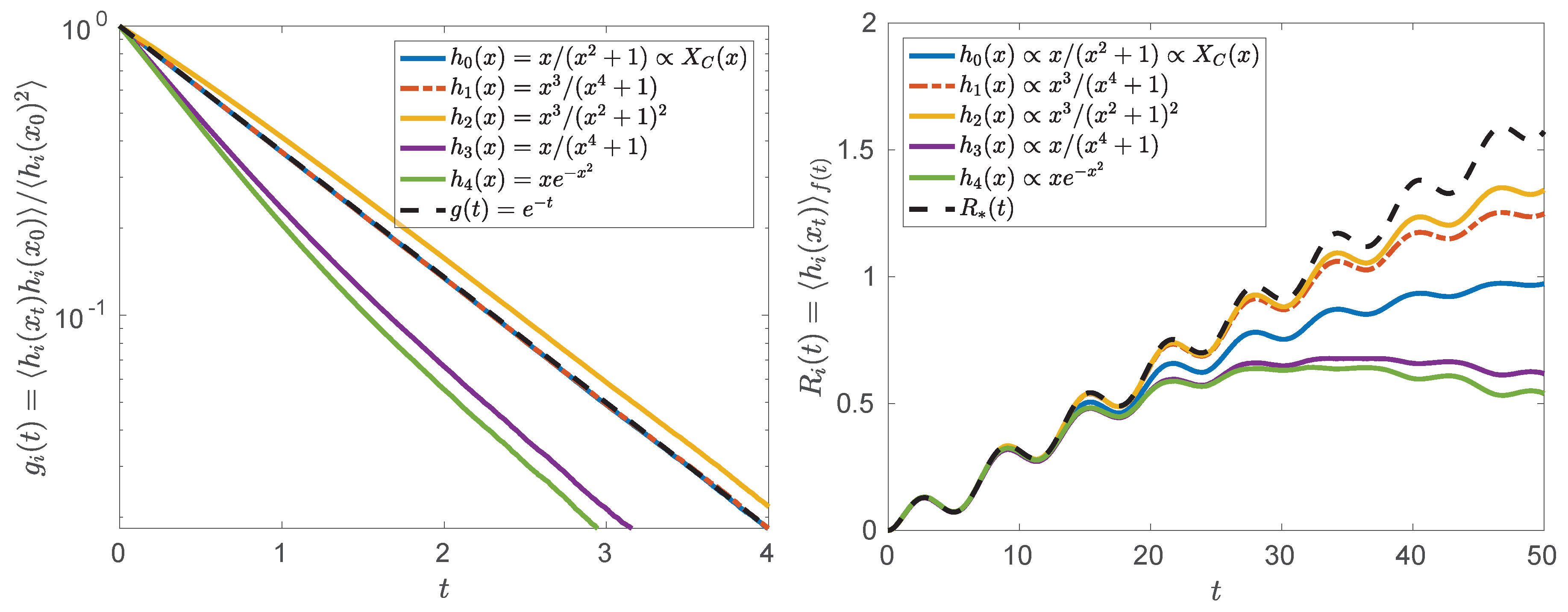
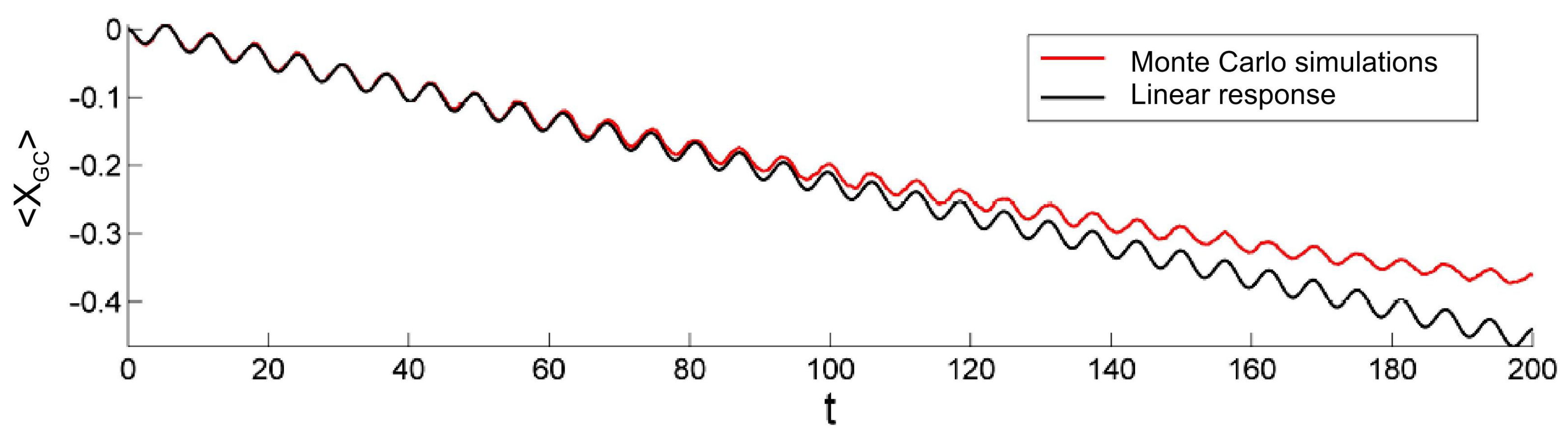
3. Linear Response and Fluctuation–Dissipation Relationship under Lévy Noise
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Processes: Stochastic Models with Infinite Variance; Chapman and Hall: New York, NY, USA, 1994. [Google Scholar]
- Meerschaert, M.M.; Scheffler, H.P. Limit Distributions for Sums of Independent Random Vectors: Heavy Tails in Theory and Practice; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Klages, R.; Radons, G.; Sokolov, I.M. (Eds.) Anomalous Transport. Foundations and Applications; Wiley-VCH: Berlin, Germany, 2008. [Google Scholar]
- Kadanoff, L. Turbulent heat flow: Structures and scaling. Phys. Today 2001, 54, 34–39. [Google Scholar] [CrossRef] [Green Version]
- Scafetta, E.R.; West, B. Solar flares intermittency and the Earth’s temperature anomalies. Phys. Rev. Lett. 2003, 90, 24701. [Google Scholar] [CrossRef] [PubMed]
- Rypdal, K. Global temperature response to radiative forcing: Solar cycle versus volcanic eruptions. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Luryi, S.; Subashiev, A. Lévy flight of holes in InP semiconductor scintillator I. Int. J. High Speed Electron. Syst. 2012, 21, 1250001. [Google Scholar] [CrossRef]
- Barthelemy, P.; Bertolotti, J.; Wiersma, D.S. A Lévy flight for light. Nature 2008, 453, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, R.M.S.; Santos, M.V.S.; Donato, C.C.; Andrade, J.S.; Oliveira, F.A. Analytical results for long-time behavior in anomalous diffusion. Phys. Rev. E 2012, 86, 012121. [Google Scholar] [CrossRef] [PubMed]
- Schumer, R.; Meerschaert, M.M.; Baeumer, B. Fractional advection-dispersion equations for modeling transport at the Earth surface. J. Geophys. Res. 2009, 114, F00A07. [Google Scholar] [CrossRef]
- Mandelbrot, B. The variation of certain speculative prices. J. Bus. 1963, 36, 394–419. [Google Scholar] [CrossRef]
- Gallet, F.; Arcizet, D.; Boheca, P.; Richerta, A. Power spectrum of out-of-equilibrium forces in living cells: Amplitude and frequency dependence. Soft Matter 2009, 5, 2947–2953. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Zhang, H.; Li, X.; Kurths, J. The switch in a genetic toggle system with Lévy noise. Sci. Rep. 2016, 6, 31505. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Serdukova, S.; Duan, J.; Kurths, J. Transitions in a genetic transcriptional regulatory system under Lévy motion. Sci. Rep. 2016, 6, 29274. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soares e Silva, M.; Stuhrmann, B.; Betz, T.; Koenderink, G.H. Time-resolved microrheology of actively remodeling actomyosin networks. New J. Phys. 2014, 16, 075010. [Google Scholar] [CrossRef] [Green Version]
- Schötz, T.; Neher, R.A.; Gerland, U. Target search on a dynamic DNA molecule. Phys. Rev. E 2011, 84, 051911. [Google Scholar] [CrossRef] [PubMed]
- Lisowski, B.; Valenti, D.; Spagnolo, B.; Bier, M.; Gudowska-Nowak, E. Stepping molecular motor amid Lévy white noise. Phys. Rev. E 2015, 91, 042713. [Google Scholar] [CrossRef] [PubMed]
- Baronchelli, A.; Radicchi, F. Lévy flights in human behavior and cognition. Chaos Solitons Fractals 2013, 56, 101–105. [Google Scholar] [CrossRef] [Green Version]
- Amor, T.A.; Reis, S.D.S.; Campos, D.; Herrmann, H.J.; Andrade, J.S., Jr. Persistence in eye movement during visual search. Sci. Rep. 2016, 6, 20815. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuśmierz, Ł.; Majumdar, S.N.; Sabhabandit, S.; Schehr, G. First order transition for the optimal search time of Lévy flights with resetting. Phys. Rev. Lett. 2014, 13, 220602. [Google Scholar] [CrossRef] [PubMed]
- Kuśmierz, Ł.; Gudowska-Nowak, E. Optimal first-arrival times in Lévy flights with resetting. Phys. Rev. E 2015, 92, 052127. [Google Scholar] [CrossRef] [PubMed]
- Kuśmierz, Ł.; Toyoizumi, T. Emergence of Lévy walks from second order stochastic optimization. Phys. Rev. Lett. 2017, 119, 250601. [Google Scholar] [CrossRef] [PubMed]
- Raposo, E.P.; Buldyrev, S.V.; Da Luz, M.G.E.; Santos, M.C.; Stanley, H.E.; Viswanathan, G.M. Dynamical robustness of Lévy search strategies. Phys. Rev. Lett. 2003, 91, 240601. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Buldyrev, S.V.; Havlin, S.; Da Luz, M.G.E.; Raposo, E.P.; Stanley, H.E. Optimizing the success of random searches. Nature 1999, 401, 911–914. [Google Scholar] [CrossRef] [PubMed]
- Sekimoto, K. Stochastic Energetics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Qian, H. Thermodynamics of the general diffusion process: Equilibrium supercurrent and nonequilibrium driven circulation with dissipation. Eur. Phys. J. Spec. Top. 2015, 224, 781–799. [Google Scholar] [CrossRef] [Green Version]
- Lévy, P. Calcul des Probabilités; Gautier-Villars: Paris, France, 1925. (In French) [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Sci. Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Janicki, A.; Weron, A. Simulation and Chaotic Behavior of α-Stable Stochastic Processes; Marcel Dekker: New York, NY, USA, 1994. [Google Scholar]
- Garbaczewski, P.; Stephanovich, V. Lévy targeting and the principle of detailed balance. Phys. Rev. E 2011, 84, 011142. [Google Scholar] [CrossRef] [PubMed]
- Eliazar, I.; Shlesinger, M.F. Lévy driven Langevin systems: Targeted stochasticity. J. Stat. Phys. 2003, 111, 739–768. [Google Scholar] [CrossRef]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; Klafter, J.; Wong, Y.M. Random walks with infinite spatial and temporal moments. J. Stat. Phys. 1982, 27, 499–512. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E.; Barkai, E.; Dubkov, A.A. Lévy flights versus Lévy walks in bounded domains. Phys. Rev. E 2015, 95, 052102. [Google Scholar] [CrossRef] [PubMed]
- Solomon, T.H.; Weeks, E.R.; Swinney, H.L. Observations of anomalous diffusion and Lévy flights in a two-dimensional rotating flow. Phys. Rev. Lett. 1993, 91, 3975. [Google Scholar] [CrossRef] [PubMed]
- Pereira, E.; Martinho, J.M.G.; Berberan-Santos, M. Photon trajectories in incoherent atomic radiation trapping as Lévy flights. Phys. Rev. Lett. 2004, 93, 120201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ott, A.; Bouchaud, J.-P.; Langevin, D.; Urbach, W. Anomalous diffusion in “living polymers”: A genuine Lévy flight? Phys. Rev. Lett. 1990, 65, 2201. [Google Scholar] [CrossRef] [PubMed]
- Belik, V.; Geisel, T.; Brockmann, D. Natural human mobility patterns and spatial spread of infectious diseases. Phys. Rev. X 2011, 8, 011001. [Google Scholar] [CrossRef]
- Mantegna, R.; Stanley, E.H. An Introduction to Econophysics: Correlations and Complexity in Finances; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ditlevsen, P.D. Observation of α-stable noise induced millennial climate changes from an ice-core record. Geophys. Res. Lett. 1999, 26, 1441–1444. [Google Scholar] [CrossRef]
- Stuhrmann, B.; Soares e Silva, M.; Depken, M.; MacKintosh, F.C.; Koenderink, G.H. Nonequilibrium fluctuations of a remodeling in vitro cytoskeleton. Phys. Rev. E 2012, 86, 020901(R). [Google Scholar] [CrossRef] [PubMed]
- Costa, T.; Boccignone, G.; Cauda, F.; Ferrano, M. The foraging brain: Evidence of Lévy dynamics in brain networks. PLoS ONE 2016, 11, e0161702. [Google Scholar] [CrossRef] [PubMed]
- Vlad, M.O.; Ross, J.; Schneider, F.W. Lévy diffusion in a force field, Huber relaxation kinetics, and nonequilibrium thermodynamics: H theorem for enhanced diffusion with Lévy white noise. Phys. Rev. E 2000, 62, 1743. [Google Scholar] [CrossRef]
- Fogedby, H.C. Langevin equations for continuous time Lévy flights. Phys. Rev. E 1994, 50, 1657. [Google Scholar] [CrossRef]
- Jespersen, S.; Metzler, R.; Fogedby, H.C. Lévy flights in external force fields: Langevin and fractional Fokker-Planck equations and their solutions. Phys. Rev. E 1999, 59, 2736. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A Math. Gen. 2004, 37, 161. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Perri, S.; Zimbardo, G.; Effenberger, F.; Fichtner, H. Parameter estimation of superdiffusive motion of energetic particles upstream of heliospheric shocks. Astron. Astrophys. 2015, 578, A2. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crooks, G.E. On thermodynamic and microscopic reversibility. J. Stat. Mech. Theor. Exp. 2011, 2011, P07008. [Google Scholar] [CrossRef]
- Kuśmierz, L.; Chechkin, A.V.; Gudowska-Nowak, E.; Bier, M. Breaking microscopic reversibility with Lévy flights. EPL 2016, 114, 60009. [Google Scholar] [CrossRef]
- Wang, J.; Xu, L.; Wang, E. Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. USA 2008, 105, 12271–12276. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, C.W. Stochastic Methods; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Dybiec, B.; Parrondo, J.M.R.; Gudowska-Nowak, E. Fluctuation–dissipation relations under Lévy noises. EPL 2012, 98, 50006. [Google Scholar] [CrossRef]
- Kuśmierz, Ł.; Rubi, J.M.; Gudowska-Nowak, E. Heat and work distributions for mixed Gauss–Cauchy process. J. Stat. Mech. 2014, 9, P09002. [Google Scholar]
- Montroll, E.W.; Shlesinger, M.F. Maximum entropy formalism, fractals, scaling phenomena and 1/f noise: A tale of tails. J. Stat. Phys. 1983, 32, 209–230. [Google Scholar] [CrossRef]
- Kharcheva, A.; Dubkov, A.; Dybiec, B.; Spagnolo, B.; Valenti, D. Spectral characteristics of steady-state Lévy flights in confinement potential profiles. J. Stat. Mech. 2016, 2016, P054039. [Google Scholar] [CrossRef]
- Kanazawa, K.; Sagawa, T.; Hayakawa, H. Heat conduction induced by non-Gaussian athermal fluctuations. Phys. Rev. E 2013, 87, 052124. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. Thermodynamics and statistical mechanics for complex systems—Foundations and applications. Acta Phys. Pol. 2015, 46, 1089. [Google Scholar] [CrossRef]
- Brockmann, D.; Sokolov, I.M. Lévy flights in external force fields: From models to equations. Chem. Phys. 2002, 284, 409–421. [Google Scholar] [CrossRef]
- Żaba, M.; Garbaczewski, P.; Stephanovich, V. Lévy flights in confining environments: Random paths and their statistics. Physica A 2013, 392, 3485–3496. [Google Scholar] [CrossRef] [Green Version]
- Prehl, J.; Boldt, F.; Hoffmann, K.H.; Essex, C. Symmetric fractional diffusion and entropy production. Entropy 2016, 18, 275. [Google Scholar] [CrossRef]
- Scafetta, N.; Grigolini, P. Scaling detection in time series: Diffusion entropy analysis. Phys. Rev. E 2001, 66, 036130. [Google Scholar] [CrossRef] [PubMed]
- Hatano, T.; Sasa, S.I. Steady-state thermodynamics of Langevin systems. Phys. Rev. Lett. 2001, 86, 3463. [Google Scholar] [CrossRef] [PubMed]
- Kubo, R. Statistical Physics II; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Ofxord University Press: Oxford, UK, 2001. [Google Scholar]
- Prost, J.; Joanny, J.-F.; Parrondo, J.M.R. Fluctuation-dissipation theorem for steady state systems. Phys. Rev. Lett. 2009, 103, 090601. [Google Scholar] [CrossRef] [PubMed]
- Gradenigo, G.; Sarracino, A.; Villamaina, D.; Vulpiani, A. Einstein’s relations in systems with anomalous diffusion. Acta Phys. Pol. B 2013, 44, 899. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Dybiec, B.; Ebeling, W. Harmonic oscillator under Lévy noise: Unexpected properties in the phase space. Phys. Rev. E 2011, 83, 041118. [Google Scholar] [CrossRef] [PubMed]
- Ebeling, W.; Romanovsky, M.Y.; Sokolov, I.M. Convoluted Gauss-Lévy distributions and exploding Coulomb clusters. Eur. Phys. J. Spec. Top. 2010, 187, 157–170. [Google Scholar] [CrossRef]
- Kuśmierz, Ł.; Ebeling, W.; Sokolov, I.M.; Gudowska-Nowak, E. Onsager’s fluctuation theory and new developents including nonequilibrium Lévy fluctuations. Acta Phys. Pol. B 2013, 44, 859. [Google Scholar] [CrossRef]
- Thiel, F.; Sokolov, I.M.; Postnikov, E.B. Nonspectral modes and how to find them in the Ornstein–Uhlenbeck process with white stable noise. Phys. Rev. E 2016, 93, 052104. [Google Scholar] [CrossRef] [PubMed]
- Dybiec, B.; Sokolov, I.M.; Chechkin, A.V. Stationary states in single-well potentials under symmetric Lévy noises. J. Stat. Mech. Theor. Exp. 2010, 2010, P07008. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E.; Sokolov, I.M. Underdamped stochastic harmonic oscillator driven by Lévy noise. Phys. Rev. E 2017, 96, 042118. [Google Scholar] [CrossRef] [PubMed]
- Touchette, H.; Cohen, E.G.D. Fluctuation relation for a Lévy particle. Phys. Rev. E 2007, 76, 020101. [Google Scholar] [CrossRef] [PubMed]
- Kanazawa, K.; Sano, T.G.; Sagawa, T.; Hayakawa, H. Minimal model of stochastic athermal systems: Origin of non-Gaussian noise. Phys. Rev. Lett. 2015, 114, 090601. [Google Scholar] [CrossRef] [PubMed]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Murphy, E.J.; Prince, P.A.; Stanley, H.E. Lévy flight search patterns of wandering albatrosses. Nature 1996, 381, 413. [Google Scholar] [CrossRef]
- Brockmann, D.; Hufnagel, L.; Geisel, T. The scaling laws of human travel. Nature 2006, 439, 462–465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reynolds, A.M.; Smith, A.D.; Reynolds, D.R.; Carreck, N.L.; Osborne, J.L. Honeybees perform optimal scale-free searching flights when attempting to locate a food source. J. Exp. Biol. 2007, 210, 3763–3770. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ariel, G.; Rabani, A.; Benisty, S.; Partridge, J.D.; Harshey, R.M.; Be’Er, A. Swarming bacteria migrate by Lévy Walk. Nat. Commun. 2015, 6, 8396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reynolds, A.M. Liberating Lévy walk research from the shackles of optimal foraging. Phys. Life Rev. 2015, 14, 59–83. [Google Scholar] [CrossRef] [PubMed]
- Bartumeus, F.; Raposo, E.P.; Viswanathan, G.M.; da Luz, M.G. Stochastic optimal foraging theory. In Dispersal, Individual Movement and Spatial Ecology; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ariel, G.; Be’er, A.; Reynolds, A. Chaotic model for Lévy walks in swarming bacteria. Phys. Rev. Lett. 2017, 118, 228102. [Google Scholar] [CrossRef] [PubMed]
- Evans, M.R.; Majumdar, S.N. Diffusion with stochastic resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Reuveni, S. First passage under restart. Phys. Rev. Lett. 2017, 118, 030603. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, J.; Goldt, S.; Seifert, U. Stochastic thermodynamics of resetting. Europhys. Lett. 2016, 113, 60009. [Google Scholar] [CrossRef] [Green Version]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuśmierz, Ł.; Dybiec, B.; Gudowska-Nowak, E. Thermodynamics of Superdiffusion Generated by Lévy–Wiener Fluctuating Forces. Entropy 2018, 20, 658. https://doi.org/10.3390/e20090658
Kuśmierz Ł, Dybiec B, Gudowska-Nowak E. Thermodynamics of Superdiffusion Generated by Lévy–Wiener Fluctuating Forces. Entropy. 2018; 20(9):658. https://doi.org/10.3390/e20090658
Chicago/Turabian StyleKuśmierz, Łukasz, Bartłomiej Dybiec, and Ewa Gudowska-Nowak. 2018. "Thermodynamics of Superdiffusion Generated by Lévy–Wiener Fluctuating Forces" Entropy 20, no. 9: 658. https://doi.org/10.3390/e20090658
APA StyleKuśmierz, Ł., Dybiec, B., & Gudowska-Nowak, E. (2018). Thermodynamics of Superdiffusion Generated by Lévy–Wiener Fluctuating Forces. Entropy, 20(9), 658. https://doi.org/10.3390/e20090658




