Study of Geo-Electric Data Collected by the Joint EMSEV-Bishkek RS-RAS Cooperation: Possible Earthquake Precursors
Abstract
:1. Introduction
- They appear selectively at some of the stations that constitute a recording network.
- They appear simultaneously at the long and short dipoles of the recording station.
- The ratio is constant for the short dipoles oriented in the same direction.
- The criterion must hold for a long and short dipole placed parallel to each other. That means that both the short and long dipoles record approximately the same mean value of the electric field.
2. Materials and Methods
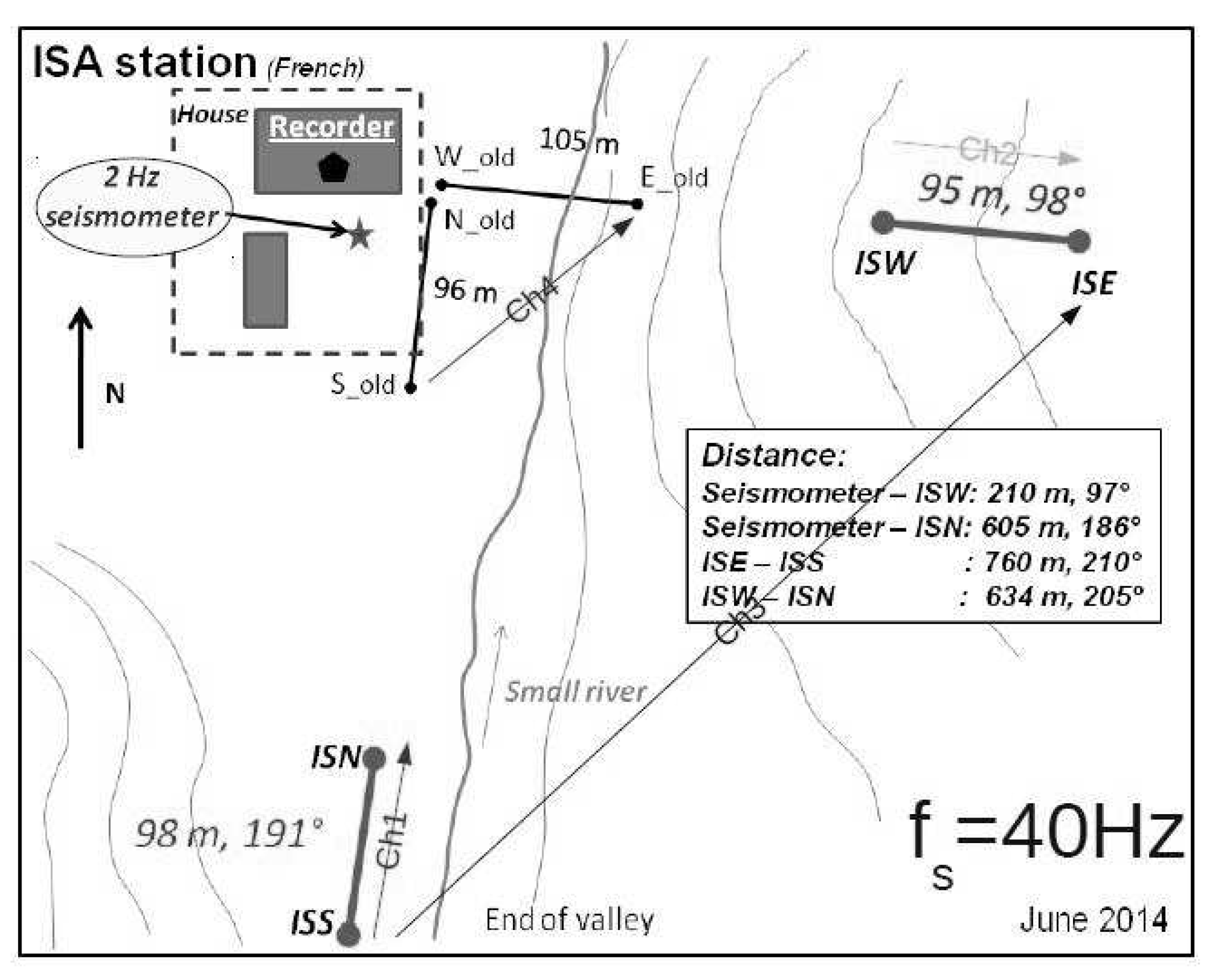
2.1. Station Configuration and Data Recording
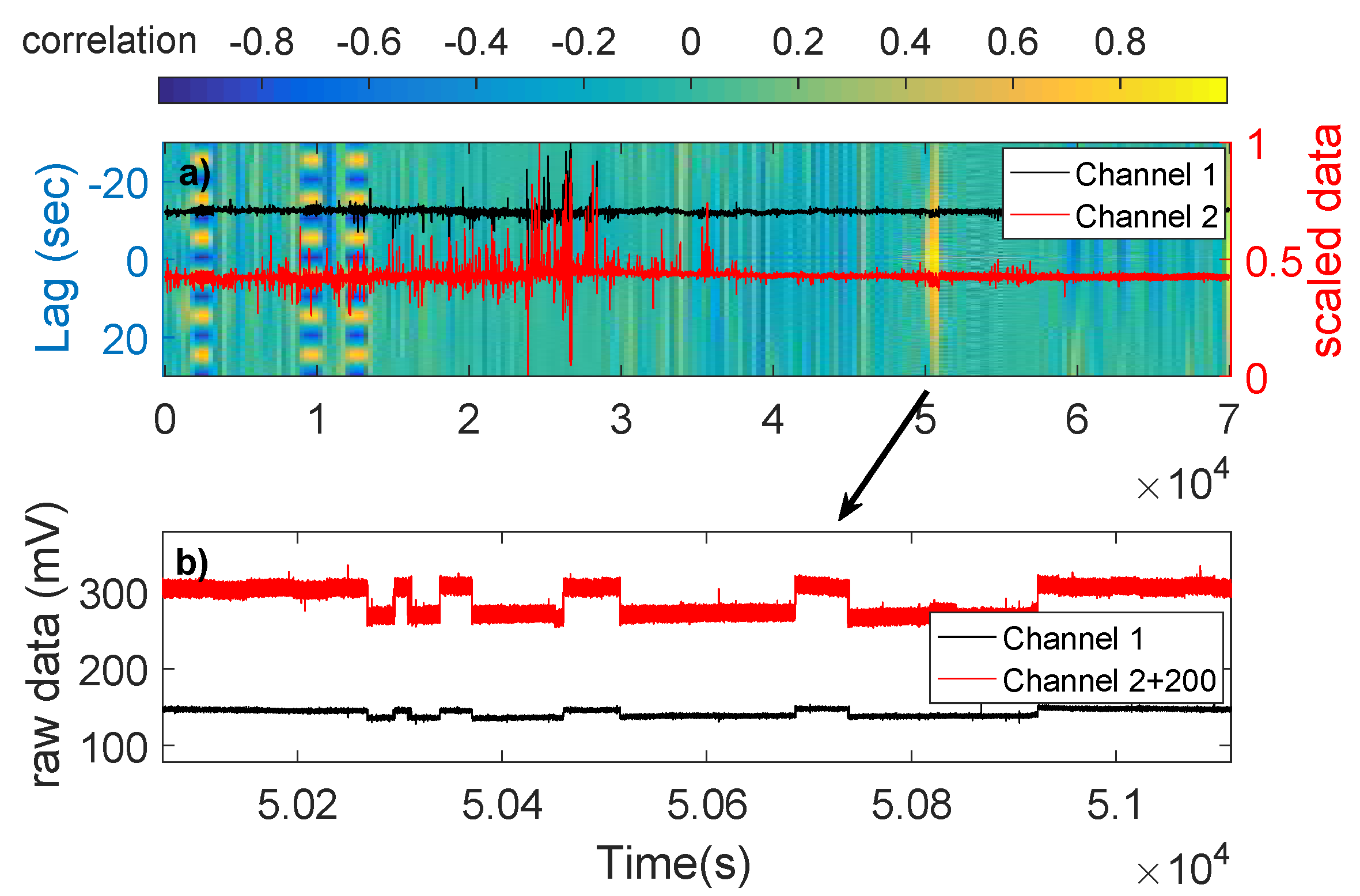
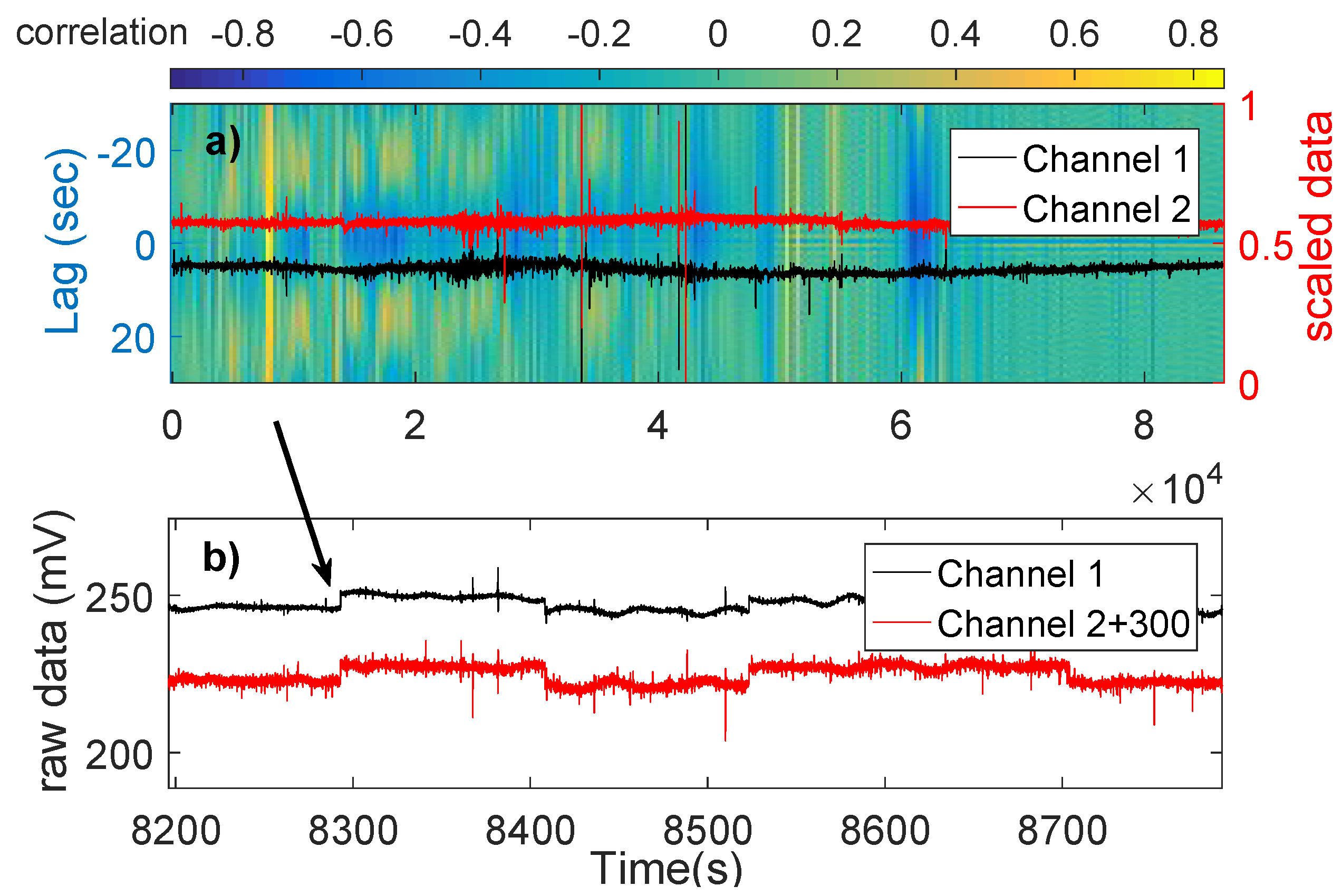
2.2. Cross-Correlogram Method Background
2.3. The Cross-Correlogram Method for the Identification of ATC
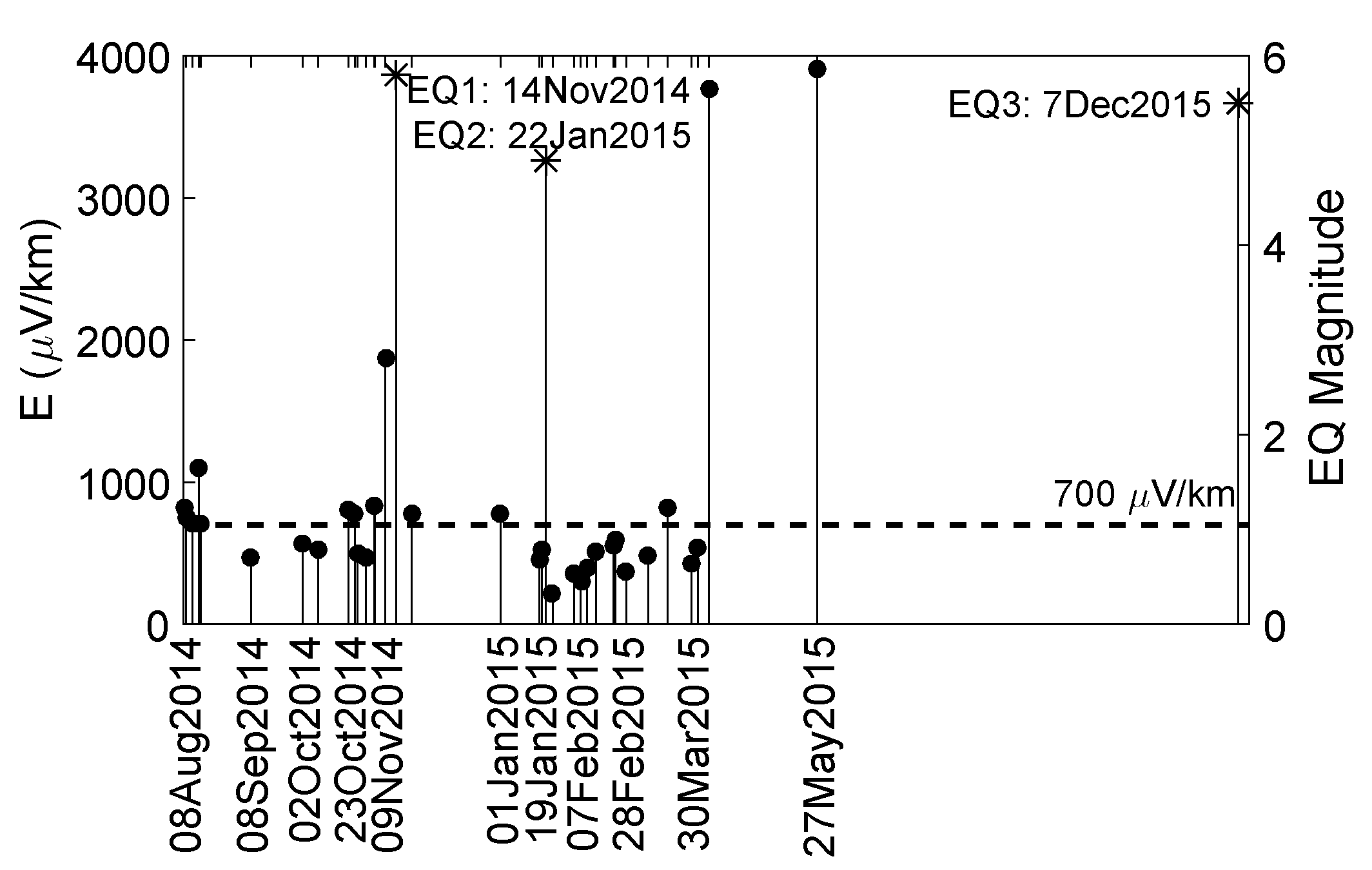
2.4. The Earthquakes Possibly Preceded by SES
3. Results
3.1. Classification of ATC-Possible SES Activities
- Type 1: 9 August 2014, 1 January 2015, and 27 May 2015. These ATC consist of rectangular pulses of almost the same amplitude.
- Type 2: 9 November 2014 and 21 November 2014. These ATC show some escalations, which means the recordings change levels constantly.
- Type 3: 23 October 2014 and 7 April 2015. These ATC show non-constant pulse amplitude.
- The ATC of 4 November 2014 is only partially recorded at one channel. If we examine a larger time-period than the 300-s windows of the cross-correlograms (see Section 2.3), we see that the ATC’s later pulses are only recorded at one of the two channels, therefore it cannot be an SES.
- Single Pulses: 8 August 2014, 12 August 2014, 15 August 2014, 16 August 2014, 26 October 2014, and 19 March 2015. Since they do not contain a number of pulses, we cannot consider them as SES activities.
- 9 August 2014: The t-test confirms the hypothesis with a p-value equal to 0.79.
- 1 January 2015: The t-test confirms the hypothesis with a p-value equal to 0.92.
- 27 May 2015: The t-test confirms the hypothesis with a p-value equal to 0.31.
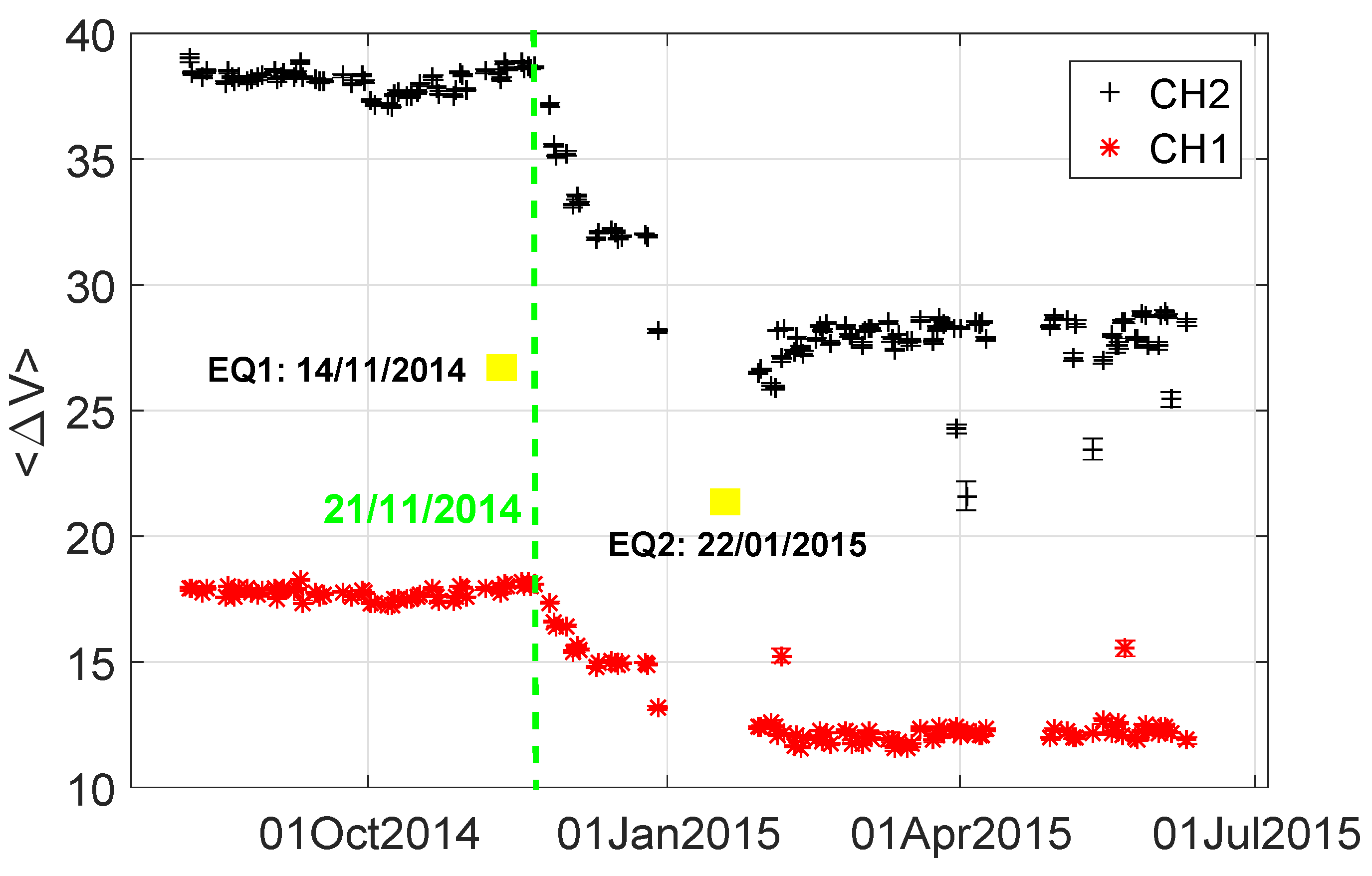
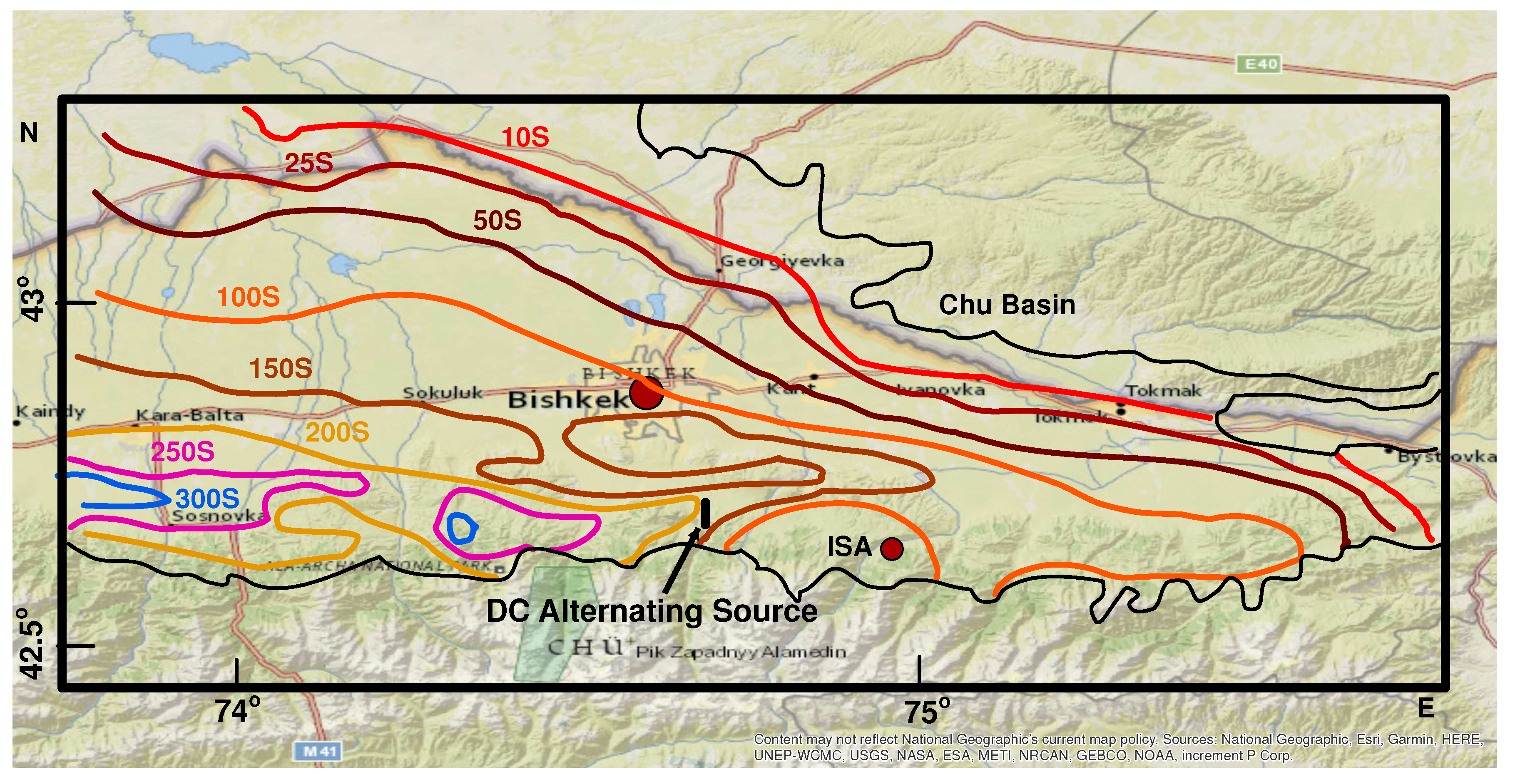
3.2. Subsurface Resistivity before Major Earthquakes
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ATC | Anomalous Telluric Currents |
| SES | Seismic Electric Signals |
| EW | East–West |
| NS | North–South |
| EMSEV | Electromagnetic Studies of Earthquakes and Volcanoes |
| RS-RAS | Bishkek Research Station of the Russian Academy of Science |
| ISA | Issyk Ata |
| USGS | United States Geological Survey |
| KNET | Kyrgyz Seismic Network |
Appendix A. Matlab Code for Cross-Correlograms
References
- Varotsos, P.; Alexopoulos, K. Physical properties of the variations of the electric field of the earth preceding earthquakes, I. Tectonophysics 1984, 110, 73–98. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Physical properties of the variations of the electric field of the earth preceding earthquakes, II. Tectonophysics 1984, 110, 99–125. [Google Scholar] [CrossRef]
- Varotsos, P. The Physics of Seismic Electric Signals; TERRAPUB: Tokyo, Japan, 2005. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, S.; Lazaridou, M. Additional evidence on some relationship between Seismic Electric Signals (SES) and earthquake focal mechanism. Tectonophysics 2006, 412, 279–288. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Fluctuations, under time reversal, of the natural time and the entropy distinguish similar looking electric signals of different dynamics. J. Appl. Phys. 2008, 103, 014906. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals. Tectonophysics 1991, 188, 321–347. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals, II. Tectonophysics 1993, 224, 1–37. [Google Scholar] [CrossRef]
- Varotsos, P. Point defect parameters in β-PbF2 revisited. Solid State Ion. 2008, 179, 438–441. [Google Scholar] [CrossRef]
- Lazaridou, M.; Varotsos, C.; Alexopoulos, K.; Varotsos, P. Point-Defect Parameters of LiF. J. Phys. C Solid State 1985, 18, 3891. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time. Precursory Seismic Electric Signals, Earthquakes and Other Complex Time-Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Lazaridou, M.; Kapiris, P. Transmission of stress induced electric signals in dielectric media. J. Appl. Phys. 1998, 83, 60–70. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Lazaridou, M.; Bogris, N.; Eftaxias, K.; Hadjicontis, V. A Review on the Statistical Significance of VAN Predictions. Phys. Chem. Earth A 1999, 24, 111–114. [Google Scholar] [CrossRef]
- Sarlis, N.; Lazaridou, M.; Kapiris, P.; Varotsos, P. Numerical Model of the Selectivity Effect and ΔV/L Criterion. Geophys. Res. Lett. 1999, 26, 3245–3248. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Long-range correlations in the electric signals that precede rupture. Phys. Rev. E 2002, 66, 011902. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Long-range correlations in the electric signals the precede rupture: Further investigations. Phys. Rev. E 2003, 67, 021109. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Attempt to distinguish electric signals of a dichotomous nature. Phys. Rev. E 2003, 68, 031106. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Tanaka, H.K.; Skordas, E.S. Some properties of the entropy in the natural time. Phys. Rev. E 2005, 71, 032102. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Seismic Electric Signals: An additional fact showing their physical interconnection with seismicity. Tectonophysics 2013, 589, 116–125. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Ramírez-Rojas, A.; Flores-Márquez, E.L. Natural time analysis: On the deadly Mexico M8.2 earthquake on 7 September 2017. Phys. A Stat. Mech. Appl. 2018, 506, 625–634. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Lazaridou-Varotsos, M.S. Earthquake Prediction by Seismic Electric Signals. The Success of the VAN Method over Thirty Years; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Mulargia, F.; Gasperini, P. Evaluating the statistical validity beyond chance of ‘VAN’ earthquake precursors. Geophys. J. Int. 1992, 111, 32–44. [Google Scholar] [CrossRef] [Green Version]
- Geller, R. Debate on ‘VAN’. Geophys. Res. Lett. 1996, 23, 1291–1452. [Google Scholar] [CrossRef]
- Lighthill, S.J. A Critical Review of VAN; World Scientific: Singapore, 1996. [Google Scholar]
- Nagao, T.; Uyeshima, M.; Uyeda, S. An independent check of VAN’s criteria for signal recognition. Geophys. Res. Lett. 1996, 23, 1441–1444. [Google Scholar] [CrossRef]
- Uyeda, S.; Al-Damegh, E.; Dologlou, E.; Nagao, T. Some relationship between VAN seismic electric signals (SES) and earthquake parameters. Tectonophysics 1999, 304, 41–55. [Google Scholar] [CrossRef]
- Kondo, S.; Uyeda, S.; Nagao, T. The selectivity of the Ioannina VAN station. J. Geodyn. 2002, 33, 433–461. [Google Scholar] [CrossRef]
- Uyeda, S. In defense of VAN’s earthquake predictions. EOS Trans. AGU 2000, 81, 3. [Google Scholar] [CrossRef]
- Sarlis, N.; Varotsos, A.P.; Skordas, E.; Uyeda, S.; Zlotnicki, J.; Nagao, T.; Rybin, A.; Lazaridou-Varotsos, S.M.; Papadopoulou, A.K. Seismic electric signals in seismic prone areas. Earthq. Sci. 2018, 31, 44–51. [Google Scholar] [CrossRef]
- Granqvist, S.; Hammarberg, B. The correlogram: A visual display of periodicity. J. Acoust. Soc. Am. 2003, 114, 2934–2945. [Google Scholar] [CrossRef] [PubMed]
- Wistbacka, G.; Andrade, P.A.; Simberg, S.; Hammarberg, B.; Södersten, M.; Švec, J.G.; Granqvist, S. Resonance Tube Phonation in Water the Effect of Tube Diameter and Water Depth on Back Pressure and Bubble Characteristics at Different Airflows. J. Voice 2018, 32, 126.e11–126.e22. [Google Scholar] [CrossRef] [PubMed]
- Öberg, F.; Askenfelt, A. Acoustical and perceptual influence of duplex stringing in grand pianos. J. Acoust. Soc. Am. 2012, 131, 856–871. [Google Scholar] [CrossRef] [PubMed]
- Bergqvist, L.; Katz-Salamon, M.; Hertegård, S.; Anand, K.; Lagercrantz, H. Mode of delivery modulates physiological and behavioral responses to neonatal pain. J. Perinatol. 2009, 29, 44. [Google Scholar] [CrossRef] [PubMed]
- Bonilha, H.S.; Deliyski, D.D. Period and glottal width irregularities in vocally normal speakers. J. Voice 2008, 22, 699–708. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.S.; Guido, R.C.; Scalassara, P.R.; Maciel, C.D.; Pereira, J.C. Wavelet time-frequency analysis and least squares support vector machines for the identification of voice disorders. Comput. Biol. Med. 2007, 37, 571–578. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Time-difference between the electric field components of signals prior to major earthquakes. Appl. Phys. Lett. 2005, 86, 194101. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. Magnetic field variations associated with SES. The instrumentation used for investigating their detectability. Proc. Jpn. Acad. Ser. B 2001, 77, 87–92. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. Magnetic field variations associated with the SES before the 6.6 Grevena-Kozani Earthquake. Proc. Jpn. Acad. Ser. B 2001, 77, 93–97. [Google Scholar] [CrossRef]
- Varotsos, P.V.; Sarlis, N.V.; Skordas, E.S. Electric Fields that “arrive” before the time derivative of the magnetic field prior to major earthquakes. Phys. Rev. Lett. 2003, 91, 148501. [Google Scholar] [CrossRef] [PubMed]
- Sarlis, N.; Varotsos, P. Magnetic field near the outcrop of an almost horizontal conductive sheet. J. Geodyn. 2002, 33, 463–476. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. On the difference in the rise times of the two SES electric field components. Proc. Jpn. Acad. Ser. B 2004, 80, 276–282. [Google Scholar] [CrossRef] [Green Version]
- Korzhenkov, A.; Deev, E. Underestimated seismic hazard in the south of the Issyk-Kul Lake region (northern Tian Shan). Geodesy Geodyn. 2017, 8, 169–180. [Google Scholar] [CrossRef]
- Bormann, P.; Fujita, K.; Mackey, K.G.; Gusev, A. Topic The Russian K-class system, its relationships to magnitudes and its potential for future development and application. In New Manual of Seismological Observatory Practice 2 (NMSOP-2); Bormann, P., Ed.; GFZ: Potsdam, Germany, 2012; pp. 1–27. [Google Scholar]
- Rybin, A.; Spichak, V.; Batalev, V.Y.; Bataleva, E.; Matyukov, V. Array magnetotelluric soundings in the active seismic area of Northern Tien Shan. Russian Geol. Geophys. 2008, 49, 337–349. [Google Scholar] [CrossRef]
- Chu, J.J.; Gui, X.; Dai, J.; Marone, C.; Spiegelman, M.W.; Seeber, L.; Armbruster, J.G. Geoelectric signals in China and the earthquake generation process. J. Geophys. Res. Solid Earth 1996, 101, 13869–13882. [Google Scholar] [CrossRef] [Green Version]
- Kayal, J.; Banerjee, B. Anomalous behaviour of precursor resistivity in Shillong area, NE India. Geophys. J. Int. 1988, 94, 97–103. [Google Scholar] [CrossRef] [Green Version]


| Date | (mV) | (mV) | |
|---|---|---|---|
| 8 August 2014 | |||
| 9 August 2014 | |||
| 12 August 2014 | |||
| 15 August 2014 | |||
| 16 August 2014 | |||
| 8 September 2014 | |||
| 2 October 2014 | |||
| 9 October 2014 | |||
| 23 October 2014 | |||
| 26 October 2014 | |||
| 27 October 2014 | |||
| 31 October 2014 | |||
| 4 November 2014 | |||
| 9 November 2014 | |||
| 21 November 2014 | |||
| 1 January 2015 | |||
| 19 January 2015 | |||
| 20 January 2015 | |||
| 25 January 2015 | |||
| 4 February 2015 | |||
| 7 February 2015 | |||
| 10 February 2015 | |||
| 14 February 2015 | |||
| 22 February 2015 | |||
| 23 February 2015 | |||
| 28 February 2015 | |||
| 10 March 2015 | |||
| 19 March 2015 | |||
| 30 March 2015 | |||
| 2 April 2015 | |||
| 7 April 2015 | |||
| 27 May 2015 |
| Date | Time | Lat. () | Long. () | K | M | r (km) |
|---|---|---|---|---|---|---|
| 15 August 2014 | 21:42:30.75 | 42.94 | 77.43 | - | 5 (mb) | 204.47 |
| 14 November 2014 | 1:24:16.48 | 42.14 | 77.23 | 14.43 | 5.2 (mww) | 194.24 |
| 5.8 (KNET) | ||||||
| 6.1 (Mpv) [42] | ||||||
| 10 January 2015 | 06:51:02.61 | 40.11 | 77.26 | - | 5.1 (mb) | 340.33 |
| 22 January 2015 | 15:52:30.71 | 42.36 | 74.95 | - | 4.9 (mb) | 30.92 |
| 17 November 2015 | 17:29:26.29 | 40.38 | 73.20 | - | 5.6 (mww) | 290.97 |
| 1 December 2015 | 06:13:43.36 | 41.38 | 73.26 | - | 5.1 (mb) | 198.82 |
| 7 December 2015 | 08:30:56.73 | 41.73 | 74.61 | - | 5.5 (mb) | 105.22 |
| Date | Time | Lat. () | Long. () | K | M | r (km) |
|---|---|---|---|---|---|---|
| 14 November 2014 | 1:24:16.48 | 42.14 | 77.23 | 14.43 | 5.8 (KNET) | 194.24 |
| 22 January 2015 | 15:52:30.71 | 42.36 | 74.95 | - | 4.9 (mb) | 30.92 |
| 7 December 2015 | 08:30:56.73 | 41.73 | 74.61 | - | 5.5 (mb) | 105.22 |
| No. of Pulse | Type | |
|---|---|---|
| 1 | rise | |
| 1 | decay | |
| 2 | rise | |
| 2 | decay | |
| 3 | rise | |
| 3 | decay | |
| 4 | rise | |
| 4 | decay |
| No. of Pulse | Type | |
|---|---|---|
| 1 | rise | |
| 1 | decay | |
| 2 | rise | |
| 2 | decay | |
| 3 | rise | |
| 3 | decay | |
| 4 | rise | |
| 4 | decay | |
| 5 | rise | |
| 5 | decay | |
| 6 | rise | |
| 6 | decay |
| No. of Pulse | Type | |
|---|---|---|
| 1 | decay | |
| 1 | rise | |
| 2 | decay | |
| 2 | rise | |
| 3 | decay | |
| 3 | rise | |
| 4 | decay | |
| 4 | rise | |
| 5 | decay | |
| 5 | rise | |
| 6 | decay | |
| 6 | rise | |
| 7 | decay | |
| 7 | rise | |
| 8 | decay | |
| 8 | rise |
| Case | ± (ms) | ± (ms) |
|---|---|---|
| 9 August 2014 | ||
| 1 January 2015 | ||
| 1 January 2015 (excl. outlier) | ||
| 27 May 2015 | ||
| source |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadopoulou, K.; Skordas, E.; Zlotnicki, J.; Nagao, T.; Rybin, A. Study of Geo-Electric Data Collected by the Joint EMSEV-Bishkek RS-RAS Cooperation: Possible Earthquake Precursors. Entropy 2018, 20, 614. https://doi.org/10.3390/e20080614
Papadopoulou K, Skordas E, Zlotnicki J, Nagao T, Rybin A. Study of Geo-Electric Data Collected by the Joint EMSEV-Bishkek RS-RAS Cooperation: Possible Earthquake Precursors. Entropy. 2018; 20(8):614. https://doi.org/10.3390/e20080614
Chicago/Turabian StylePapadopoulou, Konstantina, Efthimios Skordas, Jacques Zlotnicki, Toshiyasu Nagao, and Anatoly Rybin. 2018. "Study of Geo-Electric Data Collected by the Joint EMSEV-Bishkek RS-RAS Cooperation: Possible Earthquake Precursors" Entropy 20, no. 8: 614. https://doi.org/10.3390/e20080614






