1. Introduction
Computer simulations are widely used to reproduce the behaviour of systems [
1,
2] through which their performance can be estimated. Usually surrogate models are introduced to represent the physical realities which can be computationally expensive and are difficult to obtain analytical solutions for. In general,
f is denoted as a response function of the real system with input
and observation
which follows the form below:
Both and are regarded as random parameters. Given N samples () and corresponding observations (), the surrogate models can be built to approximate along with its statistics. The problem of proposing proper is known as the Design of Experiments (DoE) and it was developed with various mathematical theories. Basically, DoE methods can be categorized as model-free and model-oriented.
The Monte Carlo (MC) [
3,
4] method is a typical model-free DoE technique and has been widely used in applications. The main advantage of MC method is its simplicity in implementation. However, it converges at a rate of
. As a consequence, a large
N is usually needed to obtain an acceptable result and it is unsuitable for large scale high dimensional problems. A widely used way to accelerate the MC method is the quasi-MC technique [
5], for example, quasi-MC based on the Sobol set and Holton set. Another way to substitute the MC method is the Latin Hypercube Sampling (LHS) technique [
6] which can generate a near-random sample from a multidimensional distribution with even probability in a pre-defined grid, which ensures the sample is representative of the real variability.
In the context of surrogate models, given a parametric or non-parametric model, we aim to estimate the corresponding parameters or hyper-parameters to achieve the most accurate model. The model-oriented DoE is obtained via some pre-specified criteria. In parameter estimation problems, a popular approach is to consider information-based criteria [
7]. An A-optimal design minimizes the trace of the inverse of the Fisher information matrix (FIM) on the unknown parameters, whereas E-, T-, and D-optimal designs maximize the smallest eigenvalue, the trace, and the determinant of the FIM. In the Bayesian framework, the Markov Chain Monte Carlo (MCMC) method [
8] is an adaptive DoE technique which utilizes the prior and posterior information; hence, it can focus on points with more important information. The main shortage of MCMC is that it has difficulty determining the acceptance-rejection rate, and it sometimes seems cumbersome because of the long term burn-in period.
Nowadays, more efforts have been devoted to sequential sampling strategies with non-parametric Gaussian process (GP) models [
9,
10,
11]. The main idea behind those methods is to minimize the times required to call the original system which can be computationally expensive. A learning criterion should be given in prior to obtain samples sequentially. B. Echard et al. [
12] have proposed the active learning reliability method which combines the Kriging and Monte Carlo simulation methods (AK-MCS) to iteratively assess the reliability in a more efficient way. Similarly, for continuous functions, Bayesian optimization (BO) [
10], despite being designed to solve the optimization problem, also collects samples adaptively. The learning criterion is known as the acquisition function in the BO field. One can optimize the expected improvement (EI) or the probability improvement (PI) over the current best result or the lower/upper confidence bound (LCB/UCB) to decide the next point to be sampled. Unlike the A(E,T,D)-optimal designs which decide the DoE in one step, sequential sampling strategies utilize the information from the observations, hence producing more reliable and accurate results for our research goals.
We note that two main obstacles of the BO exist: first, the optimization of hyper-parameters and the inference of Gaussian processes may fail when the covariance in the Gram matrix of the kernel with respect to current DoE
is ill-conditioned; second, it is usually difficult to determine the trade-off parameter between exploration and exploitation, i.e., local optimization or global search. To solve the first problem, considering a similar situation where a parametric regression problem becomes unstable when the condition number of its design matrix is large, the state-of-the-art K-optimal design [
13] which optimizes the condition number could be a reasonable choice. In this paper, a new BO approach is proposed with the condition number of the Gram matrix being introduced as an acquisition function, namely, the Sequentially Bayesian K-optimal design (SBKO). We show that the SBKO actually evolves towards the direction of reducing the integrated posterior variance as well as the direction of maximizing the KL divergence between the prior and posterior distributions of hyper-parameters. No extra parameter is needed to balance the exploration and exploitation, because the SBKO generally tends to fill the whole design space; hence, it is suitable for global search tasks such as approximation and prediction. To solve the second problem, the property of K-optimality can be also used to modify the trade-off parameter, based on the idea that those points leading to smaller condition numbers should be explored. We combine the K-optimality and the classical BO criterion to propose the K-optimal enhanced BO (KO-BO) method. The trade-off parameters are computed automatically according to changes in the condition number brought by the associate points. Compared with the classical BO methods, the KO-BO method is more flexible in determining the trade-off parameter, and it implicitly ensures the stability of the GP model.
The paper is organized as follows. We review Gaussian process regression in
Section 2 along with the K-optimal criterion. Our main method and algorithm are in
Section 3. At the beginning of
Section 3, we present the corresponding acquisition function to incorporate the K-optimal design with the BO framework, i.e., the Sequentially Bayesian K-optimal design. Secondly, we show the connections of our method with the methods that focus on minimizing the integrated posterior variance and maximizing the information gain of the inference respectively. At the end of
Section 3, we propose the K-optimal enhanced Bayesian optimization algorithms to solve the optimization problem. The experimental results are presented in
Section 4, and the conclusions follow in
Section 5.
3. Methodology
We restate that our main goal was to choose an optimal design from the predefined input domain which is appropriate for inferring the model in the Bayesian framework. The Gaussian processes was chosen as the model, while the K-optimality was taken into consideration. As reviewed in
Section 2, the performance of the Gaussian processes was generally controlled by the covariance functions, i.e., kernels, which are continuous, positive semi-definite functions. It is notable that an inverse term of
exists in Equation (
3). When the collected samples are close enough, it will lead to potential failure to calculate
as well as the inference of the Gaussian processes, although a nugget term
was added.
In this work, we focused on an experimental design that ensured the correctness and accurateness of Bayesian inference. If the condition number of
K in Equation (
3) is bounded by a relative small constant, then the inference of Gaussian processes can be always achieved. The Sequentially Bayesian K-optimal design (SBKO) was then proposed which is straightforward and simple to present. Like the classical BO methods, the acquisition function is given as
, where
stands for the condition number and
is the updated covariance matrix, with
being the hyper-parameters of the kernel function. The term
can be omitted in the following sections without causing any misunderstanding. Hence,
is defined as follows, and the next point (
) is sampled by solving the optimization problem:
There are two main concerns about the minimization of
. On one hand, the condition number and its optimization problem are not convex. Hence, non-smooth algorithms, such as the DIviding RECTangles (DIRECT) algorithm [
15] or the genetic algorithm, are used to solve Equation (
7). A few works in the literature focused on optimizing the condition number under certain conditions. P. Maréchal and J. J. Ye investigated the optimization of condition number over a compact convex subset of the cone of symmetric positive semi-definite
matrices in 2009 [
16], while X. J. Chen, R. S. Womersley, and J. J. Ye investigated the minimization of the condition number of a Gram matrix of the polynomial regression model in 2011 [
17]. Both of the works introduced the idea of the Clarke generalized gradient which can accelerate the optimization process.
On the other hand, the hyper-parameters
control the value of
; hence, one can consider the MLE (Maximum Likelihood Estimation) or MAP (Maximum A Posterior) of
. Note that the data are sampled sequentially, which implicitly implies that the MLE (MAP) of
satisfies the criterion with current samples, and it usually does not hold when a new point is added. Instead of using the point estimate of
, one can consider the general technique [
18,
19] of integrating the acquisition function
over the posterior distribution:
where
is the posterior distribution with the DoE (
), observations (
Y) and prior distribution of the hyper-parameters (
). The expectation in Equation (
8) generally accounts for uncertainty in the hyper-parameters or the average level of
.
can be approximated by the MC estimate, where the samples of
from the posterior distribution can be obtained by the MCMC procedure. In this work, the efficient slice sampling approach proposed by I. Murray [
20] was introduced to obtain samples of
from the posterior distribution.
In fact, minimizing the condition number has more significance than generating stable inference for the GP model. In the next subsections, we show that minimizing has a close connection with the prediction uncertainty as well as the information gain.
3.1. Connection to Optimization of the Integrated Posterior Variance
The prediction uncertainty is given as the posterior variance (
) in Equation (
3). We chose to integrate the posterior variance into the input domain instead of the approximation itself; the integration accounts for every point in the whole domain, and it also quantifies the uncertainty which provides the quality of the approximation. We let the input space (
) be a first-countable space equipped with a strictly Borel measure (
), amd represented
as a convergent series according to Mercer’s theorem [
21]:
where
forms an orthonormal basis of
. Then, the next sample was obtained by minimizing its corresponding integrated posterior variance (IPV), i.e.,
where
,
,
. The fourth equation was obtained by the orthonormality of
, and we assumed that the hyper-parameters were fixed for simplicity. The last term is not easy to calculate; however, we investigated its upper bound which reflects the maximum reduction in the IPV:
where
is the maximum
and
represents the trace of a matrix. The first inequality was derived by the Cauchy–Schwarz inequality, while the last equality was given with the help of Equation (
9). Suppose the isotropic kernel functions, for example, the isotropic squared exponential covariance function or the isotropic Matérn covariance function, are used in the Gaussian process model, then
is an invariant, as well as the term
.
If we recall the SBKO criterion demonstrated in Equation (
7), we have the following results:
We let
be the singular values of
, while
were those of
. Note that we have the Cauchy’s interlacing theorem, which states that
Hence, it was derived that
According to Equations (
14) and (
15), we have the boundaries of
as follows:
By considering Equations (
11) and (
16) together, we obtained the lower bound of
as
The lower bound of is inversely proportional to , so the new sample that minimizes the condition number also maximizes the reduction of the IPV.
3.2. Connection to Optimization of the KL-Divergence
Equation (7) presents a simple way to incorporate the K-optimal design and BO framework. Such a procedure ensures the success of Bayesian inference; however, it is notable that the covariance matrix (
K) alone does not reflect how well the new sample supports the inference of model. We used Kullback–Leibler (KL) divergence [
22] from the posterior to prior as a metric to illustrate the performance of the new sample, as follows:
where
is the posterior distribution given DoE
and a new point is sampled such that
. Unlike the entropy search acquisition function which maximizes the expected reduction in the negative differential entropy (
)
w.r.t the current best location (
), Equation (
18) aims to reduce the uncertainty of the hyper-parameters, i.e., the uncertainty of the inference. We chose the inclusive direction of the KL divergence since we had
known as the prior at each step, and the KL-divergence explicitly quantified the additional information captured in
relative to the previous distribution, where a larger negative KL divergence reflects a greater information gain about
upon the possible new design (
).
We note that the new observation (
y) cannot be attained before being actually sampled at the point, so the prediction
in Equation (
3) is introduced to substitute the unknown
y. However,
has high uncertainty at some points; hence, Equation (
18) becomes unsuitable for inference. An analogue technique is taking the expectation over the prediction which is presented as follows:
The above acquisition function was introduced by Kim et al. [
23], where
is interpreted as the mutual information [
24] between the parameter variables
and the predictive observation
(which is also a random variable given
) conditional upon candidate design
, i.e.,
. Then, the next sample is obtained according to the criterion
, i.e.,
where
are omitted for simplicity, and
represents the differential entropy. The second equation is derived from the fact that
does not depend on
. Notice that
is a concave function; hence, we have the last equation with a constant
. Now that
, which is a strictly monotonically increasing function on
, given Equation (
3), we can rewrite Equation (
20) as follows:
The right-hand side of Equation (
21) is the average uncertainty of prediction over all possible parameters (models). Specifically, we investigated
only with fixed hyper-parameters (
) for simplicity. Using Equation (
16), we considered the lower bound of
as follows:
The above lower bound is an invariant if the isotropic kernel function is introduced. Since
(see Equation (
3)), it is likely to be reached when
is maximized. Hence, the minimization of
tends to optimize the KL-divergence between the prior and posterior distributions.
3.3. K-Optimal Enhanced Bayesian Optimization
Compared with the classical BO methods which aim to solve the optimization problems, the optimization process in the previous method focuses on the condition number of . Actually, the DoE generated by our method tend to be scattered throughout the whole design space (the K-optimal designs are called support points in the original paper); hence, they are suitable for the global prediction behaviour of the Gaussian process model. Based on the previous discussion, the idea of K-optimality can be used to refine the classical BO methods. In this work, we focused our research on comparison with the EI criterion, which generally outperforms the PI criterion and is simpler than the LCB criterion.
The K-optimal was introduced to enhance the performance of Bayesian optimization for the following reason. It is well-known that balancing the trade-off between exploiting (where the prediction is expected to be high) and exploring (where the prediction uncertainty is high) is a key problem in the BO framework. For instance, an additional parameter,
, is introduced for the EI algorithm, where
is replaced by
in both Equations (
4) and (
5). The value of
determines the range of exploration, i.e., the anticipated improvement is likely to be greater than
. The choice of
is an open problem for researchers, and there is no universal rule to determine the optimal value of
. An unsuitable
for the EI algorithm sometimes leads to the local optimum, whose information will be strengthened as the data number increases. Notice that since the K-optimality naturally forces the samples to spread sparsely in the design space, it may be an alternative way to perform exploration.
The natural way of introducing the K-optimality to the classical BO framework is to take account of the criteria together, where we tend to choose the one that leads to a smaller condition number when several points have comparable performances in terms of the EI criterion. Given two points
and corresponding classical acquisition function
, as well as
defined in Equation (
7), we have to decide which point should be sampled for four different situations considering the acquisition function and K-optimality simultaneously, which is illustrated in
Table 1.
The above table shows that there two situations exist where the sample strategy remains unclear to us when combining the classical BO criteria and the K-optimality directly; hence, a new method to balance the two factors is needed. Since we aimed to solve the optimal problems in the Bayesian framework, the classical BO criteria were regarded as the main factors that indicate the direction of the next sample, while K-optimality was used to tune the strength of exploration. Basically, we have stronger belief in the point that improves the optimization results while maintaining the validity of the inference.
We used the condition number
as the indicator of the strength of exploration. In this work,
was used to show the goodness of the point for the next Bayesian inference; thus, the exploration was based on the following idea: if the next point to be sampled leads to a large condition number, then we should consider extending the exploration range. We considered the analytic expression of the EI acquisition function as follows:
where
denotes the probability density function of the standard normal distribution. We then investigated how
affects the value of
by calculating the derivative
:
Hence,
is a monotonically decreasing function on
. Since we aimed to enlarge the utility of the point which leads to better inference (smaller condition number), the simplest way was to replace
with
. However, note that the condition number
is always greater than 1, and usually, it is a relative large number, so firstly, we normalized
from
to
with the help of the following function:
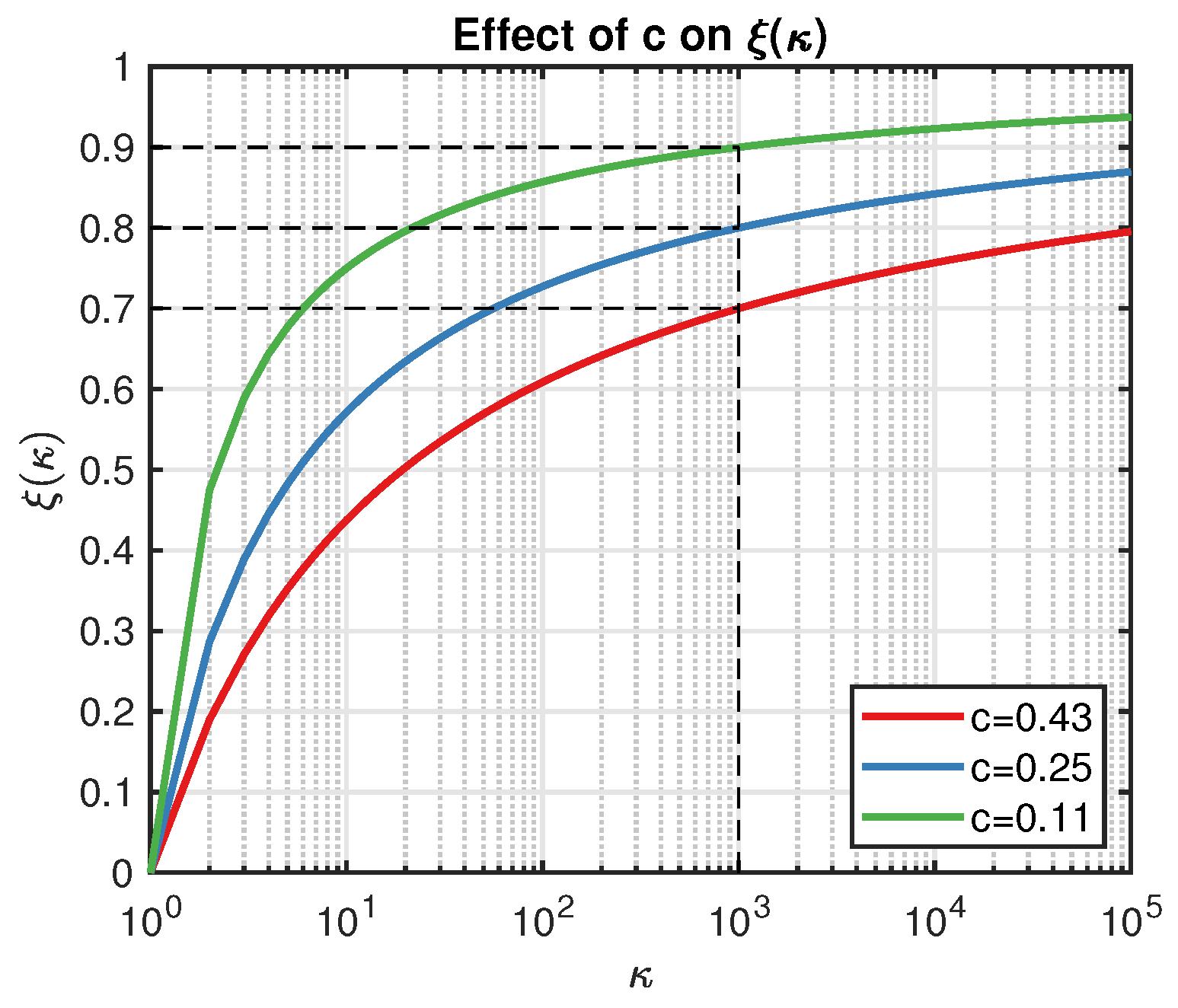
where
is the threshold of the condition number (say, greater than 1000 as a rule of thumb), and
c is a constant that controls the shape of
, as illustrated in
Figure 1. For example, let
and
; then, we have
displayed as the blue line in
Figure 1. Actually,
c determines the exploration strength
w.r.t . A smaller
c leads to a larger
, and we are less likely to trust the point that results in
. On the other hand, the smaller the
is, the fewer the points we can accept in practice. Compared with the classical EI algorithm,
is more flexible because it automatically updates its value.
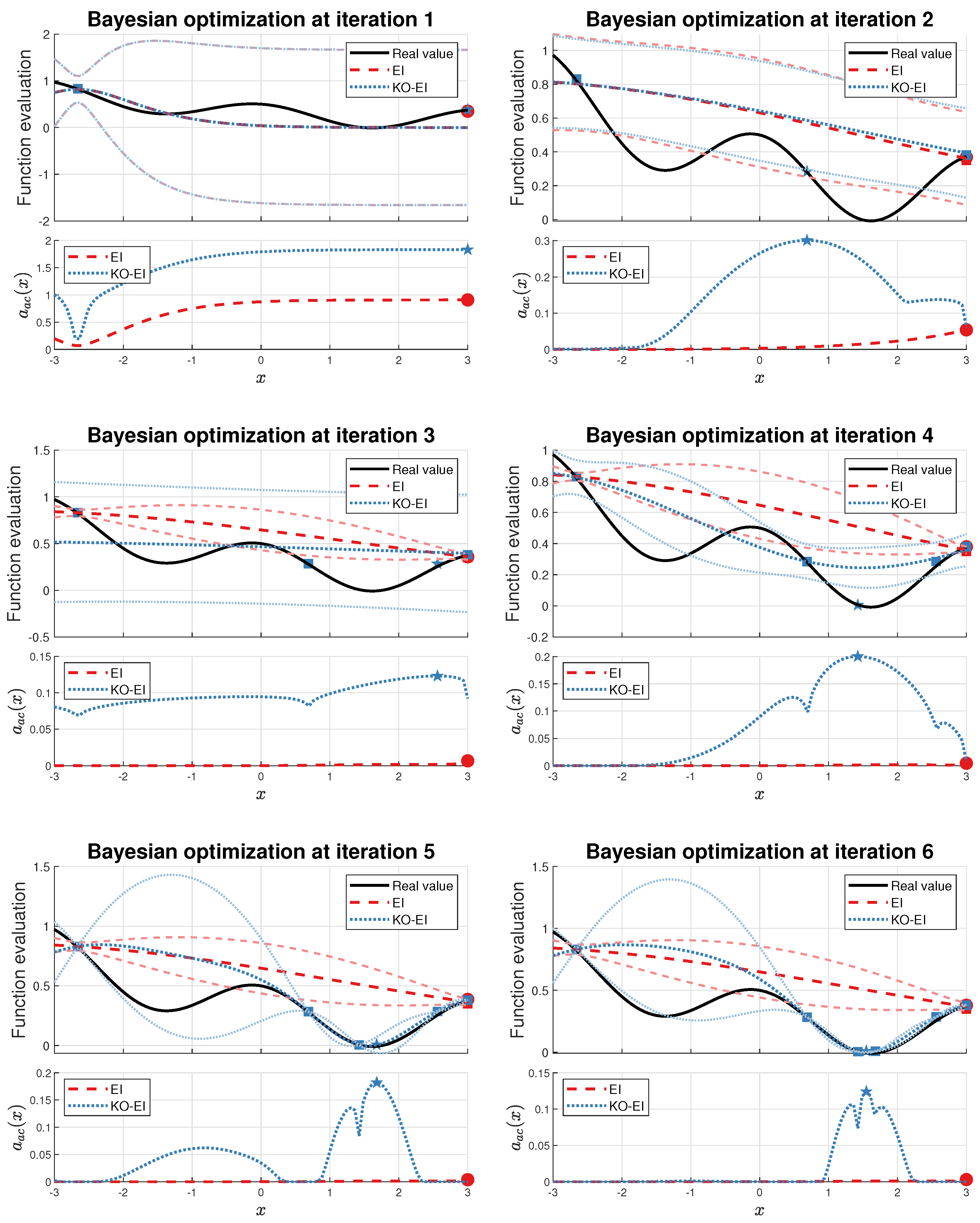
Several interesting features for the above methodology exist. Firstly, if a point is far away from the current exploitation region but it may result in better inference for the model, then the probability to keep it as the next sample still exists. Secondly, if a point can improve the current best value, however it may be derived from a false inference, then we are likely to dump the point by shrinking its utility. We wdemonstrate these properties in
Section 4.2.
5. Conclusions
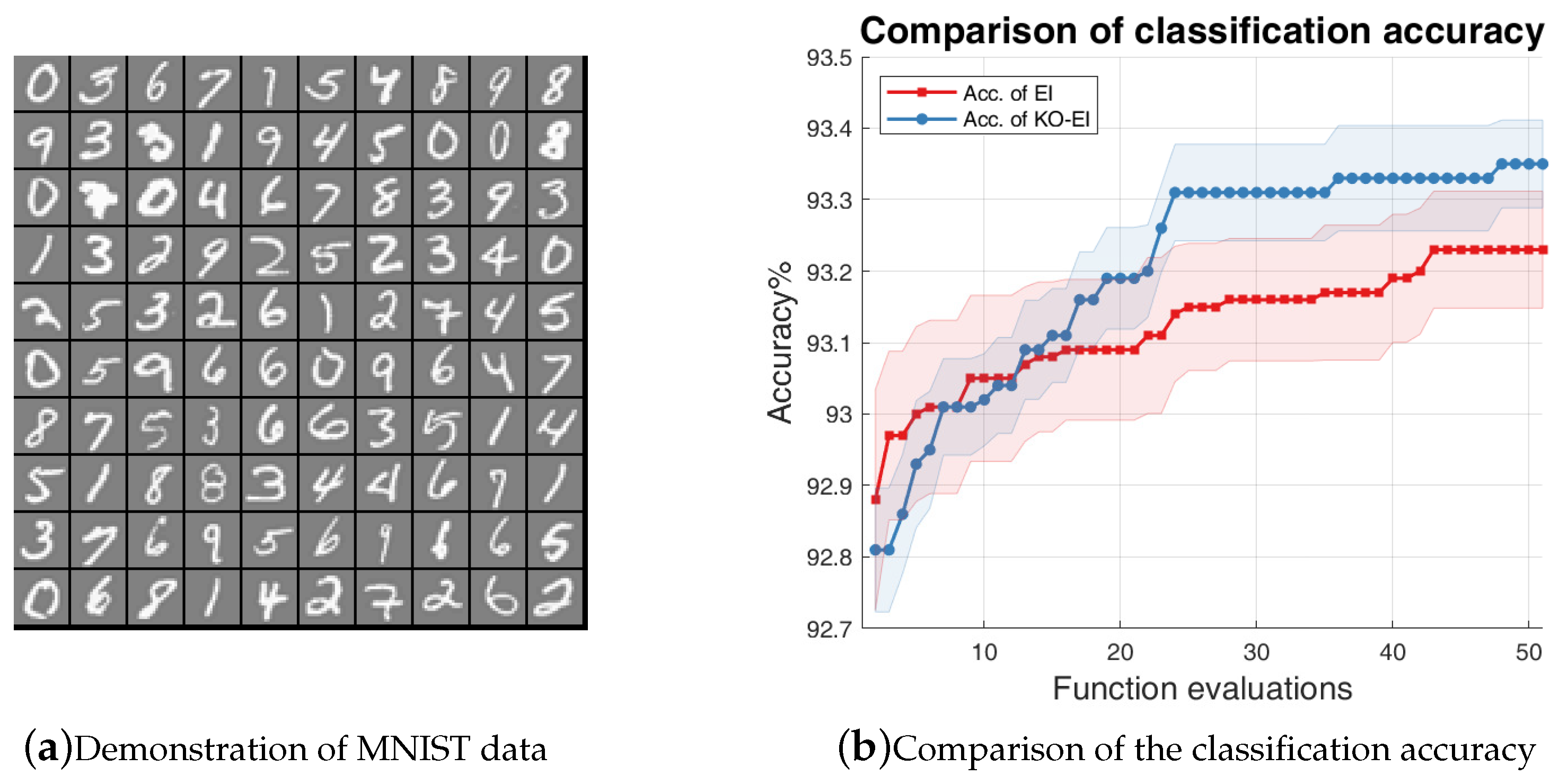
This paper examined the combination of the K-optimal design and the Bayesian optimization framework. In order to ensure the validity of Gaussian process inference, we introduced the condition number of the Gram matrix of the kernel as the acquisition function to propose the Sequentially Bayesian K-optimal design (SBKO). The SBKO is suitable for global tasks, such as approximation and prediction. On the other hand, the property of K-optimality was also used with the classical BO methods, namely the KO-BO method, in this research. The trade-off parameters were updated automatically based on the idea that points leading to smaller condition numbers should be explored. Numerical investigations on the approximation problem results showed that the SBKO generally outperforms the MC, LHS, and the MPV when the samples are compact in the input domain. Examples on the optimization problem showed that the K-optimal enhanced expected improvement (KO-EI) can deal with extreme cases where the EI criterion is trapped in a local maximum very well. Further experiments showed that the KO-EI convergences faster than the EI algorithm; however, it is much more stable.
Although the K-optimality performed well in our experiments, we also note that its calculation and optimization could still be a burden because it is not convex and there is no explicit expression of its gradient. Future work could focus on the approximation methods of the condition number, such as the Clarke generalized gradient [
16,
17], hence accelerating corresponding computation. We could also investigate the usage of our method to deal with non-convex constraints and input domains. An analysis of the theoretical boundaries of the KO-BO algorithms would be of great interest too.