Feynman Paths and Weak Values
Abstract
:1. Introduction
2. Dirac’s Notion of a Quantum Trajectory
2.1. Dirac Trajectories
2.2. The Feynman Propagator
2.3. TPAs Involving the Momentum
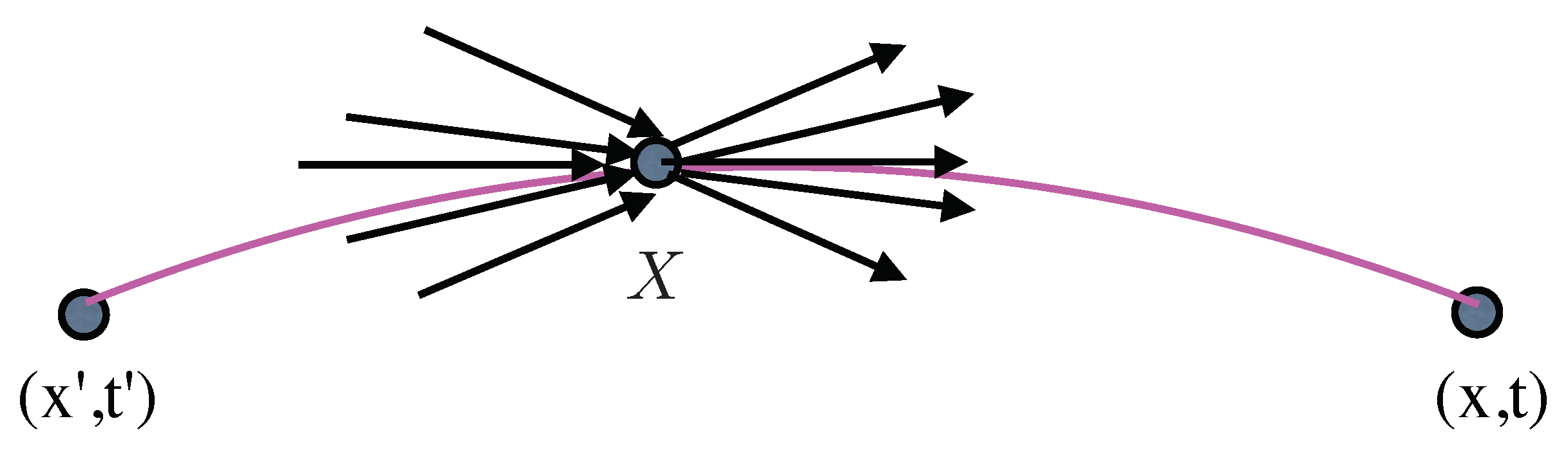
2.4. The Relation between Weak Values and TPAs
3. Weak Values Are Weighted TPAs
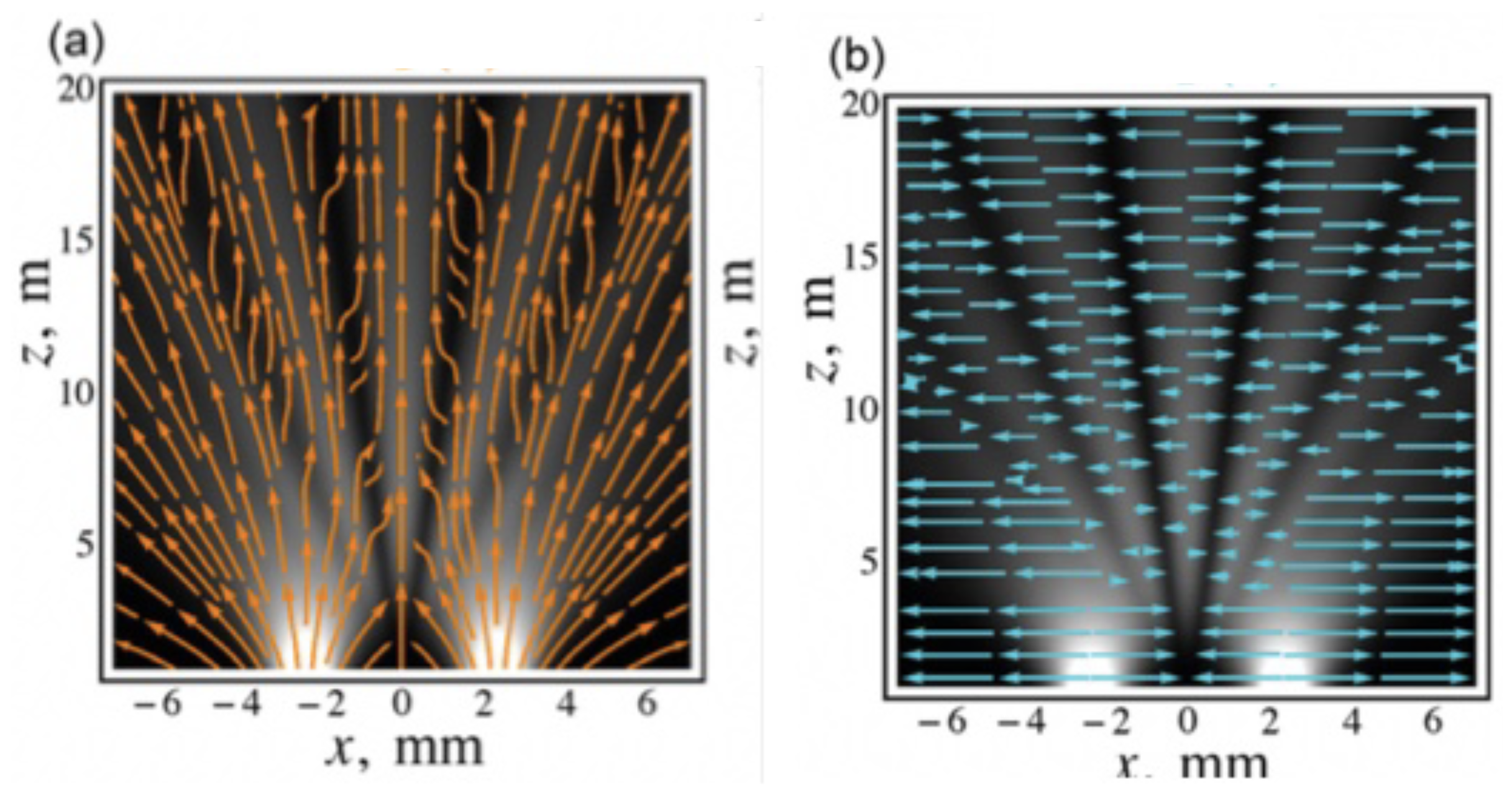
3.1. Flow Lines Constructed from Weak Values
3.2. Where Is the Quantum Potential?
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Einstein, A. Albert Einstein: Philosopher-Scientist; Schilpp, A.P., Ed.; Library of the Living Philosophers: Evanston, IL, USA, 1949; pp. 665–676. [Google Scholar]
- Heisenberg, W. Physics and Philosophy: The Revolution in Modern Science; George Allen and Unwin: London, UK, 1958. [Google Scholar]
- Jammer, M. The Philosophy of Quantum Mechanics; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Kocsis, S.; Braverman, B.; Ravets, S.; Stevens, M.J.; Mirin, R.P.; Shalm, L.K.; Steinberg, A.M. Observing the average trajectories of single photons in a two-slit interferometer. Science 2011, 332, 1170–1173. [Google Scholar] [CrossRef] [PubMed]
- Philippidis, C.; Dewdney, C.; Hiley, B.J. Quantum interference and the quantum potential. Il Nuovo Cimento B 1979, 52, 15–28. [Google Scholar] [CrossRef]
- Mahler, D.H.; Rozema, L.A.; Fisher, K.; Vermeyden, L.; Resch, K.J.; Braverman, B.; Wiseman, H.M.; Steinberg, A.M. Measuring bohm trajectories of entangled photons. In Proceedings of the 2014 Conference on Lasers and Electro-Optics (CLEO)—Laser Science to Photonic Applications, San Jose, CA, USA, 8–13 June 2014. [Google Scholar]
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P. Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys. 1948, 20, 367–387. [Google Scholar] [CrossRef]
- Schwinger, J. The theory of quantised fields I. Phys. Rev. 1951, 82, 914–927. [Google Scholar] [CrossRef]
- Dirac, P.A.M. On the analogy between Classical and Quantum Mechanics. Rev. Mod. Phys. 1945, 17, 195–199. [Google Scholar] [CrossRef]
- Nelson, E. Derivation of schrödinger’s equation from newtonian mechanics. Phys. Rev. 1966, 150, 1079–1085. [Google Scholar] [CrossRef]
- Bohm, D. A suggested interpretation of the quantum theory in terms of hidden variables, I. Phys. Rev. 1952, 85, 180–193. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1947. [Google Scholar]
- Guillemin, V.W.; Sternberg, S. Symplectic Techniques in Physics; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- De Gosson, M.; Hiley, B.J. Imprints of the quantum world in classical mechanics. Found. Phys. 2011, 41, 1415–1436. [Google Scholar] [CrossRef]
- Brown, L. Feynman’s Thesis: A New Approach to Quantum Mechanics; World Scientific Press: Singapore, 2005. [Google Scholar]
- De Gosson, M.; Hiley, B.J. Short-time quantum propagator and bohmian trajectories. Phys. Lett. 2013, 377, 3005–3008. [Google Scholar] [CrossRef] [PubMed]
- Hirschfelder, J.O.; Christoph, A.C.; Palke, W.E. Quantum mechanical streamlines I. square potential barrier. J. Chem. Phys. 1974, 61, 5435–5455. [Google Scholar] [CrossRef]
- Hirschfelder, J.O. Quantum mechanical equations of change. I. J.Chem. Phys. 1978, 68, 5151–5162. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. Non-locality and locality in the stochastic interpretation of quantum mechanics. Phys. Rep. 1989, 172, 93–122. [Google Scholar] [CrossRef]
- Hiley, B.J. Weak values: Approach through the Clifford and Moyal algebras. J. Phys. Conf. Ser. 2012, 361, 012014. [Google Scholar] [CrossRef]
- Schwinger, J. The theory of quantum fields III. Phys. Rev. 1953, 91, 728–740. [Google Scholar] [CrossRef]
- Leavens, C.R. Weak measurements from the point of view of bohmian mechanics. Found. Phys. 2005, 35, 469–491. [Google Scholar] [CrossRef]
- Wiseman, H.M. Grounding bohmian mechanics in weak values and bayesianism. New J. Phys. 2007, 9, 165–177. [Google Scholar] [CrossRef]
- Flack, R.; Hiley, B.J. Weak values of momentum of the electromagnetic field: Average momentum flow lines, not photon trajectories. arXiv, 2016; arXiv:1611.06510. [Google Scholar]
- Bohm, D.; Hiley, B.J.; Kaloyerou, P.N. An ontological basis for the quantum theory: II—A causal interpretation of quantum fields. Phys. Rep. 1987, 144, 349–375. [Google Scholar] [CrossRef]
- Monachello, V.; Flack, R.; Hiley, B.J. A method for measuring the real part of the weak value of spin using non-zero mass particles. arXiv, 2017; arXiv:1701.04808. [Google Scholar]
- Morley, J.; Edmunds, P.D.; Barker, P.F. Measuring the weak value of the momentum in a double slit interferometer. J. Phys. Conf. Ser. 2016, 701, 012030. [Google Scholar] [CrossRef]
- Moyal, J.E. Quantum mechanics as a statistical theory. Proc. Camb. Phil. Soc. 1949, 45, 99–123. [Google Scholar] [CrossRef]
- Dürr, D.; Teufel, S. Bohmian Mechanics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Bliokh, K.Y.; Bekshaev, A.Y.; Kofman, A.G.; Nori, F. Photon trajectories, anomalous velocities and weak measurements: A classical interpretation. New J. Phys. 2013, 15, 073022. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. The Undivided Universe: An Ontological Interpretation of Quantum Theory; Routledge: London, UK, 1993. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics; III, Sec 21-8; Addison-Wesley: Boston, MA, USA, 1965. [Google Scholar]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- De Broglie, L. Non-Linear Wave Mechanics: A Causal Interpretation; Elsevier: Amsterdam, The Netherlands, 1960; p. 116. [Google Scholar]
- Smolin, L. Quantum mechanics and the principle of maximal variety. Found. Phys. 2016, 46, 736–758. [Google Scholar] [CrossRef]
- Hiley, B.J. On the Nature of a Quantum Particle. 2018; in press. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flack, R.; Hiley, B.J. Feynman Paths and Weak Values. Entropy 2018, 20, 367. https://doi.org/10.3390/e20050367
Flack R, Hiley BJ. Feynman Paths and Weak Values. Entropy. 2018; 20(5):367. https://doi.org/10.3390/e20050367
Chicago/Turabian StyleFlack, Robert, and Basil J. Hiley. 2018. "Feynman Paths and Weak Values" Entropy 20, no. 5: 367. https://doi.org/10.3390/e20050367
APA StyleFlack, R., & Hiley, B. J. (2018). Feynman Paths and Weak Values. Entropy, 20(5), 367. https://doi.org/10.3390/e20050367




