1. Introduction
Sensitivity analysis (SA) is one of the most important methodologies dealing with optimization in engineering practice. It aims to quantify importance in the output of a model with regards to some input parameters or design variables [
1,
2,
3,
4]. With the results of SA, important variables of given model are chosen for further study when less important variables may be treated as constant. This could help reduce the dimension of inputs (number of input variables) and improve the model understanding.
Generally, SA methodologies can be classified into local sensitivity analysis (LSA) and global sensitivity analysis (GSA) [
1,
5]. The former only concentrate on the influence of single input parameter on model output by gradient estimating in a small neighborhood around a normal point. It is often used to provide deterministic direction to be close to the optimal object [
6]. Meanwhile, the latter one tries to quantify the output uncertainty when all input parameters are varying over entire value domain. And it does not depend on the choice of a nominal point [
5,
7]. Thus, GSA is suitable for uncertainty quantification (UQ) and reliability based design optimization (RBDO) [
8].
Numerous methodologies are developed for GSA, among which variance-based methods are widely used [
1,
5]. Variance-based methods take the well-known variance decomposition formula
V(
Y) =
V(
E(
Y|
X)) +
E(
V(
Y|
X) as their foundation. This formula has variance separated by using the variance of conditional expectation and associated residual variance. Thus, the contribution or importance of
X on
Y could be further studied. Many researchers take Sobol’s indices because they could provide a clear, accurate and robust indication of the selected uncertain inputs both quantitatively and qualitatively [
9]. Although Sobol’s indices are traditionally applied for non-statistical model output, some researchers have extended Sobol’s indices to identify uncertainty effects of inputs on reliability. Morio only studied the effects of some variable distribution parameters, such as variable means, but it did not consider the variable uncertainties themselves [
10]. Borgonovo proposed the moment-independent global sensitivity indices which are derived from conditional probability density function (PDF) [
11,
12]. Lu accepted this idea and further developed the variance-based importance measurement for global reliability sensitivity analysis (GRSA) with associated global reliability sensitivity indices [
13,
14]. Cui and Li proved the equivalence relation between these global reliability sensitivity indices and Sobol’s indices when taking the indicator function as the assumed model output.
Unlike traditional global sensitivity indices calculation, the global reliability sensitivity indices aim at calculating importance of input variables on reliability that is a statistical parameter. These indices are specifically concerned about the variance of conditional expectation of indicator function according to variance decomposition formula. However, the indicator function maps every single model output to only two real numbers 0 or 1 discretely, so the analytical method and surrogate method, which are popular with uncertainty analysis, have not been developed for GRSA because it is difficult to obtain an analytical formula of the indicator function. In this way, the Crude Monte Carlo Simulation (MCS) is always employed to calculate such measurement [
15,
16], which leads that the computation cost is unacceptable when the given model is complex. Although Li et al. used the importance sampling technologies to improve sampling efficiency [
13], quite a few samples are inevitable.
Fortunately, the conditional expectation of indicator function is equal to the conditional failure probability (CFP) that could be regarded as a continuous random variable. Thus, the variance of conditional expectation of indicator function could be replaced by the variance of CFP. In this way, if CFP could be assumed as the model output, there might be an unknown expression between CFP and corresponding conditional variable. So, the surrogate method could be used to approximate the CFP. Then, the statistical properties of CFP, such as mean and variance, may be calculated by surrogate model efficiently.
As for the issue of the statistical properties of a surrogate model, polynomial chaos expansions (PCE) technology provides a powerful tool for this application [
17,
18]. The PCE is a surrogate modelling technology with orthogonal polynomial basis functions, and it has statistical moments calculation simplified. In other words, variance information of surrogate model could be readily obtained by post-processing PCE’s coefficients analytically [
19,
20]. Therefore, it is suitable to make a surrogate model for CFP and calculate its variance. However, a challenge for PCE method in such application is that quite a few specific probability values are required. In addition, since the CFP is dependent on a set of conditional variables, each global reliability sensitivity index corresponding to different conditional variables requires a specific surrogate model. This may be time consuming when computing several indices. To circumvent this problem, the maximal entropy (ME) method is introduced since it could compute probabilities precisely and analytically only with prior moment information of model output [
21,
22,
23,
24]. Considering the orthogonal characteristics, the PCE could not only provide the first two order moments directly, but also provide higher order moments by PCE multiplication algorithm without additional sampling. In this way, the combination of PCE and ME could make GRSA efficiently. To the author’s knowledge, this idea has not been developed for global reliability sensitivity indices calculation.
Therefore, a new 2-layer PCE algorithm coupling PCE and ME is developed. That is, the first layer PCE is to generate a surrogate model by traditional algorithm. The second layer PCE is to construct several surrogate models for CFPs with the help of ME, which are referred as reliability polynomial chaos expansions (R-PCEs). The moment information that ME requires is provided by the first layer PCE when the conditional variables are given and fixed. Then, the variance of each CFP comes out by analytically post processing R-PCE coefficients, followed by global reliability sensitivity indices.
The presentation of the work is structured as follows:
Section 2 provides a brief introduction of GSA and GRSA respectively.
Section 3 presents the proposed 2-layer PCE framework and detailed calculation procedure. A numerical example and an engineering example are presented to test the performance of the proposed method in
Section 4, while
Section 5 summarizes the main contributions of this paper. The symbols used in this paper are listed in
Table A1 in
Appendix A.
3. R-PCE Framework for GRSA
3.1. PCE-Based GRSA Method
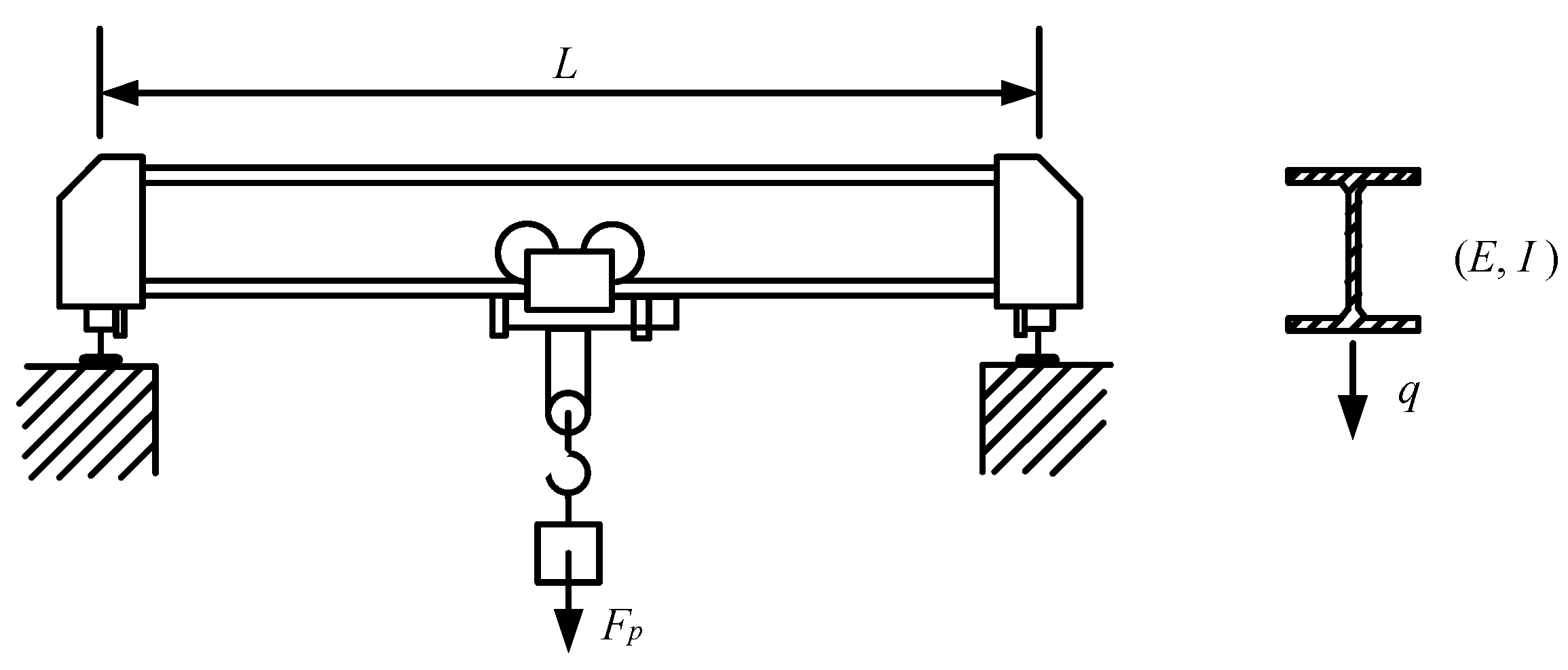
Take the limit-state function in
Section 2.2 into consideration. As mentioned above, the model output for global reliability sensitivity indices calculation is
IF, and it is difficult to compute
IF related value except for MCS. This is due to the fact that
IF only maps every single model output to two discrete real numbers 0 or 1. Either analytical methods or surrogate methods are efficient when they are applied to continuous model output rather than the discrete case. However,
E(
IF|
xi) and
E(
IF|
x~[i]) could be replaced by two CFP values
Pf(
xi) and
Pf(
x~[i]) respectively, which could be treated as continuous random variables. In this way, the key point of global reliability sensitivity index calculation is to compute variance values
V(
Pf(
xi)) and
V(
Pf(
x~[i])). Equations (17) and (18) are replaced by Equations (22) and (23):
Since the PCE technology provides an efficient surrogate modeling tool to determinate the mean as well as the variance of the model output, a PCE-based method is developed for this implement. However, several probability values required during surrogate modeling procedure may cause computational demanding. So, the analytical ME method is integrated with PCE to solve this problem. Thus, the surrogate model of CFP could be developed, which is referred as R-PCE in this work.
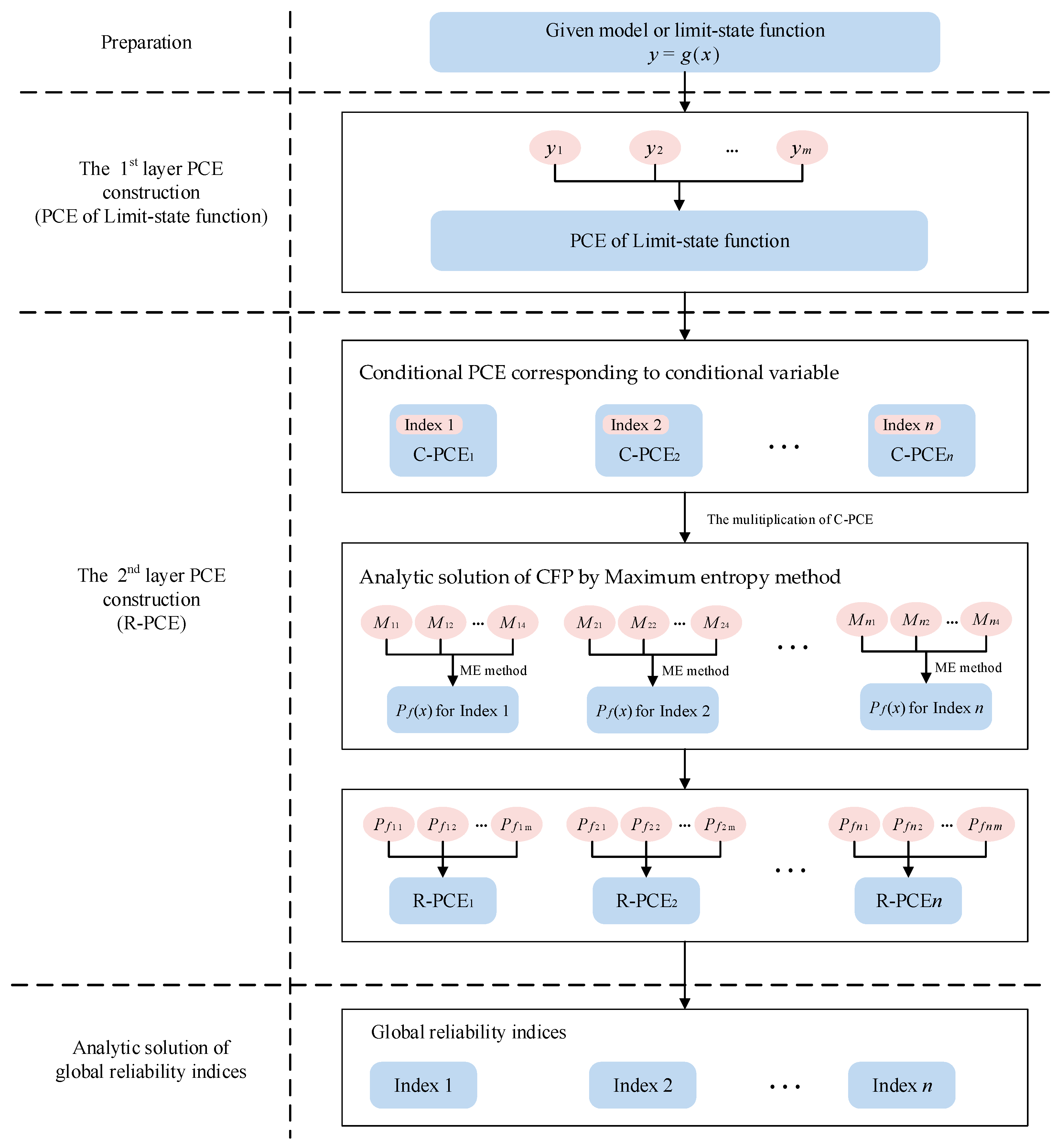
The PCE-based GRSA method involves a 2-layer PCE surrogate model construction process. The first layer PCE is to generate traditional surrogate model approximating the limit-state function. It is used to obtain mean and variance when given conditional variables are fixed in specific values. And the second layer is to construct R-PCEs for different CFPs. To obtain probability response during the surrogate modeling of R-PCE, the ME method is taken to analytically compute these probability values with the first layer PCE. Besides, since each CFP is dependent on a different conditional variable, each global reliability sensitivity index has its own R-PCE formula. The algorithm framework is shown in
Figure 1, and the whole procedure consists of four phases.
The first phase is to prepare inputs or data for GRSA.
In the second phase, the PCE technology is an efficient and accurate tool to approximate the given model with finite samples. Thus, the original model is replaced by the 1st-layer PCE in the following procedures. Besides, the first and second moment of the model output are obtained directly without traditional Mote Carlo sampling.
In the third phase, the PCE technology is developed to make the surrogate model for CFP. Unlike the surrogate model in the second phase, quite a few failure probabilities of given model require to be calculated. Unlike the model output which may be obtained by simulating directly, it is usually difficult to obtain these statistical values. Fortunately, this problem could be overcome by the ME method. According to ME, the probability distribution that best represents the current state of knowledge, which is usually presented in terms of the first
n-order moments, is the one having the largest entropy [
24]. Under this principle, the probability distribution of the model output could be analytically obtained with moment information based on the 1st-layer PCE. The details of this procedure are presented as follows.
First of all, for each global reliability sensitivity index, a set of conditional variable samples is generated by the probabilistic collocation method (PCM). Second, due to the regularity of orthogonal polynomials, the conditional variable is removed from the 1st-layer PCE. Also, the specific formula of the 1st-layer PCE with other variables could remain the form of linear combination of orthogonal polynomials, so does the statistical characteristic. For simplicity, we call it conditional PCE (C-PCE). Thus, the associated moment evaluations are also available. Third, the ME method is taken to solve failure probabilities with regards to specific conditional variable. Fourth, a set of conditional variable samples and associated conditional failure probabilities are prepared for following 2nd-layer PCE (R-PCE) construction, and this procedure is similar to PCE in the second phase. In this way, R-PCE corresponding to specific conditional variable is generated.
Finally, with the coefficients of R-PCE, we could obtain variance of each CFP and calculate global reliability sensitivity index. During the procedure, the number of sampling of both the 1st-layer PCE and the 2nd-layer PCE of proposed method is limited according to PCE sample principle. This makes proposed method efficient. The following section will provide details of how to construct the proposed 2-layer PCE.
3.2. Conditional Polynomial Chaos Expansion and Moments Calculation
Without loss of generality, PCE formula of given limit-state function is the same as Equation (8). If the value of
ξI is given as the conditional variable, Equation (8) could be simplified as:
where |
I| is the number of elements in subscript
I, {
i1, …,
is}∉
I represents that
. The coefficients are subject to:
and:
The total number of coefficients is
. Equation (24) is called as C-PCE. Thus, the mean and variance could be obtained by the following equations:
To simplify the expression, C-PCE could be rewritten as:
where
and
ψα(
ξ|
ξI) are corresponding to Equation (28) sequentially, notation “
ξ|
ξI” in
ψα(
ξ|
ξI) means that expansion base does not include conditional variable
ξI.
The mean and variance of C-PCE are given as Equations (30) and (31) respectively:
Specifically, for main effect indices, since we have
I = {
i}, Equation (29) can be further rewritten as:
and for total effect indices, since we have
I = {1, …,
n}/{
i}, Equation (29) can be further rewritten as:
The C-PCE could provide the first two order moments accurately. However, there are some difficulties for high order moment calculation. Consider the fact that the C-PCE consists of orthogonal bases, the products of two C-PCEs could also be expanded as a linear combination of orthogonal bases [
29]. Therefore, the orthogonal characteristic of PCE multiplication remains. The generalization form of orthogonal bases are presented in [
29].
Take the C-PCE with Hermite polynomial bases for example, suppose two C-PCEs
and
. If
, then the product of
u and
v has the PCE formula as:
where:
The subscripts α, β, r, and θ in Equations (34) and (35) are tuples associated with C-PCE terms, e.g., α = (α1, α2, …, αn). We say β ≤ θ if βi ≤ θi for all i = 1, 2, …, n. The operation of these subscripts, such as + or −, is also defined as component-wise. Especially, the factorial of tuples is defined like α! = ∏i αi!.
Then, the mean of
uv could be obtained as:
Based upon the preparation above, we could calculate the high-order moments of PCE by replacing
u and
v with two PCEs respectively. That is,
u and
v in Equation (34) could be replaced by
,
,
, …, respectively as Equation (37):
where ⌊•⌋ is rounded down and ⌈•⌉ is rounded up. Thus, the high order moments could be computed analytically.
3.3. The Maximum Entropy Method
Let
fy(
y) be the unknown PDF of the output of limit-state function and assume
H(
fy(
y)) to be the entropy of
fy(
y). Then we have:
where
Ωy is the domain of
y. According to the principle of ME, the failure probability distribution which best represents the current information, such as the moments, is the one with the largest entropy [
24]. Thus, the ME method for estimating
fy(
y) can be formulated as:
where
NME is the number of moments, and
μk is the
kth moment, i.e.,
μ1 =
E(
y),
μ2 =
E(
y2), etc.
It can be proved that the optimal solution for the PDF formula is given as:
Thus,
λi in Equation (40) should satisfy the following equation:
Specifically, if the first two moments of the output are available, we have:
where
and the failure probability can be calculated as:
In the proposed method, if taking Equations (27) and (28) into Equations (42) and (43), the failure probability of C-PCE could be obtained directly without additional sampling.
For more general cases, the first four moments are usually used for PDF calculation because they are corresponding to mean, variance, skewness, kurtosis respectively, which are clear in physics meaning [
30]. The 3rd moment and the 4th moment could be obtained efficiently by Equation (37) instead of traditional sampling method. Besides, since the ME method may not have the closed form solution, some optimization techniques, such as Newton method or its improved versions [
31,
32], could be utilized to solve the failure probability.
3.4. Global Reliability Sensitivity Indices Calculation
Let
denote a set of conditional variable samples, where
MR is the number of samples. As described above, when the PCE for limit-state function is given, if taking each conditional variable sample into Equation (24), it returns the mean and variance of C-PCE. Then, the CFP is calculated by ME method. In this way, we could get a set of surrogate model relationship between
and
. Similar to the traditional PCE procedure as Equation (A7) in
Appendix B, we could solve the coefficients of R-PCE. Then, the result of R-PCE is:
where
cR,j is
jth coefficient of R-PCE, and the subscript “
R” means the coefficient is used for GRSA.
ξI is independent standardized random variables corresponding to original variables
xI,
NR is the total number of coefficients, which is determined by:
where
pR is the predefined degree of R-PCE. Then, the CFP is:
And the variance of CFP is:
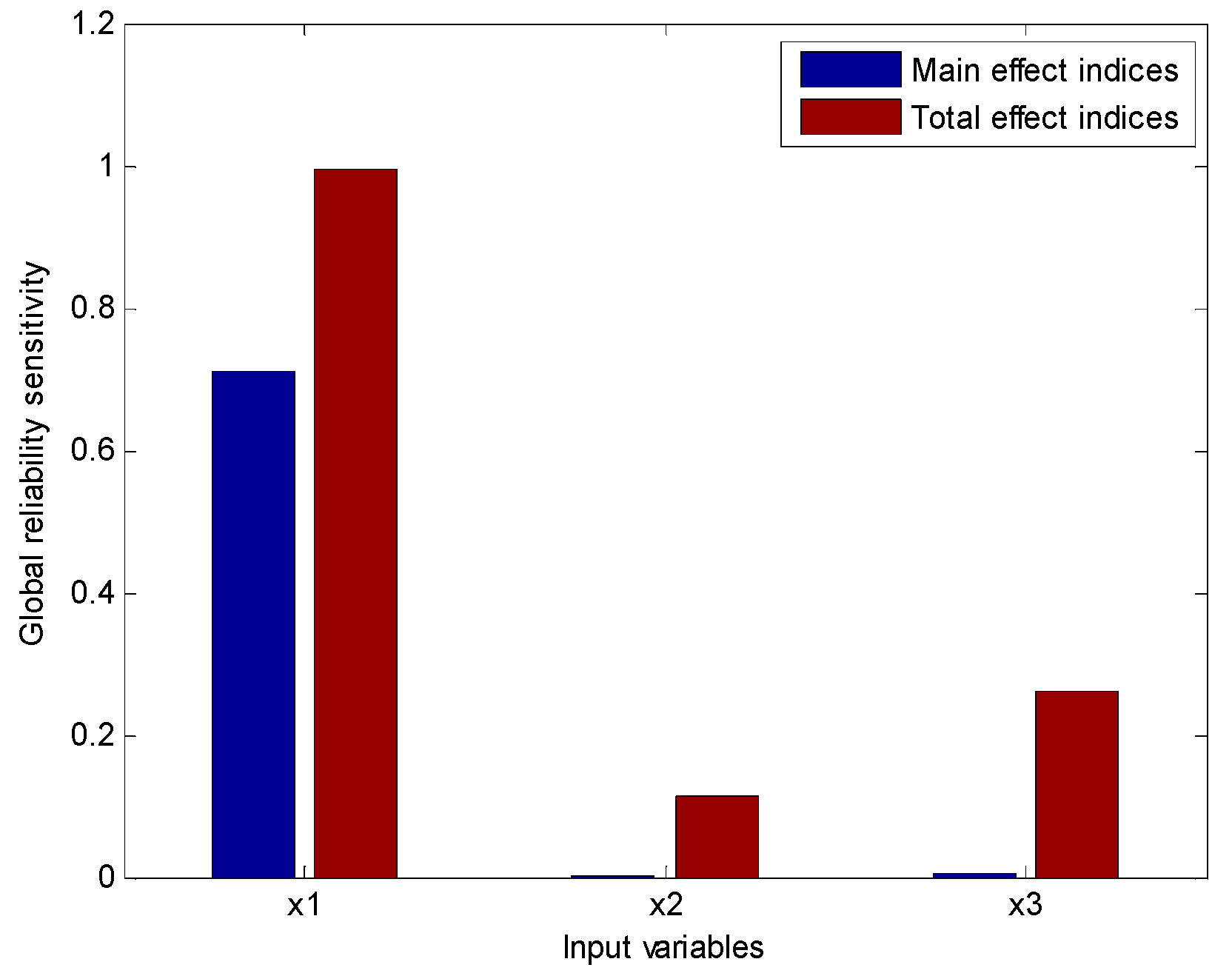
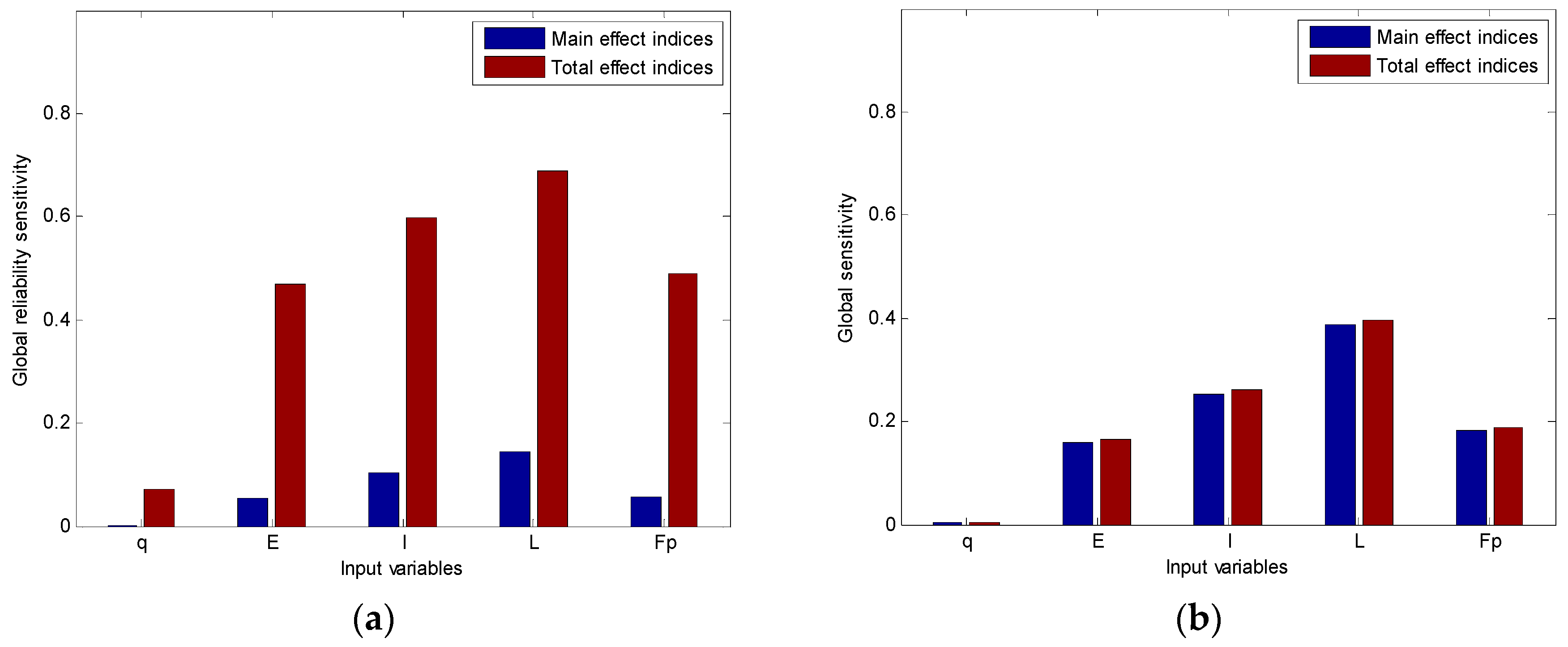
Substituting Equations (46) and (47) into Equations (22) and (23), we could calculate the main effect and the total effect of global reliability sensitivity indices.
3.5. Implementation
For a given limit-state function g = g(x), we assume here that the input random variables are independent. With preparation mentioned above, the complete algorithm description is introduced as follows:
- Step 1:
Represent distributions of the input into the associated standardized random variable. If the distribution types are not unified, we could map different distributions into the normal distribution. The following computation will be based upon standardized random variables.
- Step 2:
Compute PCE for limit-state function by Equation (A7) in
Appendix B, and it refers as
gPCE(
ξ).
- Step 3:
Based upon PCE above, compute R-PCE. First of all, generate a set of conditional variable samples. Then, integrate gPCE(ξ) and ME method to obtain the CFP value Pf(ξ|ξI), where I = {i} for main effect indices and I = {1, 2, ..., n}/{i} for total effect indices. Specifically, for each sample set , substitute it into Equations (24)–(26) to obtain C-PCE . With the moments given by C-PCE, we could calculate the with ME method analytically. Third, the R-PCE comes out as Equation (44).
- Step 4:
Compute the global reliability sensitivity indices by Equation (22), Equation (23) and Equations (46) and (47).
The step-by-step procedure of algorithm for the main effect indices and the total effect indices by the proposed 2-layer PCE method are presented in Algorithms A1 and A2 in
Appendix C respectively. The total evaluations of the limit-state function is
, where
n and
p are input variable dimension and the PCE degree respectively. If taking times of PCE evaluation in R-PCE construction process into consideration, the computation costs are
, where
pR is the degree of R-PCE. This computation burden is usually 1–2 times less than IS procedure and 2–3 times less than MCS procedure, which could be seen in the following test examples. And the efficiency of the proposed method could be further improved by adopting sparse algorithms [
6,
17,
33]. However, such work is not the scope of this paper.