A Lower Bound on the Differential Entropy of Log-Concave Random Vectors with Applications
Abstract
1. Introduction
2. Main Results
2.1. Lower Bounds on the Differential Entropy
2.2. Extension to -Concave Random Variables
2.3. Reverse Entropy Power Inequality with an Explicit Constant
2.4. New Bounds on the Rate-distortion Function
2.5. New Bounds on the Capacity of Memoryless Additive Channels
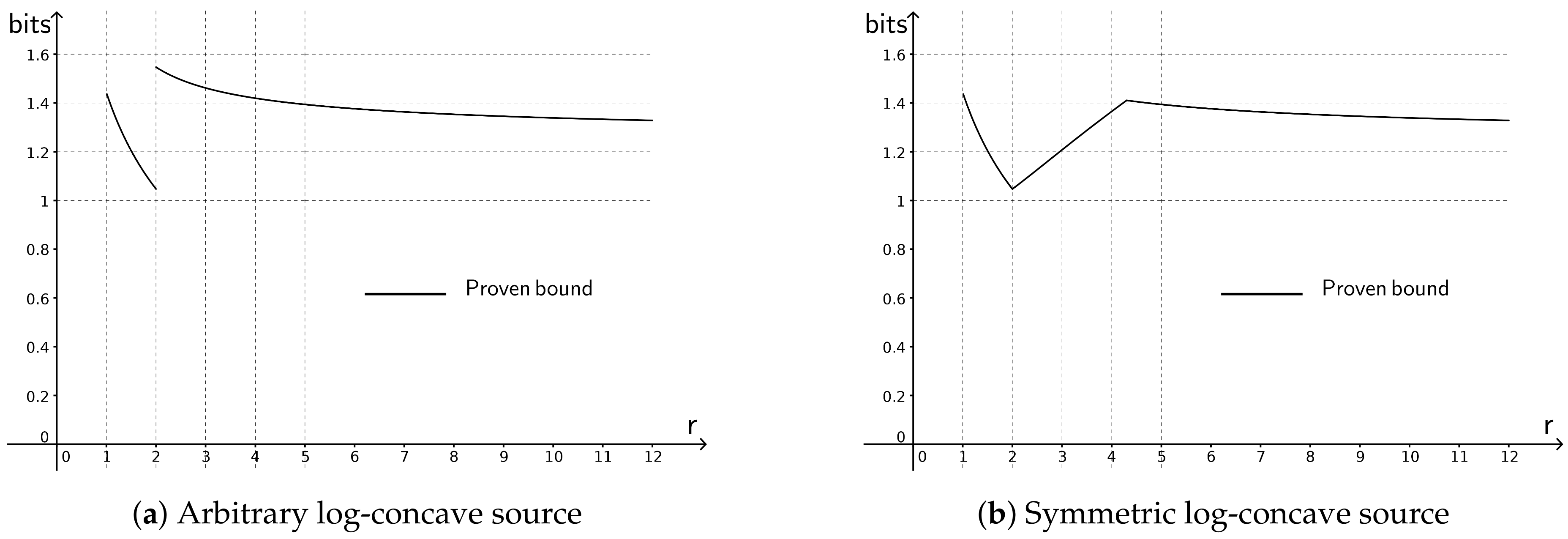
3. New Lower Bounds on the Differential Entropy
3.1. Proof of Theorem 1
3.2. Proof of Theorem 3 and Proposition 1
3.3. Proof of Theorem 4
3.4. Proof of Theorem 5
4. Extension to -Concave Random Variables
5. Reverse Entropy Power Inequality with Explicit Constant
5.1. Proof of Theorem 7
5.2. Proof of Theorem 8
6. New Bounds on the Rate-Distortion Function
6.1. Proof of Theorem 9
6.2. Proof of Theorem 10
6.3. Proof of Theorem 11
7. New Bounds on the Capacity of Memoryless Additive Channels
7.1. Proof of Theorem 12
7.2. Proof of Theorem 13
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zamir, R.; Feder, M. On Universal Quantization by Randomized Uniform/Lattice Quantizers. IEEE Trans. Inf. Theory 1992, 32, 428–436. [Google Scholar] [CrossRef]
- Prékopa, A. On logarithmic concave measures and functions. Acta Sci. Math. 1973, 34, 335–343. [Google Scholar]
- Bobkov, S.; Madiman, M. The entropy per coordinate of a random vector is highly constrained under convexity conditions. IEEE Trans. Inf. Theory 2011, 57, 4940–4954. [Google Scholar] [CrossRef]
- Bobkov, S.; Madiman, M. Entropy and the hyperplane conjecture in convex geometry. In Proceedings of the 2010 IEEE International Symposium on Information Theory Proceedings (ISIT), Austin, TX, USA, 13–18 June 2010; pp. 1438–1442. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Stam, A.J. Some inequalities satisfied by the quantities of information of Fisher and Shannon. Inf. Control 1959, 2, 101–112. [Google Scholar] [CrossRef]
- Bobkov, S.; Madiman, M. Reverse Brunn-Minkowski and reverse entropy power inequalities for convex measures. J. Funct. Anal. 2012, 262, 3309–3339. [Google Scholar] [CrossRef][Green Version]
- Cover, T.M.; Zhang, Z. On the maximum entropy of the sum of two dependent random variables. IEEE Trans. Inf. Theory 1994, 40, 1244–1246. [Google Scholar] [CrossRef]
- Madiman, M.; Kontoyiannis, I. Entropy bounds on abelian groups and the Ruzsa divergence. IEEE Trans. Inf. Theory 2018, 64, 77–92. [Google Scholar] [CrossRef]
- Bobkov, S.; Madiman, M. On the problem of reversibility of the entropy power inequality. In Limit Theorems in Probability, Statistics and Number Theory; Springer Proceedings in Mathematics and Statistics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 42, pp. 61–74. [Google Scholar]
- Ball, K.; Nayar, P.; Tkocz, T. A reverse entropy power inequality for log-concave random vectors. Studia Math. 2016, 235, 17–30. [Google Scholar] [CrossRef]
- Courtade, T.A. Links between the Logarithmic Sobolev Inequality and the convolution inequalities for Entropy and Fisher Information. arXiv, 2016; arXiv:1608.05431. [Google Scholar]
- Madiman, M.; Melbourne, J.; Xu, P. Forward and Reverse Entropy Power Inequalities in Convex Geometry. In Convexity and Concentration; Carlen, E., Madiman, M., Werner, E., Eds.; The IMA Volumes in Mathematics and Its Applications; Springer: New York, NY, USA, 2017; Volume 161, pp. 427–485. [Google Scholar]
- Shannon, C.E. Coding theorems for a discrete source with a fidelity criterion. IRE Int. Conv. Rec. 1959, 7, 142–163, Reprinted with changes in Information and Decision Processes; Machol, R.E., Ed.; McGraw-Hill: New York, NY, USA, 1960; pp. 93–126. [Google Scholar]
- Linkov, Y.N. Evaluation of ϵ-entropy of random variables for small ϵ. Probl. Inf. Transm. 1965, 1, 18–26. [Google Scholar]
- Linder, T.; Zamir, R. On the asymptotic tightness of the Shannon lower bound. IEEE Trans. Inf. Theory 1994, 40, 2026–2031. [Google Scholar] [CrossRef]
- Koch, T. The Shannon Lower Bound is Asymptotically Tight. IEEE Trans. Inf. Theory 2016, 62, 6155–6161. [Google Scholar] [CrossRef]
- Kostina, V. Data compression with low distortion and finite blocklength. IEEE Trans. Inf. Theory 2017, 63, 4268–4285. [Google Scholar] [CrossRef]
- Gish, H.; Pierce, J. Asymptotically efficient quantizing. IEEE Trans. Inf. Theory 1968, 14, 676–683. [Google Scholar] [CrossRef]
- Ziv, J. On universal quantization. IEEE Trans. Inf. Theory 1985, 31, 344–347. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ihara, S. On the capacity of channels with additive non-Gaussian noise. Inf. Control 1978, 37, 34–39. [Google Scholar] [CrossRef]
- Diggavi, S.N.; Cover, T.M. The worst additive noise under a covariance constraint. IEEE Trans. Inf. Theory 2001, 47, 3072–3081. [Google Scholar] [CrossRef]
- Zamir, R.; Erez, U. A Gaussian input is not too bad. IEEE Trans. Inf. Theory 2004, 50, 1340–1353. [Google Scholar] [CrossRef]
- Karlin, S.; Proschan, F.; Barlow, R.E. Moment inequalities of Pólya frequency functions. Pac. J. Math. 1961, 11, 1023–1033. [Google Scholar] [CrossRef][Green Version]
- Borell, C. Convex measures on locally convex spaces. Ark. Mat. 1974, 12, 239–252. [Google Scholar] [CrossRef]
- Borell, C. Convex set functions in d-space. Period. Math. Hungar. 1975, 6, 111–136. [Google Scholar] [CrossRef]
- Borell, C. Complements of Lyapunov’s inequality. Math. Ann. 1973, 205, 323–331. [Google Scholar] [CrossRef]
- Fradelizi, M.; Madiman, M.; Wang, L. Optimal concentration of information content for log-concave densities. In High Dimensional Probability VII 2016; Birkhäuser: Cham, Germany, 2016; Volume 71, pp. 45–60. [Google Scholar]
- Ball, K. Logarithmically concave functions and sections of convex sets in ℝn. Studia Math. 1988, 88, 69–84. [Google Scholar] [CrossRef]
- Brazitikos, S.; Giannopoulos, A.; Valettas, P.; Vritsiou, B.H. Geometry of Isotropic Convex Bodies; Mathematical Surveys and Monographs, 196; American Mathematical Society: Providence, RI, USA, 2014. [Google Scholar]
- Klartag, B. On convex perturbations with a bounded isotropic constant. Geom. Funct. Anal. 2006, 16, 1274–1290. [Google Scholar] [CrossRef]
- Bobkov, S.; Nazarov, F. On convex bodies and log-concave probability measures with unconditional basis. In Geometric Aspects of Functional Analysis; Springer: Berlin/Heidelberg, Germany, 2003; pp. 53–69. [Google Scholar]
- Fradelizi, M.; Guédon, O.; Pajor, A. Thin-shell concentration for convex measures. Studia Math. 2014, 223, 123–148. [Google Scholar] [CrossRef]
- Ball, K.; Nguyen, V.H. Entropy jumps for isotropic log-concave random vectors and spectral gap. Studia Math. 2012, 213, 81–96. [Google Scholar] [CrossRef][Green Version]
- Toscani, G. A concavity property for the reciprocal of Fisher information and its consequences on Costa’s EPI. Physica A 2015, 432, 35–42. [Google Scholar] [CrossRef]
- Toscani, G. A strengthened entropy power inequality for log-concave densities. IEEE Trans. Inf. Theory 2015, 61, 6550–6559. [Google Scholar] [CrossRef]
- Courtade, T.A.; Fathi, M.; Pananjady, A. Wasserstein Stability of the Entropy Power Inequality for Log-Concave Densities. arXiv, 2016; arXiv:1610.07969. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marsiglietti, A.; Kostina, V. A Lower Bound on the Differential Entropy of Log-Concave Random Vectors with Applications. Entropy 2018, 20, 185. https://doi.org/10.3390/e20030185
Marsiglietti A, Kostina V. A Lower Bound on the Differential Entropy of Log-Concave Random Vectors with Applications. Entropy. 2018; 20(3):185. https://doi.org/10.3390/e20030185
Chicago/Turabian StyleMarsiglietti, Arnaud, and Victoria Kostina. 2018. "A Lower Bound on the Differential Entropy of Log-Concave Random Vectors with Applications" Entropy 20, no. 3: 185. https://doi.org/10.3390/e20030185
APA StyleMarsiglietti, A., & Kostina, V. (2018). A Lower Bound on the Differential Entropy of Log-Concave Random Vectors with Applications. Entropy, 20(3), 185. https://doi.org/10.3390/e20030185



