1. Introduction
Bohmian mechanics differs deeply from standard quantum mechanics. In particular, in Bohmian mechanics, particles, here called Bohmian particles, follow continuous trajectories; hence, in Bohmian mechanics, there is a natural concept of time-correlation for particles’ positions. This led M. Correggi and G. Morchio [
1] and more recently Kiukas and Werner [
2] to conclude that Bohmian mechanics “cannot violate any Bell inequality” and hence is disproved by experiments. However, the Bohmian community maintains its claim that Bohmian mechanics makes the same predictions as standard quantum mechanics (at least as long as only position measurements are considered, arguing that, at the end of the day, all measurements result in position measurement, e.g., a pointer’s positions).
Here, we clarify this debate. First, we recall why two-time position correlation is at a tension with Bell inequality violation. Next, we show that this is actually not at odds with standard quantum mechanics because of certain subtleties. For this purpose, we do not go for full generality but illustrate our point with an explicit and rather simple example based on a two-particle interferometers, partly already experimentally demonstrated and certainly entirely experimentally feasible (with photons, but also feasible at the cost of additional technical complications with massive particles). The subtleties are illustrated by explicitly coupling the particles to macroscopic systems, called pointers, that measure the particles’ positions. Finally, we raise questions about Bohmian positions, about macroscopic systems, and about the large differences in appreciation of Bohmian mechanics between philosophers and physicists.
3. Two-Time Position Correlation in a Bell Test
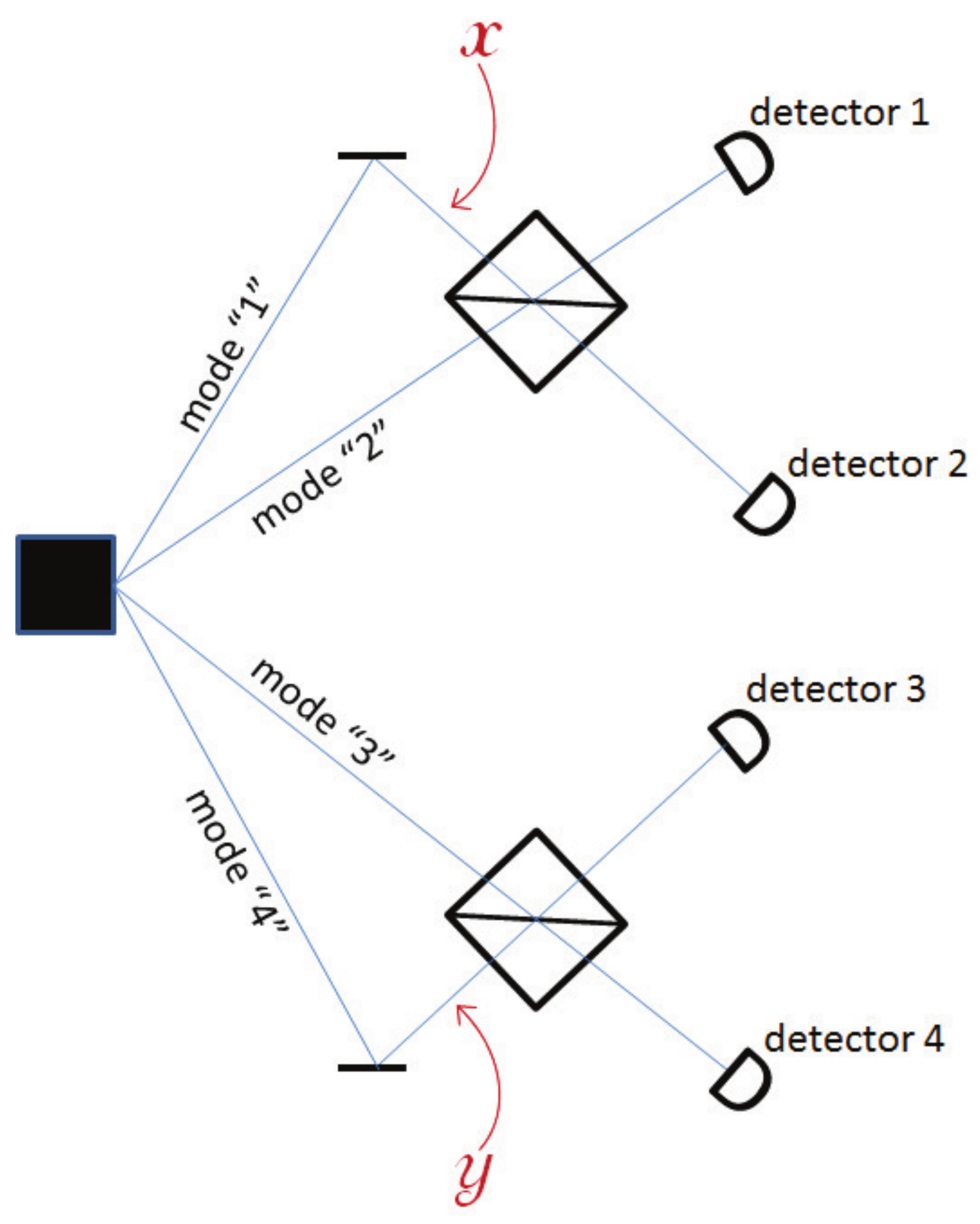
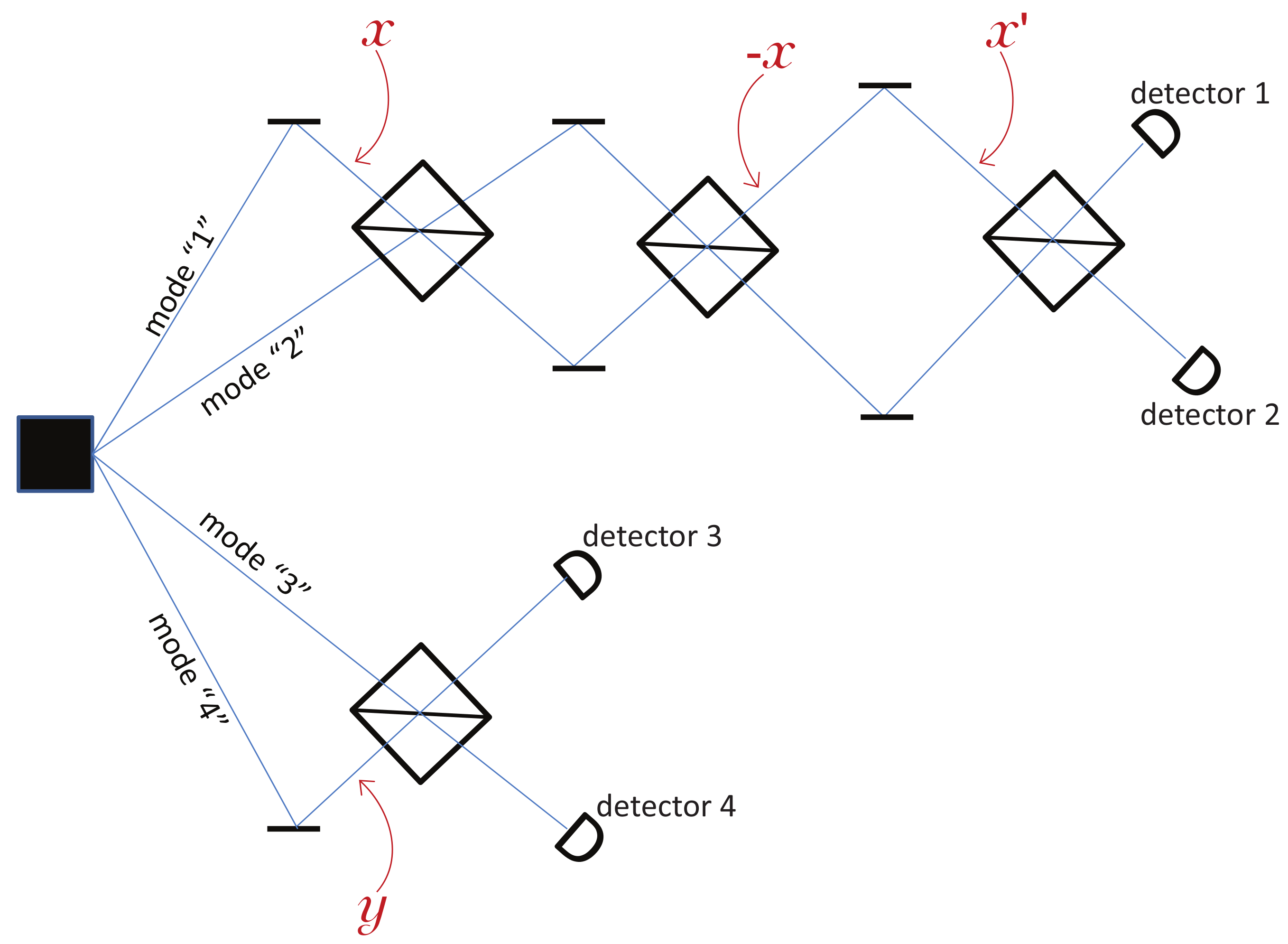
Let’s consider a two-particle experiment with 4 modes, labeled 1, 2, 3, and 4, as illustrated in
Figure 2. The source produces the quantum state:
where, e.g.,
means that there is one particle in Mode 1 and one in Mode 4, and Modes 2 and 3 are empty. This is an entangled state that can be used in a Bell inequality test. For this, Alice (who controls Modes 1 and 2) and Bob (who controls Modes 3 and 4) apply phases
x and
y to Modes 1 and 4, respectively, and combine their modes on a beam splitter, see
Figure 2. Taking into account that a reflection on a BS induces a phase
, the quantum state after the two beam splitters reads
If Modes 1, 2, 3, and 4, after the beam splitter, encounter four single-particle detectors, also labeled 1, 2, 3, and 4, then the probabilities for coincidence detection are
from which a maximal violation of the CHSH-Bell inequality of
can be obtained with appropriate choices of the phase inputs.
In Bohmian mechanics, this experiment is easily described. Denote the two particles’ positions
and
. In the initial state (Equation (
1)), the particles are either in Modes 1 and 4, a situation we denote
“1” and
“4,” or in Modes 2 and 3, i.e.,
“2” and
“3.” According to Bohmian mechanics, the particles have more precise positions, but for our argument this suffices.
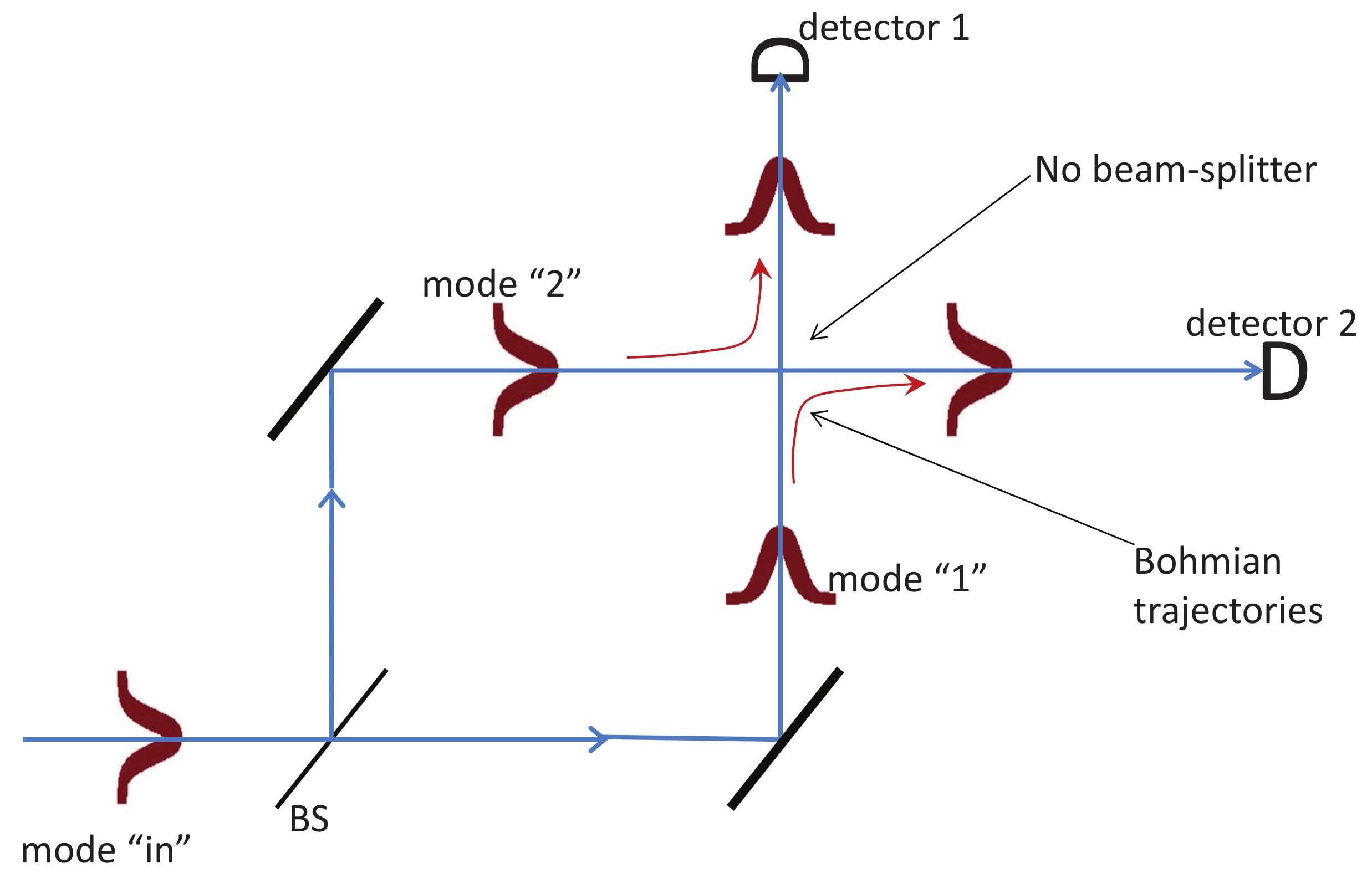
Now, according to Bohmian mechanics and Assumption
H, one does not need to actually measure the positions of the particles; it suffices to know that each is in one specific mode. Hence, one can undo Alice’s measurement as illustrated in
Figure 3. After the phase shift
, the quantum state is precisely back to the initial state
, see Equation (
1). Alice can thus perform a second measurement with a freshly chosen phase
x′ and a third beam splitter, see
Figure 3. Moreover, as Bohmian trajectories cannot cross each other (in configuration space), if
is in Mode 1 before the first BS, then
is also in Mode 1 before the last BS.
There is no doubt that, according to Bohmian mechanics, there is a well-defined joint probability distribution for Alice’s particle at two times and Bob’s particle:
′
′
, where
denotes Alice’s particle after the first beam splitter and
r′
after the third beam splitter of
Figure 3. But here comes the puzzle. According to Assumption
H, if
“1”, then any position measurement performed by Alice between the first and second beam splitter necessarily results in
. Similarly,
“2” implies
. Thus, Alice’s position measurement after the third beam splitter is determined by
r′
, and Bob’s measurement is determined by
. Hence, it seems that one obtains a joint probability distribution for Alice’s measurements results and Bob’s:
′
′
. However, such a joint probability distribution implies that Alice does not have to make any choice (she merely makes both choices, one after the other), and in such a situation there cannot be any Bell inequality violation. Hence, as claimed in [
2], it seems that the existence of two-time position correlations in Bohmian mechanics prevents the possibility of a CHSH-Bell inequality violation, in contradiction with quantum theory predictions and experimental demonstrations [
3].
Let’s have a closer look at the probability distribution that lies at the bottom of our puzzle:
′
′
. More precisely, it suffices to consider in which modes the Bohmian particles are. That is, it suffices to consider the following joint probability distribution:
where
and
number modes. This can be computed explicitly:
Note that, if one sums over
a′, i.e., traces out Alice’s second measurement, then one recovers the quantum prediction equations (Equations (
3) and (
4)):
It is important is to notice that
does not depend on Alice’s second measurement setting
x′, as one would expect. Similarly, if one traces out Alice’s first measurement,
one recovers Equations (
3) and (
4). Again, the probability that Equation (
8) does not depend on Alice’s first measurement setting.
So far so good, but now comes the catch. If one traces out Bob’s measurement, one obtains a probability distribution for Alice’s particle’s position that depends on Bob’s setting
y:
Hence, the joint probability distribution (Equation (
6)) is signaling from Bob to Alice! Is this a problem for Bohmian mechanics? Probably not, as the Bohmian particles’ positions are assumed to be “hidden”. Actually, it is already well-known that they have to be hidden in order to avoid signaling in Bohmian mechanics. Some may find this feature unpleasant, as it implies that Bohmian particles are postulated to exist “only” to immediately add that they are ultimately not fully accessible, but this is not new.
Consequently, defining a joint probability for the measurement outcomes
a,
a′, and
b in the natural way,
can be done mathematically but cannot have a physical meaning, as
would be signaling.
4. What Is Going on? Let’s Add a Position Measurement
In summary, it is the identification in Equation (
10) that confused the authors of [
1,
2] and led them to wrongly conclude that Bohmian mechanics cannot predict violations of Bell inequalities in experiments involving only position measurements. Note that the identification of Equation (
10) follows from Assumption
H, so Assumption
H is wrong. Every introduction to Bohmian mechanics should emphasize this. Indeed, Assumption
H is very intuitive and appealing, but wrong and confusing.
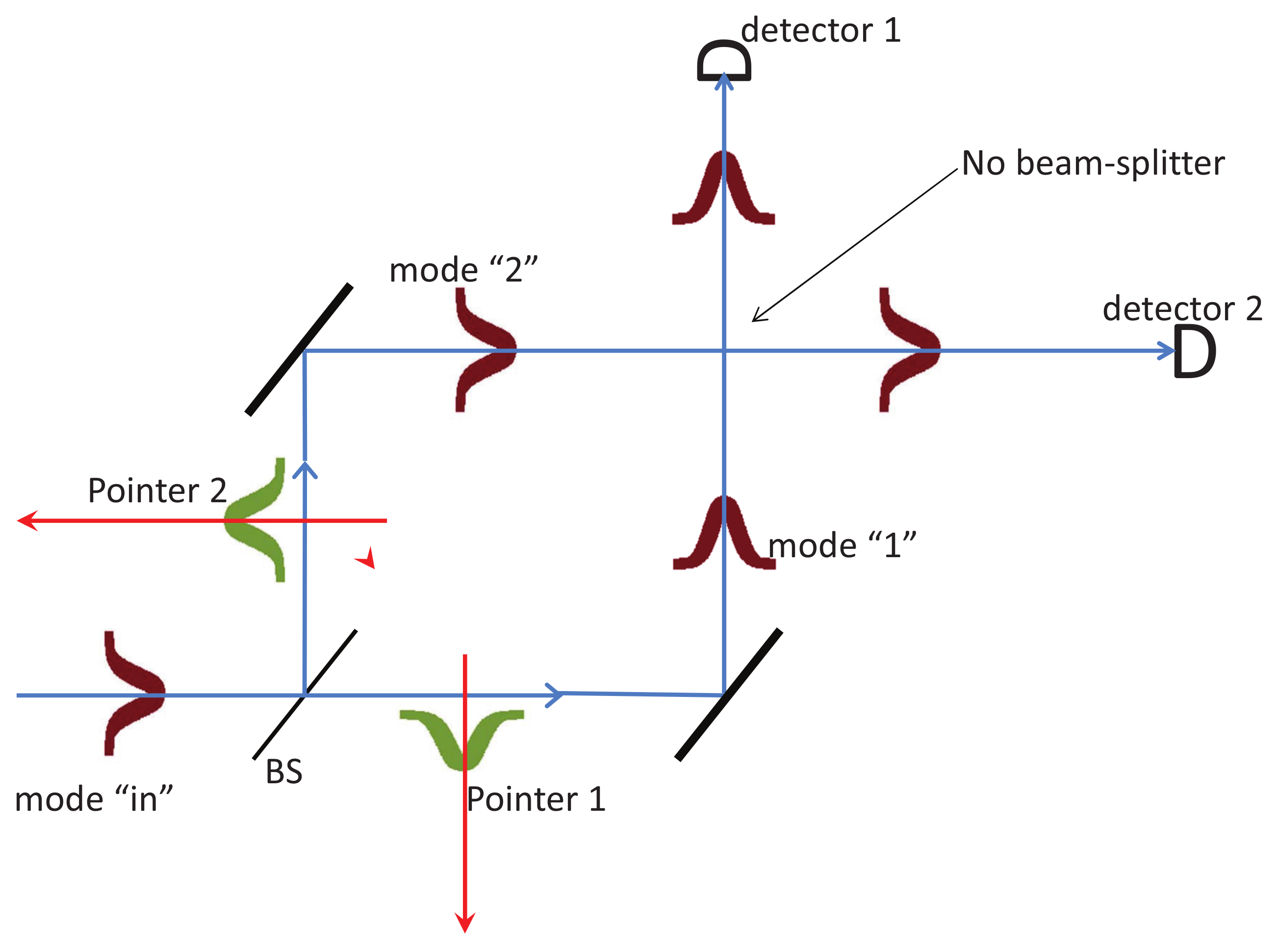
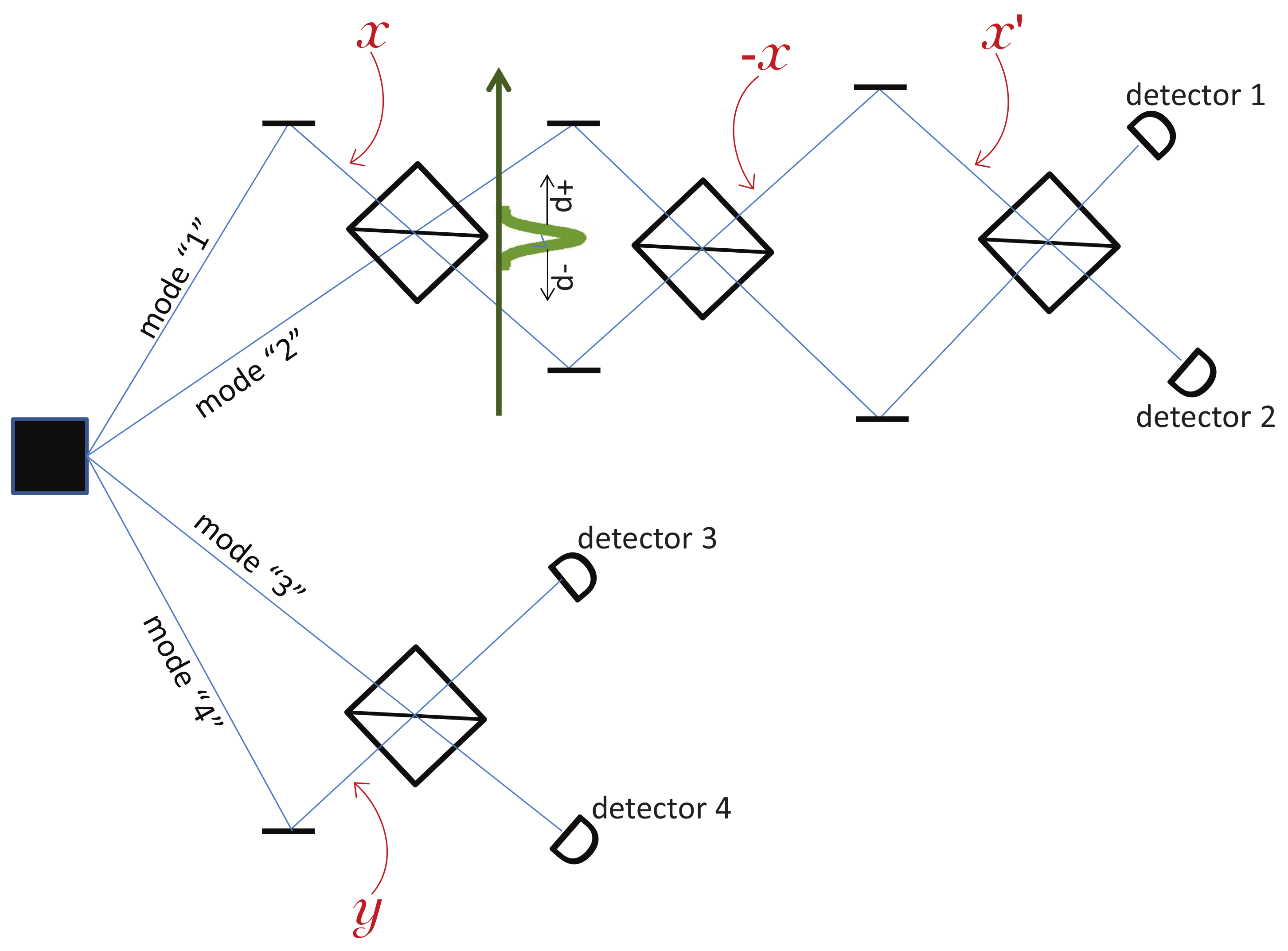
To elaborate on this, let’s add an explicit position measurement after the first beam splitter on the Alice side. The fact is that, according to both standard quantum theory and Bohmian mechanics, this position measurement perturbs the quantum state (hence the pilot wave) in such a way that the second measurement, labeled
x′ on
Figure 4, no longer shares the correlation (Equation (
9)) with the first measurement, see [
4,
5,
6].
Let’s model Alice’s first position measurement, labeled
x (i.e., corresponding to the input phase
x), by an extra system, called here the pointer, initially at rest in a Gaussian state, see
Figure 4. One should think of the pointer as a large and massive system; note that it suffices to consider the state of the center of mass of the pointer. If Alice’s particle passes through the upper part of the interferometer (
“1”), then the pointer gets a kick in the upward direction and is left with a momentum
; however, if Alice’s particle passes through the lower part of her interferometer (
“2”), then the pointer gets a kick
. We made
p large enough so that the two quantum states of the pointer
are orthogonal, i.e., according to quantum theory, we consider a strong (projective) which-path measurement. Note, however, that, immediately after the pointer has interacted with Alice’s particle, the two Gaussians corresponding to
overlap in space, so no position measurement can distinguish them. It is only after some time that the two Gaussians separate in space and that position measurements can distinguish them. Since in Bohmian mechanics there are only position measurements, this implies that, in Bohmian mechanics, it takes some time for the pointer to measure Alice’s particle.
Accordingly, if
p is large enough for the pointer to have moved by more than its spread by the time Alice’s particle hits the second BS, then the pointer acts like a standard measurement, and the second position measurement
x′ of Alice’s particle is perturbed by measurement
x, as discussed in the previous paragraph. However, if
p is small enough, then, by the time the second measurement
x′ takes place, the pointer barely moves. In this case, the second position measurement is not affected [
4,
5,
6], see also the appendix. However, it is now this second measurement
x′ that perturbs the “first” one, i.e., perturbs measurement
x. Indeed, because of the entanglement between Alice’s particle and the pointer, if one waits long enough for the pointer to move by more than its spread and then reads the result of the “first” measurement out of this pointer, then one will not find the expected result: the second measurement perturbed the “first” one. I put “first” in quotes because, in such a slow measurement, the result is actually read out of the pointer after the “second” measurement took place.
This is very similar to the so-called surrealistic trajectories, see [
4,
5,
6]. In the appendix, I recall this counter-intuitive aspect of Bohmian mechanics.
5. What about Large Systems?
So far so good. But let’s now consider, not single particles, but elephants. One of the advantages of Bohmian mechanics is that whether systems are microscopic and macroscopic makes no difference: all systems are treated alike. The price to pay, as we illustrate below, is that all the strangeness of quantum physics at the microscopic level has to show up also at the macroscopic level.
Let’s consider two elephants in the state of Equation (
1) corresponding to entangled elephants in Modes 1 & 4 superposed with elephants in Modes 2 & 3. Note that, instead of elephants, one may consider classical light pulses and replace, in Equation (
1), the one-photon state
with a coherent state
with mean photon number
as large as desired:
. The beam splitters have to be replaced by EBSs—Elephant Beam Splitters—which split elephants: an incoming elephant emerges from an EBS in a superposition of elephant-transmitted and elephant-reflected. In the case of coherent states, the transformation reads:
Note that the above deeply differs from the standard BS, which corresponds to .
The story of the single particles described above remains the same. In Bohmian mechanics, the elephants’ positions are also hidden, or at least not fully accessible. However, this is puzzling, as it means that, when one “looks slowly” (as the pointer in
Section 4, see also the Appendix) at an elephant, one may see it where it is not. Indeed, according to Bohmian mechanics, an elephant is where all the Bohmian positions of all the particles that make up the elephant are, but what does this mean if it does not correspond to where one sees the elephant? Bohmians may reply that one does not “look slowly” at elephants and that EBSs do not exist. This is certainly true of today’s technology, but there will soon be beam splitters for quantum systems large enough to be seen by the naked eye. In addition, to avoid signaling, it has to be impossible to “see” or find out in any way two-time position correlations of such quantum systems, even when they are large.
Admittedly, it is an advantage that, in Bohmian mechanics, the difference between micro- and macro-worlds is immaterial. But, accordingly and unavoidably, quantum weirdness shows up at the macro-scale.
7. Why Bohmian Mechanics
From all we have seen so far, one should, first of all, recognize that Bohmian mechanics is deeply consistent and provides a nice and explicit existence proof of a deterministic non-local hidden variables model. Moreover, the ontology of Bohmian mechanics is pretty straightforward: the set of Bohmian positions is the real stuff. This is especially attractive to philosophers. Understandably so. But what about physicists mostly interested in research? What new physics did Bohmian mechanics teach us in the last 60 years? Here, I believe it is fair to answer: Not enough! Understandably disappointing.
It is deeply disappointing that an alternative theory to quantum mechanics, a theory that John Bell thought should be taught in parallel to standard textbook quantum mechanics [
8], did not produce new physics, nor even inspirations for new ideas to be tested in the lab (though see [
9,
10,
11,
12]). How could this be? Some may conclude that not enough people worked on Bohmian mechanics. But tens or hundreds of passionate researchers worked on it for decades. Some may conclude that this lack of new ideas proves that Bohmian mechanics is a dead end. But how could a consistent theory, empirically equivalent to quantum theory, have no future?
Let me suggest some possible, albeit only partial, answers to the above puzzle. I am afraid that almost all the research on Bohmian mechanics over the last several decades remained trapped within an exceedingly narrow viewpoint and worked only on problems of interest that were highly specific to their Bohmian community. I believe this is especially disappointing, as there were several interesting open problems that Bohmian-inspired ideas could have addressed. The positive side is there are likely still interesting open problems that open-minded researchers can explore.
Let me illustrate some of the ideas I believe Bohmian mechanics should have triggered. This list is obviously subjective—it is only important that it is not empty. Bohmian mechanics, like quantum theory, is in deep tension with relativity theory. I know of Bohmians who claim that it is obvious that any non-local theory, Bohmian or not, requires a privileged universal reference frame. I also know of Bohmians who claim that it is obvious that Bohmian mechanics can be generalized to a relativistic theory (though, admittedly, I never understood their model). However, I know of no Bohmians who are inspired by their theory and its tension with relativity to try to go beyond Bohmian mechanics, as illustrated in the next two paragraphs.
According to Bohmian mechanics, particles “make decisions” at beam splitters in the sense that, after a beam splitter, the particle is definitively in one of the output modes. Admittedly, this is not a real decision as everything is determined by the initial state of the particle and of all other systems entangled with the particle. However, let me continue using this inspiring terminology. Accordingly, and following Suarez, we call such beam splitters
choice-devices [
13]. Such choice-devices take into account everything in their past. Now, a natural assumption inspired by the sketched description is that the past is not merely the past light cone, but all of the past in the inertial reference frame of the choice device. This idea led Suarze and Scarani to suggest that one should test situations in which several choice-devices, e.g., several beam splitters, are in relative motion such that what is the past for one choice-device may differ from the past of another choice-device [
14]. This has the advantage (at least for researchers in physics) that it leads to experimental predictions that differ from standard quantum predictions and that can be experimentally tested. Hence, this brings Bohmian-inspired ideas to physics. This has been tested in my lab, and the result have shown that the idea, in spite of its appeal, is wrong [
15].
Another Bohmian-inspired idea follows directly from an observation by Hiley and Bohm [
16]: “it is quite possible that quantum nonlocal connections might be propagated, not at infinite speeds (as in standard Bohmian mechanics), but at speeds very much greater than that of light. In this case, we could expect observable deviations from the predictions of current quantum theory (e.g., by means of a kind of extension of the Aspect-type experiment).” Again, this can be experimentally tested [
17,
18,
19,
20]. The results put lower bounds on this hypothetical faster-than-light-but-finite speed influence, something like 10,000 to 100,000 times the speed of light. Aspect-type experiments between two sites can only either find that hypothetical speed or set lower bounds on it. However, recently we have been able to demonstrate that, by going to more parties, one can prove that either there is no such finite-but-superluminal speed or that one can use it for faster than light communication using only classical inputs and output (i.e., measurement settings and results) [
21,
22].
I am confident that Bohmian mechanics and other alternative views on quantum mechanics will inspire further ideas that will lead to experiments that might work to extend quantum theory. The real question is whether the Bohmian community will pursue such ideas.