Entropy Measures as Geometrical Tools in the Study of Cosmology
1
Physics Department, Ariel University, Ariel 40700, Israel
2
Department of Mathematics, Ariel University, Ariel 40700, Israel
3
Department of Mathematics, Ben Gurion University, Be’er Sheva 84105, Israel
4
Department of Electrical and Electronic Engineering, Ariel University, Ariel 40700, Israel
5
School of Physics and Astronomy, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University, Tel Aviv 69978, Israel
6
Department of Physics, Bar Ilan University, Ramat Gan 52900, Israel
*
Author to whom correspondence should be addressed.
Entropy 2018, 20(1), 6; https://doi.org/10.3390/e20010006
Received: 20 October 2017
/
Revised: 27 November 2017
/
Accepted: 20 December 2017
/
Published: 25 December 2017
(This article belongs to the Special Issue Advances in Relativistic Statistical Mechanics)
Classical chaos is often characterized as exponential divergence of nearby trajectories. In many interesting cases these trajectories can be identified with geodesic curves. We define here the entropy by with being the distance between two nearby geodesics. We derive an equation for the entropy, which by transformation to a Riccati-type equation becomes similar to the Jacobi equation. We further show that the geodesic equation for a null geodesic in a double-warped spacetime leads to the same entropy equation. By applying a Robertson–Walker metric for a flat three-dimensional Euclidean space expanding as a function of time, we again reach the entropy equation stressing the connection between the chosen entropy measure and time. We finally turn to the Raychaudhuri equation for expansion, which also is a Riccati equation similar to the transformed entropy equation. Those Riccati-type equations have solutions of the same form as the Jacobi equation. The Raychaudhuri equation can be transformed to a harmonic oscillator equation, and it has been shown that the geodesic deviation equation of Jacobi is essentially equivalent to that of a harmonic oscillator. The Raychaudhuri equations are strong geometrical tools in the study of general relativity and cosmology. We suggest a refined entropy measure applicable in cosmology and defined by the average deviation of the geodesics in a congruence.
View Full-Text
Keywords:
general relativity; cosmology; Raychaudhuri equations; entropy
▼
Show Figures
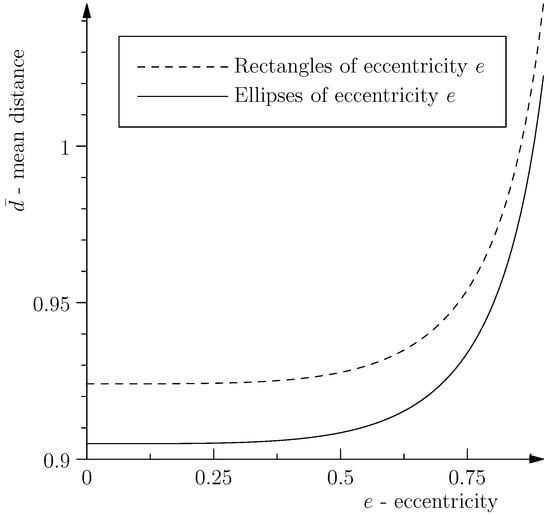
Figure 1
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited
MDPI and ACS Style
Weinstein, G.; Strauss, Y.; Bondarenko, S.; Yahalom, A.; Lewkowicz, M.; Horwitz, L.P.; Levitan, J. Entropy Measures as Geometrical Tools in the Study of Cosmology. Entropy 2018, 20, 6. https://doi.org/10.3390/e20010006
AMA Style
Weinstein G, Strauss Y, Bondarenko S, Yahalom A, Lewkowicz M, Horwitz LP, Levitan J. Entropy Measures as Geometrical Tools in the Study of Cosmology. Entropy. 2018; 20(1):6. https://doi.org/10.3390/e20010006
Chicago/Turabian StyleWeinstein, Gilbert, Yosef Strauss, Sergey Bondarenko, Asher Yahalom, Meir Lewkowicz, Lawrence P. Horwitz, and Jacob Levitan. 2018. "Entropy Measures as Geometrical Tools in the Study of Cosmology" Entropy 20, no. 1: 6. https://doi.org/10.3390/e20010006
Find Other Styles
Note that from the first issue of 2016, MDPI journals use article numbers instead of page numbers. See further details here.
