1. Introduction
There is a long history and an extensive literature of cubic equations-of-state, going back 140 years, from van der Waals renowned two-term equation for Andrew’s original p-V-T data on carbon dioxide [
1], to current research and compilations with hundreds of terms and parameters. As the thermodynamic experimental measurements have improved in accuracy, ever more complex equations have evolved [
2]. These equations are used to represent experimental thermodynamic properties for modern data banks such as the NIST compilation for CO
2 [
2,
3]. Over recent decades, ever-increasing numbers of terms and more fitted parameters are required. The Span–Wagner equation for CO
2 [
2], for example, contains hundreds of terms, each with many fitted parameters, and various adjustable fractional exponents. As even more accurate data become available from future research, these functional forms will need yet more adjustable parameters.
The basic reason of this inconvenient modeling practice is the van der Waals gas-liquid continuity hypothesis [
1]. Continuous cubic functional forms are inappropriate in the vicinity of T
c and in the supercritical mid-range between gas and liquid phases. A mesophase, confined within percolation loci that bound the existence of gas and liquid phases by higher-order discontinuities, has been identified [
4,
5,
6]. A simple numerical differentiation of NIST equations-of-state [
7] can demonstrate the supercritical mesophase and observe the phase bounds, along any isotherm, of any fluid (e.g., CO
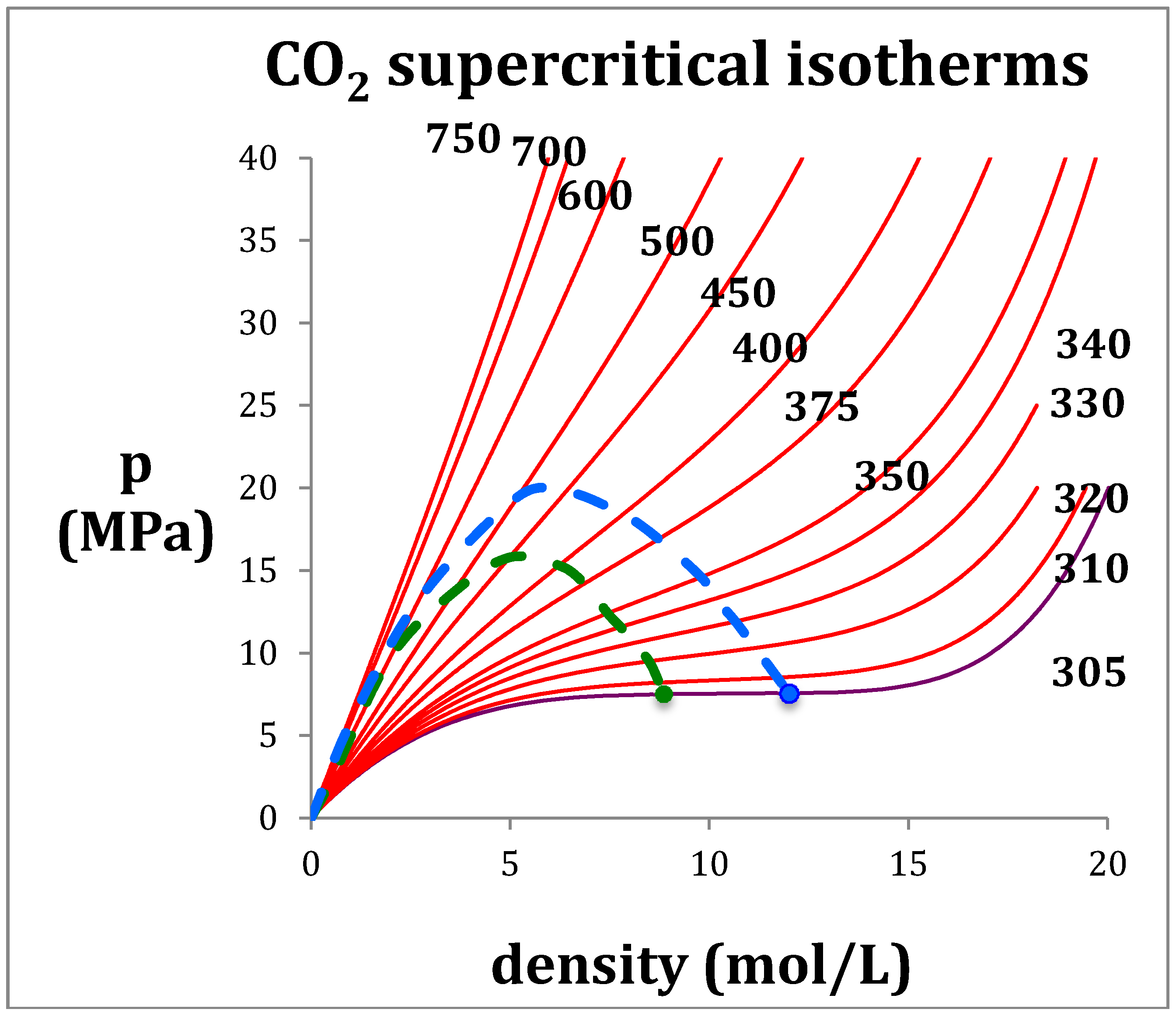
2 Figure 1) for any of the 200 fluids in the NIST Thermophysical Property data bank. These boundaries have been smoothed over by the equations-of-state used to parameterize the original experimental data.
Within the uncertainties, p(ρ,T) is a linear function of ρ in the mesophase region. The origin of the linearity is the colloidal nature of the supercritical mesophase [
6,
8] with a linear combination rule for thermodynamic state functions, similar to subcritical lever rule for the inhomogeneous 2-phase region. When appropriate functional forms are used for gaseous and liquid states separately, we find that all other isothermal thermodynamic state functions in the mesophase are linear functions of density. In the case of pressure, the negative and positive adjacent deviations for liquid and gas on either side are quadratic. The parameterizations require only physical constants belonging to the specific fluid, Boyle temperature (T
B), critical temperature (T
C), and coexisting densities along the critical isotherm, and known virial coefficients b
2(T) and b
3(T) etc. A remarkable finding is that for the gas phases below T
B, the coefficient b
4 is effectively zero within the experimental uncertainty. There is rigidity symmetry between gas and liquid phases on either side of the mesophase reported previously [
9], that relates the lower coefficients of the liquid equation to properties of the gas in the vicinity of the percolation loci.
The objective of this research is to investigate the extent that these findings can be used to describe experimental thermodynamic properties of a pure fluid over the whole range of equilibrium existence. Here, we investigate equations-of-state for gas, liquid and mesophase separately, each of which, in an initial approximation, require only measurable physical constants specific to particular fluids. Comparisons with experimental data are made via the NIST thermo-physical databank [
3]. NIST tabulations reproduce experimental data with 100% accuracy, and therefore, provide a foremost criteria for testing the alternative description to van der Waals underlying science of critical and supercritical behavior of fluids as described in references [
4,
5,
6,
7,
8,
9].
2. Rigidity and Fluid-State Bounds
Rigidity, (ω)
T, is the work required to isothermally and reversibly increase the density of a fluid. With dimensions of a molar energy, this simple state function relates directly to the change in Gibbs energy (G) with density at constant T
The inequalities that distinguish gas from liquid are:
and for the mesophase
The rigidity isotherms shown in
Figure 2 for CO
2 have been obtained from NIST Thermophysical databank [
3]. Inequalities in the derivatives of ω
T (Equations (2) and (3)) can thermodynamically define the percolation loci [
9]. It follows that at low density the percolation loci must approach the Boyle temperature (T
B) by its definition, which is obtained from the rigidity intersection interpolated at zero density. For CO
2 the limiting rigidity (RT
B: where R is the gas constant) along the percolation loci is 6.03 kJ/mol and T
B is 725 K, i.e., the temperature above which the 2nd-virial coefficient (b
2) is positive and below which it is negative; at T
B, p = ρkT and b
2 = 0. In the pressure-density plane, the percolation loci exhibit maxima as density decreases and approach zero, i.e., the ideal gas limit at low pressures and densities. The same behavior is seen for other atomic (e.g., argon) and molecular (e.g., water) fluids.
It is clear from Equation (1) that ω ≥ 0, i.e., rigidity must always be positive although it can be zero in two-phase coexistence regions. Gibbs energy cannot decrease with pressure when T is constant. From these definitions moreover, not only can there be no “continuity” of gas and liquid but the gas and liquid states are fundamentally different in their thermodynamic description. Rigidity is determined by number density fluctuations at the molecular level, which have different but complementary statistical origins in each phase, hence the symmetry [
9]. There is a distribution of many small clusters in a gas with one large void; there is a distribution of unoccupied pockets in the liquid with one large cluster. The statistical neighborhood properties of unoccupied pockets are the same as occupied sites.
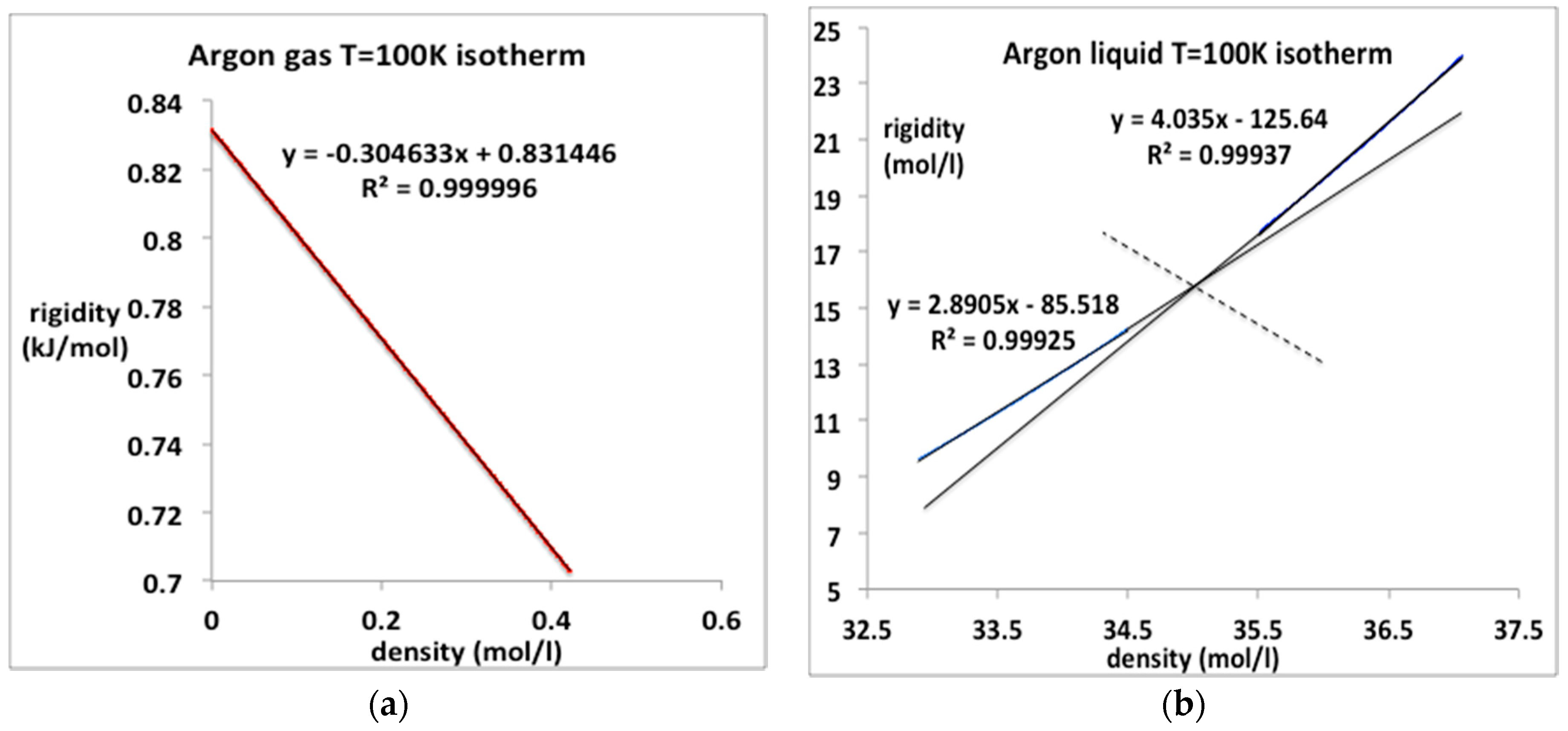
The percolation loci and the critical coexisting densities at T
c for CO
2 have been obtained by the method previously described in detail for Lennard-Jones fluids [
5] and argon [
8]. Looking at
Figure 2, the coexisting densities of the gas (ρ
G) and of liquid (ρ
L) and the meso-density gap vary linearly between the critical temperature (T
c) and Boyle temperature (T
B). If the mesophase rigidity is obtainable in terms of T
B and T
C, we can then represent the density bounds with linear functions and the rigidity in the mesophase as shown in
Figure 3a,b, and incorporate a linear equation of state for the mesophase that connects with gas and liquid at the percolation bounds PB and PA respectively.
Use of original experimental data could result in non-linear Equations (5) and (6) for density state bounds in a more refined analysis. Given these expressions for the temperature dependence of the percolation loci, and the rigidity in the mesophase (
Figure 3b), in terms of physical constants belonging to the specific fluid, we can now proceed to represent the thermodynamic surfaces using virial expansions.
The rigidity in the mesophase varies from kT at T
B to zero at T
c. It is linearly dependent on temperature in the near-critical region up about 1.25 T/T
c but there is an increasing small quadratic term as seen in
Figure 3b. The temperature dependence in the range T
c to T
B appears to be logarithmic, but without a scientific explanation, and within the uncertainty of the data, it is best represented by a simple quadratic
where T* = (T − T
c)/(T
B − T
c) and the constants c
1 and c
2 as given in
Figure 3b.
3. Pressure Surfaces p(ρ,T)
The pressure for any thermodynamic equilibrium state point can be obtained as a function of density along any isotherm. The gas equation-of-state can be parameterized using the formally exact Mayer virial expansion [
10]. The mesophase pressure increases linearly with density the region 0 > T > T
B and
ρ
PB(T) > ρ < ρ
PA(T), and for the ‘liquid’ state ρ > ρ
PA(T), we can use an empirical expansion. The isothermal equations-of-state for pressure are as follows:
For the temperature-density region Tc < T < TB and ρ < ρPA(T), Equations (8)–(10) are based upon the observation that there is a phase transition of the third-order at the mesophase bounds with a discontinuity in the derivative of ω with respect to ρ, i.e., the third derivative of Gibbs energy with respect to ρ at constant T along an isotherm. For temperatures above TB, p(ρPA,T) and ρPA, in Equation (10), are zero, whereupon the coefficients an in Equation (10) become the same as the Mayer virial coefficients bn (T) in Equation (8).
For the supercritical fluid at temperatures above T
B, Equation (8) up to order b
4 is sufficient to reproduce the pressure with five-figure accuracy, i.e., within the margin of the original experimental uncertainty, with a trend-line regression >0.999999, up to temperatures of 1000 K and pressures up to 50 Mpa. For the gas phase, at all temperatures below T
B, the 4th virial coefficient is found to be essentially zero, within the uncertainty of the experimental data; all higher terms are negligible. Thus, for the case of CO
2, the equation-of-state of the whole ‘gas’ region of
Figure 3 requires just the second and a third virial coefficients b
2(T) and b
3(T) within the experimental precision.
An overall p(ρ,T) equation of state can be integrated along any isotherm to obtain the Helmoltz energy function A(T) and hence, via the partition function, all other thermodynamic state functions and/or derivatives by long-established procedures [
11].
3.1. Supercritical CO2
In order to demonstrate a necessity of three separate equations-of-state, we take, as an example in the first instance, a supercritical isotherm T = 350 K, or T/T
c = 1.15, of CO
2. The critical and Boyle temperatures for CO
2 according to NIST databank [
3] are T
c = 305 K and T
c = 725 K. Using the same method described previously for argon [
8], the coexisting densities at T
c are found to be ρ
c(gas) = 7.771 mol/L and ρ
c(liq) = 13.46 mol/L. Substituting these physical constant values into equations (5 to 7) for T = 350 K we obtain the gas and liquid state density bounds ρ
PB(gas) = 7.305 mol/L and ρ
PA(liq) = 12.02 mol/L, and the rigidity ω(350 K) = 0.318 kT (0.925 kJ/mol).
If we try to fit the NIST data for the whole isotherm continuously from 0, just up to only 50 MPa, using a 6-term polynomial for example, we obtain the result:
with R² = 0.999125
In this typical continuous overall polynomial fit, the lower order coefficients are scientifically meaningless. By contrast, by using virial coefficients and known properties of the mesophase bounds, the NIST data for the whole range of three regions can be reproduced with essentially 100% precision when the gas, liquid and meso-states have different equations-of-state. We assume that there is a third-order phase transition, i.e., a discontinuity in the third derivative of Gibbs energy at the gas and liquid-state boundaries in accord with inequalities (2 and 3).
The experimental data from the NIST tabulations is reproduced with the same precision as the original data can be obtained, i.e., accurate to 5 figures, as evidenced by the mean-squared regression (R
2) in the trendline polynomial coefficients as given. Also shown in
Figure 4 are redefined equations to give the virial coefficients in Equations (8)–(10) as shown on the plots. The coefficient a
1 in the liquid-state expansion is taken to be equal to the value of ω
T in the mesophase to effect the third-order discontinuity between the mesophase and the liquid state. There is a symmetry between the rigidity of gas and liquid on either side of the mesophase but at this stage, this observation is empirical. As it presently lacks formal theory, we assume only the linear coefficient in Equation (10) and make no assumptions regarding higher-order coefficients at this stage.
3.2. Supercritical Argon
Modern research into fundamental equation-of-state science is more often based upon the example of argon in the first instance because of the relative simplicity of the spherical two-body pair potential and the amenability to basic theory. The literature on equation-of-state data to high temperature and pressure is both extensive and accurate to at least five figures except in the vicinity of the critical temperature (T
c) and pressure (p
c) [
3,
12]. For temperatures above the Boyle temperature there appears to be just a single continuous fluid state up to the highest pressures measured, which, in the case of argon, is 1000 MPa, according to NIST [
3,
12]. If there are no discontinuities along isotherms for T > T
B, the Mayer virial expansion is applicable over the whole accessible density range. The expansion for the pressure is
and on differentiation the rigidity is
where b
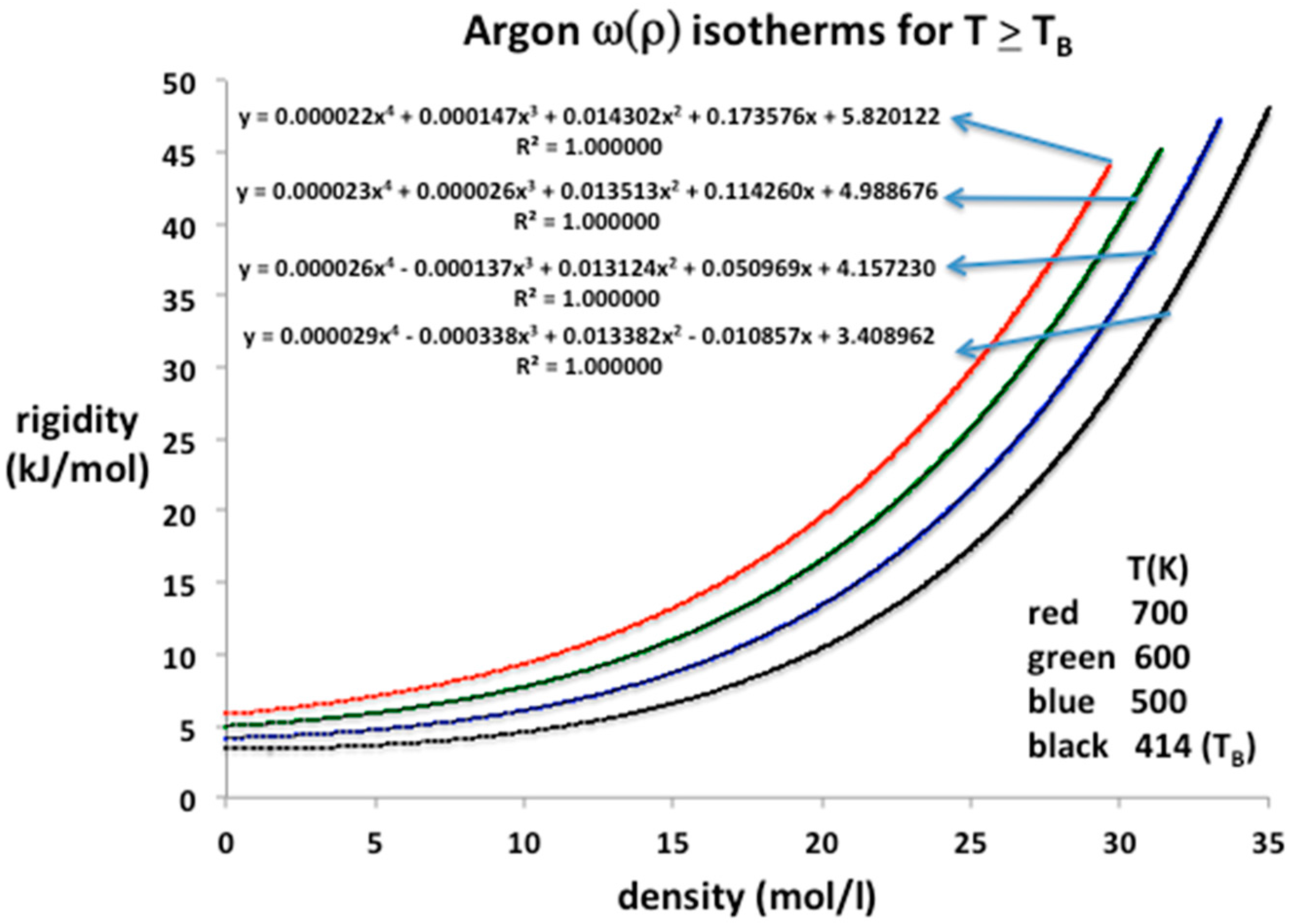
n are the temperature-dependent virial coefficients with conventional definitions. The NIST data for four supercritical isotherms above and including the Boyle temperature (T
B) can be precisely reproduced using Equation (12) and the virial coefficients determined. From Stewart and Jacobson [
13] we obtain T
B = 414 ± 0.5 for argon, which is consistent with the zero value of the second virial coefficient obtained here from parameterizations of NIST rigidity values from sound velocity compilations.
The equation-of-state isotherms are presented in
Figure 5. Also given are the polynomial trend-line parameters up to order 4. In this region, the entire experimental range of pressures, from near zero at ideal gas states at limiting low densities, up to 1000 MPa, can be represented to within the experimental five-figure precision by a three or at most four-term, closed-virial equation. Using Equation (12) we can deduce lower-order values of the virial coefficients of argon as listed in
Table 1. The values obtained for b
2 and b
3 are in agreement with the literature values within the experimental uncertainties, which can be as high as 20% in the case of b
3 [
9]. For argon at supercritical temperatures, little is presently known experimentally about b
4 and higher coefficients.
Lower-order virial coefficients, as defined by Equation (12), and calculated from the trend-line polynomial coefficients in
Figure 5, are summarized in
Table 1. All the experimental data from the NIST tabulations are reproduced with maximum precision as evidenced by the mean-squared regression in the trendline polynomial coefficients (R
2 = 1.000000 to six decimal places in every case); the coefficients have been redefined to obtain values of the virial expansion coefficients defined in Equation (11). These are in line with previous b
2(T) and b
3(T) tabulations [
14] within the uncertainties, which are rather wide, up to a few percent for b
2(T), and up to 25% in the case of b
3(T).
7. Conclusions
From the foregoing analysis, we conclude that the pressure equation-of-state, and hence all other thermodynamic state functions, can be expressed simply in terms of a few physical constants belonging to the fluid, and coefficients in virial expansions. The van der Waals equation-of-state survived for about 50 years until, increasingly, there was evidence that it could not account for the experimental data unless it was extended to include more and more terms and adjustable parameters. Modern equations-of-state with a large number of terms and adjustable parameters can reproduce experimental p-V-T data to high precision for chemical engineering applications, but they may no longer reflect an underlying physical science in the spirit of van der Waals.
We have found that the equation-of-state for the low density gas phases, in all three temperature regions T > T
B, T
B >T > Tc, and T < T
c, can all be represented by the first two or three terms of a Mayer virial expansion. For T > T
B a single virial equation can represent the whole isotherms up to the highest recorded pressures, which in the case of argon is 100 MPa. For supercritical temperatures below the Boyle temperature the gas phase can be represented by a term virial expansion to within the accuracy that the original pressures reported by NIST [
3]. The virial equations-of-state are fundamental to all atomic and molecular fluids and appear to be accurate up to second order, i.e., to quadratic terms for all temperatures below T
B. We will report detailed comparisons and virial coefficients for the case CO
2, and also some preliminary comparisons with experimental data and NIST equations, for the exemplary fluid argon, in due course.
At this stage in the development of science-based alternative forms of the equation-of-state we have not attempted to parameterise the second and third virial coefficients as functions of temperature. We note, however, there is evidence that b
2(T) may be non-analytic at the Boyle temperature. It can be represented by two different series expansions, at least in the case of a simple Lennard–Jones model, above and below T
B [
29,
30]. There are also some indications that b
3(T) exhibits a maximum at or near T
c. Also, we find that for simple fluids, e.g., argon, below T
B, the coefficient b
4(T) appears to become vanishingly small. A more accurate determination of lower-order virial coefficients from original thermodynamic data ought now to become a research priority.