Rate-Distortion Bounds for Kernel-Based Distortion Measures †
Abstract
:1. Introduction
2. Rate-Distortion Function
3. Kernel-Based Distortion Measures
3.1. Reconstruction in Input Space
3.2. Reconstruction in Feature Space
3.3. and
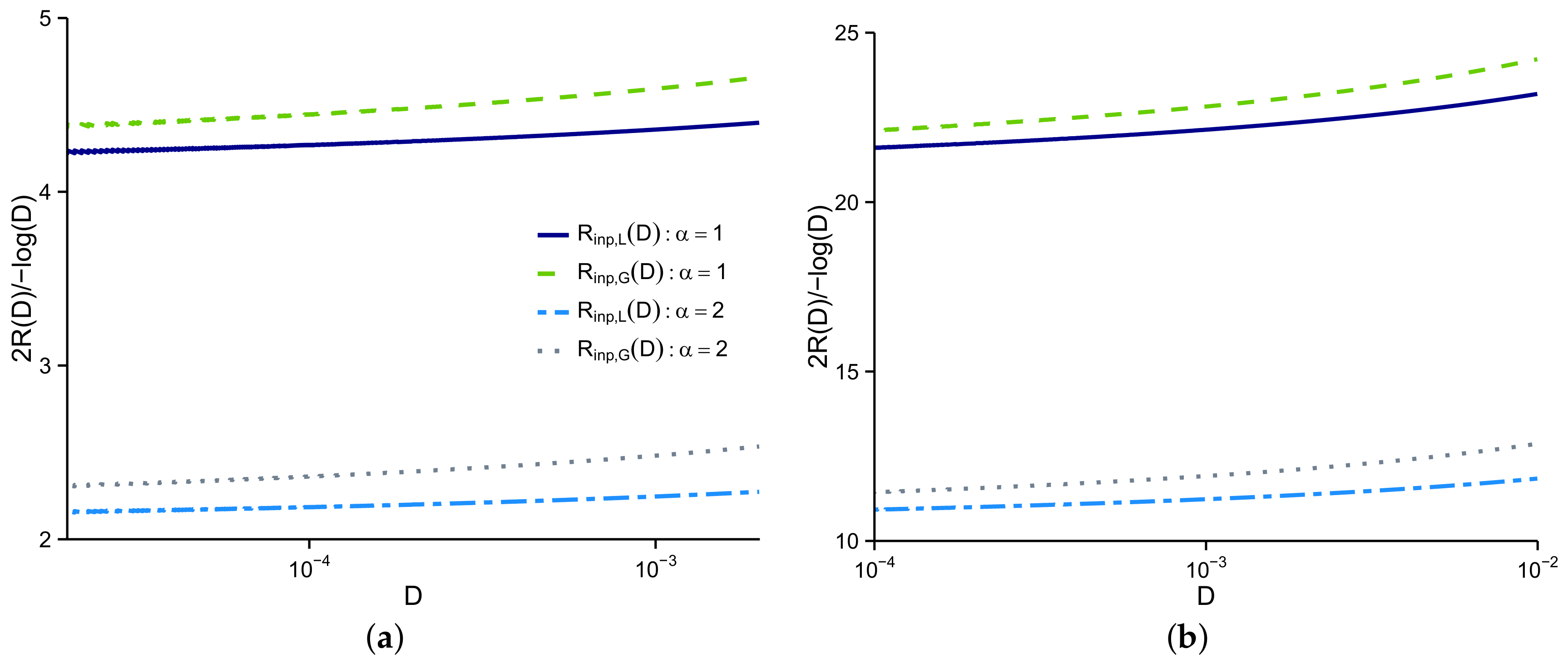
4. Rate-Distortion Bounds
4.1. Lower Bound to
4.2. Upper Bound to
4.3. Rate-Distortion Dimension
4.4. Upper Bound to
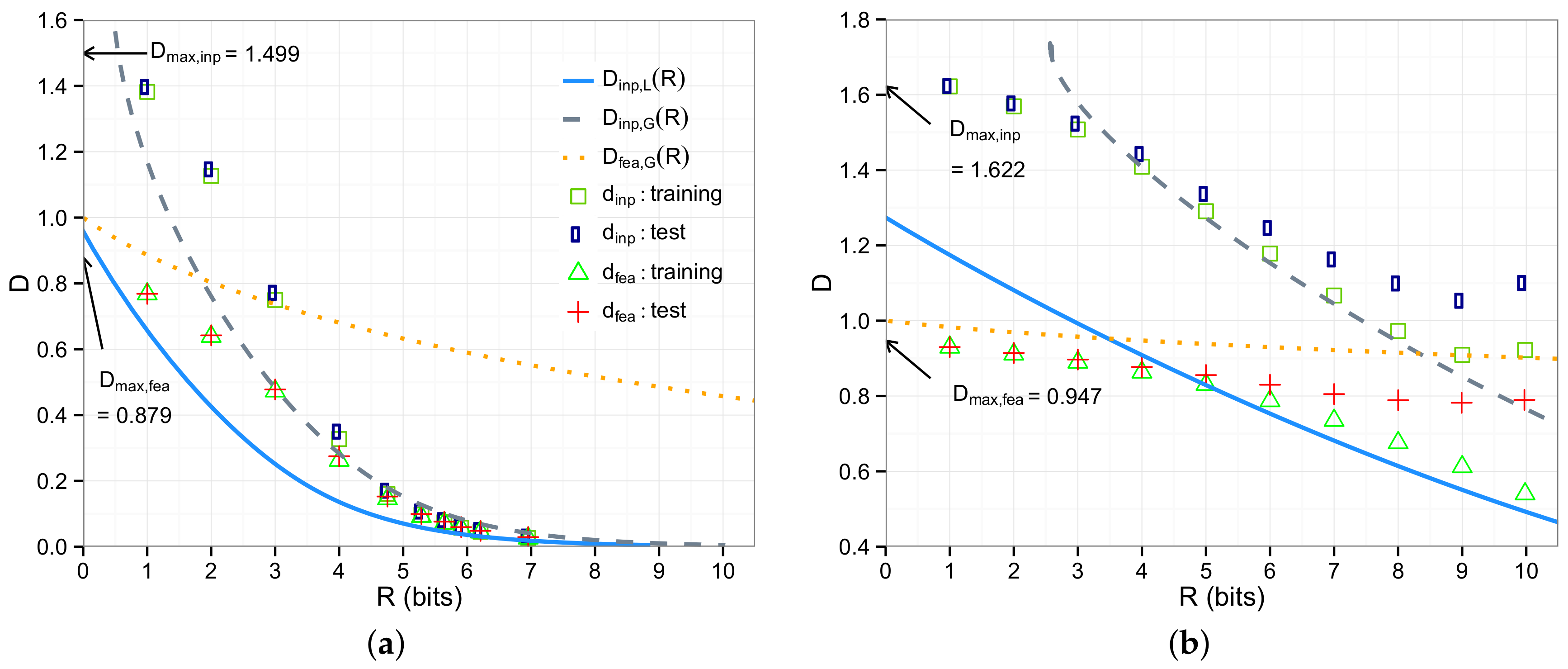
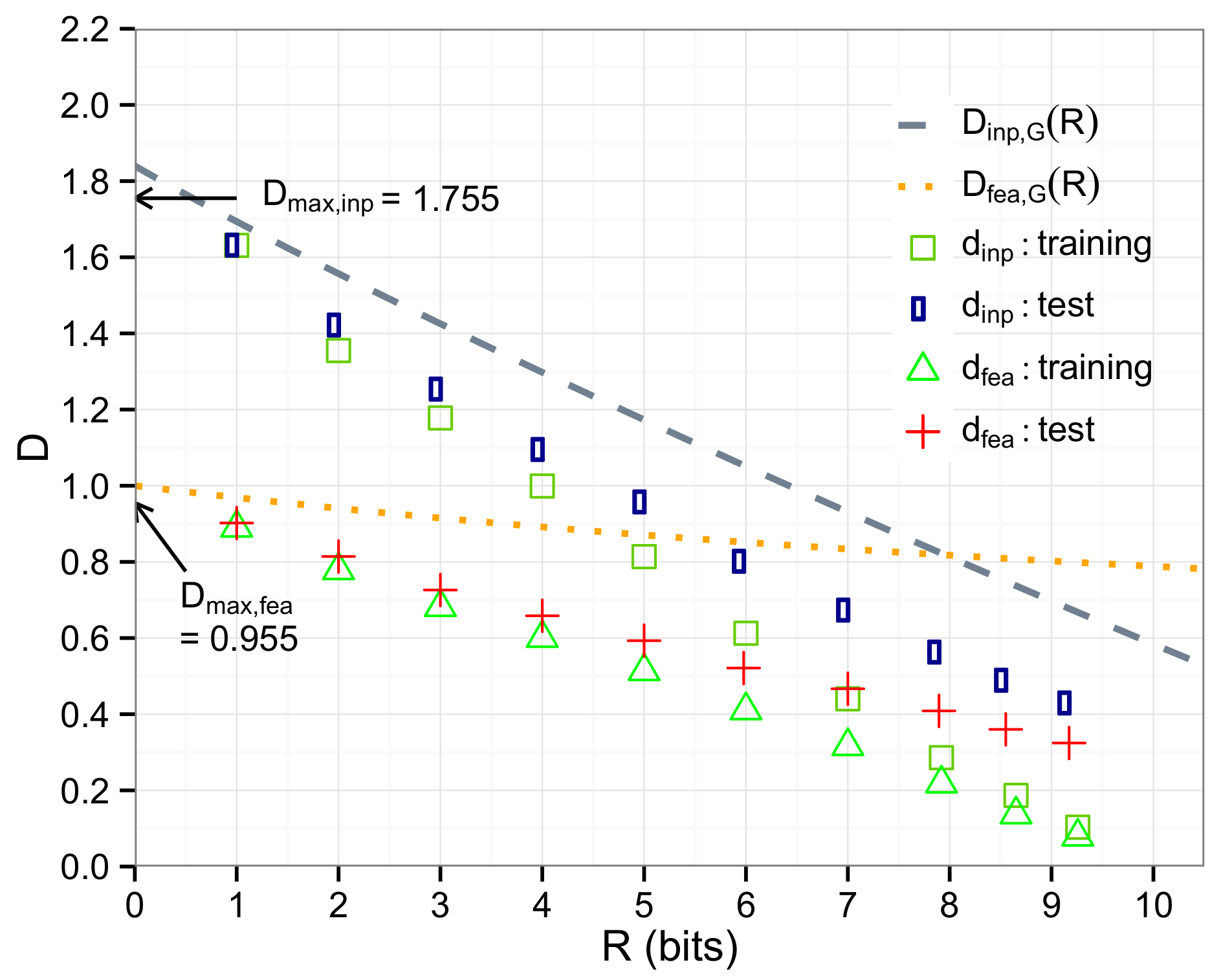
5. Experimental Evaluation
5.1. Synthetic Data
5.2. Image Data
6. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 5
References
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Aizerman, M.A.; Braverman, E.A.; Rozonoer, L. Theoretical foundations of the potential function method in pattern recognition learning. Autom. Remote Control 1964, 25, 821–837. [Google Scholar]
- Berger, T. Rate Distortion Theory: A Mathematical Basis for Data Compression; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Girolami, M. Mercer kernel-based clustering in feature space. IEEE Trans. Neural Netw. 2002, 13, 780–784. [Google Scholar] [CrossRef] [PubMed]
- Filippone, M.; Camastra, F.; Masulli, F.; Rovetta, S. A survey of kernel and spectral methods for clustering. Pattern Recognit. 2008, 41, 176–190. [Google Scholar] [CrossRef]
- Schölkopf, B.; Mika, S.; Burges, C.J.C.; Knirsch, P.; Müller, K.R.; Ratsch, G.; Smola, A.J. Input space versus feature space in kernel-based methods. IEEE Trans. Neural Netw. 1999, 10, 1000–1017. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley Interscience: Hoboken, NJ, USA, 1991. [Google Scholar]
- Gray, R.M. Entropy and Information Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Linkov, Y.N. Evaluation of ϵ-entropy of random variables for small ϵ. Probl. Inf. Transm. 1965, 1, 18–26. [Google Scholar]
- Linder, T.; Zamir, R. On the asymptotic tightness of the Shannon lower bound. IEEE Trans. Inf. Theory 1994, 40, 2026–2031. [Google Scholar] [CrossRef]
- Koch, T. The Shannon lower bound is asymptotically tight. IEEE Trans. Inf. Theory 2016, 62, 6155–6161. [Google Scholar] [CrossRef]
- Kawabata, T.; Dembo, A. The rate-distortion dimension of sets and measures. IEEE Trans. Inf. Theory 1994, 40, 1564–1572. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Fukunaga, K.; Hostetler, L. The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Trans. Inf. Theory 1975, 21, 32–40. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Watanabe, K. Rate-distortion analysis for kernel-based distortion measures. In Proceedings of the Eighth Workshop on Information Theoretic Methods in Science and Engineering, Copenhagen, Denmark, 24–26 June 2015. [Google Scholar]
- Nene, S.A.; Nayar, S.K.; Murase, H. Columbia Object Image Library (COIL-20). Available online: http://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php (accessed on 4 July 2017).
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, K. Rate-Distortion Bounds for Kernel-Based Distortion Measures. Entropy 2017, 19, 336. https://doi.org/10.3390/e19070336
Watanabe K. Rate-Distortion Bounds for Kernel-Based Distortion Measures. Entropy. 2017; 19(7):336. https://doi.org/10.3390/e19070336
Chicago/Turabian StyleWatanabe, Kazuho. 2017. "Rate-Distortion Bounds for Kernel-Based Distortion Measures" Entropy 19, no. 7: 336. https://doi.org/10.3390/e19070336




