Trajectory Shape Analysis and Anomaly Detection Utilizing Information Theory Tools †
Abstract
:1. Introduction
- For the trajectory modeling, we additionally take into account the speed attribute of the moving object, leading to a richer representation than relying solely upon the angle description for trajectory shape analysis. In order to avoid the difficult fitting problem for parametric models such as von Mises and AWLG, the general Kernel Density Estimation (KDE) is developed to obtain the probability distribution function (PDF) as the model of the trajectory shape.
- In practical implementation, probability bins are taken to approximate the shape PDF. For the sake of reducing the computational cost, we propose to take advantage of the local probability extremas to adaptively determine the probability bins used for trajectory modeling.
- The Information Bottleneck (IB) principle [14] partitions trajectories into clusters via minimizing the objective function of the loss of Mutual Information (MI) [17] between the trajectory dataset and a feature set of these trajectories (for conciseness we call this the MI based clustering in our paper). To alleviate the problem of local optima, we propose to improve the clustering performance by introducing an item of clustering quality into the objective function of IB.
- Instead of using a manually defined threshold, for the evaluation of the differences between a trajectory being tested and the medoids of the learned clusters, we employ an adaptive decision, by deploying the Shannon entropy concept [17], to look at all the differences under consideration as a whole and to make the trajectory analysis more discriminative.
2. Related Work
3. Adaptive Trajectory Modeling Based on Nonparametric KDE
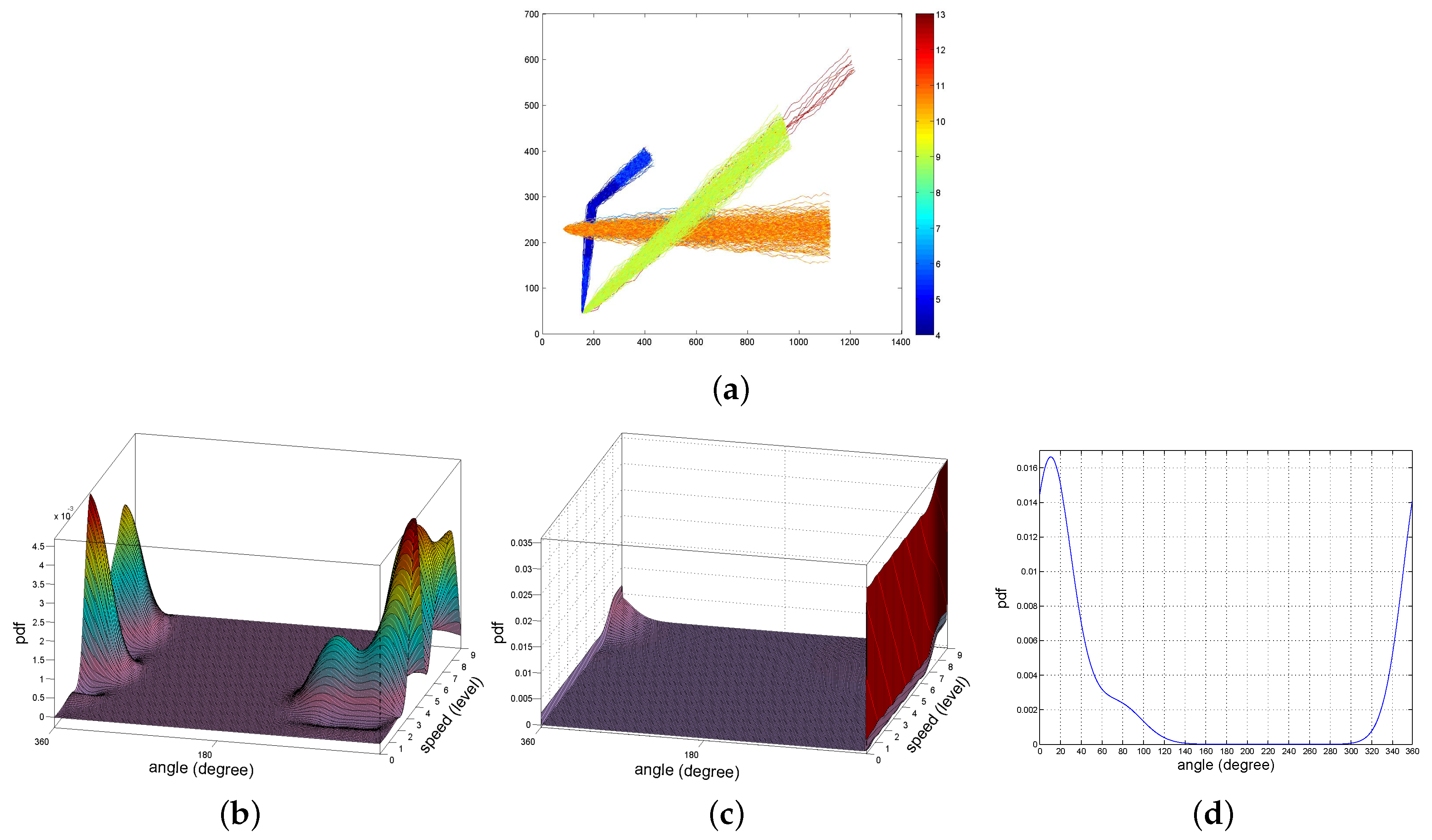
3.1. Trajectory Modeling on Speed and Angle
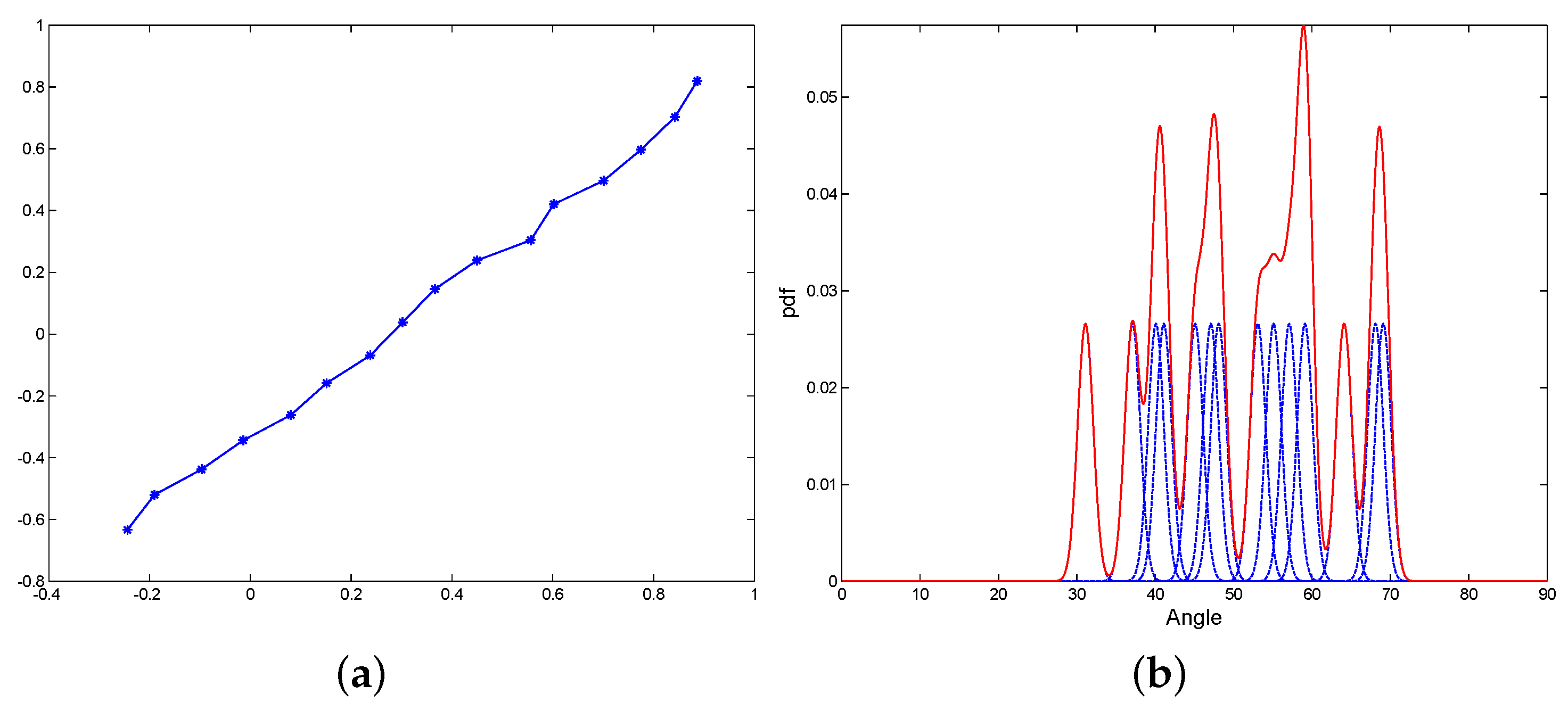
3.2. Illustration Comparing the Estimated PDFs by Different Modeling Schemes
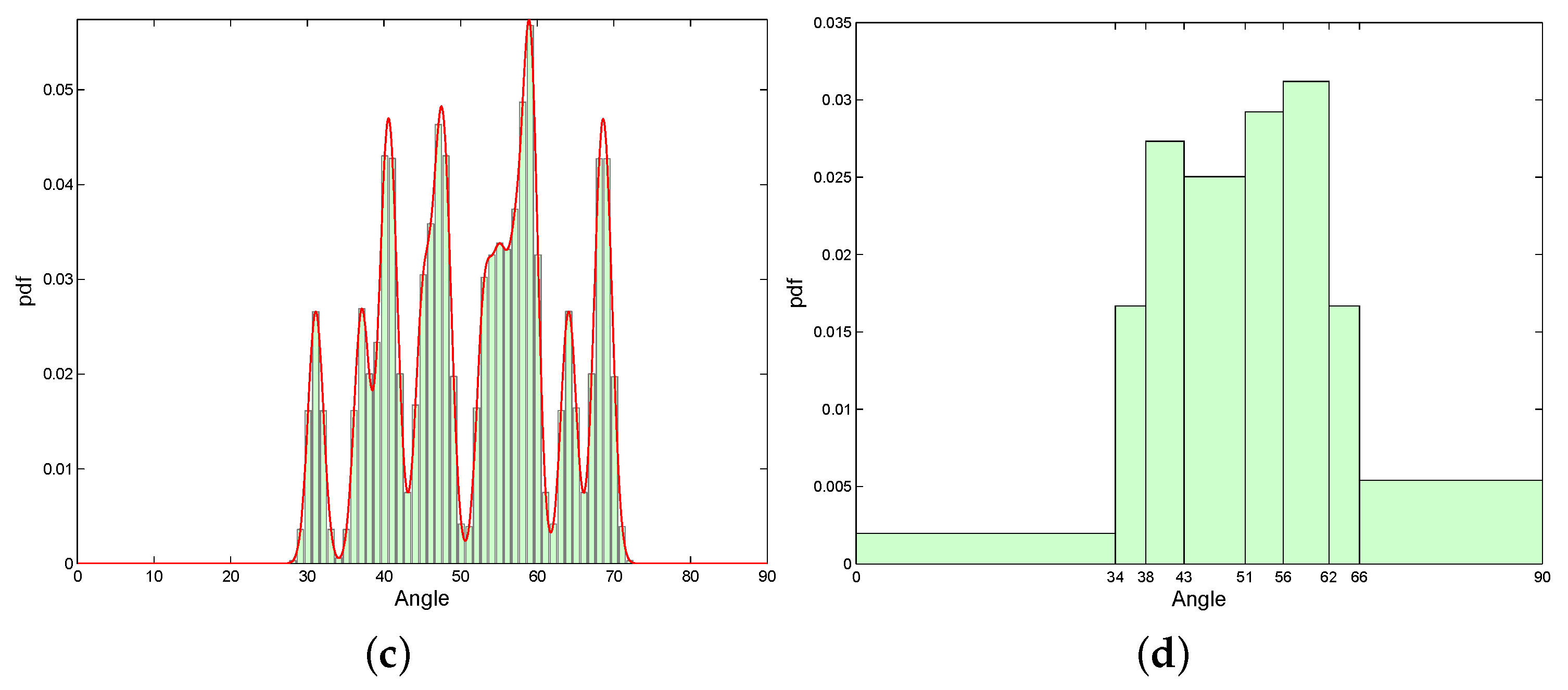
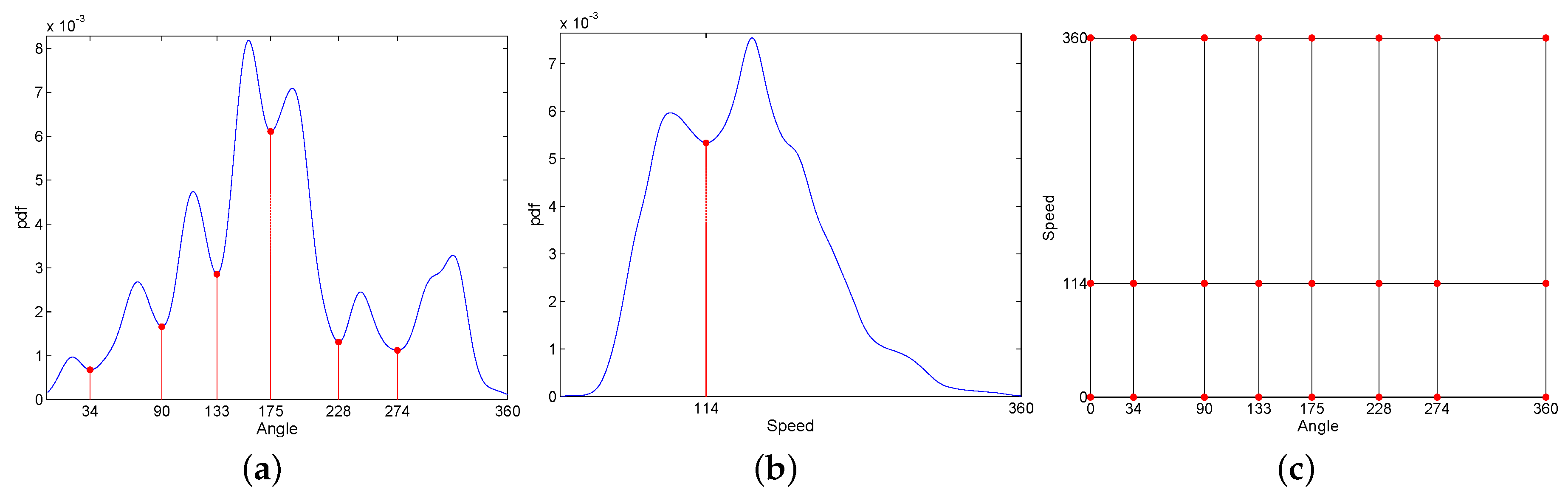
3.3. Adaptive Probability Bins
4. MI Based Trajectory Clustering
4.1. Basic Concepts of Information Theory
4.2. IB Principle for Trajectory Data
- Input probability . This is the probability of a single trajectory. We simply use to assign the uniform “importance” for all the trajectories under consideration, here .
- Conditional probability . This probability of the feature point given the trajectory can be obtained from the discrete probability distribution of shape feature of , . That is, this probability is the height of the bin located at .
- Output probability . This is the probability of the feature point , given all the trajectories in the dataset. This can be obtained by the full probability formula
4.3. New Objective Function
5. Shannon Entropy Based Trajectory Anomaly Detection
6. Experiments on Synthetic and Real Trajectory Data
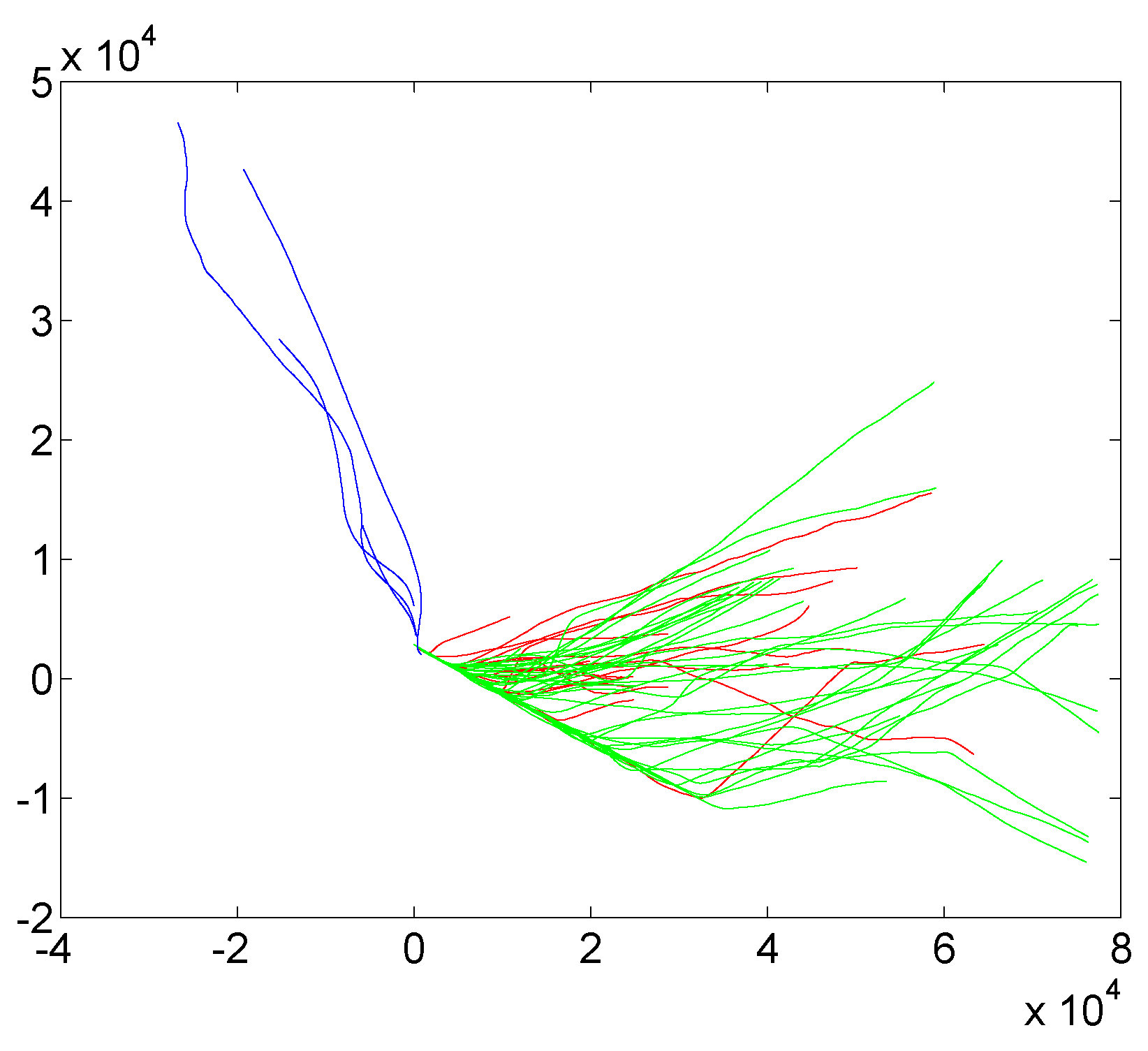
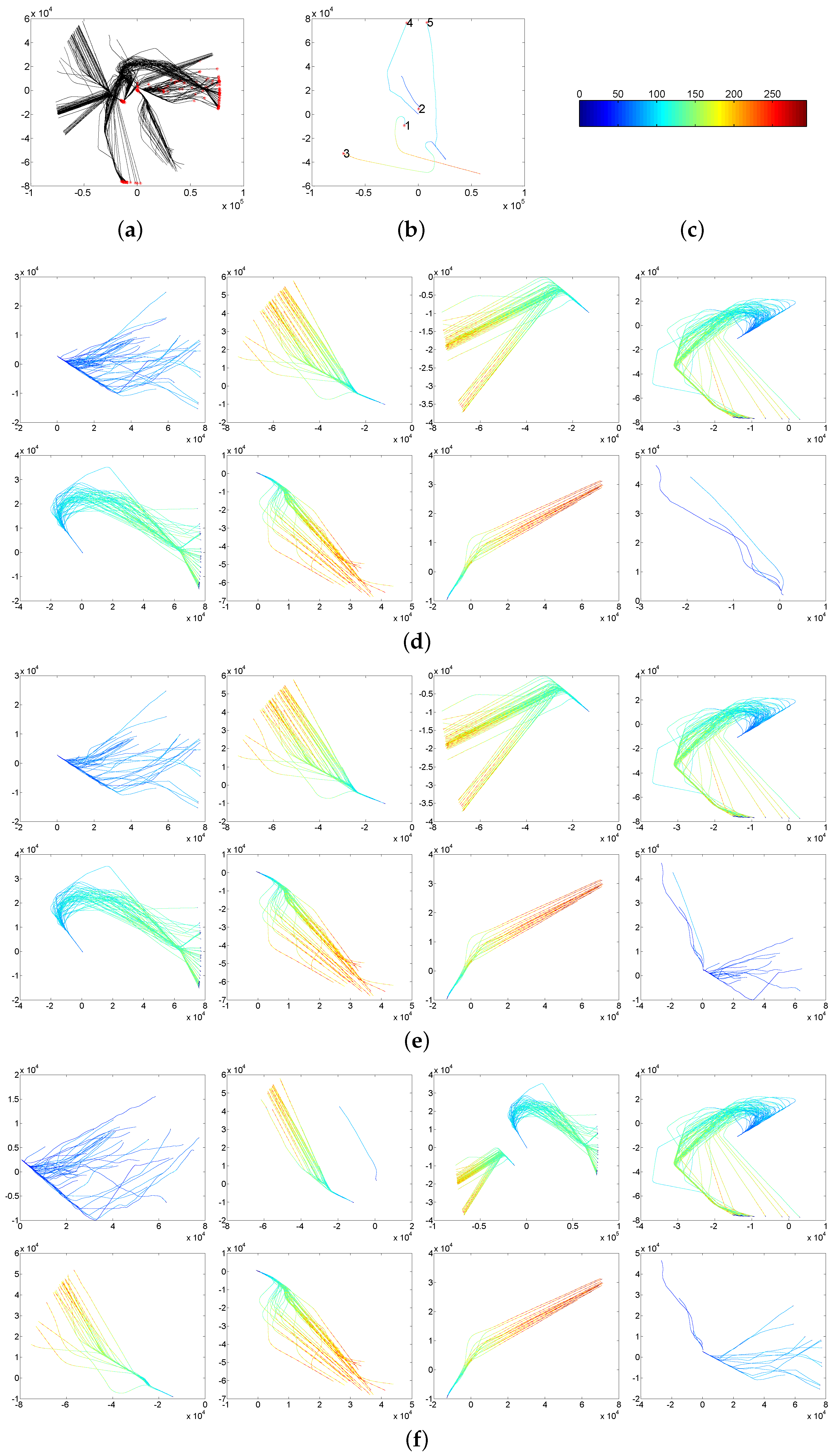
6.1. Aircraft Trajectory Dataset
6.2. MIT Trajectory Dataset
6.3. Synthetic Trajectory Dataset
7. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dee, H.M.; Velastin, S.A. How close are we to solving the problem of automated visual surveillance? Mach. Vis. Appl. 2008, 19, 329–343. [Google Scholar] [CrossRef]
- Ciccio, C.D.; van der Aa, H.; Cabanillas, C.; Mendling, J.; Prescher, J. Detecting flight trajectory anomalies and predicting diversions in freight transportation. Decis. Support Syst. 2016, 88, 1–17. [Google Scholar] [CrossRef]
- Smart, E.; Brown, D. A Two-Phase Method of Detecting Abnormalities in Aircraft Flight Data and Ranking Their Impact on Individual Flights. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1253–1265. [Google Scholar] [CrossRef]
- Morris, B.T.; Trivedi, M.M. Understanding vehicular traffic behavior from video: a survey of unsupervised approaches. J. Electron. Imaging 2013, 22, 041113. [Google Scholar] [CrossRef]
- Hu, W.; Xie, D.; Tan, T.; Maybank, S. Learning Activity Patterns Using Fuzzy Self-Organizing Neural Network. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 1618–1626. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection: A Survey. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Calderara, S.; Prati, A.; Cucchiara, R. Mixtures of von Mises Distributions for People Trajectory Shape Analysis. IEEE Trans. Circuits Syst. Video Technol. 2011, 21, 457–471. [Google Scholar] [CrossRef]
- Prati, A.; Calderara, S.; Cucchiara, R. Using Circular Statistics for Trajectory Shape Analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Mariescu-Istodor, R.; Tabarcea, A.; Saeidi, R.; Fränti, P. Low Complexity Spatial Similarity Measure of GPS Trajectories. In Proceedings of the 10th International Conference on Web Information Systems and Technologies, Barcelona, Spain, 3–5 April 2014; pp. 62–69. [Google Scholar]
- Markovic, I.; Cesic, J.; Petrovic, I. Von Mises Mixture PHD Filter. IEEE Signal Process. Lett. 2015, 22, 2229–2233. [Google Scholar] [CrossRef]
- Sieranoja, S.; Kinnunen, T.; Fränti, P. GPS Trajectory Biometrics: From Where You Were to How You Move. In Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR); Robles-Kelly, A., Loog, M., Biggio, B., Escolano, F., Wilson, R., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 450–460. [Google Scholar]
- Calderara, S.; Prati, A.; Cucchiara, R. Learning People Trajectories using Semi-directional Statistics. In Proceedings of the Sixth IEEE International Conference on Advanced Video and Signal Based Surveillance, Genova, Italy, 2–4 September 2009; pp. 213–218. [Google Scholar]
- Ding, H.; Trajcevski, G.; Scheuermann, P.; Wang, X.; Keogh, E. Querying and Mining of Time Series Data: Experimental Comparison of Representations and Distance Measures. Proc. VLDB Endow. 2008, 1, 1542–1552. [Google Scholar] [CrossRef]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. In Proceedings of the 37th annual Allerton Conference on Communication, Control, and Computing, Chicago, IL, USA, 22–24 September 1999; pp. 368–377. [Google Scholar]
- Guo, Y.; Xu, Q.; Liang, S.; Fan, Y.; Sbert, M. XaIBO: An Extension of aIB for Trajectory Clustering with Outlier. In Neural Information Processing; Lecture Notes in Computer Science; Arik, S., Huang, T., Lai, W.K., Liu, Q., Eds.; Springer: Cham, Switzerland, 2015; Volume 9490, pp. 423–431. [Google Scholar]
- Slonim, N. The Information Bottleneck: Theory and Applications. Ph.D. Thesis, Hebrew University of Jerusalem, Jerusalem, Israel, 2002. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: San Francisco, CA, USA, 2006. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]
- Junejo, I.N.; Javed, O.; Shah, M. Multi Feature Path Modeling for Video Surveillance. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 26 August 2004; Volume 2, pp. 716–719. [Google Scholar]
- Anjum, N.; Cavallaro, A. Multifeature Object Trajectory Clustering for Video Analysis. IEEE Trans. Circuits Syst. Video Technol. 2008, 18, 1555–1564. [Google Scholar] [CrossRef]
- De Vries, G.; van Someren, M. Clustering Vessel Trajectories with Alignment Kernels under Trajectory Compression. In Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2010; pp. 296–311. [Google Scholar]
- De Vries, G.K.D.; Someren, M.V. Machine learning for vessel trajectories using compression, alignments and domain knowledge. Exp. Syst. Appl. 2012, 39, 13426–13439. [Google Scholar] [CrossRef]
- Annoni, R.; Forster, C.H.Q. Analysis of Aircraft Trajectories Using Fourier Descriptors and Kernel Density Estimation. In Proceedings of the15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012; pp. 1441–1446. [Google Scholar]
- Zheng, Y. Trajectory Data Mining: An Overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–41. [Google Scholar] [CrossRef]
- Cilibrasi, R.; Vitányi, P.M.B. Clustering by Compression. IEEE Trans. Inf. Theory 2005, 51, 1523–1545. [Google Scholar] [CrossRef]
- Izakian, H.; Pedrycz, W. Anomaly Detection and Characterization in Spatial Time Series Data: A Cluster-Centric Approach. IEEE Trans. Fuzzy Syst. 2014, 22, 1612–1624. [Google Scholar] [CrossRef]
- Ge, W.; Collins, R.T.; Ruback, R.B. Vision-based Analysis of Small Groups in Pedestrian Crowds. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1003–1016. [Google Scholar] [PubMed]
- Steeg, G.V.; Galstyan, A.; Sha, F.; DeDeo, S. Demystifying Information-Theoretic Clustering. arXiv, 2013; arXiv:1310.4210. [Google Scholar]
- Laxhammar, R.; Falkman, G. Online Learning and Sequential Anomaly Detection in Trajectories. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1158–1173. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Li, N.; Zhou, Z.H.; Chen, C.; Sun, L.; Li, S. iBAT: Detecting Anomalous Taxi Trajectories from GPS Traces. In Proceedings of the 13th International Conference on Ubiquitous Computing, Beijing, China, 17–21 September 2011; pp. 99–108. [Google Scholar]
- Wand, M.P.; Jones, M.C. Kernel Smoothing, Monographs on Statistics and Applied Probability; CRC Press: Boca Raton, FL, USA, 1995; Volume 60, p. 91. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Lin, J. Divergence Measures Based on the Shannon Entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Slonim, N.; Tishby, N. Agglomerative Information Bottleneck. Adcances Neural Inf. Process. Syst. 1999, 12, 617–623. [Google Scholar]
- Kailath, T. The Divergence and Bhattacharyya Distance Measures in Signal Selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar] [CrossRef]
- Aircraft Trajectory Dataset. Available online: https://c3.nasa.gov/dashlink/resources/132/ (accessed on 9 June 2017).
- Gariel, M.; Srivastava, A.N.; Feron, E. Trajectory Clustering and an Application to Airspace Monitoring. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1511–1524. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, Q.; Fan, Y.; Liang, S.; Sbert, M. Fast Agglomerative Information Bottleneck Based Trajectory Clustering. In Proceedings of the 23rd International Conference on Neural Information Processing, Kyoto, Japan, 16–21 October 2016; pp. 425–433. [Google Scholar]
- Morris, B.; Trivedi, M. Learning Trajectory Patterns by Clustering: Experimental Studies and Comparative Evaluation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 312–319. [Google Scholar]
- MIT Trajectory Dataset. Available online: http://www.ee.cuhk.edu.hk/~xgwang/MITtrajsingle.html (accessed on 9 June 2017).
- Wang, X.; Ma, K.T.; Ng, G.W.; Grimson, W.E.L. Trajectory Analysis and Semantic Region Modeling Using A Nnonparametric Bayesian Model. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Synthetic Trajectory Dataset. Available online: https://avires.dimi.uniud.it/papers/trclust/ (accessed on 9 June 2017).
- Piciarelli, C.; Micheloni, C.; Foresti, G.L. Trajectory-Based Anomalous Event Detection. IEEE Trans. Circuits Syst. Video Technol. 2008, 18, 1544–1554. [Google Scholar] [CrossRef]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On Clustering Validation Techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Larsen, B.; Aone, C. Fast and Effective Text Mining Using Linear-time Document Clustering. In Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; pp. 16–22. [Google Scholar]
- Hu, W.; Li, X.; Tian, G.; Maybank, S.; Zhang, Z. An Incremental DPMM-Based Method for Trajectory Clustering, Modeling, and Retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1051–1065. [Google Scholar] [PubMed]
- May, R.; Hanrahan, P.; Keim, D.A.; Shneiderman, B.; Card, S. The State of Visual Analytics: Views on what visual analytics is and where it is going. In Proceedings of the IEEE Symposium on Visual Analytics Science and Technology, Salt Lake City, UT, USA, 25–26 October 2010; pp. 257–259. [Google Scholar]

| Adaptive | Equal | |||
|---|---|---|---|---|
| Number of Bins | Runtime | Number of Bins | Runtime | |
| Aircraft | 14 | 0.000012 | 21 | 0.000017 |
| MIT | 40 | 0.000026 | 50 | 0.000036 |
| Synthetic | 4 | 0.000004 | 9 | 0.000009 |
| Minimum Speed | Maximum Speed | Accelerated Speed | Operation | |
|---|---|---|---|---|
| clusters 1, 2 | 10 | 160 | 10 | speed up |
| clusters 3, 4 | 200 | 350 | −10 | slow down |
| cluster 5 | 30 | 320 | 20 | speed up |
| Proposed Approach | Original IB | k-means | ||||
|---|---|---|---|---|---|---|
| Average | Standard Error | Average | Standard Error | Average | Standard Error | |
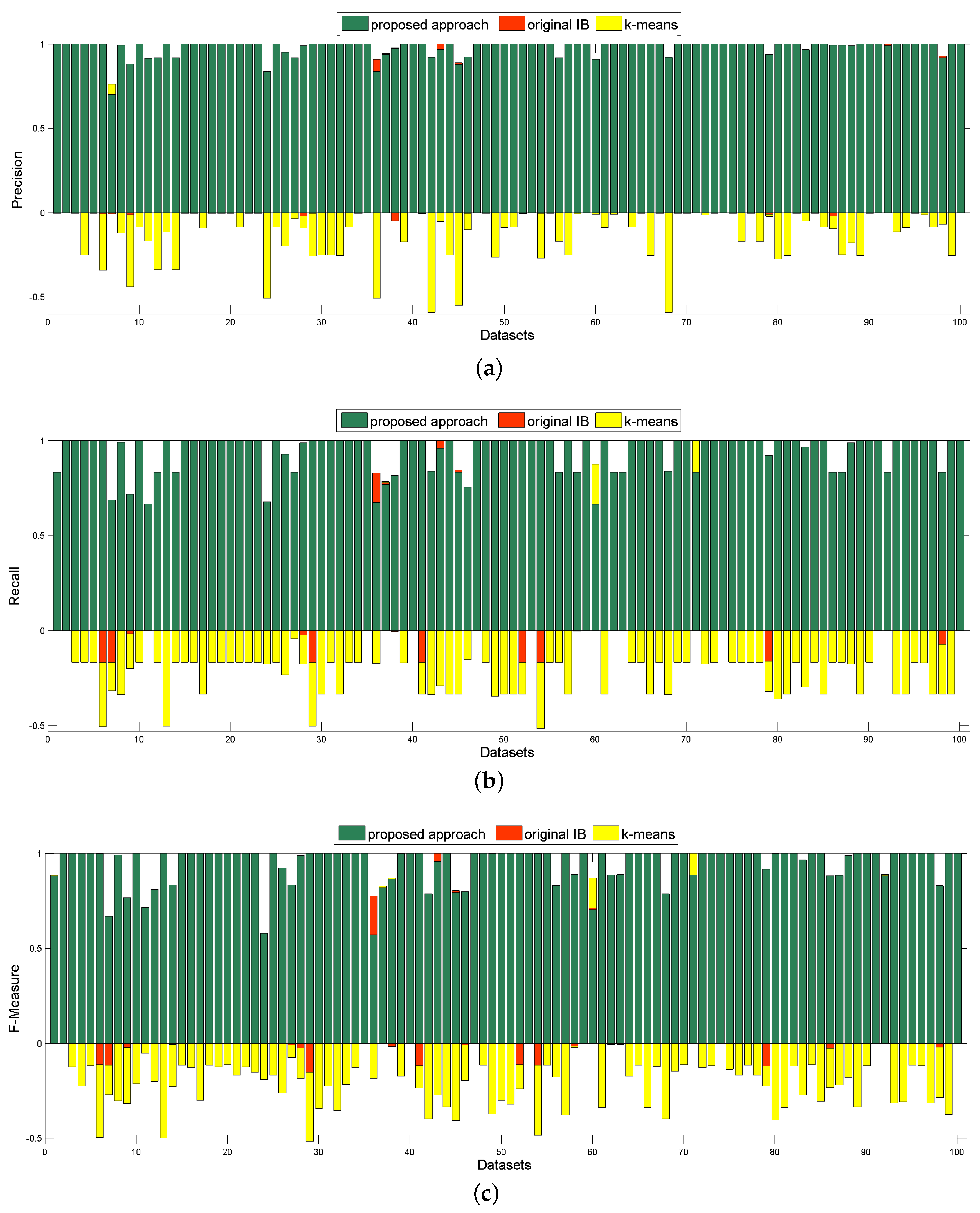
| precision | 0.9791 | 0.0046 | 0.9792 | 0.0045 | 0.8683 | 0.0170 |
| recall | 0.9447 | 0.0096 | 0.9341 | 0.0103 | 0.7649 | 0.0129 |
| F-Measure | 0.9475 | 0.0096 | 0.9402 | 0.0097 | 0.7703 | 0.0155 |
| Proposed Approach | SHNN-CAD (k = 3) | SHNN-CAD (k = 4) | SHNN-CAD (k = 5) | |
|---|---|---|---|---|
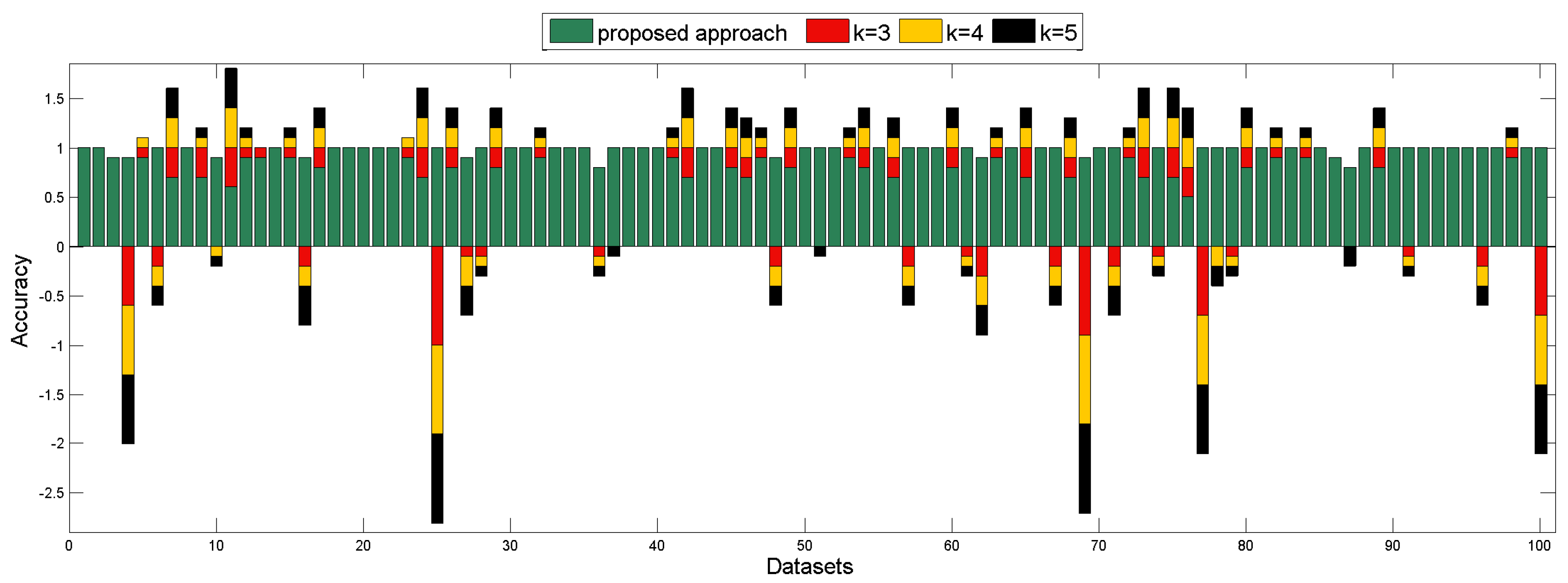
| average | 0.9160 | 0.9190 | 0.9100 | 0.9010 |
| standard error | 0.0114 | 0.0193 | 0.0194 | 0.0199 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Xu, Q.; Li, P.; Sbert, M.; Yang, Y. Trajectory Shape Analysis and Anomaly Detection Utilizing Information Theory Tools. Entropy 2017, 19, 323. https://doi.org/10.3390/e19070323
Guo Y, Xu Q, Li P, Sbert M, Yang Y. Trajectory Shape Analysis and Anomaly Detection Utilizing Information Theory Tools. Entropy. 2017; 19(7):323. https://doi.org/10.3390/e19070323
Chicago/Turabian StyleGuo, Yuejun, Qing Xu, Peng Li, Mateu Sbert, and Yu Yang. 2017. "Trajectory Shape Analysis and Anomaly Detection Utilizing Information Theory Tools" Entropy 19, no. 7: 323. https://doi.org/10.3390/e19070323
APA StyleGuo, Y., Xu, Q., Li, P., Sbert, M., & Yang, Y. (2017). Trajectory Shape Analysis and Anomaly Detection Utilizing Information Theory Tools. Entropy, 19(7), 323. https://doi.org/10.3390/e19070323





