Optimal Nonlinear Estimation in Statistical Manifolds with Application to Sensor Network Localization
Abstract
:1. Introduction
2. Nonlinear Estimation via Natural Gradient MLE
| Algorithm 1: The natural gradient based iterative MLE algorithm. |
|
- The natural gradient estimator updates the underlying manifold metric (i.e., FIM) at each iteration as well, which evaluates the estimate accuracy.
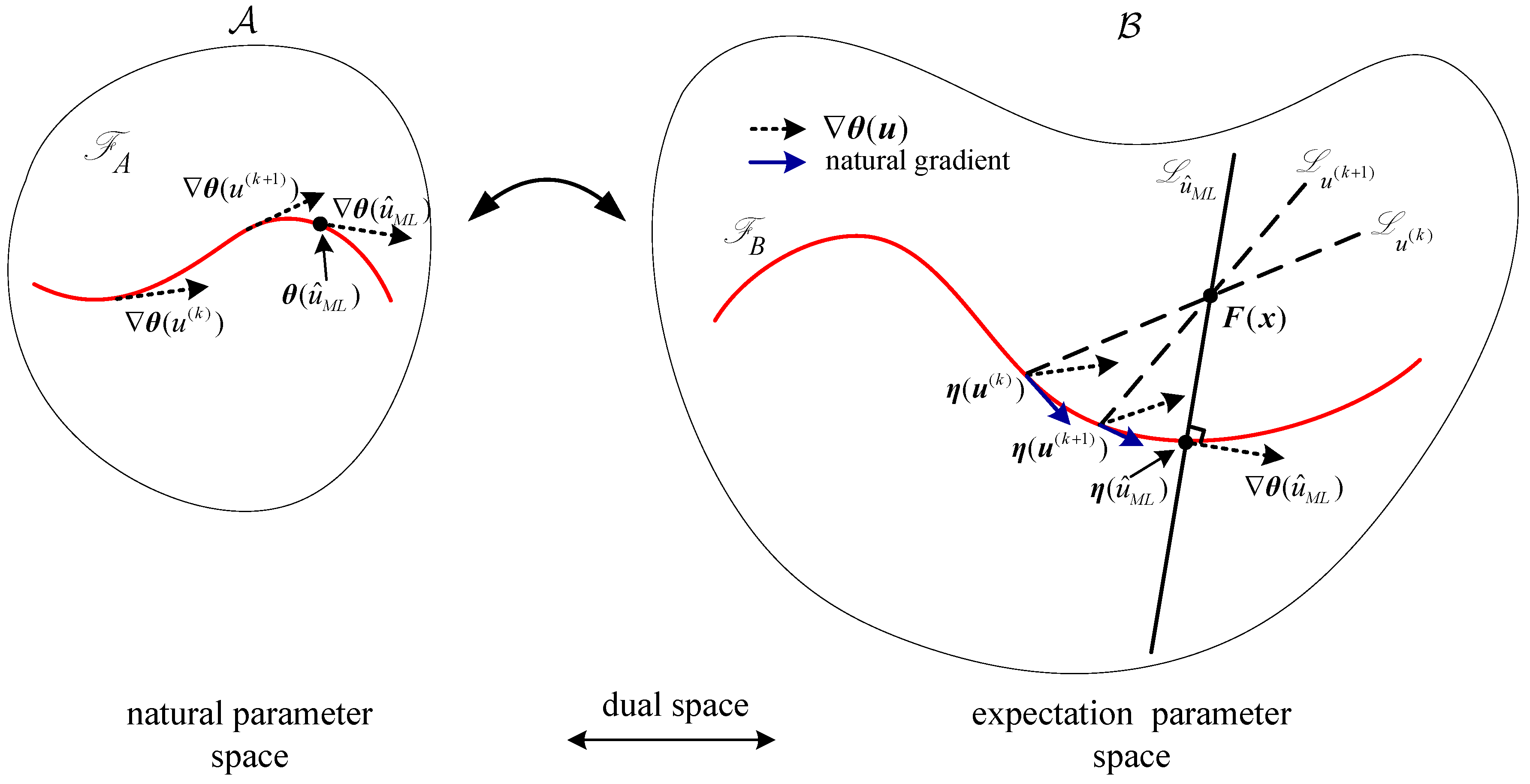
- Updates in the classical steepest descent types are performed via the standard gradient and are well-matched to the Euclidean distance measure as well as the gradient adaptation. For the cases where the underlying parameter spaces are not Euclidean but are curved, i.e., Riemannian, does not represent the steepest descent direction in the parameter space, and thus the standard gradient adaptation is no longer appropriate. The natural gradient updates in Equation (14) improve the steepest descent update rule by taking the geometry of the Riemannian manifold into account to calculate the learning directions. In other words, it modifies the standard gradient direction according to the local curvature of the parameter space in terms of the Riemannian metric tensor , thus offers faster convergence than the steepest descent method.
- The Newton methodimproves the steepest descent method by using the second-order derivatives of the cost function, i.e., the inverse of the Hessian of to adjust the gradient search direction. When is a quadratic function of , the inverse of the Hessian is equal to , and thus Newton’s method and the natural gradient approach are identical [22]. However, in more general contexts, the two techniques are different. Generally, the natural gradient approach increases the stability of the iteration with respect to Newton’s method through replacing the Hessian by its expected value, i.e., the Riemannian metric tensor .
- The natural gradient approach is identical to the Fisher scoring method in cases where the Fisher information matrix coincides with the Riemannian metric tensor of the underlying parameter space. In such cases, the natural gradient approach is a Riemannian-based version of the Fisher scoring method performed on manifolds, and it is very appropriate when the cost function is related to the Riemannian geometry of the underlying parameter space [23]. Once these methods are entered into the manifold, additional insights into their geometric meaning may be deduced in the framework of differential and information geometry.
3. Information Geometric Interpretation for Natural Gradient MLE
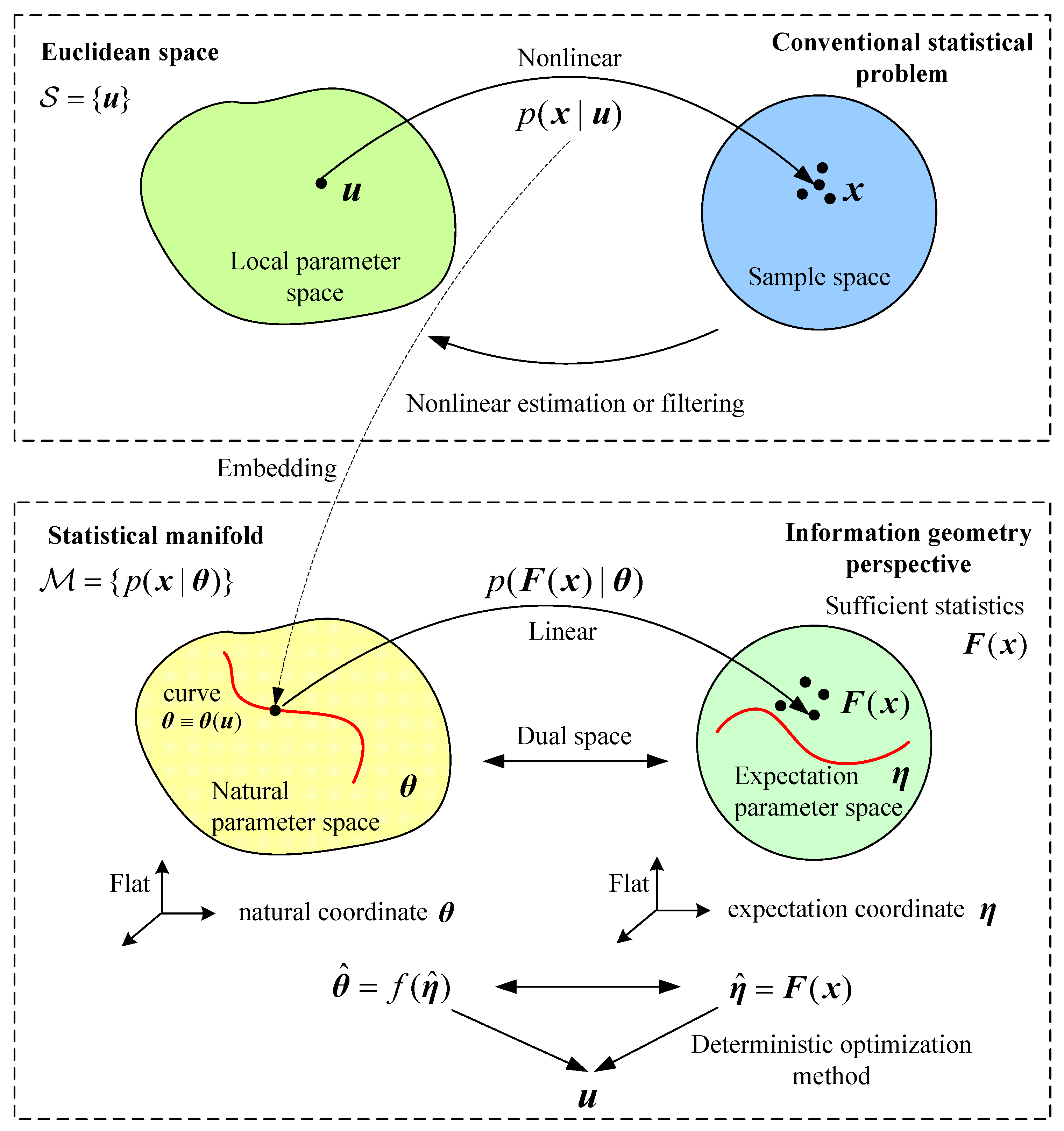
3.1. Principles of Information Geometry
3.2. Information Geometric Interpretation for Natural Gradient MLE
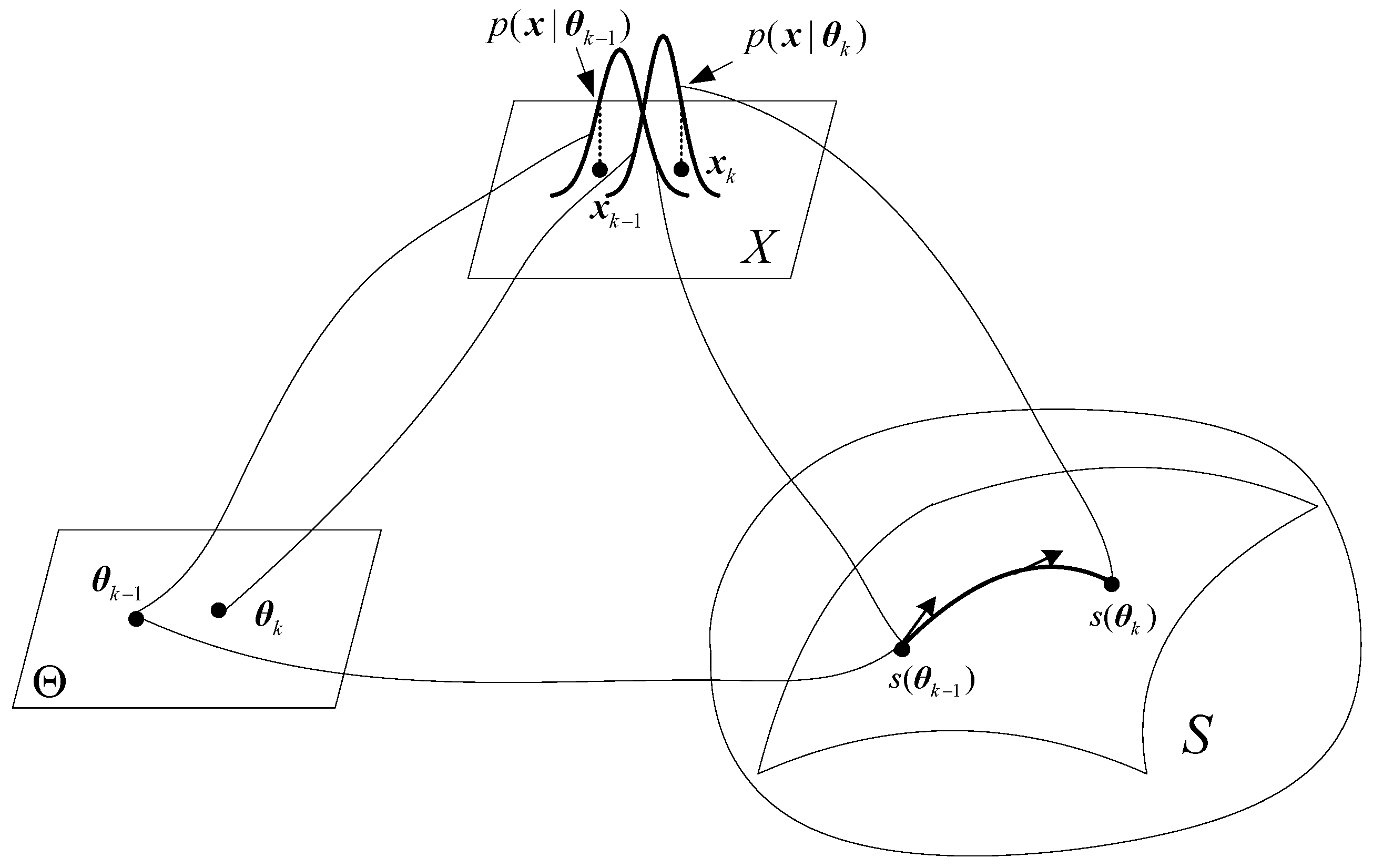
- Statistical problems can be described in manifolds in a number of ways. In the parameter estimation problems as we have discussed here the parameter belongs to a curved manifold, whereas the observations may lie on an enveloping manifold. The filtering process is thus implemented by means of projection in the manifolds.
- The iterative estimator is optimal in the MLE sense as the filtering itself involves no information loss. The stochastic filtering problem becomes an optimization problem defined over a statistical manifold.
- As seen from Algorithm 1, the algorithm implementation is relatively simple and straightforward by distribution reparameterization and operating in the dual flat manifolds. Though a Newton method-based MLE estimator can be derived directly via the likelihood. However, in most cases the operation is not trivial.
- The initial guess is important to facilitate convergence of the estimator to the true value. This can be varied and such initial value sampling may provide more certainty about reaching a global minimum. This has not been examined here.
4. Examples of Implementation of Natural Gradient MLE
4.1. An One Parameter Estimation Example of Curved Gaussian Distribution
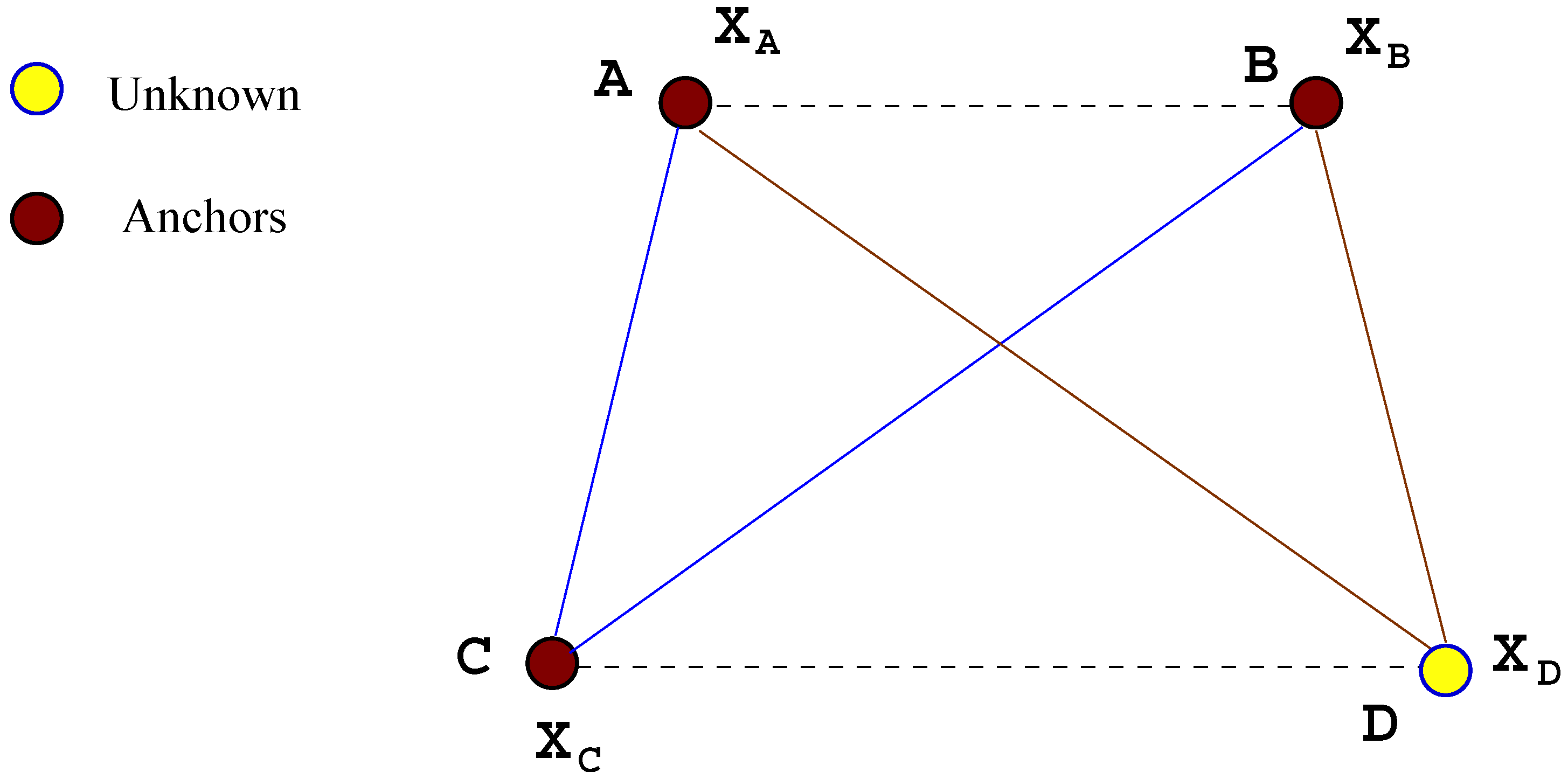
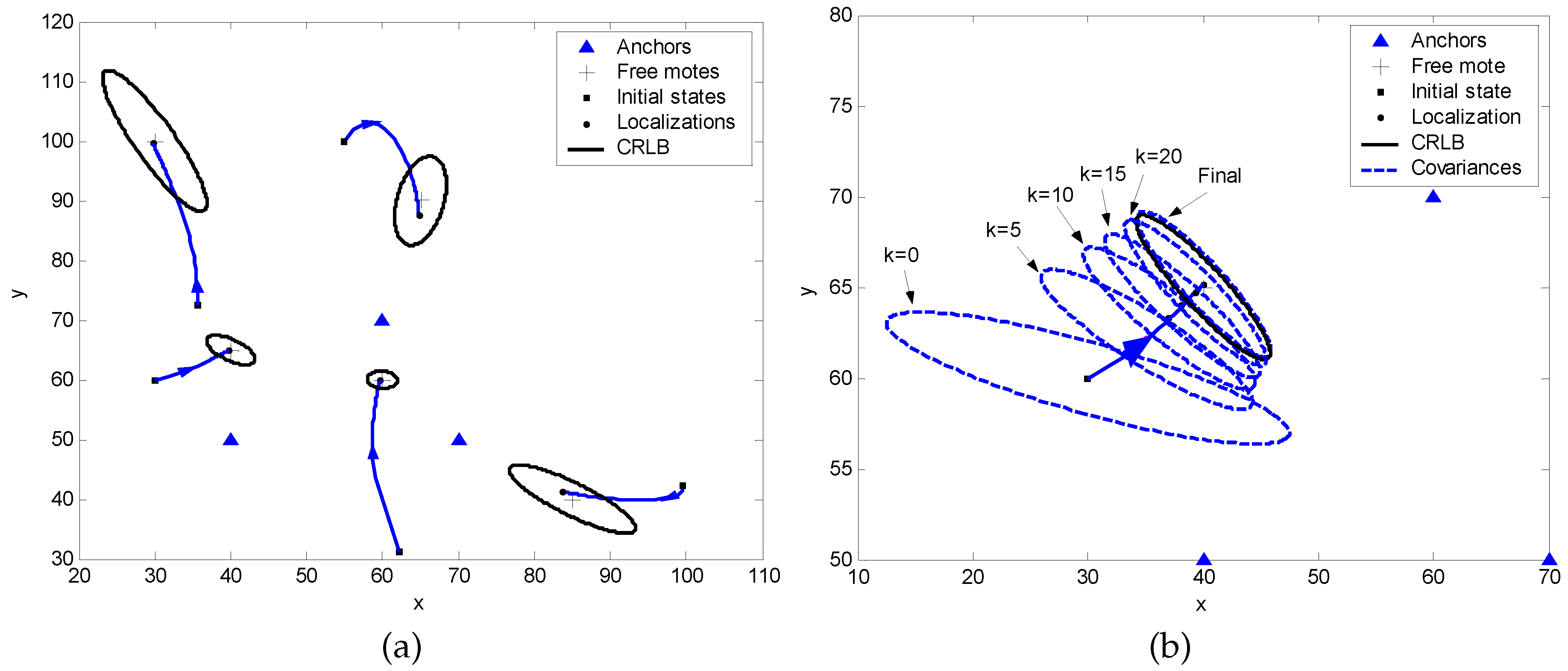
4.2. A Mote Localization Example via RIPS Measurements
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rao, C.R. Information and accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- Chentsov, N.N. Statistical Decision Rules and Optimal Inference; Leifman, L.J., Ed.; Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 1982; Volume 53. [Google Scholar]
- Efron, B. Defining the curvature of a statistical problem (with applications to second order efficiency). Ann. Stat. 1975, 3, 1189–1242. [Google Scholar] [CrossRef]
- Efron, B. The geometry of exponential families. Ann. Stat. 1978, 6, 362–376. [Google Scholar] [CrossRef]
- Amari, S. Differential geometry of curved exponential families-curvatures and information loss. Ann. Stat. 1982, 10, 357–385. [Google Scholar] [CrossRef]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; Kobayashi, S., Takesaki, M., Eds.; Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 2000; Volume 191. [Google Scholar]
- Amari, S. Information geometry of statistical inference—An overview. In Proceedings of the IEEE Information Theory Workshop, Bangalore, India, 20–25 October 2002. [Google Scholar]
- Smith, S.T. Covariance, subspace, and intrinsic Cramér–Rao bounds. IEEE Trans. Signal Process. 2005, 53, 1610–1630. [Google Scholar] [CrossRef]
- Srivastava, A. A Bayesian approach to geometric subspace estimation. IEEE Trans. Signal Process. 2000, 48, 1390–1400. [Google Scholar] [CrossRef]
- Srivastava, A.; Klassen, E. Bayesian and geometric subspace tracking. Adv. Appl. Probab. 2004, 36, 43–56. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Patrangenaru, V. Nonparametric estimation of location and dispersion on Riemannian manifolds. J. Stat. Plan. Inference 2002, 108, 23–35. [Google Scholar] [CrossRef]
- Richardson, T. The geometry of turbo-decoding dynamics. IEEE Trans. Inf. Theory 2000, 46, 9–23. [Google Scholar] [CrossRef]
- Ikeda, S.; Tanaka, T.; Amari, S. Information geometry of turbo and low-density parity-check codes. IEEE Trans. Inf. Theory 2004, 50, 1097–1114. [Google Scholar] [CrossRef]
- Haenggi, M. A geometric interpretation of fading in wireless networks: Theory and application. IEEE Trans. Inf. Theory 2008, 54, 5500–5510. [Google Scholar] [CrossRef]
- Westover, M.B. Asymptotic geometry of multiple hypothesis testing. IEEE Trans. Inf. Theory 2008, 54, 3327–3329. [Google Scholar] [CrossRef]
- Li, Q.; Georghiades, C.N. On a geometric view of multiuser detection for synchronous DS/CDMA channels. IEEE Trans. Inf. Theory 2000, 46, 2723–2731. [Google Scholar]
- Cheng, Y.; Wang, X.; Moran, B. Sensor network performance evaluation in statistical manifolds. In Proceedings of the 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010. [Google Scholar]
- Cheng, Y.; Wang, X.; Caelli, T.; Li, X.; Moran, B. On information resolution of radar systems. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3084–3102. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Y.; Moran, B. Bearings-only tracking analysis via information geometry. In Proceedings of the 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010. [Google Scholar]
- Wang, X.; Cheng, Y.; Morelande, M.; Moran, B. Bearings-only sensor trajectory scheduling using accumulative information. In Proceedings of the International Radar Symposium, Leipzig, Germany, 7–9 September 2011. [Google Scholar]
- Altun, Y.; Hofmann, T.; Smola, A.J.; Hofmann, T. Exponential families for conditional random fields. In Proceedings of the 20th Annual Conference on Uncertainty in Artificial Intelligence, Banff, AB, Canada, 7–11 July 2004. [Google Scholar]
- Amari, S.; Douglas, S.C. Why natural gradient? In Proceedings of the IEEE International Conference on Acoustics Speech Signal Process, Seattle, WA, USA, 12–15 May 1998. [Google Scholar]
- Manton, J.H. On the role of differential geometry in signal processing. In Proceedings of the IEEE International Conference on Acoustics Speech Signal Process, Philadelphia, PA, USA, 18–23 March 2005. [Google Scholar]
- Amari, S. Information geometry on hierarchy of probability distributions. IEEE Trans. Inf. Theory 2001, 47, 1701–1711. [Google Scholar] [CrossRef]
- Brun, A.; Knutsson, H. Tensor glyph warping-visualizing metric tensor fields using Riemannian exponential maps. In Visualization and Processing of Tensor Fields: Advances and Perspectives, Mathematics and Visualization; Laidlaw, D.H., Weickert, J., Eds.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Maroti, M.; Kusy, B.; Balogh, G.; Volgyesi, P.; Molnar, K.; Nadas, A.; Dora, S.; Ledeczi, A. Radio Interferometric Positioning; Tech. Rep. ISIS-05-602; Institute for Software Integrated Systems, Vanderbilt University: Nashville, TN, USA, 2005. [Google Scholar]
- Kusy, B.; Ledeczi, A.; Maroti, M.; Meertens, L. Node-density independent localization. In Proceedings of the 5th International Conference on Information Processing in Sensor Networks, Nashville, TN, USA, 19–21 April 2006. [Google Scholar]
- Wang, X.; Moran, B.; Brazil, M. Hyperbolic positioning using RIPS measurements for wireless sensor networks. In Proceedings of the 15th IEEE International Conference on Networks (ICON2007), Adelaide, Australia, 19–21 November 2007. [Google Scholar]
- Scala, B.F.; Wang, X.; Moran, B. Node self-localisation in large scale sensor networks. In Proceedings of the International Conference on Information, Decision and Control (IDC 2007), Adelaide, Australia, 11–14 February 2007. [Google Scholar]
- Yang, Z.; Laaksonen, J. Principal whitened gradient for information geometry. Neural Netw. 2008, 21, 232–240. [Google Scholar] [CrossRef] [PubMed]


| Measure | Results |
|---|---|
| Number of Monte Carlo runs | |
| Standard deviation of sensor noise | m |
| Location of the free mote | |
| CRLB for estimating the state | |
| Sample mean of the estimator | |
| Sample covariance of the estimator | Cov |
| Average RMS location error | m |
| Number of iterations M | , when m |
| (—iteration stopping threshold) | , when m |
| (—learning rate) | , when m |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Wang, X.; Moran, B. Optimal Nonlinear Estimation in Statistical Manifolds with Application to Sensor Network Localization. Entropy 2017, 19, 308. https://doi.org/10.3390/e19070308
Cheng Y, Wang X, Moran B. Optimal Nonlinear Estimation in Statistical Manifolds with Application to Sensor Network Localization. Entropy. 2017; 19(7):308. https://doi.org/10.3390/e19070308
Chicago/Turabian StyleCheng, Yongqiang, Xuezhi Wang, and Bill Moran. 2017. "Optimal Nonlinear Estimation in Statistical Manifolds with Application to Sensor Network Localization" Entropy 19, no. 7: 308. https://doi.org/10.3390/e19070308







