On Unsteady Three-Dimensional Axisymmetric MHD Nanofluid Flow with Entropy Generation and Thermo-Diffusion Effects on a Non-Linear Stretching Sheet
Abstract
:1. Introduction
2. Problem Formulation
3. Entropy Generation Analysis
4. Method of Solution
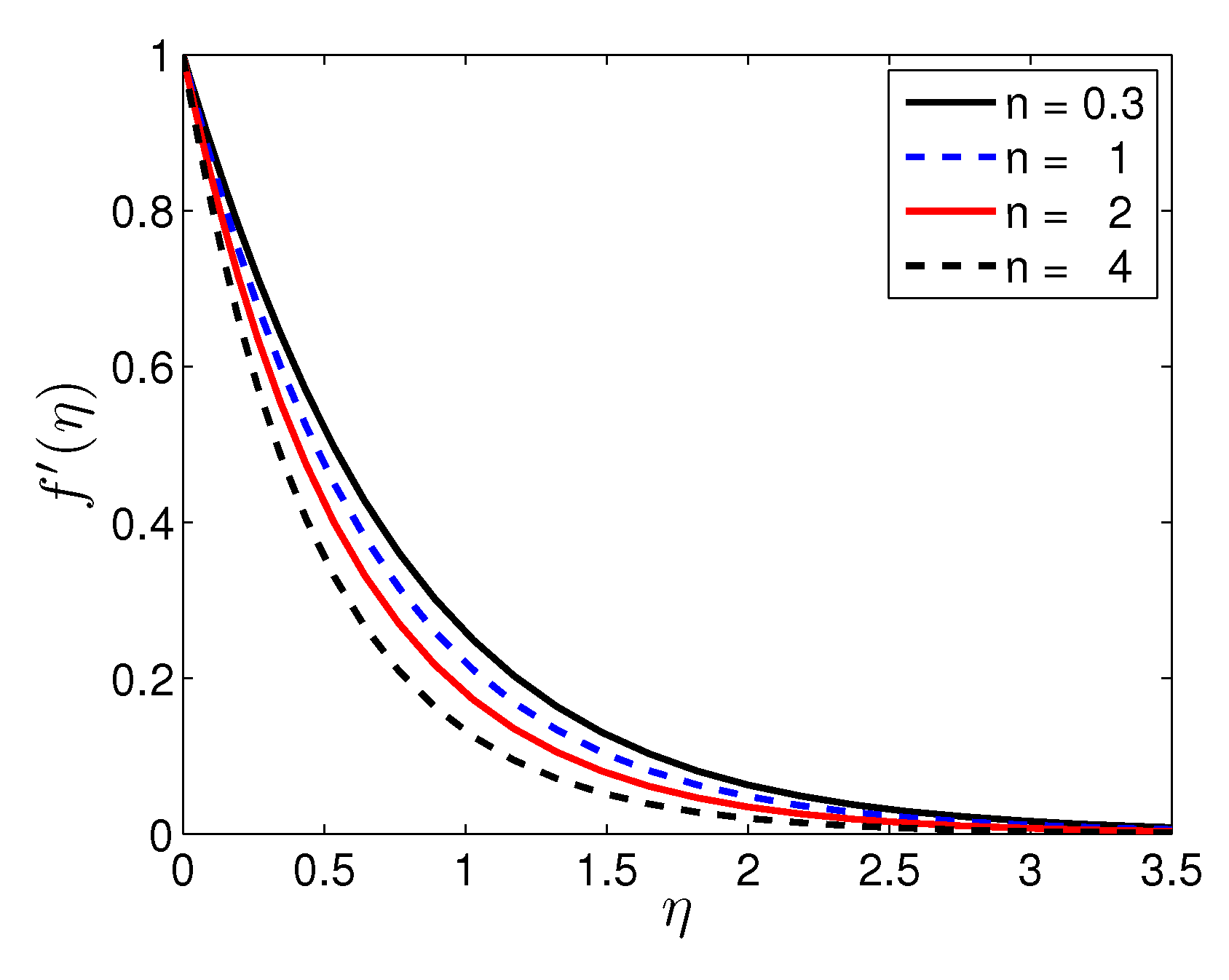
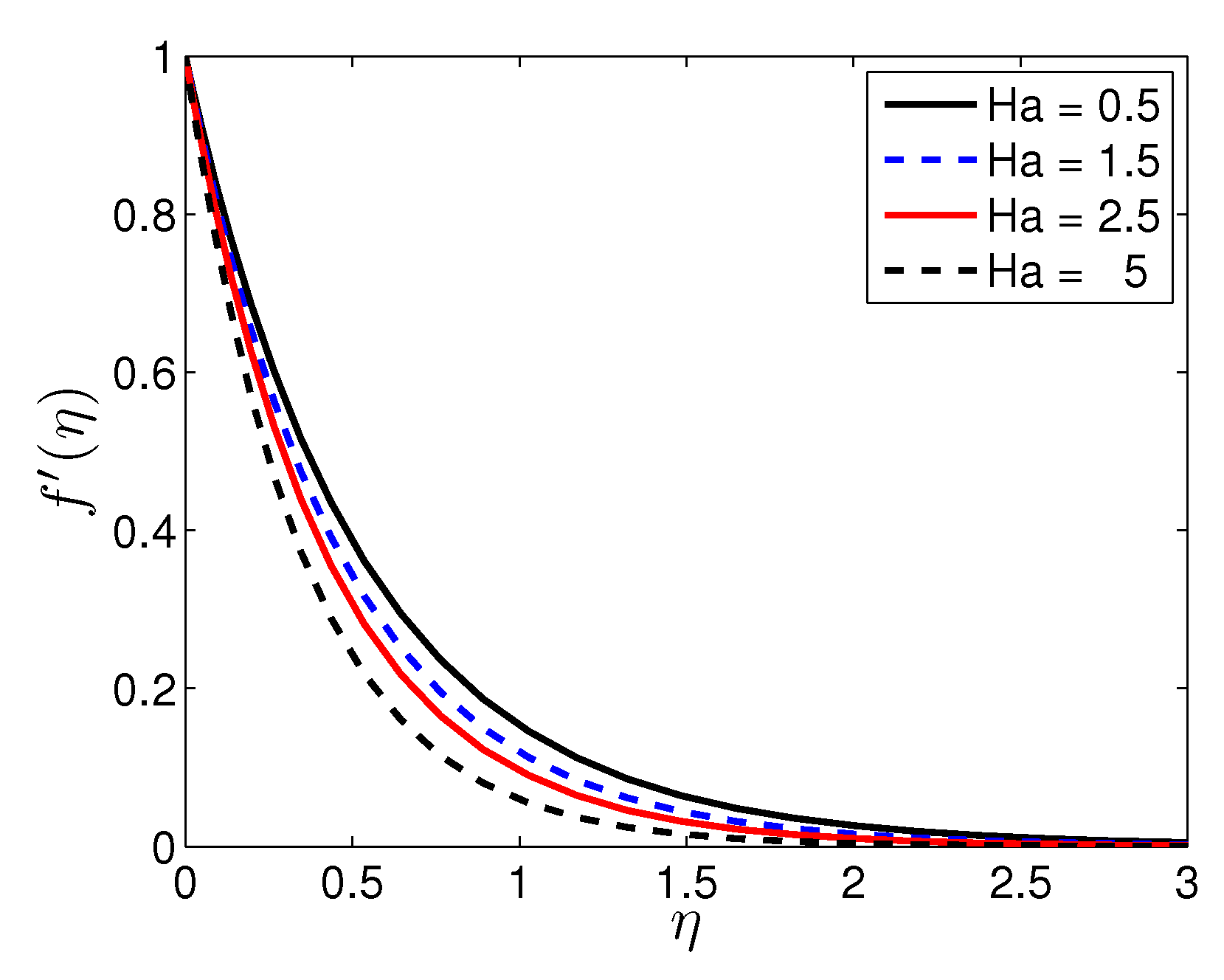
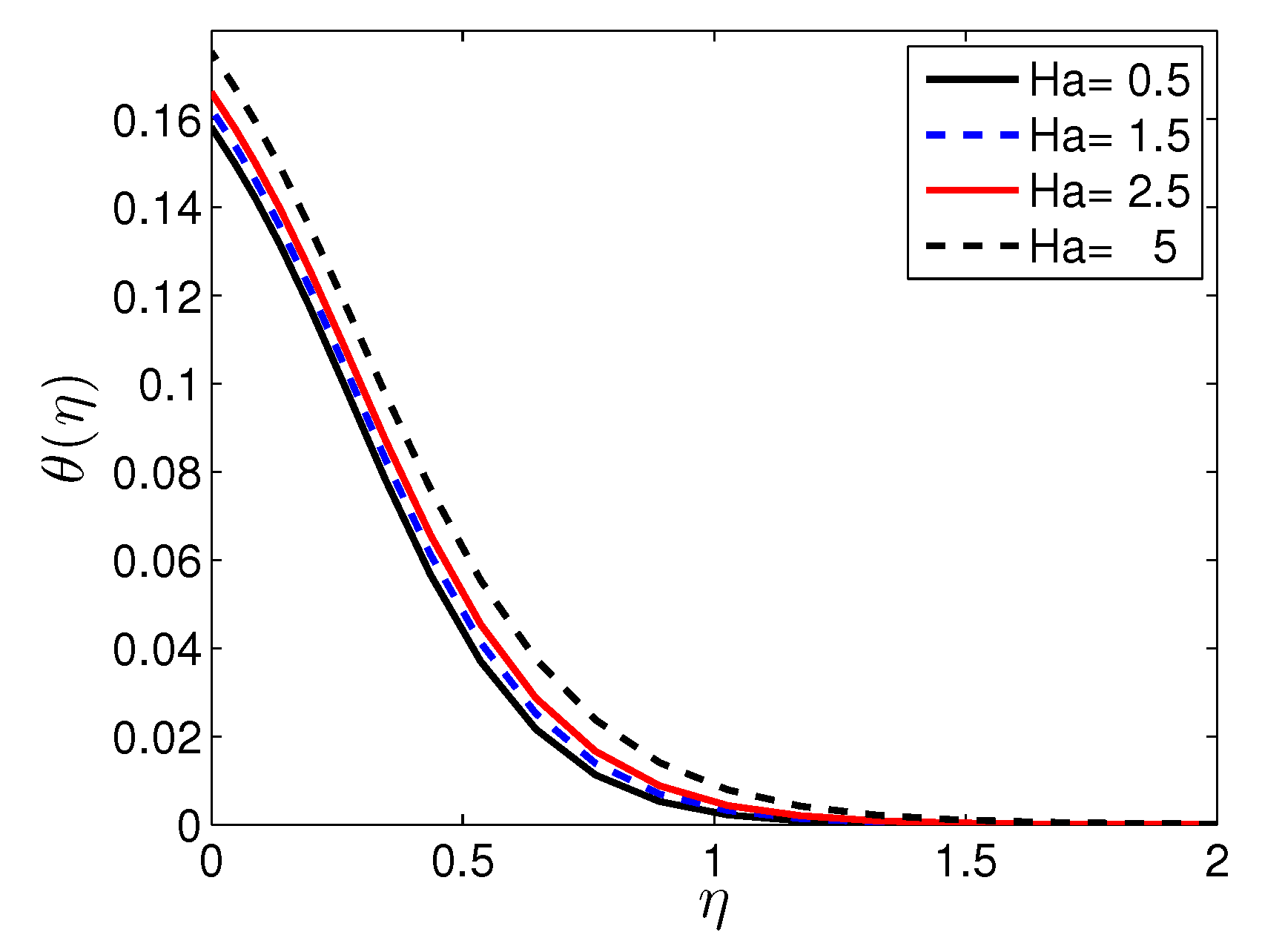
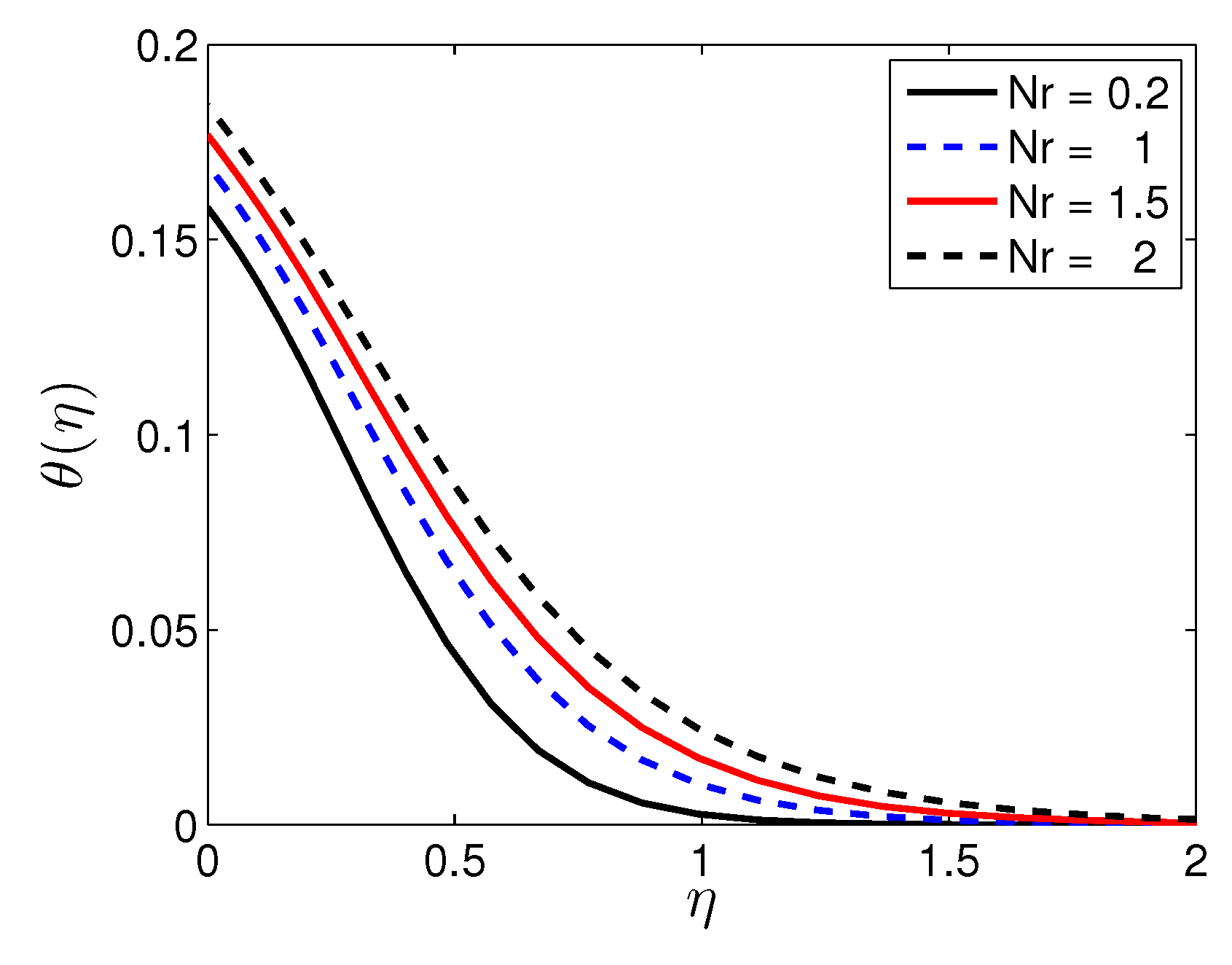
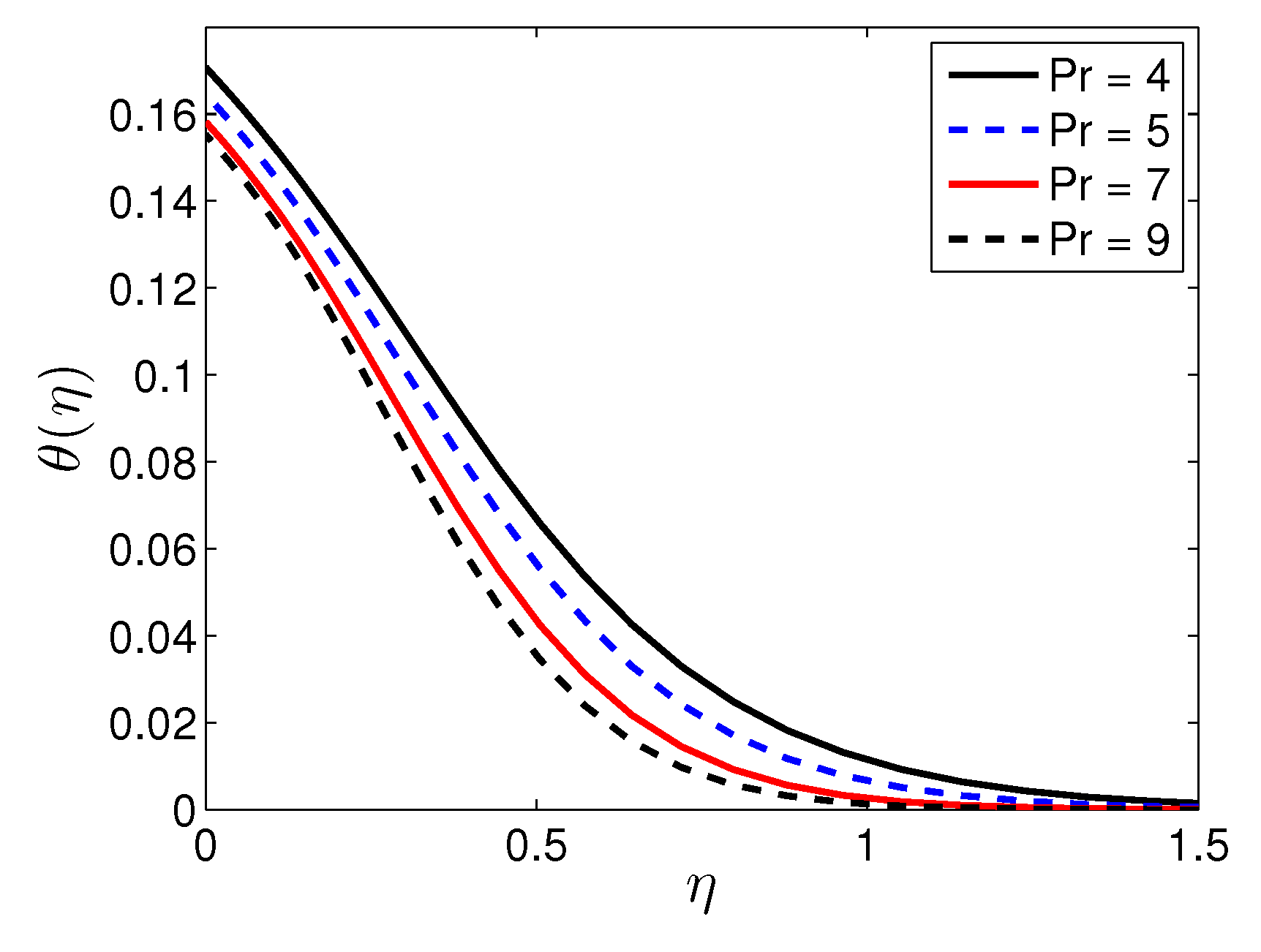
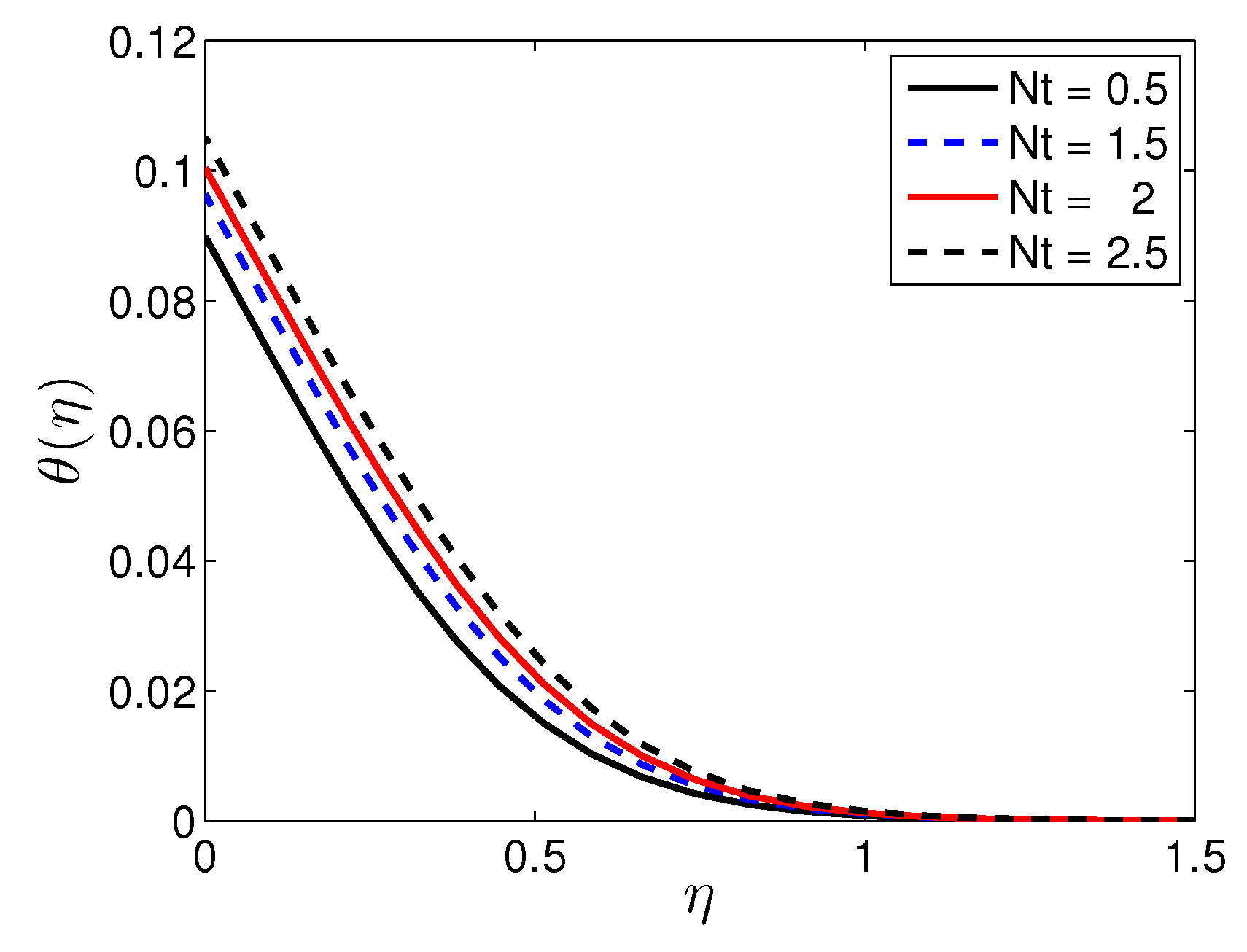
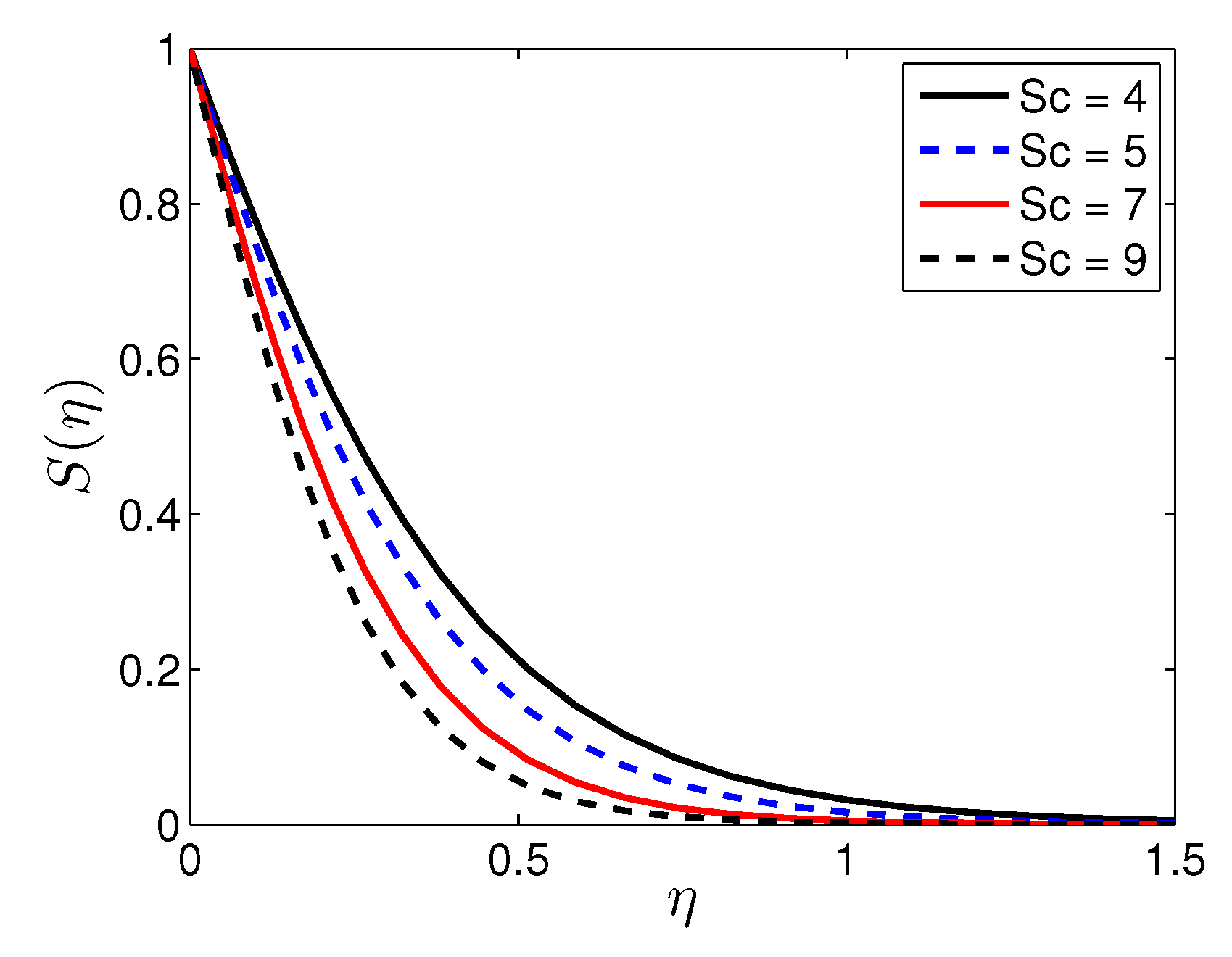
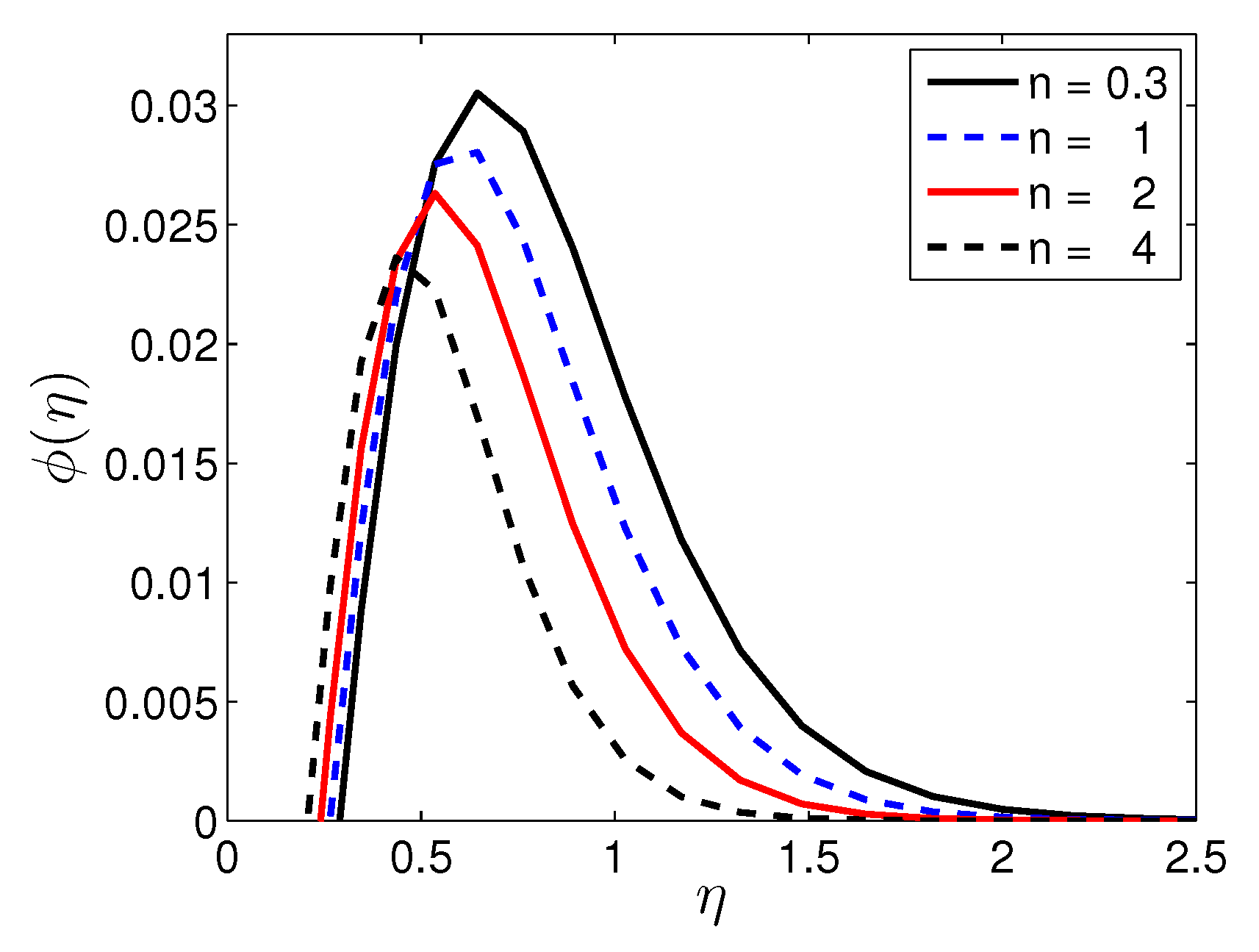
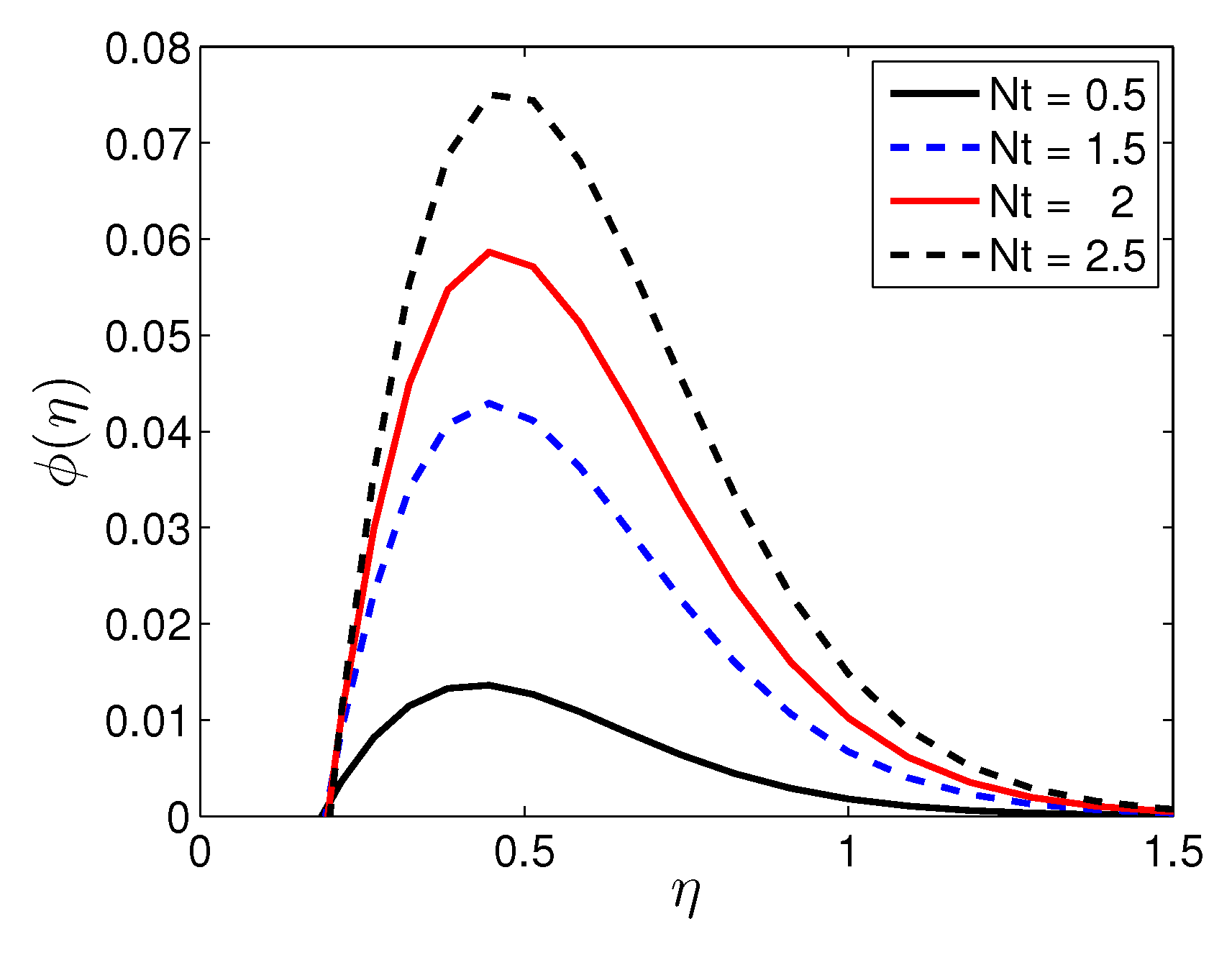
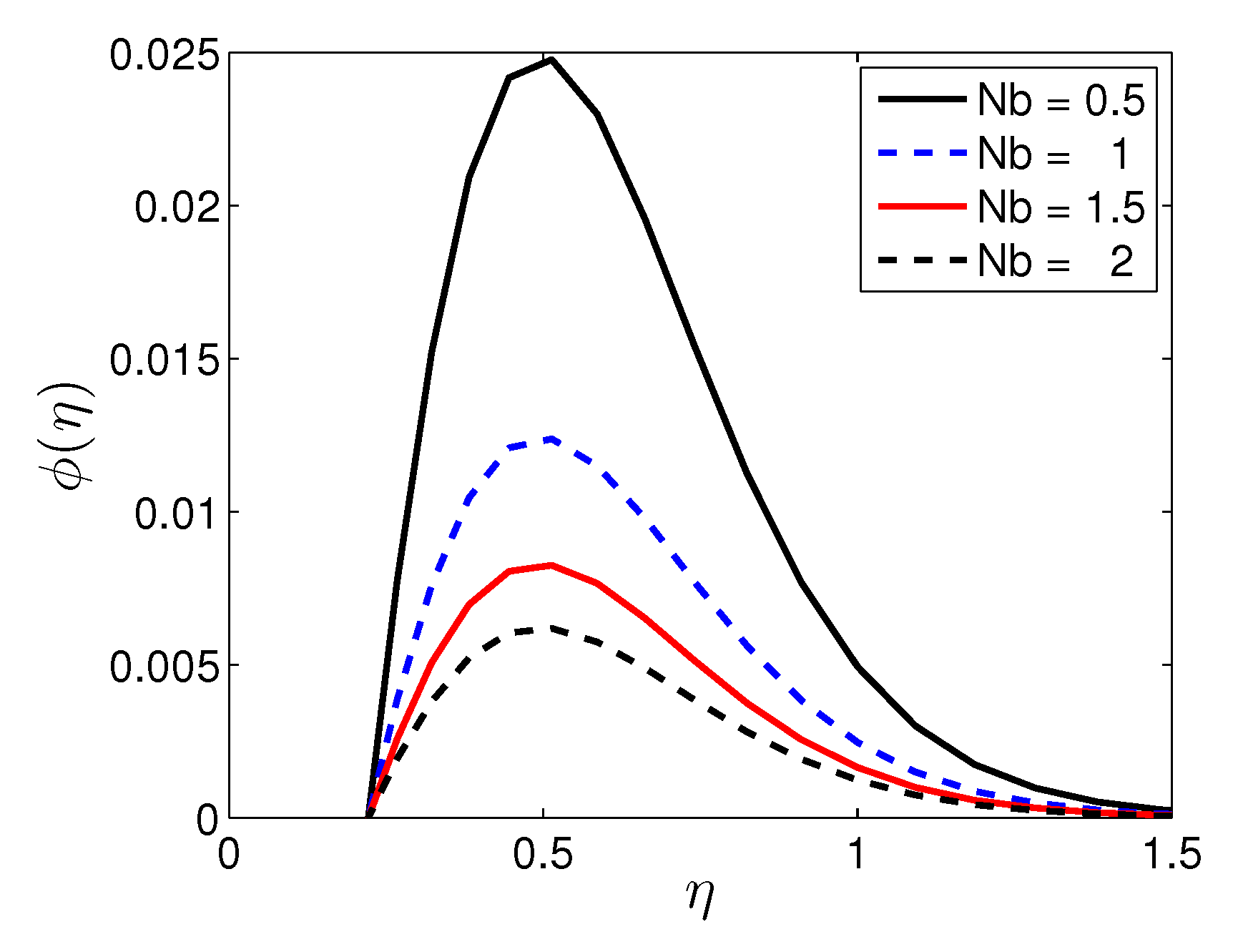
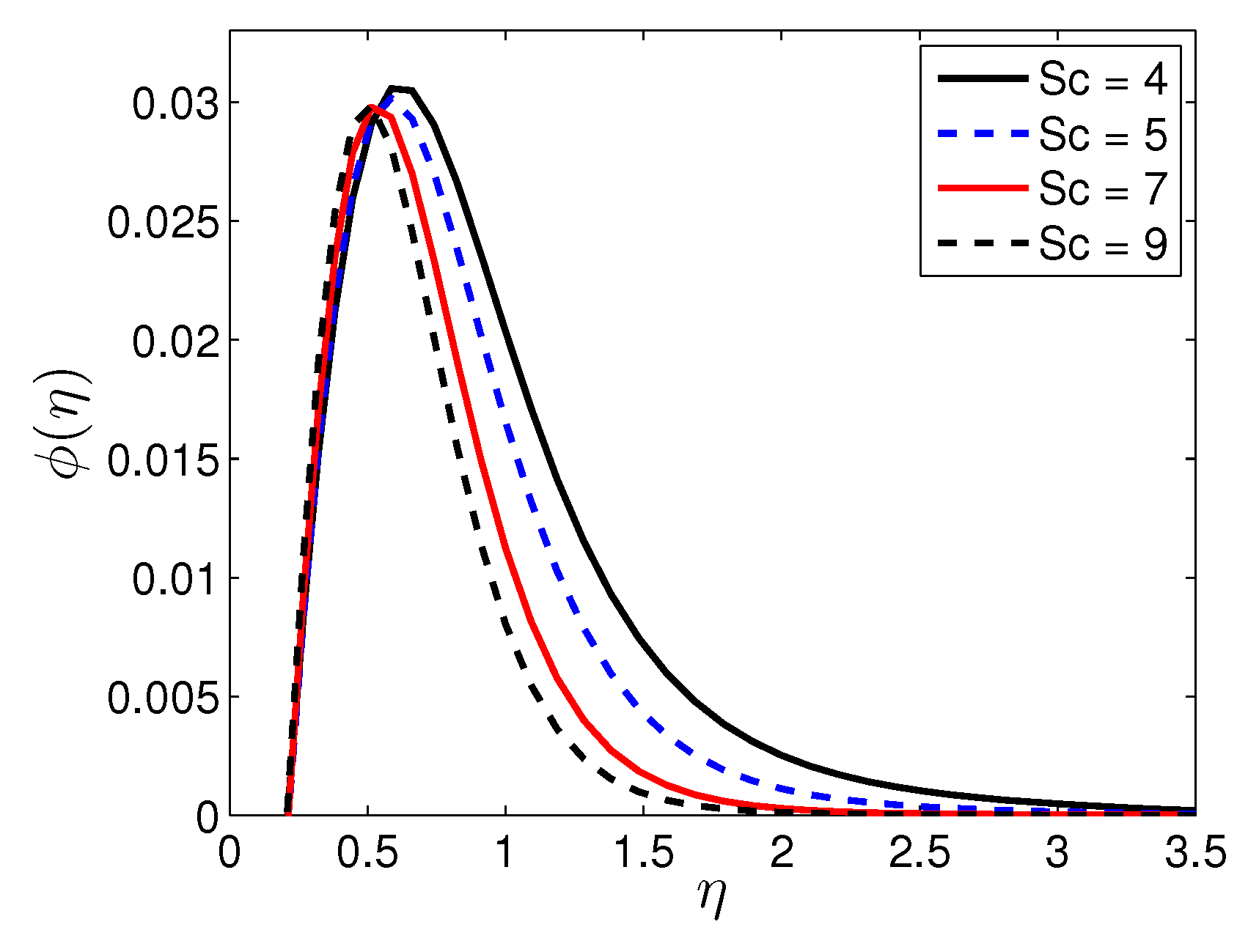
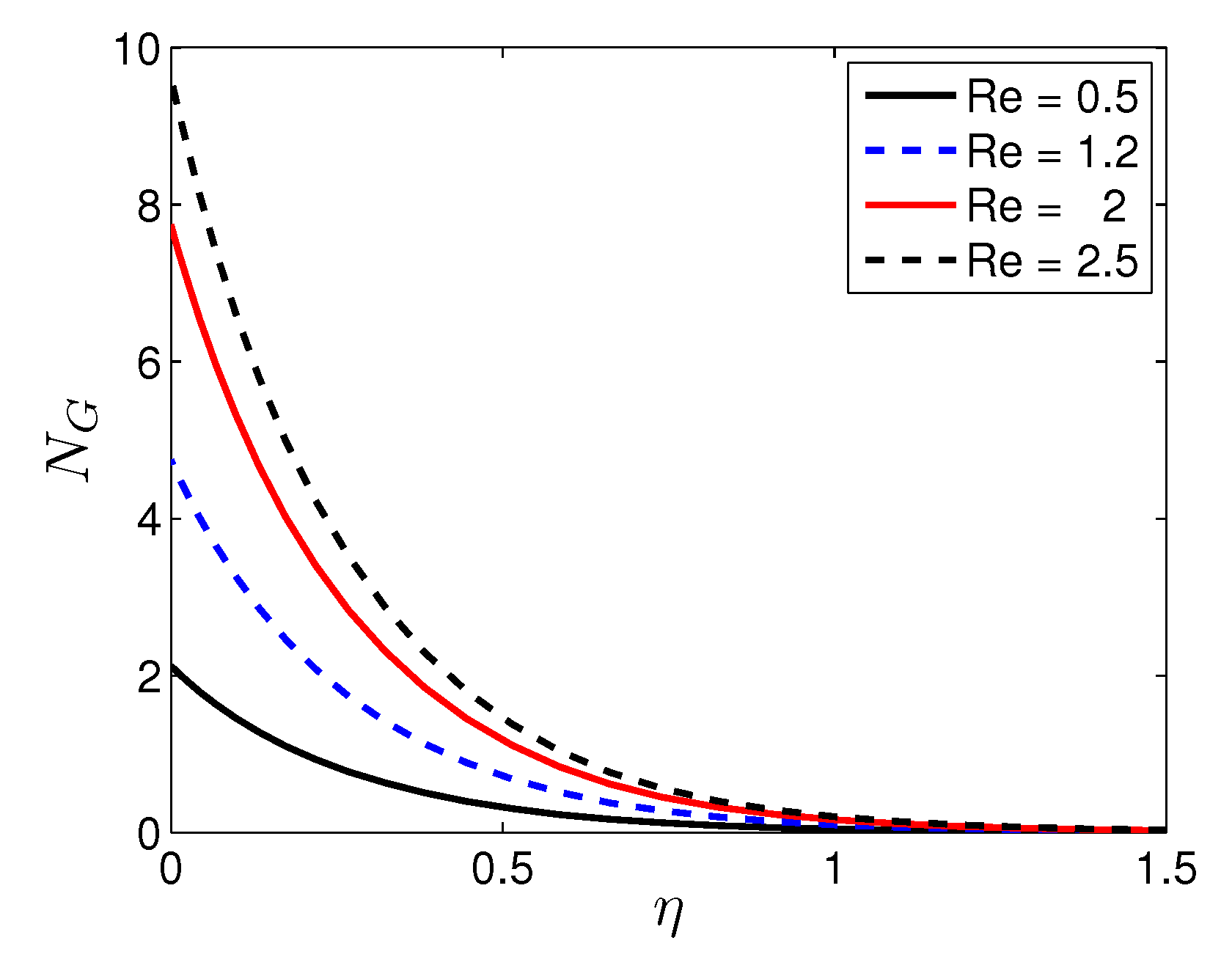
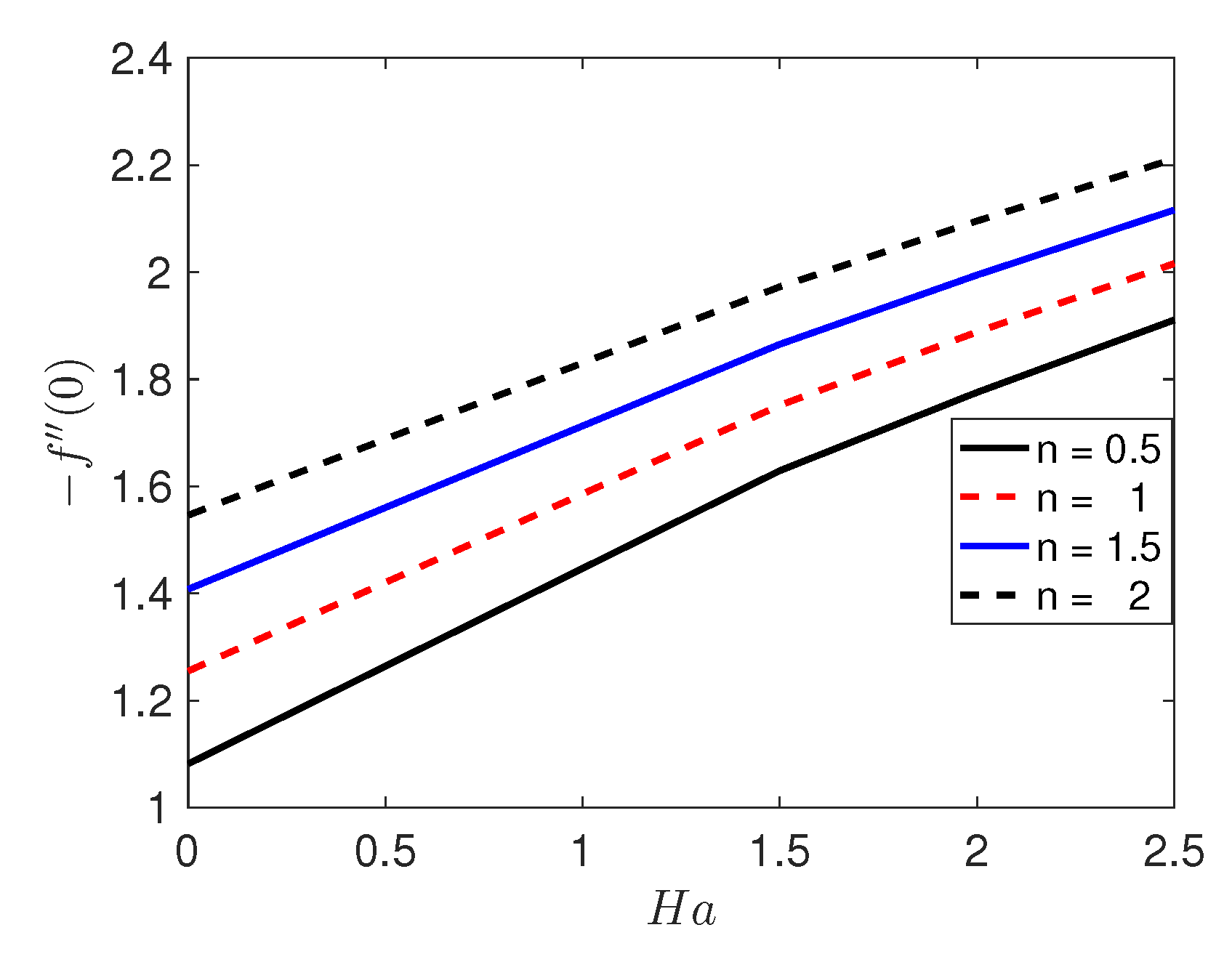
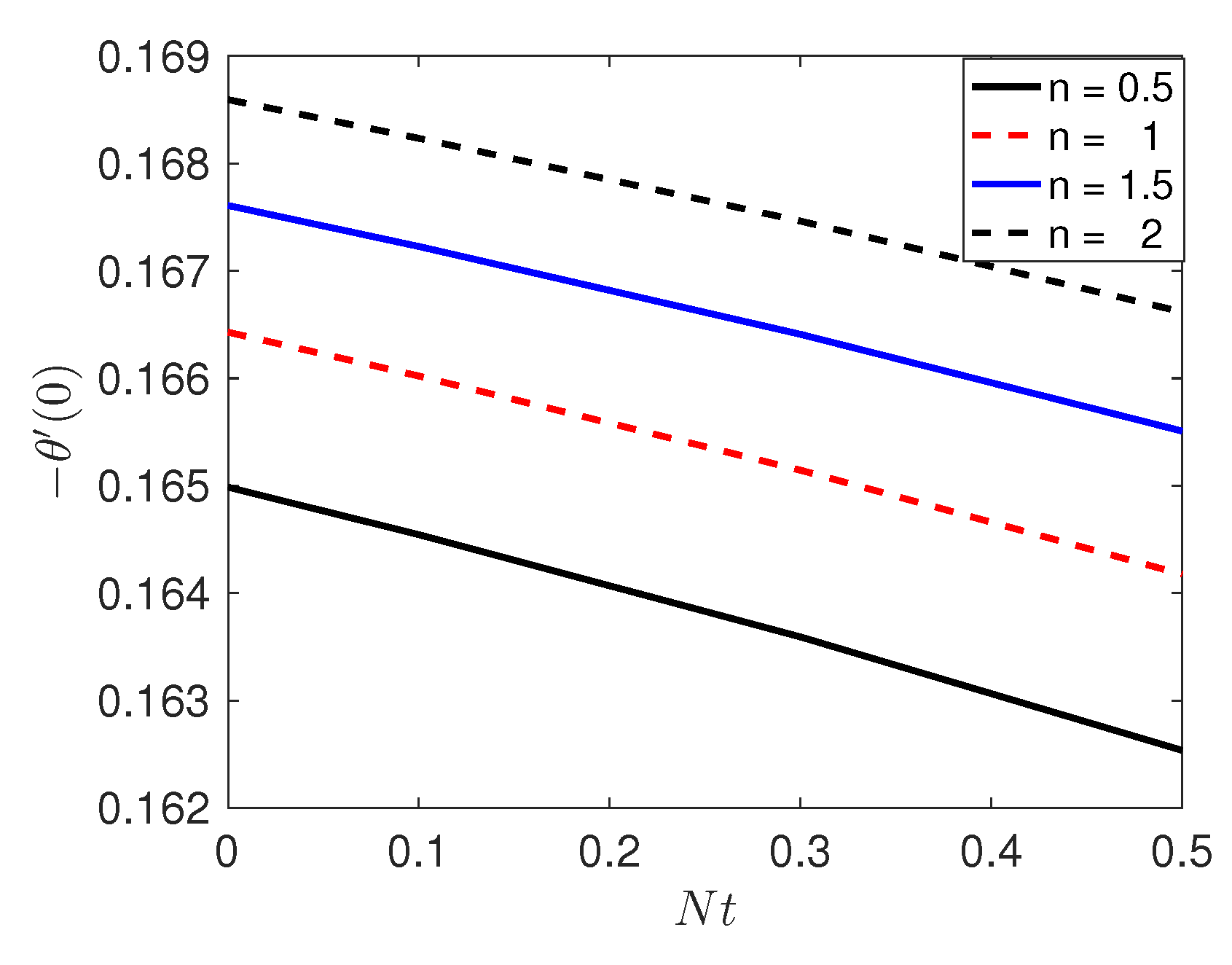
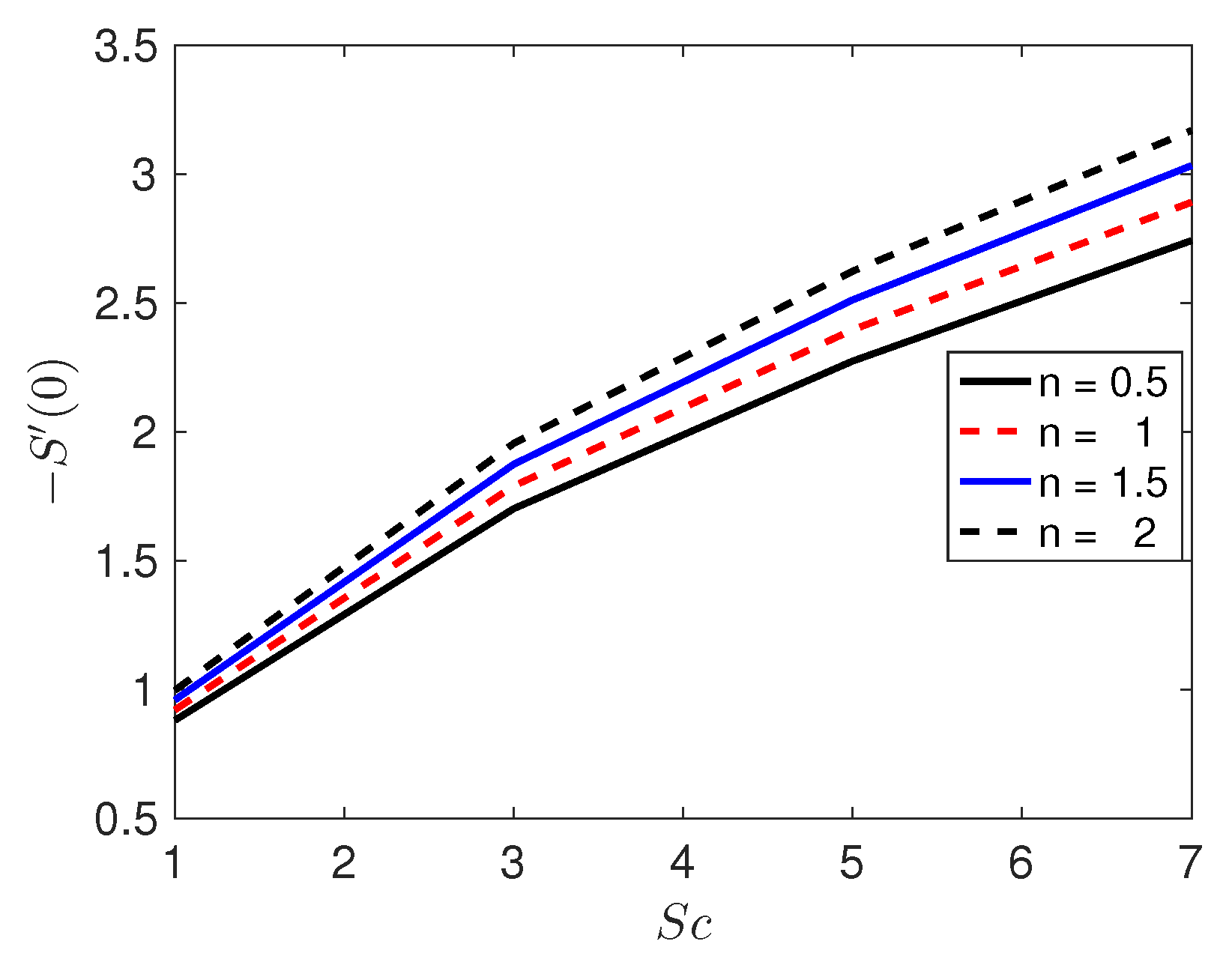
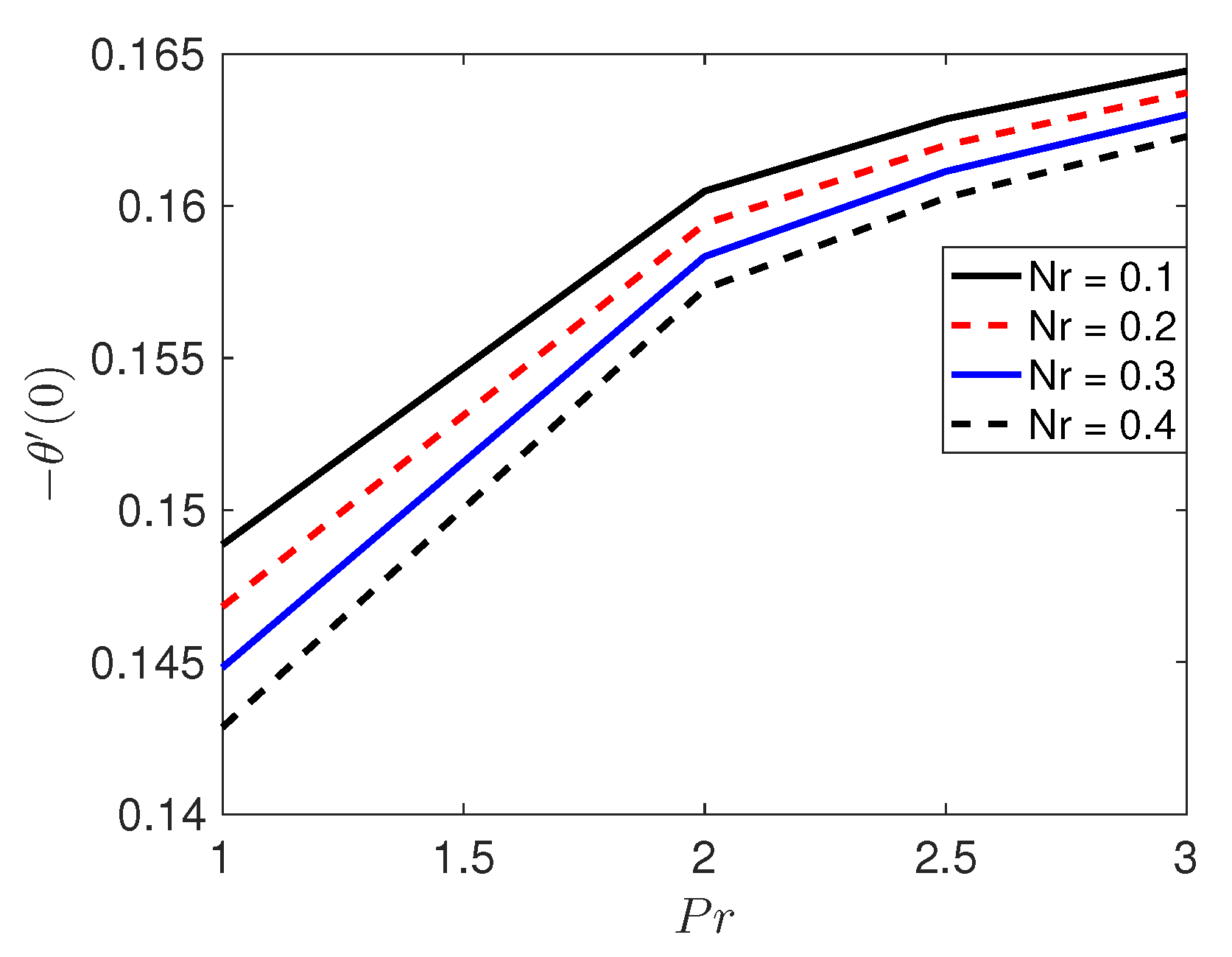
5. Results and Discussion
6. Conclusions
- The heat transfer rate increases with increasing sheet stretching.
- An increase in the Reynolds number and the Brinkman number corresponds to a significant increase in the entropy generation number. Therefore, it can be ascertained that the entropy generation number is highly affected by viscous dissipation when the nanofluid flow has a large Reynolds number.
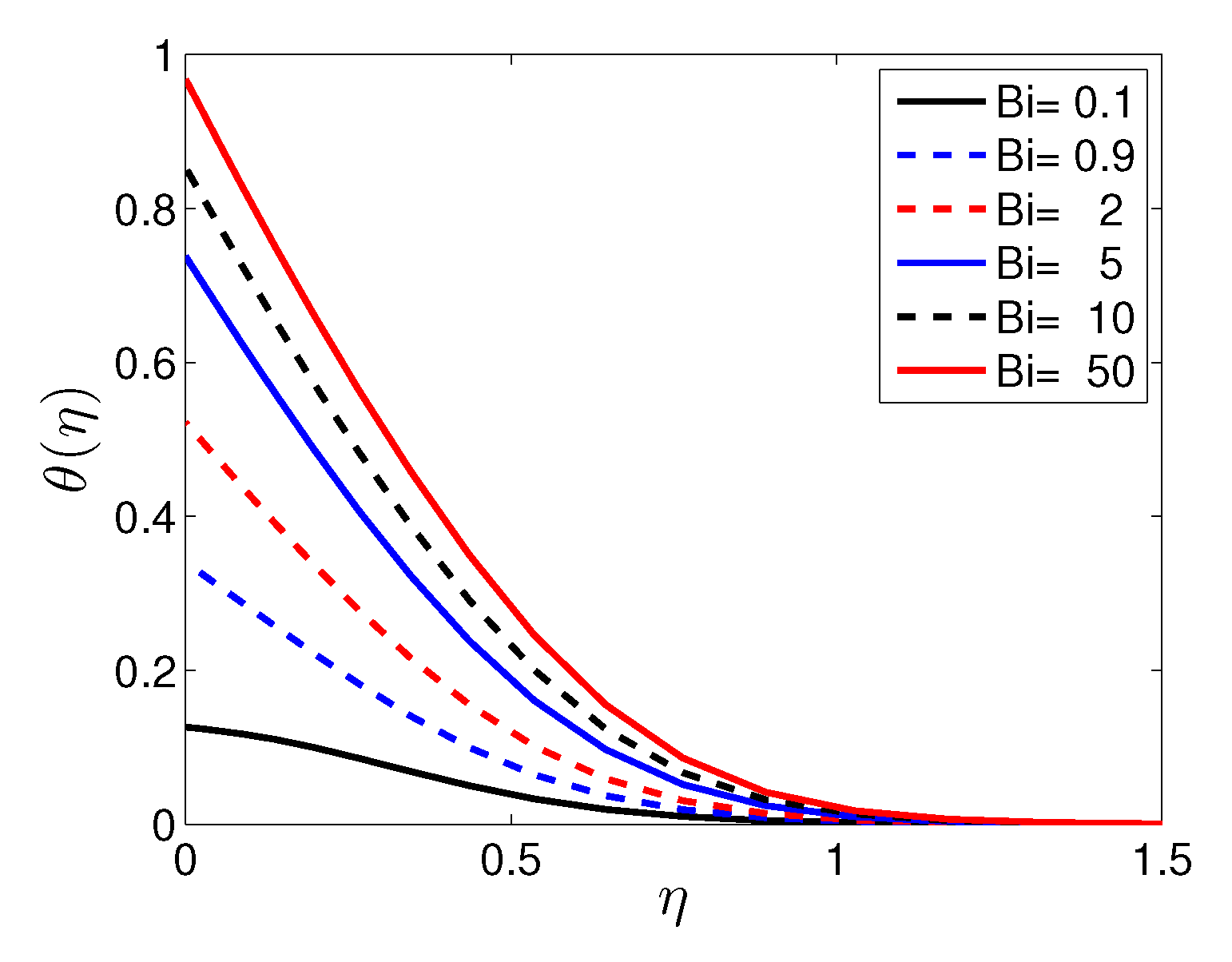
- An increase in the Biot and Hartmann numbers corresponds to a significant increase in the entropy generation number in the vicinity of the sheet surface. The significance of the Biot and Hartmann numbers gradually fades with distance from the sheet.
- The entropy generation rate can be minimized by controlling the physical parameters.
- The number of collocation points has a significant influence on the accuracy of the solutions.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| cylindrical polar coordinate axes | |
| magnetic field strength (kg·sA) | |
| u | velocity in radial direction (m·s) |
| constants | |
| w | velocity in axial direction (m·s) |
| kinematic viscosity (ms) | |
| T | temperature variable (K) |
| electrical conductivity (m) | |
| temperature of fluid at sheet (K) | |
| density of fluid (kg·m) | |
| ambient temperature of fluid (K) | |
| thermal diffusion of fluid (ms) | |
| C | solute concentration of fluid (kg·m) |
| solute concentration at wall (kg·m) | |
| solute concentration far away from the disk (kg·m) | |
| nanoparticle concentration | |
| nanoparticle concentration at wall | |
| nanoparticle concentration far away from the disk | |
| ratio of nanoparticle heat capacity | |
| Brownian mention coefficient (kg·ms) | |
| Thermophoretic diffusion coefficient (kg·msK) | |
| Dufour diffusion coefficient | |
| specific heat (msK) | |
| thermal conductivity (W·mK) | |
| radiative heat flux (kg·m) | |
| solute diffusion coefficient | |
| Soret diffusion coefficient | |
| R | chemical reaction parameter |
| heat capacity of the nanoparticle | |
| heat capacity of fluid | |
| Stefan–Boltzmann constant | |
| mean absorption coefficient | |
| constants | |
| constants | |
| heat transfer coefficient (W·m K) | |
| Biot number | |
| dimensionless variable | |
| dimensionless temperature | |
| S | dimensionless solute concentration |
| dimensionless nanoparticle concentration | |
| f | dimensionless velocity |
| A | unsteadiness parameter |
| Hartmann number | |
| thermal radiation parameter | |
| Prandtl number | |
| Brownian mention parameter | |
| Thermophoresis parameter | |
| Dufour parameter | |
| Schmidt number | |
| Soret parameter | |
| skin friction coefficient | |
| Nusselt number | |
| Sherwood number | |
| velocity of the stretching sheet | |
| Reynolds number | |
| heat flux (W·m) | |
| mass flux (kg·ms) | |
| volumetric entropy generation per unit length (W·m K) | |
| dimensionless entropy generation rate | |
| Brinkman number | |
| dimensionless parameter | |
| Hartmann number | |
| diffusive constant parameter | |
| difference between ()(K) |
References
- Dessie, H.; Kishan, N. Unsteady MHD flow of heat and mass transfer of nanofluids over stretching sheet with a non-uniform heat/source/sink considering viscous dissipation and chemical reaction. Int. J. Eng. Res. Afr. 2015, 14. [Google Scholar] [CrossRef]
- Chol, S. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. FED 1995, 231, 99–106. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Ahmed, N.; Goswami, J.; Barua, D. Effects of chemical reaction and radiation on an unsteady MHD flow past an accelerated infinite vertical plate with variable temperature and mass transfer. Indian J. Pure Appl. Math. 2013, 44, 443–466. [Google Scholar] [CrossRef]
- Ahmed, J.; Mahmood, T.; Iqbal, Z.; Shahzad, A.; Ali, R. Axisymmetric flow and heat transfer over an unsteady stretching sheet in power law fluid. J. Mol. Liq. 2016, 221, 386–393. [Google Scholar] [CrossRef]
- Mohammadiun, H.; Rahimi, A.; Kianifar, A. Axisymmetric stagnation-point flow and heat transfer of a viscous, compressible fluid on a cylinder with constant heat flux. Sci. Iran. 2013, 20, 185–194. [Google Scholar] [CrossRef]
- Xiao, B.; Yang, Y.; Chen, L. Developing a novel form of thermal conductivity of nanofluids with Brownian motion effect by means of fractal geometry. Powder Technol. 2013, 239, 409–414. [Google Scholar] [CrossRef]
- Cai, J.; Hu, X.; Xiao, B.; Zhou, Y.; Wei, W. Recent developments on fractal-based approaches to nanofluids and nanoparticle aggregation. Int. J. Heat Mass Transf. 2017, 105, 623–637. [Google Scholar] [CrossRef]
- Shankar, B.; Yirga, Y. Unsteady heat and mass transfer in MHD flow of nanofluids over stretching sheet with a non-uniform heat source/sink. Int. J. Math. Comput. Sci. Eng. 2013, 7, 1267–1275. [Google Scholar]
- Shahzad, A.; Ali, R.; Khan, M. On the exact solution for axisymmetric flow and heat transfer over a nonlinear radially stretching sheet. Chin. Phys. Lett. 2012, 29, 084705. [Google Scholar] [CrossRef]
- Ahmad, S.; Ashraf, M.; Syed, K. Effects of thermal radiation on MHD axisymmetric stagnation point flow and heat transfer of a micropolar fluid over a shrinking sheet. World Appl. Sci. J. 2011, 15, 835–848. [Google Scholar]
- Mabood, F.; Shafiq, A.; Hayat, T.; Abelman, S. Radiation effects on stagnation point flow with melting heat transfer and second order slip. Results Phys. 2017, 7, 31–42. [Google Scholar] [CrossRef]
- Prasad, K.; Vaidya, H.; Vajravelu, K.; Datti, P.; Umesh, V. Axisymmetric mixed convective MHD flow over a slender cylinder in the presence of chemically reaction. Int. J. Appl. Mech. Eng. 2016, 21, 121–141. [Google Scholar] [CrossRef]
- Sarada, K.; Shanker, B. The effect of chemical reaction on an unsteady MHD free convection flow past an infinite vertical porous plate with variable suction. Int. J. Eng. Mod. Res. 2013, 3, 725–735. [Google Scholar]
- Hunegnaw, A.; Kishan, N. Unsteady MHD heat and mass transfer flow over stretching sheet in porous medium with variable properties considering viscous dissipation and chemical reaction. Am. Chem. Sci. J. 2014, 4, 901–917. [Google Scholar] [CrossRef]
- Barik, R. Heat and Mass Transfer Effects on Unsteady MHD Flow through an Accelerated Isothermal Vertical Plate Embedded in Porous Medium in the Presence of Heat Source and Chemical Reaction. Eur. J. Adv. Eng. Technol. 2016, 3, 56–61. [Google Scholar]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.E.S. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy 2016, 18, 123. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bhatti, M.M.; Abbas, M.A.; Ali, M.E.S. Entropy generation on MHD blood flow of nanofluid due to peristaltic waves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.S.; Yang, Z. Entropy generation on MHD eyring—Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Rashidi, M.; Mohammadi, F.; Abbasbandy, S.; Alhuthali, M. Entropy generation analysis for stagnation point flow in a porous medium over a permeable stretching surface. J. Appl. Fluid Mech. 2015, 8, 753–765. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.S. Numerical simulation of entropy generation with thermal radiation on MHD Carreau nanofluid towards a shrinking sheet. Entropy 2016, 18, 200. [Google Scholar] [CrossRef]
- Freidoonimehr, N.; Rahimi, A.B. Comment on “Effects of thermophoresis and Brownian motion on nanofluid heat transfer and entropy generation” by M. Mahmoodi, Sh. Kandelousi, Journal of Molecular Liquids, 211 (2015) 15–24. J. Mol. Liq. 2016, 216, 99–102. [Google Scholar] [CrossRef]
- Agbaje, T.; Mondal, S.; Makukula, Z.; Motsa, S.; Sibanda, P. A new numerical approach to MHD stagnation point flow and heat transfer towards a stretching sheet. Ain Shams Eng. J. 2016, in press. [Google Scholar] [CrossRef]
- Kaladhar, K.; Motsa, S.; Srinivasacharya, D. Mixed Convection Flow of Couple Stress Fluid in a Vertical Channel with Radiation and Soret Effects. J. Appl. Fluid Mech. 2016, 9, 43–50. [Google Scholar]
- Nield, D.; Kuznetsov, A. The onset of convection in a horizontal nanofluid layer of finite depth: A revised model. Int. J. Heat Mass Transf. 2014, 77, 915–918. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Analytical and numerical solutions for axisymmetric flow of nanofluid due to non-linearly stretching sheet. Int. J. Non Linear Mech. 2015, 71, 22–29. [Google Scholar] [CrossRef]
- Sajid, M.; Hayat, T.; Asghar, S.; Vajravelu, K. Analytic solution for axisymmetric flow over a nonlinearly stretching sheet. Arch. Appl. Mech. 2008, 78, 127–134. [Google Scholar] [CrossRef]
- Pal, D. Heat and mass transfer in stagnation-point flow towards a stretching surface in the presence of buoyancy force and thermal radiation. Meccanica 2009, 44, 145–158. [Google Scholar] [CrossRef]
- Arikoglu, A.; Ozkol, I.; Komurgoz, G. Effect of slip on entropy generation in a single rotating disk in MHD flow. Appl. Energy 2008, 85, 1225–1236. [Google Scholar] [CrossRef]
- Bellman, R.E.; Kalaba, R.E. Quasilinearization and Nonlinear Boundary-Value Problems; RAND Corporation: New York, NY, USA, 1965. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.M.; Thomas, A., Jr. Spectral Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Oxford, UK, 2000. [Google Scholar]
- Motsa, S.; Sibanda, P.; Shateyi, S. On a new quasi-linearization method for systems of nonlinear boundary value problems. Math. Methods Appl. Sci. 2011, 34, 1406–1413. [Google Scholar] [CrossRef]
- Rashidi, M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]

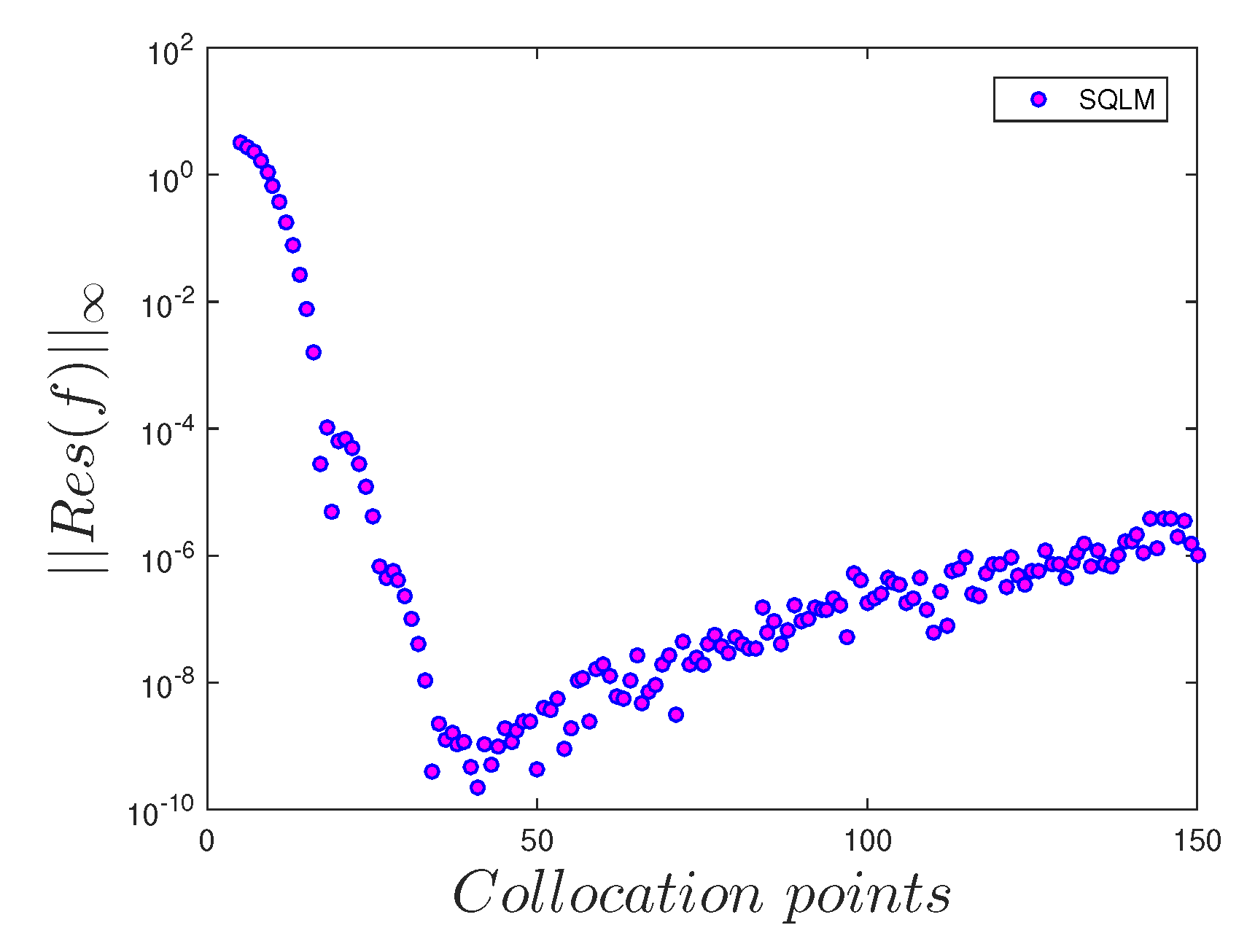
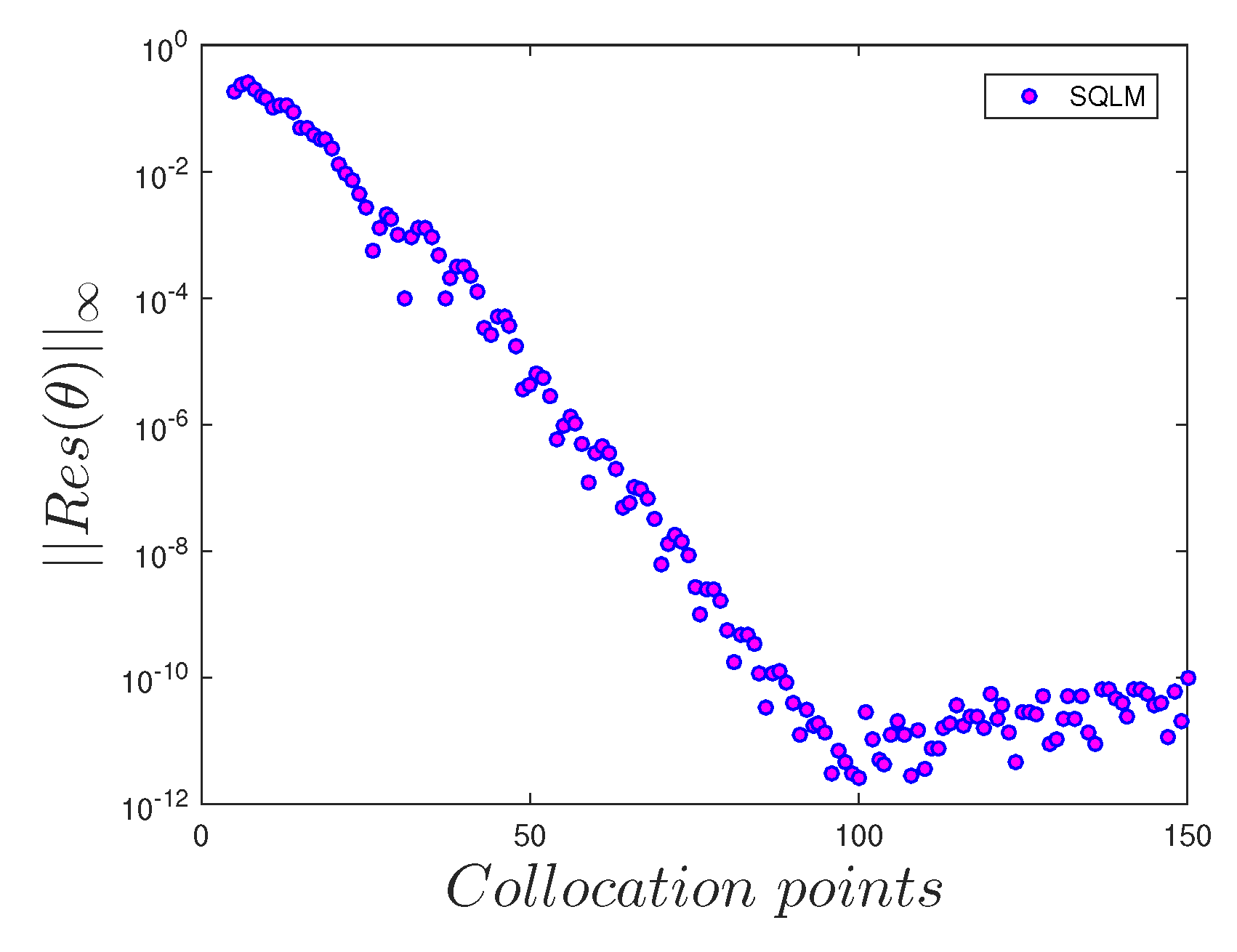
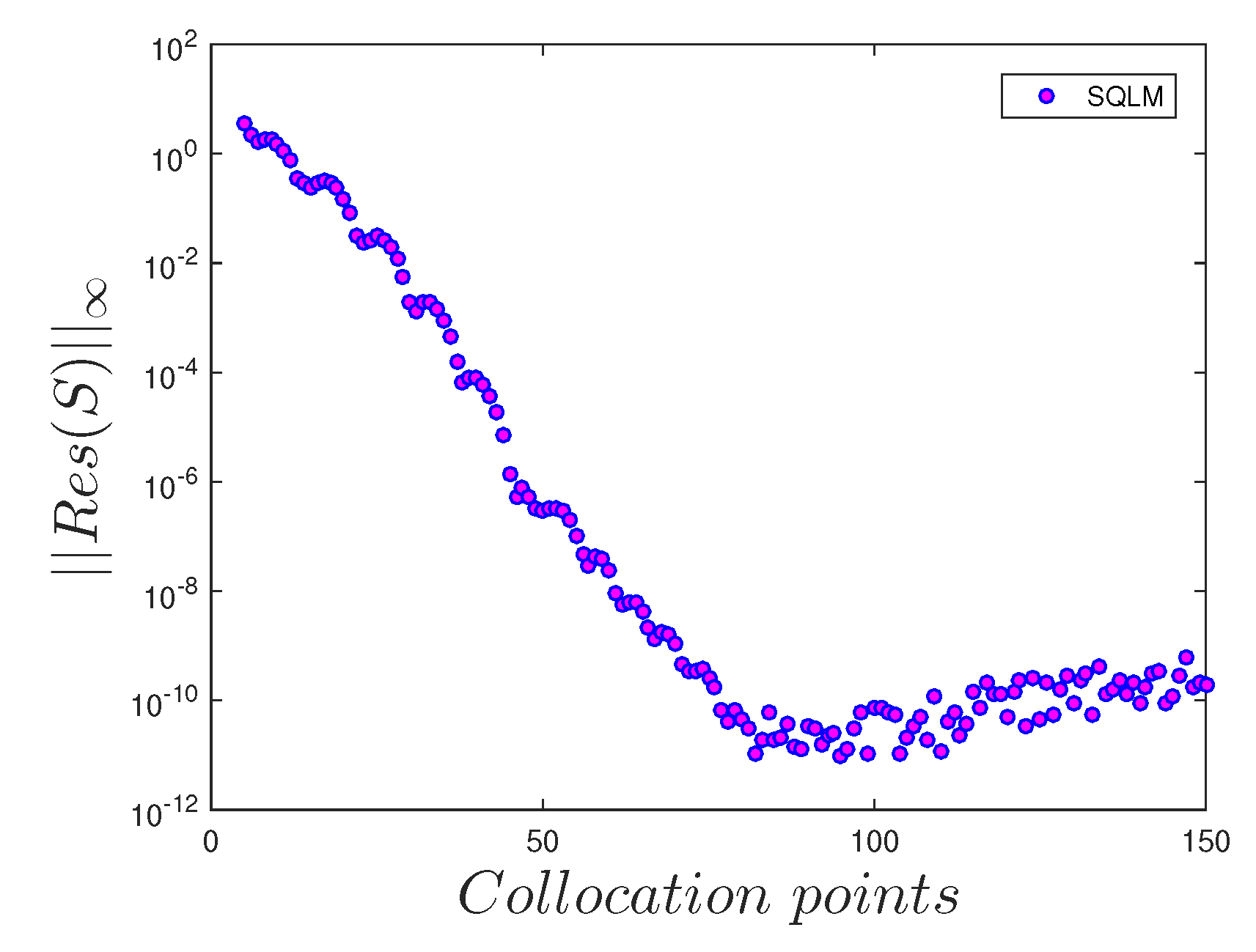

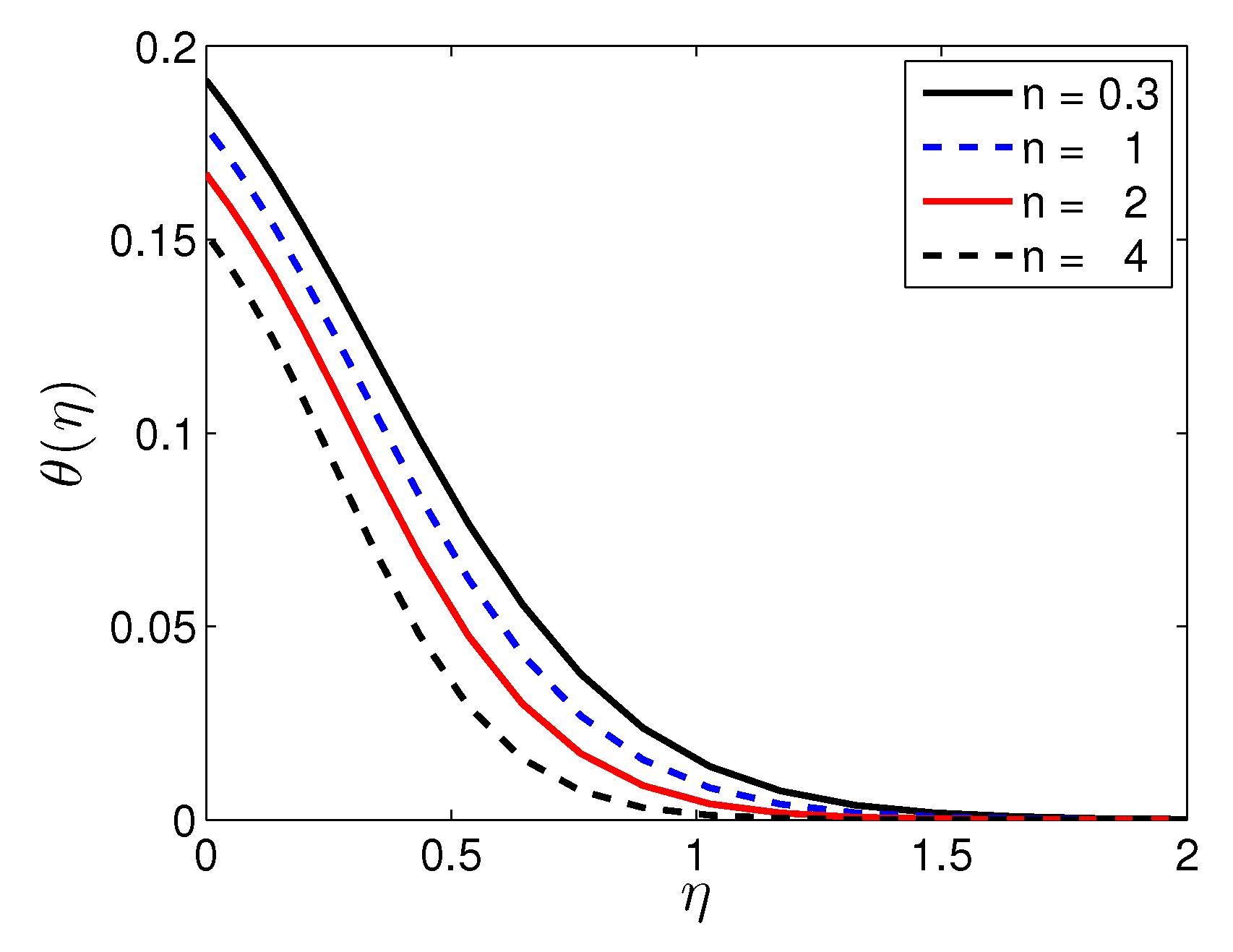
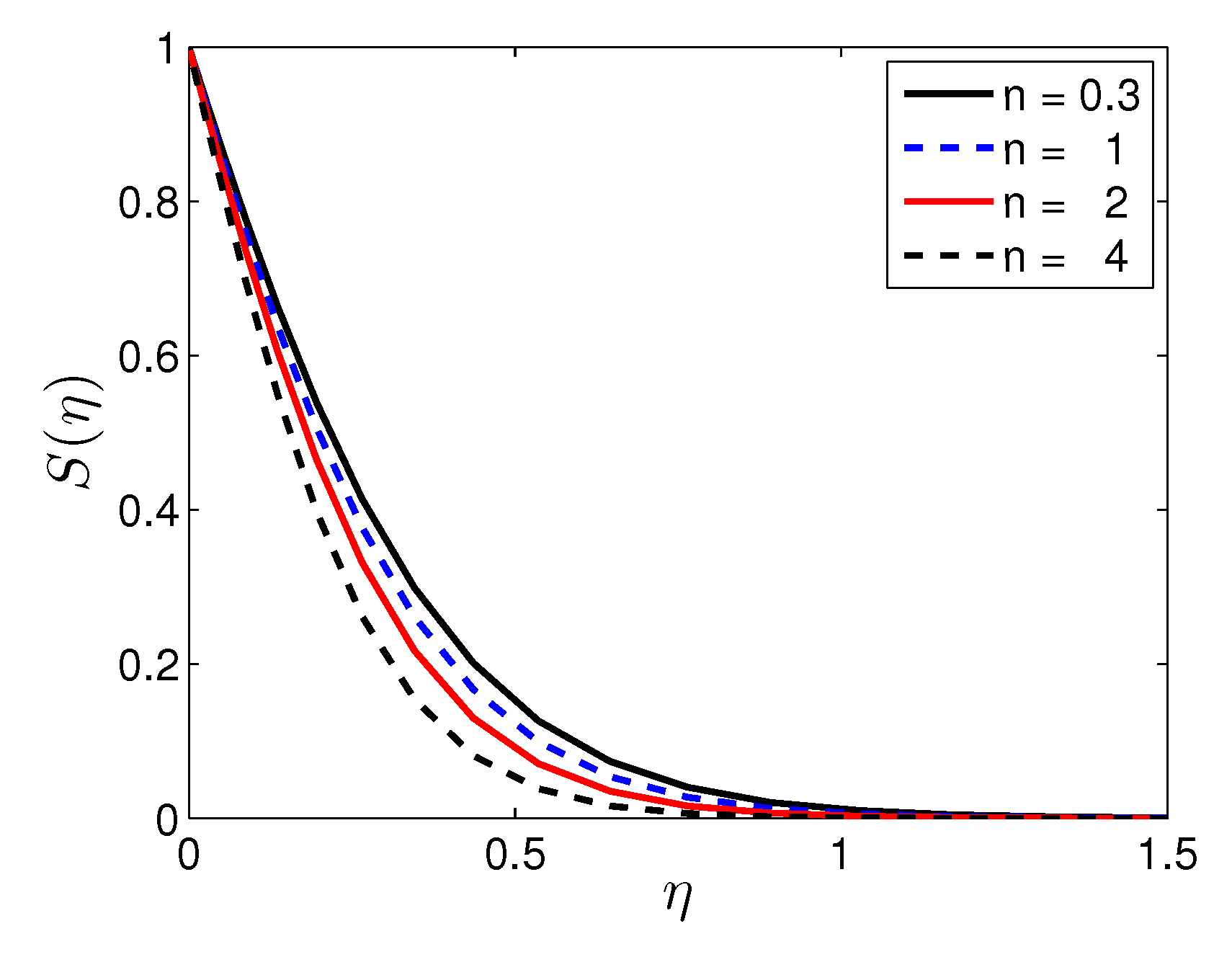
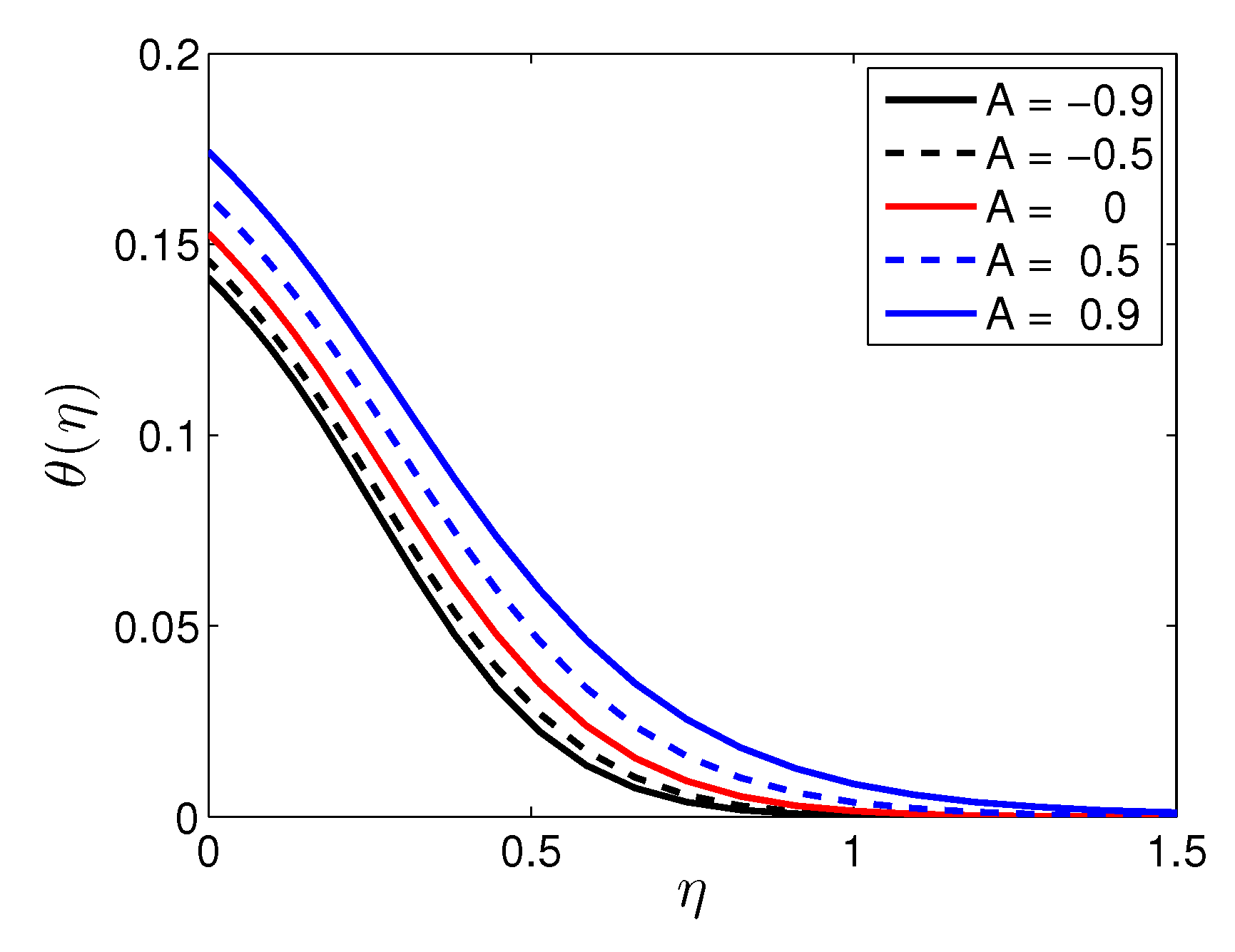
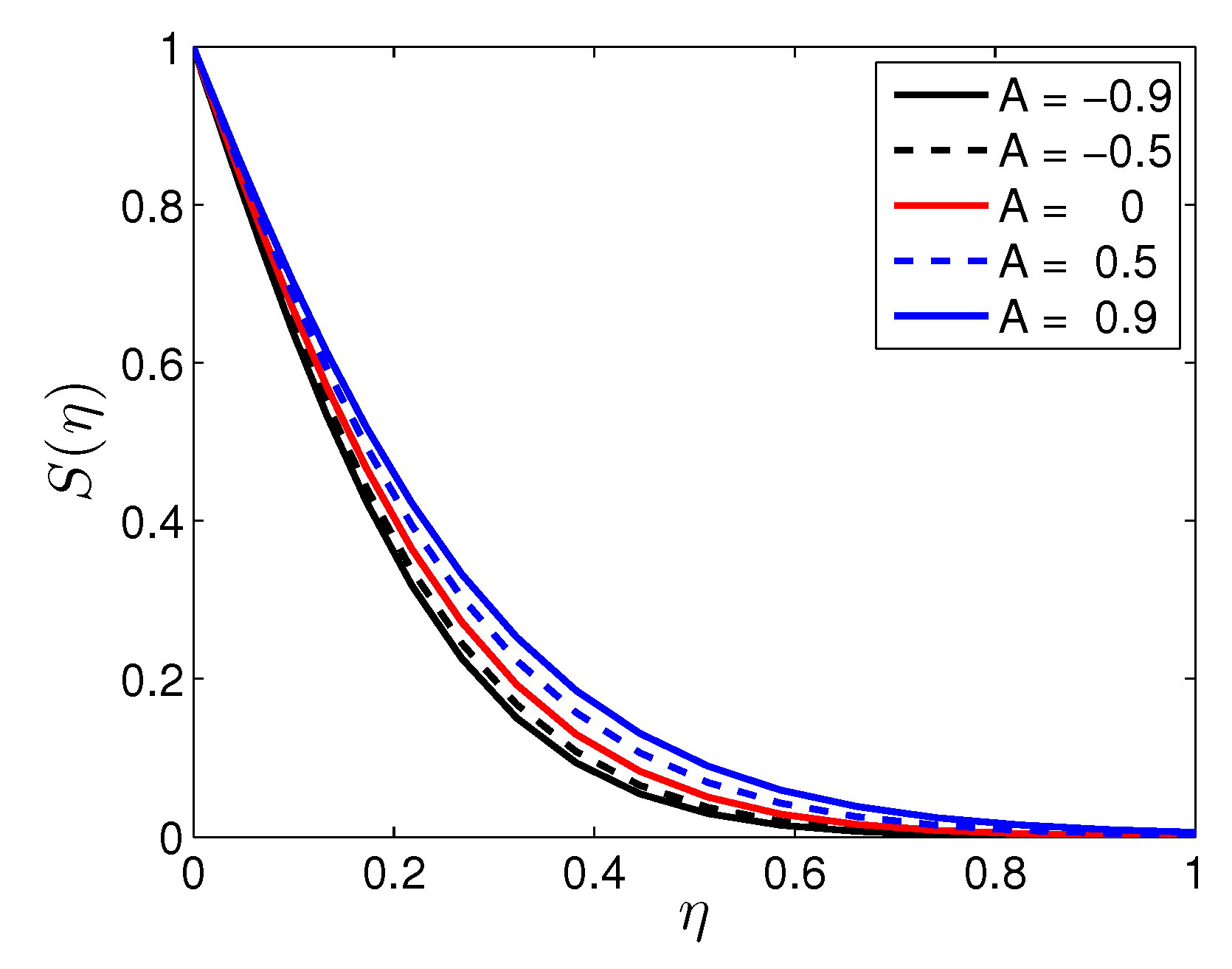

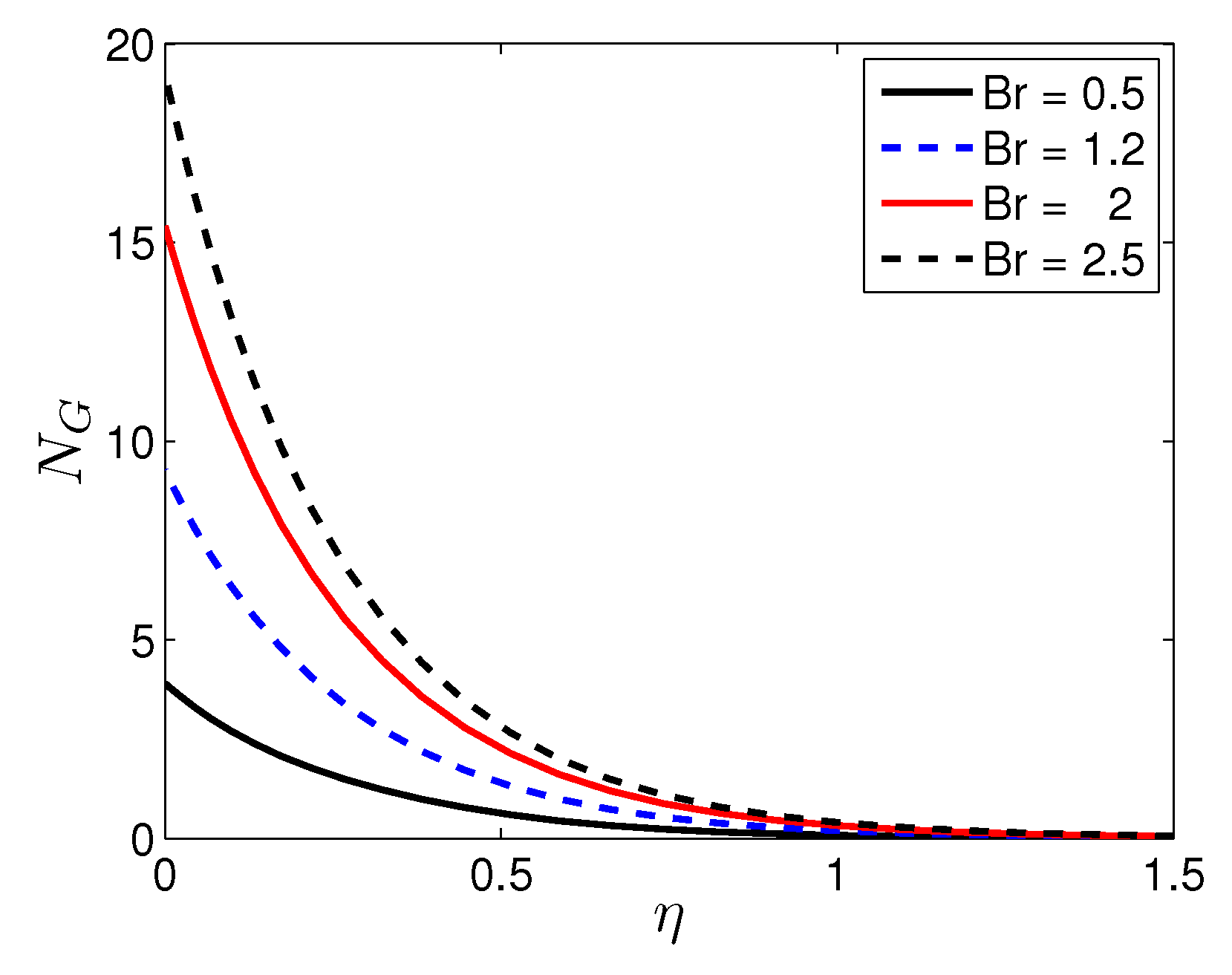
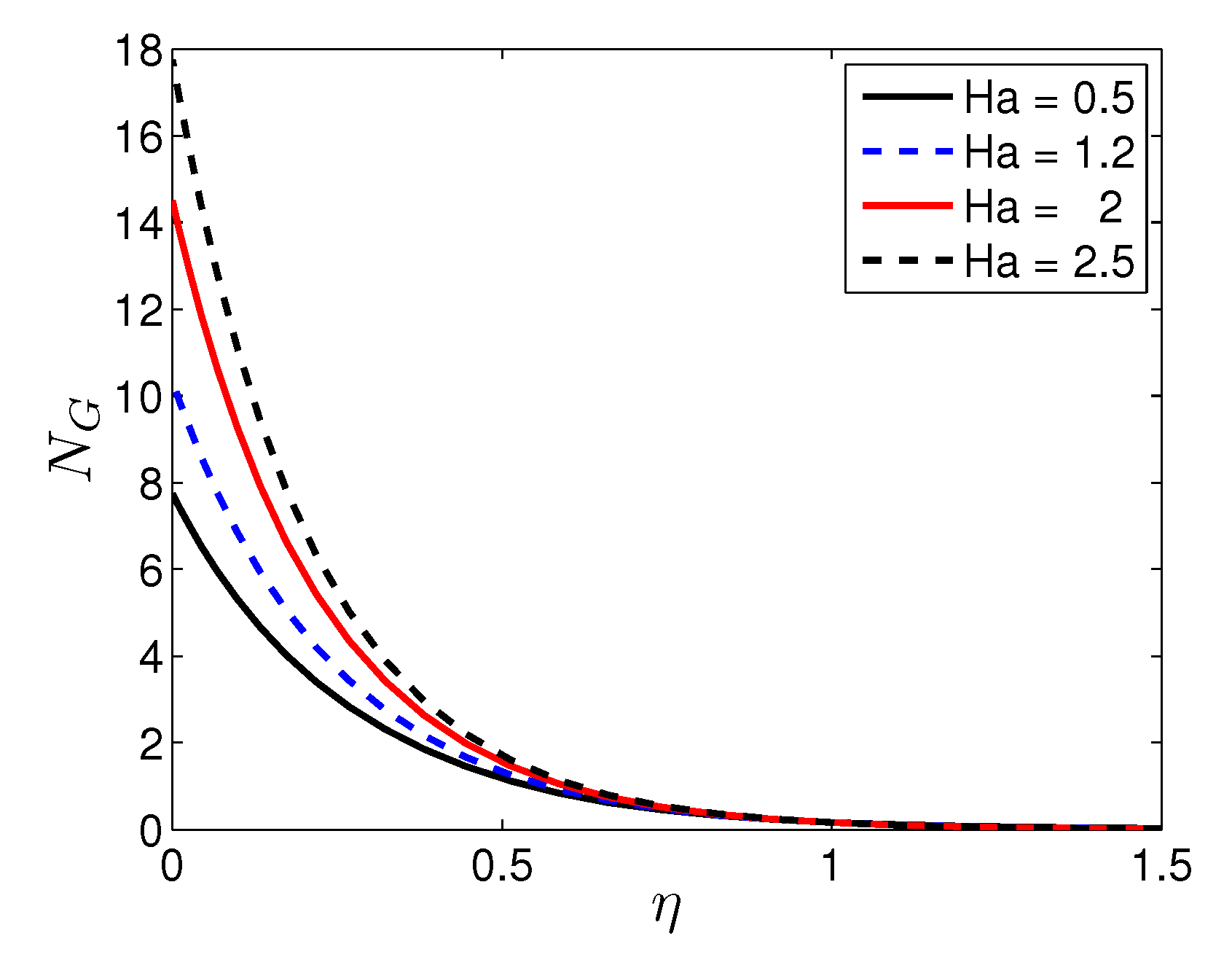
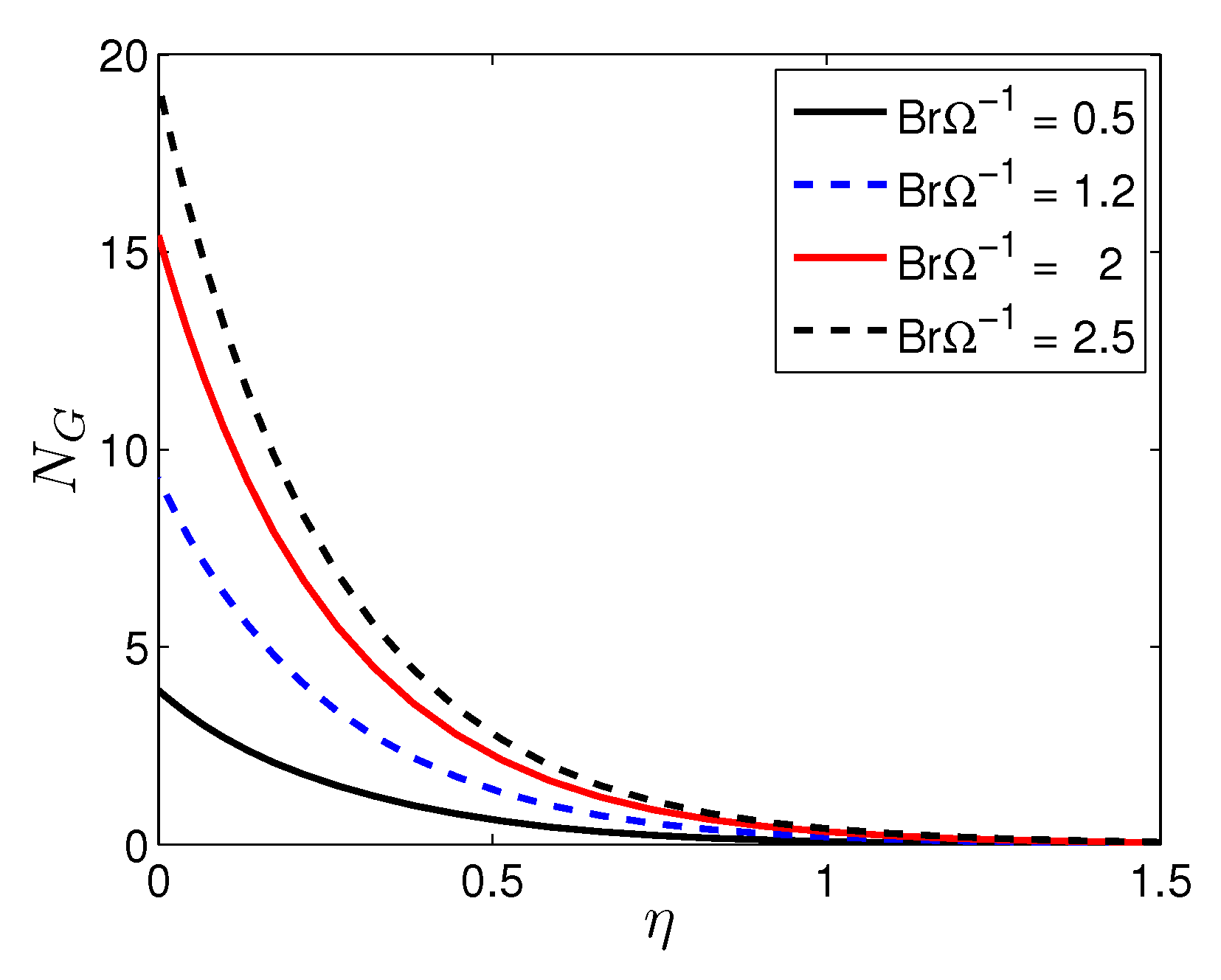
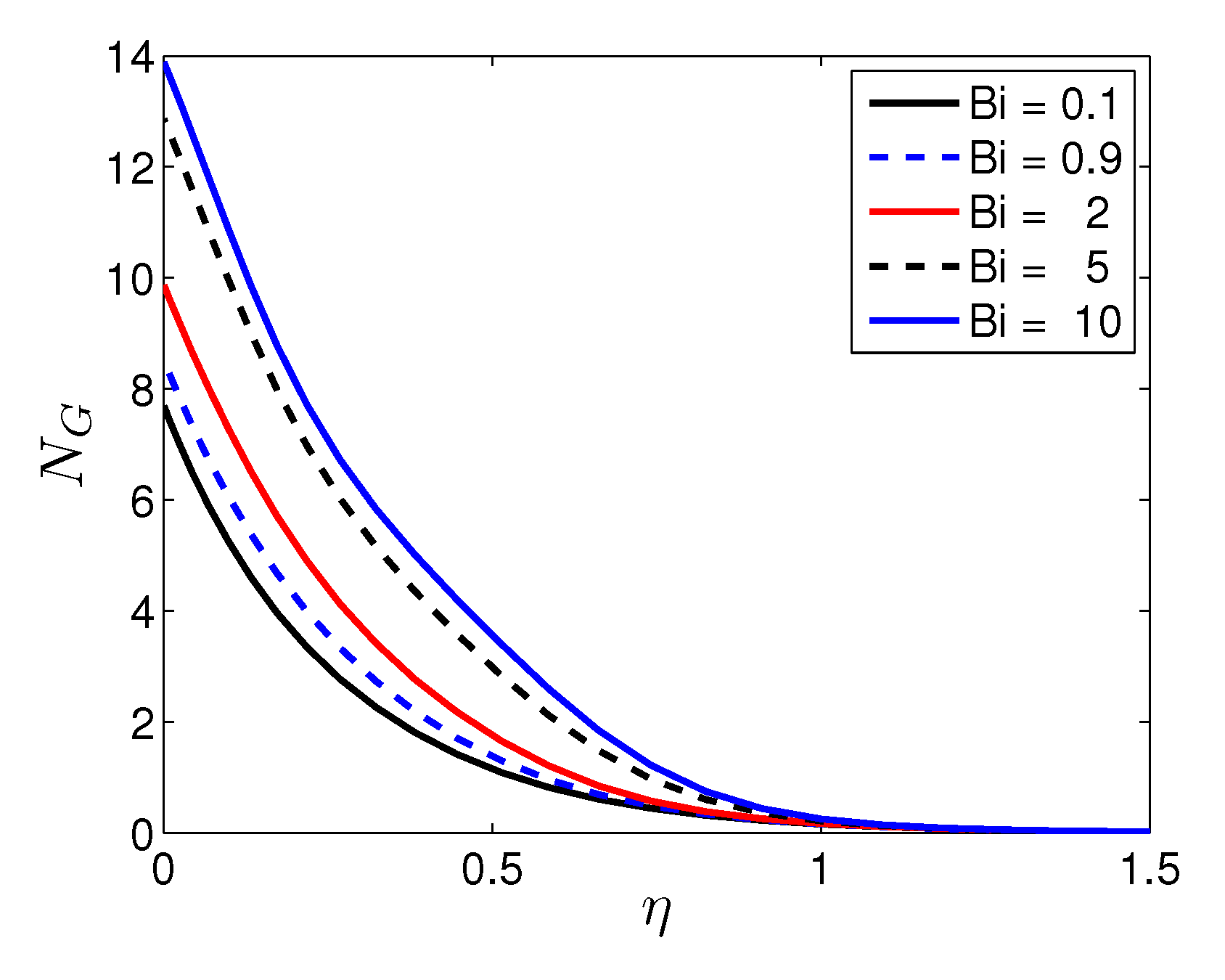
| n | Mustafa et al. [27] | Present Results | |||
|---|---|---|---|---|---|
| 0.5 | 0.1 | 20 | 5 | ||
| 0.5 | |||||
| 0.7 | |||||
| 1.0 | 0.5 | 5 | 5 | ||
| 10 | |||||
| 20 | |||||
| 2.5 | 0.5 | 20 | 0.7 | ||
| 5 | |||||
| 7 |
| n | A | ||||||
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 2 | 0.3 | 0.5 | 0.2 | 7 | |||
| 4 | |||||||
| −0.5 | |||||||
| 3 | 0 | 0.5 | 0.2 | 7 | |||
| 0.5 | |||||||
| 1.5 | |||||||
| 3 | 0.3 | 2.5 | 0.2 | 7 | |||
| 5 | |||||||
| 1 | |||||||
| 3 | 0.3 | 0.5 | 1.5 | 7 | |||
| 2 | |||||||
| 4 | |||||||
| 3 | 0.3 | 0.5 | 0.2 | 5 | |||
| 9 |
| Biot Number | Maximum Temperature | Change in Maximum Temperature |
|---|---|---|
| 0.1 | 0.1264 | |
| 0.9 | 0.3401 | 169.07 |
| 2 | 0.5218 | 53.43 |
| 5 | 0.7377 | 41.38 |
| 10 | 0.853 | 15.63 |
| 50 | 0.9678 | 13.46 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almakki, M.; Dey, S.; Mondal, S.; Sibanda, P. On Unsteady Three-Dimensional Axisymmetric MHD Nanofluid Flow with Entropy Generation and Thermo-Diffusion Effects on a Non-Linear Stretching Sheet. Entropy 2017, 19, 168. https://doi.org/10.3390/e19070168
Almakki M, Dey S, Mondal S, Sibanda P. On Unsteady Three-Dimensional Axisymmetric MHD Nanofluid Flow with Entropy Generation and Thermo-Diffusion Effects on a Non-Linear Stretching Sheet. Entropy. 2017; 19(7):168. https://doi.org/10.3390/e19070168
Chicago/Turabian StyleAlmakki, Mohammed, Sharadia Dey, Sabyasachi Mondal, and Precious Sibanda. 2017. "On Unsteady Three-Dimensional Axisymmetric MHD Nanofluid Flow with Entropy Generation and Thermo-Diffusion Effects on a Non-Linear Stretching Sheet" Entropy 19, no. 7: 168. https://doi.org/10.3390/e19070168







