1. Introduction
The rate-distortion function,
, shows the minimum achievable rate to reproduce source outputs with the expected distortion not exceeding
D. The Shannon lower bound (SLB) has been used for evaluating
[
1,
2]. The tightness of the SLB for the entire range of the positive rate identifies the entire
for pairs of a source and distortion measure such as the Gaussian source with squared distortion [
1], the Laplacian source with absolute magnitude distortion [
2], and the gamma source with Itakura–Saito distortion [
3]. However, such pairs are rare examples. In fact, for a fixed distortion measure, there exists only a single source that makes the SLB tight for all
D, as we will prove in
Section 2.3. The necessary and sufficient condition for the tightness of the SLB was first obtained for the squared distortion [
4], discussed for a general difference distortion measure
d [
2], and recently described in terms of
d-tilted information [
5]. While these results consider the tightness of the SLB for each point of
(i.e., for each
D), we discuss the tightness for all
D in this paper. More specifically, if we focus on the minimum distortion at zero rate (denoted by
), the tightness of the SLB at
characterizes a condition between the source density and the distortion measure.
If the SLB is not tight, the explicit evaluation of the rate-distortion function has been obtained only in limited cases [
6,
7,
8,
9]. Little is inferred on the behavior of
when the distortion measure is varied from a known case, since
does not continuously change even if the distortion measure is continuously modified. Although the SLB is easily obtained for difference distortion measures, it is unknown how accurate the SLB is without the explicit evaluation, upper bound, or numerical calculation of the rate-distortion function.
In this paper, we consider the constrained optimization of the definition of
from an information geometrical viewpoint [
10]. More specifically, we show that it is equivalent to a projection of the source distribution to the mixture family defined by the distortion measure. If the source is included in the mixture family, the SLB is tight; if it is not tight, the gap between
and its SLB evaluates the minimum Kullback–Leibler divergence from the source to the mixture family (Lemma 1). Then, using the bounds of the rate-distortion function of the
-th power difference distortion measure obtained in [
11], we evaluate the projections of the source distribution to the mixture families associated with this distortion measure (Theorem 3).
Operational rate-distortion results have been obtained for the uniform scalar quantization of the generalized Gaussian source under the
-th power distortion measure [
12,
13]. We prove that only the
-generalized Gaussian distribution has the potential to be the source whose SLB is tight; that is, identical to the rate-distortion function for the entire rage of positive rate. This fact brings knowledge on the tightness of the SLB of an
-insensitive distortion measure, which is obtained by truncating the loss function near zero error [
14,
15,
16]. The above result implies that the SLB is not tight if the source is the
-generalized Gaussian and the distortion has another power
. We demonstrate that even in such a case, a novel upper bound to
can be derived from the condition for the tightness of the SLB. The fact that the Laplacian (
) and the Gaussian (
) sources have the tight SLB specifically derives a novel upper bound to
of
-th power distortion measure, which has a constant gap from the SLB for all
D. By the relationship between the SLB and the projection in the information geometry, the gap evaluates the projections of the
-generalized Gaussian source to the mixture families of
-generalized Gaussian models. Extending the above argument to
-insensitive loss, we derive an upper bound to the distortion-rate function, which is tight in the limit of zero rate.
4. Rate-Distortion Bounds for Mismatching Pairs
From Corollary 1, the SLB cannot be tight for all D if the distortion measure has a different exponent from that of the source (i.e., ). In this section, we show that even in such a case, accurate upper and lower bounds to of Laplacian and Gaussian sources can be derived from the fact that for and .
We denote the rate-distortion function and bounds to it by indicating the parameters and of the source and the distortion measure. More specifically, denotes the rate-distortion function for the source with respect to the distortion measure .
We first prove the following lemma:
Lemma 2. If for all D, thenholds for , where denotes the expectation with respect to , andis satisfied for the optimal conditional reproduction distribution in(3). Proof. implies that
for the optimal reproduction distribution
in (
3) and
minimizing (
2), and
. It follows that
☐
Let
, which is equivalent to
The above lemma implies that
achieving
has the expected
-distortion,
with the rate
if
for all
D.
Thus, we obtain the following upper bound to
if
.
We also have the SLB for
,
Therefore, we arrive at the following theorem:
Theorem 2. If , for , the rate-distortion function is lower- and upper-bounded aswhere the lower and upper bounds are given by (20) and (19). The left inequality becomes equality only for . The gap between the bounds iswhich is constant with respect to D. Furthermore, the upper bound is tight at ; that is, Since the upper bound is tight at
, it is the smallest upper bound that has a constant deviation from the SLB. In addition, the SLB is asymptotically tight in the limit
for the distortion measure
in general [
2,
21], and the condition for the asymptotic tightness has been weakened recently [
22]. These facts suggest that the rate-distortion function
is near the SLB at low distortion levels and then approaches the upper bound
as the average distortion
D grows to
. In terms of the distortion-rate function, the theorem also implies that the encoder
designed for
-distortion has the loss in
-distortion, due to the mismatch of the orders, at most by the constant factor
.
From Lemma 1 in
Section 2.2, by examining the correspondence between the slope parameter
and the distortion level
D, we obtain the next theorem, which evaluates the m-projection of the source to the mixture family,
If the upper bound
is replaced by the asymptotically tight upper bound [
2,
21], asymptotically tighter bounds to the m-projection are obtained.
Theorem 3. If , for , the m-projection of the generalized Gaussian source to the mixture family of is evaluated asfor related to by (9), where is given by (21). For , the m-projection is upper bounded asFurthermore, the inequality (22) holds with equality for , where is the slope parameter of at
.
Proof. The first part of the theorem is a corollary of Theorem 2 and Lemma 1. The second part corresponds to the case of
, since
D monotonically decreases as
s grows. Because
yields
, we have (
22). It follows from (
13) that
.
Since for
, the optimal reconstruction distribution is given by
, (
22) holds with equality. ☐
Since we know that if and , the SLB is tight for all D, we have the following corollaries.
Corollary 3. The rate-distortion function of the Laplacian source, , is lower- and upper-bounded as Corollary 4. The rate-distortion function of the Gaussian source, , is lower- and upper-bounded as Example 1. If we put in Corollary 4 (
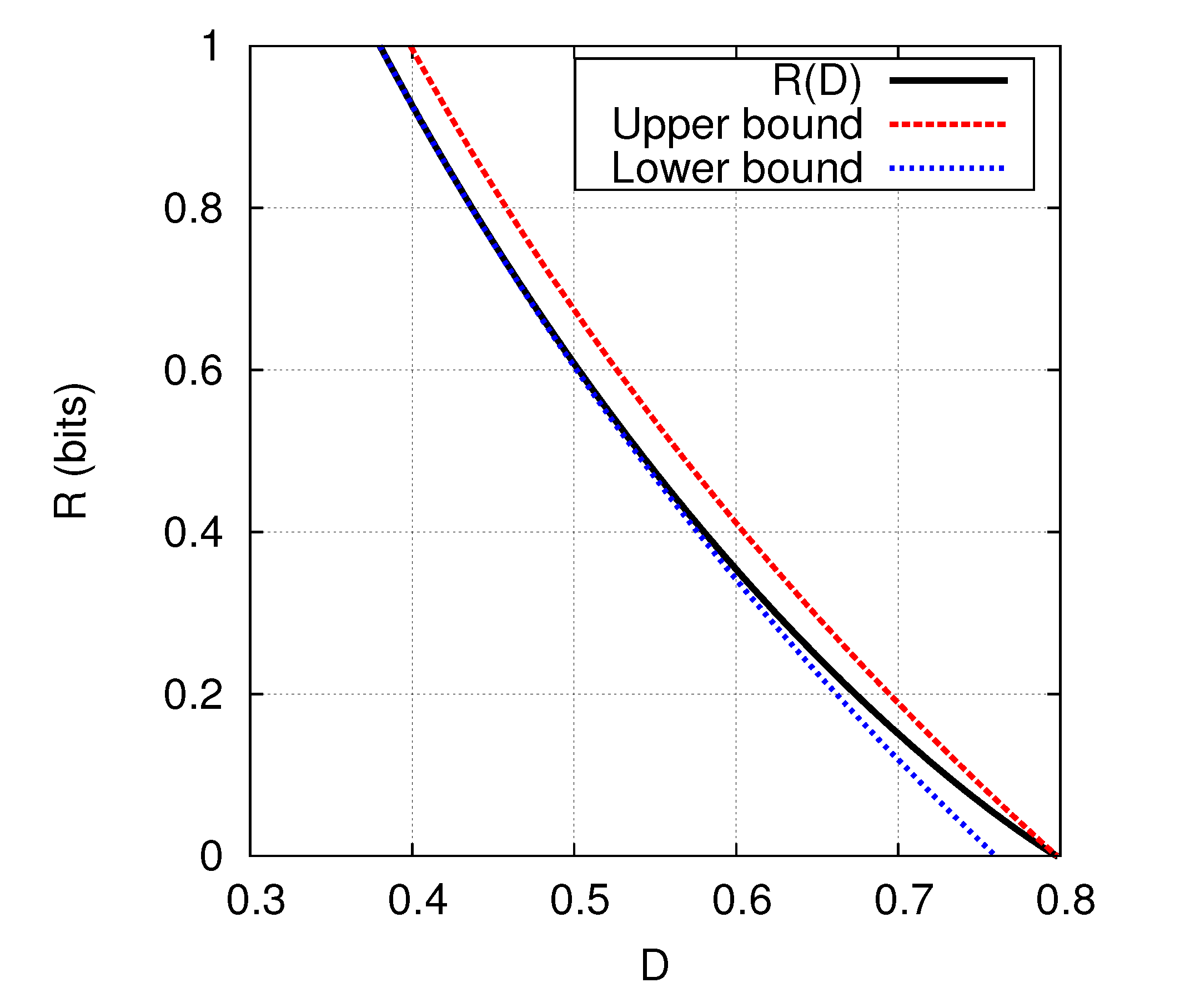
), we haveThe explicit evaluation of is obtained through a parametric form using the slope parameter s [6]. While the explicit parametric form requires evaluations of the cumulative distribution function of the Gaussian distribution, the bounds in (23) demonstrate that it is well approximated by an elementary function of D. In fact, the gap between the upper and lower bounds is (bit). The bounds in (23) are compared with for in Figure 1. Example 2. If we put in Corollary 3 (
), we havefor the Laplacian source and the squared distortion measure . The gap between the bounds is (bit). The upper bound in Theorem 2 implies the following:
Corollary 5. Under the γ-th power distortion measure, if for all D, the γ-generalized Gaussian source has the greatest rate-distortion function among all β-generalized Gaussian sources with a fixed , satisfying for all D.
Proof. Since
, the upper bound in (
19) is expressed as
, which is equal to the rate-distortion function of the
-generalized Gaussian source under the
-th power distortion measure if its SLB is tight for all
D. ☐
The preceding corollary is well-known in the case of the squared distortion measure, while the Gaussian source has the largest rate-distortion function not only among all
-generalized Gaussian sources, but also among all the sources with a fixed variance ([
2], Theorem 4.3.3).
5. Distortion-Rate Bounds for -Insensitive Loss
As another example of a distortion measure that is not matching with the
-generalized Gaussian source in the sense of Theorem 1, we consider the following
-th power
-insensitive distortion measure generalizing (
17),
where
. Such distortion measures are used in support vector regression models [
14,
15].
In this section, we focus on the Laplacian source (
), for which similarly to
Section 4, we can evaluate
where
and
. Such an explicit evaluation appears to be prohibitive for
. The above expected distortion is achievable by
with the rate
since
holds for all
D. Thus, we obtain the following upper bound, which is expressed by a closed form in the case of the distortion-rate function.
Theorem 4. The distortion-rate function of the Laplacian source under the γ-th power ϵ-insensitive distortion measure (24) is upper-bounded asIn addition, the upper bound is tight at ; that is, Upper and (Shannon) lower bounds which are accurate asymptotically as
have been obtained for the distortion measure (
24) [
16]. They are proved to have approximation error at most
as
. Combined with these bounds, the upper bound (
25), being accurate at high distortion levels, provides a good approximation of the rate-distortion function for the entire range of
D. This is demonstrated in
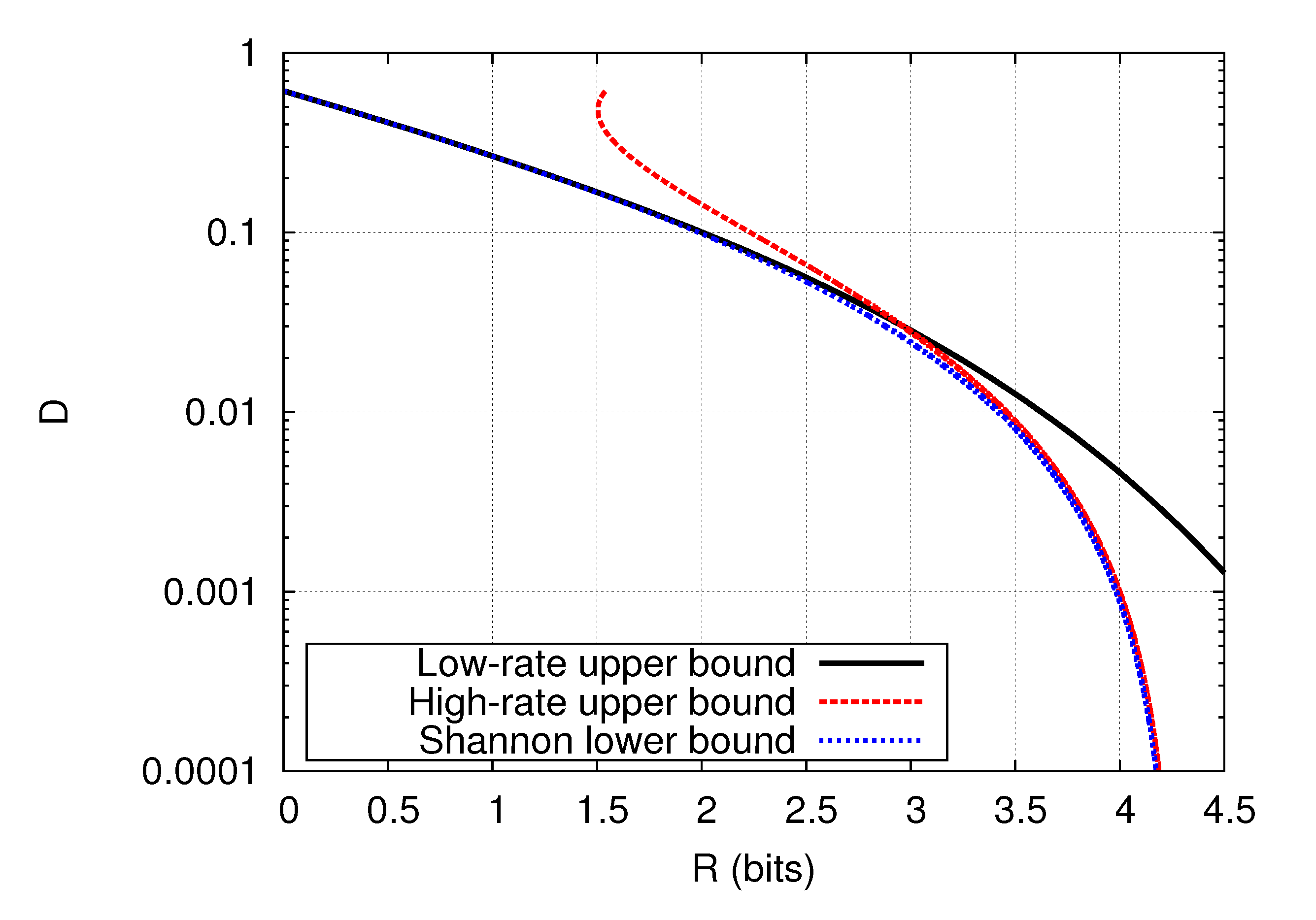
Figure 2 for the case of
,
, and
, where the upper bound (
25) and that in [
16] are referred to as low-rate and high-rate upper bounds because they are effective at low and high rates, respectively. Although the rate-distortion function of this case is still unknown, it lies between the upper bounds and the SLB. Hence, the figure implies that the SLB is accurate for all
R, and the rate-distortion function is almost identified except for the region around
(bits) where there is a relatively large gap between the upper bounds and the SLB.