Lyapunov Spectra of Coulombic and Gravitational Periodic Systems
Abstract
:1. Introduction
2. Model
3. Lyapunov Characteristic Exponents
3.1. Theoretical Overview
3.2. Numerical Approach
4. N-Body Simulation
4.1. Equations of Motion
4.2. Time Evolution of Tangent-Space Vectors
4.2.1. Coulombic System
4.2.2. Gravitational System
4.3. p-Volume and Lyapunov Spectrum
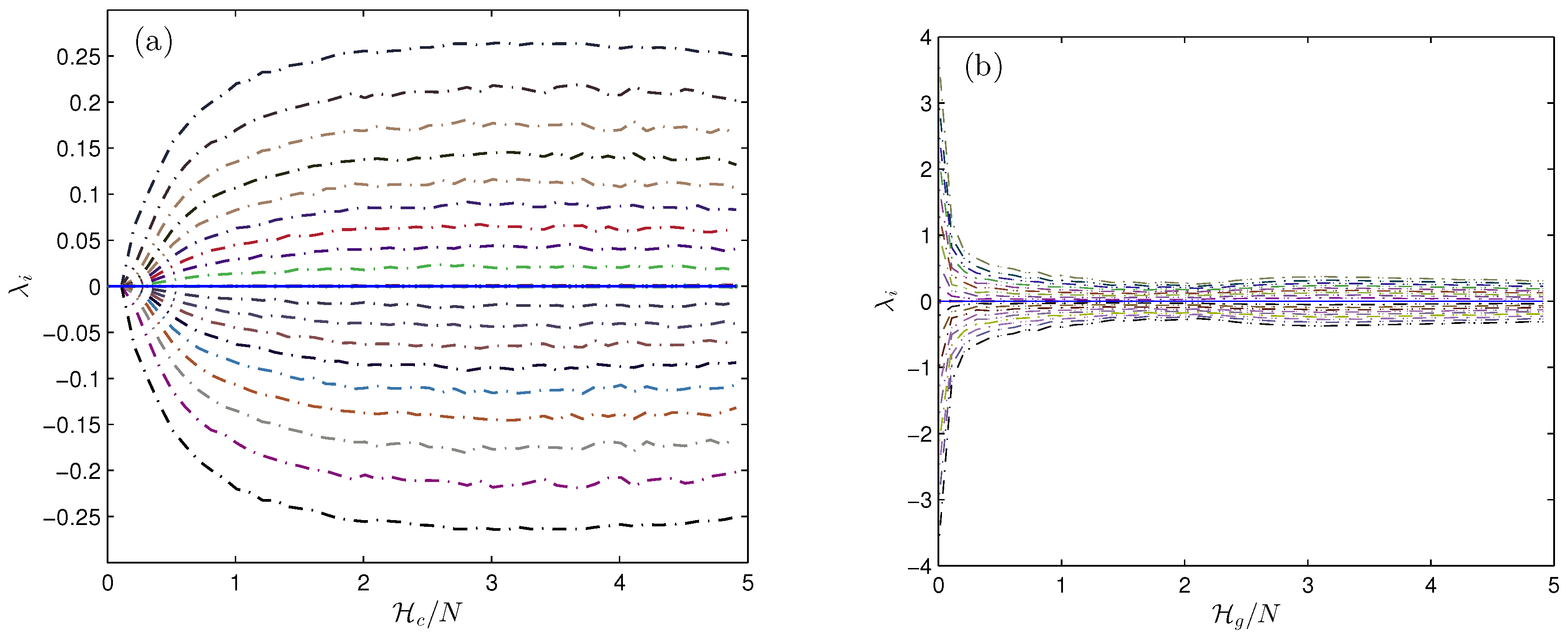
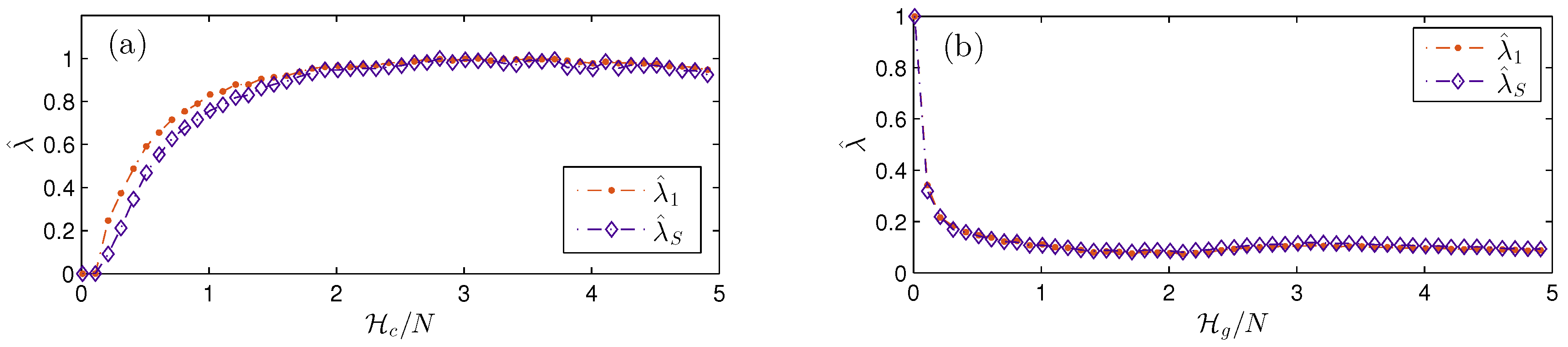
4.4. Results
5. Discussion
- (a)
- The sum of LCEs was found to converge to zero for all energies and N.
- (b)
- For the ordered set (), the results show that
- (c)
- In addition, our results show that
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| LCE | Lyapunov characterstic exponent |
| KS | Kolmogorov–Sinai |
| MD | Molecular dynamics |
| HMF | Hamiltonian Mean Field |
References
- Klinko, P.; Miller, B.N. Dynamical study of a first order gravitational phase transition. Phys. Lett. A 2004, 333, 187–192. [Google Scholar] [CrossRef]
- Wang, G.; Sevick, E.M.; Mittag, E.; Searles, D.J.; Evans, D.J. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys. Rev. Lett. 2002, 89, 050601. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, C.; Liphardt, J.; Ritort, F. The nonequilibrium thermodynamics of small systems. Phys. Today 2005, 58, 43–48. [Google Scholar] [CrossRef]
- Ritort, F. The nonequilibrium thermodynamics of small systems. C. R. Phys. 2007, 8, 528–539. [Google Scholar] [CrossRef]
- Schnell, S.K.; Vlugt, T.J.; Simon, J.M.; Bedeaux, D.; Kjelstrup, S. Thermodynamics of a small system in a μT reservoir. Chem. Phys. Lett. 2011, 504, 199–201. [Google Scholar] [CrossRef]
- Frisch, H.L.; Lebowitz, J.L. The Equilibrium Theory of Classical Fluids: A Lecture Note and Reprint Volume; WA Benjamin: Los Angeles, CA, USA, 1964. [Google Scholar]
- Kumar, P.; Miller, B.N.; Pirjol, D. Thermodynamics of a one-dimensional self-gravitating gas with periodic boundary conditions. Phys. Rev. E 2017, 95, 022116. [Google Scholar] [CrossRef] [PubMed]
- Rybicki, G.B. Exact statistical mechanics of a one-dimensional self-gravitating system. Astrophys. Space Sci. 1971, 14, 56–72. [Google Scholar] [CrossRef]
- Yawn, K.R.; Miller, B.N. Equipartition and Mass Segregation in a One-Dimensional Self-Gravitating System. Phys. Rev. Lett. 1997, 79, 3561–3564. [Google Scholar] [CrossRef]
- Miller, B.N.; Youngkins, P. Phase Transition in a Model Gravitating System. Phys. Rev. Lett. 1998, 81, 4794–4797. [Google Scholar] [CrossRef]
- Lauritzen, A.; Gustainis, P.; Mann, R.B. The 4-body problem in a (1+1)-dimensional self-gravitating system. J. Math. Phys. 2013, 54, 072703. [Google Scholar] [CrossRef]
- Kumar, P.; Miller, B.N. Chaotic dynamics of one-dimensional systems with periodic boundary conditions. Phys. Rev. E 2014, 90, 062918. [Google Scholar] [CrossRef] [PubMed]
- Milner, V.; Hanssen, J.L.; Campbell, W.C.; Raizen, M.G. Optical Billiards for Atoms. Phys. Rev. Lett. 2001, 86, 1514–1517. [Google Scholar] [CrossRef] [PubMed]
- Chalony, M.; Barré, J.; Marcos, B.; Olivetti, A.; Wilkowski, D. Long-range one-dimensional gravitational-like interaction in a neutral atomic cold gas. Phys. Rev. A 2013, 87, 013401. [Google Scholar] [CrossRef]
- Springiel, V.; Frenk, C.S.; White, S.D.M. The large-scale structure of the universe. Nature 2006, 440, 1137–1144. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, E. Simulations of structure formation in the universe. Annu. Rev. Astron. Astrophys. 1998, 36, 599–654. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles; CPC Press: Boca Raton, FL, USA, 1988. [Google Scholar]
- Hernquist, L.; Bouchet, F.R.; Suto, Y. Application of the Ewald method to cosmological N-body simulations. Astrophys. J. Suppl. 1991, 75, 231–240. [Google Scholar] [CrossRef]
- Kunz, H. The one-dimensional classical electron gas. Ann. Phys. 1974, 85, 303–335. [Google Scholar] [CrossRef]
- Schotte, K.D.; Truong, T.T. Phase transition of a one-dimensional Coulomb system. Phys. Rev. A 1980, 22, 2183–2188. [Google Scholar] [CrossRef]
- Miller, B.N.; Rouet, J.L. Ewald sums for one dimension. Phys. Rev. E 2010, 82, 066203. [Google Scholar] [CrossRef] [PubMed]
- Krylov, N.; Migdal, A.; Sinai, Y.G.; Zeeman, Y.L. Works on the Foundations of Statistical Physics by Nikolai Sergeevich Krylov; Princeton Series in Physics; Princeton University Press: Princeton, NJ, USA, 1979. [Google Scholar]
- Pesin, J.B. Characteristic Liapunov indices and ergodic properties of smooth dynamical systems with invariant measure. Sov. Math. Dokl. 1976, 17, 196. [Google Scholar]
- Pesin, Y.B. Characteristic Lyapunov exponents and smooth ergodic theory. Russ. Math. Surv. 1977, 32, 55–114. [Google Scholar] [CrossRef]
- Benettin, G.; Froeschle, C.; Scheidecker, J.P. Kolmogorov entropy of a dynamical system with an increasing number of degrees of freedom. Phys. Rev. A 1979, 19, 2454–2460. [Google Scholar] [CrossRef]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: Cambridge, UK, 2002; pp. 137–145. [Google Scholar]
- Sprott, J. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003; pp. 116–117. [Google Scholar]
- Butera, P.; Caravati, G. Phase transitions and Lyapunov characteristic exponents. Phys. Rev. A 1987, 36, 962–964. [Google Scholar] [CrossRef]
- Caiani, L.; Casetti, L.; Clementi, C.; Pettini, M. Geometry of Dynamics, Lyapunov Exponents, and Phase Transitions. Phys. Rev. Lett. 1997, 79, 4361–4364. [Google Scholar] [CrossRef]
- Casetti, L.; Pettini, M.; Cohen, E.G.D. Geometric approach to Hamiltonian dynamics and statistical mechanics. Phys. Rep. 2000, 337, 237–341. [Google Scholar] [CrossRef]
- Dellago, C.; Posch, H.A. Lyapunov instability, local curvature, and the fluid-solid phase transition in two-dimensional particle systems. Phys. A Stat. Mech. Appl. 1996, 230, 364–387. [Google Scholar] [CrossRef]
- Barre, J.; Dauxois, T. Lyapunov exponents as a dynamical indicator of a phase transition. Europhys. Lett. 2001, 55, 2. [Google Scholar] [CrossRef]
- Monechi, B.; Casetti, L. Geometry of the energy landscape of the self-gravitating ring. Phys. Rev. E 2012, 86, 041136. [Google Scholar] [CrossRef] [PubMed]
- Dellago, C.; Posch, H. Kolmogorov-Sinai entropy and Lyapunov spectra of a hard-sphere gas. Phys. A Stat. Mech. Appl. 1997, 240, 68–83. [Google Scholar] [CrossRef]
- Milanović, L.; Posch, H.A.; Thirring, W. Statistical mechanics and computer simulation of systems with attractive positive power-law potentials. Phys. Rev. E 1998, 57, 2763–2775. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Gouda, N. Relaxation and Lyapunov time scales in a one-dimensional gravitating sheet system. Phys. Rev. E 2000, 61, 948–951. [Google Scholar] [CrossRef]
- Benettin, G.; Galgani, L.; Giorgilli, A.; Strelcyn, J.M. Lyapunov Characteristic Exponents for smooth dynamical systems and for hamiltonian systems; a method for computing all of them. Part 1: Theory. Meccanica 1980, 15, 9–20. [Google Scholar] [CrossRef]
- Shimada, I.; Nagashima, T. A numerical approach to ergodic problem of dissipative dynamical systems. Prog. Theor. Phys. 1979, 61, 1605–1616. [Google Scholar] [CrossRef]
- Sandri, M. Numerical calculation of Lyapunov exponents. Math. J. 1996, 6, 78–84. [Google Scholar]
- Oseledec, V.I. A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems. Trans. Mosc. Math. Soc. 1968, 19, 197–231. [Google Scholar]
- Shilov, G.E.; Silverman, R.A. An Introduction to the Theory of Linear Spaces; Dover: Mineola, NY, USA, 2012. [Google Scholar]
- Kumar, P.; Miller, B.N. Dynamics of Coulombic and gravitational periodic systems. Phys. Rev. E 2016, 93, 040202. [Google Scholar] [CrossRef] [PubMed]
- Ginelli, F.; Takeuchi, K.A.; Chaté, H.; Politi, A.; Torcini, A. Chaos in the Hamiltonian mean-field model. Phys. Rev. E 2011, 84, 066211. [Google Scholar] [CrossRef] [PubMed]
- Bonasera, A.; Latora, V.; Rapisarda, A. Universal Behavior of Lyapunov Exponents in Unstable Systems. Phys. Rev. Lett. 1995, 75, 3434–3437. [Google Scholar] [CrossRef] [PubMed]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, P.; Miller, B.N. Lyapunov Spectra of Coulombic and Gravitational Periodic Systems. Entropy 2017, 19, 238. https://doi.org/10.3390/e19050238
Kumar P, Miller BN. Lyapunov Spectra of Coulombic and Gravitational Periodic Systems. Entropy. 2017; 19(5):238. https://doi.org/10.3390/e19050238
Chicago/Turabian StyleKumar, Pankaj, and Bruce N. Miller. 2017. "Lyapunov Spectra of Coulombic and Gravitational Periodic Systems" Entropy 19, no. 5: 238. https://doi.org/10.3390/e19050238
APA StyleKumar, P., & Miller, B. N. (2017). Lyapunov Spectra of Coulombic and Gravitational Periodic Systems. Entropy, 19(5), 238. https://doi.org/10.3390/e19050238





