2.1. The Committor
Consider a system of two metastable states
and
denoting reactants and products respectively. Trajectories are computed, starting from any phase space point
and are terminated when they reach either
R or
P. The committor,
, is the probability that a pathway initiated at
will make it to the product state (
P) before the reactant state (
R). The committor is zero at
R and one at
P, and its range is
. The iso-committor surfaces are the set of all phase space points such that the committor function of these points is a constant. It forms a foliation that is useful for the definition of the reaction coordinate. The calculation of the committor function attracted considerable attention. Pioneering work on committors was done in the context of Transition Path Theory (TPT [
18,
22,
23,
24]). Indeed the algorithm proposed in the present work is similar to these previous studies. It is also similar in spirit to references [
25,
26]. However, there are conceptual and algorithmic differences between these investigations, which are discussed later in the article.
For overdamped Langevin dynamics, a partial differential equation (PDE) determines the iso-committor surfaces [
27]. The solution of the PDE is rapid and efficient. However, it is limited to a small number of degrees of freedom since the complexity of the solution increases exponentially with the dimensionality of the system. Studies of committors [
26,
28,
29,
30] in systems with high dimension use estimates based on trajectory sampling. Trajectory-based formulation makes it possible to use arbitrary dynamics and not limit the choice to overdamped Langevin. Nevertheless, even with trajectory-based approaches calculating exact iso-committor surfaces is computationally challenging. To exhaustively compute the committor function an ensemble of stochastic trajectories is required for each phase space point between
R and
P.
Given the staggering costs of computing the exact committor surfaces, it is not a surprise that approximate approaches to determine this function are used. Among these approaches are the use of planes in a specific orientation with respect to the SDP curve [
17], maximum likelihood determination of function parameters [
29], and more [
25,
28]. In these approaches several different approximations were used: (i) the committor is assumed to depend only on a small number of coarse variables; (ii) Some techniques use only a small displacement from the mean curve; (iii) The committor is assumed to be a linear function of several coordinates. The assumptions mentioned above leave room for improvements, or for the use of alternative approaches to supplant current methodologies.
In the present manuscript, we suggest an alternative calculation of the committor function using Milestoning with several coarse variables [
31,
32,
33]. Milestoning is a theory and an algorithm that computes efficiently the kinetics and thermodynamics of a system using short-time trajectories between boundaries of cells or milestones. In the next section, we briefly review the critical elements of Milestoning and refer the interested reader to other papers [
7,
31,
32,
33] for a complete description.
2.2. Milestoning
We consider a system with two metastable states, a reactant state
R and a product state
P. A coordinate vector
represents a single configuration and
denotes a trajectory as a function of time
. The dynamics that we consider are classical but otherwise left for the user to choose. We are interested in conversions of reactants to products and Milestoning is a technique to sample these transitions efficiently. In the past we showed how Milestoning can be used to determine pathways of maximum flux [
13]. Here we study another reaction coordinate (the committor). A brief review of Milestoning therefore follows. In Milestoning we consider only short trajectories between boundaries of cells that are called milestones (
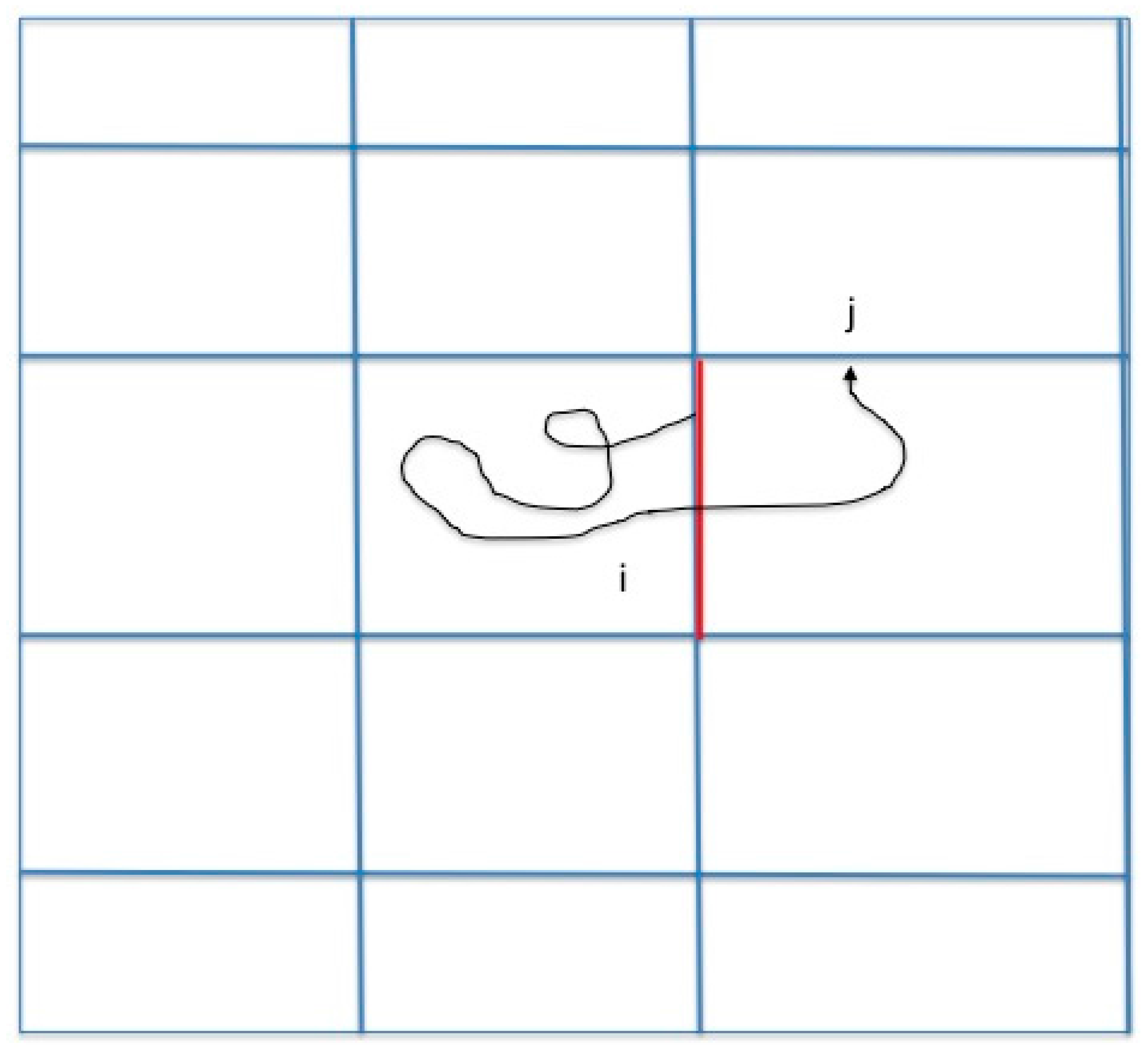
Figure 1).
A critical operator of the Milestoning theory is the matrix
, which is the probability that trajectories initiated at milestone
will reach milestone
before any other milestone. It is also called the kernel. The transition matrix is time independent and is especially useful for a stationary process. It is obtained from the time-dependent transition probability,
(the probability density of a transition between
and
per unit time at time
). We integrate
to obtain
. Note that the matrix is normalized with respect to the final state
and it may represent a non-Markovian process. For the process to be Markovian the transition probability per unit time must be of the form
, i.e., decaying exponentially in the time
[
7]. The average lifetime of a trajectory initiated at milestone
until it hits for the first time another milestone is
. The kernel is computed numerically from the trajectories (see below) and it frequently deviates from the Markovian form.
The kinetic of the complete process is determined by the distribution of the first passage times from reactants to products. The complete distribution is hard to determine computationally, and typically only the first moment or the mean first passage time is reported. Milestoning, however, makes it possible to determine all the moments of the distribution from local information. The local information is the moments of the milestones’ life times, or the time moments of
. Given this information, explicit expressions for the moments of the first passage time are derived (see [
33]). For example, a local moment that we need can be
. Another example is
. A Markovian model agrees with the general process only in the zero and first time moments [
33], which may be a problem if higher time moments are needed. For the calculation of the committor function only the zero moment is necessary, making it possible to use Markovian modeling, with the Markov model properly defined. As discussed earlier
must decays exponentially in time with relaxation time of
.
To use Milestoning the following two conditions must be met. First, the milestones must be able to differentiate between reactants and products, i.e., there is a subset of milestones that bounds the reactants and another subset of milestones that bound the products and the two sets have zero overlap. Second, there is a sequence of transitions between milestones connecting the reactant and product with non-zero probability. In other words we require that the Mean First Passage Time (MFPT) between the reactant and the product is finite.
A fundamental Milestoning equation determines the stationary flux
(the number of trajectories that pass milestone
per unit time under stationary conditions) [
31,
33].
We use bold-faced symbols to denote vectors and matrices. The length of the vector
is the number of milestones
, and the dimensionality of
is
. The origin of this equation is the time dependent formulation of Milestoning discussed at length elsewhere [
31]:
where
is the distribution at zero time (initial conditions). Note that the time range is between 0 and infinite. Integration over time for the delta function in the first term on the right gives one half since the Dirac’s delta function is symmetric. The above equation is a general statement of conservation of trajectories in time. A trajectory that passes a milestone at time
and is counted for in the flux vector
must originate from other milestones at an earlier time
(counted in the flux vector
) and propagate to the milestone of observation after time
with a probability determined by the kernel
. The process is homogeneous in time and therefore the kernel depends only on the time difference.
If we consider the limit of long time
of the time dependent equation and use Laplace transforms we obtain Equation (1) [
31]. We can understand this result, however, on a more physical ground. At stationary conditions the flux that passes at each milestone is a time-independent constant, per definition. We therefore have
. Moreover, we always set the kernel to have a short range in time. In molecular simulations it decays to zero in sub-nanosecond timescales in most practical applications. Consider the convolution on the right hand side. If
is large, so must be
to ensure non-zero values of the kernel as a function of the time difference
. So we must also have
and
approaching infinity to avoid
approaching zero. As a result we have
which is a time independent flux that can be taken out from the convolution integral. Finally the remaining integral becomes
. Summarizing the above considerations we obtain
from the long time limit of the time-dependent equation, which is Equation (1).
According to Equation (1) the stationary flux is the left eigenvector of the kernel with an eigenvalue one. The matrix is a probability matrix for stochastic transitions between pairs of milestones. The elements of the matrix are all non-negative and the summation of the entries of any row is one. For this matrix the absolute magnitudes of the eigenvalues are equal or smaller than one.
In the exact variant of Milestoning [
33], the kernel is a function of the phase space positions in the initiating and terminating milestones. That is
where
is a phase space point in milestone
. The exact kernel is a high dimensional operator which makes its direct use challenging. A systematic simplification is desired and discussed below. We can write the flux through milestone
without loss of generality, as a product.
where
is a scalar which is the overall weight of a milestone and
is the normalized probability density at milestone
(
). We can redefine the kernel after averaging over the positions in the milestone and summing over the final state.
Equation (3) is then plugged in Equation (1) to provide an equation for the milestone weights—
:
The lower formula in Equation (4) is easy to solve since the number of milestones and not the distribution within the milestone determines the dimensionality of the matrix. The complication using Equation (4) is that, in general,
is not known. In exact Milestoning we determine progressively more accurate approximations to
and to the flux
using iterations of Equation (1) [
33]
The superscript denotes the iteration number. For example,
is our first approximation to the flux at milestone
. We choose
and we sample configurations in the milestone according to the canonical distribution. With initial distributions at hand, we compute the short trajectories between the milestones and estimate the elements of the matrix
according to Equation (3). We continue to determine the weights of the milestones (Equation (4)) and the fluxes
. The exact version of Milestoning uses the newly generated distribution of terminating trajectories at the milestones to define
and re-computes the weight of the next iteration, repeating the calculations until the process converges. The process is assumed converged if the fluxes remain constant, or an observable of interest, such as the MFPT, does not change its value significantly from iteration to iteration. In the simpler version of Milestoning [
7] we stop after determining
assuming that the Boltzmann distribution is adequate. Rapid convergence of averages with respect to the distribution
is expected for systems at, or close to equilibrium. We tested the use of a single iteration for the system of solvated alanine dipeptide [
34] and numerous other applications.
In the present manuscript, we use Milestoning with a single iteration. However, the procedure described here is directly applicable also for exact Milestoning [
33]. We estimate the transition kernel from trajectories as:
where
is the total number of times a trajectory crossed (or was initiated at) milestone
and
is the number of trajectories that cross milestone
after they passed (or initiated at) milestone
. Note that to normalize
we must have
.
Instead of running many short trajectories between milestones it is also possible to use Milestoning as an analysis tool and to extract the necessary transitions from a long trajectory. A long trajectory, with many reactive events at equilibrium is an exact representation of the dynamics and it can be used to study the committor function and the time scales of the reaction. Hence, the distribution extracted from the long trajectory is exact (the accuracy is restricted only by statistics). We simply monitor the long trajectory and record the milestones that it crosses and the position of the trajectory in the milestone at the crossing to determine the desired distribution function. With the exact results for the distribution at hand, there is no need for the iterations described in Equation (5). We can answer the question “Given that milestone was crossed, what is the probability that the next milestone to be crossed is ?” exactly. The answer to that question, which can be estimated numerically from the data collected from the long trajectory, is the matrix element .
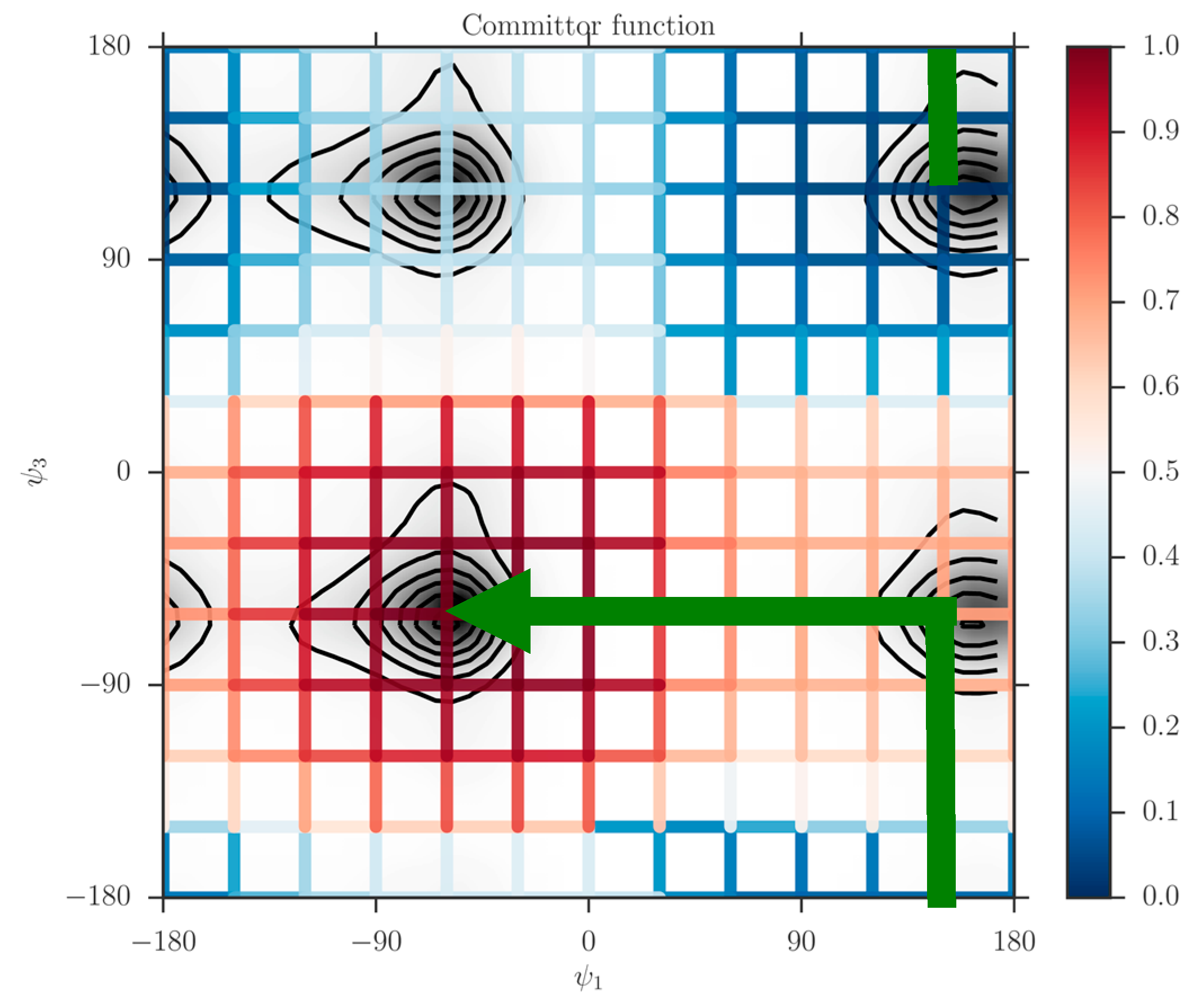
When the milestones are iso-committors or so-called optimal milestones [
27], they are (of course) assigned constant probability to reach the product before the reactant and as a result the kernel in Equation (1) is also an independent of the coordinates in the milestone. The collection of the milestones with the same committor value defines an iso-committor surface. The optimality of the committor hyper-surfaces adds another motivation to the present manuscript. The iso-committor surfaces that we determine with the approach discussed in the next section can be used to redefine the milestones and conduct a new analysis of the long trajectory results with optimal milestones.
2.3. The Committor Function and Milestoning
The theory and algorithm that we propose below follow closely the mathematical approach described in reference [
35]. On the physics side, our algorithm is similar to the Transition Path Theory of E and Vanden Eijnden, which made the committor a core function of their theory [
22,
24], and to the explicit formulation of Cameron and Vanden-Eijnden [
18]. Our results are analogous to Equation (6) of [
18]. However, their core operator,
, is an infinitesimal Markovian propagator in time, our is
, which describes also non-Markovian and stationary (time-independent) flux [
7].
The current formulation uses only a single function that is readily available in Milestoning simulations: the kernel. The kernel, , provides transition probabilities between nearby milestones and is estimated from short trajectories or trajectory fragments between the milestones. It is time independent and is equally applicable to systems in equilibrium or not (if an appropriate function can be found for a non-equilibrium process).
In the Milestoning context, we define the committor function as “Given that we start a trajectory at milestone what is the probability that it will make it to one of the milestones surrounding the product state before the milestones that surround the reactant”? In contrast, we define the kernel as a local function that provides transition probabilities between nearby milestones without crossing other milestones during the transition. In this section, we outline two approaches to determine the committor from the kernel.
The committor
is assumed constant in milestone
and is defined as the probability of making it from
to the product before reaching the reactant for the first time. We denote all the milestones that emerge from the reactants by
and all the milestones that lead to the product by
. We adjust the kernel such that all probabilities
for all
i exiting the reactants are zero. We also set
. The last choice implies that
. Hence, all the trajectories that make it to the product get “stuck” in the product state. Starting from a milestone
there may not be a non-zero element
and therefore the product state cannot be reached in a single “step”. Multiple “steps” are necessary, and depending on the values of the kernel, the number of steps can be large, as illustrated in the example below. To distinguish the adjusted transition probability from the usual kernel of Milestoning we denote the new definition by
. A simple example below illustrates the new construction. Consider a system with four milestones, one that leads to the reactants, one that leads to products, and two intermediate states. Once the flux makes it to the reactant it vanishes. Once the flux reaches the product, it stays in the product with probability one. The
is therefore:
First, we consider the calculation of the flux by power iteration . Let us assume that the initial flux is . After one multiplication by the transition matrix, we obtain a vector . After 10 iterations converged (with error smaller than 10−3) to . The elements of the stationary vector are all zero excluding the product entry.
The committor function is obtained by similar power iterations of the matrix
on the right side.
Interestingly the matrix converged after only 4 iterations (with errors less than 10
−3) to:
Equation (7) is also an iterative adjustment of a vector, consider:
Equation (8) defines iterations of matrix-vector multiplications that converge to the same desired result as Equation (7) in the limit of . For high powers of the transition matrix , the resulting matrix is guaranteed to converge to a fixed value since the absolute magnitudes of the eigenvalues of this matrix are less or equal one. As we multiply the matrix by itself all of its elements are approaching zero excluding the column of the product state (i.e., only for ). These matrix entries are the probabilities that a trajectory that starts at milestone will terminate at the product state and not at the reactant in, at most, steps. Hence, these elements are the values of the committor function of milestone . When multiple milestones bound the product, the value of the committor is a sum over the entries leading to the product. .
We can use Equation (8) as a base for an iterative algorithm to determine . We multiply the current estimate for the committor vector, by and check if the resulting vector converged to the asymptotic value. A convergence check is provided by where is the error tolerance.
The dimensionality of the matrix is the number of milestones, , which is of order of 100 to 10,000. Multiplying a matrix by a vector requires operations if the matrix is dense. The multiplication requires only the non-zero elements of the matrix (in our case about operations) if the matrix is sparse. However, the multiplications are repeated many times and can be computationally expensive. The iteration will converge more rapidly if the eigenvalue gap is significant. In other words, that the difference between the largest and the rest of the eigenvalues is big.
The second algorithm to determine the committors from a Milestoning kernel is based on solving linear equations. The advantage of the linear formulation is that many algorithms are available to address this type of linear problems. Consider trajectories that start at milestone
. The committor value of milestone
is
. In a single transition, the trajectories cross milestones
with probabilities
for all
. The sum
is set to one, and therefore all the trajectories that start at
are accounted for. The committor values of all the trajectories after the first step is the sum of the probabilities that they made it to milestone
multiplied by their committor values
:
. This probability must be equal to the initial value of the committor
. We have:
If we insert the boundary conditions
and
to the equation we have for all
We can write more compactly Equation (10) as
Equation (11) is a straightforward linear equation for the committor coefficients that is solved by standard approaches. Note that because of the boundary conditions for at the reactant and the product the equation is not homogeneous and has a unique solution.
The solution of Equation (11) is the same as the solution of Equation (8). We show that by substituting in (11) the solution from Equation (8)
The last equality is a result of the convergence of the power iterations, which proves that the solution of Equation (8) solves Equation (11). Since the solution is unique we demonstrate the equivalence of the two approaches.
For an illustration, we are using a long time trajectory to determine the kernel in the examples provided in this manuscript. The long path is decomposed to trajectory fragments between milestones to obtain transition statistics. Instead of a long trajectory, it is possible to use an ensemble of short trajectories with initial conditions sampled at the milestones [
31,
33,
34]. Use of multiple paths is much more efficient than the calculations of a single trajectory, and motivation for the use of the Milestoning algorithm [
34]. Nevertheless, a single long trajectory is trivial to conduct using any Molecular Dynamics software. The sampling of initial conditions and on-the-fly recording of crossing events with short trajectories are more complex to implement and require additional programming. Here we use a single trajectory to illustrate that straightforward MD software (or pre-computed trajectories) can be used as well to determine committors. There is another advantage of using a long trajectory in the context of Milestoning. The calculation of MFPT is exact in the over damped limit of Langevin dynamics if the milestones are iso-committors [
27]. It is possible to use the procedure described in this paper to redefine the milestones as iso-committors. In exact Milestoning or variants of Milestoning that use many short trajectories re-definition of the milestones implies calculations of new trajectories. However, if a long trajectory is at hand there is no need to re-compute dynamic pathways; only a new analysis of transition events through the new milestones is required.