Divergence and Sufficiency for Convex Optimization

Abstract

Logarithmic score and information divergence appear in information theory, statistics, statistical mechanics, and portfolio theory. We demonstrate that all these topics involve some kind of optimization that leads directly to regret functions and such regret functions are often given by Bregman divergences. If a regret function also fulfills a sufficiency condition it must be proportional to information divergence. We will demonstrate that sufficiency is equivalent to the apparently weaker notion of locality and it is also equivalent to the apparently stronger notion of monotonicity. These sufficiency conditions have quite different relevance in the different areas of application, and often they are not fulfilled. Therefore sufficiency conditions can be used to explain when results from one area can be transferred directly to another and when one will experience differences.

1. Introduction

One of the main purposes of information theory is to compress data so that data can be recovered exactly or approximately. One of the most important quantities was called entropy because it is calculated according to a formula that mimics the calculation of entropy in statistical mechanics. Another key concept in information theory is information divergence (KL-divergence) that is defined for probability vectors P and Q as

$$D\left(P\parallel Q\right)=\sum _{x}P(x)ln\frac{P(x)}{Q(x)}.$$

It was introduced by Kullback and Leibler in 1951 in a paper entitled On Information and Sufficiency [1]. The link from information theory back to statistical physics was developed by E.T. Jaynes via the maximum entropy principle [2,3,4]. The link back to statistics is now well established [5,6,7,8,9].

Related quantities appear in information theory, statistics, statistical mechanics, and finance, and we are interested in a theory that describes when these relations are exact and when they just work by analogy. First we introduce some general results about optimization on state spaces of finite dimensional C*-algebras. This part applies exactly to all the topics under consideration and lead to Bregman divergences or more general regret functions. Secondly, we introduce several notions of sufficiency and show that this leads to information divergence. In a number of cases it is not possible or not relevant to impose the condition of sufficiency, which can explain why regret function are not always equal to information divergence.

2. Structure of the State Space

Our knowledge about a system will be represented by a state space. I many applications the state space is given by a set of probability distributions on a sample space. In such cases the state space is a simplex, but it is well-known that the state space is not a simplex in quantum physics. For applications in quantum physics the state space is often represented by a set of density matrices, i.e., positive semidefinite complex matrices with trace 1. In some cases the states are represented as elements of a finite dimensional $C^{*}$-algebra, which is a direct sum of matrix algebras. A finite dimensional $C^{*}$-algebra that is a sum of $1\times 1$ matrices has a state space that is a simplex, so the state spaces of finite dimensional $C^{*}$-algebras contain the classical probability distributions as special cases.

The extreme points in the set of states are the pure states. The pure states of a $C^{*}$-algebra can be identified with projections of rank 1. Two density matrices $s_1$ and $s_2$ are said to be orthogonal if $s_1{s}_2=s_2{s}_1=0.$ Any state s has a decomposition

$$s=\sum {\lambda }_i{s}_i$$

where $s_i$ are orthogonal pure states. Such a decomposition is not unique, but for a finite dimensional $C^{*}$-algebra the coefficients ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$ are unique and are called the spectrum of the state.

Sometimes more general state spaces are of interest. In generalized probabilistic theories a state space is a convex set where mixtures are defined by randomly choosing certain states with certain probabilities [10,11]. A convex set where all orthogonal decompositions of a state have the same spectrum, is called a spectral state space. Much of the theory in this paper can be generalized to spectral sets. The most important spectral sets are sets of positive elements with trace 1 in Jordan algebras. The study of Jordan algebras and other spectral sets is relevant for the foundation of quantum theory [12,13,14,15], but in this paper we will restrict our attention to states on finite dimensional $C^{*}$-algebras. Nevertheless some of the theorems and proofs are stated in such a way that they hold for more general state spaces.

3. Optimization

Let $\mathcal{S}$ denote a state space of a finite dimensional $C^{*}$-algebra and let $\mathcal{A}$ denote a set of self-adjoint operators. Each $a\in \mathcal{A}$ is identified with a real valued measurement. The elements of $\mathcal{A}$ may represent feasible actions (decisions) that lead to a payoff like the score of a statistical decision, the energy extracted by a certain interaction with the system, (minus) the length of a codeword of the next encoded input letter using a specific code book, or the revenue of using a certain portfolio. For each $s\in \mathcal{S}$ the mean value of the measurement $a\in \mathcal{A}$ is given by

$$⟨a,s⟩=\mathrm{tr}(\mathrm{as}).$$

In this way the set of actions may be identified with a subset of the dual space of $\mathcal{S}$.

Next we define

$$F\left(s\right)=\underset{a\in \mathcal{A}}{sup}⟨a,s⟩.$$

We note that F is convex, but F need not be strictly convex. In principle $F(s)$ may be infinite, but we will assume that $F(s)<\infty$ for all states s. We also note that F is lower semi-continuous. In this paper we will assume that the function F is continuous. The assumption that F is a real valued continuous function is fulfilled for all the applications we consider.

If s is a state and $a\in \mathcal{A}$ is an action then we say that a is optimal for s if $⟨a,s⟩=F\left(s\right)$. A sequence of actions $a_n\in \mathcal{A}$ is said to be asymptotically optimal for the state s if $⟨a,s⟩\to F\left(s\right)$ for $n\to \infty .$

If $a_i$ are actions and $\left(t_i\right)$ is a probability vector then we we may define the mixed action $\sum t_i·a_i$ as the action where we do the action $a_i$ with probability $t_i.$ We note that $⟨\sum t_i·a_i,s⟩=\sum t_i·⟨a_i,s⟩.$ We will assume that all such mixtures of feasible actions are also feasible. If $a_1\left(s\right)\ge a_2\left(s\right)$ almost surely for all states we say that $a_1$ dominates $a_2$ and if $a_1\left(s\right)>a_2\left(s\right)$ almost surely for all states s we say that $a_1$ strictly dominates $a_2.$ All actions that are dominated may be removed from $\mathcal{A}$ without changing the function $F.$ Let ${\mathcal{A}}_F$ denote the set of self-adjoint operators (observables) a such that $⟨a,s⟩\le F\left(s\right).$ Then $F\left(s\right)={sup}_{a\in {\mathcal{A}}_F}⟨a,s⟩.$ Therefore we may replace $\mathcal{A}$ by ${\mathcal{A}}_F$ without changing the optimization problem.

In the definition of regret we follow Servage [16] but with different notation.

Definition 1.

Let F denote a convex function on the state space $\mathcal{S}$. If $F\left(s\right)$ is finite the regret of the action a is defined by

$$D_F\left(s,a\right)=F\left(s\right)-⟨a,s⟩.$$

(1)

The notion of regret has been discussed in detail in [17,18,19]. In [20] it was proved that if a regret based decision procedure is transitive then it must be equal to a difference in expected utility as in Equation (1), which rules out certain non-linear models in [17,19].

Proposition 1.

The regret $D_F$ of actions has the following properties:

• $D_F\left(s,a\right)\ge 0$ with equality if a is optimal for s.
• $s\to D_F\left(s,a\right)$ is a convex function.
• If $\overline{a}$ is optimal for the state $\overline{s}=\sum t_i·s_i$ where $\left(t_1,t_2,\dots ,t_{\ell }\right)$ is a probability vector then

  $$\sum t_i·D_F\left(s_i,a\right)=\sum t_i·D_F\left(s_i,\overline{a}\right)+D_F\left(\overline{s},a\right).$$
• $\sum t_i·D_F\left(s_i,a\right)$ is minimal if a is optimal for $\overline{s}=\sum t_i·s_i$.

If the state is $s_1$ but one acts as if the state were $s_0$ one may compare what one achieves and what could have been achieved. If the state $s_0$ has a unique optimal action a we may simply define the regret of $s_0$ by

$$D_F\left(s_1,s_0\right)=D_F\left(s_1,a\right).$$

The following definition leads to a regret function that is essentially equivalent to the so-called generalized Bregman divergences defined by Kiwiel [21,22].

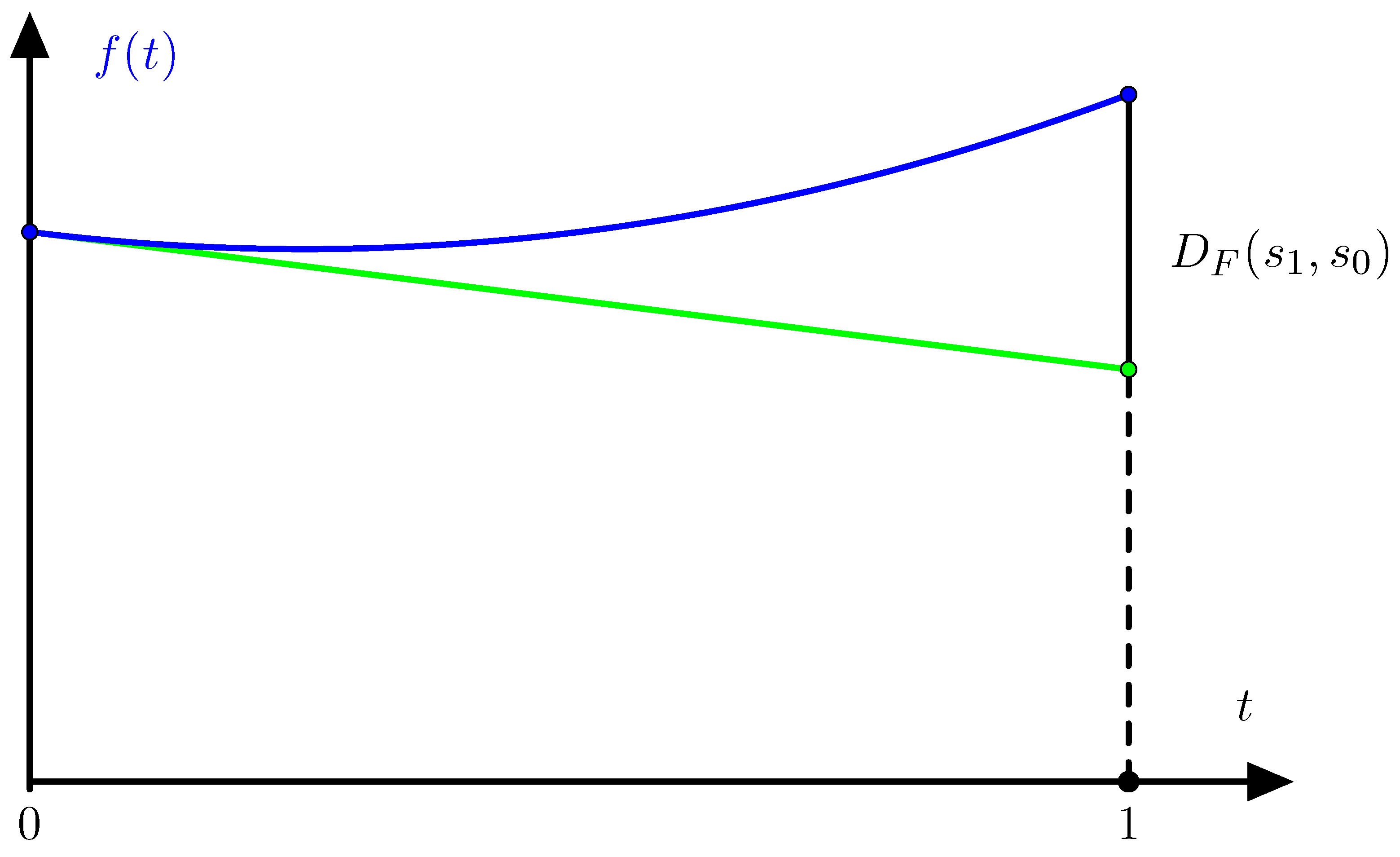
Definition 2.

Let F denote a convex function on the state space $\mathcal{S}$. If $F\left(s_1\right)$ is finite then we define the regret of the state $s_0$ as

$$D_F\left(s_1,s_0\right)=\underset{\left(a_n\right)}{inf}\underset{n\to \infty }{lim}{D}_F\left(s_1,a_n\right)$$

where the infimum is taken over all sequences of actions $\left(a_n\right)$ that are asymptotically optimal for $s_0.$

With this definition the regret is always defined with values in $[0,\infty ]$ and the value of the regret $D_F\left(s_1,s_0\right)$ only depends on the restriction of the function F to the line segment from $s_0$ to $s_1$. Let f denote the function $f(t)=F\left((1-t)s_0+t{s}_1\right)$ where $t\in [0,1]$. As illustrated in Figure 1 we have

$$D_F\left(s_1,s_0\right)=f\left(1\right)-\left(f\left(0\right)+f_{+}^{\prime }(0)\right)$$

(2)

where $f_{+}^{\prime }(0)$ denotes the right derivative of f at $t=0$. Equation (2) is even valid when the regret is infinite if we allow the right derivative to take the value −∞.

Figure 1. The regret equals the vertical distance between curve and tangent.

If the state $s_0$ has the unique optimal action $a\in \mathcal{A}$ then

$$F\left(s_1\right)=D_F\left(s_1,s_0\right)+⟨a,s_1⟩$$

(3)

so the function F can be reconstructed from $D_F$ except for an affine function of $s_1.$ The following proposition follows from Alexandrov’s theorem ([23], Theorem 25.5).

Proposition 2.

A convex function on a finite dimensional convex set is differentiable almost everywhere with respect to the Lebesgue measure.

A state $s_0$ where F is differentiable has a unique optimal action. Therefore Equation (3) holds for almost any state $s_0$. In particular the function F can be reconstructed from $D_F$ except for an affine function.

Proposition 3.

The regret $D_F$ of states has the following properties:

• $D_F\left(s_1,s_0\right)\ge 0$ with equality if there exists an action a that is optimal for both $s_1$ and $s_0$.
• $s_1\to D_F\left(s_1,s_0\right)$ is a convex function.

Further, the following two conditions are equivalent:

• $D_F\left(s_1,s_0\right)=0$ implies $s_1=s_0$.
• The function F is strictly convex.

We say that a regret function $D_F$ is strict if F is strictly convex. The two last properties Proposition 1 do not carry over to regret for states except if the regret is a Bregman divergence as defined below. The regret is called a Bregman divergence if it can be written in the following form

$$\begin{array}{cc}\hfill D_F\left(s_1,s_0\right)& =F\left(s_1\right)-\left(F\left(s_0\right)+⟨s_1-s_0,\nabla F\left(s_0\right)⟩\right)\hfill \end{array}$$

(4)

where $⟨·,·⟩$ denotes the (Hilbert-Schmidt) inner product. In the context of forecasting and statistical scoring rules the use of Bregman divergences dates back to [24]. A similar but less general definition of regret was given by Rao and Nayak [25] where the name cross entropy was proposed. Although Bregman divergences have been known for many years they did not gain popularity before the paper [26] where a systematic study of Bregman divergences was presented.

We note that if $D_F$ is a Bregman divergence and $s_0$ minimizes F then $\nabla F\left(s_0\right)=0$ so that the formula for the Bregman divergence reduces to

$$D_F\left(s_1,s_0\right)=F\left(s_1\right)-F\left(s_0\right).$$

Bregman divergences satisfy the Bregman identity

$$\sum t_i·D_F\left(s_i,s\right)=\sum t_i·D_F\left(s_i,\overline{s}\right)+D_F\left(\overline{s},s\right),$$

(5)

but if F is not differentiable this identity can be violated.

Example 1.

Let the state space be the interval $\left[0,1\right]$ with two actions $⟨a_0,s⟩=1-2s$ and $⟨a_1,s⟩=2s-1.$ Let $s_0=0$ and $s_1=1.$ Let further $t_0=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ and $t_1=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right..$ Then $\overline{s}=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right..$ If $s=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ then

$$\sum t_i·D_F\left(s_i,s\right)=0,$$

but

$$\begin{array}{ccc}\hfill \sum t_i·D_F\left(s_i,\overline{s}\right)& =& \frac{1}{3}·\left(⟨a_0,0⟩-⟨a_1,0⟩\right)+\frac{2}{3}·\left(⟨a_1,1⟩-⟨a_1,1⟩\right)\hfill \\ & =& \frac{1}{3}·\left(1-\left(-1\right)\right)\hfill \\ & =& \frac{2}{3}.\hfill \end{array}$$

Clearly the Bregman identity (5) is violated and $\sum t_i·D_F\left(s_i,s\right)$ will increase if s is replaced by $\overline{s}$.

The following proposition is easily proved.

Proposition 4.

For a convex and continuous function F on the state space $\mathcal{S}$ the following conditions are equivalent:

• The function F is differentiable in the interior of any face of $\mathcal{S}$.
• The regret $D_F$ is a Bregman divergence.
• The Bregman identity (5) is always satisfied.
• For any probability vectors $\left(t_1,t_2,\dots ,t_n\right)$ the sum $\sum t_i·D_F\left(s_i,s\right)$ is always minimal when $s=\sum t_i·s_i$.

4. Examples

In this section we shall see how regret functions are defined in some applications.

4.1. Information Theory

We recall that a code is uniquely decodable if any finite sequence of input symbols give a unique sequence of output symbols. It is well-known that a uniquely decodable code satisfies Kraft’s inequality (see [27] and ([28], Theorem 3.8))

$$\sum _{a\in \mathbb{A}}{\beta }^{-\ell \left(a\right)}\le 1$$

(6)

where $\ell \left(a\right)$ denotes the length of the codeword corresponding to the input symbol $a\in \mathbb{A}$ and $\beta$ denotes the size of the output alphabet $\mathbb{B}$. Here the length of a codeword is an integer. If $P={\left(p_a\right)}_{a\in \mathbb{A}}$ is a probability vector over the input alphabet, then the mean code-length is

$$\sum _{a\in \mathbb{A}}\ell \left(a\right)·p_a.$$

Our goal is to minimize the expected code-length. Here the state space consist of probability distributions over the input alphabet and the actions are code-length functions.

Shannon established the inequality

$$-\sum _{a\in \mathbb{A}}{log}_b\left(p_a\right)·p_a\le min\sum _{a\in \mathbb{A}}\ell \left(a\right)·p_a\le -\sum _{a\in \mathbb{A}}{log}_b\left(p_a\right)·p_a+1.$$

It is a combinatoric problem to find the optimal code-length function. In the simplest case with a binary output alphabet the optimal code-length function is determined by the Huffmann algorithm.

A code-length function dominates another code-length function if all letters have shorter code-length. If a code-length function is not dominated by another code-length function then for all $a\in \mathbb{A}$ the length is bounded by $\ell \left(a\right)\le \left|\mathbb{A}\right|-1.$ For fixed alphabets $\mathbb{A}$ and $\mathbb{B}$ there exists only a finite number of code-length functions ℓ that satisfy Kraft’s inequality and are not dominated by other code-length functions that satisfying Kraft’s inequality.

4.2. Scoring Rules

The use of scoring rules has a long history in statistics. An early contribution was the idea of minimizing the sum of square deviations that dates back to Gauss and works perfectly for Gaussian distributions. In the 1920s, Ramsay and de Finetti proved versions of the Dutch book theorem where determination of probability distributions were considered as dual problems of maximizing a payoff function [29]. Later it was proved that any consistent inference procedure corresponds to optimizing with respect to some payoff function. A more systematic study of scoring rules was given by McCarthy [30].

Consider an experiment with $\mathcal{X}=\left\{1,2,\dots ,\ell \right\}$ as sample space. A scoring rule f is defined as a function $\mathcal{X}\times M_1^{+}\left(\mathcal{X}\right)\to \mathbb{R}$ such that the score is $f\left(x,Q\right)$ when a prediction has been given in terms of a probability distribution Q and $x\in \mathcal{X}$ has been observed. A scoring rule is proper if for any probability measure $P\in M_1^{+}\left(\mathcal{X}\right)$ the score ${\sum }_{x\in \mathcal{X}}P\left(x\right)·f\left(x,Q\right)$ is minimal when $Q=P.$ Here the state space consist of probability distributions over $\mathcal{X}$ and the actions are predictions over $\mathcal{X}$, which are also probability distributions over $\mathcal{X}$.

There is a correspondence between proper scoring rules and Bregman divergences as explained in [31,32]. If $D_F$ is a Bregman divergence and g is a function with domain $\mathcal{X}$ then f given by $f\left(x,Q\right)=g\left(x\right)-D_F\left({\delta }_x,Q\right)$ defines a scoring rule.

Assume that f is a proper scoring function. Then a function F can be defined as

$$F(P)=\sum _{x\in \mathcal{X}}P\left(x\right)·f\left(x,P\right).$$

This lead to the regret function

$$D_F\left(P,Q\right)=F(P)-\sum _{x\in \mathcal{X}}P\left(x\right)·f\left(x,Q\right).$$

(7)

Since f is assumed to be proper $D_F\left(P,Q\right)\ge 0$. The Bregman identity (5) follows by straight forward calculations. With these two results we see that the regret function $D_F$ is a Bregman divergence and that

$$\begin{array}{cc}\hfill D_F\left({\delta }_y,Q\right)& ={\displaystyle \sum _{x\in \mathcal{X}}}{\delta }_y\left(x\right)·f\left(x,{\delta }_y\right)-{\displaystyle \sum _{x\in \mathcal{X}}}{\delta }_y\left(x\right)·f\left(x,Q\right)\hfill \\ & =f\left(y,{\delta }_y\right)-f\left(y,Q\right).\hfill \end{array}$$

(8)

Hence a proper scoring rule f has the form $f\left(x,Q\right)=g(x)-D_F\left({\delta }_x,Q\right)$ where $g(x)=f\left(x,{\delta }_x\right)$. A strictly proper scoring rule can be defined as a proper scoring rule where the corresponding Bregman divergence is strict.

Example 2.

The Brier score is given by

$$f\left(x,Q\right)=\frac{1}{n}\left(\sum _{y\in \mathcal{X}}{\left(Q\left(y\right)-{\delta }_x\left(y\right)\right)}^2\right).$$

The Brier score is generated by the strictly convex function $F\left(P\right)=\frac{1}{n}{\sum }_{x\in \mathcal{X}}P{\left(x\right)}^2$.

4.3. Statistical Mechanics

Thermodynamics is the study of concepts like heat, temperature and energy. A major objective is to extract as much energy from a system as possible. The idea in statistical mechanics is to view the macroscopic behavior of a thermodynamic system as a statistical consequence of the interaction between a lot of microscopic components where the interacting between the components are governed by very simple laws. Here the central limit theorem and large deviation theory play a major role. One of the main achievements is the formula for entropy as a logarithm of a probability.

Here we shall restrict the discussion to the most simple kind of thermodynamic system from which we want to extract energy. We may think of a system of non-interacting spin particles in a magnetic field. For such a system the Hamiltonian is given by

$$\widehat{H}\left(\sigma \right)=-\mu \sum h_j{\sigma }_j$$

where $\sigma$ is the spin configuration, $\mu$ is the magnetic moment, $h_j$ is the strength of an external magnetic field, and ${\sigma }_j=\pm 1$ is the spin of the the j’th particle. If the system is in thermodynamic equilibrium the configuration probability is

$$P_{\beta }\left(\sigma \right)=\frac{exp\left(-\beta \widehat{H}\left(\sigma \right)\right)}{Z_{\beta }}$$

where $Z\left(\beta \right)$ is the partition function

$$Z\left(\beta \right)=\sum _{\sigma }exp\left(-\beta \widehat{H}\left(\sigma \right)\right).$$

Here $\beta$ is the inverse temperature ${\left(kT\right)}^{-1}$ of the spin system and $k=1.381\times {10}^{-23}\raisebox{1ex}{$\mathrm{J}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{K}$}\right.$ is Boltzmann’s constant.

The mean energy is given by

$$\sum _{\sigma }{P}_{\beta }\left(\sigma \right)\widehat{H}\left(\sigma \right),$$

which will be identified with the internal energy U defined in thermodynamics. The Shannon entropy can be calculated as

$$\begin{array}{cc}\hfill -{\displaystyle \sum _{\sigma }}{P}_{\beta }\left(\sigma \right)ln{P}_{\beta }\left(\sigma \right)& =-{\displaystyle \sum _{\sigma }}{P}_{\beta }\left(\sigma \right)ln\frac{exp\left(-\beta \widehat{H}\left(\sigma \right)\right)}{Z_{\beta }}\hfill \\ & =-{\displaystyle \sum _{\sigma }}{P}_{\beta }\left(\sigma \right)\left(-\beta \widehat{H}\left(\sigma \right)-lnZ\left(\beta \right)\right)\hfill \\ & =\beta ·U+lnZ\left(\beta \right).\hfill \end{array}$$

The Shannon entropy times k will be identified with the thermodynamic entropy S.

The amount of energy that can be extracted from the system if a heat bath is available, is called the exergy [33]. We assume that the heat bath has temperature $T_0$ and the internal energy and entropy of the system are $U_0$ and $S_0$ if the system has been brought in equilibrium with the heat bath. The exergy can be calculated by

$$\begin{array}{cc}\hfill Ex& =U-U_0-T_0\left(S-S_0\right)\hfill \\ & =U-U_0-k{T}_0\left(\beta ·U+lnZ\left(\beta \right)-{\beta }_0{U}_0-lnZ\left({\beta }_0\right)\right)\hfill \\ & =k{T}_0\left(\left({\beta }_0-\beta \right)·U+ln\frac{Z\left({\beta }_0\right)}{Z\left(\beta \right)}\right).\hfill \end{array}$$

The information divergence between the actual state and the corresponding state that is in equilibrium with the environment is

$$\begin{array}{cc}\hfill D\left(P_{\beta }∥P_{{\beta }_0}\right)& ={\displaystyle \sum _{\sigma }}{P}_{\beta }\left(\sigma \right)ln\frac{P_{\beta }\left(\sigma \right)}{P_{{\beta }_0}\left(\sigma \right)}\hfill \\ & ={\displaystyle \sum _{\sigma }}{P}_{\beta }\left(\sigma \right)ln\frac{\frac{exp\left(-\beta \widehat{H}\left(\sigma \right)\right)}{Z\left(\beta \right)}}{\frac{exp\left(-{\beta }_0\widehat{H}\left(\sigma \right)\right)}{Z\left({\beta }_0\right)}}\hfill \\ & ={\displaystyle \sum _{\sigma }}{P}_{\beta }\left(\sigma \right)\left(-\beta \widehat{H}\left(\sigma \right)+{\beta }_0\widehat{H}\left(\sigma \right)+ln\frac{Z\left({\beta }_0\right)}{Z\left(\beta \right)}\right)\hfill \\ & =\left({\beta }_0-\beta \right)·{\displaystyle \sum _{\sigma }}{P}_{\beta }\left(\sigma \right)\widehat{H}\left(\sigma \right)+ln\frac{Z\left({\beta }_0\right)}{Z\left(\beta \right)}\hfill \\ & =\left({\beta }_0-\beta \right)·U+ln\frac{Z\left({\beta }_0\right)}{Z\left(\beta \right)}.\hfill \end{array}$$

Hence

$$Ex=k{T}_{0}D\left(P_{\beta }∥P_{{\beta }_0}\right).$$

This equation appeared already in [34].

4.4. Portfolio Theory

The relation between information theory and gambling was established by J. L. Kelly [35]. Logarithmic terms appear because we are interested in the exponent in the exponential growth rate of our wealth. Later Kelly’s approach has been generalized to trading of stocks although the relation to information theory is weaker [36].

Let $X_1,X_2,\dots ,X_k$ denote price relatives for a list of k assets. For instance $X_5=1.04$ means that 5-th asset increases its value by 4%. Such price relatives are mapped into a price relative vector $\overrightarrow{X}=\left(X_1,X_2,\dots ,X_k\right).$

Example 3.

A special asset is the safe asset where the price relative is 1 for any possible price relative vector. Investing in this asset corresponds to placing the money at a safe place with interest rate equal to 0%.

A portfolio is a probability vector $\overrightarrow{b}=\left(b_1,b_2,\dots ,b_k\right)$ where for instance $b_5=0.3$ means that 30% of the money is invested in asset no. 5. We note that a portfolio may be traded just like the original assets. The price relative for the portfolio $\overrightarrow{b}$ is $X_1·b_1+X_2·b_2+\dots +X_k·b_k=⟨\overrightarrow{X},\overrightarrow{b}⟩.$ The original assets may be considered as extreme points in the set of portfolios. If an asset has the property that the price relative is only positive for one of the possible price relative vectors, then we may call it a gambling asset.

We now consider a situation where the assets are traded once every day. For a sequence of price relative vectors ${\overrightarrow{X}}_1,\overrightarrow{X_2},\dots {\overrightarrow{X}}_n$ and a constant re-balancing portfolio $\overrightarrow{b}$ the wealth after n days is

$$\begin{array}{ccc}\hfill S_n& =& {\displaystyle \prod _{i=1}^n}⟨{\overrightarrow{X}}_i,\overrightarrow{b}⟩\hfill \end{array}$$

(9)

$$\begin{array}{cc}=& exp\left({\displaystyle \sum _{i=1}^n}ln\left(⟨{\overrightarrow{X}}_i,\overrightarrow{b}⟩\right)\right)\hfill \end{array}$$

(10)

$$\begin{array}{cc}=& exp\left(n·E\left[ln⟨\overrightarrow{X},\overrightarrow{b}⟩\right]\right)\hfill \end{array}$$

(11)

where the expectation is taken with respect to the empirical distribution of the price relative vectors. Here $E\left[ln⟨\overrightarrow{X},\overrightarrow{b}⟩\right]$ is proportional to the doubling rate and is denoted $W\left(\overrightarrow{b},P\right)$ where P indicates the probability distribution of $\overrightarrow{X}$. Our goal is to maximize $W\left(\overrightarrow{b},P\right)$ by choosing an appropriate portfolio $\overrightarrow{b}.$ The advantage of using constant rebalancing portfolios was demonstrated in [37].

Definition 3.

Let ${\overrightarrow{b}}_1$ and ${\overrightarrow{b}}_2$ denote two portfolios. We say that ${\overrightarrow{b}}_1$ dominates ${\overrightarrow{b}}_2$ if $⟨{\overrightarrow{X}}_j,{\overrightarrow{b}}_1⟩\ge ⟨{\overrightarrow{X}}_j,{\overrightarrow{b}}_2⟩$ for any possible price relative vector ${\overrightarrow{X}}_j$ $j=1,2,\dots ,n.$ We say that ${\overrightarrow{b}}_1$ strictly dominates ${\overrightarrow{b}}_2$ if $⟨{\overrightarrow{X}}_j,{\overrightarrow{b}}_1⟩>⟨{\overrightarrow{X}}_j,{\overrightarrow{b}}_2⟩$ for any possible price relative vector ${\overrightarrow{X}}_j$ $j=1,2,\dots ,n.$ A set A of assets is said to dominate the set of assets B if any asset in B is dominated by a portfolio of assets in $A.$

The maximal doubling rate does not change if dominated assets are removed. Sometimes assets that are dominated but not strictly dominated may lead to non-uniqueness of the optimal portfolio.

Let ${\overrightarrow{b}}_P$ denote a portfolio that is optimal for P and define

$$G(P)=W\left({\overrightarrow{b}}_P,P\right).$$

(12)

The regret of choosing a portfolio that is optimal for Q when the distribution is P is given by the regret function

$$D_G(P,Q)=W\left({\overrightarrow{b}}_P,P\right)-W\left({\overrightarrow{b}}_Q,P\right).$$

(13)

If ${\overrightarrow{b}}_Q$ is not uniquely determined we take a minimum over all $\overrightarrow{b}$ that are optimal for $Q.$

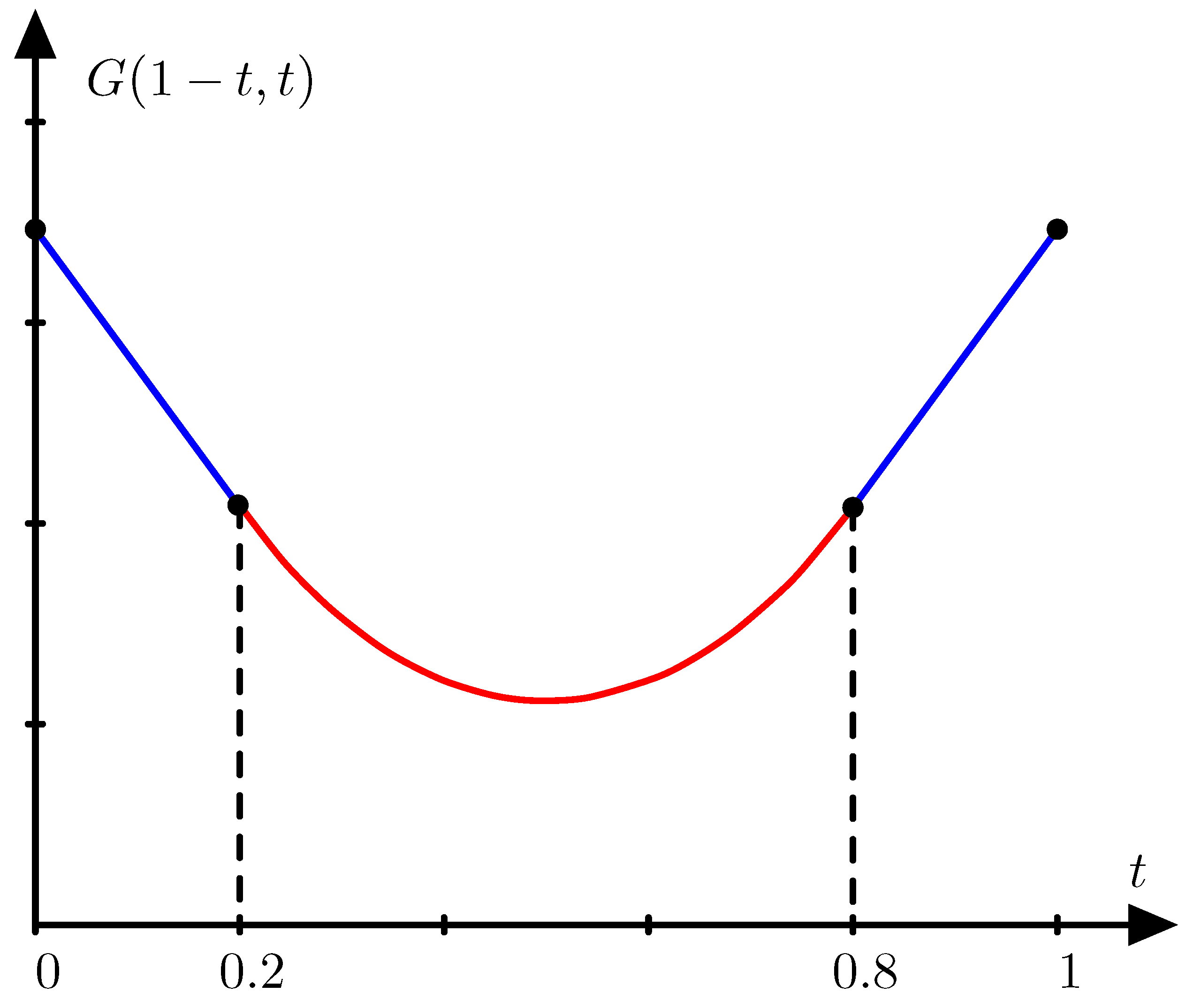
Example 4.

Assume that the price relative vector is $\left(2,\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)$ with probability $1-t$ and $\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,2\right)$ with probability t. Then the portfolio concentrated on the first asset is optimal for $t\le \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$ and the portfolio concentrated on the second asset is optimal for $t>\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$. For values of t between $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$ and $\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$ the optimal portfolio invests money on both assets as illustrated in Figure 2.

Figure 2. The function G for the price relative vectors in Example 4.

Lemma 1.

If there are only two price relative vectors and the regret function is strict then either one of the assets dominates all other assets or two of the assets are orthogonal gambling assets that dominate all other assets.

Proof. 

We will assume that no assets are dominated by other assets. Let

$$\begin{array}{ccc}\hfill \overrightarrow{X}& =& \left(X_1,X_2,\dots ,X_k\right)\hfill \\ \hfill \overrightarrow{Y}& =& \left(Y_1,Y_2,\dots ,Y_k\right)\hfill \end{array}$$

denote the two price relative vectors. Without loss of generality we may assume that

$$\frac{X_1}{Y_1}\ge \frac{X_2}{Y_2}\ge \dots \ge \frac{X_k}{Y_k}.$$

If $\frac{X_i}{Y_i}=\frac{X_{i+1}}{Y_{i+1}}$ then $\frac{X_i}{X_{i+1}}=\frac{Y_i}{Y_{i+1}}$ so that if $X_i\le X_{i+1}$ then $Y_i\le Y_{i+1}$ and the asset i is dominated by the asset $i+1.$ Since we have assumed that no assets are dominated we may assume that

$$\frac{X_1}{Y_1}>\frac{X_2}{Y_2}>\dots >\frac{X_k}{Y_k}.$$

If $P=\left(1-t,t\right)$ is a probability vector over the two price relative vectors then according to [36] the portfolio $\overrightarrow{b}=\left(b_1,b_2,\dots ,b_n\right)$ is optimal if and only if

$$(1-t)\frac{X_i}{b_1{X}_1+\dots +b_k{X}_k}+t\frac{Y_i}{b_1{Y}_1+\dots +b_k{Y}_k}\le 1$$

for all $i\in \left\{1,2,\dots ,k\right\}$ with equality if $b_i>0.$ Assume that the portfolio $\overrightarrow{b}={\delta }_j$ is optimal. Now

$$\left(1-t\right)\frac{X_{j+1}}{X_j}+t\frac{Y_{j+1}}{Y_j}\le 1$$

is equivalent to

$$t\le \frac{\frac{X_j}{Y_{j+1}}-\frac{X_{j+1}}{Y_{j+1}}}{\frac{X_j}{Y_j}-\frac{X_{j+1}}{Y_{j+1}}}.$$

(14)

Similarly

$$\left(1-t\right)\frac{X_{j-1}}{X_j}+t\frac{Y_{j-1}}{Y_j}\le 1$$

is equivalent to

$$t\ge \frac{\frac{X_j}{Y_{j-1}}-\frac{X_{j-1}}{Y_{j-1}}}{\frac{X_j}{Y_j}-\frac{X_{j-1}}{Y_{j-1}}}.$$

(15)

We have to check that

$$\frac{\frac{X_j}{Y_{j-1}}-\frac{X_{j-1}}{Y_{j-1}}}{\frac{X_j}{Y_j}-\frac{X_{j-1}}{Y_{j-1}}}<\frac{\frac{X_j}{Y_{j+1}}-\frac{X_{j+1}}{Y_{j+1}}}{\frac{X_j}{Y_j}-\frac{X_{j+1}}{Y_{j+1}}},$$

which is equivalent with

$$0<X_j{Y}_{j-1}-Y_{j-1}{X}_{j+1}-Y_j{X}_{j-1}-\left(X_j{Y}_{j+1}-Y_{j+1}{X}_{j-1}-Y_j{X}_{j+1}\right).$$

The right hand side equals the determinant

$$\left|\begin{array}{cc}{X}_{j+1}-X_{j-1}& X_j-X_{j-1}\\ Y_{j+1}-Y_{j-1}& Y_j-Y_{j-1}\end{array}\right|,$$

which is positive because asset j is not dominated by a portfolio based on asset $j-1$ and asset $j+1.$

We see that the portfolio concentrated in asset j is optimal for t in an interval of positive length and the regret between distributions in such an interval will be zero. In particular the regret will not be strict.

Strictness of the regret function is only possible if there are only two assets and if a portfolio concentrated on one of these assets is only optimal for a singular probability measure. According to the formulas for the end points of intervals (14) and (15) this is only possible if the assets are gambling assets. ☐

Theorem 1.

If the regret function is strict it equals information divergence, i.e.,

$$D_G(P,Q)=D\left(P\parallel Q\right).$$

(16)

Proof. 

If the regret function is strict then it is also strict when we restrict to two price relative vectors. Therefore any two price relative vectors are orthogonal gambling assets. If the assets are orthogonal gambling assets we get the type of gambling described by Kelly [35], for gambling equations can easily be derived [36]. ☐

5. Sufficiency Conditions

In this section we will introduce some conditions on a regret function. Under some mild conditions they turn out to be equivalent.

Theorem 2.

Let $D_F$ denote a regret function based on a continuous and convex function F defined on the state space of a finite dimensional $C^{*}$-algebra. If the state space has at least three orthogonal states then the following conditions are equivalent:

• The function F equals entropy times a negative constant plus an affine function.
• The regret $D_F$ is proportional to information divergence.
• The regret is monotone.
• The regret satisfies sufficiency.
• The regret is local.

In the rest of this section we will describe each of these equivalent conditions and prove that they are actually equivalent. The theorems and proofs will be stated so that they hold even for more general state spaces than the ones considered in this paper.

5.1. Entropy and Information Divergence

Definition 4.

Let s denote an element in a state space. The entropy of s is defined as

$$H\left(s\right)=inf\left(-\sum _{i=1}^n{\lambda }_{i}ln\left({\lambda }_i\right)\right)$$

where the infimum is taken over all decompositions $s={\sum }_{i=1}^n{\lambda }_i{s}_i$ of s into pure states $s_i$.

This definition of the entropy of a state was first given by Uhlmann [38]. Using the fact that entropy is decreasing under majorization we see that the entropy of s is attained at an orthogonal decomposition [13] and we obtain the familiar equation

$$H(s)=-\mathrm{tr}\left[sln(s)\right].$$

In general this definition of entropy does not provide a concave function on a convex set. For instance, the entropy of points in the square has local maximum in the four different points. A characterization of the convex sets with concave entropy functions is lacking.

Definition 5.

If the entropy is a concave function then the regret function $D_{-H}$ is called information divergence.

The information divergence is also called Kullback–Leibler divergence, relative entropy or quantum relative entropy. In a C*-algebra we get

$$\begin{array}{cc}\hfill D_{-H}\left(s_1,s_2\right)& =-H\left(s_1\right)-\left(-H\left(s_2\right)+⟨s_1-s_2,-\nabla H\left(s_2\right)⟩\right)\hfill \\ & =H\left(s_2\right)-H\left(s_1\right)+⟨s_1-s_2,\nabla H\left(s_2\right)⟩\hfill \\ & =\mathrm{tr}\left[f\left(s_2\right)\right]-\mathrm{tr}\left[f\left(s_1\right)\right]+\mathrm{tr}\left[\left(s_1-s_2\right)f^{\prime }\left(s_2\right)\right]\hfill \\ & =\mathrm{tr}\left[f\left(s_2\right)-f\left(s_1\right)+\left(s_1-s_2\right)f^{\prime }\left(s_2\right)\right]\hfill \end{array}$$

where $f\left(x\right)=-xln\left(x\right).$ Now $f^{\prime }\left(x\right)=-ln\left(x\right)-1$ so that

$$\begin{array}{cc}\hfill f\left(s_2\right)-f\left(s_1\right)+\left(s_1-s_2\right)f^{\prime }\left(s_2\right)& =-s_{2}ln\left(s_2\right)+s_{1}ln\left(s_1\right)+\left(s_1-s_2\right)\left(-ln\left(s_2\right)-1\right)\hfill \\ & =s_1\left(ln\left(s_1\right)-ln\left(s_2\right)\right)+s_2-s_1.\hfill \end{array}$$

Hence

$$D_{-H}\left(s_1,s_2\right)=\mathrm{tr}\left[s_1\left(ln\left(s_1\right)-ln\left(s_2\right)\right)+s_2-s_1\right].$$

For states $s_1,s_2$ it reduces to the well-known formula

$$D_{-H}\left(s_1,s_2\right)=\mathrm{tr}\left[s_{1}ln\left(s_1\right)-s_{1}ln\left(s_2\right)\right].$$

5.2. Monotonicity

We consider a set $\mathcal{T}$ of maps of the state space into itself. The set $\mathcal{T}$ will be used to represent those transformations that we are able to perform on the state space before we choose a feasible action $a\in \mathcal{A}$. Let $\mathrm{\Phi }:\mathcal{S}\curvearrowright \mathcal{S}$ denote a map. Then the dual map ${\mathrm{\Phi }}^{*}$ maps actions into actions and is given by

$$⟨a,\mathrm{\Phi }\left(s\right)⟩=⟨{\mathrm{\Phi }}^{*}(a),s⟩.$$

Proposition 5 (The principle of lost opportunities).

If ${\mathrm{\Phi }}^{*}$ maps the set of feasible actions $\mathcal{A}$ into itself then

$$F\left(\mathrm{\Phi }\left(s\right)\right)\le F\left(s\right).$$

(17)

Proof. 

If $a\in \mathcal{A}$ then

$$\begin{array}{ccc}\hfill ⟨a,\mathrm{\Phi }\left(s\right)⟩& =& ⟨{\mathrm{\Phi }}^{*}(a),s⟩\hfill \\ & \le & F\left(s\right)\hfill \end{array}$$

because ${\mathrm{\Phi }}^{*}(a)\in \mathcal{A}$. Inequality (17) follows because $F\left(\mathrm{\Phi }\left(s\right)\right)={sup}_a⟨a,\mathrm{\Phi }\left(s\right)⟩.$ ☐

Corollary 1 (Semi-monotonicity)

Let Φ denote a map of the state space into itself such that ${\mathrm{\Phi }}^{*}$ maps the set of feasible actions $\mathcal{A}$ into itself and let $s_2$ denote a state that minimizes the function F. If $D_F$ is a Bregman divergence then

$$D_F\left(\mathrm{\Phi }\left(s_1\right),\mathrm{\Phi }\left(s_2\right)\right)\le D_F\left(s_1,s_2\right).$$

(18)

Proof. 

Since $s_2$ minimizes F and F is differentiable we have $\nabla F\left(s_2\right)=0$. Since $s_2$ minimizes F and $F\left(\mathrm{\Phi }\left(s_2\right)\right)\le F\left(s_2\right)$ we also have that $\mathrm{\Phi }\left(s_2\right)$ minimizes F and that $\nabla F\left(\mathrm{\Phi }\left(s_2\right)\right)=0$. Therefore

$$\begin{array}{cc}\hfill D_F\left(\mathrm{\Phi }\left(s_1\right),\mathrm{\Phi }\left(s_2\right)\right)& =F\left(\mathrm{\Phi }\left(s_1\right)\right)-\left(F\left(\mathrm{\Phi }\left(s_2\right)\right)+⟨\mathrm{\Phi }\left(s_1\right)-\mathrm{\Phi }\left(s_2\right),\nabla F\left(\mathrm{\Phi }\left(s_2\right)\right)⟩\right)\hfill \\ & =F\left(\mathrm{\Phi }\left(s_1\right)\right)-F\left(\mathrm{\Phi }\left(s_2\right)\right)\hfill \\ & \le F\left(s_1\right)-F\left(s_2\right)\hfill \\ & =D_F\left(s_1,s_2\right),\hfill \end{array}$$

which proves the inequality. ☐

Next we introduce the stronger notion of monotonicity.

Definition 6.

Let $D_F$ denote a regret function on the state space $\mathcal{S}$ of a finite dimensional C*-algebra. Then $D_F$ is said to be monotone if

$$D_F\left(\mathrm{\Phi }\left(s_1\right),\mathrm{\Phi }\left(s_2\right)\right)\le D_F\left(s_1,s_2\right)$$

for any affine map $\mathrm{\Phi }:S\to S.$

Proposition 6.

If a regret function $D_F$ based on a convex and continuous function F is monotone then it is a Bregman divergence.

Proof. 

Assume that $D_F$ is monotone. We have to prove that F is differentiable. Since F is convex it is sufficient to prove that any restriction of F to a line segment is differentiable. Let $s_0$ and $s_1$ denote states that are the end points of a line segment. The restriction of F to the line segment is given by the convex and continuous function $f(t)=F((1-t)s_0+t{s}_1)$ so we have to prove that f is differentiable.

If $0<t_1<t_2<1$ then according to Equation (2) we have

$$D_F\left((1-t_2)s_0+t_2{s}_1,(1-t_1)s_0+t_1{s}_1\right)=f\left(t_2\right)-\left(f\left(t_1\right)+\left(t_2-t_1\right)·f_{+}^{\prime }\left(t_1\right)\right)$$

where $f_{+}^{\prime }$ denotes the derivative from the right. A dilation by a factor $r\le 1$ around $s_0$ decreases the regret so that

$$r\to f\left(r·t_2\right)-\left(f\left(r·t_1\right)+r·\left(t_2-t_1\right)·f_{+}^{\prime }\left(r·t_1\right)\right)$$

(19)

is increasing. Since f is convex the function $r\to f_{+}^{\prime }\left(r·t_1\right)$ is increasing. Assume that f is not differentiable so that $r\to f_{+}^{\prime }\left(r·t_1\right)$ has a positive jump as illustrated on Figure 3.

Figure 3. Example of a dilation that increases regret.

This contradicts that the function (19) is increasing. Therefore $f_{+}^{\prime }$ is continuous and f is differentiable. ☐

Recently it has been proved that information divergence on a complex Hilbert space is decreasing under positive trace preserving maps [39,40]. Previously this was only known to hold if some extra condition like complete positivity or 2-positivity was assumed [41].

Theorem 3.

Information divergence is monotone under any positive trace preserving map on the states of a finite dimensional $C^{*}$-algebra.

Proof. 

Any finite dimensional $C^{*}$-algebra $\mathcal{B}$ can be embedded in $\mathbb{B}\left(\mathbb{H}\right)$ and there exist a conditional expectation $\mathbb{E}:\mathbb{B}\left(\mathbb{H}\right)\to \mathcal{B}.$ If $\mathrm{\Phi }$ is a positive trace preserving map of the density matrices of $\mathcal{B}$ into it self then $\mathrm{\Phi }\circ \mathbb{E}$ is positive and trace preserving on $\mathbb{B}\left(\mathbb{H}\right).$ According to Müller-Hermes and Reeb [39] we have

$$D\left(\mathrm{\Phi }\circ \mathbb{E}\left(s_1\right)∥\mathrm{\Phi }\circ \mathbb{E}\left(s_2\right)\right)\le D\left(s_1∥s_2\right)$$

for density matrices in $\mathbb{B}\left(\mathbb{H}\right).$ In particular this inequality holds for density matrices in $\mathcal{B}$ and for such matrices we have $\mathbb{E}\left(s_i\right)=s_i$. ☐

5.3. Sufficiency

The notion of sufficiency plays an important role in statistics and related fields. We shall present a definition of sufficiency that is based on [42], but there are a number of other equivalent ways of defining this concept. We refer to [43] where the notion of sufficiency is discussed in great detail.

Definition 7.

Let ${\left(s_{\theta }\right)}_{\theta }$ denote a family of states and let Φ denote an affine map $\mathcal{S}\to \mathcal{T}$ where $\mathcal{S}$ and $\mathcal{T}$ denote state spaces. A recovery map is an affine map $\mathrm{\Psi }:\mathcal{T}\to \mathcal{S}$ such that $\mathrm{\Psi }\left(\mathrm{\Phi }\left(s_{\theta }\right)\right)=s_{\theta }.$ The map Φ is said to be sufficient for ${\left(s_{\theta }\right)}_{\theta }$ if Φ has a recovery map.

Proposition 7.

Assume $D_F$ is a regret function based on a convex and continuous function F and assume that Φ is sufficient for $s_1$ and $s_2$ with recovery map Ψ. Assume that both ${\mathrm{\Phi }}^{*}$ and ${\mathrm{\Psi }}^{*}$ map the set of feasible actions $\mathcal{A}$ into itself. Then

$$D_F\left(\mathrm{\Phi }\left(s_1\right),\mathrm{\Phi }\left(s_2\right)\right)=D_F\left(s_1,s_2\right).$$

Proof. 

According to the principle of lest opportunities (Proposition 5) we have

$$\begin{array}{cc}\hfill F\left(s_2\right)& =F\left(\mathrm{\Psi }\left(\mathrm{\Phi }\left(s_2\right)\right)\right)\hfill \\ & \le F\left(\mathrm{\Phi }\left(s_2\right)\right)\hfill \\ & \le F\left(s_2\right).\hfill \end{array}$$

Therefore $F\left(\mathrm{\Phi }\left(s_2\right)\right)=F\left(s_2\right).$ Let a denote an action that is optimal for $s_2.$ Then

$$\begin{array}{cc}\hfill F\left(\mathrm{\Phi }\left(s_2\right)\right)& =F\left(s_2\right)\hfill \\ & =⟨a,s_2⟩\hfill \\ & =⟨a,\mathrm{\Psi }\left(\mathrm{\Phi }\left(s_2\right)\right)⟩\hfill \\ & =⟨{\mathrm{\Psi }}^{*}(a),\mathrm{\Phi }\left(s_2\right)⟩\hfill \end{array}$$

and we see that ${\mathrm{\Psi }}^{*}(a)$ is optimal for $\mathrm{\Phi }\left(s_2\right).$ Now

$$\begin{array}{cc}\hfill D_F\left(s_1,s_2\right)& ={\displaystyle \underset{a}{inf}}\left(F\left(s_1\right)-⟨a,s_1⟩\right)\hfill \\ & ={\displaystyle \underset{a}{inf}}\left(F\left(s_1\right)-⟨{\mathrm{\Psi }}^{*}(a),\mathrm{\Phi }\left(s_1\right)⟩\right)\hfill \end{array}$$

where the infimum is taken over actions a that are optimal for $s_2.$ Then

$$\begin{array}{cc}\hfill {\displaystyle \underset{a}{inf}}\left(F\left(s_1\right)-⟨{\mathrm{\Psi }}^{*}(a),\mathrm{\Phi }\left(s_1\right)⟩\right)& \ge {\displaystyle \underset{\tilde{a}}{inf}}\left(F\left(\mathrm{\Phi }\left(s_1\right)\right)-⟨\tilde{a},\mathrm{\Phi }\left(s_1\right)⟩\right)\hfill \\ & =D_F\left(\mathrm{\Phi }\left(s_1\right),\mathrm{\Phi }\left(s_2\right)\right)\hfill \end{array}$$

so we have $D_F\left(s_1,s_2\right)\ge D_F\left(\mathrm{\Phi }\left(s_1\right),\mathrm{\Phi }\left(s_2\right)\right).$ The reverse inequality is proved in the same way. ☐

The notion of sufficiency as a property of divergences was introduced in [44]. The crucial idea of restricting the attention to maps of the state space into itself was introduced in [45]. It was shown in [45] that a Bregman divergence on the simplex of distributions on an alphabet that is not binary and satisfies sufficiency equals information divergence up a multiplicative factor. Here we extend the notion of sufficiency from Bregman divergences to regret functions.

Definition 8.

Let $D_F$ denote a regret function based on a convex and continuous function F on a state space $\mathcal{S}$. We say $D_F$ satisfies sufficiency if

$$D_F\left(\mathrm{\Phi }\left(s_1\right),\mathrm{\Phi }\left(s_2\right)\right)=D_F\left(s_1,s_2\right)$$

for any affine map $\mathcal{S}\to \mathcal{S}$ that is sufficient for $\left(s_1,s_2\right).$

Proposition 8.

Let $D_F$ denote a regret function based on a convex and continuous function F on a state space $\mathcal{S}$. If the regret function $D_F$ is monotone then it satisfies sufficiency.

Proof. 

Assume that the regret function $D_F$ is monotone. Let $s_1$ and $s_2$ denote two states and let $\mathrm{\Phi }$ and $\mathrm{\Psi }$ denote maps on the state space such that $\mathrm{\Phi }\left(\mathrm{\Psi }\left(s_i\right)\right)=s_i,i=1,2$ . Then

$$\begin{array}{cc}\hfill D_F\left(s_1,s_2\right)& =D_F\left(\mathrm{\Phi }\left(\mathrm{\Psi }\left(s_1\right)\right),\mathrm{\Phi }\left(\mathrm{\Psi }\left(s_2\right)\right)\right)\hfill \\ & \le D_F\left(\mathrm{\Psi }\left(s_1\right),\mathrm{\Psi }\left(s_2\right)\right)\hfill \\ & \le D_F\left(s_1,s_2\right).\hfill \end{array}$$

Hence $D_F\left(\mathrm{\Psi }\left(s_1\right),\mathrm{\Psi }\left(s_2\right)\right)=D_F\left(s_1,s_2\right).$ ☐

Combining the previous results we get that information divergence satisfies sufficiency. Under some conditions there exists an inverse version of Proposition 8 stating that if monotonicity holds with equality then the map is sufficient. In statistics where the state space is a simplex, this result is well established. For density matrices over the complex numbers it has been proved for completely positive maps in [43]. Some new results on this topic can be found in [46].

5.4. Locality

Often it is relevant to use the following weak version of the sufficiency property.

Definition 9.

Let $D_F$ denote a regret function based on a convex and continuous function F on a state space $\mathcal{S}$. The regret function $D_F$ is said to be local if

$$D_F\left(s_1,t·s_1+\left(1-t\right)·\sigma \right)=D_F\left(s_1,t·s_1+\left(1-t\right)·\rho \right)$$

when the states σ and ρ are orthogonal to $s_1$ and $t\in \left]0,1\right[.$

Example 5.

On a 1-dimensional simplex (an interval) or on the Block sphere any regret function $D_F$ is local. The reason is that if σ and ρ are states that are orthogonal to $s_1$ then $\sigma =\rho .$

Proposition 9.

Let $D_F$ denote a regret function based on a convex and continuous function F on a state space $\mathcal{S}$. If the regret function $D_F$ satisfies sufficiency then $D_F$ is local.

Proof. 

Let $\sigma$ and $\rho$ be states that are orthogonal to $s_1.$ Let p denote the projection supporting the state $s_0$. Let the maps $\mathrm{\Phi }$ and $\mathrm{\Psi }$ be defined by

$$\begin{array}{cc}\hfill \mathrm{\Phi }\left(s\right)& =\mathrm{tr}(ps)·s_1+(1-\mathrm{tr}(ps))·\rho ,\hfill \\ \hfill \mathrm{\Psi }\left(s\right)& =\mathrm{tr}(ps)·s_1+(1-\mathrm{tr}(ps))·\sigma .\hfill \end{array}$$

Then $\mathrm{\Phi }\left(s_1\right)=\mathrm{\Psi }\left(s_1\right)=s_1$ and $\mathrm{\Phi }\left(\sigma \right)=\rho$ and $\mathrm{\Psi }\left(\rho \right)=\sigma .$ Therefore

$$\begin{array}{cc}\hfill \mathrm{\Phi }\left(t·s_1+\left(1-t\right)·\sigma \right)& =t·s_1+\left(1-t\right)·\rho \hfill \\ \hfill \mathrm{\Psi }\left(t·s_1+\left(1-t\right)·\rho \right)& =t·s_1+\left(1-t\right)·\sigma \hfill \end{array}$$

and

$$D_F\left(s_1,t·s_1+\left(1-t\right)·\sigma \right)=D_F\left(s_1,t·s_1+\left(1-t\right)·\rho \right),$$

which proves the Proposition. ☐

Theorem 4.

Let $\mathcal{S}$ be the state space of a $C^{*}$-algebra with at least three orthogonal states, and let $D_F$ denote a regret function based on a convex and continuous function F on the state space $\mathcal{S}$. If the regret function $D_F$ is local then it is the Bregman divergence generated by the entropy times a negative constant.

Proof. 

In the following proof we will assume that the regret function is based on the convex function $F:\mathcal{S}\to \mathbb{R}.$ First we will prove that the regret function is a Bregman divergence.

Let K denote the convex hull of a set $s_0,s_1,\dots s_n$ of orthogonal states. For $x\in [0,1]$ let $g_i$ denote the function $g_i\left(x\right)=D_F\left(s_i,x{s}_i+\left(1-x\right)s_{i+1}\right)$. Note that $g_i$ is decreasing and continuous from the left. Let $P=\sum p_i{s}_i$ and $Q=\sum q_i{s}_i$ where $p_i,q_i\in \left]0,1\right[$ for all $i=0,1,2,\dots n$. If F is differentiable in P then locality implies that

$$\begin{array}{ccc}\hfill D_F\left(P,Q\right)& =& \sum p_i{D}_F\left(s_i,Q\right)-\sum p_i{D}_F\left(s_i,P\right)\hfill \\ & =& \sum p_i{g}_i\left(q_i\right)-\sum p_i{g}_i\left(p_i\right)\hfill \\ & =& \sum p_i\left(g_i\left(q_i\right)-g_i\left(p_i\right)\right).\hfill \end{array}$$

Note that $P\to D_F\left(P,Q\right)$ is a convex function and thereby it is continuous. Assume that $P_0$ is an arbitrary element in K and let ${\left(P_n\right)}_{n\in \mathbb{N}}$ denote a sequence such that $P_n\to P_0$ for $n\to \infty .$ The sequence ${\left(P_n\right)}_{n\in \mathbb{N}}$ can be chosen so that regret is differentiable in $P_n$ for all $n\in \mathbb{N}.$ Further the sequence $P_n$ can be chosen such that $p_{n,i}$ is increasing for all $i\ne j.$ Then

$$D_F\left(P_0,Q\right)=\sum p_{0,i}\left(g_i\left(q_i\right)-g_i\left(p_{0,i}\right)\right)+p_{0,j}{g}_j\left(p_{0,j}\right)-p_{0,j}\underset{n\to \infty }{lim}{g}_j\left(p_{n,j}\right).$$

Similarly, if the sequence $P_n$ can be chosen such that $p_{n,i}$ is increasing for all $i\ne j,j+1$ then

$$\begin{array}{c}{D}_F\left(P_0,Q\right)=\sum p_{0,i}\left(g_i\left(q_i\right)-g_i\left(p_{0,i}\right)\right)+p_{0,j}{g}_j\left(p_{0,j}\right)-p_{0,j}{\displaystyle \underset{n\to \infty }{lim}}{g}_j\left(p_{n,j}\right)\hfill \\ \hfill +p_{0,j+1}{g}_{j+1}\left(p_{0,j+1}\right)-p_{0,j+1}{\displaystyle \underset{n\to \infty }{lim}}{g}_{j+1}\left(p_{n,j+1}\right),\end{array}$$

which implies that $p_{0,j+1}{g}_{j+1}\left(p_{0,j+1}\right)-p_{0,j+1}{lim}_{n\to \infty }{g}_{j+1}\left(p_{n,j+1}\right)=0$ and that

$$\underset{n\to \infty }{lim}{g}_{j+1}\left(p_{n,j+1}\right)=g_{j+1}\left(p_{0,j+1}\right)$$

for all j. Therefore

$$D_F\left(P_0,Q\right)=\sum p_{0,i}\left(g_i\left(q_i\right)-g_i\left(p_{0,i}\right)\right)$$

(20)

for all $P_0,Q$ in the interior of K. In the following calculations we will assume that the distributions lie in the interior of K. The validity of the Bregman identity (5) follows directly from Equation (20) implying that $D_F$ is a Bregman divergence.

As a function of Q the regret is minimal when $Q=P.$ In the following calculations we write $x=p_i$, $z=p_j$, $y=q_i$, and $w=q_j$. If $p_{\ell }=q_{\ell }$ for $\ell \ne i,j$ then non-negativity of regret can be written as

$$x\left(g_i\left(y\right)-g_i\left(x\right)\right)+z\left(g_j\left(w\right)-g_j\left(z\right)\right)\ge 0$$

and we note that this inequality should hold as long as $x+z=y+w\le 1.$ Permutation of i and j leads to the inequality

$$x\left(g_j\left(y\right)-g_j\left(x\right)\right)+z\left(g_i\left(w\right)-g_i\left(z\right)\right)\ge 0$$

that implies

$$x\left(g_{ij}\left(y\right)-g_{ij}\left(x\right)\right)+z\left(g_{ij}\left(w\right)-g_{ij}\left(z\right)\right)\ge 0$$

(21)

where $g_{ij}=\frac{g_i+g_j}{2}.$

Assume that $x=z=\frac{y+w}{2}$ in Inequality (21). Then

$$\begin{array}{ccc}\hfill x\left(g_{ij}\left(y\right)-g_{ij}\left(x\right)\right)+x\left(g_{ij}\left(w\right)-g_{ij}\left(x\right)\right)& \ge & 0\hfill \\ \hfill g_{ij}\left(y\right)-g_{ij}\left(x\right)+g_{ij}\left(w\right)-g_{ij}\left(x\right)& \ge & 0\hfill \\ \hfill \frac{g_{ij}\left(y\right)+g_{ij}\left(w\right)}{2}& \ge & g_{ij}\left(x\right)\hfill \end{array}$$

so that $g_{ij}$ is mid-point convex, which for a measurable function implies convexity. Therefore $g_{ij}$ is differentiable from left and right.

If $y=w$ and $x=y+ϵ$ and $z=y-ϵ$ then we have

$$\left(y+ϵ\right)\left(g_{ij}\left(y\right)-g_{ij}\left(y+ϵ\right)\right)+\left(y-ϵ\right)\left(g_{ij}\left(y\right)-g_{ij}\left(y-ϵ\right)\right)\ge 0$$

with equality when $ϵ=0.$ We differentiate with respect to $ϵ$ from right.

$$\left(g_{ij}\left(y\right)-g_{ij}\left(y+ϵ\right)\right)+\left(y+ϵ\right)\left(-g_{ij+}^{\prime }\left(y+ϵ\right)\right)-\left(g_{ij}\left(y\right)-g_{ij}\left(y-ϵ\right)\right)+\left(y-ϵ\right)\left(g_{ij-}^{\prime }\left(y-ϵ\right)\right),$$

which is positive for $ϵ=0$ so that

$$\begin{array}{ccc}\hfill -y·g_{ij+}^{\prime }\left(y\right)+y·g_{ij-}^{\prime }\left(y\right)& \ge & 0\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill y·g_{ij-}^{\prime }\left(y\right)& \ge & y·g_{ij+}^{\prime }\left(y\right).\hfill \end{array}$$

(23)

Since $g_{ij}$ is convex we have $g_{ij-}^{\prime }\left(y\right)\le g_{ij+}^{\prime }\left(y\right)$ which in combination with Inequality (23) implies that $g_{ij-}^{\prime }\left(y\right)=g_{ij+}^{\prime }\left(y\right)$ so that $g_{ij}$ is differentiable. Since $g_i=g_{ij}+g_{ik}-g_{jk}$ the function $g_i$ is also differentiable.

As a function of Q the Bregman divergence $D_F(P,Q)$ has a minimum at $Q=P$ under the condition $\sum q_i=1$. Since the functions $g_i$ are differentiable we can characterize this minimum using Lagrange multipliers. We have

$$\frac{\partial }{\partial q_i}{D}_F\left(P,Q\right)=p_i{g}_i^{\prime }\left(q_i\right)$$

and

$$\frac{\partial }{\partial q_i}{D}_F{\left(P,Q\right)}_{\mid Q=P}=p_i·g_i^{\prime }\left(p_i\right).$$

Further $\frac{\partial }{\partial q_i}\sum q_i=1$ so there exist a constant $c_K$ such that $p_i·g_i^{\prime }\left(p_i\right)=c_K.$ Hence $g_i^{\prime }\left(p_i\right)=\frac{c_K}{p_i}$ so that $g_i\left(p_i\right)=c_K·ln\left(p_i\right)+m_i$ for some constant $m_i.$

Now we get

$$\begin{array}{ccc}\hfill D_F\left(P,Q\right)& =& \sum p_i\left(g_i\left(q_i\right)-g_i\left(p_i\right)\right)\hfill \\ & =& \sum p_i\left(\left(c_K·ln\left(q_i\right)+m_i\right)-\left(c_K·ln\left(p_i\right)+m_i\right)\right)\hfill \\ & =& -c_K·\sum p_{i}ln\frac{p_i}{q_i}\hfill \\ & =& D_{-c_K·H}\left(P,Q\right).\hfill \end{array}$$

Therefore, an affine function exists, defined by K such that

$$F_{\mid K}(P)=-c_K·H_{\mid K}(P)+g_K$$

(24)

for all P in the interior of K. Since $H_K$ is continuous on K Equation (24) holds for any $P\in K$. If each of the sets K and L is a simplex and $x\in K\cap L$ then

$$-c_K·H_{\mid K}\left(x\right)+g_K\left(x\right)=-c_L·H_{\mid L}\left(x\right)+g_L\left(x\right)$$

so that

$$\left(c_L-c_K\right)·H_{\mid K}\left(x\right)=g_L\left(x\right)-g_K\left(x\right).$$

If $K\cap L$ has dimension greater than zero then the right hand side is affine so the left hand side is affine, which is only possible when $c_K=c_L.$ Therefore we also have $g_L\left(x\right)=g_K\left(x\right)$ for all $x\in K\cap L.$ Therefore the functions $g_K$ can be extended to a single affine function on the whole of $\mathcal{S}.$ ☐

6. Applications

6.1. Information Theory

If only integer values of a code-length function ℓ are allowed then there are only finitely many actions that are not dominated. Therefore the function F given by

$$F\left(P\right)=-\underset{\ell }{min}\sum \ell \left(a\right)·p_a$$

is piece-wise linear. In particular F is not differentiable so that the regret is not a Bregman divergence and cannot be monotone according to Proposition 6. In information theory monotonicity of a divergence function is closely related to the data processing inequality and since the data processing inequality is one of the most important tools for deriving inequalities in information theory we need to modify our notion of code-length function in order to achieve a data processing inequality.

We now formulate a version of Kraft’s inequality that allows the code length function to be non-integer valued.

Theorem 5.

Let $\ell :\mathbb{A}\to \mathbb{R}$ be a function. Then the function ℓ satisfies Kraft’s inequality (6) if and only if for all $\epsilon >0$ there exists an integer n and a uniquely decodable fixed-to-variable length block code $\kappa :{\mathbb{A}}^n\to {\mathbb{B}}^{*}$ such that

$$\left|{\overline{\ell }}_{\kappa }\left(a^n\right)-\frac{1}{n}\sum _{i=1}^n\ell \left(a_i\right)\right|\le \epsilon$$

where ${\overline{\ell }}_{\kappa }\left(a^n\right)$ denotes the length ${\ell }_{\kappa }\left(a^n\right)$ divided by $n.$ The uniquely decodable block code can be chosen to be prefix free.

Proof. 

Assume that ℓ satisfies Kraft’s inequality. Then

$$\sum _{a_1{a}_2\dots a_n\in {\mathbb{A}}^n}{\beta }^{-{\sum }_{i=1}^n\ell \left(a_i\right)}={\left(\sum _{a\in \mathbb{A}}{\beta }^{-\ell \left(a\right)}\right)}^n\le 1^n=1.$$

Therefore the function $\tilde{\ell }:{\mathbb{A}}^n\to \mathbb{N}$ given by

$$\tilde{\ell }\left(a_1{a}_2\dots a_n\right)=⌈\sum _{i=1}^n\ell \left(a_i\right)⌉$$

is integer valued and satisfies Kraft’s inequality (6) and there exists a prefix-free code $\kappa :{\mathbb{A}}^n\to {\left\{0,1\right\}}^{*}$ such that ${\ell }_{\kappa }\left(a_1{a}_2\dots a_n\right)=\tilde{\ell }\left(a_1{a}_2\dots a_n\right).$ Therefore

$$\left|{\overline{\ell }}_{\kappa }\left(a_1{a}_2\dots a_n\right)-\frac{1}{n}\sum _{i=1}^n\ell \left(a_i\right)\right|=\frac{1}{n}\left|⌈\sum _{i=1}^n\ell \left(a_i\right)⌉-\sum _{i=1}^n\ell \left(a_i\right)\right|\le \frac{1}{n}$$

so for any $\epsilon >0$ choose n such that $1/n\le \epsilon .$

Assume that for all $\epsilon >0$ there exists a uniquely decodable fixed-to-variable length code $\kappa :{\mathbb{A}}^n\to {\left\{0,1\right\}}^{*}$ such that

$$\left|{\overline{\ell }}_{\kappa }\left(a_1{a}_2\dots a_n\right)-\frac{1}{n}\sum _{i=1}^n\ell \left(a_i\right)\right|\le \epsilon$$

for all strings $a_1{a}_2\dots a_n\in {\mathbb{A}}^n.$ Then $n{\overline{\ell }}_{\kappa }\left(a_1{a}_2\dots a_n\right)$ satisfies Kraft’s Inequality (6) and

$$\begin{array}{cc}\hfill {\left({\displaystyle \sum _{a\in \mathbb{A}}}{\beta }^{-\ell \left(a\right)}\right)}^n& ={\displaystyle \sum _{a_1{a}_2\dots a_n\in {\mathbb{A}}^n}}{\beta }^{-{\sum }_{i=1}^n\ell \left(a_i\right)}\hfill \\ & \le {\displaystyle \sum _{a_1{a}_2\dots a_n\in {\mathbb{A}}^n}}{\beta }^{-n\left({\overline{\ell }}_{\kappa }\left(a_1{a}_2\dots a_n\right)-\epsilon \right)}\hfill \\ & ={\beta }^{n\epsilon }{\displaystyle \sum _{a_1{a}_2\dots a_n\in {\mathbb{A}}^n}}{\beta }^{-n{\overline{\ell }}_{\kappa }\left(a_1{a}_2\dots a_n\right)}\hfill \\ & \le {\beta }^{n\epsilon }.\hfill \end{array}$$

Therefore ${\sum }_{a\in \mathbb{A}}{\beta }^{-\ell \left(a\right)}\le {\beta }^{\epsilon }$ for all $\epsilon >0$ and the result is obtained. ☐

Like in Bayesian statistics we focus on finite sequences. Contrary to Bayesian statistics we should always consider a finite sequence as a prefix of longer finite sequences. Contrary to frequential statistics we do not have to consider a finite sequence as a prefix of an infinite sequence.

If we minimize the mean code-length over functions that satisfy Kraft’s inequality (6), but without an integer constraint the code-length should be $\ell \left(a\right)=-{log}_{\beta }\left(p_a\right)$ and the function F is given by

$$F\left(P\right)=\sum _a{p}_a·{log}_{\beta }\left(p_a\right).$$

The function F is proportional to the Shannon entropy and the (negative) proportionality factor is determined by the size of the output alphabet.

In lossy source coding and rate distortion theory it is important to choose a distortion function with tractable properties. The notion of sufficiency for divergence functions was introduced in [44] in order to characterize such tractable distortions functions. In this paper the main result was that sufficiency together with properties related to Bregman divergence lead directly to the information bottleneck method introduced by N. Tishby [47]. Logarithmic loss has also been studied for lossy compression in [48].

6.2. Statistics

In statistics one is often interested in scoring rules that are local, which means a scoring rule where the payoff only depends on the probability of the observed value and not on the predicted distribution over unobserved values. The notion of locality has recently been extended by Dawid, Lauritzen and Parry [49], but here we shall focus on the original definition. The basic result is that the only local strictly proper scoring rule is logarithmic score that was proved by Bernardo under the assumption that scoring rule is given by a smooth function [50].

Definition 10.

A local strictly proper scoring rule is a scoring rule of the form $f\left(x,Q\right)=g\left(Q\left(x\right)\right).$

Theorem 6.

On a finite space a local strictly proper scoring rule is given by a local regret function.

Proof. 

The regret function of a local strictly proper scoring rule is given by

$$D\left(P,Q\right)=\sum _{x}P\left(x\right)\left(g\left(P\left(x\right)\right)-g\left(Q\left(x\right)\right)\right).$$

If $Q=\left(1-t\right)P+t{Q}_i$ and P and Q are mutually singular then

$$\begin{array}{cc}\hfill D\left(P,Q\right)& ={\displaystyle \sum _x}P\left(x\right)\left(g\left(P\left(x\right)\right)-g\left(\left(1-t\right)P\left(x\right)+t{Q}_i\left(x\right)\right)\right)\hfill \\ & ={\displaystyle \sum _x}P\left(x\right)\left(g\left(P\left(x\right)\right)-g\left(\left(1-t\right)P\left(x\right)+0\right)\right)\hfill \end{array}$$

and we see that the regret does not depend on $Q_i$ because $Q_i$ vanish on the support of $P.$ Therefore the regret function is local. ☐

Corollary 2.

On a finite space with at least three elements a local strictly proper scoring rule is given by a function g of the form $g\left(x\right)=a·ln\left(x\right)+b$ for some constants a and $b.$

Also the notion of sufficiency plays an important role in statistics. Here we will restrict the discussion to 1-dimensional exponential families. A natural exponential family is a family of probability distributions of the form

$$\frac{\mathrm{d}{P}_{\beta }}{\mathrm{d}Q}=\frac{exp\left(\beta x\right)}{Z\left(\beta \right)}$$

where Q is a reference measure on the real numbers and Z is the moment generating function given by $Z\left(\beta \right)=\int exp\left(\beta x\right)\mathrm{d}Qx$. Then $x_1^n\to x_1+x_2+\dots +x_n$ is a sufficient statistic for the family ${\left(P_{\beta }^{\otimes n}\right)}_{\beta }.$

Example 6.

In a Bernoulli model a sequence $x_1^n\in {\left\{0,1\right\}}^n$ is predicted with probability

$$\prod _{i=1}^n{p}^{x_i}{\left(1-p\right)}^{1-x_i}=exp\left(\left(\sum _{i=1}^n{x}_1\right)ln\left(p\right)+\left(n-\sum _{i=1}^n{x}_1\right)ln\left(1-p\right)\right).$$

The function $x_1^n\to x_1+x_2+\dots +x_n$ induces a sufficient map Φ from probability distributions on ${\left\{0,1\right\}}^n$ to probability distributions on $\left\{0,1,2,\dots ,n\right\}.$ The reverse map maps a measure concentrated in $j\in \left\{0,1,2,\dots ,n\right\}$ into a uniform distributions over sequences $x_1^n\in {\left\{0,1\right\}}^n$ that satisfy ${\sum }_{i=1}^n{x}_1=j.$

The mean value of $P_{\beta }$ is

$$\int x·\frac{exp\left(\beta x\right)}{Z\left(\beta \right)}\mathrm{d}Qx.$$

The set of possible mean values is called the mean value range and is an interval. Let $P^{\mu }$ denote the element in the exponential family with mean value $\mu .$ Then a Bregman divergence on the mean value range is defined by $D\left(\lambda ,\mu \right)=D\left(P^{\lambda }∥P^{\mu }\right).$ Note that the mapping $\mu \to P^{\mu }$ is not affine so the Bregman divergence $D\left(\lambda ,\mu \right)$ will in general not be given by the formula for information divergence with the family of binomial distributions as the only exception. Nevertheless the Bregman divergence $D\left(\lambda ,\mu \right)$ encodes important information about the exponential family. In statistics it is common to use squared Euclidean distance as distortion measure, but often it is better to use the Bregman divergence $D\left(\lambda ,\mu \right)$ as a distortion measure. Note that $D\left(\lambda ,\mu \right)$ is only proportional to squared Euclidean distance for the Gaussian location family.

Example 7.

An exponential distribution has density

$$f_{\lambda }\left(x\right)=\left\{\begin{array}{cc}\frac{1}{\lambda }exp\left(-\frac{x}{\lambda }\right),\hfill & \mathrm{for}x\ge 0;\hfill \\ 0,\hfill & else.\hfill \end{array}\right.$$

This leads to a Bregman divergence on the interval $\left[0;\infty \right[$ given by

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{f}_{\lambda }\left(x\right)ln\left(\frac{f_{\lambda }\left(x\right)}{f_{\mu }\left(x\right)}\right)\mathrm{d}x& =\frac{\lambda }{\mu }-1-ln\left(\frac{\lambda }{\mu }\right)\hfill \\ & =D_{-ln}\left(\lambda ,\mu \right).\hfill \end{array}$$

This Bregman divergence is called the Isakura-Saito distance. The Isakura-Saito distance is defined as an unbounded set so our previous results cannot be applied. Affine bijections on $\left[0;\infty \right[$ have the form $\mathrm{\Phi }\left(x\right)=k·x$ for some constant $k>0$. The Isakura-Saito distance obviously satisfy sufficiency for such maps and it is a simple exercise to check that the Isakura-Saito distance is the only Bregman divergence on $[0,\infty [$ that satisfies sufficiency. Any affine map $\left[0;\infty \right[\to \left[0;\infty \right[$ is composed of a map $x\to k·x$ where $k\ge 0$ and a right translation $x\to x+t$ where $t\ge 0.$ The Itakura-Saito distance decreases under right translations because

$$\begin{array}{cc}\hfill \frac{\partial }{\partial t}{D}_{-ln}\left(\lambda +t,\mu +t\right)& =\frac{\partial }{\partial t}\left(\frac{\lambda +t}{\mu +t}-1-ln\left(\frac{\lambda +t}{\mu +t}\right)\right)\hfill \\ & =\frac{\left(\mu +t\right)-\left(\lambda +t\right)}{{\left(\mu +t\right)}^2}-\frac{1}{\lambda +t}+\frac{1}{\mu +t}\hfill \\ & =-\frac{{\left(\lambda -\mu \right)}^2}{\left(\lambda +t\right){\left(\mu +t\right)}^2}\le 0.\hfill \end{array}$$

Thus the Isakura-Saito distance is monotone.

Both sufficiency and the Bregman identity are closely related to inference rules. In [51] I. Csiszár explained why information divergence is the only divergence function on the cone of positive measures that lead to certain tractable inference rules. One should observe that his inference rules are closely related to sufficiency and the Bregman identity, and the present paper may be viewed as a generalization of these results of I. Csiszár.

In the minimum description length approach to statistics [9] it is common to minimize the maximal regret of the model where the maximum is taken over all possible data sequences. For most exponential families this approach is computationally difficult and may cause problems with normalization of the optimal distribution over the parameter. In general this approach will also depend on the length of the data sequence in a way that is not transitive. That means that one cannot analyze a subsequence before the length of the whole data sequence is known. In [52] it was proved that for one dimensional exponential family there are essentially three exponential families where these problems are avoided. The exponential families are the Gaussian location family, the Gamma distributions, and the Tweedie distributions of order $\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. The statistical analysis of the Gaussian location family reduces to minimizing the sum of squares. Similarly, the Gamma distributions can be analyzed using the Isakura–Saito distance (or information divergence), but the Tweedie family of order $\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ is an exotic object that has not been analyzed in similar detail. For exponential models in two or more dimensions similar results are not known, but in general one should expect that most models are complicated to analyze exactly while certain models simplify due to some type of inner symmetry of the model.

6.3. Statistical Mechanics

Statistical mechanics can be stated based on classical mechanics or quantum mechanics. For our purpose this makes no difference because our theorems are valid for both classical systems and quantum systems.

As we have seen before

$$Ex=k{T}_0·D\left(s∥s_0\right).$$

(25)

Our general results for Bregman divergences imply that the Bregman divergence based on this exergy satisfies

$$D_{Ex}\left(s_1,s_2\right)=k{T}_0·D\left(s_1∥s_2\right).$$

Therefore

$$D_{Ex}\left(\mathrm{\Phi }\left(s_1\right),\mathrm{\Phi }\left(s_2\right)\right)=D_{Ex}\left(s_1,s_2\right)$$

for any map that is sufficient for $\left\{s_1,s_2\right\}.$ The equality holds for any regret function that is reversible and conserves the state that is in equilibrium with the environment. Since a different temperature of the environment leads to a different state that is in equilibrium the equality holds for any reversible map that leave some equilibrium state invariant. We see that $D_{Ex}\left(s_1,s_2\right)$ is uniquely determined as long as there exists a sufficiently large set of maps that are reversible.

In this exposition we have made some short-cuts. First of all we did not derive Equation (25). In particular the notion of temperature was used without discussion. Secondly we identified the internal energy with the mean value of the Hamiltonian and identified the thermodynamic entropy with k times the Shannon entropy. Finally, in the argument above we need to verify in all details that the set of reversible maps is sufficiently large to determine the regret function. For classical thermodynamics a comprehensive exposition was made by Lieb and Yngvason [53,54]. In their exposition randomness was not taken into account. With the present framework it is also possible to handle randomness so that one can make a bridge between thermodynamics and statistical mechanics. The approach of Lieb and Yngvason was recently improved by C. Marletto [55] uses the formalism of constructor theory to derive results. The basic idea in constructor theory is to distinguish between possible and impossible transformation in a way that is closely related to the ideas presented in this paper. A detailed exposition of such relations will be given in a future paper.

According to Equation (25) any bit of information can be converted into an amount of energy! One may ask how this is related to the mixing paradox (a special case of Gibbs’ paradox). Consider a container divided by a wall with a blue and a yellow gas on each side of the wall as illustrated in Figure 4. The question is how much energy can be extracted by mixing the blue and the yellow gas?

Figure 4. Mixing of a blue and a yellow gas.

We loose one bit of information about each molecule by mixing the blue and the green gas, but if the color is the only difference no energy can be extracted. This seems to be in conflict with Equation (25), but in this case different states cannot be converted into each other by reversible processes. For instance one cannot convert the blue gas into the yellow gas. To get around this problem one can restrict the set of preparations and one can restrict the set of measurements. For instance one may simply ignore measurements of the color of the gas. What should be taken into account and what should be ignored, can only be answered by an experienced physicist. Formally this solves the mixing paradox, but from a practical point of view nothing has been solved. If for instance the molecules in one of the gases are much larger than the molecules in the other gas then a semi-permeable membrane can be used to create an osmotic pressure that can be used to extract some energy. It is still an open question as to which differences in properties of the two gases that can be used to extract energy.

6.4. Monotone Regret for Portfolios

We know that in general a local regret function on a state space with at least three orthogonal states is proportional to information divergence. In portfolio theory we get the stronger result that monotonicity implies that we are in the situation of gambling introduced by Kelly [35].

Theorem 7.

Assume that none of the assets are dominated by a portfolio of other assets. If the regret function $D_G(P,Q)$ given by (13) is monotone then the regret function equals information divergence and the measures P and Q are supported by k distinct price relative vectors of the form $\left(o_1,0,0,\dots 0\right)$, $\left(0,o_2,0,\dots 0\right),$ until $\left(0,0,\dots o_k\right).$

Proof. 

If there are more than three price relative vectors then a monotone regret function is always proportional to information divergence which is a strict regret function. Therefore we may assume that there are only two price relative vectors. Assume that the regret function is not strict. Then the function G defined by (12) is not strictly convex. Assume that $D_G(P,Q)=0$ so that G is affine between P and Q. Let $\mathrm{\Phi }$ be a contraction around one of the end points of intersection between the state space and the line through P and Q. Then monotonicity implies that $D_G(\mathrm{\Phi }(P),\mathrm{\Phi }(Q))=0$ so that G is affine on the line between $\mathrm{\Phi }(P)$ and $\mathrm{\Phi }(Q)$. This holds for contractions around any point. Therefore G is affine on the whole state space which implies that there is a single portfolio that dominates all assets. Such a portfolio must be supported on a single asset. Therefore monotonicity implies that if two assets are not dominated then the regret function is strict and according to Theorem 1 we have already proved that a strict regret function in portfolio theory is proportional to information divergence. ☐

Example 8.

If the regret function divergence is monotone and one of the assets is the safe asset then there exists a portfolio $\overrightarrow{b}$ such that $b_i·o_i\ge 1$ for all $i.$ Equivalently $b_i\ge o_i^{-1}$ which is possible if and only if $\sum o_i^{-1}\le 1.$ One says that the gamble is fair if $\sum o_i^{-1}=1$. If the gamble is super-fair, i.e., $\sum o_i^{-1}<1$, then the portfolio $b_i=o_i^{-1}/\sum o_i^{-1}$ gives a price relative equal to ${\left(\sum o_i^{-1}\right)}^{-1}>1$ independently of what happens, which is a Dutch book.

Corollary 3.

In portfolio theory the regret function $D_G(P,Q)$ given by (13) is monotone if and only if it is strict.

Proof. 

We use that in portfolio theory the regret function is monotone if and only it is proportional to information. ☐

7. Concluding Remarks

Convexity of a Bregman divergence is an important property that was first studied systematically in [56] and extended from probability distributions to matrices in [57]. In [58] it was proved that if f is a function such that the Bregman divergence based on $\mathrm{tr}(f(\rho ))$ is monotone on any (simple) C*-algebra then the Bregman divergence is jointly convex. As we have seen monotonicity implies that the Bregman divergence must be proportional to inform divergence, which is jointly convex in both arguments. We also see that in general joint convexity is not a sufficient condition for monotonicity, but in the case where the state space has only two orthogonal states it is not known if joint convexity of a Bregman divergence is sufficient to conclude that the Bregman divergence is monotone.

One should note that the type of optimization presented in this paper is closely related to a game theoretic model developed by F. Topsøe [59,60]. In his game theoretic model he needed what he called the perfect match principle. Using the terminology presented in this paper the perfect match principle states that the regret function is a strict Bregman divergence. As we have seen the perfect match principle is only fulfilled in portfolio theory if all the assets are gambling assets. Therefore, the theory of F. Topsøe can only be used to describe gambling while our optimization model can describe general portfolio theory and our sufficient conditions can explain exactly when our general model equals gambling. The formalism that has been developed in this paper is also closely related to constructor theory [61], but a discussion will be postponed to another article.

The original paper of Kullback and Leibler [1] was called “On Information and Sufficiency”. In the present paper, we have made the relation between information divergence and the notion of sufficiency more explicit. The results presented in this paper are closely related to the result that a divergence that is both an f-divergence and a Bregman divergence is proportional to information divergence (see [44] or [62] and references therein). All f-divergences satisfy a sufficiency condition, which is the reason why this class of divergences has played such a prominent role in the study of the relation between information theory and statistics. One major question has been to find reasons for choosing between the different f-divergences. For instance f-divergences of power type (often called Tsallis divergences or Cressie-Read divergences) are popular [5], but there are surprisingly few papers that can point at a single value of the power $\alpha$ that is optimal for a certain problem except if this value is 1. In this paper we have started with Bregman divergences because each optimization problem comes with a specific Bregman divergence. Often it is possible to specify a Bregman divergence for an optimization problem and only in some of the cases this Bregman divergence is proportional to information divergence.

The idea of sufficiency has different relevance in different applications, but in all cases information divergence prove to be the quantity that convert the general notion of sufficiency into a number. In information theory information divergence appear as a consequence of Kraft’s inequality. For code length functions of integer length we get functions that are piecewise linear. Only if we are interested in extend-able sequences we get a regret function that satisfies a data processing inequality. In this sense information theory is a theory of extend-able sequences. For scoring functions in statistics the notion of locality is important. These applications do not refer to sequences. Similarly the notion of sufficiency that plays a major role in statistics, does not refer to sequences. Both sufficiency and locality imply that regret is proportional to information divergence, but these reasons are different from the reasons why information divergence is used in information theory. Our description of statistical mechanics does not go into technical details, but the main point is that the many symmetries in terms of reversible maps form a set of maps so large that our result on invariance of regret under sufficient maps applies. In this sense statistical mechanics and statistics both apply information divergence for reasons related to sufficiency. For portfolio theory the story is different. In most cases one has to apply the general theory of Bregman divergences because we deal with an optimization problem. The general Bregman divergences only reduce to information divergence when the assets are gambling assets.

Often one talks about applications of information theory in statistics, statistical mechanics and portfolio theory. In this paper we have argued that information theory is mainly a theory of sequences, while some problems in statistics and statistical mechanics are also relevant without reference to sequences. It would be more correct to say that convex optimization has various application such as information theory, statistics, statistical mechanics, and portfolio theory and that certain conditions related to sufficiency lead to the same type of quantities in all these applications.