1. Introduction: Turbulence as a Maximum Energy Dissipation State?
A well-known feature of any turbulent flow is the Kolmogorov–Richardson cascade by which energy is transferred from scale to scale until scales at which it can be dissipated. This cascade is a nonlinear, non-equilibrium process. It is believed to be the origin of the significant enhancement of dissipation observed in turbulent flow, often characterized via the introduction of a turbulent viscosity.
It has then sometimes been suggested that turbulence is a state of
maximum energy dissipation. This principle inspired early works by Malkus [
1,
2] or Spiegel [
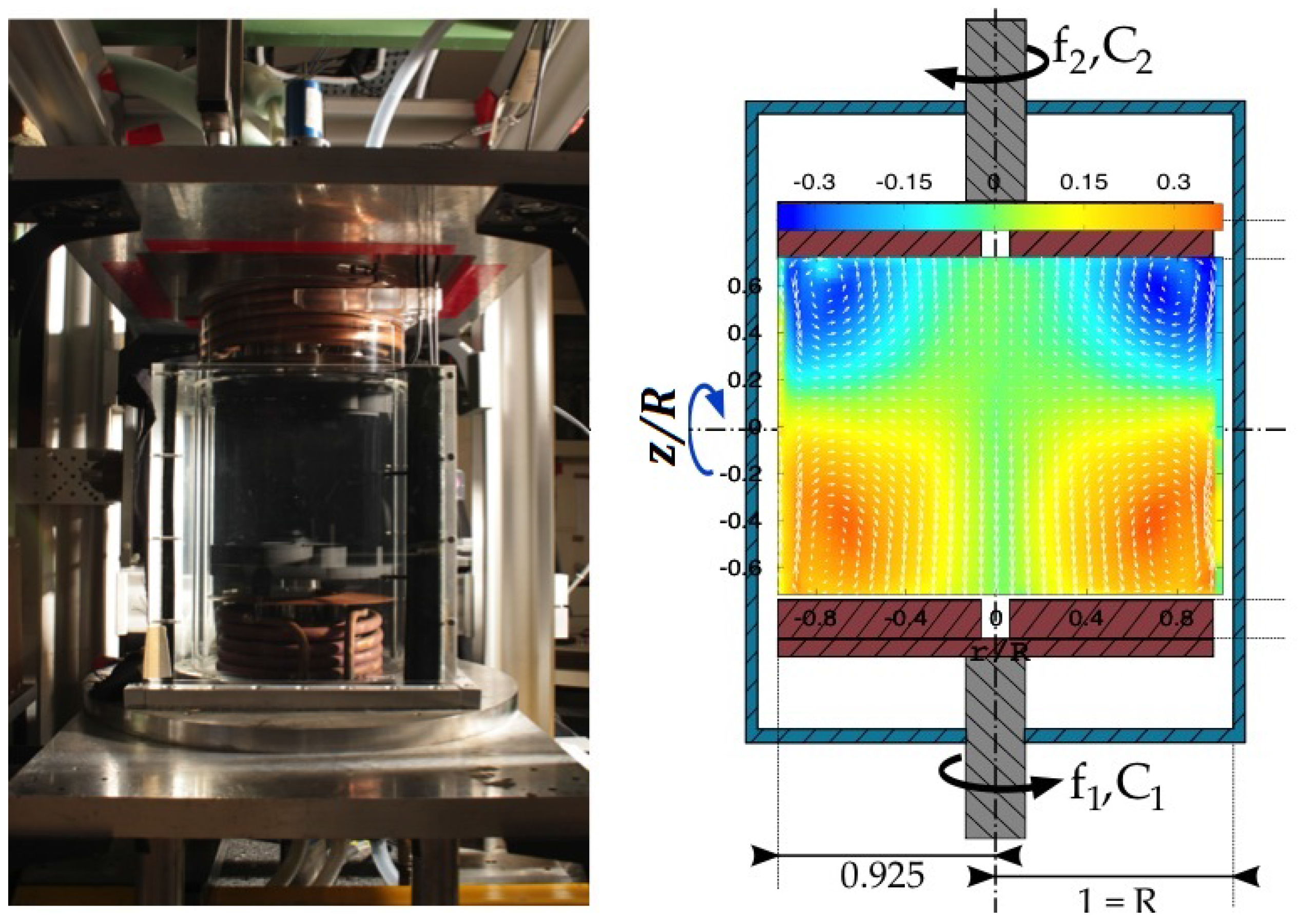
3] to compute analytically the heat or momentum profiles in thermal boundary layers or linear shear flows. While there were many criticisms about this principle, there are a few experimental situations where this principle seems to work. A good example is provided by the von Kármán flow. This flow is generated by two-counter rotating impellers inside a cylindrical vessel filled e.g., with water (see
Figure 1). The impellers produce a source of angular momentum at the top and bottom of the vessel, angular momentum that is then transferred and mixed within the flow throughout the turbulent motions [
4], in analogy with heat transferred through a Rayleigh–Bénard cell. For most impellers, the resulting mean large scale stationary motion is the superposition of a two-cell azimuthal motion, and a two cell poloidal motion bringing the flow from the top and bottom end of the experiment towards its center plane
(see
Figure 1). This mean flow is thus symmetrical with respect to the plane
. For some types of impellers, however, this symmetrical state is unstable, and bifurcates after a certain time towards another state that breaks the system symmetry [
5,
6]—see
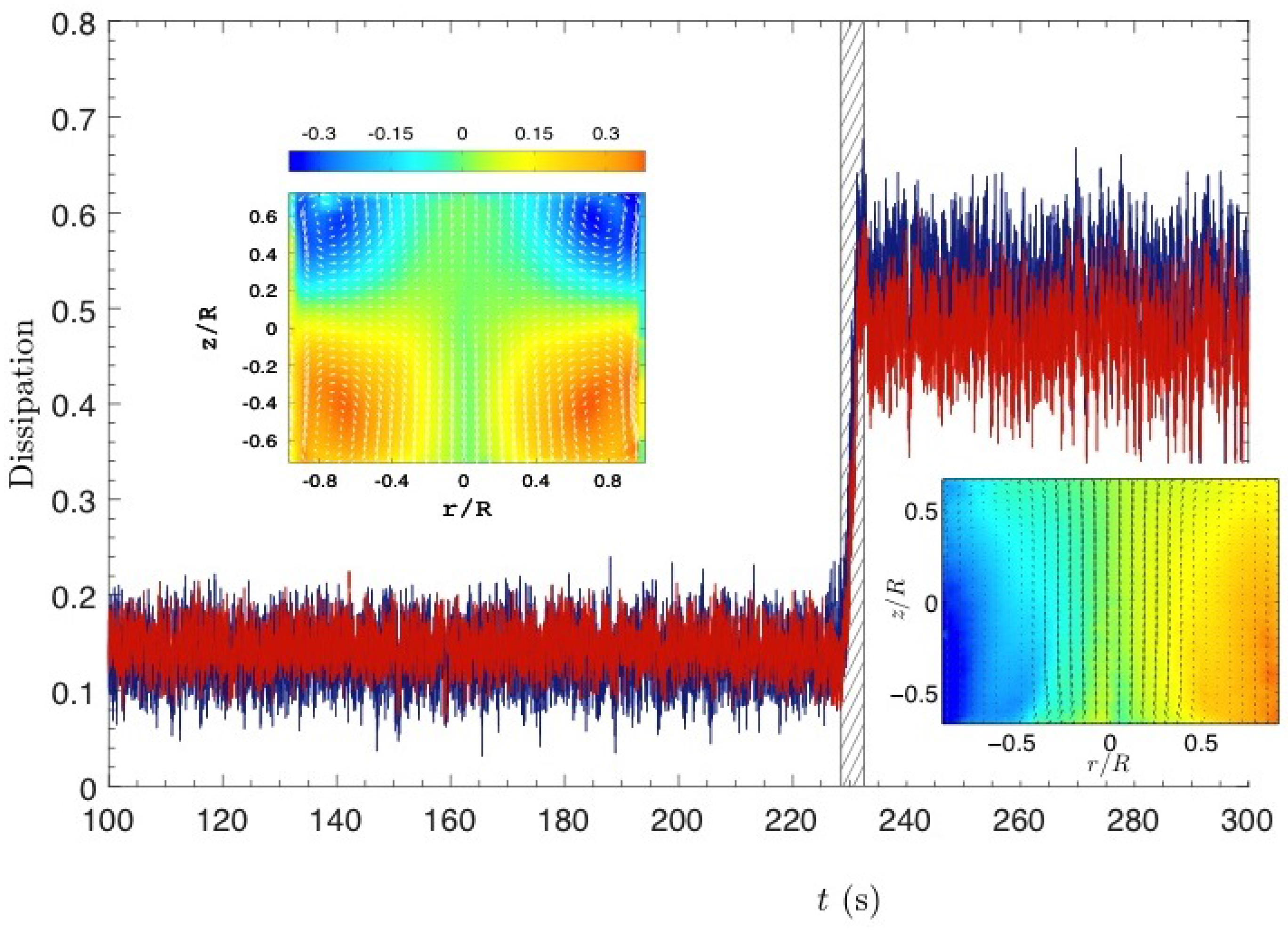
Figure 2. This state corresponds to a global rotation in the direction of either the top or the bottom impeller. The energy dissipation corresponding to either one of these three states can be measured through monitoring of the torque applied to the impellers by the flow. When monitored during a bifurcation (see
Figure 3), this energy dissipation displays a jump (by a factor 4) at the moment of the bifurcation from the symmetrical state towards either one of the non-symmetrical states. Once the system is in the bifurcated state, it never bifurcates back towards the symmetrical state, indicating that the most stable state is the state with larger dissipation.
This observation is in agreement with a general principle inspired from the Malkus principle, which could be formulated as follows:
Principle A: In certain non-equilibrium systems with coexistence of several stationary states, the most stable one is that of Maximum Energy Dissipation.
This principle is of course very appealing. There is, however, no derivation of it from any first principles, and we are not aware of any theories that could lead to its proof (while there are probably many immediate counter-examples that can be provided). If it is true or approximately true for some types of flows (like the von Kármán flow, or the Rayleigh–Bénard flow or the plane Couette flow), it may then lead to interesting applications allowing the computation of mean velocity or temperature profile without the need to integrate all of the Navier–Stokes equations. A way to proceed with its justification is to transform it into an equivalent principle, that uses notions more rooted in non-equilibrium physics. Indeed, energy dissipation is not a useful quantity to work with in general because of its dependence on the small scale processes that produce it. In general, energy dissipation is a signature of entropy production. The connection between energy dissipation and entropy production was heuristically made by Lorenz [
7] and theoretically discussed in nonlinear chemical thermodynamics by Dewar [
8] and Moroz [
9,
10]. This last notion seems more appealing to work with and a first natural step is to modify slightly the principle A into a more appealing version as:
Principle B: In certain non-equilibrium systems with coexistence of several stationary state, the most stable one is that of Maximum Entropy Production (MEP).
From the point of view of non-equilibrium physics, this principle appears as a counterpart of the well known principle of Maximum Entropy that governs stability of equilibria in statistical physics, the analog of equilibria here being the stationary states. This principle was discovered by Ziegler [
11,
12] and it is sometimes referred to as Ziegler’s principle. It has found several applications in climate dynamics: first, it was used by Paltridge [
13] to derive a good approximation of the mean temperature distribution in the mean atmosphere of the Earth. This approach has been extend to more exhaustive climate models by Herbert [
14]. Kleidon et al. [
15] used an atmospheric general circulation model to show that MEP states can be used as a criterion to determine the boundary layer friction coefficients. MEP seems also a valuable principle to describe planetary atmospheres, as those of Mars and Titan, where it has been used to determine latitudinal temperature gradients [
16]. MEP have been also applied to several geophysical problems: to describe thermally driven winds [
17], convection [
18], and oceanic circulation [
19]. A detailed overview on the usefulness of MEP in climate science can be found in [
20,
21] and references therein. It is therefore interesting to evaluate the soundness of this principle and understand its limitations and its possible improvements, in order to extend as possible the scope of its applications. The usual path to prove the validity of a principle is to provide some rigorous demonstration of the principle itself. This task has been attempted without convincing results in the past [
8,
22,
23]. In the absence of any theory of out-of-equilibrium systems, we may turn to equilibrium theory as a guide to find a path for justification of the selection of stationary states. In equilibrium systems or conceptual models, this selection can be studied using the dynamical systems theory, where other quantities than thermodynamics entropy are relevant. One of these quantities is the Kolmogorov Sinai Entropy (KSE) [
24], which is indeed different from the thermodynamic one. The KSE appears a good candidate for the selection of preferred metastable states because it is related to the concept of mixing time [
25]. The goal of this paper is therefore to show that the MEP principle could find a justification in a linked relationship, which involves studying the connections among MEP, KSE and mixing times. The paper follows this structure: after discussing the relation between MEP and the Prigogine minimization principle (
Section 2), we connect MEP and maximum KSE in conceptual models of turbulence (
Section 3). In
Section 4, we establish the link between maximum KSE and mixing times for Markov chains. Then, we summarize the results and discuss the implications of our findings.
2. Maximization or Minimization of Entropy Production?
At first sight, Principle B appears in conflict with an established result of Prigogine, according to which the stationary states of a system close to equilibrium are states with
minimum entropy production. In fact, both principles can be reconciled if Principle B is viewed as a MaxMin, principle: Martyushev et al. [
26] and Kleidon [
21] suggest that Prigogine’s principle selects the steady state of minimum entropy production compared to transient states. For a steady-state condition, the minimum entropy production principle does not give any further information if many steady state conditions are possible given the imposed boundary conditions. To provide a simple example, let us consider a system characterized by two parameters,
T and
U, where
T controls the departure from equilibrium and
U labels an additional constraint of the system, allowing the existence of several stationary states at a given
T (see
Figure 4). In our von Kármán system,
T could for example label the velocity fluctuations, and
U the angular momentum transport. In the
T direction, application of the Prigogine principle selects the value of
T corresponding to the stationary state. When there are several possible stationary states, the Principle B then selects the most stable state as the one with the largest entropy production, thereby fixing the corresponding value of
U. This was precisely the procedure followed by Paltridge.
On the other hand, it appears that the stability of the stationary state may depend on boundary conditions. For example, Niven [
27] or Kawazura and Yoshida [
28] provide explicit examples of out-of-equilibrium systems, in which the entropy production is
maximized for fixed temperature boundary conditions, while it is
minimized for fixed heat flux boundary conditions. In the experimental von Kármán system discussed in
Section 1, we observe a similar phenomenon: for fixed propeller velocities, the selected stationary state is the one of maximum dissipation. However, when one changes the boundary conditions into fixed applied torque at each propeller, the stationary state regime disappears and is replaced by a dynamical regime, in which the system switches between different meta-stable states of low and high energy dissipation [
6]. This case is discussed in more detail in
Section 6. It shows, however, that we cannot trust the Maximum Entropy Production principle blindly, and must find ways to understand why and when it works, using tools borrowed from non-equilibrium theories. A justification has been attempted [
8], and dismissed [
22,
23], following the ideas of Jaynes that non-equilibrium systems should be characterized by a probability distribution on the trajectories in phase space, instead of just the points in phase space at equilibrium. A more pragmatic way to evaluate the validity of Principle B is to consider its application to toy models of non-equilibrium statistics, which mimics the main processes at work in the von Kármán flow, and that can guide us on a way to a justification (or dismissal). This is the topic of the next section.
3. From Maximum Entropy Production to Maximum Kolmogorov–Sinai Entropy in Toy Models of Turbulence
3.1. From Passive Scalar Equation to Markovian Box Models
In the von Kármán flow, angular momentum is transported from the vessel ends towards the center. In Rayleigh–Bénard, the temperature is transported from the bottom to the top plates. In shear flows, the linear momentum is transported from one side to the other. On Earth, the heat is transported from the equator towards the pole. All these systems in which Principle B seems to provide a non-trivial answer have then in common that they deal with the transport of a scalar quantity
T by a given velocity field
, which may be sketched as:
with appropriate boundary conditions. Here,
is the diffusivity. To transform this process into a tractable toy model, we stick to a one-dimensional case and divide the accessible space
ℓ into
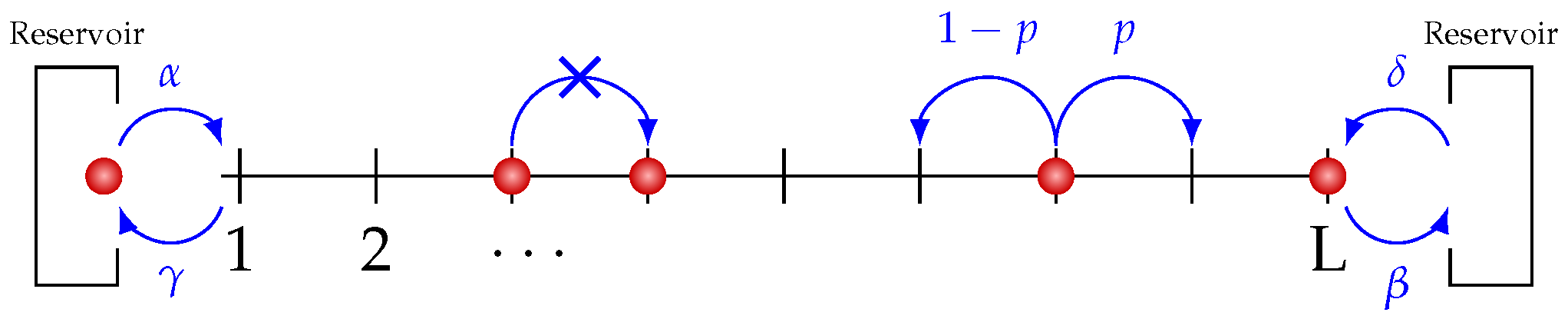
L boxes. We impose the boundary conditions through two reservoirs located at each end of the chain (mimicking e.g., the top and bottom propeller or solar heat flux at pole and equator). The boxes contain bosonic or fermionic particles that can jump in between two adjacent boxes via decorrelated jumps (to the right or to the left) following a 1D Markov dynamics governed by a coupling with the two reservoirs imposing a difference of chemical potential at the ends. The different jumps are described as follows. At each time step, a particle can jump right with probability
or jump left with probability
.
is a parameter depending on the number of particles inside the box and on the nature of particles. Choices of different
give radically different behaviors. For fermionic particles, it prevents a jump on to a site, if this site is already occupied by a particle. The corresponding process is called the Asymmetric Exclusion Process (ASEP). For boson,
and the process is called Zero Range Process (ZRP). At the edges of the lattice, the probability rules are different: at the left edge, a particle can enter with probability
and exit with probability
, whereas, at the right edge, a particle can exit with probability
and enter with probability
. See
Figure 5 for a visual description.
Without loss of generality, we may consider only , which corresponds to a particle flow from the left to the right and note . After a sufficiently long time, the system reaches a non-equilibrium steady state, with a well defined density profile (or fugacity profile) across the boxes ranging between , the density of the left reservoir and , the density of the right reservoir, given by and , where for ASEP (fermion) and for ZRP (boson). In the sequel, we fix and and denote the parameter that measures the balance between the input rate of the left reservoir (the equivalent of the heat or momentum injection), and the removal rate of the right reservoir (the equivalent of the heat or momentum dissipation). Once (say) and are fixed, we can compute all the other parameters , and of the model. In the sequel, we fix and vary and/or U.
Taking the continuous limit of this process, it may be checked that the fugacity
of stationary solutions of a system consisting of boxes of size
follow the continuous equation [
29]:
corresponding to stationary solution of a passive scalar equation with velocity
U and diffusivity
. Therefore, the fugacity
Z is a passive scalar obeying a convective-diffusion equation. We thus see that
corresponds to a purely conductive regime, whereas the larger the
U, the more convective the regime. This toy model therefore mimics in the continuous limit the behavior of scalar transport in the von Kármán, Rayleigh–Bénard, Couette or Earth system we are trying to understand. The toy model is a discrete Markov process with
states. It is characterized by its transition matrix
, which is irreducible. Thus, the probability measure on the states converges to the stationary probability measure
which satisfies:
This Markov property makes our model simple enough so that exact computations are analytically tractable and numerical simulations are possible up to
(ASEP model) to
(ZRP model) on a laptop computer. The idea now is to apply the Principle B in these toy models and see what useful information we can derive from it.
3.2. Maximum Entropy Production in Zero Range and Asymmetric Exclusion Process
We turn to the definition of entropy production in our toy model system. For a macroscopic system subject to thermodynamic forces
and fluxes
, the thermodynamic entropy production is given by: [
30,
31]:
The fluxes to consider for a diffusive particles model are fluxes of particles and the thermodynamic forces can be written
, where
T is the temperature and
the chemical potential proportional to
for an ideal gas [
30]. Thus, as the temperature here is fixed, the thermodynamic Entropy production of a given stationary state takes the form:
where
is the stationary density distribution and
the particle fluxes in the stationary state, where all fluxes become equal and independent from the site.
and
J are both (nonlinear) function of
U. It is easy to show [
32] that this definition is just the continuous limit of the classical thermodynamic entropy production in an ideal gas, which reads:
In the case of bosonic particles (ZRP model), this entropy production takes a compact analytical shape in the (thermodynamic) limit
[
33]:
Because
, the entropy production is positive if and only if
. This means that fluxes are in the opposite direction of the gradient. We remark than that if
, then
. Indeed,
J is proportional to
U in this model. Moreover,
is zero also when
. This happens when
U increases,
decreases and
increases until they take the same value. Thus, there exists a large enough
U, for which
. Between these two values of
U, the entropy production has at least one maximum. By computing numerically the entropy production, we observe in fact that it is also true for the fermionic particles, even though we cannot prove it analytically. This is illustrated in
Figure 6 for
(ZRP) and
(ASEP).
The value of
at which this maximum occurs depends on the distance to equilibrium of the system, characterized by the parameter
. In the case of the ZRP model, it can be computed as [
33]:
where
. This means that at equilibrium (
,
), the maximum is attained for
, i.e., the symmetric case. Numerical simulations of the ASEP system suggest that this behavior is qualitatively valid also for fermionic particles: the entropy production displays a maximum, which varies linearly in
. Such behavior therefore appears quite generic for this class of toy model. When the system is close to equilibrium (
), the maximum is very near zero, and, the density profile is linear, corresponding to a
conductive case. When the system is out-of-equilibrium (
), the maximum is shifted towards larger values of
, corresponding to a
convective state, with flattened profile. An example is provided in
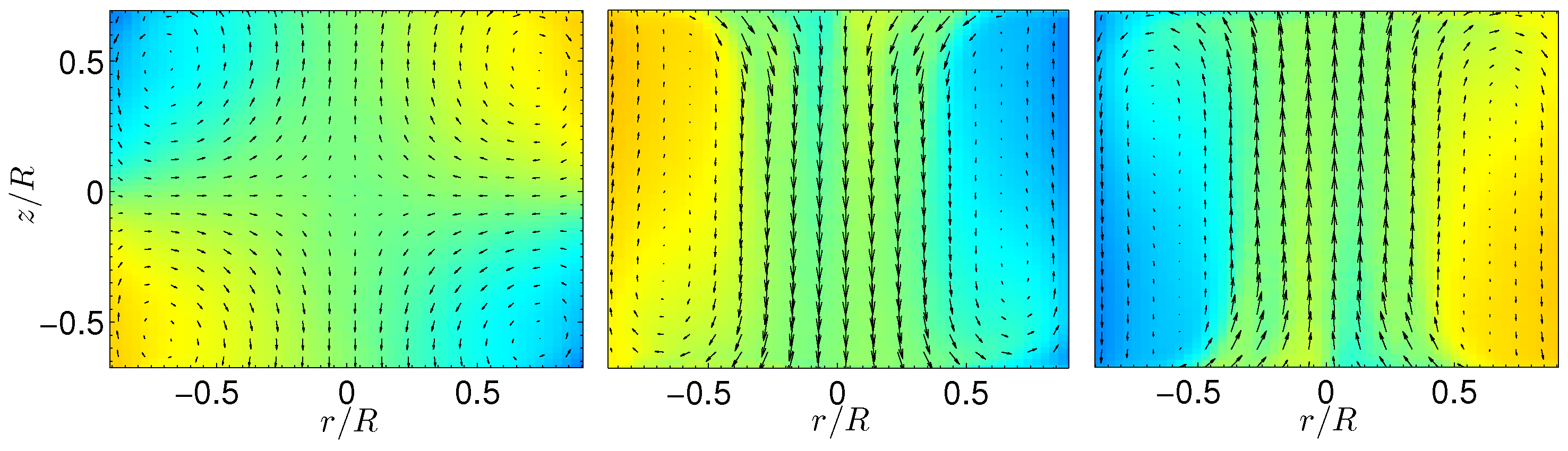
Figure 7 for the ZRP and ASEP model.
Our toy models are examples of systems with deviation from equilibrium (labelled by
), admitting several stationary states (labelled by
U). Thus, if we were to apply our MinMax/Principle B to these toy models, we would select the model corresponding to
as the most stable one, i.e., the conductive state with a linear profile at equilibrium, and the convective state with flattened profile at non-equilibrium. Interestingly enough, this selection corresponds qualitatively to the type of profiles that are selected by the nonlinear dynamics in the von Kármán, Rayleigh–Bénard or Couette system, as illustrated in
Figure 8 for the Von Kármán flow: for low levels of fluctuations (low Reynolds or impeller with bent blades) corresponding to close to equilibrium state, the most stable state is the symmetric state, with linear angular momentum profile. At larger fluctuation rates, the most stable state is the bifurcated state, with flat angular momentum at the center.
The ability of Principle B, based only on entropy, i.e., equilibrium notions, to predict at least qualitatively the correct behavior of scalar transport in several non-equilibrium turbulent systems is puzzling. It would be more satisfying to connect this Principle to other notions that seem more appropriate in the case of the non-equilibrium system. This is the topic of the next section.
3.3. From Maximum Entropy Production to Kolmogorov–Sinai Entropy
The physical meaning of the thermodynamic entropy production is the measure of irreversibility: the larger
, the more irreversible the system [
34]. It is, however, only a
static quantity, being unconnected to the behavior of trajectories in the phase space. In that respect, it is not in agreement with the ideas of Jaynes that non-equilibrium systems should be characterized by a probability distribution on the trajectories in phase space, instead of just the points in phase space at equilibrium. In the context of Markov chains, Jaynes’ idea provides a natural generalization of equilibrium statistical mechanics [
35], by considering the Kolmogorov–Sinai entropy (KSE). There are many ways to estimate the Kolmogorov–Sinai entropy associated with a Markov chain [
35,
36]. The most useful one in our context is the one defined as the time derivative of the Jaynes entropy. To characterize the dynamics of the system during the time interval
, one considers the possible dynamical trajectories
and the associated probabilities
. The dynamical trajectories entropy—the Jaynes entropy—reads:
For a Markov chain, we find that:
Thus, the Kolmogorov–Sinai Entropy for the Markov chain is:
where
is the stationary measure and
the transition matrix.
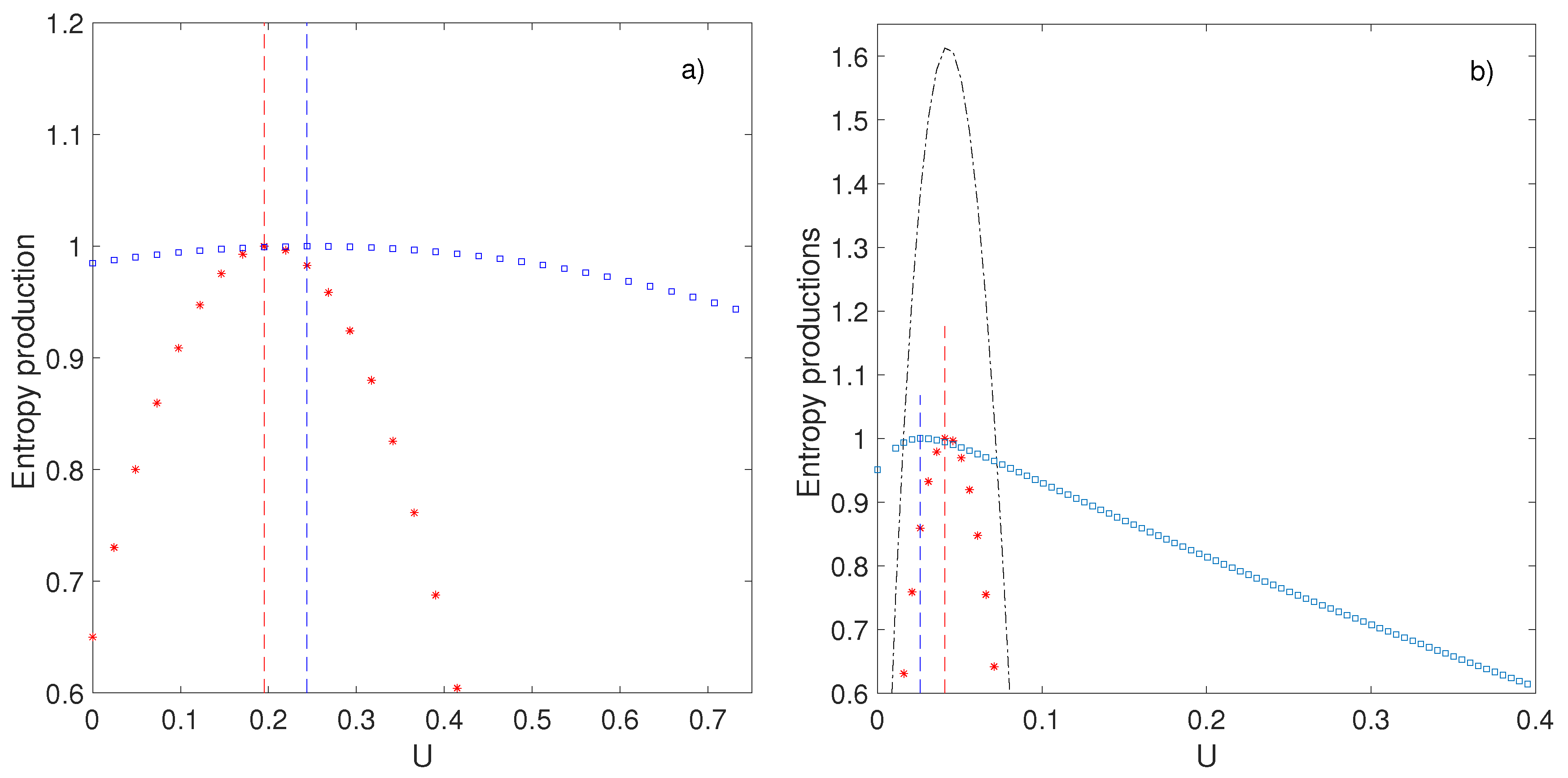
In the case of bosonic particles (ZRP model), the KSE can be computed analytically and it admits a maximum as a function of
U [
33]. The value of
U corresponding to this maximum can also be computed analytically, and leads to:
Such first order approximation appears to be valid even far from equilibrium (see
Figure 9). Comparing with the value for the maximum of entropy production, we see that the two maxima coincide, to first order in
and
: in the continuous limit, Principle B provides the same kind of information than a third principle that we may state as:
Principle C: In certain non-equilibrium systems with coexistence of several stationary state, the most stable one is that of Maximum Kolmogorov–Sinai Entropy.
Is this third principle any better that the principle B? In our toy models, it seems to give the same information than the Principle B: for ZRP, we have shown analytically that the maxima of each principle coincide to first order in
and
. Numerical simulation of the ASEP system suggests that it is also true for fermionic particles: for a given value of
, the difference between the two maxima
decreases with increasing
L [
32]. For a fixed
L, the difference between the two maxima increases with
, but never exceeds a few percent at
[
32] (see
Figure 9).
In a turbulent system, the test of this principle is more elaborate because the computation of is not straightforward. It would, however, be interesting to test it in numerical simulations.
4. From Maximum Kolmogorov–Sinai Entropy to Minimum Mixing Time in Markov Chains
Principle C is appealing because it involves a quantity clearly connected with dynamics in the phase space, but it is still unclear why the maximization of the entropy associated with paths in the phase space should select the most stable stationary state, if any. To make such a link, we need to somehow connect to the relaxation towards a stationary state, i.e., the time a system takes to reach its stationary state. In Markov chains, such a time is well defined and is called the mixing time. Intuitively, one may think that the smaller the mixing time, the most probable it is to observe a given stationary state. Thus, there should be a link between the maximum of Kolmogorov–Sinai entropy and the minimum mixing time. This link has been derived in [
25], for general Markov chains defined by their adjacency matrix
A and transition matrix
P, defined as follows:
if and only if there is a link between the nodes
i and
j and 0 otherwise.
, where
is the probability for a particle in
i to hop on the
j node. Specifically, it has been shown that Kolmogorov–Sinai entropy increases with decreasing mixing time (see Figure 1 in [
25]). More generally, for a given degree of sparseness of the matrix
A (with a number of 0), the Markov process maximizing the Kolmogorov–Sinai entropy is close (using an appropriate distance) to the Markov process minimizing the mixing time. The degree of closeness depends on the sparseness and becomes very large with decreasing sparseness, i.e., for unconstrained dynamics (Figure 3 in [
25]).
This result provides us with a fourth principle in Markov chains.
Principle D: In certain non-equilibrium systems with coexistence of several stationary states, the most stable one is that of Minimum Mixing Time.
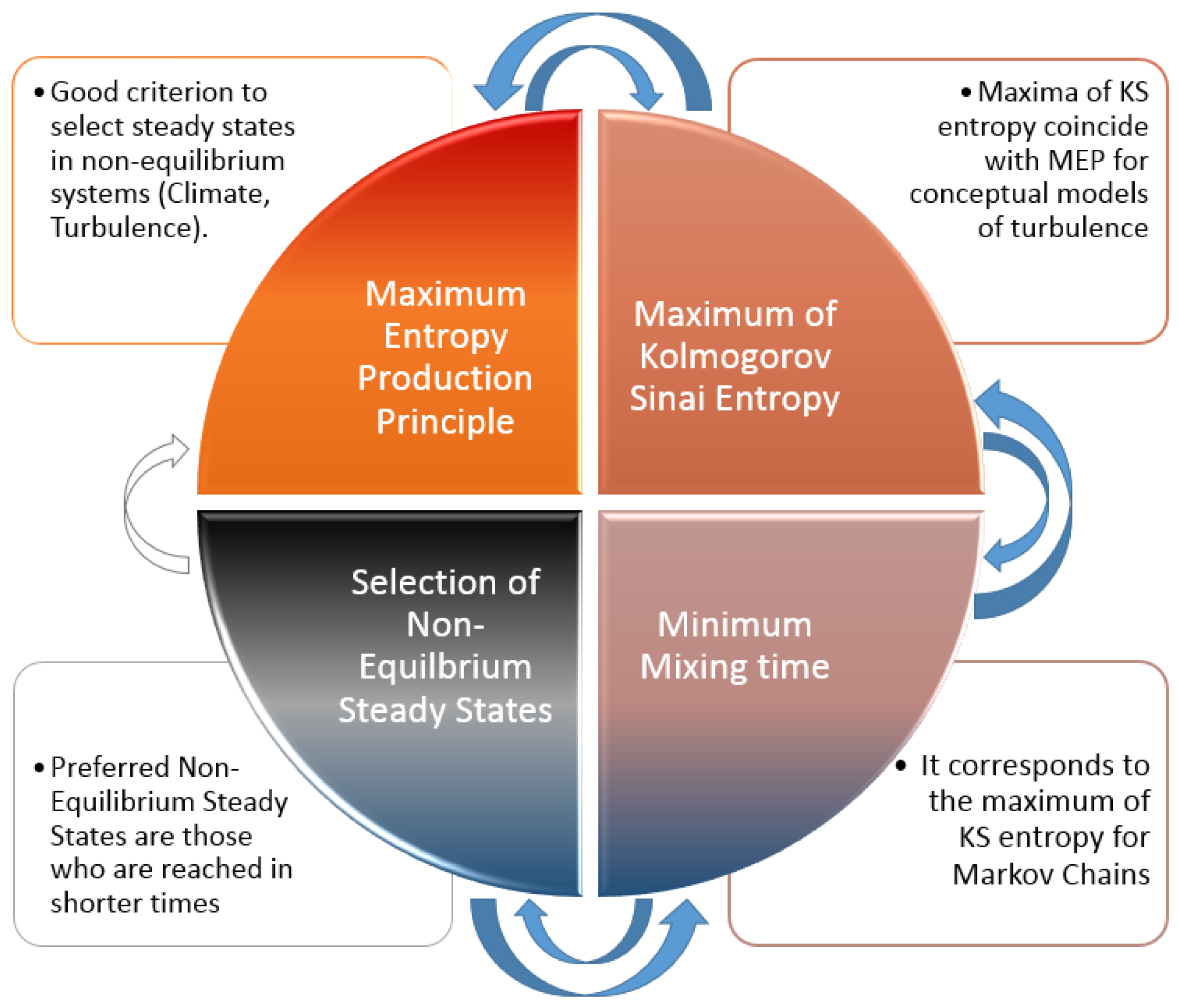
Given what we have seen before, there are four general principles that select the same stationary state, in the limit of large size and small deviations from out-of-equilibrium (see
Figure 10). Among all four, the Principle that provides the better understanding of its application is Principle D because the smaller the mixing time, the less time it is required to reach a given state and so the most probable the corresponding state. This phenomenological understanding can actually be given a deeper meaning when switching from Markov chains to Langevin systems.
5. From Minimum Mixing Time in Markov Chains to Mean Escape Rate in Langevin Systems
The notions we have derived in Markov chains have actually a natural counterpart in general Langevin systems. Consider indeed the general Langevin model:
where
is the force and
is a delta-correlated Gaussian noise:
The probability distribution of
x,
then obeys a Fokker–Planck equation:
where
is the current. It is well known (see e.g., [
37]) that the discretization of the Langevin model on a lattice of grid spacing
a (so that
) is a Markov chain, governed by the master equation:
where
is the probability of having the particle at node
n and
are the probability of forward and backward jump at node
n, given by:
From this, we can compute the Kolmogorov–Sinai entropy as [
38]
which in the continuous limit
becomes:
which is the well known entropy production.
On the other hand, the dissipated power in the Langevin process can easily be computed as:
The Kolmogorov–Sinai entropy and the dissipated power are thus proportional to each other. In such an example, it is thus clear that maxima of
and maxima of entropy production coincide.
On the other hand, when
f derives from a potential,
, there may be several meta-stable positions at
U local minima. In such a case, it is known from diffusion maps theory and spectral clustering [
39] that the exit times from the meta-stable states are connected to the smallest eigenvalues of the operator
, such that
, which is the equivalent of the Liouville operator in Markov chain. More specifically, if
U has
N local minima, then the spectra of
has a cluster of
N eigenvalues
located near 0, each of which being associated with the exit time it takes to get out from the local minima
to the state corresponding to the deepest minimum (the equilibrium state). For example,
, where
is the mean exit time to jump the highest barrier of energy onto the deepest well. From that, we see from that the smaller the eigenvalue (equivalent to the mixing time), the longer the time it takes to jump from this metastable state, and so the
more stable is this state. This provides a quantitative justification of the notion that
the most stable stationary states are the ones with the minimum mixing time. It is worth mentioning that Langevin systems are now incorporated in numerical weather prediction to provide some flexibility to the sub-grid scales’ parameterizations [
40]. Models based on these so-called stochastic parameterizations have usually better prediction skills than models based on deterministic parameterizations. Stochastic parameterization is therefore increasingly used in different aspects of weather and climate modeling [
41]. We might speculate that, in these large simulations, the stochasticity helps models to reach more realistic results by favoring jumps to
more stable states as outlined above. Another way to select these more realistic states could possibly be to search for the ones that maximize dissipation or entropy production, as was done empirically in a simple way in Paltridge’s model [
13,
14].
6. Summary: Turbulence as a Minimum Mixing Time State?
Considering a
mixing time to characterize turbulence is natural, given the well known enhancement of mixing properties observed in turbulent flows. The mixing time defined for Markov chains is also comparable to the mixing time one would naturally define for turbulence, namely the smallest time after which a given partition of a scale quantity is uniformly spread over the volume. This time corresponds to the one defined by Arnold for dynamical systems [
42] when introducing the concept of strong mixing. Here, it is the time associated with eigenvalues of the Liouville operator of the processes describing the turbulence action. In the specific example we consider here, namely von Kármán flow, the turbulence is characterized by a symmetry along the rotation axis, which favors stationary states in which angular momentum is mixed along meridional planes [
43,
44]. In this case, there is a clear connection between the equation obeying the angular momentum and the classical Fokker–Planck equation, Equation (
15). One can thus hope in such a case to find a Langevin process describing the angular momentum mixing. This was actually done in [
43] and was shown to reproduce very well the power statistics in both regimes of constant torque and constant speed forcing, in cases where there is only one stationary state. For multiple stationary states, obtained in the regime with fixed applied torque, the corresponding Langevin process has been derived in [
45] and it turns out to be a nonlinear stochastic oscillator, featuring multiple metastable states and limit cycles. Such an oscillator is found to describe the dynamics of the reduced frequency
, which is a global observable respecting the symmetries of the flow. The challenge is then to compute the mixing times of the different metastable states arising in the nonlinear stochastic oscillator.
In [
46,
47,
48], we have shown that the mixing time
of turbulent flows can be easily obtained by fitting the Langevin process (or aut-regressive process)
to data. Here,
is a global quantity tracing the symmetry of the flows,
is a random variable normally distributed, and
is the so called auto-regressive coefficient. The link with the mixing time is made through the parameter
, which is indeed proportional to
: the larger this quantity, the slower the mixing in the system because the dynamics weight more the present observation
when updating
. In [
46], only flow configurations with a single stationary state have been analysed and
computed using the complete time series. To extend the results to the flow regimes featuring multistability, we use the strategy outlined in [
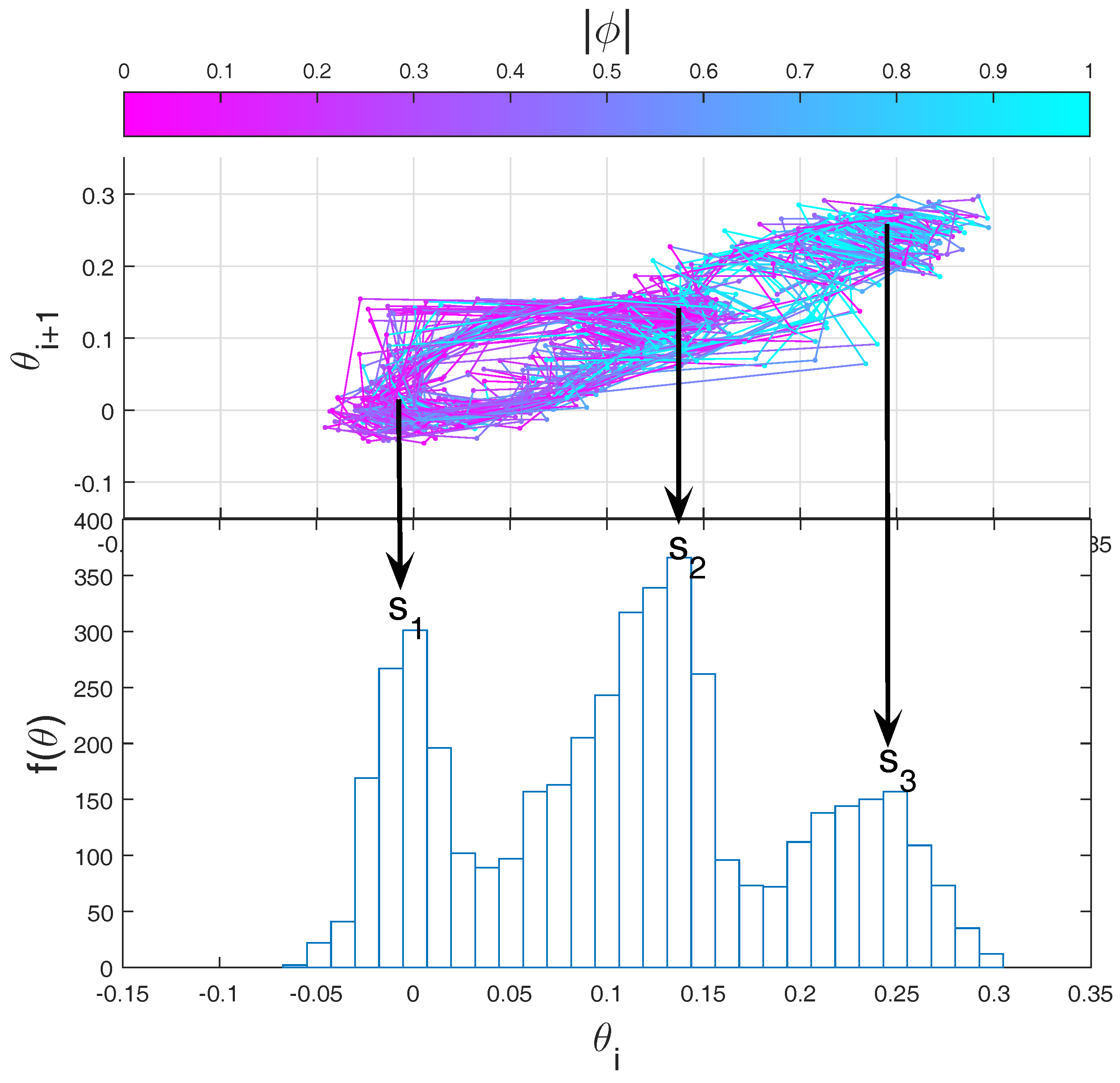
49]. First of all, we reconstruct the dynamics by using the embedding methodology on the series of partial maxima of
, denoted as
. A 2D section of the attractor is shown in the upper panel of
Figure 11 and it is obtained by plotting
as a function of the subsequent maxima
. The histogram of
is reported in the lower panel and shows the correspondence to three metastable states
. Since we are not dealing with a stationary process, we cannot compute a single
for the full time series of
. The method introduced in [
49] consists of computing a value of
for each
, taking the 50 previous observations of the complete time series. The distribution of
is shown in colorscale in
Figure 11. It is evident that the most represented states (
and
) are those with the minimum mixing time, whereas the most unstable one (
) is the one with the largest mixing time. This example shows that the results outlined in
Section 5 can be extended to higher dimensions and that there is a simple strategy to compute the mixing times in complex systems.
It is quite plausible that such study can be generalized to turbulent systems with other symmetry, such as symmetry by translation along an axis. The turbulent shear flow enters into that category. Finally, we note that in Rayleigh-Bénard systems or in stratified turbulence, the temperature is also a quantity that is mixed within the flow, which should also be liable to a Langevin description. It is therefore not a coincidence that shear flow, Rayleigh-Bénard convection and von Kármán flows are so far the only systems in which the principle of Maximum Energy dissipation has been applied with some success. They are systems where a Langevin description is possible, and where the Maximum Energy dissipation principle in fact coincides with the Minimum Mixing time principle, connected to the longest exit time from meta-stable states. As observed by [
50], these flows tends to be in a steady state with a distribution of eddies that produce the maximum rate of entropy increase in the non-equilibrium surroundings. In more general turbulence, it is not clear that such a Langevin description is possible, so that the statement of
Turbulence as a minimum Mixing Time State might actually be limited to quite special situations, where symmetry or dynamics impose pure mixing of a quantity (like angular momentum, momentum or temperature). Shear flow, Rayleigh Bénard convection and von Kármán flows belong to this category.
Other conceptual pathways allow for linking MEP to the underlying dynamics of the system: Moroz [
51] suggests that the dissipation time minimization is linked to the least action principle, used in chemistry, biology and physics to derive the equations of motion. Although this theoretical formulation goes in the same direction of the results provided in this paper, our approach provides a rather practical way to connect dynamics and thermodynamics through statistical quantities directly computable from experimental time series.