Tensor Singular Spectrum Decomposition Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis
Abstract
:1. Introduction
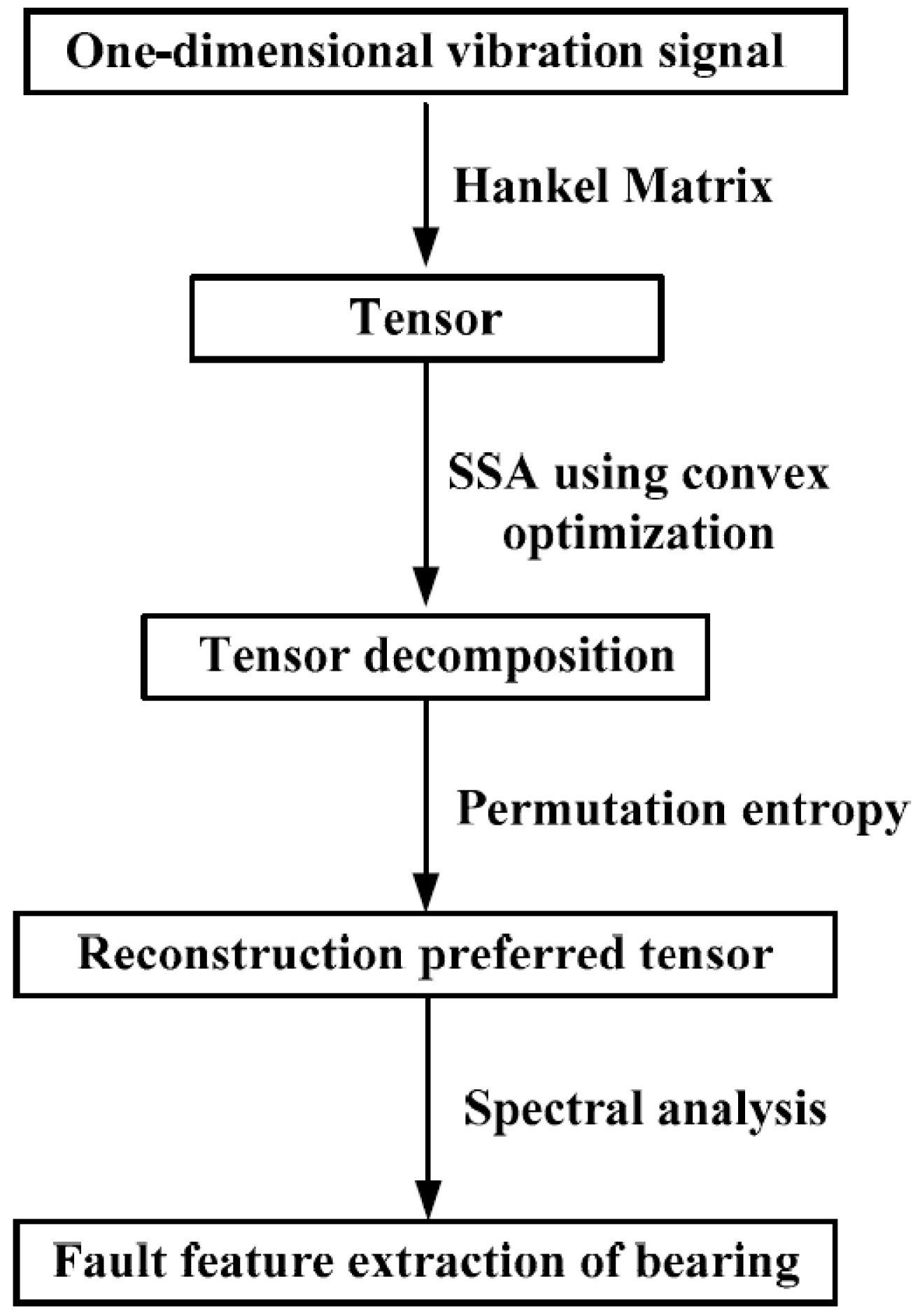
2. Theory Description
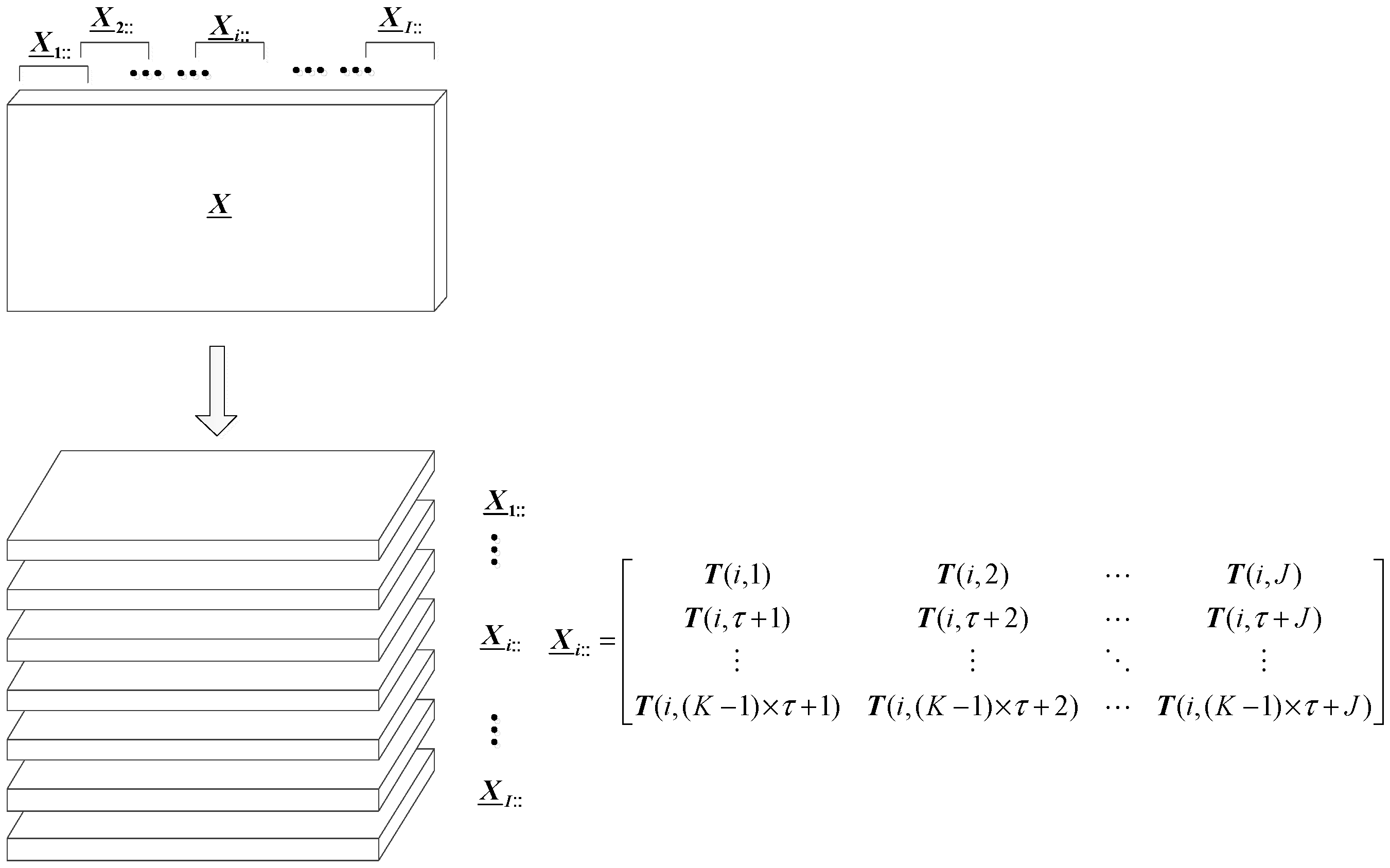
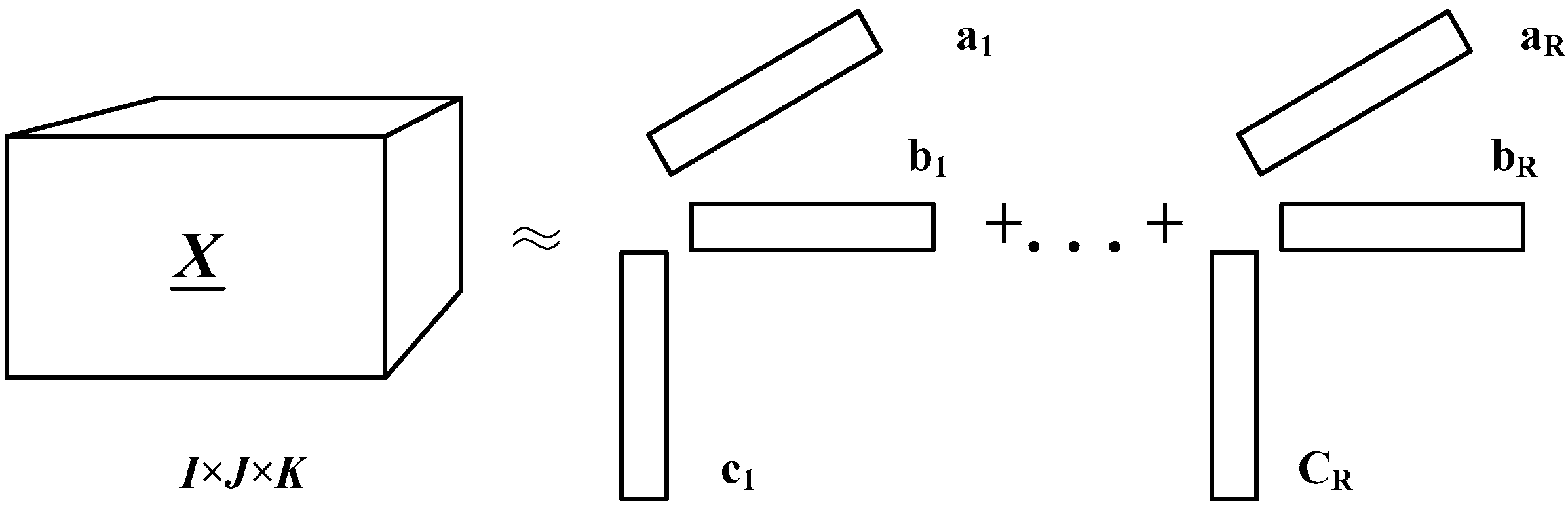
2.1. Tensor Singular Spectrum Analysis
2.2. The Rank Estimation of Tensor Based on Convex Optimization
2.3. The Desired Tensor Selection Based on PE
3. Test with Numerical Simulation Signal
3.1. The Performance of Abnormal Signal Detection Using PE
3.2. The Feature Extraction Result Provided by Proposed Method
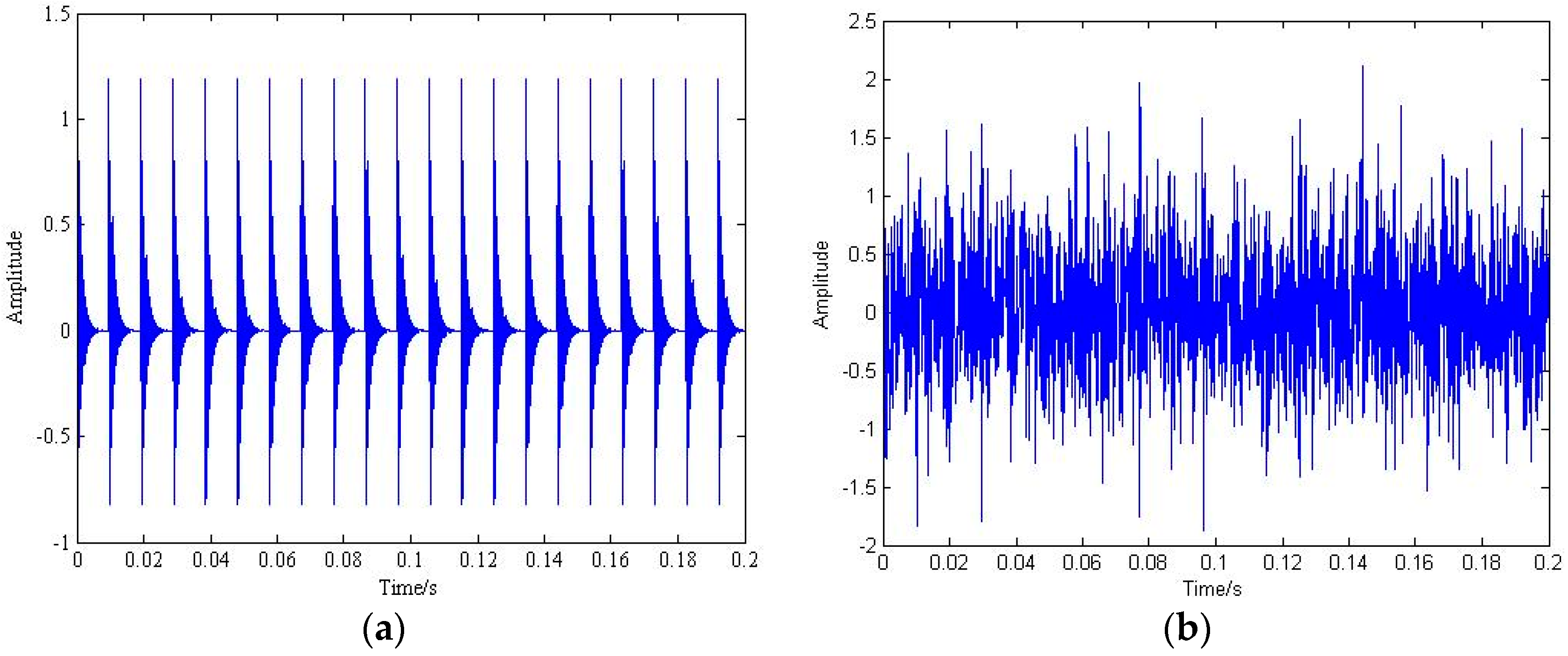
4. Applications to Rolling Bearing Fault Feature Extraction
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Veer, K.; Agarwal, R. Wavelet and short-time Fourier transform comparison-based analysis of myoelectric signals. Ournal Appl. Stat. 2015, 42, 1591–1601. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. In Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences; The Royal Society: London, UK, 1998; Volume 454, pp. 903–995. [Google Scholar]
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Yang, Z.; Zhong, J. A hybrid EEMD-based SampEn and SVD for acoustic signal processing and fault diagnosis. Entropy 2016, 18, 112. [Google Scholar] [CrossRef]
- Wu, F.; Qu, L. An improved method for restraining the end effect in empirical mode decomposition and its applications to the fault diagnosis of large rotating machinery. J. Sound Vib. 2008, 314, 586–602. [Google Scholar] [CrossRef]
- Chen, J.; Dou, Y.; Li, Y.; Li, J. Application of Shannon Wavelet Entropy and Shannon Wavelet Packet Entropy in Analysis of Power System Transient Signals. Entropy 2016, 18, 437. [Google Scholar] [CrossRef]
- Wang, D.; Tsui, K.L. Dynamic Bayesian wavelet transform: New methodology for extraction of repetitive transients. Mech. Syst. Signal Process. 2017, 88, 137–144. [Google Scholar] [CrossRef]
- Wang, D. An extension of the infograms to novel Bayesian inference for bearing fault feature identification. Mech. Syst. Signal Process. 2016, 80, 19–30. [Google Scholar] [CrossRef]
- Huang, N.E. Hilbert-Huang Transform and Its Applications; World Scientific: Singapore, 2014. [Google Scholar]
- Abeysekera, S.S.; Boashash, B. Methods of signal classification using the images produced by the Wigner-Ville distribution. Pattern Recognit. Lett. 1991, 12, 717–729. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J. Gear-box fault detection using time-frequency based methods. Annu. Rev. Control 2015, 40, 50–58. [Google Scholar] [CrossRef]
- Nejad, A.R.; Odgaard, P.F.; Gao, Z.; Moan, T. A prognostic method for fault detection in wind turbine drivetrains. Eng. Fail. Anal. 2014, 42, 324–336. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Nejad, A.R. Frequency based wind turbine gearbox fault detection applied to a 750 kW wind turbine. In Proceedings of the IEEE Conference on Control Applications, Antibes, France, 8–10 October 2014; pp. 1383–1388. [Google Scholar]
- Fadlallah, B.; Chen, B.; Keil, A.; Principe, J.C. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Wang, J.; Zhao, H.; Principe, J.C. Insights into entropy as a measure of multivariate variability. Entropy 2016, 18, 196. [Google Scholar] [CrossRef]
- Chen, B.; Yuan, Z.; Zheng, N.; Principe, J.C. Kernel minimum error entropy algorithm. Neurocomputing 2013, 121, 160–169. [Google Scholar] [CrossRef]
- Chen, B.; Zhu, Y.; Hu, J. Mean-square convergence analysis of ADALINE training with minimum error entropy criterion. IEEE Trans. Neural Netw. 2010, 21, 1168–1179. [Google Scholar] [CrossRef] [PubMed]
- Hitchcock, F.L. The expression of a tensor or a polyadic as a sum of products. J. Math. Phys. 1927, 6, 164–189. [Google Scholar] [CrossRef]
- Carroll, J.D.; Chang, J.J. Analysis of individual differences in multidimensional scaling via an N-way generalization of “Eckart-Young” decomposition. Psychometrika 1970, 35, 283–319. [Google Scholar] [CrossRef]
- Harshman, R.A. Foundations of the PARAFAC procedure: Models and conditions for an “explanatory” multi-modal factor analysis. UCLA Work. Pap. Phon. 1970, 16, 1–84. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Kouchaki, S.; Sanei, S.; Arbon, E.L.; Dijk, D.-J. Tensor based singular spectrum analysis for automatic scoring of sleep EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Romero, C.E.; Yao, Z. Wind power forecasting based on principle component phase space reconstruction. Renew. Energy 2015, 81, 737–744. [Google Scholar] [CrossRef]
- Tomasi, G.; Bro, R. PARAFAC and missing values. Chemom. Intell. Lab. Syst. 2005, 75, 163–180. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Nocedal, J.; Wright, S.J. Penalty and augmented Lagrangian methods. In Numerical Optimization; Springer: New York, NY, USA, 2006; pp. 497–528. [Google Scholar]
- Rufai, M.A.; Anbarjafari, G.; Demirel, H. Lossy image compression using singular value decomposition and wavelet difference reduction. Digit. Signal Process. 2014, 24, 117–123. [Google Scholar] [CrossRef]
- Parekh, A.; Selesnick, I.W. Enhanced low-rank matrix approximation. IEEE Signal Process. Lett. 2016, 23, 493–497. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Bayram, İ. Enhanced Sparsity by Non-Separable Regularization. IEEE Trans. Signal Process. 2015, 64, 2298–2313. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z.; Xiao, H. A Novel Mechanical Fault Diagnosis Scheme Based on the Convex 1-D Second-Order Total Variation Denoising Algorithm. Appl. Sci. 2016, 6, 403. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z.; Xiao, H.; Yu, X. Quaternion singular spectrum analysis using convex optimization and its application to fault diagnosis of rolling bearing. Measurement 2017, 103, 321–332. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Theodossiades, S.; Natsiavas, S. Non-linear dynamics of gear-pair systems with periodic stiffness and backlash. J. Sound Vib. 2000, 229, 287–310. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, M.; Deng, W.; Yang, X. A New Feature Extraction Method Based on EEMD and Multi-Scale Fuzzy Entropy for Motor Bearing. Entropy 2016, 19, 14. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar]
- Harshman, R.A.; Berenbaum, S.A. Basic concepts underlying the PARAFAC-CANDECOMP three-way factor analysis model and its application to longitudinal data. In Present and Past in Middle Life; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Burdick, D.S. An introduction to tensor products with applications to multiway data analysis. Chemom. Intell. Lab. Syst. 1995, 28, 229–237. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403. [Google Scholar] [CrossRef] [PubMed]
- Randall, R.B.; Antoni, J.; Chobsaard, S. The relationship between spectral correlation and envelope analysis in the diagnostics of bearing faults and other cyclostationary machine signals. Mech. Syst. Signal Process. 2001, 15, 945–962. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. A stochastic model for simulation and diagnostics of rolling element bearings with localized faults. J. Vib. Acoust. 2003, 125, 282–289. [Google Scholar] [CrossRef]
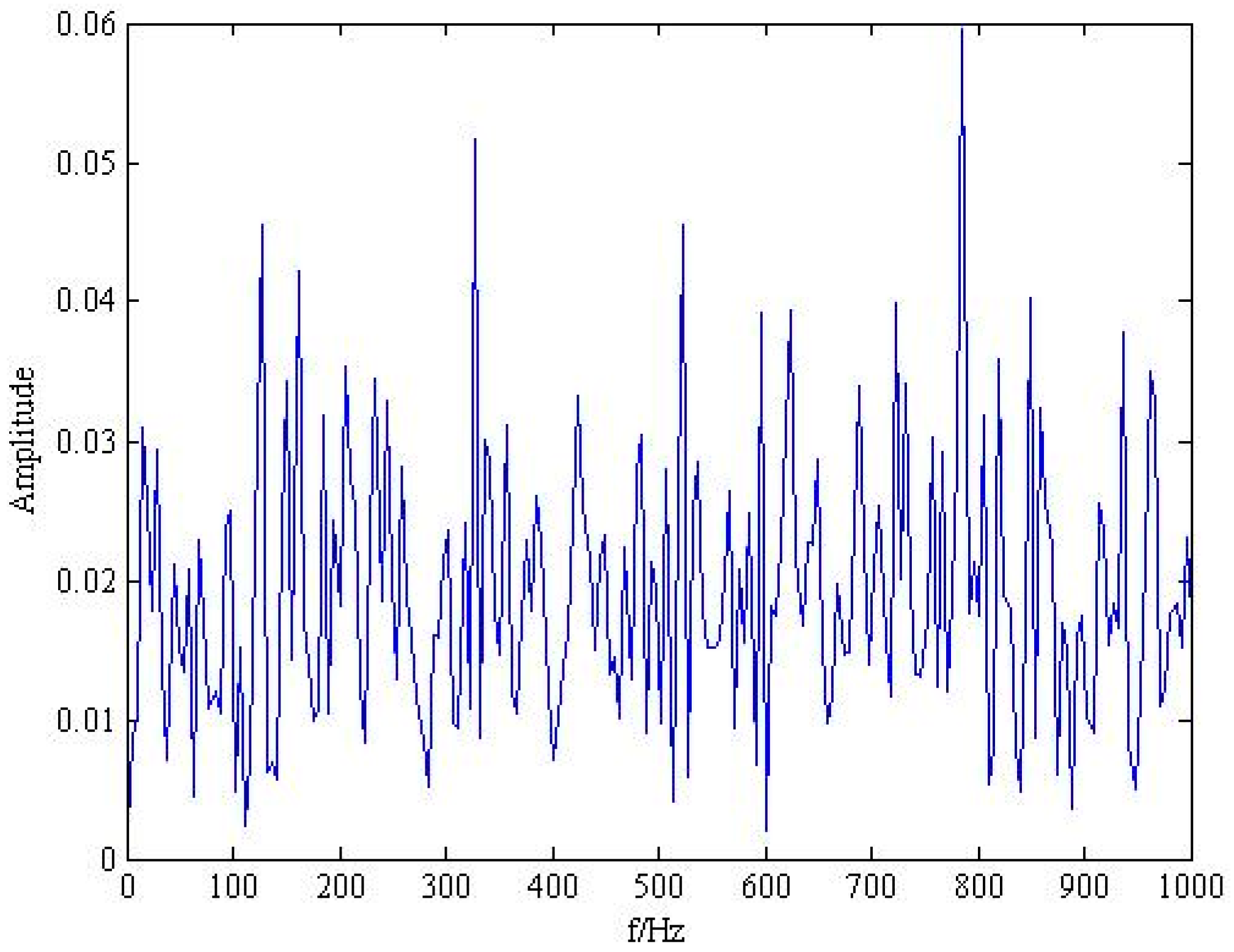
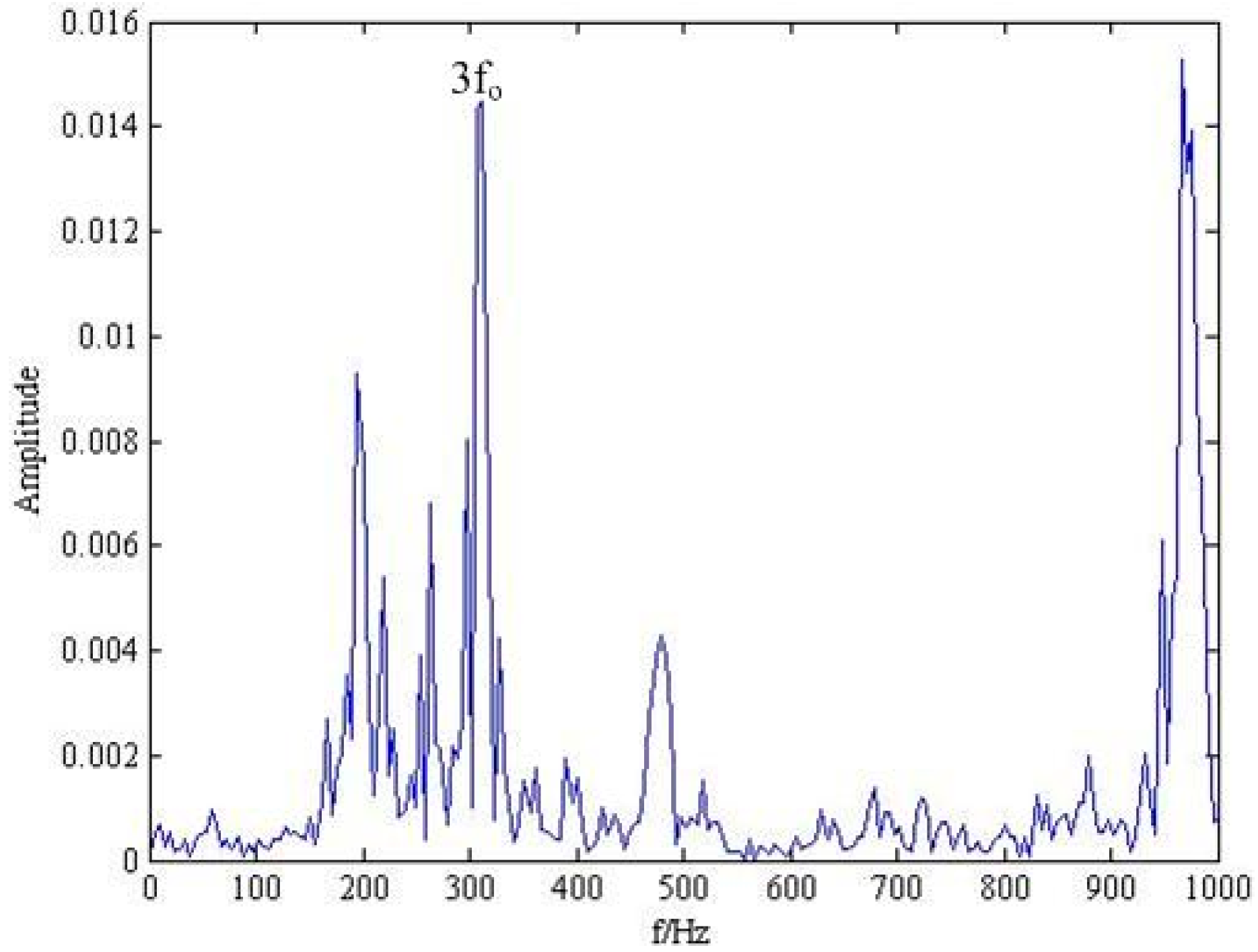
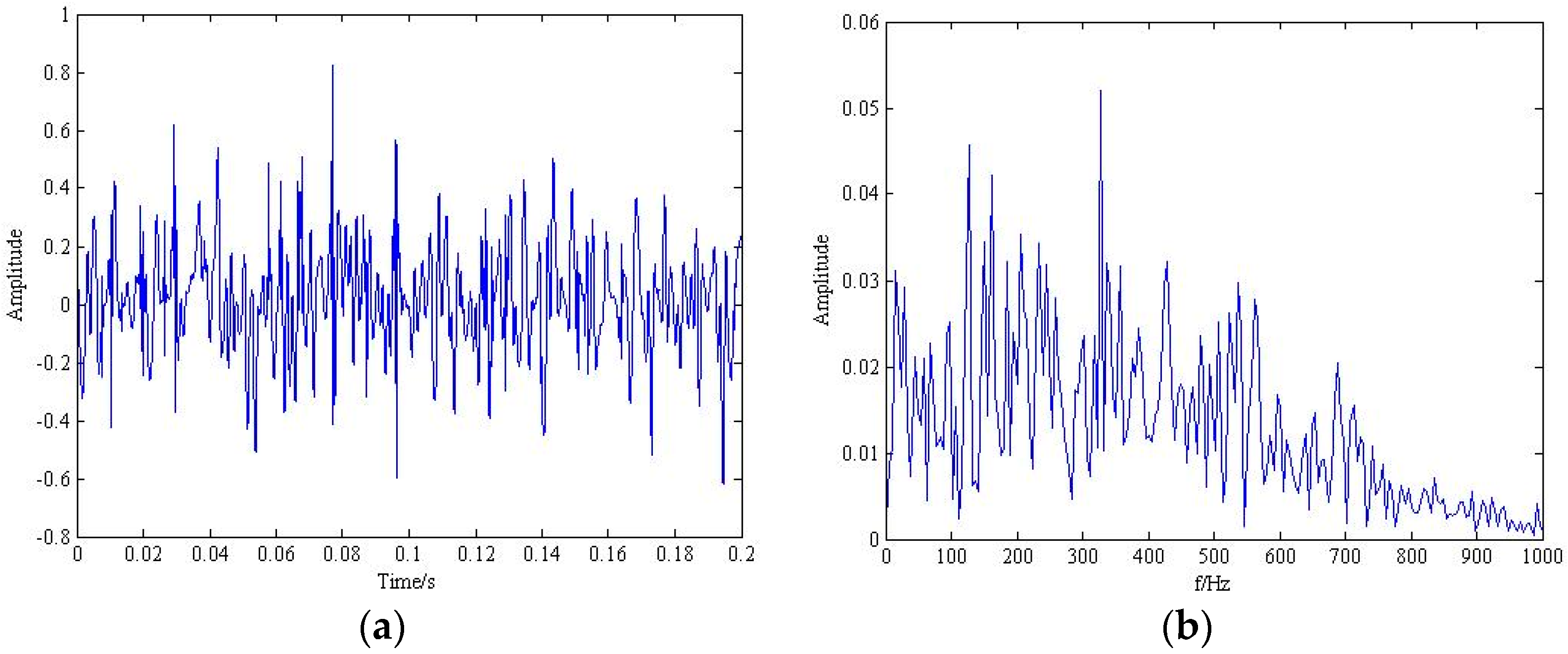
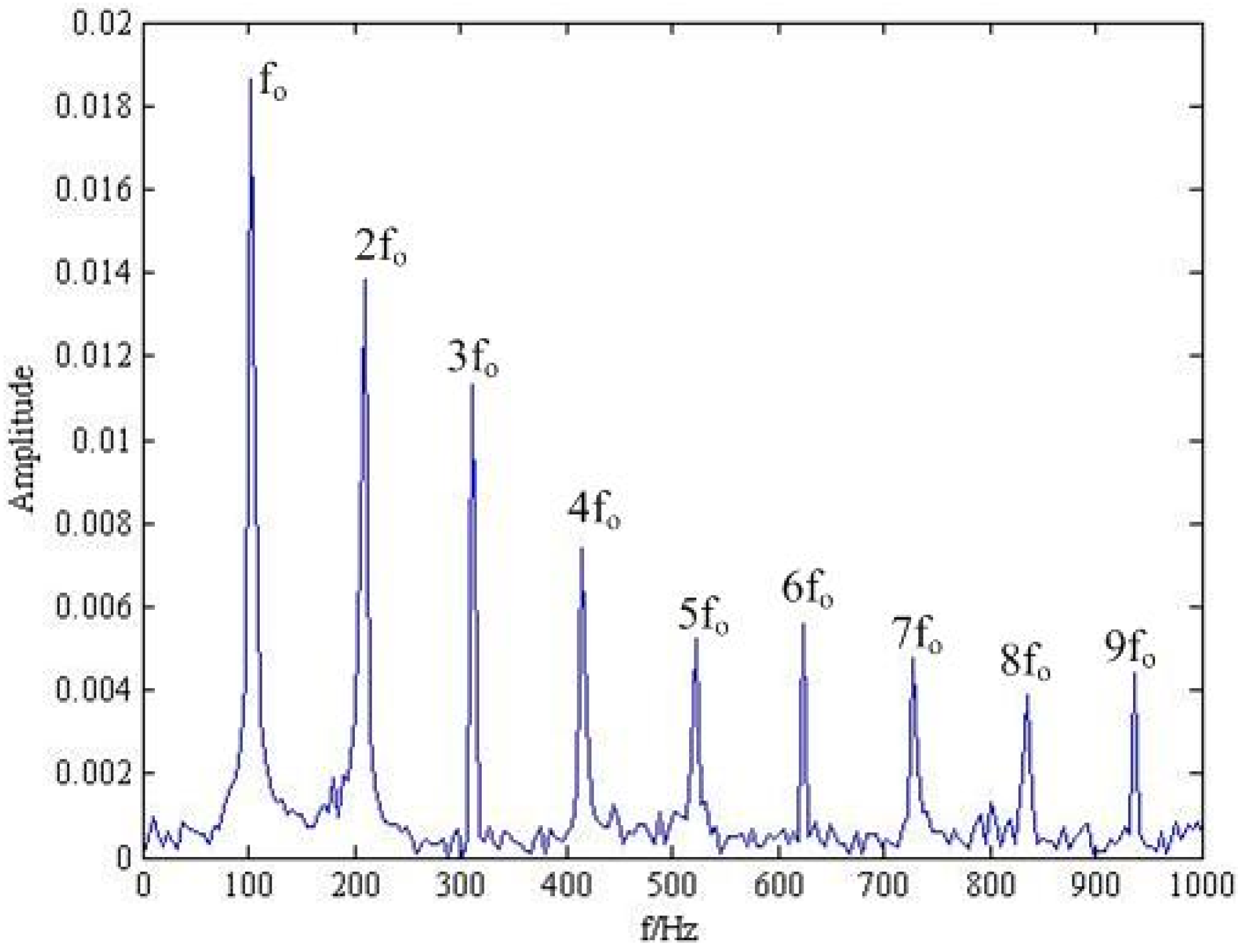

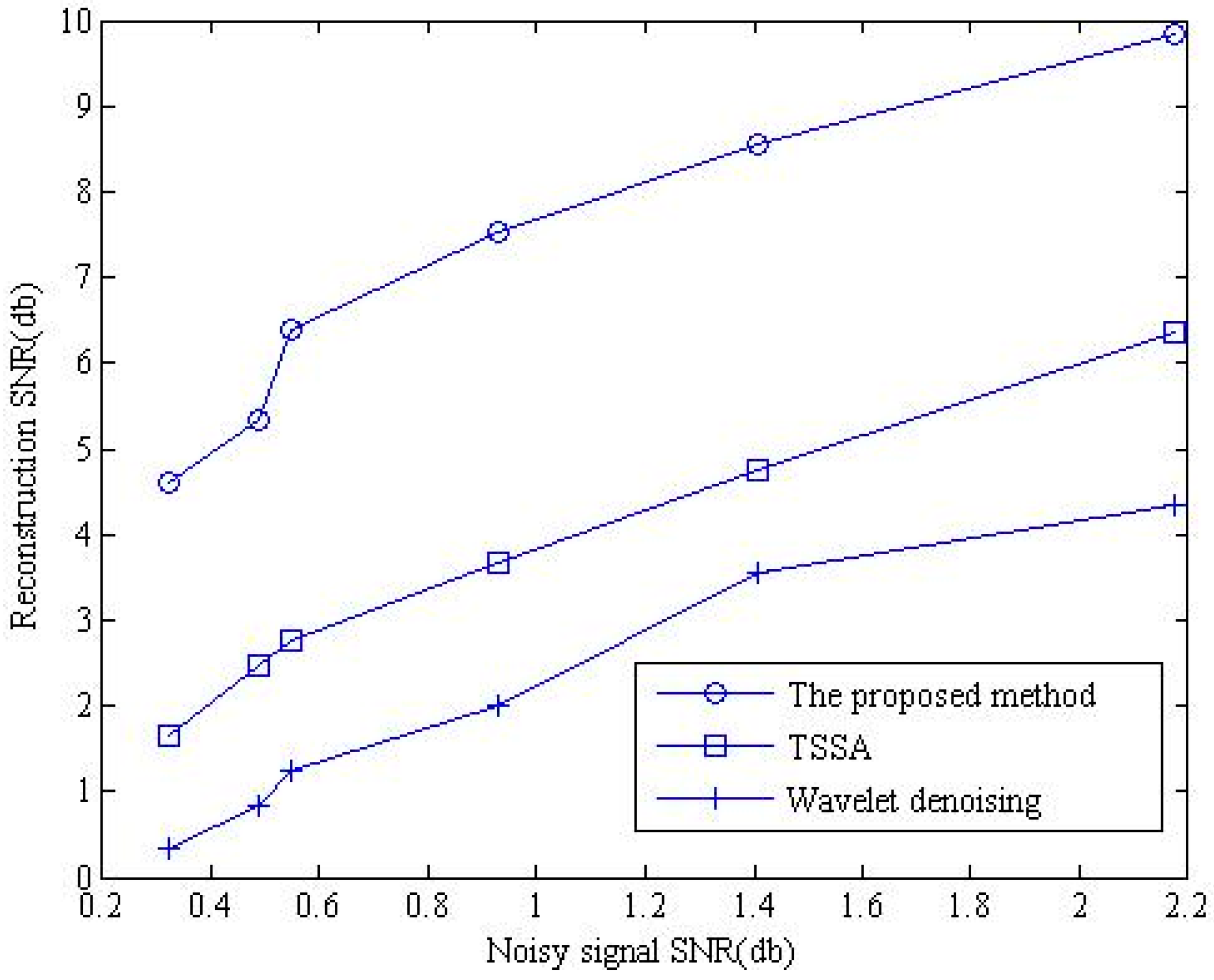
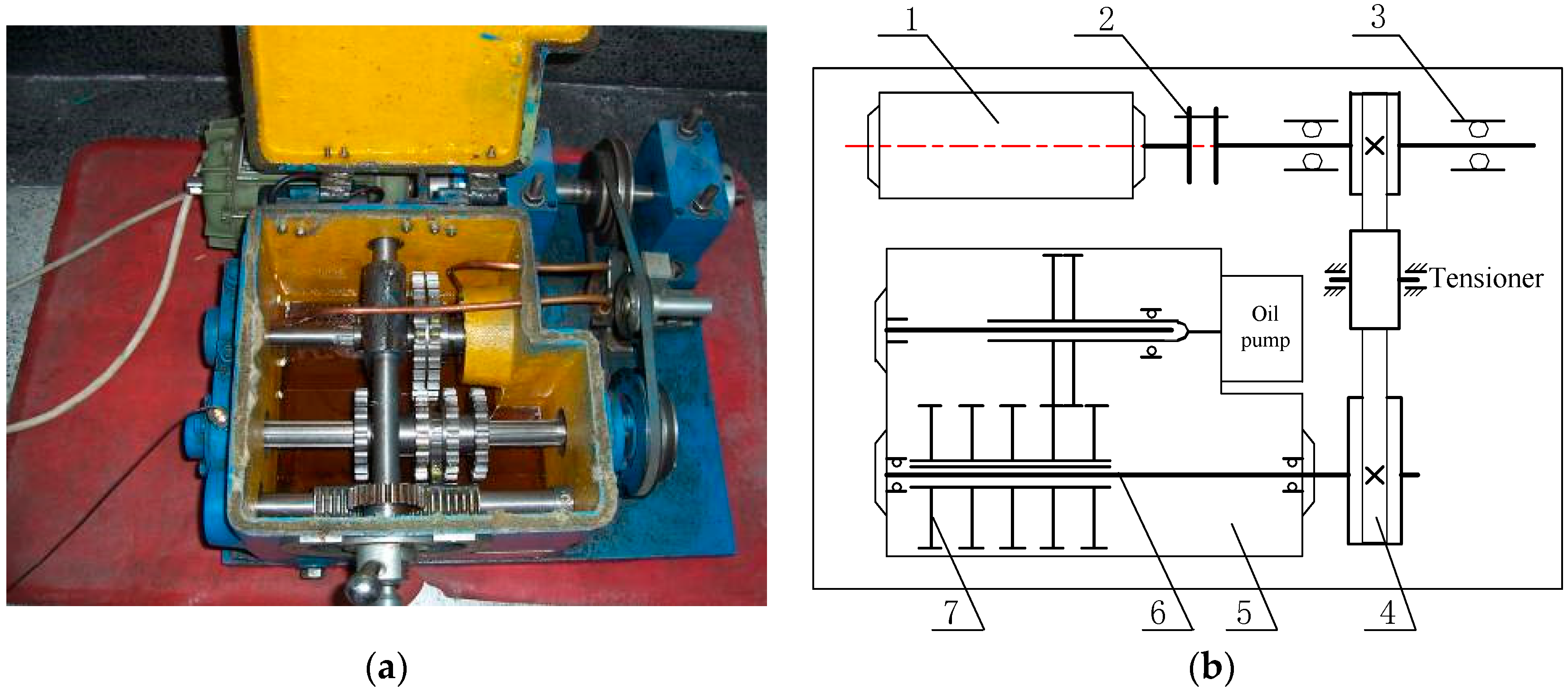

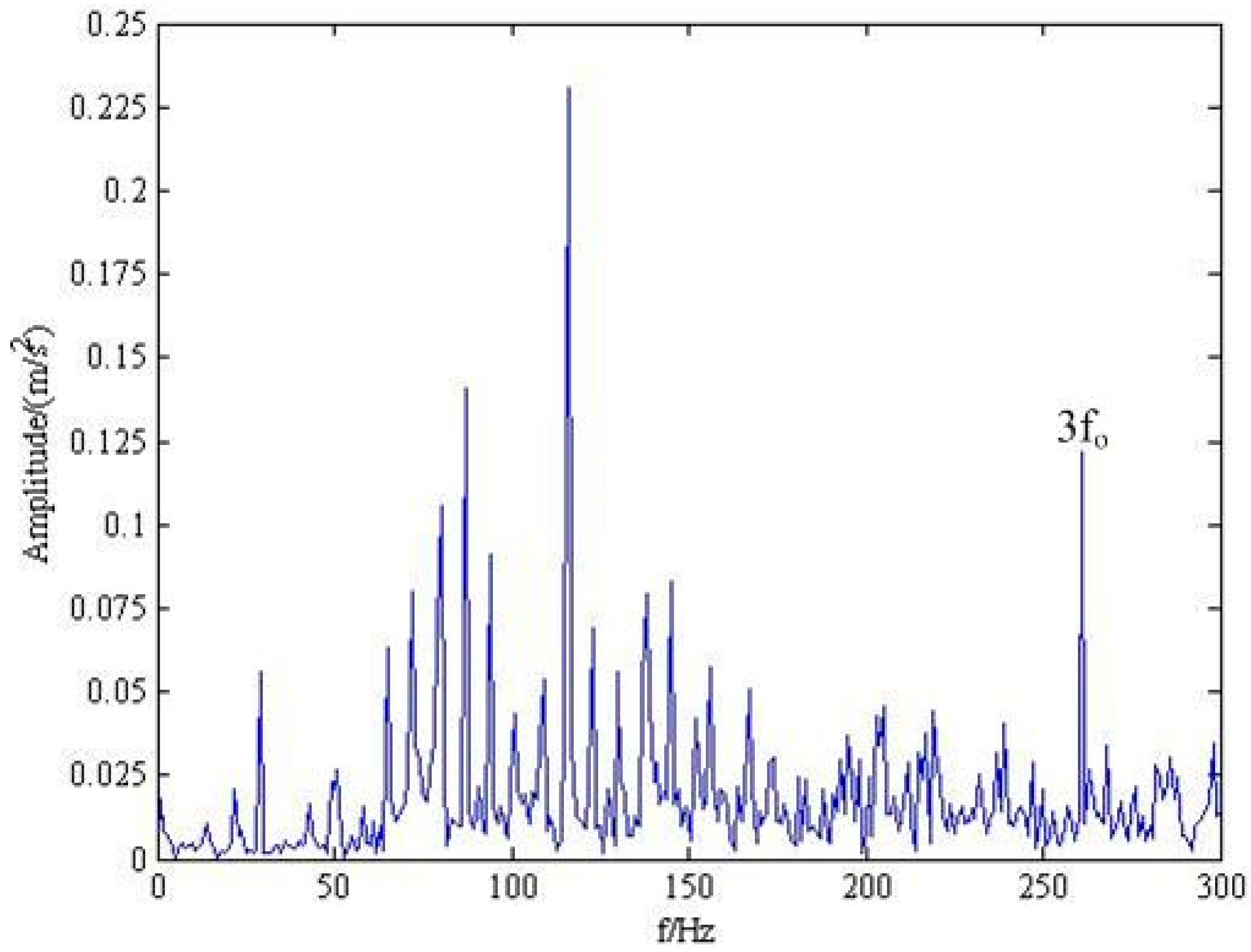

| Inner Race fi (Hz) | Outer Race fo (Hz) | Rolling Element fro (Hz) |
|---|---|---|
| 156 | 103.9 | 59.7 |
| (Hz) | (Hz) | (Hz) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.0003 | 17 | 0 | 0.01 | 2000 | 1 | 0 | 0 | 800 |
| Rotating Speed r/min | Rotating Frequency/Hz | Sampling Frequency/Hz | Sampling Time/s | Outer Fault Frequency/Hz |
|---|---|---|---|---|
| 1450 | 24.17 | 16384 | 1 | 87.01 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, C.; Lv, Y.; Ge, M.; Xiao, H.; Yu, X. Tensor Singular Spectrum Decomposition Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy 2017, 19, 139. https://doi.org/10.3390/e19040139
Yi C, Lv Y, Ge M, Xiao H, Yu X. Tensor Singular Spectrum Decomposition Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy. 2017; 19(4):139. https://doi.org/10.3390/e19040139
Chicago/Turabian StyleYi, Cancan, Yong Lv, Mao Ge, Han Xiao, and Xun Yu. 2017. "Tensor Singular Spectrum Decomposition Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis" Entropy 19, no. 4: 139. https://doi.org/10.3390/e19040139






