Abstract
Quantifying synergy among stochastic variables is an important open problem in information theory. Information synergy occurs when multiple sources together predict an outcome variable better than the sum of single-source predictions. It is an essential phenomenon in biology such as in neuronal networks and cellular regulatory processes, where different information flows integrate to produce a single response, but also in social cooperation processes as well as in statistical inference tasks in machine learning. Here we propose a metric of synergistic entropy and synergistic information from first principles. The proposed measure relies on so-called synergistic random variables (SRVs) which are constructed to have zero mutual information about individual source variables but non-zero mutual information about the complete set of source variables. We prove several basic and desired properties of our measure, including bounds and additivity properties. In addition, we prove several important consequences of our measure, including the fact that different types of synergistic information may co-exist between the same sets of variables. A numerical implementation is provided, which we use to demonstrate that synergy is associated with resilience to noise. Our measure may be a marked step forward in the study of multivariate information theory and its numerous applications.
1. Introduction
Shannon’s information theory is a natural framework for studying the correlations among stochastic variables. Claude Shannon proved that the entropy of a single stochastic variable uniquely quantifies how much information is required to identify a sample value from the variable, which follows from four quite plausible axioms (non-negativity, continuity, monotonicity and additivity) [1]. Using similar arguments, the mutual information between two stochastic variables is the only pairwise correlation measure which quantifies how much information is shared. However, higher-order informational measures among three or more stochastic variables remain a long-standing research topic [2,3,4,5,6].
A prominent higher-order informational measure is synergistic information [3,4,5,7,8,9,10], however it is still an open question how to measure it. It should quantify the idea that a set of variables taken together can convey more information than the summed information of its individual variables. Synergy is studied for instance in the context of regulatory processes in cells and networks of neurons. To illustrate the idea at a high level, consider the recognition of a simple object, say a red square, implemented by a multi-layer neuronal network. Some input neurons will implement local edge detection, and some other input neurons will implement local color detection, but the presence of the red square is not defined solely by the presence of edges or red color alone: it is defined as a particular higher-order relation between edges and color. Therefore, a neuronal network which successfully recognizes an object must integrate the multiple pieces of information in a synergistic manner. However, it is unknown exactly how and where this is implemented in any dynamical network because no measure exists to quantify synergistic information among an arbitrary number of variables. Synergistic information appears to play a crucial role in all complex dynamical systems ranging from molecular cell biology to social phenomena, and some argue even in quantum entanglement [11].
We consider the task of predicting the values of an outcome variable using a set of source variables . The total predictability of given is quantified information-theoretically by the classic Shannon mutual information:
Here:
is the entropy of and denotes the total amount of information needed on average to determine a unique value of , in bits. It is also referred to as the uncertainty about . The conditional variant obeys the chain rule and is written explicitly as:
This denotes the remaining entropy of given that the value for is observed. We note that and easily extend to vector-valued variables, for details see for instance Cover and Thomas [12].
In this article we address the problem of quantifying synergistic information between and . To illustrate information synergy, consider the classic example of the XOR-gate of two i.i.d. binary inputs, defined by the following (deterministic) input-output table (Table 1).

Table 1.
Transition table of the binary XOR-gate.
A priori the outcome value of is 50/50 distributed. It is easily verified that observing both inputs and simultaneously fully predicts the outcome value , while observing either input individually does not improve the prediction of at all. Indeed, we find that:
In words this means that in this case the information about the outcome is not stored in either source variable individually, but is stored synergistically in the combination of the two inputs. In this case stores whether , which is independent of the individual values of either or .
Two general approaches to quantify synergy exist in the current literature. On the pragmatic and heuristic side, methods have been devised to approximate synergistic information using simplifying assumptions. An intuitive example is the “whole minus sum” (WMS) method [10] which simply subtracts the sum of pairwise (“individual”) mutual information quantities from the total mutual information, i.e., . This formula is based on the assumption that the are uncorrelated; in the presence of correlations this measure may become negative and ambiguous.
On the theoretical side, the search is ongoing for a set of necessary and sufficient conditions for a general synergy measure to satisfy. To our knowledge, the most prominent systematic approach is the Partial Information Decomposition framework (PID) proposed by Williams and Beer [3]. Here, synergistic information is implicitly defined by additionally defining so-called “unique” and “shared” information; together they are required to sum up to the total mutual information , among other conditions. However, it appears that the original axioms of Shannon’s information theory are insufficient to uniquely determine the functions in this decomposition framework [13], so two approaches exist: extending or changing the set of axioms [3,7,8,14], or finding “good enough” approximations [3,6,9,10].
Our work differs crucially from both abovementioned approaches. In fact, we will define “synergy” from first principles which is incompatible with PID. We use a simple example to motivate our intuitive incongruence of PID; however, no mathematical argument are found in favor of either framework. Our proposed procedure of calculating synergy is based upon a newly introduced notion of perfect “orthogonal decomposition” among stochastic variables. We will prove important basic properties which we feel any successful synergy measure should obey, such as non-negativity and insensitivity to reordering subvariables. We will also derive a number of intriguing properties, such as an upper bound on the amount of synergy that any variable can have about a given set of variables. Finally, we provide a numerical implementation which we use for experimental validation and to demonstrate that synergistic variables tend to have increased resilience to localized noise, which is an important property at large and specifically in biological systems.
2. Definitions
2.1. Preliminaries
Definition 1: Orthogonal Decomposition
Following the intuition from linear algebra we refer to two stochastic variables as orthogonal in case they are independent, i.e., . Given a joint distribution of two stochastic variables we say that a decomposition is an orthogonal decomposition of with respect to in case it satisfies the following five properties:
In words, is decomposed into two orthogonal stochastic variables so that (i) the two parts taken together are informationally equivalent to ; (ii) the orthogonal part has zero mutual information about ; and (iii) the parallel part has the same mutual information with as the original variable has.
Our measure of synergy is defined in terms of orthogonal decompositions of MSRVs. However this decomposition is not a trivial procedure and is even impossible to do exactly in certain cases. A deeper discussion of its applicability and limitations is deferred to Section 7.1; here we proceed with defining synergistic information.
2.2. Proposed Framework
2.2.1. Synergistic Random Variable
Firstly we define as a synergistic random variable (SRV) of if and only if it satisfies the conditions:
In words, an SRV stores information about as a whole but no information about any individual which constitutes . Each SRV is defined by a conditional probability distribution and is thus conditionally independent of any other SRV given , i.e., . We denote the collection of all possible SRVs of as the joint random variable . We sometimes refer to as a set because the ordering of its marginal distributions (SRVs) is irrelevant due to their conditional independence.
2.2.2. Maximally Synergistic Random Variables
The set may in general be uncountable, and many of its members may have extremely small mutual information with , which would prevent any practical use. Therefore we introduce the notion of maximally synergistic random variables (MSRV) which we will also use in some derivations. We do not have a proof yet that this set is countable, however our numerical results (see especially the figure in Section 6.2) show that a typical MSRV has substantial mutual information with (about 75% of the maximum possible). This suggests that either the set of MSRVs is countable or that the mutual information of a small set of MSRVs rapidly converges to the maximum possible mutual information, enabling a practical use.
We define the set of MSRVs of , denoted , as the smallest possible subset of which still makes redundant, i.e.:
Here, denotes the cardinality of set which is minimized. Intuitively, one could imagine building by iteratively removing an SRV from in case it is completely redundant given another SRV , i.e., if . The result is a set with the same informational content (entropy) as since only redundant variables are discarded. In case multiple candidates for would exist then any candidate among them will induce the same synergy quantity in our proposed measure, as will be clear from the definition in Section 2.2.5 and further proven in Appendix A.2 and Appendix A.3.
2.2.3. Synergistic Entropy of
We interpret as representing all synergistic information that any stochastic variable could possibly store about . Therefore we define the synergistic entropy of as . This will be the upper bound on the synergistic information of any other variable about .
2.2.4. Orthogonalized SRVs
In order to prevent doubly counting synergistic information we orthogonalize all MSRVs. Let us denote for the th permuted sequence of all MSRVs in out of all possibilities which are arbitrarily labeled by integers . Then we convert into a set of orthogonal MSRVs, or OSRVs for short, for a given ordering:
In words, we iteratively take each MSRV in and add its orthogonal part to the set in the specific order . As a result, each OSRV in is completely independent from all others in this set. is still informationally equivalent to because during its construction we only discard completely redundant variables given other SRVs.
Note that each orthogonal part is an SRV if is an SRV (or MSRV), which follows from the contradiction of the negation: if is not an SRV then and consequently which contradicts since by the above definition of orthogonal decomposition.
2.2.5. Total Synergistic Information
We define the total amount of synergistic information that stores about as:
In words, we propose to quantify synergy as the sum of the mutual information that contains about each MSRV of , after first making the MSRVs independent and then reordering them to maximize this quantity. Note that the optimal ordering is dependent on , making the calculation of the set of MSRVs used to calculate synergy also dependent on .
Intuitively, we first “extract” all synergistic entropy of a set of variables by constructing a new set of all possible maximally synergistic random variables (MSRVs) of , denoted , where each MSRV has non-zero mutual information with the set but zero mutual information with any individual . This set of MSRVs is then transformed into a set of independent orthogonal SRVs (OSRV), denoted , to prevent over counting. Then we define the amount of synergistic information in outcome variable about the set of source variables as the sum of OSRV-specific mutual information quantities, .
We illustrate our proposed measure on a few simple examples in Section 5 and compare to other measures. In the next Section we will prove several desired properties which this definition satisfies; here we finish with an informal outline of the intuition behind this definition and refer to corresponding proofs where appropriate.
Outline of Intuition of the Proposed Definition
Our initial idea was to quantify synergistic information directly as , however we found that this results in undesired counting of non-synergistic information which we demonstrate in Section 4.3 and in Appendix A.2.1. That is, two or more SRVs taken together do not necessarily form an SRV, meaning that their combination may store information about individual inputs. For this reason we use the summation over individual OSRVs. Intuitively, each term in the sum quantifies a “unique” amount of synergistic information which none of the other terms quantifies, due to the independence among all OSRVs in . That is, no synergistic information is doubly counted, which we also discuss in Appendix A.2 by proving that never exceeds . On the other hand, no possible type of synergistic information is ignored (undercounted). This can be seen from the fact that only fully redundant variables are ever discarded in the above process; also we prove for example in Section 3.6 in the sense that for any arbitrary there exists a such that equals the maximum , namely .
This summation is sensitive to the ordering of the orthogonalization of the SRVs. The reason for maximizing over these orderings is the possible presence of synergies among the SRVs themselves. We prove that handles correctly such “synergy-among-synergies”, i.e., does not lead to over counting or undercounting, in Appendix A.3.
3. Basic Properties
Here we first list important minimal requirements that the above definitions obey. The first four properties typically appear in the related literature either implicitly or explicitly as desired properties; the latter two properties are direct consequences of our first principle to use SRVs to encode synergistic information. The corresponding proofs are straightforward and sketched briefly.
3.1. Non-Negativity
This follows from the non-negativity of the underlying mutual information function, making every term in the sum of Equation (5) non-negative.
3.2. Upper-Bounded by Mutual Information
This follows from the Data-Processing Inequality [12] where is first processed into and then follows because we can write:
Here, is understood to denote the element in after maximizing the sequence used to construct for computing .
3.3. Equivalence Class of Reordering in Arguments
This follows from the same property of the underlying mutual information function and that of the sum in Equation (5).
3.4. Zero Synergy about a Single Variable
This follows from the constraint that any SRV must be ignorant about any individual variable in , so .
3.5. Zero Synergy in a Single Variable
This also follows from the constraint that any SRV must be ignorant about any individual variable in : all terms in the sum in Equation (5) are necessarily zero.
3.6. Identity Maximizes Synergistic Information
This follows from the fact that each is computed from and is therefore completely redundant given , so each term in the sum in Equation (5) must be maximal and equal to . Since all are independent, .
4. Consequential Properties
We now list important properties which are induced by our proposed synergy measure along with their corresponding proofs.
4.1. Upper Bound on the Mutual Information of an SRV
The maximum amount of mutual information (and entropy) of an SRV of a set of variables can be derived analytically. We start with the case of two input variables, i.e., , and then generalize. Maximizing under the two constraints and from Equation (2) leads to:
using that by construction. Since the first term in the third line does not change by varying we can maximize only by minimizing the second term . Since and from relabeling (reordering) the inputs we also have the constraint , leading to:
This can be rewritten as:
The generalization to variables is fairly straightforward by induction (see Appendix A.1) and here illustrated for the case for one particular labeling (ordering) :
Since this inequality must be true for all labelings of the , in particular for the labeling that maximizes , and extending this result to any , we find that:
Corollary. Suppose that is completely synergistic about , i.e., . Then their mutual information is bounded as follows:
Finally, we assume that the SRV is “efficient” in the sense that it contains no additional entropy that is unrelated to , i.e., . After all, if it would contain additional entropy then by our orthogonal decomposition assumption we can distill only the dependent part exactly. Therefore the derived upper bound of any SRV is also the upper bound on its entropy.
4.2. Non-Equivalence of SRVs
It is indeed possible to have at least two non-redundant MSRVs in , i.e., where , or even . In words, this means that there can be multiple types of synergistic relation with which are not equivalent. This is demonstrated by the following example: with and uniform distribution , where and . The fact that these functions are MSRVs is verified numerically by trying all combinations. It can also be seen visually in Figure 1; adding additional states for or or changing their distribution will break the symmetries needed to stay uncorrelated with the individual inputs. In this case so the two MSRVs are mutually independent, whereas . In fact, as shown in Section 4.1 this is actually the maximum possible mutual information that any SRV can store about . Since the MSRVs are a subset of the SRVs it follows trivially that SRVs can be non-equivalent or even independent.
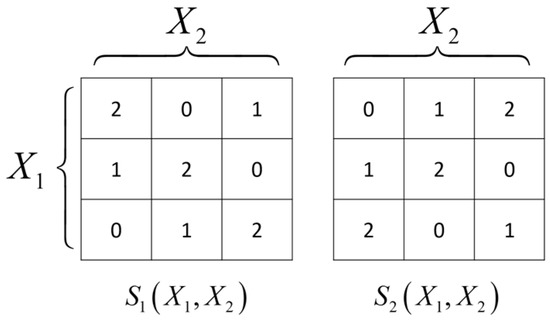
Figure 1.
The values of the two MSRVs and which are mutually independent but highly synergistic about two 3-valued variables and . and are uniformly distributed and independent.
4.3. Synergy among MSRVs
The combination of two (or more) MSRVs , , cannot be an SRV, i.e., . Otherwise it would be a contradiction: if would be true then it follows that , since both and S2 would be completely redundant given , and therefore discarded in the construction of MSRV.
This means that all combinations of MSRVs, such as , must necessarily have non-zero mutual information about at least one of the individual source variables, i.e., , violating Equation (2). Since each individual MSRV has zero mutual information with each individual source variable by definition, it must be true that this “non-synergistic” information results from synergy among MSRVs. We emphasize that this type of synergy among the is different from the synergy among the which we intend to quantify in this paper, and could more appropriately be considered as a “synergy of synergies”.
The fact that multiple MSRVs are possible is already proven by the example used in the previous proof in Section 4.2. The synergy among these two MSRVs in this example is indeed easily verified: and , whereas .
Since MSRVs are a subset of the SRVs it follows that also SRVs can have such “synergy-of-synergies”. In fact, the existence of multiple MSRVs means that there are necessarily SRVs which are synergistic about another SRV, and conversely, if there is only one MSRV then there cannot be any set of SRVs which are synergistic about another SRV.
Corollary. Alternatively quantifying synergistic information using directly the mutual information could violate the fourth desired property, “Zero synergy about a single variable”, because if consists of two or more MSRVs then . In this case the choice would have non-zero synergistic information about , which is undesired.
4.4. XOR-Gates of Random Binary Inputs Always Form an MSRV
Lastly we use our definition of synergy to prove the common intuition that the XOR-gate is maximally synergistic about a set of i.i.d. binary variables (bits), as suggested in the introductory example.
We start with the case of two bits . As SRV we take . The entropy of this SRV equals 1, which is in fact the upper bound of any SRV for this , Equation (17). Therefore no other SRV can make completely redundant such that it would prevent from becoming an MSRV (Section 2.2.2). It is only possible for another SRV to make redundant in case the converse is also true, in which case the two SRVs are equivalent. An example of this would be the NOT-XOR gate which is informationally equivalent to XOR. Here we consider equivalent SRVs as one and the same.
For the more general case of bits , consider as SRV the set of XOR-gates where . It is easily verified that does not contain mutual information about any individual bit , so indeed . Moreover it is also easily verified that all are independent, so the entropy which equals the upper bound on any SRV. Following the same reasoning as the two-bit case, is indeed an MSRV. We remark that conversely, each possible set of XOR gates is not necessarily an MSRV because, e.g., is redundant given both and . That is, some (sets of) XOR-gates are redundant given others and will therefore not be member of the set by construction.
The converse is proved for the case of two independent input bits in Appendix A.4, that is, the only possible MSRV of two bits is the XOR-gate.
5. Examples
In this Section we derive the SRVs and MSRVs for some small example input-output relations to illustrate how synergistic information is calculated using our proposed definition. This also allows comparing our approach to that of others in the field, particularly PID-like frameworks even though the community has not yet settled on a satisfactory definition of such a framework.
5.1. Two Independent Bits and XOR
Let be two independent input bits, so . Let be a -valued SRV of .
We derive in Appendix A.4 that any SRV in this case is necessarily a (stochastic) function of the XOR relation . One could thus informally write with the understanding that the function could be either a deterministic function or result in a stochastic variable. Therefore, the set consists of all possible deterministic and stochastic mappings . A deterministic example would be and a stochastic example could be written loosely as the mixture where the probability satisfies the first condition in Equation (2).
The set is indeed an uncountably large set in this case. However in Appendix A.4 we also derive that there is only a single MSRV in the set : the XOR-gate itself. It makes all other SRVs redundant. This confirms our conjecture in Section 2.2.2 that although is uncountable, may typically still be countable.
For any output stochastic variable the amount of synergistic information is simply equal to , according to Equation (5). This implies trivially that the XOR-gate has maximum synergistic information for two independent input bits, as is shown schematically in Figure 2a.
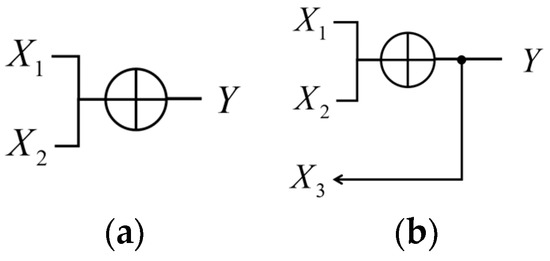
Figure 2.
Two independent input bits and as output the XOR-gate. (a) The relation . In (b) an additional input bit is added which copies the XOR output, adding individual (unique) information .
5.2. XOR-Gate and Redundant Input
Suppose now that an extra independent input bit is added as and that the output is still (see Figure 2b). This case highlights a crucial difference between our method and that of PID-like frameworks.
In our method this leaves the perceived amount of synergistic information stored in unchanged as it still stores the XOR-gate. Adding unique or “individual” information can never reduce this.
In PID-like frameworks, however, synergistic information and individual information are treated on equal footing and subtracted; intuitively, the more individual information is in the output, the less synergy it computes. As a result, various canonical PID-based synergy measures all reach “the desired answer of 0 bits” for this so-called XorLoses example [10].
5.3. AND-Gate
Our method nevertheless still differs from that of Bertschinger et al. [14] as demonstrated in the simple case of the AND-gate of two independent random bits, i.e., . In our method the outcome of the AND-gate is simply correlated (using mutual information) with that of the XOR-gate as shown in Section 5.1, i.e.:
Their proposed method in contrast calculates that the individual information with either input equals which they infer as fully “shared” (intuitively speaking, both inputs are said to provide exactly the same individual information to the output). The total information with both inputs equals . Since in the PID framework all four types of information are required to sum up to the total mutual information and no “unique” information exists, their method infers the synergy equals . Indeed, Griffith and Koch [10] state that for this example all but one PID-like measure result in 0.189 bits of synergy; only the original measure also results in 0.5 bits which agrees with our method.
6. Numerical Implementation
We have implemented the numerical procedures to compute the above as part of a Python library named jointpdf (https://bitbucket.org/rquax/jointpdf). Here, a set of discrete stochastic variables is represented by a matrix of joint probabilities of dimensions , where is the number of variables and is the number of possible values per variable. This matrix is uniquely identified by independent parameters each on the unit line.
In brief, finding an MSRV S amounts to numerically optimizing a subset of the (bounded) parameters of Pr(X,S) in order to maximize I(S:X) while satisfying the conditions for SRVs in Equation (2). Then we approximate the set of OSRVs by constructing it iteratively. For finding the next OSRV SN in addition to an existing set S1,…,SN−1, the independence constraint is added to the numerical optimization. The procedure finishes once no more OSRVs are found. The optimization of their ordering is implemented by restarting the sequence of numerical optimizations from different starting points and taking the result with highest synergistic information. Orthogonal decomposition is also implemented even though it is not used since the OSRV set is built directly using this optimization procedure. This uses the fact that each decomposed part of an SRV must also be an SRV (assuming perfect orthogonal decomposition) and can therefore be found directly in the optimization. For all numerical optimizations the algorithm scipy.optimize.minimize (version 0.11.0) is used. Once the probability distribution is extended with the set of OSRVs, the amount of synergistic information has a confidence interval due to the approximate nature of the numerical optimizations. That is, one or more OSRVs may turn out to store a small amount of unwanted information about individual inputs. We subtract these unwanted quantities from each mutual information term in Equation (5) in order to estimate the synergistic information in each OSRV. However, these subtracted terms could be (partially) redundant, the extent of which cannot be determined in general. Thus, once the optimal sequence of OSRVs is found we take the lower bound on the estimated synergistic information as:
This corresponds to the case where each subtracted mutual information term is fully independent so that they can be summed, leading to this WMS form [6]. On the other hand, the corresponding upper bound would occur if all subtracted mutual information terms would be fully redundant, in which case:
We take the middle point between these bounds as the best estimate . The corresponding measure of uncertainty is then defined as the relative error:
The following numerical results have been obtained for the case of two input variables, X1 and X2, and one output variable Y. Their joint probability distribution Pr(X1,X2,Y) is randomly generated unless otherwise stated. Once an OSRV is found it is added to this distribution as an additional variable. All variables are constrained to have the same number of possible values (“state space”) in our experiments. All results reported in this section have been obtained by sampling random probability distributions. This results in interesting characteristics pertaining to the entire space of probability distributions but offers a limitation when attempting to translate the results to any specific application domain such as neuronal networks or gene-regulation models, since domains focus only on specific subspaces of probability distributions.
6.1. Success Rate and Accuracy of Finding SRVs
Our first result is on the ability of our numerical algorithm to find a single SRV as function of the number of possible states per individual variable. Namely, our definition of synergistic information in Equation (5) relies on perfect orthogonal decomposition; we showed that perfect orthogonal decomposition is impossible for at least one type of relation among binary variables (Appendix A.6), whereas previous work hints that continuous variables might be (almost) perfectly decomposed (Section 7.1).
Figure 3 shows the probability of successfully finding an SRV for variables with a state space of 2, 3, 4 and 5 values. Success is defined as a relative error on the entropy of the SRV of less than 10%. In Figure 3 we also show the expected relative error on the entropy of an SRV once successfully found. This is relevant for our confidence in the subsequent results. For 2 or 3 values per variable we find a relative error in the low range of 1%–3%, indicating that finding an SRV is a bimodal problem: either it is successfully found with relatively low error or it is not found successfully and has high error. For 4 or more values per variable a satisfactory SRV is always successfully found. This indicates that additional degrees of freedom aid in finding SRVs.
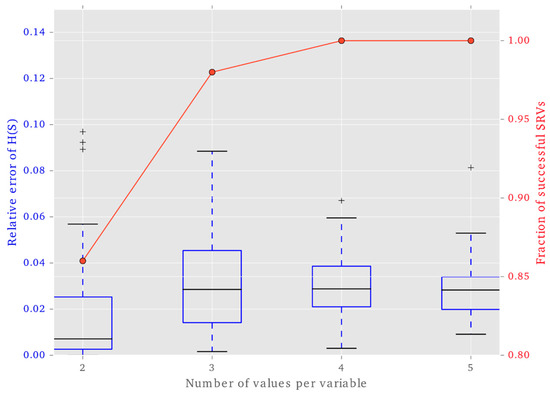
Figure 3.
Effectiveness of the numerical implementation to find a single SRV. The input consists of two variables with 2, 3, 4, or 5 possible values each (x-axis). Red line with dots: probability that an SRV could be found with at most 10% relative error in 50 randomly generated Pr(X1,X2,Y) distributions. The fact that it is lowest for binary variables is consistent with the observation that perfect orthogonal decomposition is impossible in this case under at least one known condition (Appendix A.6). The fact that it converges to 1 is consistent with our suggestion that orthogonal decomposition could be possible for continuous variables (Section 7.1). Blue box plot: expected relative error of the entropy of a single SRV, once successfully found.
6.2. Efficiency of a Single SRV
Once an SRV is successfully found, the next question is how much synergistic information it actually contains compared to the maximum possible. According to Equation (17) and its preceding, the upper bound is the minimum of and . Thus, a single added variable as SRV has in principle sufficient entropy to store this information. However, depending on it is possible that a single SRV cannot store all synergistic information at once, regardless of how much entropy it has, as demonstrated in Section 4.3. This happens if two or more SRVs would be mutually “incompatible” (cannot be combined into a single, large SRV). Therefore we show the expected synergistic information in a single SRV normalized by the corresponding upper bound in Figure 4.
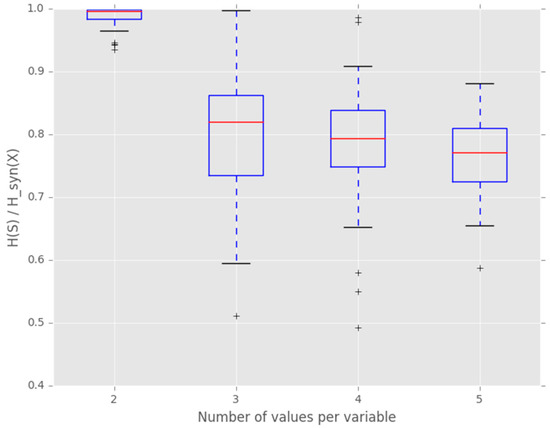
Figure 4.
Synergistic entropy of a single SRV normalized by the theoretical upper bound. The input consists of two randomly generated stochastic variables with 2, 3, 4, or 5 possible values per variable (x-axis). The SRV is constrained to have the same number of possible values. The initial downward trend shows that individual SRVs become less efficient in storing synergistic information as the state space per variable grows. The apparent settling to a non-zero constant suggests that estimating synergistic information does not require a diverging number of SRVs to be found for any number of values per variable.
The decreasing trend indicates that this incompatibility among SRVs plays a significant role as the state space of the variables grows. This would imply that an increasing number of SRVs must be found in order to estimate the total synergistic information . Fortunately, Figure 4 also suggests that the efficiency settles to a non-zero constant which suggests that the number of needed SRVs does not grow to impractical numbers.
6.3. Resilience Implication of Synergy
Finally we compare the impact of two types of perturbations in two types of input-output relations, namely the case of a randomly generated versus the case that is an SRV of . A “local” perturbation is implemented by adding a random vector with norm 0.1 to the point in the unit hypercube that defines the marginal distribution of a randomly selected input variable, so or . Conversely, a “non-local” perturbation is similarly applied to while keeping the marginal distributions and unchanged. The impact is quantified by the relative change of the mutual information due to the perturbation. That is, we ask whether a small perturbation disrupts the information transmission when viewing as a communication channel.
In Figure 5 we show that a synergistic is significantly less susceptible to local perturbations compared to a randomly generated . For non-local perturbations the difference in susceptibility is smaller but still significant. The null-hypothesis of equal population median is rejected both for local and non-local perturbations (Mood’s median test, p-values and respectively; threshold ).
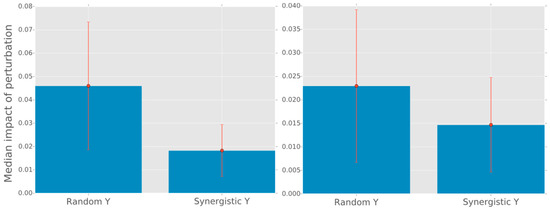
Figure 5.
Left: The median relative change of the mutual information after perturbing a single input variable’s marginal distribution (“local” perturbation). Error bars indicate the 25th and 75th percentiles. A perturbation is implemented by adding a random vector with norm 0.1 to the point in unit hypercube that defines the marginal distribution . Each bar is based on 100 randomly generated joint distributions , where in the synergistic case is constrained to be an SRV of . Right: the same as left except that the perturbation is “non-local” in the sense that it is applied to while keeping and unchanged.
The difference in susceptibility for local perturbations is intuitive because an SRV has zero mutual information with individual inputs, so it is arguably insensitive to changes in individual inputs. We still find a non-zero expected impact; this could be partly explained by our algorithm’s relative error being on the order of 3% which is the same order as the relative impact found (2%). In order to test this intuition we devised the non-local perturbations to compare against. A larger susceptibility is indeed found for non-local perturbations, however it remains unclear why synergistic variables are still less susceptible in the non-local case compared to randomly generated variables. Nevertheless, our numerical results indicate that synergy plays a significant role in resilience to noise. This is relevant especially for biological systems which are continually subject to noise and must be resilient to it. A simple use-case on using the jointpdf package to estimate synergies, as is done here, is included in Appendix A.8.
7. Limitations
7.1. Orthogonal Decomposition
Our formulation is currently dependent on being able to orthogonally decompose MSRVs exactly. To the best of our knowledge our decomposition formulation has not appeared in previous literature. However from similar work we gather that it is not a trivial procedure, and we derive that it is even impossible to do exactly in certain cases, as we explore next.
7.1.1. Related Literature on Decomposing Correlated Variables
Our notion of orthogonal decomposition is related to the ongoing study of “common random variable” definitions dating back to around 1970. In particular our definition of appears equivalent to the definition by Wyner [15], here denoted , in case it holds that . That is, in Appendix A.7 we show that under this condition their satisfies all three requirements in Equation (1) which do not involve (which remains undefined in Wyner’s work). In brief, their is the “smallest” common random variable which makes and conditionally independent, i.e., . Wyner shows that . In cases where their minimization is not able to reach the desired equality condition it is an open question whether this implies that our does not exist for the particular . The required minimization step to calculate is highly non-trivial and solutions are known only for very specific cases [16,17].
To illustrate a different approach in this field, Gács and Körner [18] define their common random variable as the “largest” random variable which can be extracted deterministically from both and individually, i.e., for functions and chosen to maximize . They show that and it appears in practice that typically the “less than” relation actually holds, preventing its use for our purpose. Their variable is more restricted than ours but has applications in zero-error communication and cryptography.
7.1.2. Sufficiency of Decomposition
Our definition of orthogonal decomposition is sufficient to be able to define a consistent measure of synergistic information. However we leave it as an open question whether Equation (1) is actually more stringent than strictly necessary. Therefore, our statement is that if orthogonal decomposition is possible then our synergy measure is valid; in case it is not possible then it remains an open question whether this implies the impossibility to calculate synergy using our method. For instance, for the calculation of synergy in the case of two independent input bits there is actually no need for any orthogonal decomposition step among SRVs, such as in the examples in Section 4.2 and in Section 5. Important future work is thus to try to minimize the reliance on orthogonal decomposition while leaving the synergy measure intact.
7.1.3. Satisfiability of Decomposition
Indeed it turns out that it is not always possible to achieve a perfect orthogonal decomposition according to Equation (1), depending on and . For example, we demonstrate in Appendix A.6 that for the case of binary-valued and , it is impossible to achieve the decomposition in case depends on as .
On the other hand, one sufficient condition for being able to achieve a perfect orthogonal decomposition is being able to restate and as and for independent from each other. In this case it is easy to see that and are a valid orthogonal decomposition. Such a restating could be reached by reordering and relabeling of variables and states.
As an example consider and denoting the sequences of positions (paths) of two causally non-interacting random walkers on the plane which are under influence of the same constant drift tendency (e.g., a constant wind speed and direction). This drift creates a spurious correlation (mutual information) between the two walkers. From sufficiently long paths this constant drift tendency can however be estimated and subsequently subtracted from both paths to create drift-corrected paths and which are independent by construction, reflecting only the internal decisions of each walker. The two walkers therefore have a mutual information equal to the entropy of the “wind” stochastic variable whose value is generated once at the beginning of the two walks and then kept constant.
We propose the following more general line of reasoning to (asymptotically) reach this restating of and or at least approximate it. Nevertheless the remainder of the paper simply assumes the existence of the orthogonal decomposition and does not use any particular method to achieve it.
Consider the Karhunen-Loève transform (KLT) [19,20,21] which can restate any stochastic variable as:
Here, is the mean of , the are pairwise independent random variables, and the coefficients are real scalars. This transform could be seen as the random variables analogy to the well-known principle component analysis or the Fourier transform.
Typically this transform is defined for a range of random variables in the context of a continuous stochastic process . Here each is decomposed by which are defined through the themselves as:
Here, the scalar coefficients become functions on which must be pairwise orthogonal (zero inner product) and square-integrable. Otherwise the abovementioned transform applies to each single in the same way, now with t-dependent coefficients . Nevertheless, for our purpose we leave it open how the are chosen; through being part of a stochastic process or otherwise. We also note that the transform works similarly for the discrete case, which is often applied to image analysis.
Let us now choose a single sequence of as our variable “basis”. Now consider two random variables and which can both be decomposed into as the sequences and , respectively. In particular, the mutual information must be equal before and after this transform. Then the desired restating of and into and is achieved by:
The choice of the common could either be natural, such as a common stochastic process of which both and are part, or a known common signal which two receivers intermittently record. Otherwise could be found through a numerical procedure to attempt a numerical approximation, as is done for instance in image analysis tasks.
8. Discussion
Most theoretical work on defining synergistic information uses the PID framework [3], which (informally stated) requires that . That is, the more synergistic information stores about , the less information it can store about an individual and vice versa because those two types of information are required to sum up to the quantity as non-negative terms. Our approach is incompatible with this viewpoint. That is, in our framework the amount of synergistic information makes no statement on the amount of “individual” information that may also store about . In fact, the proposed synergistic information can be maximized by the identity , which obviously also stores maximum information about all individual variables . To date no synergy measure has been found which has earned the consensus of the PID framework (or similar) community, typically by offering counter-examples. This led us to explore this completely different viewpoint. If our proposed measure would prove successful then it may imply that the decomposition requirement is too strong for a synergy measure to obey, and that synergistic information and individual information cannot be treated on equal footing (increasing one means decreasing the other by the same amount). Whether our proposed synergy measure can be used to define a different notion of non-negative information decomposition is left as an open question.
Our intuitive argument against the decomposition requirement is exemplified in Section 4.2 and Section 4.3. This example demonstrates that two independent SRVs can exist which are not synergistic when taken together. That is, there are evidently two distinct (independent or uncorrelated) ways in which a variable can be completely synergistic about (it could be set equal to one or the other SRV). However, we show it is impossible for to store information about both these SRVs simultaneously (maximum synergy) while still having zero information about all individual input variables —in fact this leads to maximum mutual information with all individual inputs in the example. This suggests that synergistic information and “individual” information cannot simply be considered on equal footing or as mutually exclusive.
Therefore we propose an alternative viewpoint. Whereas synergistic information could be measured by , the amount of “individual information” could foreseeably be measured by a similar procedure. For instance, the sequence could be replaced by the individual inputs after which the same procedure in Equation (5) as for is repeated. This would measure the amount of “unique” information that stores about individual inputs which is not also stored in (combinations of) other inputs. This measure would be upper bounded by . For completely random and independent inputs, this individual information in would be upper bounded by whereas if were synergistic then its total mutual information would be upper bounded by (since it is then an SRV). This suggests that both quantities measure different but not fully independent aspects. How the two measures relate to each other is subject of future work.
Our proposed definition builds upon the concept of orthogonal decomposition. It allows us to rigorously define a single, definite measure of synergistic information from first principles. However further research is needed to determine for which cases this decomposition can be done exactly, approximately, or not at all, and in which cases a decomposition is even necessary. Even if in a specific case it would turn out to be not exactly computable (due to imperfect orthogonal decomposition) then our definition can still serve as a reference point. To the extent that a necessary orthogonal decomposition must be numerically approximated (or bounded), the resulting amount of synergistic information must also be considered an approximation (or bound).
Our final point of discussion is that the choice of how to divide a stochastic variable into subvariables is crucial and determines the amount of information synergy found. This choice strongly depends on the specific research question. For instance, the neurons of a brain may be divided into the two cerebral hemispheres, into many anatomical regions, or into individual neurons altogether, where at each level the amount of information synergy may differ. In this article we are not concerned with choosing the division and will calculate the amount of information synergy once the subvariables have been chosen.
9. Conclusions
In this paper we propose a measure to quantify synergistic information from first principles. Briefly, we first “extract” all synergistic entropy of a set of variables by constructing a new set of all possible maximally synergistic random variables (MSRVs) of , denoted , where each MSRV has non-zero mutual information with the set but zero mutual information with any individual . This set of MSRVs is then transformed into a set of independent orthogonal SRVs (OSRV), denoted , to prevent over counting. Then we define the amount of synergistic information in outcome variable about the set of source variables as the sum of OSRV-specific mutual information quantities, .
Our proposed measure satisfies important desired properties, e.g., it is non-negative and bounded by mutual information, invariant under reordering of , and always has zero synergy if the input is a single variable. We also prove four important properties of our synergy measure. In particular, we derive the maximum mutual information in case is an SRV; we demonstrate that synergistic information can be of different types (multiple, independent SRVs); and we prove the fact that the combination of multiple SRVs may store non-zero information about an individual in a synergistic way. This latter property leads to the intriguing concept of “synergy among synergies”, which we show must necessarily be excluded from quantifying synergy in about but which might turn out to be an interesting subject of study in its own right. Finally, we provide a software implementation of the proposed synergy measure.
The ability to quantify synergistic information in an arbitrary multivariate setting is a necessary step to better understand how dynamical systems implement their complex information processing capabilities. Our proposed framework based on SRVs and orthogonal decomposition provides a new line of thinking and produces a general synergy measure with important desired properties. Our initial numerical experiments suggest that synergistic relations are less sensitive to noise, which is an important property of biological and social systems. Studying synergistic information in complex adaptive systems will certainly lead to substantial new insights into their various emergent behaviors.
Acknowledgments
The authors acknowledge the financial support of the Future and Emerging Technologies (FET) program within Seventh Framework Programme (FP7) for Research of the European Commission, under the FET-Proactive grant agreement TOPDRIM, number FP7-ICT-318121, as well as the financial support of the Future and Emerging Technologies (FET) program within Seventh Framework Programme (FP7) for Research of the European Commission, under the FET-Proactive grant agreement Sophocles, number FP7-ICT-317534. PMAS acknowledges the support of the Russian Scientific Foundation, Project number 14-21-00137.
Author Contributions
Rick Quax, Omri Har-Shemesh and Peter Sloot conceived the research, Rick Quax and Omri Har-Shemesh performed the analytical derivations, Rick Quax performed the numerical simulations, Rick Quax and Peter Sloot wrote the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
A.1. Upper Bound of Possible Entropy of an SRV by Induction
A.1.1. Base Case
The base case is that it is true that , which is proven for in Section 4.1.
A.1.2. Induction Step
We will prove that the base case induces .
An must be chosen which satisfies:
Here, the negative maximization term arises from applying the base case. We emphasize that this upper bound relation must be true for all choices of orderings of all labels (since the labeling is arbitrary and due to the desired property in Section 3.3). Therefore, must satisfy all simultaneous instances of the above inequality, one for each possible ordering. Any that satisfies the “most constraining” inequality, i.e., where the r.h.s. is minimal, necessarily also satisfies all inequalities. The r.h.s. is minimized for any ordering where the with overall maximum is part of the subset . In other words, for the inequality with minimal r.h.s. it is true that, due to considering all possible reorderings,
Substituting this above we find indeed that
A.2. Does Not “Overcount” Any Synergistic Information
All synergistic information that any can store about is encoded by the set of SRVs which is informationally equivalent to , i.e., they have equal entropy and zero conditional entropy. Therefore should be an upper bound on since otherwise some synergistic information must have been doubly counted. In this section we derive that . In Appendix A.2.1 we use the same derivation to demonstrate that a positive difference is undesirable at least in some cases.
Here we start with the proof that in case consists of two OSRVs, taken as base case for a proof by induction. Then we also work out the case so that the reader can see how the derivation extends for increasing . Then we provide the proof by induction in .
Let consist of an arbitrary number of OSRVs. Let denote the first OSRVs for . Let be defined using instead of , i.e., only the first terms in the sum in Equation (5).
For we use the property by construction of :
For we similarly use the independence properties and :
Essentially, the proof for each proceeds by rewriting each conditional mutual information term as a mutual information term and four added entropy terms (third equality above) of which two cancel out ( above) and the remaining two terms summed together are non-negative ( above). Thus, by induction:
Thus we find that it is not possible for our proposed to exceed the mutual information . This suggests that does not “overcount” any synergistic information.
A.2.1. Also Includes Non-Synergistic Information
In the derivation of the previous section we observe that, conversely, can exceed and we will now proceed to show that this is undesirable at least in some cases.
The positive difference must arise from one of the non-negative terms in square brackets in all derivations above. Suppose that and therefore has zero information with any individual OSRV by definition. That is, does not correlate with any possible synergistic relation (SRV) about . In our view, should thus be said to store zero synergistic information about . However, even though by construction, this does not necessarily imply , among others, and therefore any term in square brackets above can still be positive. In other words, it is possible for to “cooperate” or have synergy with one or more OSRVs to have non-zero mutual information about another OSRV. A concrete example of this is given in Section 4.3. This would lead to a non-zero synergistic information if quantified by , which is undesirable in our view. In contrast, our proposed definition for in Equation (5) purposely ignores this “synergy-of-synergies” and in fact will always yield in case , which is desirable in our view and proved in Section 3.5.
A.3. Synergy Measure Correctly Handles Synergy-of-Synergies among SRVs
By “correctly handled” we mean that synergistic information is neither overcounted nor undercounted. We already start by the conjecture that “non-synergistic” redundancy among a pair of SRVs does not lead to under or overcounting synergistic information. That is, suppose that , which we consider “non-synergistic” mutual information. If correlates with one or neither SRV then the optimal ordering is trivial. If it correlates with both then any ordering will do, assuming that their respective “parallel” parts (see Section 2.1.1) are informationally equivalent and it does not matter which one is retained in . The respective orthogonal parts are retained in any case. Therefore we now proceed to handle the case where there is synergy among SRVs.
First we illustrate the apparent problem which we handle in this section. Suppose that and further suppose that while . In other words, by this construction the pair synergistically makes fully redundant, and no non-synergistic redundancy among the SRVs exists. Finally, let . At first sight it appears possible that happens to be constructed using an ordering such that appears after and . This is unwanted because then will not be part of the used to compute , i.e., the term disappears from the sum, which potentially leads to the contribution of to the synergistic information being ignored.
In this Appendix we show that the contribution is always counted towards by construction, and that the only possibility for the individual term to disappear is if its synergistic information is already accounted for.
First we interpret each such (synergistic) mutual information from a set of SRVs to another, single SRV as a ( to ) hyperedge in a hypergraph. In the above example, there would be a hyperedge from the pair to . Let the weight of this hyperedge be equal to the mutual information. In the Appendix A.3.1 below we prove that in this setting, one hyperedge from n − 1 SRVs to one SRV implies a hyperedge from all other possible n − 1 subsets to the remaining SRV, at the same weight. That is, the hypergraph for forms a fully connected “clique” of three hyperedges.
In this setting, finding a “correct” ordering translates to letting appear before all have appeared in case there is a hyperedge and . This translates to traversing a path of steps through the hyperedges in reverse order, each time choosing one SRV from the ancestor set that is not already previously chosen, such that for each SRV either (i) not all ancestor SRVs were chosen, or (ii) it has zero mutual information with . In other words, in case there is an such that then any ordering with as last element will suffice. Only if correlates with all SRVs then one of the SRVs will be (partially) discarded by the order maximization process in . This is desirable because otherwise could exceed or even . Intuitively, if correlates with SRVs then it automatically correlates with the th SRV as well, due to the redundancy among the SRVs. Counting this synergistic information would be overcounting this redundancy, leading to the violation of the boundedness by mutual information.
An example that demonstrates this phenomenon is given by consisting of three i.i.d. binary variables. It has four pairwise-independent MSRVs, namely the three pairwise XOR functions and one nested “XOR-of-XOR” function (verified numerically). However, one pairwise XOR is synergistically fully redundant given the two other pairwise XORs, so the entropy , which equals . Taking e.g., yields indeed 3 bits of synergistic information according to our proposed definition of , correctly discarding the synergistic redundancy among the four SRVs. However, if the synergistically redundant SRV would not be discarded from the sum then we would find 4 bits of synergistic information in about , which is counterintuitive because it exceeds , , and . Intuitively, the fact that correlates with two pairwise XORs necessarily implies that it also correlates with the third pairwise XOR, so this redundant correlation should not be counted.
A.3.1. Synergy among SRVs Forms a Clique
Given is a particular set of SRVs in arbitrary order. Suppose that the set is fully synergistic about , i.e., and we first assume that . This assumption is dropped in the subsection below. The question is: are then also synergistic about , and about ? We will now prove that in fact they are indeed synergistic at exactly the same amount, i.e., . The following proof is thus for the case of two variables being synergistic about a third, but trivially generalizes to variables (in case the condition is also generalized for variables).
First we find that the given condition leads to known quantities for two conditional mutual information terms:
Then we use this to derive a different combination (the third combination is derived similarly):
In conclusion, we find that if a set of SRVs synergistically stores mutual information about at amount , then all subsets of SRVs of will store exactly the same synergistic information about the respective remaining SRV. If each such synergistic mutual information from a set of SRVs to another SRV is considered as a directed ( to ) hyperedge in a hypergraph, then the resulting hypergraph of SRVs will have a clique in .
A.3.2. Generalize to Partial Synergy among SRVs
Above we assumed . Now we remove this constraint and thus let all mutual informations of (or in general) to be arbitrary. We then proceed as above, first:
Then:
We see that again is obtained for the mutual information among variables, but a correction term appears to account for a difference in the mutual information quantities among variables.
A.4. SRVs of Two Independent Binary Variables are Always XOR Gates
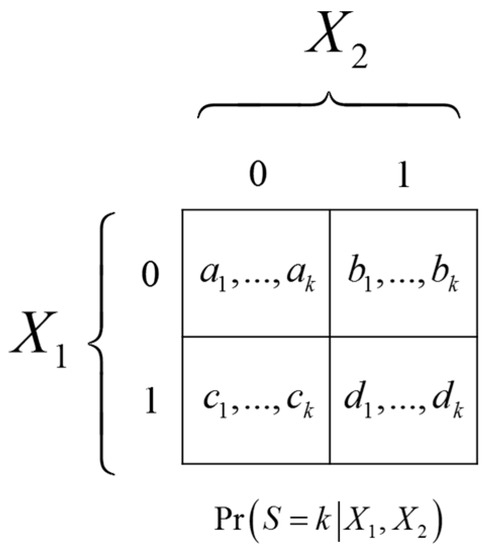
Figure 6.
The conditional probabilities of an SRV conditioned on two independent binary inputs. Here e.g., and ai denotes the probability that S equals to state i in casein case .
For to satisfy the conditions for being an SRV in Equation (2) the conditional probabilities must satisfy the following constraints. Firstly, it must be true that which implies , and similarly , leading to:
Secondly, in order to ensure that it must be true that , meaning that the four -vectors cannot be all equal:
The first set of constraints implies that the diagonal probability vectors must be equal, which can be seen by summing the two equalities:
The second constraint then requires that the non-diagonal probability vectors must be unequal, i.e.:
The mutual information equals the entropy computed from the average of the four probability vectors minus the average entropy computed of one of the probability vectors. First let us define the shorthand:
Then the mutual information equals:
Let and . Due to the equality of diagonal probability vectors the above simplifies to:
In words, the mutual information that any SRV stores about two independent bits is equal to the mutual information with the XOR of the bits, . Intuitively, one could therefore think of as the result of the following sequence of (stochastic) mappings: .
A corollary of this result is that the deterministic XOR function is an MSRV of two independent bits since this maximizes due to the data-processing inequality condition.
To be more precise and as an aside, the MSRV would technically also have to include all additional stochastic variables (“noise sources”) which are used in any SRVs, in order for to make all SRVs redundant and thus satisfy Equation (3). For instance, for to make, e.g., redundant it would also have to store the outcome of the independent random probability as a stochastic variable, meaning that the combined variable must actually be the MSRV, and so forth for the uncountably many SRVs in . However we assume that these noise sources like are independent of the inputs and outputs . Therefore in the mutual information terms in calculating the synergistic information in Equation (5) they do not contribute anything, meaning that we may ignore them in writing down MSRVs.
A.5. Independence of the Two Decomposed Parts
From the first constraint it follows that:
Here we used the shorthand . From the resulting combined with the second constraint it follows that and must be independent, namely:
A.6. Impossibility of Decomposition for Binary Variables
Consider as stochastic binary variables. The orthogonal decomposition imposes constraints on and which cannot always be satisfied perfectly for the binary case, as we show next. We use the following model for and :
In particular, we will show that cannot be computed from without storing information about , violating the orthogonality condition. Being supposedly independent from , we encode by its dependence on fully encoded by two parameters as:
Intuitively, in the case of binary variables, cannot store information about without also indirectly storing information about . A possible explanation is that the binary case has an insufficient number of degrees of freedom for this.
To satisfy the condition it must be true that and therefore that , among others. Let us find the conditions for this equality:
The conditions for satisfying this equality are either or . The first condition describes the trivial case where is independent from . The second condition is less trivial but severely constrains the relations that can have with . In fact it constrains the mutual information to exactly zero regardless of and , as we show next. Using the shorthand ,
Using the substitution and after some algebra steps it can be verified that indeed simplifies to zero.
Extending the parameters to also depend on would certainly be possible and add degrees of freedom, however this can only create a non-zero conditional mutual information, . As soon as is calculated then these extra parameters will be summed out into certain parameters, which we demonstrated will lead to zero mutual information under the orthogonality constraint.
This result demonstrates that a class of correlated binary variables and exists for which perfect orthogonal decomposition is impossible. Choices for binary and for which decomposition is indeed possible do exist, such as the trivial independent case. Exactly how numerous such cases are is currently unknown, especially when the number of possible states per variable is increased.
A.7. Wyner’s Common Variable Satisfies Orthogonal Decomposition if
Wyner’s common variable is defined as a non-trivial minimization procedure, namely where means that the minimization considers only random variables which make and independent, i.e., . Wyner showed that in general [15]. Here we show that for cases where the equality condition is actually reached, satisfies all three orthogonal decomposition conditions which do not involve also . Wyner leaves undefined and therefore his work cannot satisfy those conditions, but this shows at least one potential method of computing .
The two starting conditions are:
From the second condition it follows that:
Similarly:
Then from the first condition we can derive:
from which follows:
Firstly this implies the “non-spuriousness” condition on the last line. Then from combining Equations (A12) and (A13) with either Equation (A10) or Equation (A11) we find, respectively,
These are the “parallel” and “parsimony” conditions, concluding the proof.
A.8. Use-Case of Estimating Synergy Using the Provided Code
Our code can be run using any Python interface. As an example, suppose that a particular probability distribution is given of two “input” stochastic variables, each having three possible values. We generate a random probability distribution as follows:
- from jointpdf import JointProbabilityMatrix
- # randomly generated joint probability mass function p(A,B)
- # of 2 discrete stochastic variables, each having 3 possible values
- p_AB = JointProbabilityMatrix(2,3)
We add a fully redundant (fully correlated) output variable as follows:
- # append a third variable C which is deterministically computed from A and B, i.e., such that I(A,B:C)=H(C)
- p_AB.append_redundant_variables(1)
- p_ABC = p_AB # rename for clarity
Finally we compute the synergistic information with the following command:
- # compute the information synergy that C contains about A and B
- p_ABC.synergistic_information([2], [0,1])
With the jointpdf package it is also easy to marginalize stochastic variables out of a joint distribution, add variables using various constraints, compute various information-theoretic quantities, and estimate distributions from data samples. It is implemented for discrete variables only. More details can be found on its website (https://bitbucket.org/rquax/jointpdf).
References
- Shannon, C.E.; Weaver, W. Mathematical Theory of Communication; University Illinois Press: Champaign, IL, USA, 1963. [Google Scholar]
- Watanabe, S. Information theoretical analysis of multivariate correlation. IBM J. Res. Dev. 1960, 4, 66–82. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv 2010. [Google Scholar]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: An experimentalist’s perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef] [PubMed]
- Schneidman, E.; Bialek, W.; Berry, M.J. Synergy, redundancy, and independence in population codes. J. Neurosci. 2003, 23, 11539–11553. [Google Scholar] [PubMed]
- Griffith, V.; Chong, E.K.P.; James, R.G.; Ellison, C.J.; Crutchfield, J.P. Intersection Information Based on Common Randomness. Entropy 2014, 16, 1985–2000. [Google Scholar] [CrossRef]
- Lizier, J.T.; Flecker, B.; Williams, P.L. Towards a synergy-based approach to measuring information modification. In Proceedings of the 2013 IEEE Symposium on Artificial Life (ALIFE), Singapore, 16–19 April 2013; pp. 43–51.
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared Information—New Insights and Problems in Decomposing Information in Complex Systems. In Proceedings of the European Conference on Complex Systems 2012; Springer: Cham, Switzerland, 2013; pp. 251–269. [Google Scholar]
- Olbrich, E.; Bertschinger, N.; Rauh, J. Information Decomposition and Synergy. Entropy 2015, 17, 3501–3517. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. In Guided Self-Organization: Inception; Springer: Berlin/Heidelberg, Germany, 2014; pp. 159–190. [Google Scholar]
- Brukner, C.; Zukowski, M.; Zeilinger, A. The essence of entanglement. arXiv 2001. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 1991; Volume 6. [Google Scholar]
- Wibral, M.; Lizier, J.T.; Priesemann, V. Bits from Brains for Biologically Inspired Computing. Front. Robot. AI 2015. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Wyner, A. The common information of two dependent random variables. IEEE Trans. Inf. Theory 1975, 21, 163–179. [Google Scholar] [CrossRef]
- Witsenhausen, H.S. Values and bounds for the common information of two discrete random variables. SIAM J. Appl. Math. 1976, 31, 313–333. [Google Scholar] [CrossRef]
- Xu, G.; Liu, W.; Chen, B. Wyners common information for continuous random variables—A lossy source coding interpretation. In Proceedings of the 45th Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 23–25 March 2011; pp. 1–6.
- Gács, P.; Körner, J. Common information is far less than mutual information. Probl. Control Inf. Theory 1973, 2, 149–162. [Google Scholar]
- Karhunen, K. Zur Spektraltheorie Stochastischer Prozesse; Finnish Academy of Science and Letters: Helsinki, Finland, 1946. (In Germany) [Google Scholar]
- Loeve, M. Probability Theory, 4th ed.; Graduate Texts in Mathematics (Book 46); Springer: New York, NY, USA, 1994; Volume 2. [Google Scholar]
- Phoon, K.K.; Huang, H.W.; Quek, S.T. Simulation of strongly non-Gaussian processes using Karhunen–Loeve expansion. Probabilistic Eng. Mech. 2005, 20, 188–198. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).