Breakdown Point of Robust Support Vector Machines
Abstract
:1. Introduction
1.1. Background
1.2. Our Contribution
2. Brief Introduction to Learning Algorithms
3. Robust Variants of SVM
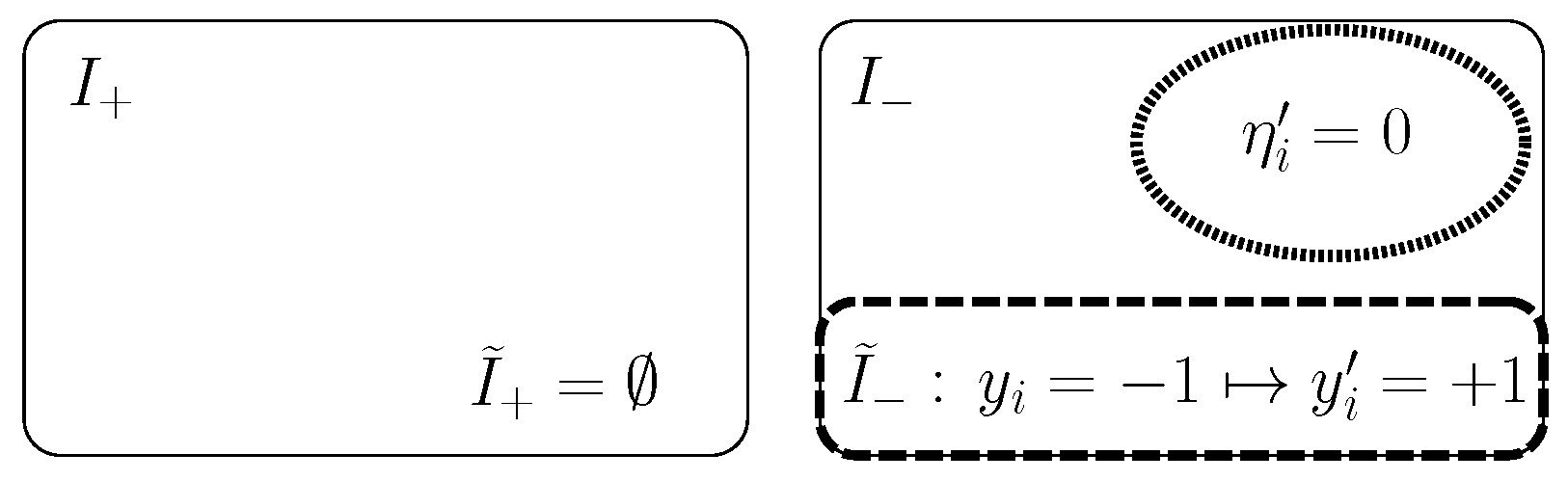
3.1. Outlier Indicators for Robust Learning Methods
3.2. Learning Algorithm
| Algorithm 1 Learning Algorithm of Robust -SVM |
Input: Training dataset , Gram matrix defined as , and training labels . The matrix is defined as . Let be the initial decision function.
|
3.3. Dual Problem and Its Interpretation
4. Breakdown Point of Robust SVMs
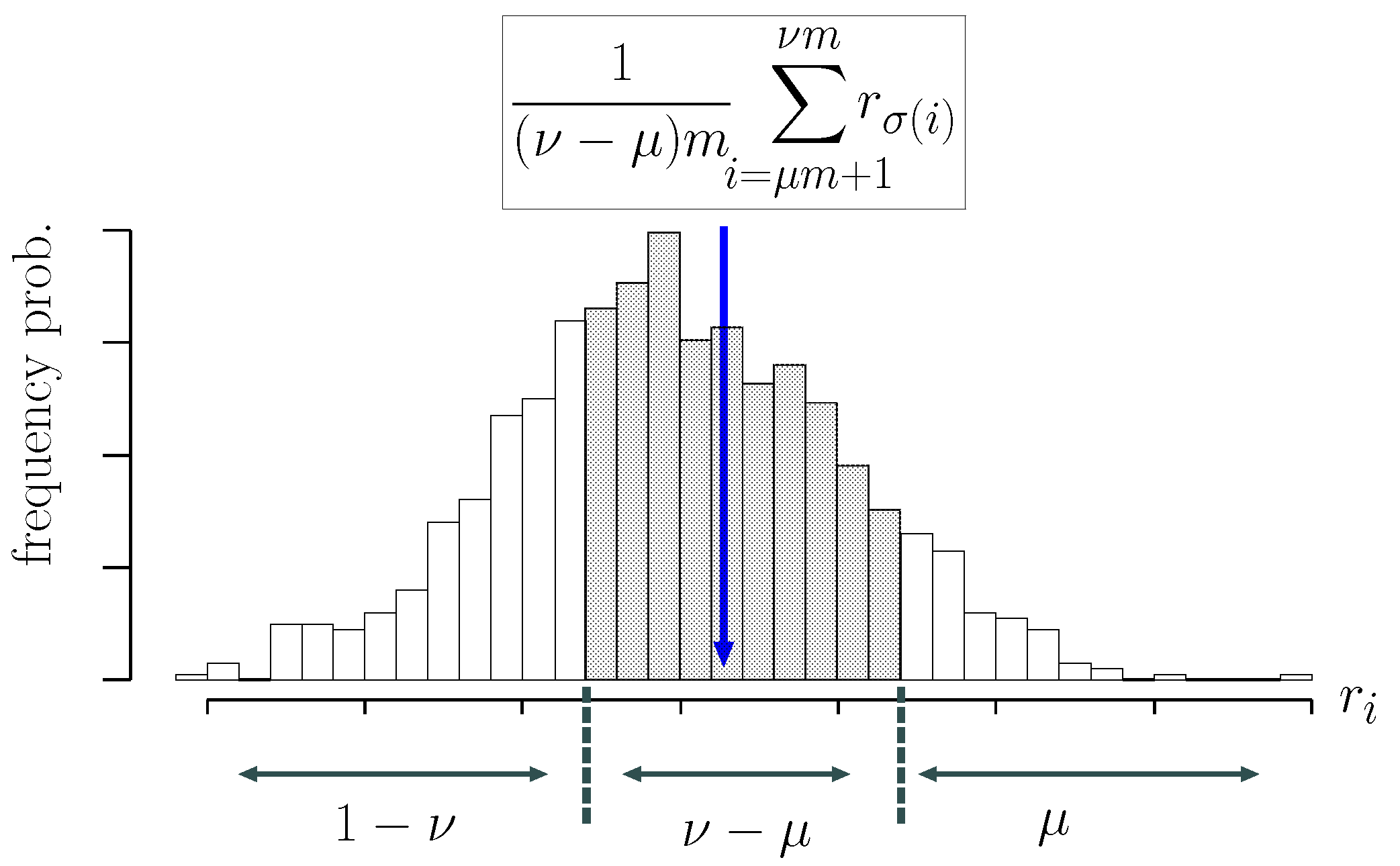
4.1. Finite-Sample Breakdown Point
4.2. Breakdown Point of Robust -SVM
- (i)
- The inequalityholds.
- (ii)
- Uniform boundedness,holds, where is the family of contaminated datasets defined from D.
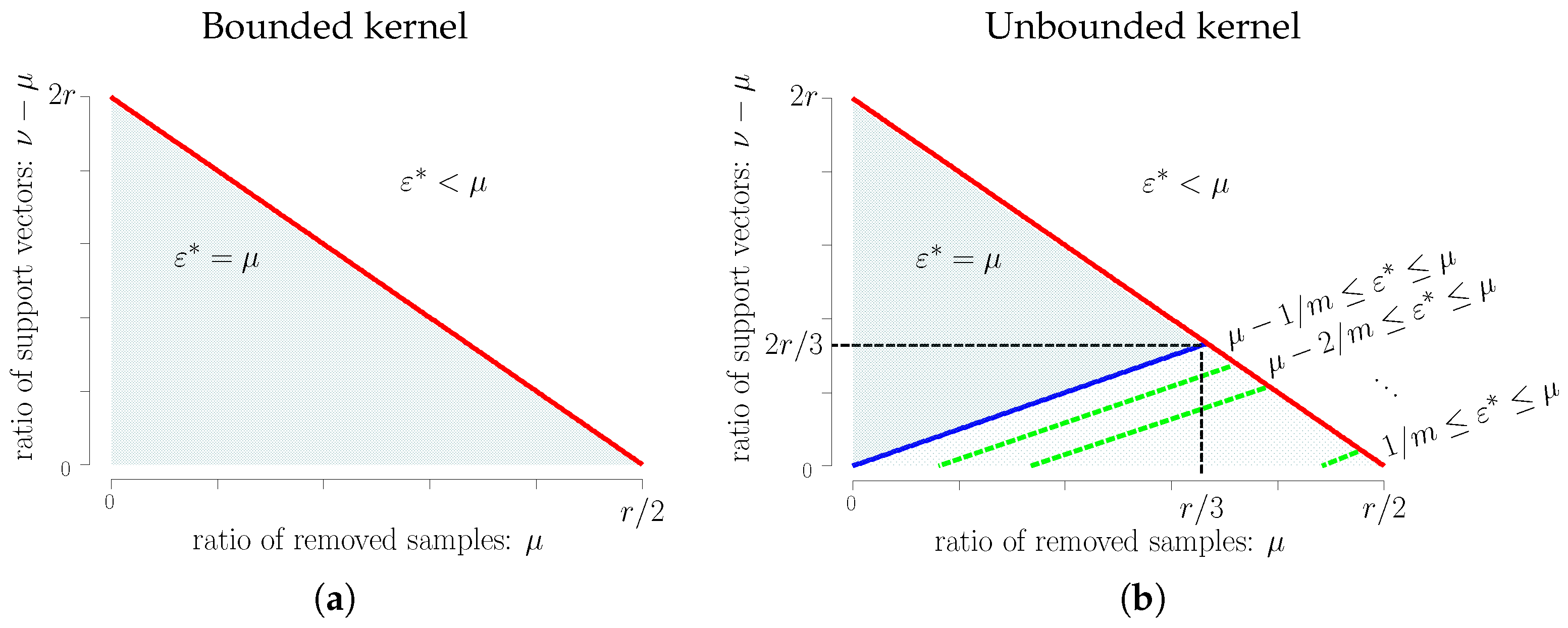
- Bounded kernel: For , the breakdown point of is less than μ. For , the breakdown point of is equal to μ.
- Unbounded kernel: For , the breakdown point of is less than μ. For , the breakdown point of is equal to μ. When , the breakdown point of is equal to μ, and the breakdown point of is bounded from below by and from above by μ, where depends on ν and μ, as shown in Theorem 3.
4.3. Breakdown Point Revisited
4.3.1. Effective Case of Breakdown Point
4.3.2. Other Robust Estimators
5. Admissible Region for Learning Parameters
6. Numerical Experiments
6.1. DCA versus Global Optimization Methods
6.2. Computational Cost
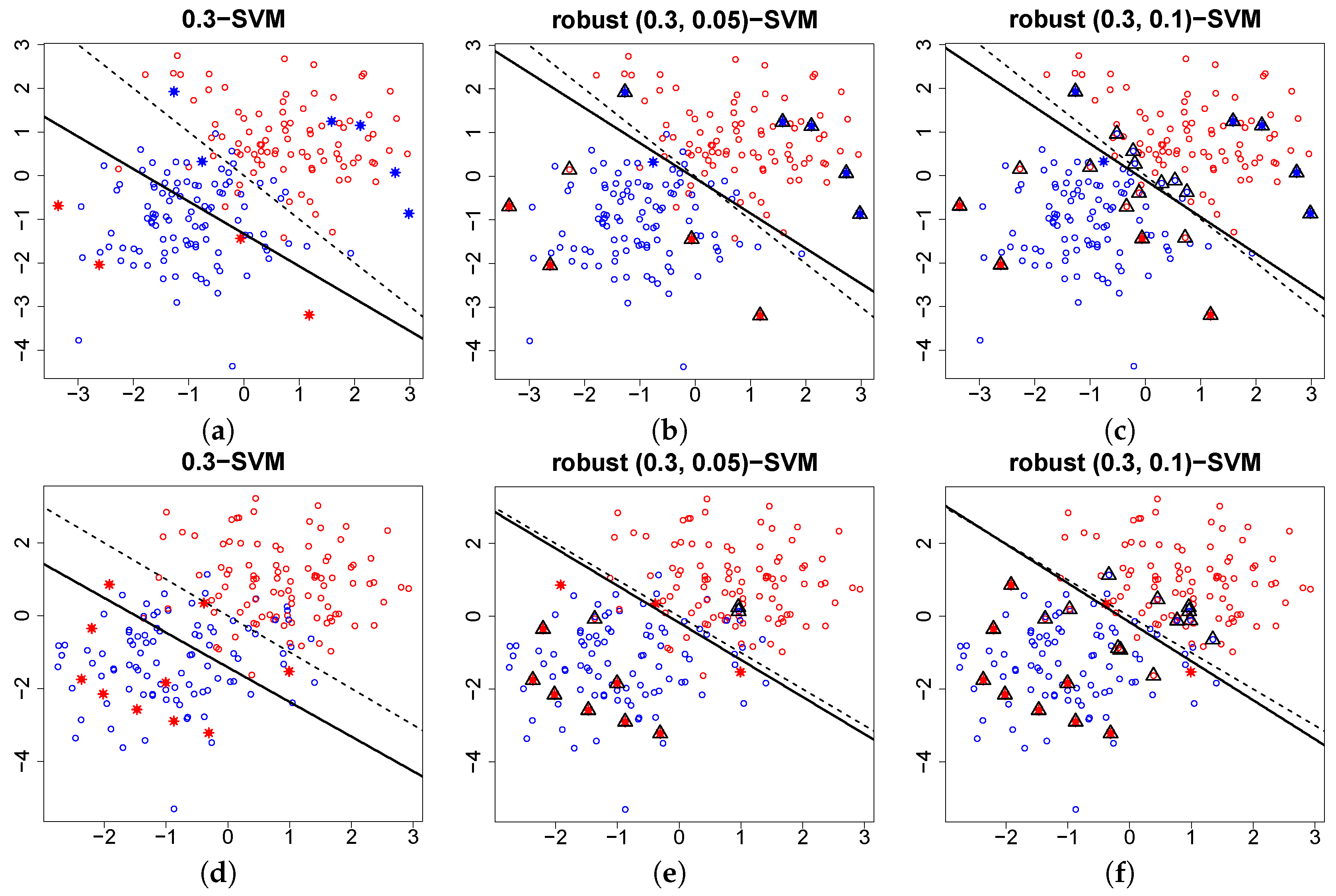
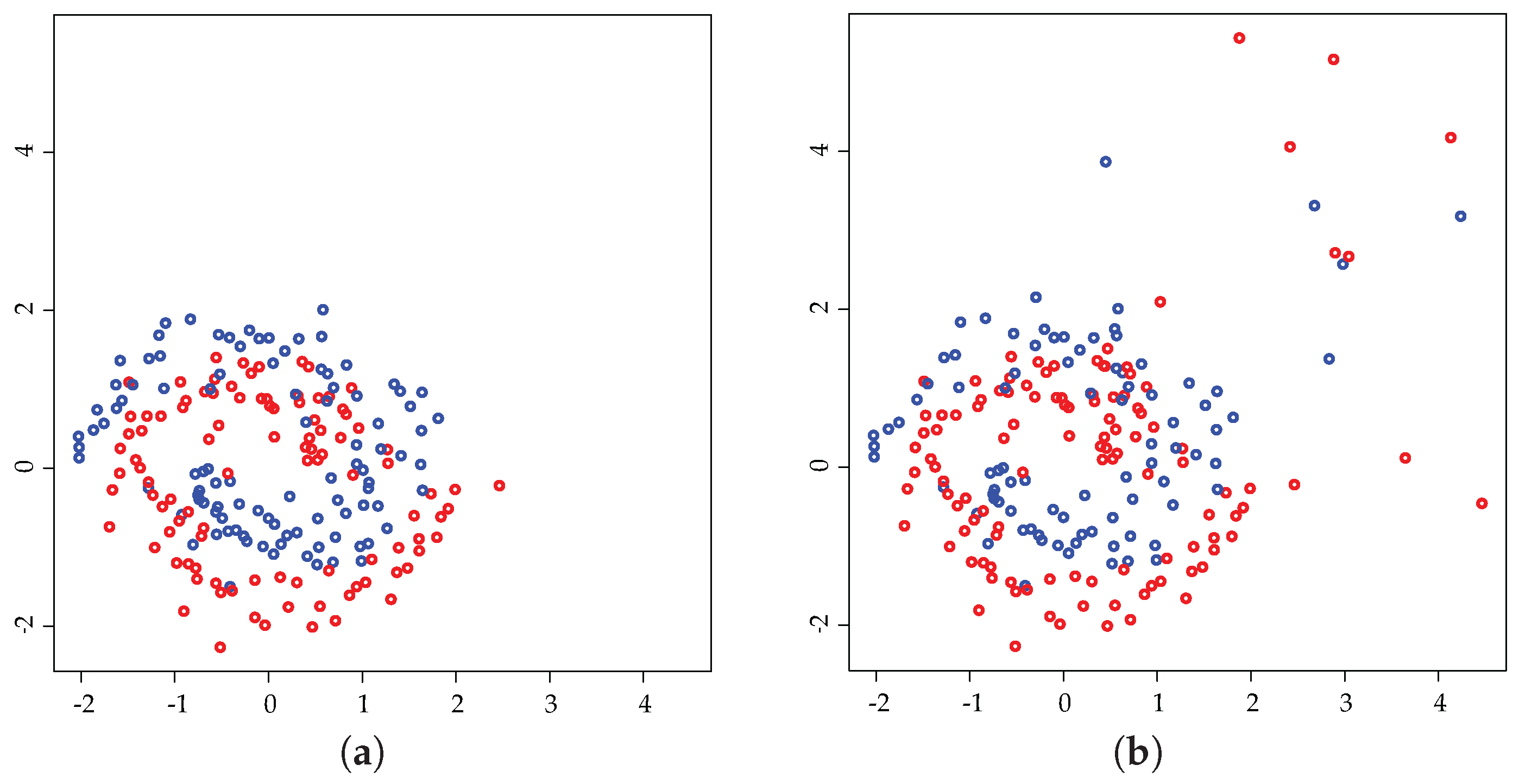
6.3. Outlier Detection
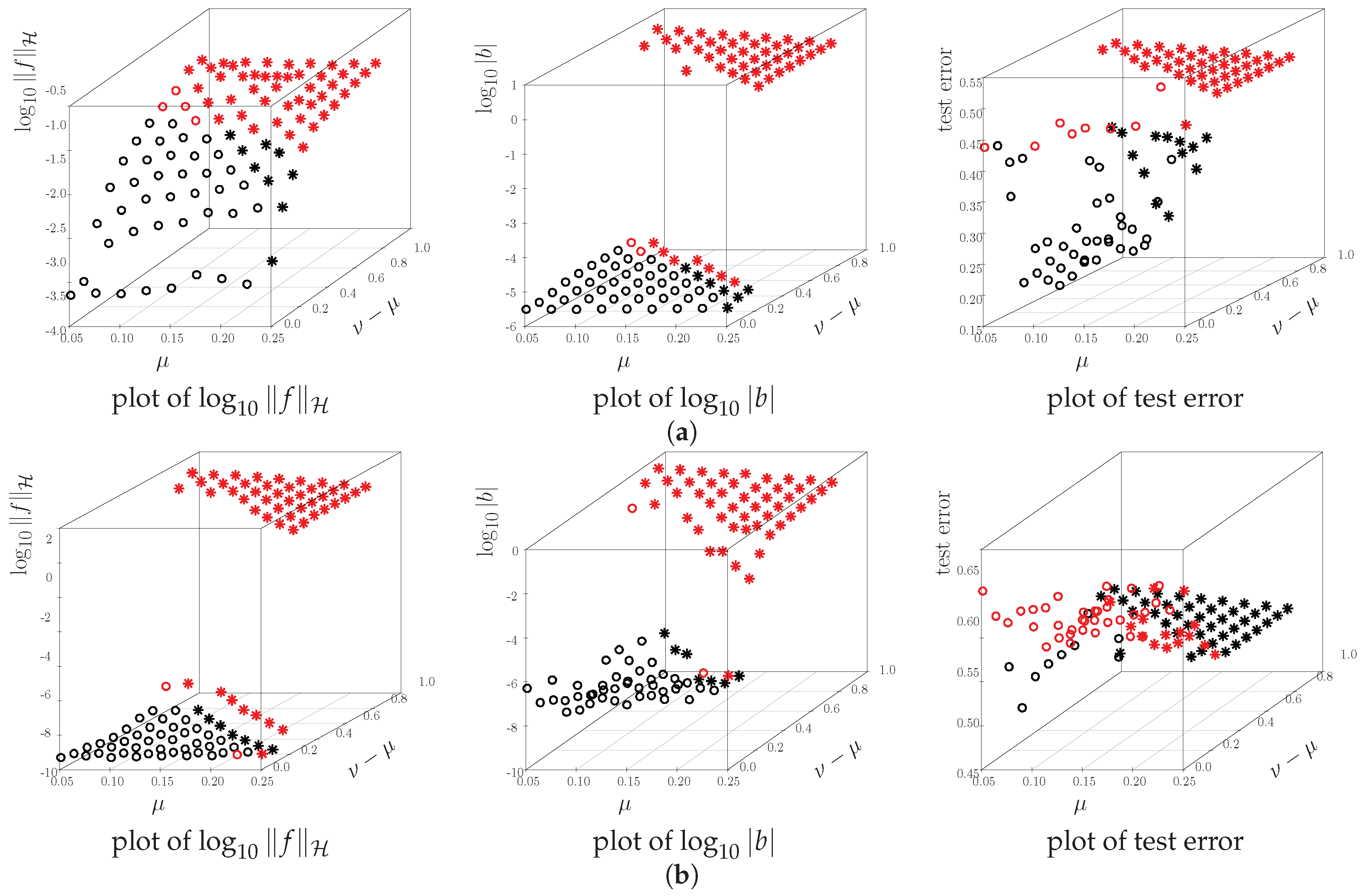
6.4. Breakdown Point
6.5. Prediction Accuracy
7. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
Appendix C. Proof of Theorem 3
- The function is increasing for .
- The function is decreasing for .
- (i)
- for all , holds and
- (ii)
- there exists an index such that .
Appendix D. Proof of Theorem 4
References
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Berlinet, A.; Thomas-Agnan, C. Reproducing Kernel Hilbert Spaces in Probability and Statistics; Kluwer Academic: Boston, MA, USA, 2004. [Google Scholar]
- Perez-Cruz, F.; Weston, J.; Hermann, D.J.L.; Schölkopf, B. Extension of the ν-SVM Range for Classification. In Advances in Learning Theory: Methods, Models and Applications 190; IOS Press: Amsterdam, The Netherlands, 2003; pp. 179–196. [Google Scholar]
- Schölkopf, B.; Smola, A.; Williamson, R.; Bartlett, P. New support vector algorithms. Neural Comput. 2000, 12, 1207–1245. [Google Scholar] [CrossRef] [PubMed]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Bartlett, P.L.; Jordan, M.I.; McAuliffe, J.D. Convexity, classification, and risk bounds. J. Am. Stat. Assoc. 2006, 101, 138–156. [Google Scholar] [CrossRef]
- Steinwart, I. On the influence of the kernel on the consistency of support vector machines. J. Mach. Learn. Res. 2001, 2, 67–93. [Google Scholar]
- Zhang, T. Statistical behavior and consistency of classification methods based on convex risk minimization. Ann. Stat. 2004, 32, 56–134. [Google Scholar] [CrossRef]
- Shen, X.; Tseng, G.C.; Zhang, X.; Wong, W.H. On ψ-learning. J. Am. Stat. Assoc. 2003, 98, 724–734. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, M.; Xu, L.; White, M.; Schuurmans, D. Relaxed Clipping: A Global Training Method for Robust Regression and Classification. In Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2010; pp. 2532–2540. [Google Scholar]
- Collobert, R.; Sinz, F.; Weston, J.; Bottou, L. Trading Convexity for Scalability. In Proceedings of the ICML06, 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; ACM Press: New York, NY, USA, 2006; pp. 201–208. [Google Scholar]
- Wu, Y.; Liu, Y. Robust truncated hinge loss support vector machines. J. Am. Stat. Assoc. 2007, 102, 974–983. [Google Scholar] [CrossRef]
- Yu, Y.; Aslan, Ö.; Schuurmans, D. A Polynomial-Time Form of Robust Regression. In Advances in Neural Information Processing Systems 25; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 2483–2491. [Google Scholar]
- Feng, Y.; Yang, Y.; Huang, X.; Mehrkanoon, S.; Suykens, J.A. Robust Support Vector Machines for Classification with Nonconvex and Smooth Losses. Neural Comput. 2016, 28, 1217–1247. [Google Scholar] [CrossRef] [PubMed]
- Tsyurmasto, P.; Uryasev, S.; Gotoh, J. Support Vector Classification with Positive Homogeneous Risk Functionals; Technical Report, Research Report 2013-4; Department of Industrial and Systems Engineering, University of Florida: Gainesville, FL, USA, 2013. [Google Scholar]
- Xu, L.; Crammer, K.; Schuurmans, D. Robust Support Vector Machine Training Via Convex Outlier Ablation. In Proceedings of the AAAI, Boston, MA, USA, 16–20 July 2006; pp. 536–542.
- Fujiwara, S.; Takeda, A.; Kanamori, T. DC Algorithm for Extended Robust Support Vector Machine; Technical Report METR 2014–38; The University of Tokyo: Tokyo, Japan, 2014. [Google Scholar]
- Takeda, A.; Fujiwara, S.; Kanamori, T. Extended robust support vector machine based on financial risk minimization. Neural Comput. 2014, 26, 2541–2569. [Google Scholar] [CrossRef] [PubMed]
- Maronna, R.; Martin, R.D.; Yohai, V. Robust Statistics: Theory and Methods; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Schapire, R.E.; Freund, Y.; Bartlett, P.L.; Lee, W.S. Boosting the margin: A new explanation for the effectiveness of voting methods. Ann. Stat. 1998, 26, 1651–1686. [Google Scholar] [CrossRef]
- Kimeldorf, G.S.; Wahba, G. Some results on Tchebycheffian spline functions. J. Math. Anal. Appl. 1971, 33, 82–95. [Google Scholar] [CrossRef]
- Wahba, G. Advances in Kernel Methods; Chapter Support Vector Machines, Reproducing Kernel Hilbert Spaces, and Randomized GACV; MIT Press: Cambridge, MA, USA, 1999; pp. 69–88. [Google Scholar]
- Takeda, A.; Sugiyama, M. ν-Support Vector Machine as Conditional Value-at-Risk Minimization. In Proceedings of the ICML, ACM International Conference Proceeding Series, Yokohama, Japan, 3–5 December 2008; Cohen, W.W., McCallum, A., Roweis, S.T., Eds.; ACM: New York, NY, USA, 2008; Volume 307, pp. 1056–1063. [Google Scholar]
- Rockafellar, R.T.; Uryasev, S. Conditional value-at-risk for general loss distributions. J. Bank. Financ. 2002, 26, 1443–1472. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Le Thi, H.A.; Dinh, T.P. Convex analysis approach to d.c. programming: Theory, algorithms and applications. Acta Math. Vietnam. 1997, 22, 289–355. [Google Scholar]
- Yuille, A.L.; Rangarajan, A. The concave-convex procedure. Neural Comput. 2003, 15, 915–936. [Google Scholar] [CrossRef] [PubMed]
- Crisp, D.J.; Burges, C.J.C. A Geometric Interpretation of ν-SVM Classifiers. In Advances in Neural Information Processing Systems 12; Solla, S.A., Leen, T.K., Müller, K.-R., Eds.; MIT Press: Cambridge, MA, USA, 2000; pp. 244–250. [Google Scholar]
- Kanamori, T.; Takeda, A.; Suzuki, T. Conjugate relation between loss functions and uncertainty sets in classification problems. J. Mach. Learn. Res. 2013, 14, 1461–1504. [Google Scholar]
- Takeda, A.; Mitsugi, H.; Kanamori, T. A Unified Robust Classification Model. In Proceedings of the 29th International Conference on Machine Learning (ICML-12), ICML’12, Edinburgh, Scotland, 26 June–1 July 2012; Langford, J., Pineau, J., Eds.; Omnipress: New York, NY, USA, 2012; pp. 129–136. [Google Scholar]
- Bertsekas, D.; Nedic, A.; Ozdaglar, A. Convex Analysis and Optimization; Athena Scientific: Belmont, MA, USA, 2003. [Google Scholar]
- Donoho, D.; Huber, P. The Notion of Breakdown Point. In A Festschrift for Erich L. Lehmann; CRC Press: Boca Raton, FL, USA, 1983; pp. 157–184. [Google Scholar]
- Hampel, F.R.; Rousseeuw, P.J.; Ronchetti, E.M.; Stahel, W.A. Robust Statistics. The Approach Based on Influence Functions; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1986. [Google Scholar]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Christmann, A.; Steinwart, I. On robustness properties of convex risk minimization methods for pattern recognition. J. Mach. Learn. Res. 2004, 5, 1007–1034. [Google Scholar]
- Le Thi, H.A.; Dinh, T.P. The DC (Difference of Convex Functions) Programming and DCA Revisited with DC Models of Real World Nonconvex Optimization Problems. Ann. Oper. Res. 2005, 133, 23–46. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Steinwart, I. On the optimal parameter choice for ν-support vector machines. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1274–1284. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y. Adaptively weighted large margin classifiers. J. Comput. Graph. Stat. 2013, 22, 416–432. [Google Scholar] [CrossRef] [PubMed]
| Setting | Err. (%) | in Robust -SVM Using Linear Kernel | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dim. | Cov. | #Initial Points | #Initial Points | #Initial Points | |||||||
| 1 | 5 | 10 | 1 | 5 | 10 | 1 | 5 | 10 | |||
| 2 | I | 7.9 | 87 | 96 | 97 | 90 | 99 | 99 | 93 | 99 | 99 |
| 5 | I | 1.3 | 98 | 99 | 100 | 100 | 100 | 100 | 99 | 100 | 100 |
| 10 | I | 0.1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2 | 26.4 | 78 | 84 | 88 | 76 | 85 | 90 | 75 | 85 | 86 | |
| 5 | 24.0 | 46 | 84 | 90 | 53 | 83 | 90 | 66 | 90 | 90 | |
| 10 | 32.7 | 16 | 59 | 73 | 31 | 72 | 77 | 46 | 85 | 92 | |
| Linear Kernel | Sonar () | BreastCancer () | Spam () | |||
|---|---|---|---|---|---|---|
| Robust -SVM, | Time (s) | SV Ratio | Time (s) | SV Ratio | Time (s) | SV Ratio |
| 1.10 (0.22) | 0.79 (0.14) | 1.02 (0.17) | 0.21 (0.11) | 13.38 (3.90) | 0.27 (0.22) | |
| 0.87 (0.15) | 0.75 (0.20) | 0.73 (0.13) | 0.18 (0.06) | 11.29 (2.41) | 0.64 (0.27) | |
| 1.17 (0.19) | 0.57 (0.12) | 0.80 (0.13) | 0.22 (0.07) | 9.65 (2.13) | 0.24 (0.04) | |
| 0.81 (0.09) | 0.58 (0.16) | 0.63 (0.07) | 0.28 (0.05) | 8.64 (2.12) | 0.36 (0.21) | |
| 1.11 (0.18) | 0.49 (0.10) | 0.83 (0.14) | 0.30 (0.03) | 8.65 (1.25) | 0.30 (0.02) | |
| 0.90 (0.15) | 0.62 (0.16) | 0.76 (0.12) | 0.36 (0.02) | 8.72 (1.77) | 0.38 (0.04) | |
| Robust -SVM, | ||||||
| 0.12 (0.02) | 0.00 (0.00) | 0.15 (0.02) | 0.00 (0.00) | 1.62 (0.08) | 0.00 (0.00) | |
| 1 | 0.61 (0.07) | 0.45 (0.08) | 0.60 (0.16) | 0.04 (0.01) | 7.38 (2.36) | 0.08 (0.01) |
| 1.02 (0.11) | 0.54 (0.13) | 0.68 (0.18) | 0.03 (0.01) | 10.16 (3.31) | 0.11 (0.16) | |
| 1.07 (0.13) | 0.47 (0.09) | 0.63 (0.17) | 0.05 (0.06) | 20.98 (5.95) | 0.30 (0.32) | |
| Data | Outlier | Linear Kernel | Gaussian Kernel | ||||
|---|---|---|---|---|---|---|---|
| Robust -SVM | Robust C-SVM | ν-SVM | Robust -SVM | Robust C-SVM | ν-SVM | ||
| Sonar: , | 0% | *0.258(.032) | 0.270(.038) | * 0.256(.051) | * 0.179(.038) | **0.188(0.043) | *0.181(0.039) |
| , | 5% | * 0.256(0.039) | 0.273(0.047) | *0.258(0.046) | *0.225(0.042) | **0.229(0.051) | * 0.224(0.061) |
| , | 10% | * 0.297(0.060) | 0.306(0.067) | *0.314(0.060) | *0.249(0.059) | ** 0.230(0.046) | *0.259(0.062) |
| . | 15% | * 0.329(0.061) | 0.339(0.064) | *0.345(0.062) | *0.280(0.053) | ** 0.280(0.050) | *0.294(0.064) |
| BreastCancer: , | 0% | 0.033(.010) | *0.035(0.008) | * 0.033(0.006) | ** 0.032(0.008) | *0.035(0.012) | 0.033(0.010) |
| , | 5% | 0.034(0.009) | * 0.034(0.010) | *0.043(0.015) | ** 0.032(.005) | *0.033(0.007) | 0.033(0.006) |
| , | 10% | 0.055(0.015) | * 0.051(0.026) | *0.076(0.036) | ** 0.035(0.008) | *0.043(0.025) | 0.038(0.008) |
| 15% | 0.136(0.058) | * 0.120(0.050) | *0.148(0.058) | **0.160(0.083) | * 0.145(0.070) | 0.150(0.110) | |
| PimaIndiansDiabetes: | 0% | **0.237(0.018) | * 0.232(0.014) | 0.246(0.018) | * 0.238(0.021) | *0.240(0.019) | 0.243(0.022) |
| , , | 5% | **0.239(0.019) | * 0.237(0.016) | 0.269(0.036) | * 0.264(0.025) | *0.267(0.024) | 0.273(0.024) |
| , | 10% | ** 0.280(0.046) | *0.299(0.042) | 0.330(0.030) | *0.302(0.039) | * 0.293(0.036) | 0.315(0.038) |
| 15% | ** 0.338(0.042) | *0.349(0.030) | 0.351(0.026) | * 0.344(0.028) | *0.344(0.031) | 0.353(0.016) | |
| spam: , | 0% | **0.083(0.005) | 0.088(0.006) | *0.083(0.005) | **0.081(0.005) | 0.086(0.006) | * 0.081(0.006) |
| , | 5% | ** 0.094(0.008) | 0.104(0.013) | *0.109(0.010) | **0.095(0.008) | 0.097(0.009) | * 0.095(0.008) |
| , | 10% | ** 0.129(0.022) | 0.152(0.020) | *0.166(0.067) | ** 0.129(0.015) | 0.133(0.017) | 0.141(.030) |
| 15% | ** 0.201(0.029) | 0.240(0.030) | *0.256(0.091) | ** 0.206(0.018) | 0.223(0.030) | 0.240(0.055) | |
| Satellite: , | 0% | **0.097(0.004) | *0.096(0.003) | ** 0.094(0.003) | *0.069(0.031) | 0.067(0.004) | ** 0.063(0.004) |
| , | 5% | **0.101(0.003) | * 0.100(0.005) | **0.100(0.004) | *0.072(0.015) | 0.078(0.007) | **0.078(0.043) |
| , | 10% | ** 0.148(0.020) | *0.161(0.026) | **0.161(0.019) | *0.117(0.034) | 0.126(0.040) | **0.137(0.027) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanamori, T.; Fujiwara, S.; Takeda, A. Breakdown Point of Robust Support Vector Machines. Entropy 2017, 19, 83. https://doi.org/10.3390/e19020083
Kanamori T, Fujiwara S, Takeda A. Breakdown Point of Robust Support Vector Machines. Entropy. 2017; 19(2):83. https://doi.org/10.3390/e19020083
Chicago/Turabian StyleKanamori, Takafumi, Shuhei Fujiwara, and Akiko Takeda. 2017. "Breakdown Point of Robust Support Vector Machines" Entropy 19, no. 2: 83. https://doi.org/10.3390/e19020083
APA StyleKanamori, T., Fujiwara, S., & Takeda, A. (2017). Breakdown Point of Robust Support Vector Machines. Entropy, 19(2), 83. https://doi.org/10.3390/e19020083





