Cosine Similarity Entropy: Self-Correlation-Based Complexity Analysis of Dynamical Systems
Abstract
:1. Introduction
2. Sample Entropy, Fuzzy Entropy and a Multiscale Approach
| Algorithm 1. Sample Entropy |
| For a time series with a given embedding dimension (m), tolerance () and time lag (): |
|
| Algorithm 2. Fuzzy Entropy |
| For a time series with given embedding dimension (m), tolerance () and time lag (): |
|
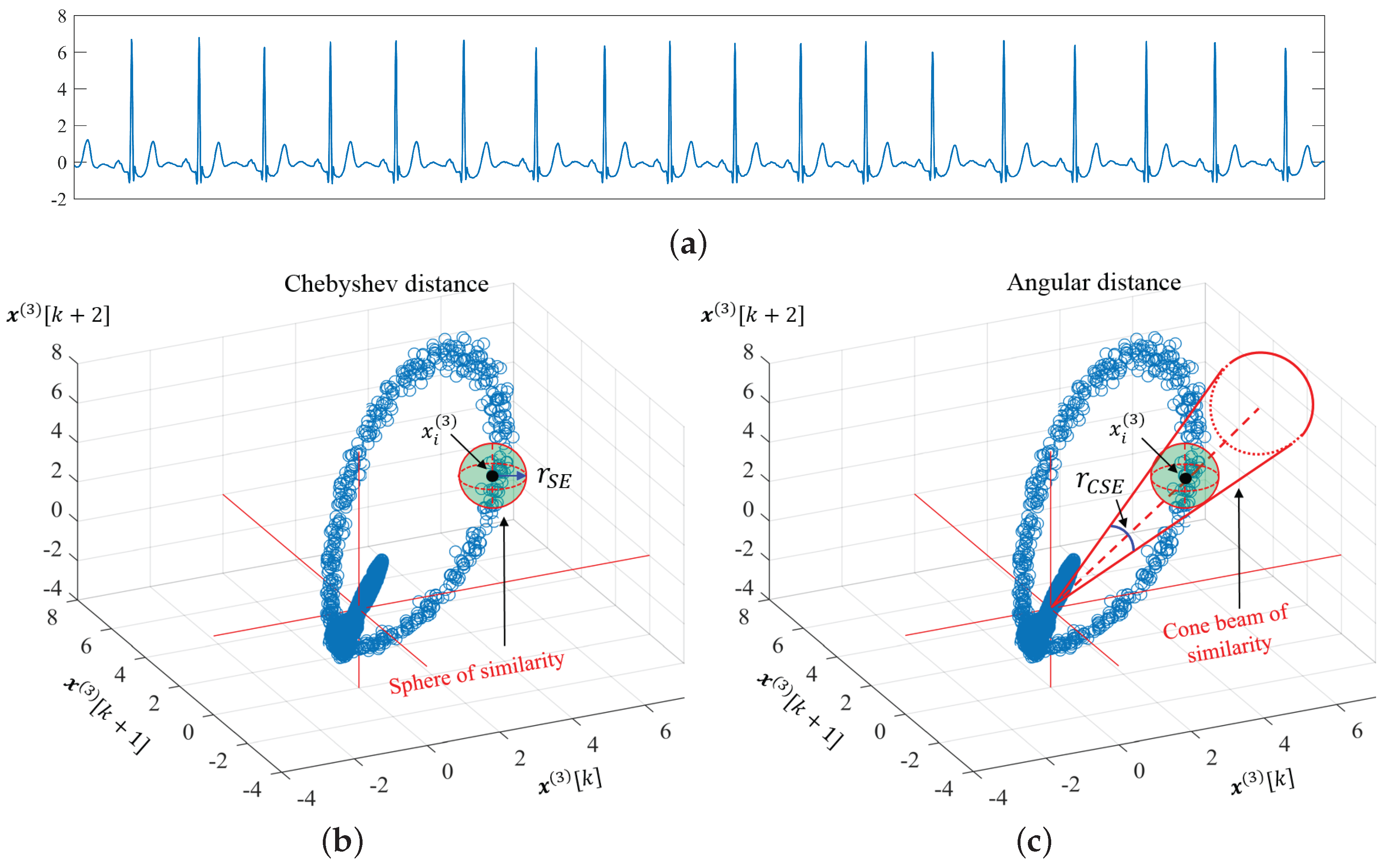
3. Cosine Similarity Entropy (CSE)
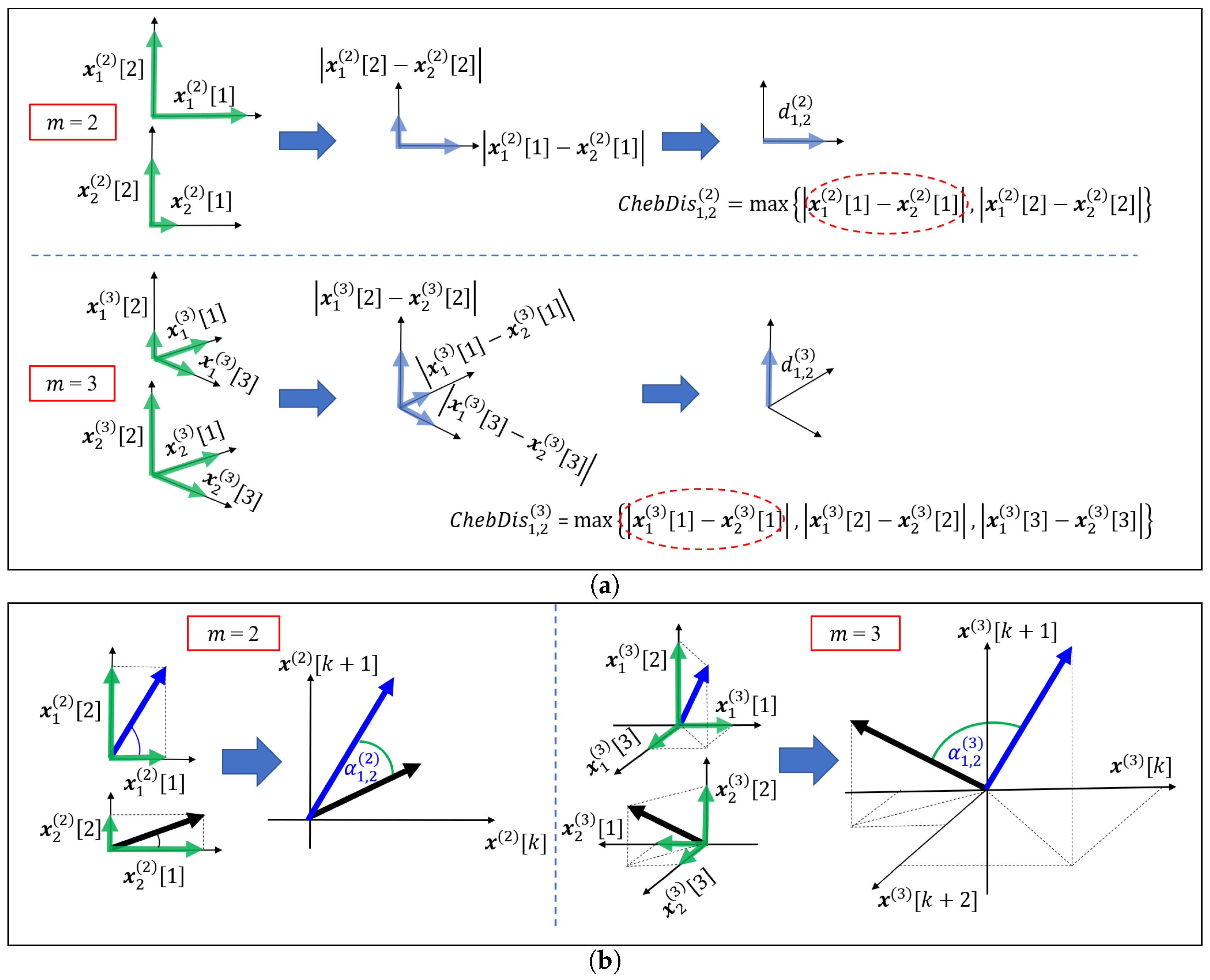
3.1. Angular Distance
3.2. Properties of Angular Distance
3.3. Cosine Similarity Entropy and Multiscale Cosine Similarity Entropy
| Algorithm 3. Cosine Similarity Entropy |
| For a time series with given embedding dimension (m), tolerance () and time lag (): |
|
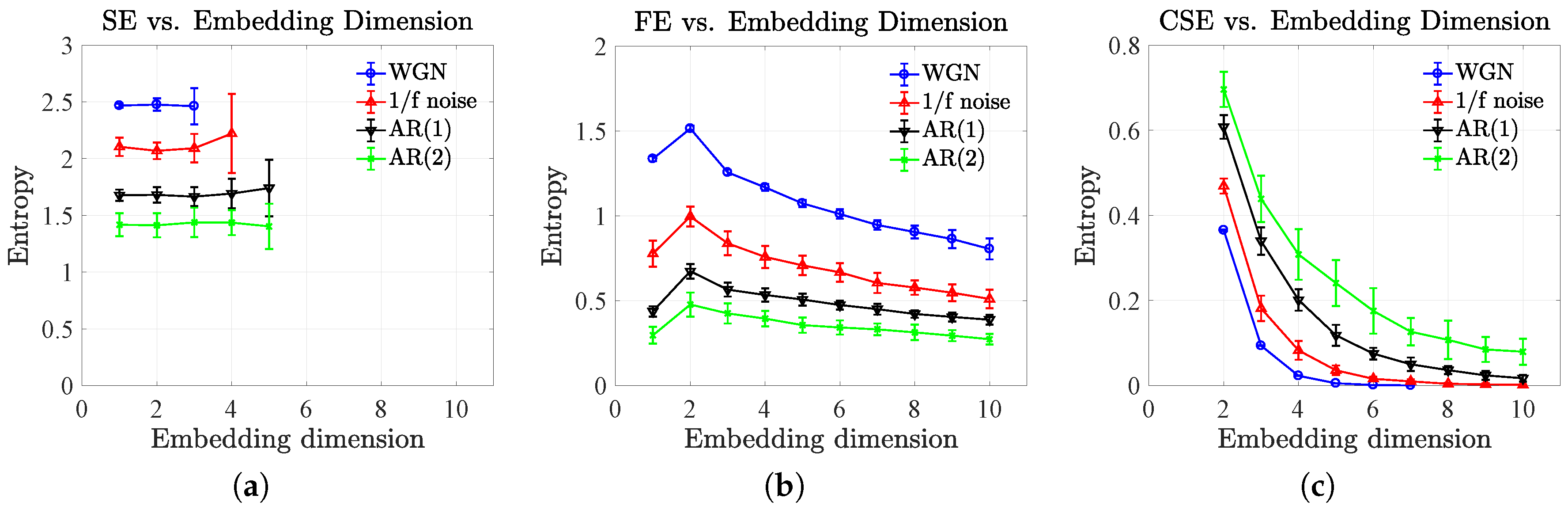
4. Selection of Parameters
4.1. Selection of the Tolerance ( ) for CSE
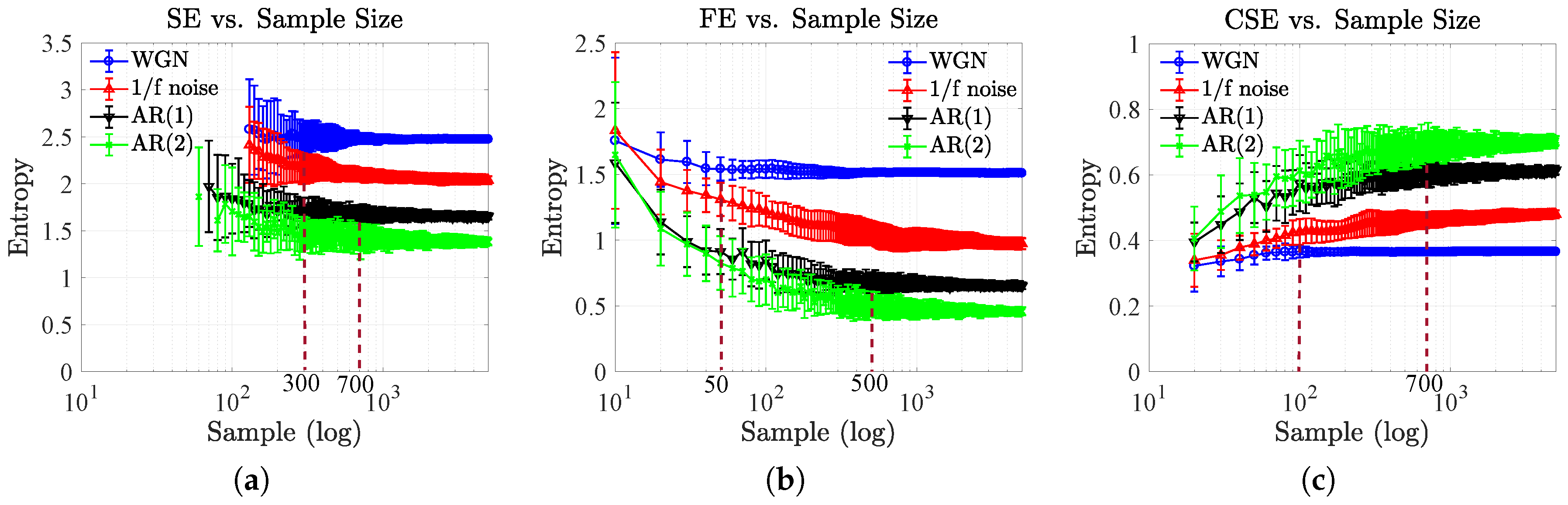
4.2. Effect of Sample Size and Embedding Dimension
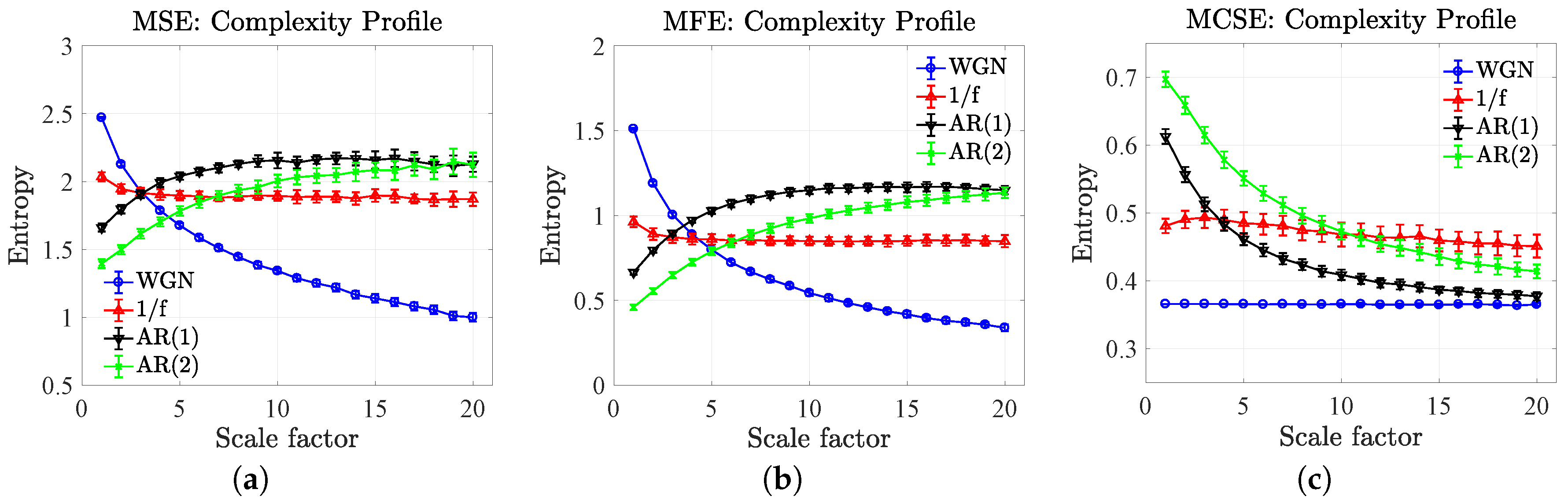
5. A Comparison of Complexity Profiles Using MSE, MFE and MCSE
5.1. Complexity Profiles of Synthetic Noises
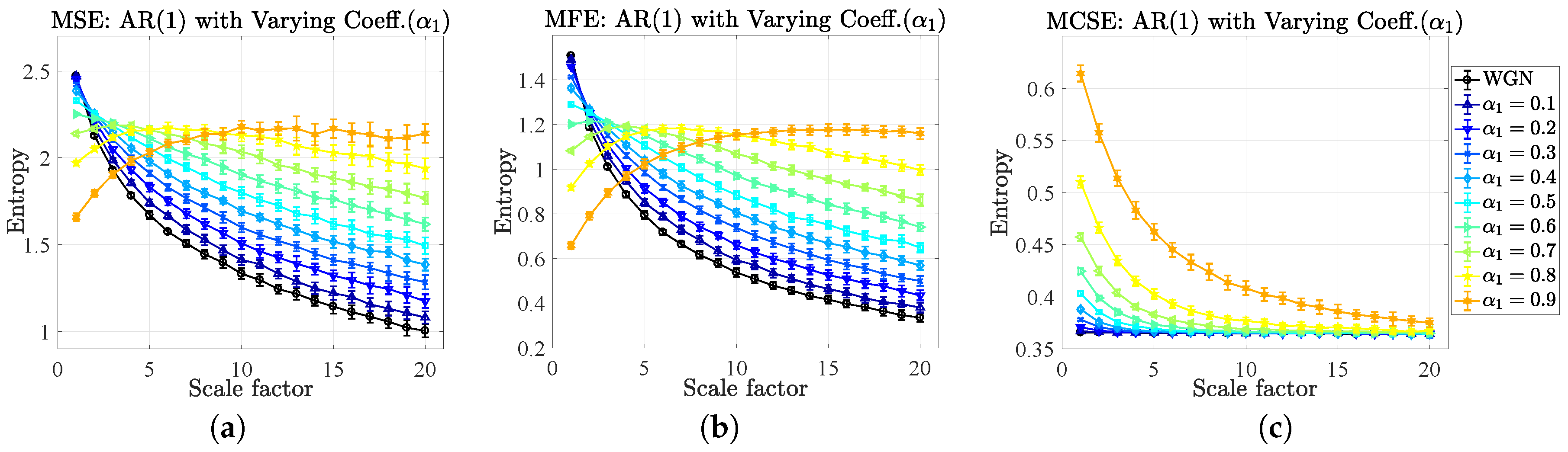
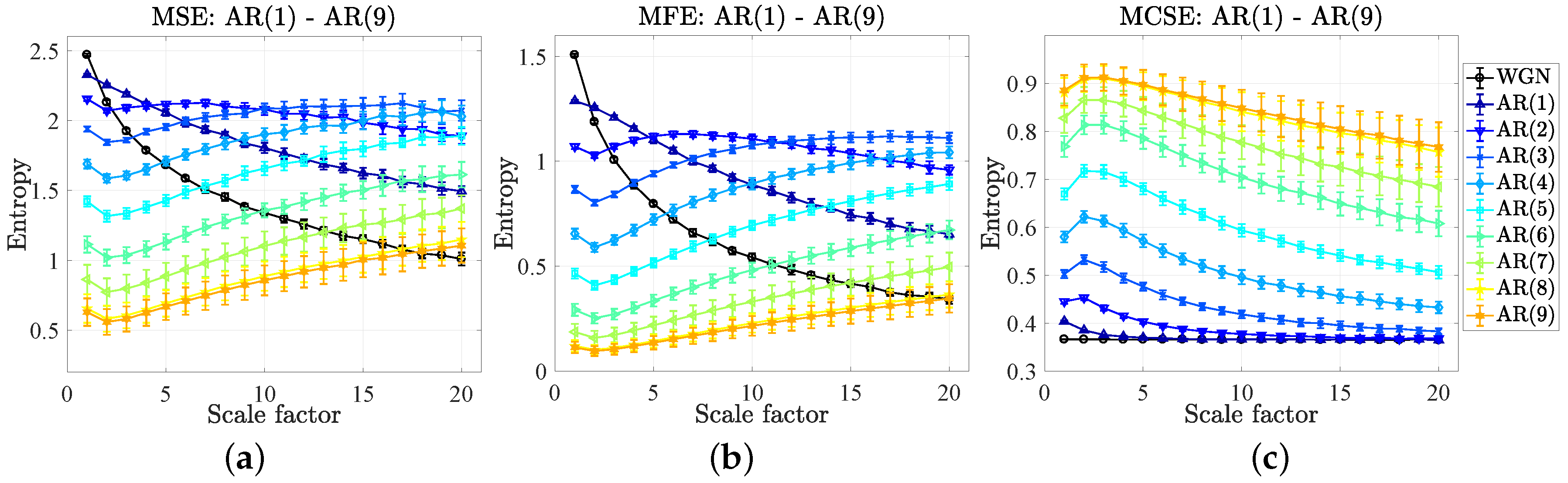
5.2. Complexity Profiles of Autoregressive Models
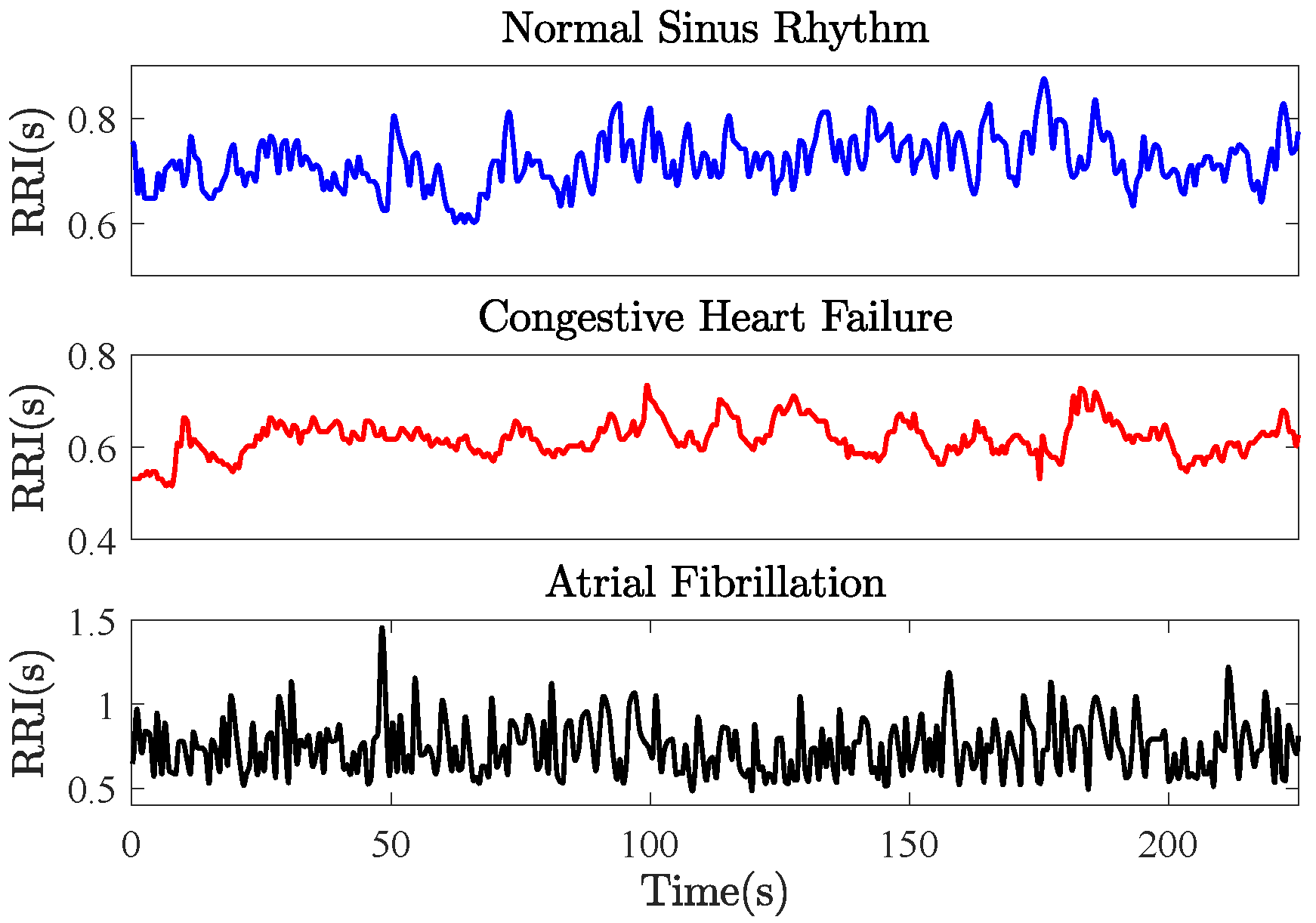
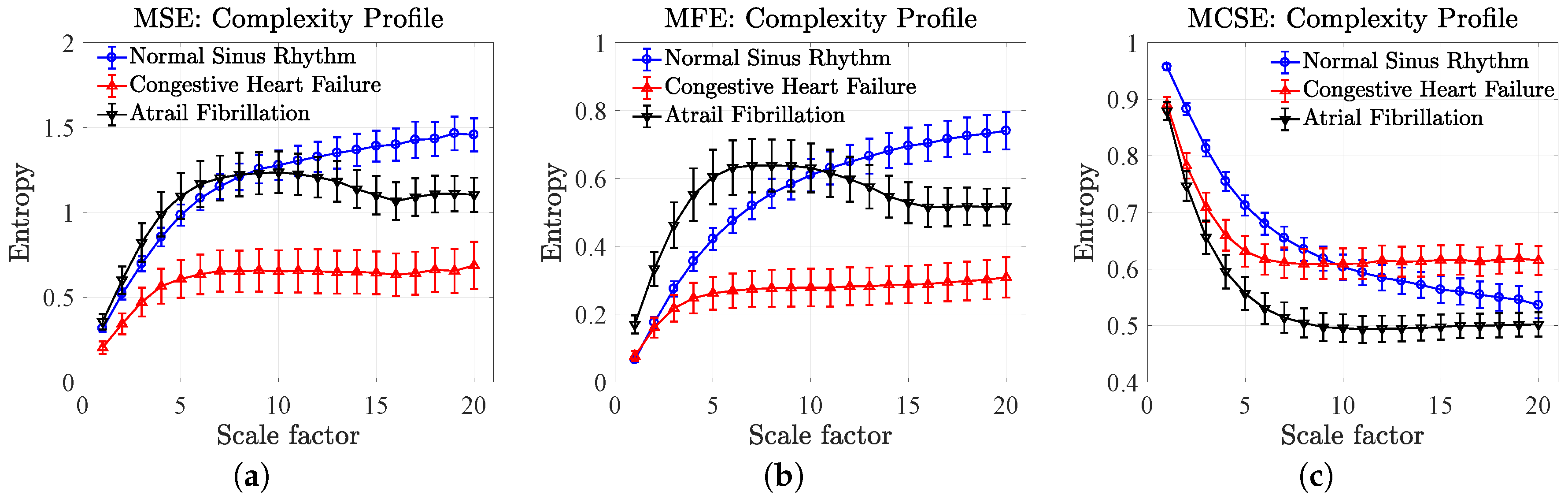
5.3. Complexity Profiles of Heart Rate Variability
6. Discussion and Conclusions
- The results of the MSE and MFE have unveiled that the high to low mean entropies (complexity) were in agreement with the high to low values of the correlation coefficients of the AR(1) only at the large scale factor, while the results of the MCSE correctly indicate the corresponding orders of the mean entropies over all the scale factors, which is rather significant at the small scale factor.
- The results of the MSE and MFE have showed that the values of mean entropies at the first scale factor (from high to low) correspond to the small to large orders of the AR(p), while the results of the MCSE have disclosed the correct corresponding orders of the mean entropies over all the scale factors, illustrating as the robust nature of the proposed algorithms.
- The MSE resulted in equal complexity (overlapped mean entropies) for the NSR and the AF, which were higher than the complexity of the CHF at the first scale factor. When increasing the scale factor, the complexity of the three HRVs increased toward the largest scale factor, where the order of degrees of complexity from high to low corresponds to the NSR, AF and CHF.
- The MFE resulted in equal complexity (overlapped mean entropies) for both the NSR and CHF, which were higher than the complexity of the AF at the first scale factor. When increasing the scale factor, the complexity of the three HRVs increased toward the largest scale factor, where the degrees of complexity from high to low correspond to the NSR, AF and CHF, analogous to the results of the MSE.
- The MCSE resulted in equal structural complexity measures for both the CHF and AF (overlapped mean entropies), which were higher than the complexity of the NRS at the first scale factor. When increasing the scale factor, the complexity of the three HRVs decreased, and, at the largest scale factor, the degrees of structural complexity from high to low correspond to the CHF, NRS and AF.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Autoregressive Models
| Correlation Coefficient | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| AR(1) | 0.5 | - | - | - | - | - | - | - | - |
| AR(2) | 0.5 | 0.25 | - | - | - | - | - | - | - |
| AR(3) | 0.5 | 0.25 | 0.125 | - | - | - | - | - | - |
| AR(4) | 0.5 | 0.25 | 0.125 | 0.0625 | - | - | - | - | - |
| AR(5) | 0.5 | 0.25 | 0.125 | 0.0625 | 0.0313 | - | - | - | - |
| AR(6) | 0.5 | 0.25 | 0.125 | 0.0625 | 0.0313 | 0.0156 | - | - | - |
| AR(7) | 0.5 | 0.25 | 0.125 | 0.0625 | 0.0313 | 0.0156 | 0.0078 | - | - |
| AR(8) | 0.5 | 0.25 | 0.125 | 0.0625 | 0.0313 | 0.0156 | 0.0078 | 0.0039 | - |
| AR(9) | 0.5 | 0.25 | 0.125 | 0.0625 | 0.0313 | 0.0156 | 0.0078 | 0.0039 | 0.0019 |
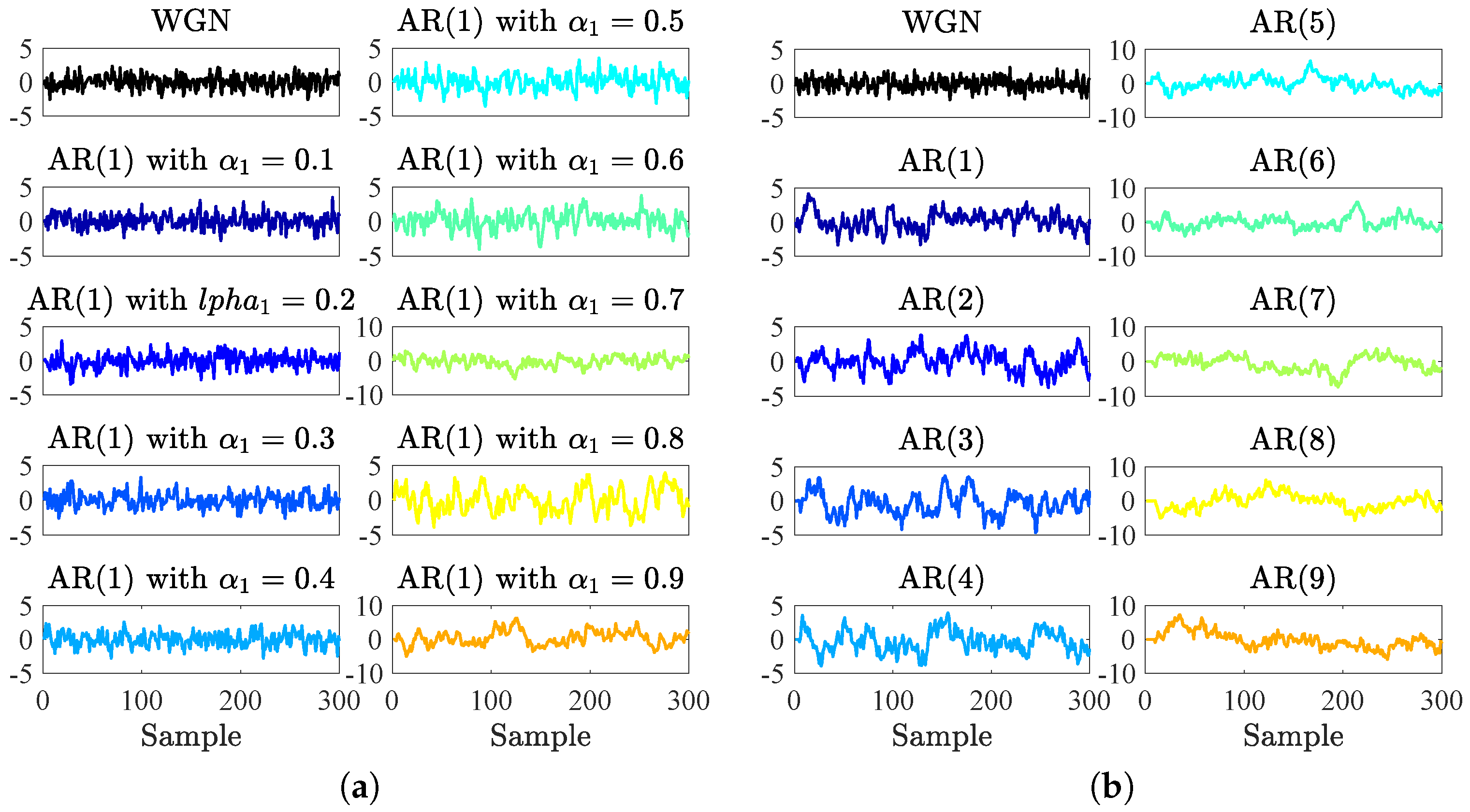
Appendix B. Heart Rate Variability Database
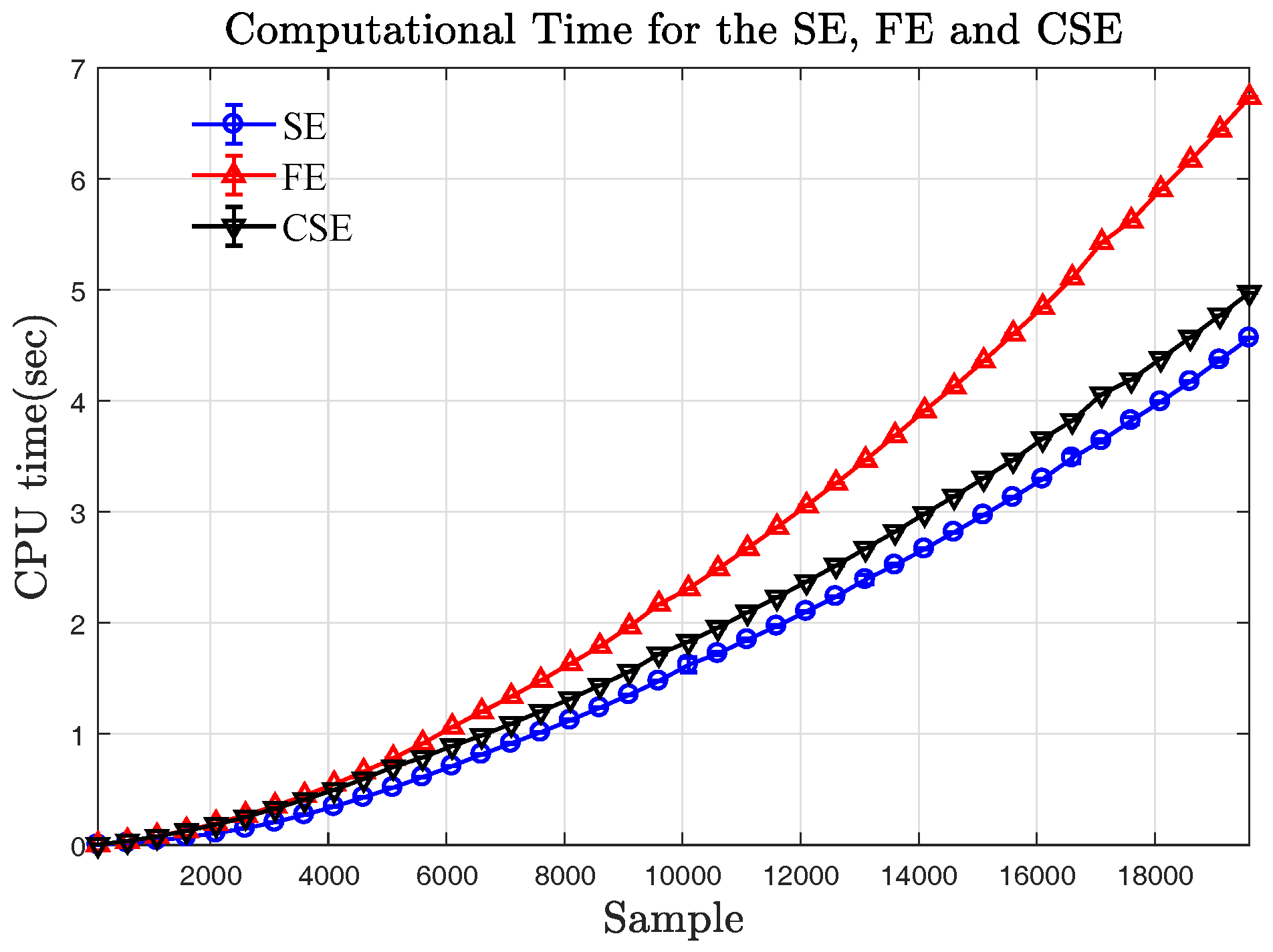
Appendix C. Computational Time
References
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Assessing serial irregularity and its implications for health. Ann. N. Y. Acad. Sci. 2001, 954, 245–267. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence; Rand, D., Young, L.S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a time series. Phys. Rev. Lett. 1980, 45, 52–56. [Google Scholar] [CrossRef]
- Gautama, T.; Mandic, D.P.; Van Hulle, M.M. The delay vector variance method for detecting determinism and nonlinearity in time series. Phys. D 2004, 190, 167–176. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. 2000, 278, H2039–H2049. [Google Scholar]
- Alcaraz, R.; Abásolo, D.; Hornero, R.; Rieta, J. Study of sample entropy ideal computational parameters in the estimation of atrial fibrillation organization from the ECG. Comput. Cardiol. 2010, 37, 1027–1030. [Google Scholar]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Molina-Picó, A.; Cuesta-Frau, D.; Aboy, M.; Crespo, C.; Miró-Martínez, P.; Oltra-Crespo, S. Comparative study of approximate entropy and sample entropy robustness to spikes. Artif. Intell. Med. 2011, 53, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol. 2002, 283, R789–R797. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W.; Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.B.; He, W.X.; Liu, H. Measuring time series regularity using nonlinear similarity-based sample entropy. Phys. Lett. A 2008, 372, 7140–7146. [Google Scholar] [CrossRef]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.B.; Guo, J.Y.; Zheng, Y.P. Using the modified sample entropy to detect determinism. Phys. Lett. A 2010, 374, 3926–3931. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Y.; Sun, X.; Li, D.; Voss, L.J.; Sleigh, J.W.; Hagihira, S.; Li, X. EEG entropy measures in anesthesia. Front. Comput. Neurosci. 2015, 9, 16. [Google Scholar] [CrossRef] [PubMed]
- Gan, C.; Learmonth, G. Comparing entropy with tests for randomness as a measure of complexity in time series. arXiv, 2015; arXiv:stat.ME/1512.00725. [Google Scholar]
- Trifonov, M. The structure function as new integral measure of spatial and temporal properties of multichannel EEG. Brain Inform. 2016, 3, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 6–9. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; HauSDorff, J.M. Multiscale entropy analysis of human gait dynamics. Phys. A 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 21906. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Ghiran, I.; Peng, C.K.; Nicholson-Weller, A.; Goldberger, A.L. Complex dynamics of human red blood cell flickering: Alterations with in vivo aging. Phys. Rev. E 2008, 78, 20901. [Google Scholar] [CrossRef] [PubMed]
- Carter, T. An Introduction to Information Theory and Entropy. Available online: http://astarte.csustan.edu/~tom/SFI-CSSS/info-theory/info-lec.pdf (accessed on 30 September 2017).
- Steele, M.J. The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities; The Mathematical Association of America: Washington, DC, USA, 2004. [Google Scholar]
- Deza, E.; Deza, M.M. Encyclopedia of Distances; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Kryszkiewicz, M. The Triangle Inequality Versus Projection onto a Dimension in Determining Cosine Similarity Neighborhoods of Non-negative Vectors. In Rough Sets and Current Trends in Computing; Yao, J., Yang, Y., Słowiński, R., Greco, S., Li, H., Mitra, S., Polkowski, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 229–236. [Google Scholar]
- Kryszkiewicz, M. The Cosine Similarity in Terms of the Euclidean Distance. In Encyclopedia of Business Analytics and Optimization; IGI Global: Hershey, PA, USA, 2014; pp. 2498–2508. [Google Scholar]
- Abbad, A.; Abbad, K.; Tairi, H. Face Recognition Based on City-block and Mahalanobis Cosine Distance. In Proceedings of the International Conference on Computer Graphics, Imaging and Visualization (CGiV), Beni Mellal, Morocco, 29 March–1 April 2016; pp. 112–114. [Google Scholar]
- Senoussaoui, M.; Kenny, P.; Stafylakis, T.; Dumouchel, P. A Study of the cosine distance-based mean shift for telephone speech diarization. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 217–227. [Google Scholar] [CrossRef]
- Sahu, L.; Mohan, B.R. An Improved K-means Algorithm Using Modified Cosine Distance Measure for Document Clustering Using Mahout with Hadoop. In Proceedings of the International Conference on Industrial and Information Systems (ICIIS), Gwalior, India, 15–17 December 2014; pp. 1–5. [Google Scholar]
- Ji, J.; Li, J.; Tian, Q.; Yan, S.; Zhang, B. Angular-similarity-preserving binary signatures for linear subspaces. IEEE Trans. Image Process. 2015, 24, 4372–4380. [Google Scholar] [CrossRef] [PubMed]
- Pearson, K. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1985, 58, 240–242. [Google Scholar] [CrossRef]
- Stigler, S.M. Francis Galton’s account of the invention of correlation. Stat. Sci. 1989, 4, 73–79. [Google Scholar] [CrossRef]
- Székely, G.J.; Rizzo, M.L.; Bakirov, N.K. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- Josh Patterson, A.G. Deep Learning a Practitioner’s Approach, 1st ed.; O’Reilly Media: Sevastopol, CA, USA, 2015; p. 536. [Google Scholar]
- Pincus, S.M.; Goldberger, A.L. Physiological time-series analysis: What does regularity quantify? Am. J. Physiol. 1994, 266, H1643–H1656. [Google Scholar] [PubMed]
- Kaffashi, F.; Foglyano, R.; Wilson, C.G.; Loparo, K.A.; Kenneth, A.L. The effect of time delay on approximate & sample Entropy calculations. Phys. D 2008, 237, 3069–3074. [Google Scholar]
- Richman, J.S.; Lake, D.E.; Moorman, J. Sample entropy. Methods Enzymol. 2004, 384, 172–184. [Google Scholar] [PubMed]
- Gautama, T.; Mandic, D.P.; Van Hulle, M.M. A Differential Entropy Based Method for Determining the Optimal Embedding Parameters of a Signal. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Hong Kong, China, 6–10 April 2003; Volume 6, pp. 29–32. [Google Scholar]
- Shalizi, C.R. Methods and Techniques of Complex Systems Science: An Overview. In Complex Systems Science in Biomedicine; Deisboeck, T.S., Kresh, J.Y., Eds.; Springer: Boston, MA, USA, 2006; pp. 33–114. [Google Scholar]
- Lipsitz, L.A.; Goldberger, A.L. Loss of complexity and aging. Potential applications of fractals and chaos theory to senescence. J. Am. Med. Assoc. 1992, 267, 1806–1809. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; HauSDorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.B.; Mark, R.G. A new method for detecting atrial fibrillation using RR intervals. In Proceedings of the International Conference on Computers in Cardiology, Aachen, Germany, 4–7 October 1983; pp. 227–230. [Google Scholar]

| Approach/Type of Signal | SE (SD of Entropies) | FE (SD of Entropies) | CSE (SD of Entropies) |
|---|---|---|---|
| WGN | 0.0586 | 0.0146 | 0.0011 |
| noise | 0.0975 | 0.0880 | 0.0287 |
| AR(1) | 0.0656 | 0.0505 | 0.0267 |
| AR(2) | 0.0982 | 0.0580 | 0.0401 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chanwimalueang, T.; Mandic, D.P. Cosine Similarity Entropy: Self-Correlation-Based Complexity Analysis of Dynamical Systems. Entropy 2017, 19, 652. https://doi.org/10.3390/e19120652
Chanwimalueang T, Mandic DP. Cosine Similarity Entropy: Self-Correlation-Based Complexity Analysis of Dynamical Systems. Entropy. 2017; 19(12):652. https://doi.org/10.3390/e19120652
Chicago/Turabian StyleChanwimalueang, Theerasak, and Danilo P. Mandic. 2017. "Cosine Similarity Entropy: Self-Correlation-Based Complexity Analysis of Dynamical Systems" Entropy 19, no. 12: 652. https://doi.org/10.3390/e19120652





