Analyzing Information Distribution in Complex Systems

Abstract

Information theory is often utilized to capture both linear as well as nonlinear relationships between any two parts of a dynamical complex system. Recently, an extension to classical information theory called partial information decomposition has been developed, which allows one to partition the information that two subsystems have about a third one into unique, redundant and synergistic contributions. Here, we apply a recent estimator of partial information decomposition to characterize the dynamics of two different complex systems. First, we analyze the distribution of information in triplets of spins in the 2D Ising model as a function of temperature. We find that while redundant information obtains a maximum at the critical point, synergistic information peaks in the disorder phase. Secondly, we characterize 1D elementary cellular automata rules based on the information distribution between neighboring cells. We describe several clusters of rules with similar partial information decomposition. These examples illustrate how the partial information decomposition provides a characterization of the emergent dynamics of complex systems in terms of the information distributed across their interacting units.

1. Introduction

The universe is full of systems that comprise a large number of interacting elements. Even if the immediate local interactions of these elements are rather simple, the global observable behaviour that they give rise to is often complex. Such systems, intuitively understood to be physical manifestations of the expression “the whole is more than the sum of its parts”, are aptly called complex systems. Canonical examples of complex systems include the human brain, ant colonies and financial markets. Indeed, most of these systems have many relatively simple parts (e.g., neurons) interacting nonlinearly, whose collective behavior engenders complex phenomena (e.g., consciousness).

In addition to physical systems, many mathematical models have been developed that capture the essence of different complex systems. These theoretical models are particularly interesting because one has complete knowledge of how their various parts are connected together and which rules they obey while interacting with each other. Nevertheless, the emergent global structures are often so complex that their exact evolution is difficult to predict from the initial conditions and the interaction rules without actually simulating the system. Cellular automata and the Ising model are quintessential examples of such models.

One way to analyze these complex models is to treat them as information processing systems and measure the amount of information that their elements have about each other. Often, such analysis is done by using a well-known quantity from classical information theory, mutual information, and its various derivations, which measure statistical dependencies between a pair of random variables. These measures are particularly useful because of their sensitivity to both linear as well as nonlinear interactions between random variables. Among other things, they allow one to quantify the amount of information that is stored [1], transferred [2,3,4,5] and modified [6] in different parts of the system.

However, only measuring the information that is processed between two sub-components is rather restrictive. Indeed, even the simplest of logic gates has more elements, being composed of a pair of inputs and an output, which statistical dependencies we are interested to characterize. While one could consider the inputs as a single sub-component, this would not capture the intricate interactions among the inputs themselves. In particular, components in the input ensemble can provide information uniquely, redundantly, or synergistically about the output [7].

To capture this distribution of information between two inputs and a single output, an extension to classical information theory is needed [7]. Recently, several axiomatic frameworks have been developed to account for such extension and they are often referred to as partial information decomposition (PID) [7,8,9,10,11]. For a review of the uses of partial information decomposition in Neuroscience, see [12,13]. In this article, we capitalize on a recently developed numerical estimator for PID [14] for a particular version of PID [8], and use it to characterize the emergent dynamics of several complex systems (2D Ising model and 1D cellular automata) in terms of the information distribution across their interacting sub-units.

The remaining of this article is organized as follows. In the Background sections, we give a brief overview of partial information decomposition including its numerical estimation, as well as the basics of Ising and elementary cellular automata models. The Methods section details both the numerical simulation and PID analyses for both systems. The Results section describes the results of applying the PID estimator to the dynamics of neighboring cells in the Ising model and elementary cellular automata. We conclude by discussing the implications of the obtained results and related work, as well as the limitations of applying the current approach to other systems such as artificial neural networks, and provide suggestions for future work.

2. Background

2.1. Partial Information Decomposition

Mutual information measures the amount of information two random variables, or more generally, two random vectors have about each other. However, it is often worthwhile to ask how much information an ensemble of input (source) random variables carries about some output (target) variable. A trivial solution would be to measure the mutual information between the whole input ensemble considered as a single random vector and the output. However, this would not capture the interactions between the input variables themselves. Moreover, by considering the input ensemble as a single unit, knowledge about how the interactions between specific individual units and the output differ is lost.

This section briefly reviews the partial information decomposition proposed by [8]—a specific mathematical framework for decomposing mutual information between a group of input variables and single source variable.

2.1.1. Formulation

The simplest non-trivial system to analyze that has an ensemble of inputs and a single output is a system with two inputs. Given this setup, one can ask how much information one input variable has about the output that the other does not, how much information they share about the output, and how much information they jointly have about the output such that both inputs must be present for this information to exist.

More formally, let Y and Z be two random variables that are considered as sources to a third random variable X. The mutual information between the pair $(Y,Z)$ and X is defined in terms of entropies as

$$MI(X;Y,Z)=H\left(X\right)-H\left(X\right|Y,Z).$$

The partial information decomposition framework aims to decompose this mutual information into unique, redundant and complementary information terms.

Unique information quantifies the amount of information that only one of the input variables has about the output variable. The unique information that Y has about the output X is denoted as $UI(X:Y\backslash Z)$. Similarly, $UI(X:Z\backslash Y)$ denotes the unique information that Z has about the target X.

Shared information quantifies the amount of information both inputs share about the output variable. It is also sometimes called redundant information because, if both inputs contain the same information about the output, it would suffice to observe only one of the input variables. The shared information is denoted as $SI(X:Y;Z)$. (To be consistent with “Elements of Information Theory”, the notation used in this article for PID terms deviates a little from the one introduced by Bertschinger et al. [8]. Specifically, a colon (:) is used to partition the set of random variables to a single output (on the left-hand side) and a set of inputs (on the right-hand side). As before, a semicolon (;) is used to separate the input variables on the right-hand side, signifying that these variables are considered to be separate entities, not part of a single random vector.)

Complementary or synergistic information quantifies the amount of information that is only present when both inputs are considered jointly. The complementary information is denoted as $CI(X:Y;Z)$.

It is generally agreed [7,8,9,10] that mutual information can be decomposed into the four terms just described as follows:

$$MI(X;Y,Z)=SI(X:Y;Z)+UI(X:Y\backslash Z)+UI(X:Z\backslash Y)+CI(X:Y;Z).$$

(1)

The same sources also agree on the decomposition of information that a single variable, either Y or Z, has about the output X:

$$\begin{array}{c}MI(X;Y)=UI(X:Y\backslash Z)+SI(X:Y;Z),\hfill \\ MI(X;Z)=UI(X:Z\backslash Y)+SI(X:Y;Z).\hfill \end{array}$$

(2)

It is important to note that thus far in this section, no formulas for actually calculating the PID terms have been given, and only several relationships that such a decomposition should satisfy have been stated. The only computable quantities so far are the mutual information terms on the left-hand side of Equations (1) and (2). The discussion of computing the specific PID terms is developed in the next section, which is heavily inspired by an intuitive overview of the paper “Quantifying Unique Information” by Bertschinger et al. [8], provided by Wibral et al. [13].

2.1.2. Calculating PID Terms

It turns out that the current tools from classical information theory—entropy and various forms of mutual information—are not enough to calculate any of the terms of the PID [7]. Indeed, there are only three Equations (1) and (2) relating to the four variables of interest, making the system undetermined. In order to make the problem tractable, a definition of at least one of the PID terms must be given [8].

Taking inspiration from decision theory, Bertschinger et al. [8] were able to provide such a definition for unique information. Their insight was that, if a variable contains unique information, there must be a way to exploit it. In other words, there must exist a situation such that an agent having access to unique information has an advantage over another agent who does not possess this knowledge. Given such a situation, the agent in possession of unique information can prove it to others by designing a bet on the output variable, such that, on average, the bet is won by the designer.

In particular, suppose there are two agents, Alice and Bob, Alice having access to the random variable Y and Bob having access to the random variable Z from Equation (1). Neither of them have access to the other player’s random variable, and both of them can observe, but not directly modify, the output variable X. Alice can prove to Bob that she has unique information about X via Y by constructing a bet on the outcomes of X. Since Alice can only directly modify Y and observe the outcome X, her reward will depend only on the distribution $p(X,Y)$. Similarly, Bob’s reward will depend only on the distribution $p(X,Z)$. From this, it follows that the results of the bet are not dependent on the full distribution $p(X,Y,Z)$, but rather only on its marginals $p(X,Y)$ and $p(X,Z)$.

Let $p\equiv p(X,Y,Z)$ be the original joint probability distribution that we are interested in computing the PID of, and let $\Delta$ be the set of all joint probability distributions of X, Y and Z. Under the assumption that the unique information depends only on the two marginal distributions of p, a set of probability distributions ${\Delta }_p$ can be defined such that the unique information stays constant for any element in this set. Such a set consist only of the probability distributions that have the same marginal distributions of the pairs $(X,Y)$ and $(X,Z)$ as p. It is defined as follows:

$$\begin{array}{c}{\Delta }_p=\{q\in \Delta :q(X=x,Y=y)=p(X=x,Y=y)\\ \mathrm{and}q(X=x,Z=z)=p(X=x,Z=z)\mathrm{for}\mathrm{all}x\in X,y\in Y,z\in Z\}\end{array}$$

Putting the observation that unique information is constant on ${\Delta }_p$ and Equation (2) together, it becomes apparent that shared information will also be constant on ${\Delta }_p$. Thus, only complementary information varies when considering arbitrary distribution q from ${\Delta }_p$. The last observation makes sense intuitively and is to be expected, since “complementary information should capture precisely the information that is carried by the joint dependencies between X, Y and Z” [8].

Using the chain rule for information as well as decompositions (1) and (2), the following identities can be derived:

$$\begin{array}{c}MI(X;Y|Z)=UI(X:Y\backslash Z)+CI(X:Y;Z),\hfill \\ MI(X;Z|Y)=UI(X:Z\backslash Y)+CI(X:Y;Z).\hfill \end{array}$$

(3)

Now, if a distribution $q_0\in {\Delta }_p$ could be found that yields vanishing synergy, the unique information could be calculated using quantities from classical information theory. Indeed, from Equation (3), it can be seen that when synergy is 0, the mutual information and unique information terms coincide. Bertschinger et al. [8] prove that a distribution $q_0\in {\Delta }_p$ with this property only exists for specific measures of unique, shared and complementary information. They define the suitable measure for unique information as follows:

$$\widetilde{UI}(X:Y\backslash Z)=\underset{q\in \Delta p}{min}M{I}_q(X;Y|Z),$$

(4)

$$\widetilde{UI}(X:Z\backslash Y)=\underset{q\in {\Delta }_p}{min}M{I}_q(X;Z|Y),$$

(5)

where the subscript q under the mutual information symbol means that the quantity is calculated over the distribution q.

Replacing these measures with the corresponding quantities in Equations (1) and (2), measures for shared and complementary information can be defined as follows:

$$\widetilde{SI}(X:Y;Z)=\underset{q\in {\Delta }_p}{max}M{I}_q(X;Y)-M{I}_q(X;Y|Z),$$

(6)

$$\widetilde{CI}(X:Y;Z)=MI(X;Y,Z)-\underset{q\in {\Delta }_p}{min}M{I}_q(X;Y,Z).$$

(7)

These four constrained optimization problems (Equations (4)–(7)) are all equivalent in the sense that it would suffice to solve only one of these problems and the obtained optimal joint distribution q would produce the optimal value for all the remaining three measures as well.

2.1.3. Numerical Estimator

Bertschinger et al. showed that “the optimization problems involved in the definitions of $\widetilde{UI}$, $\widetilde{SI}$ and $\widetilde{CI}$ … are convex optimization problems on convex sets” [8]. A notable property of convex functions is that their local and global minimums coincide, making the optimization problems that involve such functions relatively easy to solve. Indeed, many effective algorithms have been developed that solve even large convex problems both efficiently and reliably [15].

However, in this particular case, the convex optimization problem is not trivial because “the optimization problems … can be very ill-conditioned, in the sense that there are directions in which the function varies fast, and other directions in which the function varies slowly [8].” This means that there exists extremely small eigenvalues in the positive definite matrix that needs to be inverted as part of the convex optimization procedure, making the method numerically unstable. To tackle this problem in [14], the optimization problem is analyzed in detail and found that the problematic issues occur mostly at the boundary of the feasible region. Hence, the authors proposed and compared several versions of interior point methods to provide a fast estimator of PID terms together with a certificate of its approximation quality.

The analyzed numerical estimator takes the approach of solving the optimization problem given in Equation (7) and then using the resulting distribution q to find the other quantities of interest. The user interface of the estimator is rather simple, abstracting away all the technical details of its inner workings: it takes as input a probability distribution $p(X,Y,Z)$ and outputs the scalars $MI(X;Y,Z)$, $UI(X:Y\backslash Z)$, $UI(X:Z\backslash Y)$, $SI(X:Y;Z)$ and $CI(X:Y;Z)$. For all of the analyses conducted, the convex program is solved in CVXOPT [16] ,using an interior point method. When the interior point method failed to converge, we refined the solution by solving iteratively the Karush–Kuhn–Tucker equations of the program until a desired level of tolerance was reached. See [14] for a detailed study of the performance of different algorithms to solve the optimization problem in Equation (7).

2.2. Ising Model

The Ising model, first conceived by Wilhelm Lenz in 1920 [17], is a mathematical model of ferromagnetism. The model abstracts away the rather complex details of atomic structures of magnets, consisting simply of a discrete lattice of cells or sites, denoted as $s_i$, each of which has an associated binary value of either −1 or +1 [18]. Conceptually, the lattice can be thought of as a physical material, where the sites roughly represent the unpaired electrons of its atoms. The binary value of each site intuitively corresponds to the direction of the electron’s spin. A value of −1 means that the spin is considered to point down, otherwise it is said to be pointing up. A given set of spins, denoted as $\mathit{s}$ (without the subscript), is called the configuration of the lattice [18].

The probability of a configuration $\mathit{s}$ at thermal equilibrium is given by the Boltzmann distribution:

$$P_{\beta }\left(\mathit{s}\right)=\frac{e^{-\beta E\left(\mathit{s}\right)}}{{\sum }_{\mathit{s}}{e}^{-\beta E\left(\mathit{s}\right)}},$$

(8)

where the sum in the denominator is over all possible spin configurations, $E\left(\mathit{s}\right)$ denotes the energy associated with the configuration $\mathit{s}$, and $\beta =\frac{1}{k_{B}T}$, where T is the temperature and $k_B$ is the Boltzmann constant. Thus, $\beta$ is proportional to the inverse temperature of the system.

The probability of a configuration $\mathit{s}$ depends on two quantities: the internal energy of the configuration under discussion, and the temperature. Two observations that stem from Equation (8) are of importance. First, the lower the energy $E\left(\mathit{s}\right)$ of a configuration $\mathit{s}$, the higher its probability. Second, the higher the temperature T (or equivalently, the lower the parameter $\beta$), the more diffuse the distribution becomes. The latter mathematical property models the physical fact that, at high temperatures, the thermal “oscillation” of the atoms break the alignment of the spins, demagnetizing the material.

Assuming that the external magnetic field interacting with the lattice is omitted, and the interaction strength between pairs of nearest neighbors is fixed to be equal to the Boltzmann constant $k_B$, the energy of a spin configuration $\mathit{s}$ simplifies to

$$H\left(\mathit{s}\right)=-\sum _{\langle ij\rangle }{s}_i{s}_j,$$

(9)

where the sum is over all different nearest neighboring pairs of spins (each pair counted only once). The minus sign in front of the sum accounts for a lower energy state (and, thus, with a higher probability) is achieved when neighboring spins take on the same value, as this yields a positive product. It can be intuitively thought as if the spins are intrinsically trying to align with their neighbors, while the temperature of the system quantifies the amount of prohibition that prevents them from doing so.

The Ising model in two or more dimensions exhibits a second order phase transition with a critical temperature $T_c$ such that, for temperatures $T<T_c$, the expected magnetization (net alignment of spins) quickly rises to be different from zero. The Ising model is thus a prototypical example of many complex systems exhibiting collective order even under the constant presence of a source of disorder.

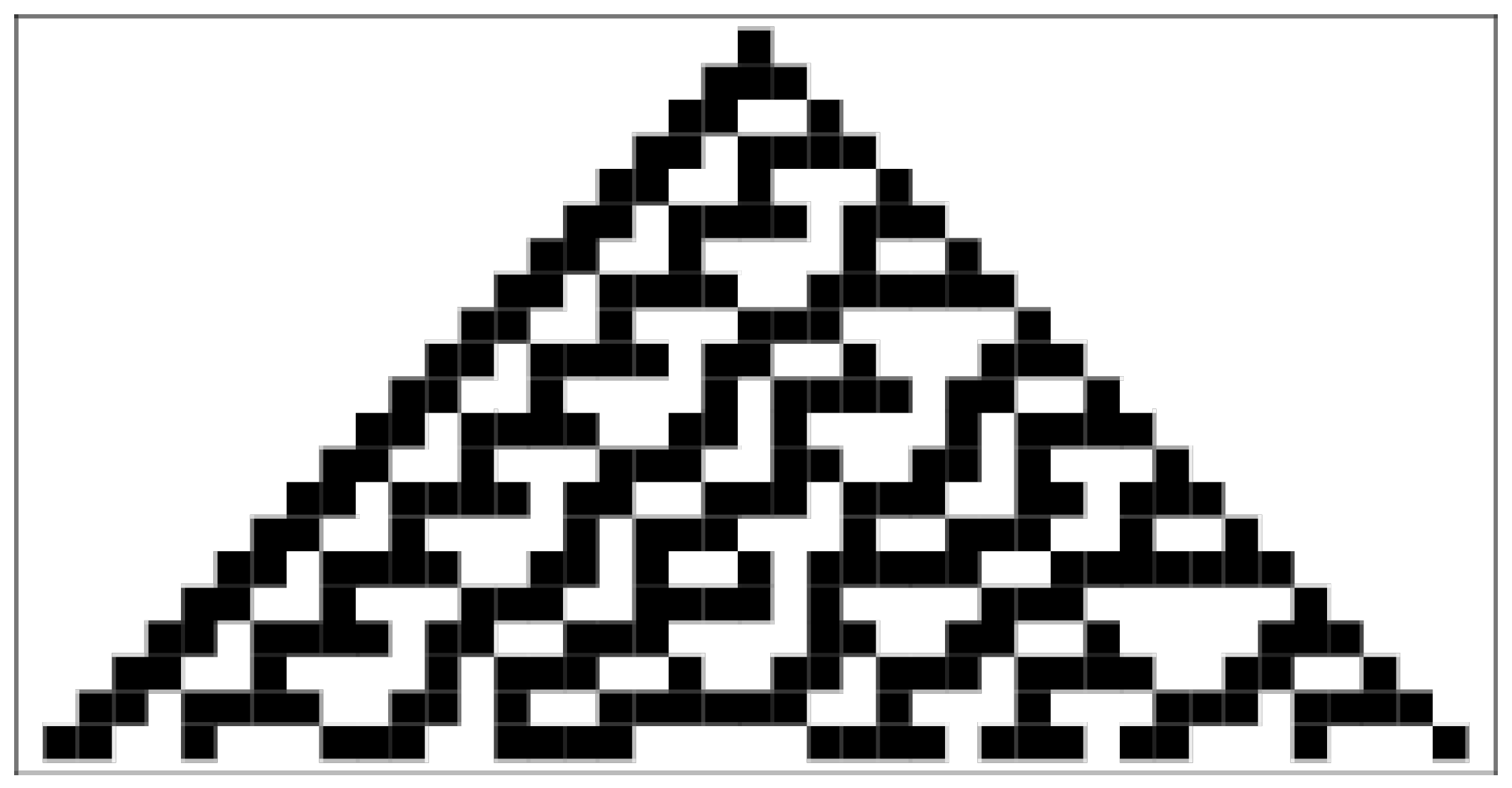
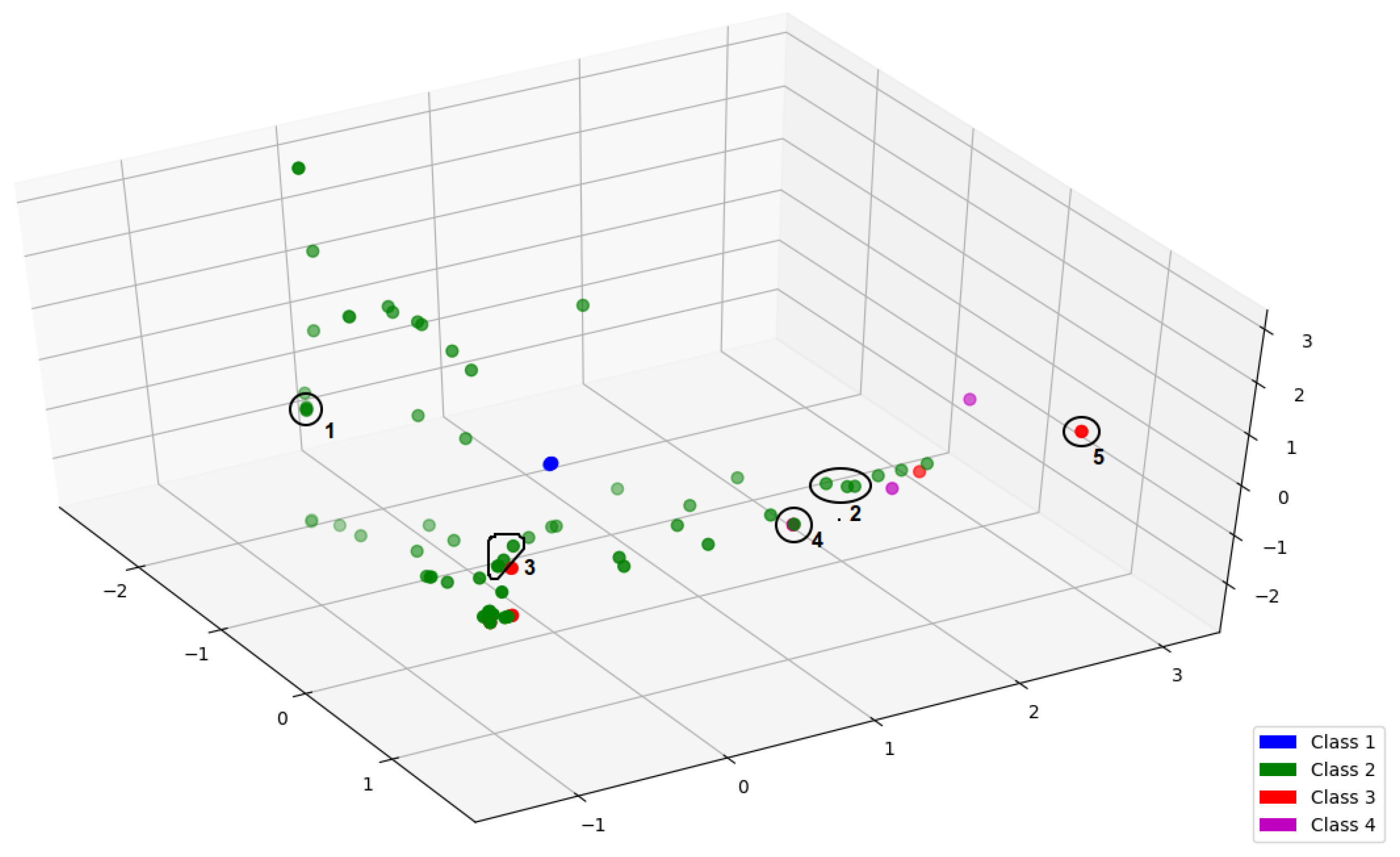
2.3. Elementary Cellular Automata

Elementary cellular automata (ECA) are discrete dynamical complex systems that consist of a one-dimensional array of cells, each of which has an associated binary value. Every automaton is uniquely defined by its rule table—a function that maps the value of a cell to a new value based on the cell’s current value and the values of its two immediate neighbors. Since each rule table corresponds to a unique 8-bit binary number, there are only $2^8=256$ elementary cellular automata in total, each of which is associated with a unique decimal number from 0 to 255.

Elementary cellular automata can be simulated in time by simultaneously applying the update rule to each cell in the one-dimensional array, producing a two-dimensional plot where the vertical axis represents time. The result of evolving the rule 30, given an initial lattice configuration of all white cells except the center, can be seen in Figure 1. Notably, the figure shows that the evolution of the dynamics can be rather non-trivial. Indeed, cellular automata are interesting precisely because, despite their simplicity, the patterns that emerge as a function of the rule table and the initial configuration can be quite complex. For example, elementary cellular automata have been shown to be capable of generating random numbers [19], modelling city traffic [20] and simulating any Turing machine [21]. On the other hand, many rules quickly converge into an uninteresting homogeneous or repetitive state.

Because the set of all elementary cellular automata is rather diverse, consisting of both computationally interesting as well as uninteresting rules, it would make sense to try to group them based on the apparent complexity of their behaviour. In his seminal paper “Universality and Complexity in Cellular Automata” [23], Stephen Wolfram did just that.

After qualitatively analyzing the global structures that the different rules give rise to, given random initial states, Wolfram proposed a classification scheme that partitions all elementary cellular automata into four classes. The proposed classes are as follows:

• Class 1: Cellular automata that converge to a homogeneous state. For example, rule 0, which takes any state into a 0 state, belongs to this class.
• Class 2: Ceullar automata that converge to a repetitive or periodic state. For example, rule 184, which has been used to model traffic, belongs to this class.
• Class 3: Cellular automata that evolve chaotically. For example, rule 30, which Mathematica uses as a random number generator [24], belongs to this class.
• Class 4: Cellular automata in which persistent propagating structures are formed. For example, rule 110, which is capable of universal computation, belongs to this class. It is conjectured that other rules in this class are also universal.

3. Methods

3.1. Methodology for Analyzing the Ising Model

To estimate the PID terms in the Ising model, a two-dimensional model with Glauber dynamics [25], periodic boundary conditions and a square lattice of size 128 × 128 was simulated. A single simulation consisted of a burn-in period of ${10}^4$ updates, followed by ${10}^5$ updates from which the samples were gathered. As in the paper by Barnett et al. [26], “each update comprised L (potential) spin-flips according to Glauber transition probabilities”, where L is the size of the lattice. Hence, the probability to accept a transition is given by

$$P(\mathit{s}\to {\mathit{s}}_{\mathit{n}})=\frac{1}{1+e^{\frac{\Delta E(\mathit{s}\to {\mathit{s}}_{\mathit{n}})}{T}}},$$

(10)

where $\mathit{s}$ and ${\mathit{s}}_{\mathit{n}}$ denote the old and new lattice configurations, respectively, T stands for temperature and $\Delta E(\mathit{s}\to {\mathit{s}}_{\mathit{n}})=E\left(\mathit{s}\right)-E\left({\mathit{s}}_{\mathit{n}}\right)$ is the difference between the energies of the two successive configurations.

In other words, using Algorithm 1 as a subprocedure, the model was simulated according to Algorithm 2 with $B={10}^4$, $N={10}^5$ and $L=128\times 128$. This procedure was performed at 102 temperature points spaced evenly over the interval [2.0, 2.8], which encloses the theoretical phase transition at $T_c\approx 2.269$.

Algorithm 1: A single Glauber dynamics update, which consists of L spin-flip attempts

Algorithm 2: The full Glauber dynamics algorithm

The obtained ${10}^5$ lattice configurations at each temperature point were subsequently used to construct the probability distributions that the PID estimator takes as input. One-hundred sites were chosen uniformly at random at the beginning of the simulation, and they stayed the same for all temperature points. Figure 2 illustrates the 100 randomly chosen sites of the $128\times 128$ lattice. For each site, the relative frequency of the spin configurations of its local neighborhood (the site itself along with four of its neighbors) was measured, yielding a total of 100 joint probability distributions of five random variables per temperature point. An example of one such distribution at temperature $T\approx 2.119$ is given by

Table 1. Joint probability distribution of a random site and its four neighbors at temperature $T\approx 2.119$. The column labels represent the location of the sites with respect to the neighboring center (C) site: upper (U), right (R), down (D), left (L).

C	U	R	D	L	Pr
−1	−1	−1	−1	−1	0.004
−1	−1	−1	−1	1	0.002
−1	−1	−1	1	−1	0.003
−1	−1	−1	1	1	0.003
..	..	..	..	..	..
1	1	1	−1	1	0.035
1	1	1	1	−1	0.033
1	1	1	1	1	0.776

, where the first random variable C represents the center site, and the following four random variables represent its immediate neighbors. For example, the last row of the table illustrates that the configuration where all the spins point upwards at a specific location on the lattice has a probability of $0.776$, meaning that it appears approximately $0.776\times {10}^5$ = 77,600 times out of a total of ${10}^5$ configurations sampled. The high probability of “all aligned” spins is to be expected, since the samples are taken while the Ising model is in the ordered, low temperature regime.

Having created 100 probability distributions for each of the 102 temperature points, it remains to feed the distributions into the PID estimator for analysis. However, this can not be done naively with the current setup, as the estimator works with probability distributions of 3 random vectors only, where one of them is thought of as an output and the remaining as inputs. Thus, the distributions of the same form as the one in Table 1 must be reconfigured such that they are understood by the estimator, i.e., it must be decided how neighboring sites are partitioned into 2 sets of inputs and an output. Two different setups were considered. First, the center site was taken to be the output, and only 2 neighbors were chosen without repetitions uniformly at random (out of the possible set of 4 neighbors) as inputs. Second, the center was again considered as an output, but, in this experiment, all 4 neighbors were taken into consideration as inputs: the full set of neighbors was randomly partitioned into 2 disjoint pairs, such that each pair was a two-dimensional random vector. After estimating the PID terms, an arithmetic mean across the sites was taken at each temperature point, yielding 102 average PID vectors, one for each temperature point.

Due to the randomness present in the Glauber dynamics and in choosing the 100 sites from the lattice for analysis, the results may vary across different runs. To gain more confidence in the results, the whole experiment described above (simulating the Ising model, choosing 100 random sites for analysis, estimating the PID of the local neighborhood of the sites) was repeated 8 times and the results averaged. In the very first run, each initial spin configuration was initialized randomly at each temperature point as in line 2 of Algorithm 2, and the configuration that was arrived at after the burn in period of ${10}^4$ updates was saved. For the subsequent 7 runs, the very first lattice configuration for temperature point $T_i$ was chosen to be equivalent to the saved lattice configuration from the very first run at temperature point $T_i$. After doing the first run separately to obtain the initial configurations, the 7 remaining simulations to gather the relevant lattice configurations were run for 8 days on 41 computing nodes in parallel in a computer cluster.

3.2. Methodology for Analyzing the Elementary Cellular Automata

The average information distribution was estimated in all 88 inequivalent elementary cellular automata. (While there are 256 different rules in total, some of them are computationally equivalent. In particular, exchanging the roles of black and white in the rule table and reflecting the rule through a vertical axis does not change the computational capabilities of the automaton. Not considering rules that are equivalent under these transformations yields 88 rules that are of interest). To gather the probability distributions for the PID estimator, 88 automata with ${10}^4$ cells were simulated for ${10}^3$ time steps using periodic boundary conditions. For each automaton, a random initial configuration was generated, such that each cell at time step $t=0$ was associated with a value taken uniformly at random from the set $\{0,1\}$.

The input pair for the PID was taken to be the cell’s 2 neighbors (considered as a single random vector) and the cell itself at time step t, while the output was the cell’s value at the next time step $t+1$. This is indeed a logical setup to use, as it ensures that the input set contains all the variables that the output is a function of. Using these random variables, a single global distribution was generated for each rule. Note that this differs from the methodology that was used in the case of the Ising model, where a subset of the sites was chosen for analysis, yielding 100 different local distributions and PID values, the latter of which were subsequently averaged to obtain estimates of the global measures.

Because the emergent dynamics of a cellular automaton depend on the initial configuration of the lattice, the above experiment (generating initial configurations for each of the 88 automata, simulating the dynamics and generating the distribution that is fed into the estimator) was repeated 5 times, after which the resulting 5 PIDs of each rule were averaged.

4. Results

Next, we provide the results of applying a PID estimator to the dynamics of neighboring units in two different complex systems. The focus of the first section is on the Ising model, while the second concentrates on elementary cellular automata.

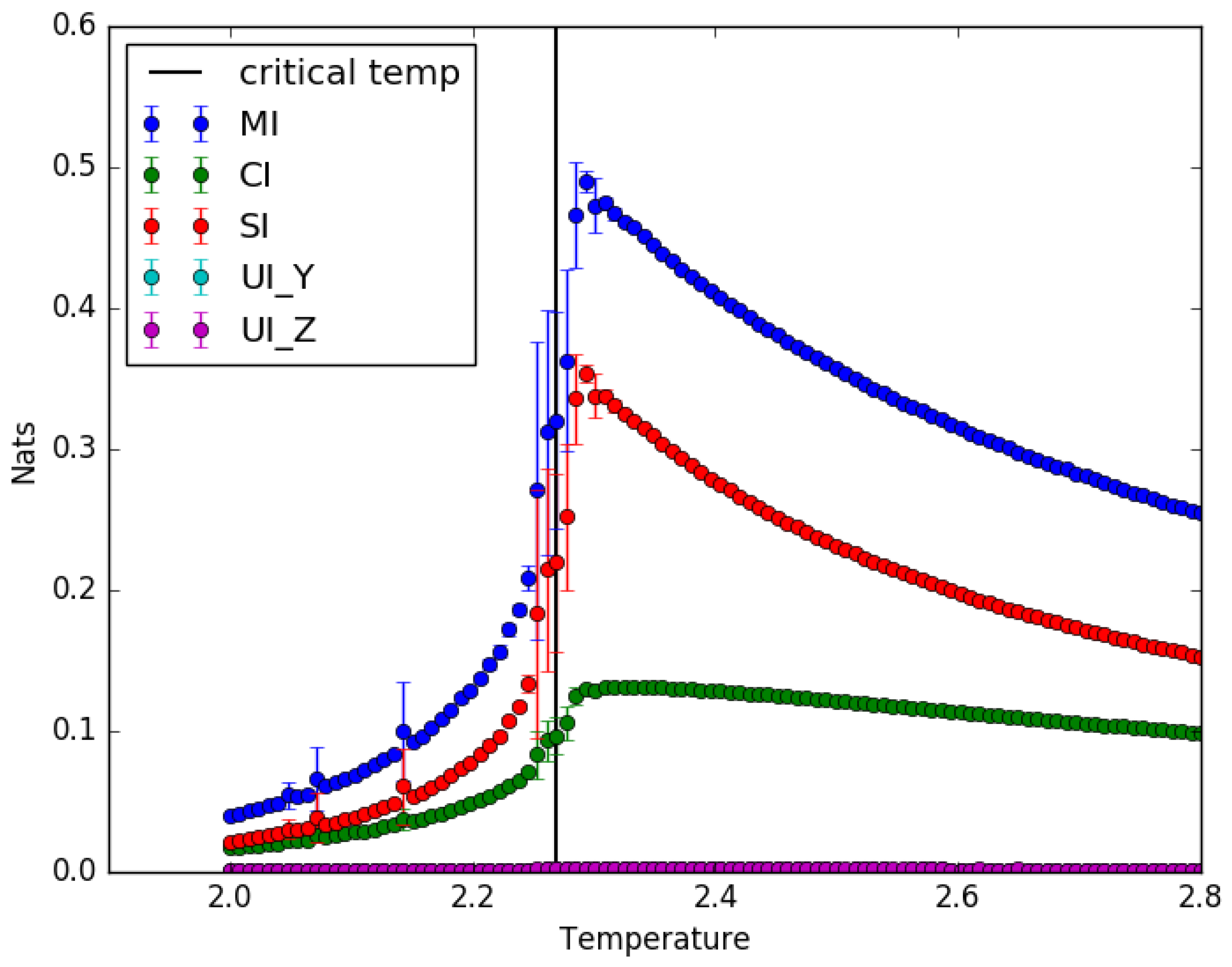
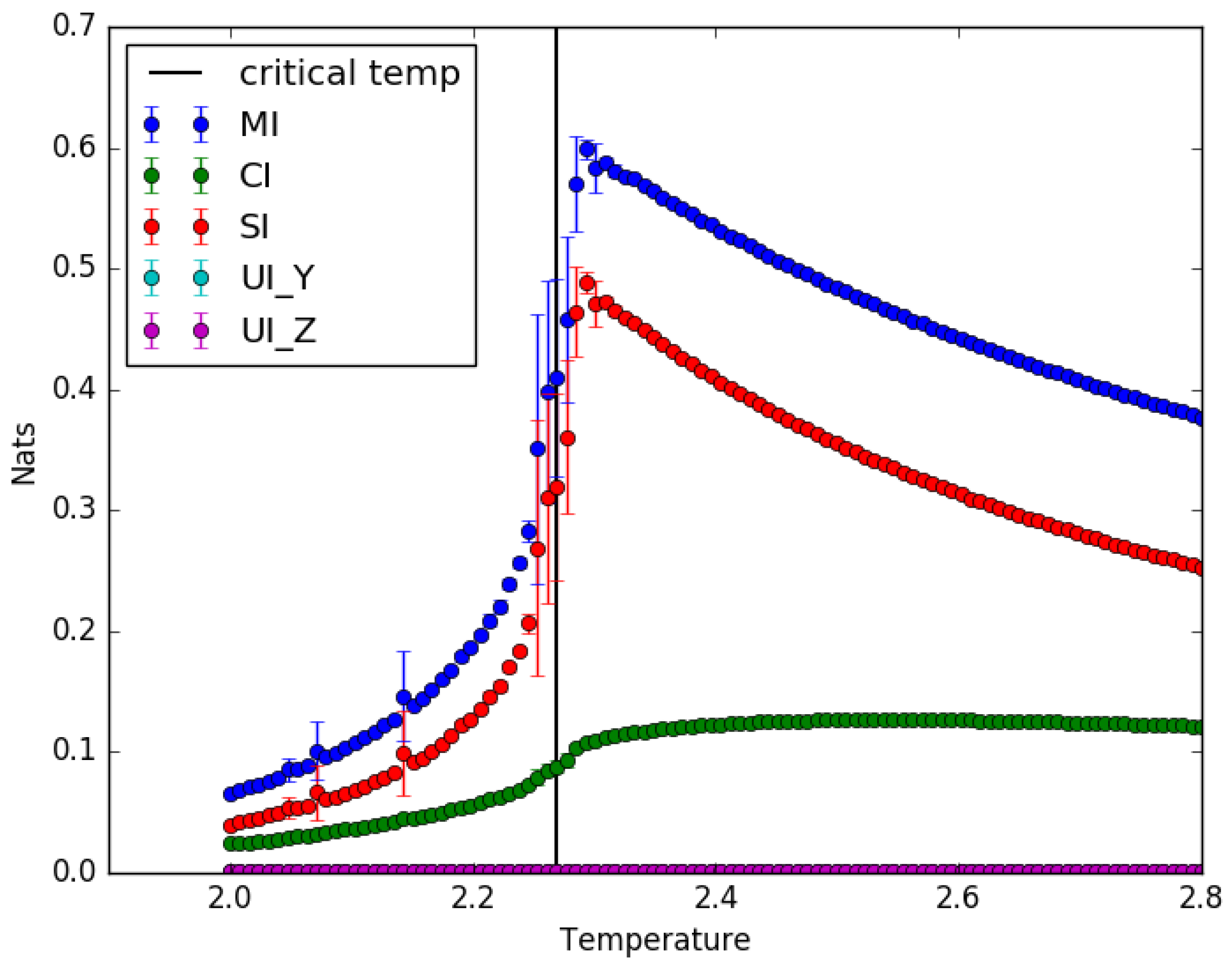
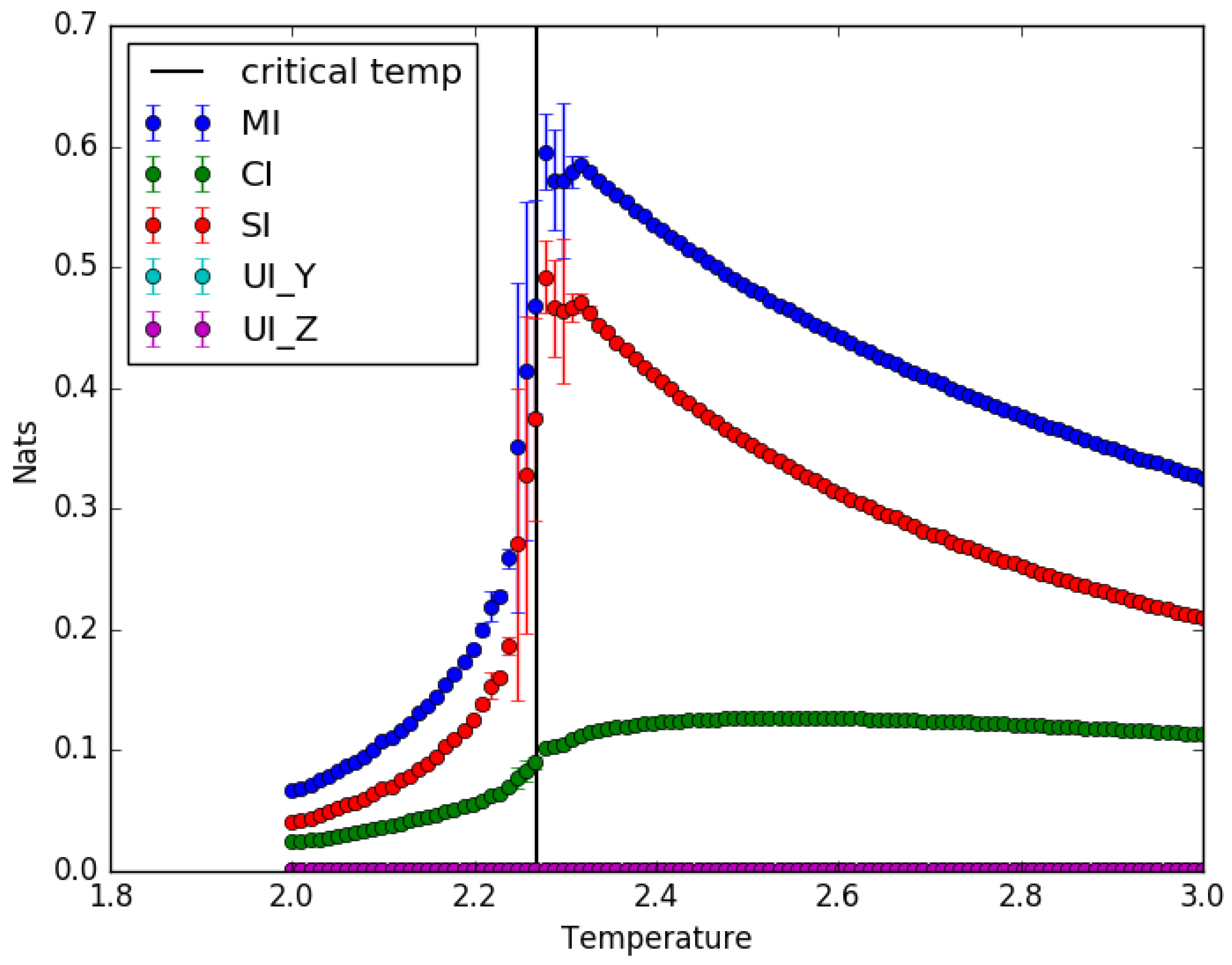
4.1. Ising Model: Partial Information Decomposition as a Function of Temperature

First, we consider the case in which the partial information decomposition is evaluated for triplets of neighboring spins in the lattice. In Figure 3, the average mutual information and PID terms are given as a function of the temperature.

As seen from the figure, mutual information peaks around the phase transition (more precisely, at $T\approx 2.293$)—a phenomenon that agrees with previous theoretical and numerical work [26]. In addition, since, in the experiment under discussion, the mutual information was measured between a site and two of its neighbors, as opposed to measuring it between two neighboring sites only, it would be reasonable to expect the resulting mutual information to be higher in the current experiment. Indeed, two neighbors should have more information about their center site than a single neighbor has. Barnett et al. [26] observed that the mutual information between two neighboring sites (the quantity $I_{pw}$ in the paper) achieves a maximum value of less than $0.3$. In agreement with intuition, the blue graph representing mutual information in Figure 3 achieves a peak value of just under $0.5$.

Observing the partial information decomposition terms of the Ising model in Figure 3, one can see that the non-zero terms seem to peak around the phase transition, just as mutual information itself does. Shared information is the most dominant of the partial information decomposition near the phase transition (before and after) and it reaches its maximum at the critical point. Indeed, shared information follows a curve similar to the mutual information, with the exception of being shifted downwards about $0.15$ nats for temperatures near the phase transition. The synergistic information as a function of temperature follows a different graph with noteworthy differences. First, numerically, it peaks slightly before mutual information does at $T\approx 2.333$. In addition, its overall behaviour also deviates from that of mutual information, with the graph being quite a bit flatter, not exhibiting a sharp peak.

The unique information terms are always near 0, no matter which neighbor is considered. First, it is reasonable that both of the unique information terms are identical, as the neighbors are chosen randomly. Second, the fact that there is no unique information in the system is also intuitively plausible, as each neighbor interacts with the center site in an identical fashion. Indeed, from corollary 8 in [8], a symmetry in the probability distributions $p(X,Y)=p(X,Z)$ between the two inputs Y and Z ensures that both unique information terms should be identically zero. This symmetry between two random neighbors in a 2D Ising model is expected to be maintained across all temperatures unless the neighboring sites would belong to different frozen clusters, which is a negligible event. Moreover, all computations of PID are averaged over many different sites.

In Figure 4, the results of measuring information-theoretic functionals between the center sites and all of their neighbors are illustrated. As expected, the mutual information term increases in value (about $0.1$ nat at the critical point) compared to Figure 3 because, considering all four of the sites that interact with the center site, as opposed to just two, should reduce the amount of uncertainty one has about the center. Further inspection reveals that the PID term most responsible for the increased mutual information is shared information. The complementary and unique information terms have roughly the same values in both experiments. Specifically, at all temperature points, unique information terms are 0 and synergistic information varies around $0.1$ nats in the disorder regime.

An unanticipated difference between the first (two neighbors) and second (four neighbors) experiment is that, when all neighbors are considered, the synergistic information term is flatter than before and peaks even deeper in the disorder phase, at temperature $T\approx 2.554$, while shared information does not change its maximum point across the two experiments.

As for the behaviour of synergistic information, we do not have an analytical explanation for the observed phenomenon. That said, it is possible that it is related to the peak of global transfer entropy (a form of conditional mutual information) in the disorder phase of the Ising model, as demonstrated by Barnett et al. [26]. According to Equation (3), when unique information vanishes, synergy becomes equal to conditional mutual information as well. However, the exact relationship between the synergy and transfer entropy in the Ising model remains unclear, as the random variables considered as arguments to the conditional mutual information functional in this paper do not correspond to the ones used by Barnett et al.

To confirm that the observed phenomena are not specific to a lattice of size 128 × 128, but are general characteristics of the computational properties of the Ising model, the simulations were repeated with a smaller, 64 × 64 lattice. The experimental setup was analogous to the one used in the previous experiments, with the exception that the measurements were averaged over six different runs (instead of eight) and, for each run, 50 different random sites were chosen for PID analysis (instead of 100). The simulations were run on 102 temperature points spaced evenly over the interval [2.0, 2.8].

Figure 5 depicts the results when only two random immediate neighbors are considered as input to the center site in the PID framework. Although the mutual, shared and synergistic information graphs are more shaky at the phase transition due to random fluctuations, in general, the graphs are almost identical to the corresponding graphs in Figure 3. The mutual and shared information quantities peak at $T\approx 2.277$, while synergistic information peaks at $T\approx 2.327$.

The results of measuring PID terms when all neighboring sites are considered as inputs to the center site are illustrated in Figure 6. Both mutual and shared information again peak at $T\approx 2.277$. Complementary information peaks at $T\approx 2.515$, a little closer to the phase transition than was the case when the lattice size was twice the size (Figure 4). This observation validates that the peak in synergy does not gradually move closer to the phase transition with increasing lattice sizes, suggesting that it could be a general property of the model.

4.2. PID of Elementary Cellular Automata

In Figure 7, all 88 inequivalent elementary cellular automata have been depicted based on their PID terms. Each point represents a single rule, and the points are colored according to their Wolfram’s class. Because there are four terms in PID, principal component analysis was used to project the four-dimensional PID vectors into three-dimensional space. It is important to explicitly mention that some “points” in the plot are actually clusters of several rules, but, due to their almost identical PID terms, they overlap with each other, yielding a single visual mark on the plot. For example, the cluster numbered as 1 appears to be a single point, but there are actually five different rules present at this location.

From the figure, it can be seen that the rules corresponding to Wolfram’s class I are all clustered together in a single location separate from the rest of the automata. This is natural, as these class I rules quickly converge to a homogeneous all-white state, such that there is no uncertainty left in the system. In an all-white state, the entropy of the system is 0 implying that mutual information, and, accordingly, all of the PID terms to be 0 as well. While various other clusters appear, they do not correspond well to Wolfram’s three other classes, meaning that there is no straightforward relationship between Wolfram’s classification and the information distribution in elementary cellular automata.

To further investigate this claim, we show the distribution of PID values across Wolfram’s classes in Figure 8. From Figure 8a, it can be seen that, in general, the synergy goes up when the complexity of the automata in terms of Wolfram’s classification increases. However, there are many outliers in the second class and the variance of the third class is extremely high, making it hard to further draw any specific conclusions. On average, shared information seems to be higher in class 2 automata, while it is almost 0 for the majority of class 3 and 4 automata. Focusing on the last two panels (Figure 8c,d), it shows that, for these rules, two neighbors at the previous time step have usually more information about a cell’s value at current time step than its own previous value does.

In Figure 9, the top panels show the space-time diagrams of two different rules, where the dynamics were generated using random initial states. The two considered automata belong to Wolfram’s second class because they quickly converge into a repetitive state. The diagrams look very alike visually as well, containing densely populated diagonal lines. It would not be unreasonable to expect these rules to be clustered together in Figure 7. Interestingly, however, these rules are partitioned into two different clusters that are spaced far apart from each other. In particular, rule 6 (and similarly rules 38 and 134) appears in cluster 2, while the automaton 130 (and similarly rules 24 and 152) belong to cluster 3. At first glance, this partitioning might be rather confusing, but the solution to the conundrum becomes apparent when one zooms in on the space-time diagrams. As can be seen from the bottom panels in Figure 9, the intricate structure of the diagonal lines is different between rules 6 and 130. It turns out that rules such as 6, 38 and 134 all have diagonal lines that are composed of small “inverted L” type blocks, while the diagonals of rules 130, 24, and 152 are much simpler, having a thickness of just a single cell. More generally, the PID terms seem to depend heavily on the specific local details of the emergent repeating, ubiquituous patterns in the space-time diagrams of cellular automata.

To better understand why the specific details of the diagonals yield a radical change in the PID terms, a closer quantitative look at the PID of the rules under discussion is in order. The mutual information of all of the six rules is almost exclusively divided between synergy and the unique information provided by the neighbors, leaving the remaining PID terms close to 0. The first three rules each have roughly about $0.55$ nats of synergy and $0.25$ nats of unique information. In contrast, the last three rules have no complementary information, but their neighbors have about twice as much unique information about the cell’s next state, approximately $0.62$ nats each. Thus, almost all of the information in the systems with simpler diagonals is provided uniquely by the neighbors of a site.

The former numeric observations are not surprising because, looking at the dynamics of rule 130 from Figure 9d, the new states are almost always uniquely determined by the neighbors alone. Indeed, the ubiquitous white background arises mainly because, if the right neighbor of a cell is white, this cell’s next value will also be white. If, however, the left neighbor is white and the right is black, the cell’s next state will be black. The latter relationship produces the diagonals. In the case of rule 6, there is a lot more synergy in the system because neither the cell’s previous state or the neighbors are able to produce the complex “reversed L” shaped diagonals alone. The rather high unique information comes from the fact that the left neighbor being black completely determines that the cell’s value will be white in the next step.

Some other clusters are not as straightforward to analyze, but, nevertheless, in many cases, it is still possible to give some intuitive justifications of the characterization that the PID has produced. For example, Figure 10 depicts the rules in cluster 4, which all have exactly $0.5$ nats of synergy and $0.5$ nats of unique information from the neighbors. While the automata look rather different from the distance, zooming into the lattices again reveals the similarities. Looking at the zoomed space-time diagrams in Figure 11, it can be seen that what the automata under observation have in common is that they all contain rather complex stairway-like structures traveling from the upper right to the lower left.

Another noteworthy collection of rules is cluster 5, which consists of three automata that Wolfram has classified as chaotic. All the automata belonging to this cluster have 1 nat of mutual information, which is all exclusively provided by complementary information. The cluster is interesting because it shows that, at least for some subset of automata, their qualitative characterization coincides with the quantitative one provided by the PID.

5. Discussion

This section starts by putting the results obtained in the two complex systems into a larger context and by discussing their implications. The possibility of analyzing other dynamical complex systems with the information-theoretic tools used in this article is critically examined in the second section. Finally, we will conclude with several suggestions for further work.

5.1. Implications of the Results

In the paper “Information flow in a kinetic Ising model peaks in the disordered phase” [26], it is shown that global transfer entropy peaks in the disorder phase in the Ising model, just before the phase transition. This result might suggest the possibility that global transfer entropy might be used as an indicator of an impending phase transition before it actually takes place. In a subsequent commentary discussing this work [27], Lionel Barnett, one of the authors of the paper, argues that this result might also generalize to other real-world dynamical complex systems that undergo phase transitions. The practical importance of this could be high as a predictor of imminent phase transitions, but it needs to be tested in practice with real data.

In this article, it was found that one of the PID terms, complementary information or synergy also obtains a maximum in the disorder regime in the Ising system. Taking the commentary by Barnett into account, it would be worthwhile to study various real-world systems near phase transitions in terms of partial information decomposition. In particular, it would be interesting to measure the synergy between various components with the hope of predicting the arising phase transition in advance.

As for elementary cellular automata, the obtained characterization of the rules based on the PID can be a complementary perspective to Wolfram’s classification. Wolfram’s classification relies largely on human intuition and was developed by qualitatively analysing the space-time diagrams of all elementary cellular automata. In contrast, the characterization based on partial information decomposition is automatic and more grounded theoretically, not relying on qualitative observations. While Wolfram’s classification is able to differentiate between different automata based on the global behaviour of the emergent structures, it is agnostic to the subtle details in the structures themselves. As for the characterization based on the PID terms, the opposite seems to be true.

5.2. Related Work

There is a large body of previous work in applying information theory to analyze dynamical complex systems that undergo phase transitions. Specifically, it has been shown that mutual information and other related information-theoretic measures peak at the critical point where the systems undergo an order–disorder transition. Such is the case for several mathematical models like random Boolean networks [28] and Vicsek’s self-propelled particle model [29].

As for real-world systems, Harre and Bossomaier [30] measured mutual information between pairs of selected stocks and found that the peaks in information take place around known market crashes. In another paper [31], to better understand phase transitions in cognitive behaviours, the same authors analyzed mutual information between successive moves in the game of Go as a function of players’ skill level. They found that information peaks around the transition from amateur to professional, “agreeing with other evidence that a radical shift in strategic thinking occurs at this juncture” [32].

Particularly relevant to the work at hand is the above-mentioned information-theoretic analysis of the Ising model. It has been analytically shown that, in a two-dimensional Ising model, the mutual information between joint states of two spin systems peaks at the critical temperature [33]. Barnett et al. [26] show empirically that mutual information measured between pairs of neighboring spins peaks at the phase transition. In the current paper, this result is replicated and extended by also measuring the decomposition terms of this mutual information. They further discovered that another related quantity called global transfer entropy peaks strictly in the disorder phase before the phase transition.

Not directly related to this article, but contextually rather relevant, are various works that have made use of information theory to quantitatively validate long-held hypotheses about information storage and transfer in elementary cellular automata. In the article “Local measures of information storage in complex distributed computation” [1], Lizier et al. found quantitative evidence that specific structures in elementary cellular automata called blinkers and background domains are “dominant information storage processes in these systems.” In another closely related paper [34], the same authors conclude that “local transfer entropy provides the first quantitative evidence for the long-held conjecture that the emergent traveling coherent structures known as particles … are the dominant information transfer agents in cellular automata.”

Of particular interest to this paper is the work done by Chliamovitch et al. [35], in which the behaviour of multi-information, a generalization of mutual information to multiple variables, in elementary cellular automata was studied. It was found that, while it could be possible to establish a classification of cellular automata rules based on this measure, it would not correspond with Wolfram’s four classes. This is because multi-information failed to discriminate between all pairs of Wolfram’s classes except between classes I and IV.

5.3. Limitations

The two complex systems analyzed in this paper have an important property in common that makes their investigation with PID estimators very convenient, not to say possible. First, they are both binary, meaning that the individual elements of the systems can only be in two different states. Second, in both systems, each local part of the model is directly influenced by only a handful of other agents. Indeed, in the Ising model, the energy of a single site depends only on the spins of its four immediate neighbors, while the next value of a cell in elementary cellular automata is determined by the three cells in its local neighborhood. What follows is a discussion of why both of these characteristics are paramount to successful analysis of information distribution in complex systems.

First, the systems being binary, or more generally, discrete with relatively few possible states, ensures that the number of rows in the probability distribution that the PID numerical estimator takes as input is relatively small. The number of rows of the distribution increases polynomially in the number of states of the random variables that it contains. For example, a distribution with three random variables with 20 possible states would have 8000 rows. Such a large distribution is challenging for the numerical estimators we used, and the version at the moment we conducted this research was able to handle distributions with roughly 2500 rows. This challenge also can arise when the analyzed system has continuous elements, since a naive discretization strategy, or, in other words, dividing the continuous signal into a finite number of different states, will result in a large number of number of states. To analyze the performance of the estimator on discretized versions of continuous signals, a multivariate Gaussian probability distribution was generated, discretized, and fed into the estimator. The convergence of this discretization approach together with the study of the optimization challenges in the numerical estimators of PID are presented in [14].

Second, the systems having few directly interdependent components again ensures that the number of rows in the distributions is relatively small, the latter increasing polynomially in the number of random variables that the three random vectors contain. There is, however, an even more fundamental problem that has nothing to do with the numerical estimator, but rather with the fact that the PID mathematical framework has currently been developed for two logical input sets only. In particular, if the number of inputs in the system grows, and they are not naturally divisible into two distinct sets, it becomes increasingly hard to reasonably choose the two subsets of input channels. Even if the input space is composed of two logical sets, taking only a small subset of components from each might not yield desirable results. This is because there is exponentially many ways to choose the subsets with respect to each other, and there is often no straightforward way to know which configuration is the “right” one.

To better understand the argument put forth in the last paragraph, it is instructive to look at the results of another preliminary experiment that was carried out as part of this research. In particular, the average information distribution between the nodes in a feed-forward neural network was analyzed while it was trained on a classification task. The model consisted of two hidden layers, each containing 300 neurons. While such models usually have continuous activation functions, it is not feasible to discretize these continuous signals with fine enough granularity without making their analysis with the estimator unfeasible. Thus, binary activations were used in the hidden layers of the network, as introduced by Courbariaux et al. [36]. The output layer of the network consisted of softmax units. The network was trained on the MNIST handwritten digit database [37] for 150 epochs. The training and validation learning curves of this classifier exhibited smooth decaying graphs saturating at certain base levels.

To estimate the information distribution in the system, 200 triplets were taken for analysis. For each triplet, the two inputs were taken to be two random nodes from the last hidden layer of the network, and the output was taken to be the true target decimal value. The 200 probability distributions were subsequently fed into the PID numerical estimator and the results averaged. This procedure was repeated for each epoch, but the 200 triplets remained the same throughout the experiment.

We observed that the mutual information behaves similarly to the reflection of the training loss over the horizontal axis. This agrees with the observation made in Bard Sorngard’s master’s thesis “Information Theory for Analyzing Neural Networks” [38], in which the mutual information between the neurons in a toy neural network was measured during training. We also observed that the unique information terms follow the mutual information curve almost exactly, and that complementary and redundant information terms are both essentially 0. It is the authors’ belief that the PID terms are rather uninteresting largely because the inputs do not come from two logically distinct subsystems (especially given the limitation that we used a PID framework so far restricted to characterize the information relations between one output and two input variables). Every neuron in the last layer has 299 neighbors, and there is no fundamental reason to prefer one neighbor over the other. This illustrates some challenges in finding a natural partition of a complex system in meaningful triplets of random variables to which one could apply most of the current versions of partial information decomposition.

5.4. Future Work

There are various promising research directions in the domain of partial information decomposition itself. First, the mathematical framework of partial information decomposition used here has so far been developed for the bivariate input case. The general decomposition of multi-variate information remains to be further developed, and it is expected to open the door to a refined characterization of information distribution in many classes of complex systems not considered in this article.

In the case of the Ising model, it might be of interest to study more theoretically how information is distributed between the different parts of the model. This would provide some further insight as to why the PID functionals behave as they do in this specific model. In addition, the results obtained in the Ising system should inspire further research into real-world complex systems in which it would be of importance to predict the occurrence of a phase transition in advance.

A system of major importance in which Ising models have been shown to be a good fit is the dynamics of ganglion cells in the vertebrate retina [39]. This system has been extensively researched as an excellent model to study neuronal population codes. In particular, a pressing question is to what degree these neurons code visual information in a redundant or independent manner, a question that can be directly addressed by the framework analyzed here.

In this paper, elementary cellular automata were studied, in which, by definition, each cell is directly influenced by only three cells in its local neighborhood. However, these relatively simple systems are just a special case of a larger class of models, called one-dimensional cellular automata, where cells can depend on an arbitrary fixed number of nearby cells. It is up to further work to study the information distribution in cellular automata that are not elementary. Das et al. [40] used genetic algorithms to discover different rules that are able to perform specific computational tasks, like classifying whether the majority of cells in the initial configuration have a value of 1. It could be worthwhile to study the information distribution in different automata that solve common tasks.

Finally, there is more work to be done in analyzing the information distribution in artificial neural networks. The PID measurements obtained from analyzing feed-forward neural networks in this work were uninteresting largely because there was no natural partitioning of nodes belonging to the same layer in this model. However, such a partitioning does exist in recurrent neural networks, where each neuron has both bottom-up inputs from the previous layer and lateral contextual inputs from the same layer at the previous time step. Applying the current numerical estimator to recurrent networks can prove to be difficult, however, as for the authors’ knowledge, there is no existing work validating that binarizing the activations of a recurrent network yields a reasonable model.

More generally, we consider that, provided a meaningful partition of nodes in the network and armed with multivariate approaches [41,42], the concepts and tools from information theory can play an important role in characterizing and bringing a novel perspective on the training of neural networks.

6. Conclusions

Most of this paper is devoted to applying PID to empirically analyze the distribution of information in two well-known dynamical complex systems.

First, it was observed that complementary or synergistic information peaks in the disorder regime of the Ising model. If such phenomenon is to be generalizable to other phase transitions, this result could be of practical value. Second, a novel quantitative characterization of elementary cellular automata based on information distribution was obtained. The proposed characterization is complementary, and orthogonal, to the popular qualitative classification proposed by S. Wolfram. Third, feedforward neural networks were found to be difficult to characterize in information distribution terms within the current bivariate PID framework. Some more promising research directions in the study of neural networks and information dynamics include recurrent neural networks and multivariate formulations of PID.