Modal Strain Energy-Based Debonding Assessment of Sandwich Panels Using a Linear Approximation with Maximum Entropy
Abstract
:1. Introduction
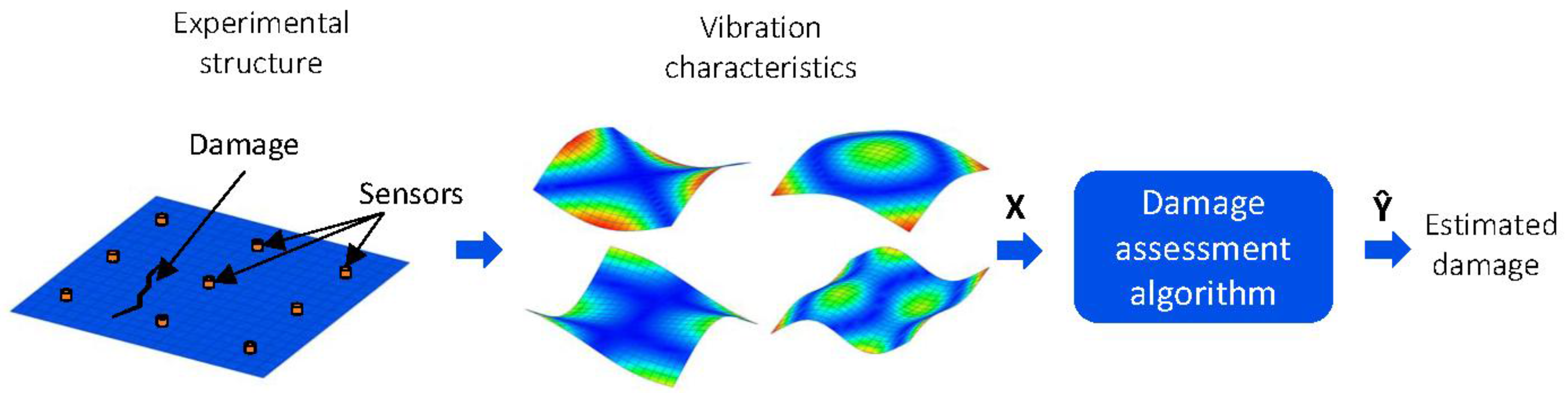
2. Damage Assessment Algorithm
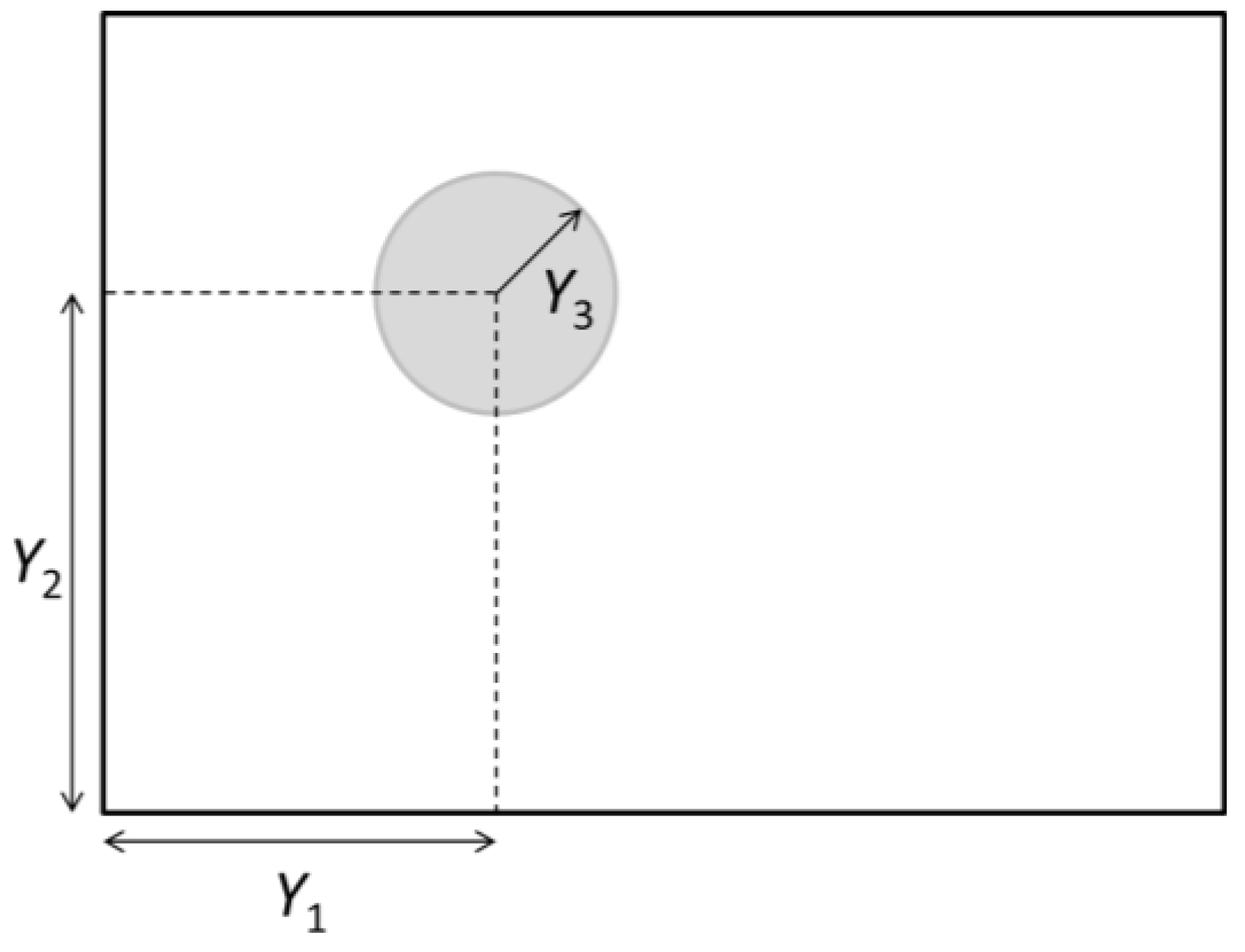
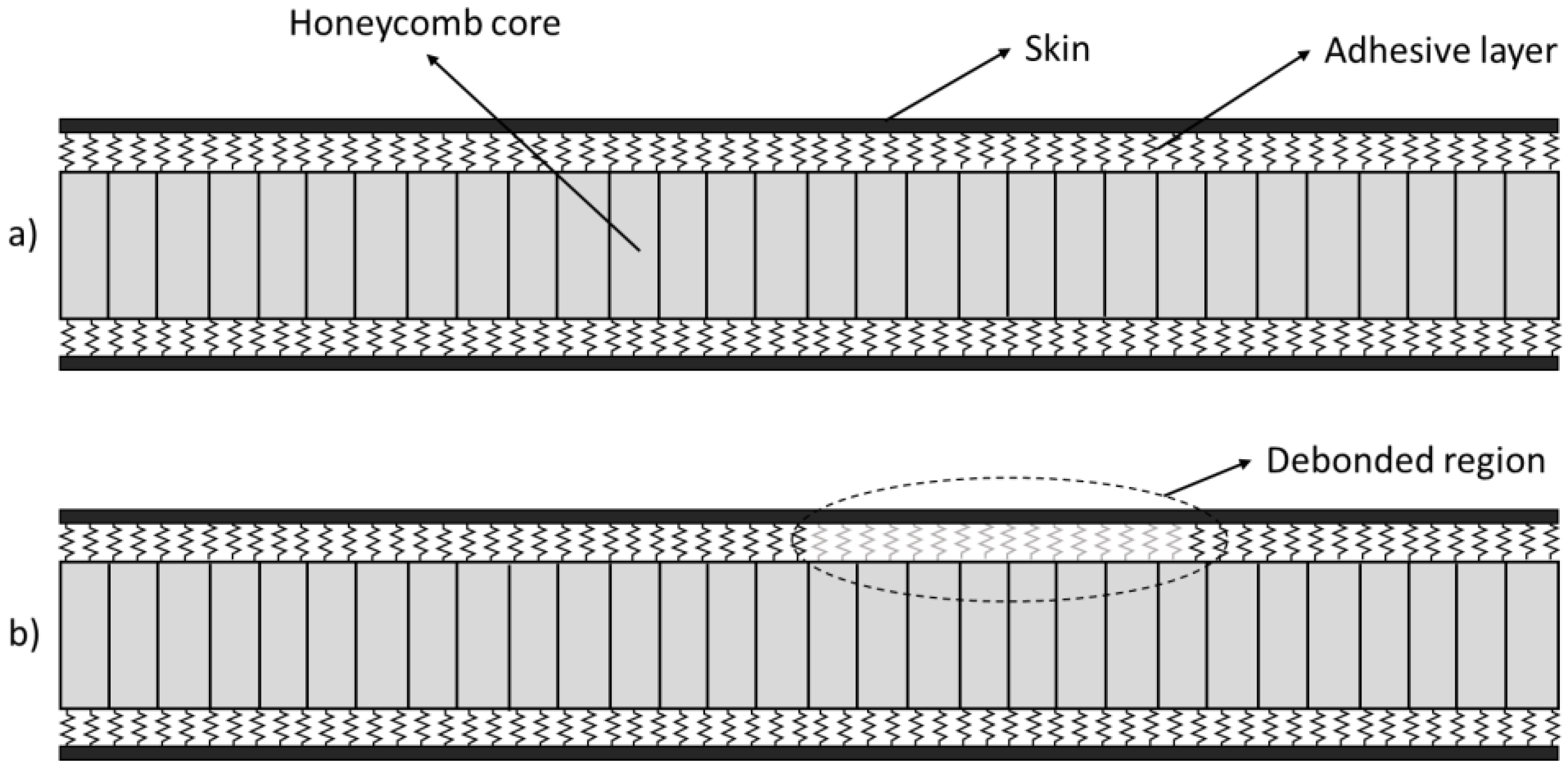
2.1. Damage Parameterization
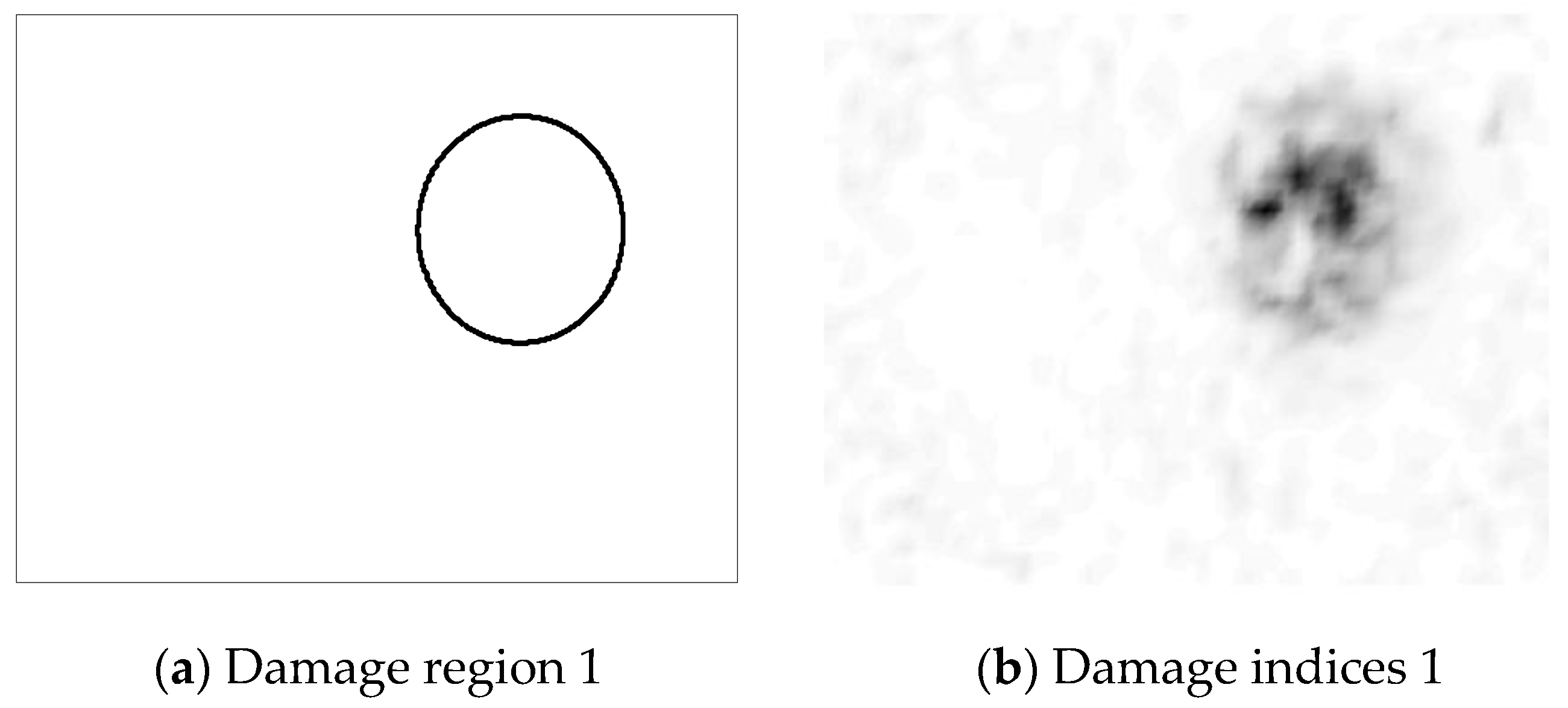
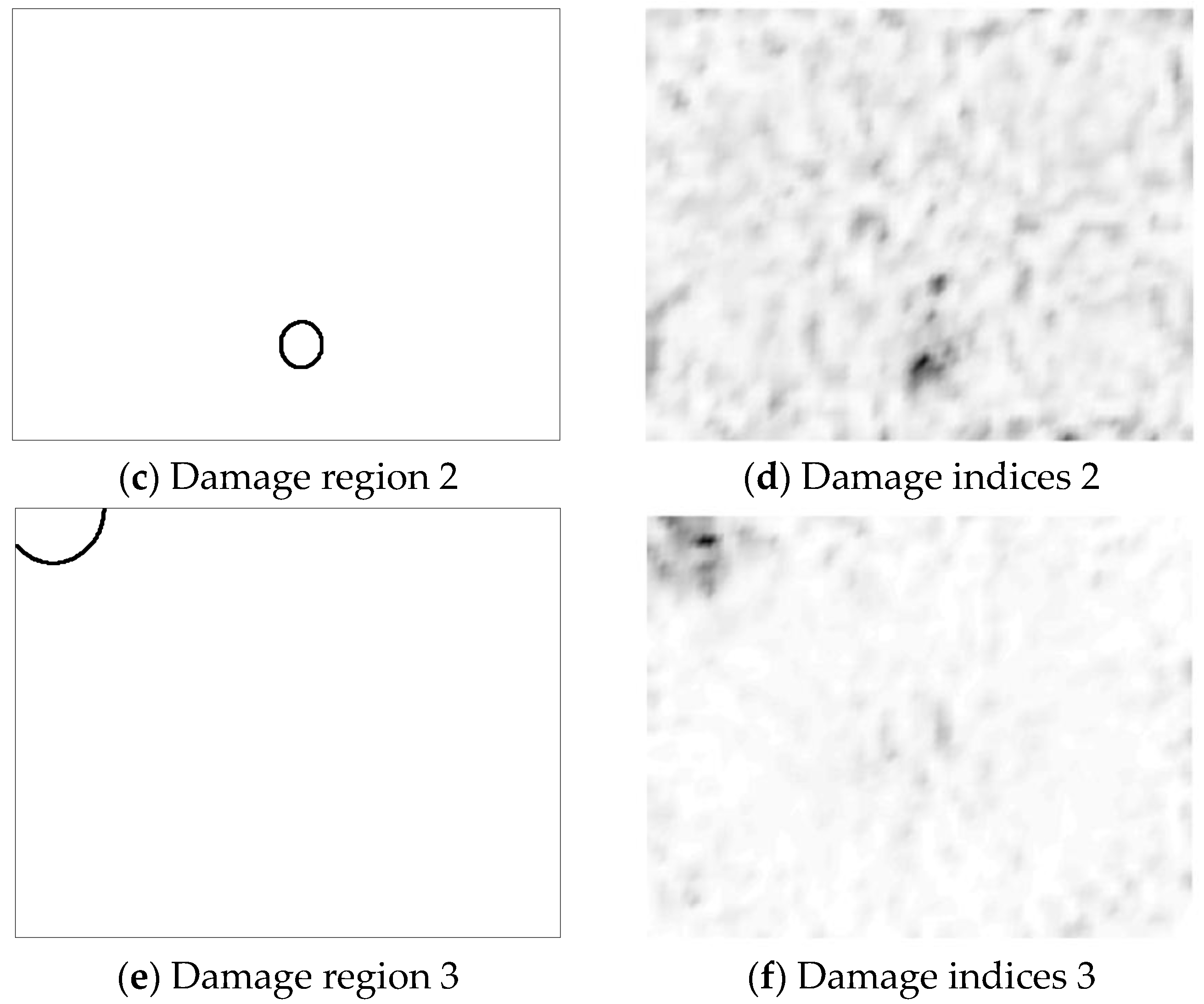
2.2. Damage Indices
2.3. Principal Component Analysis
2.4. Kernel PCA
2.5. Linear Approximation with Maximum Entropy (LME)
3. Methodology
3.1. Building of the Databases
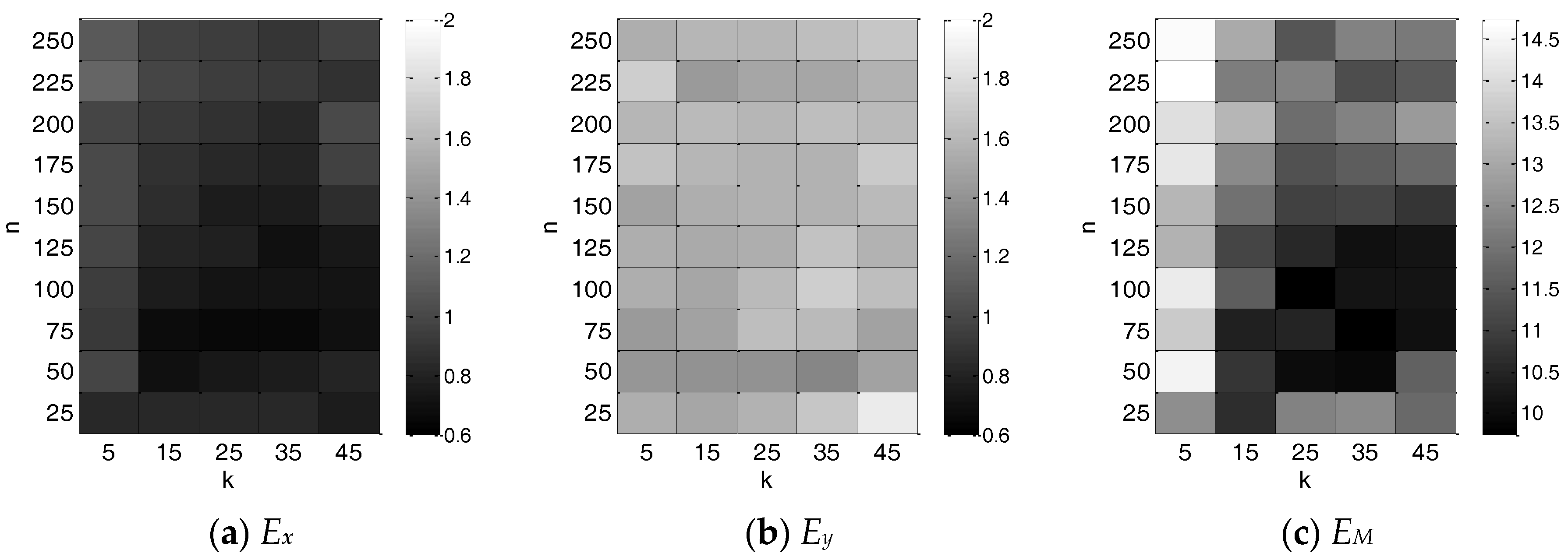
3.2. Selection of Parameters
3.3. Evaluation of the Algorithm
- (1)
- Extraction of a feature vector from the testing database.
- (2)
- Selection of the parameter in Equation (27), so that k neighbors contribute to the solution.
- (3)
- Solving of the system of nonlinear equations presented in Equation (30).
- (4)
- Computation of the weight functions using Equation (28).
- (5)
- Localization and quantification of the damage using Equation (23).
- (6)
- Computation of the localization and quantification errors using Equations (31)–(33).
- (7)
- Repetition of Steps 1–6 for all the feature vectors in the testing database.
3.4. Experimental Validation
4. Application Case
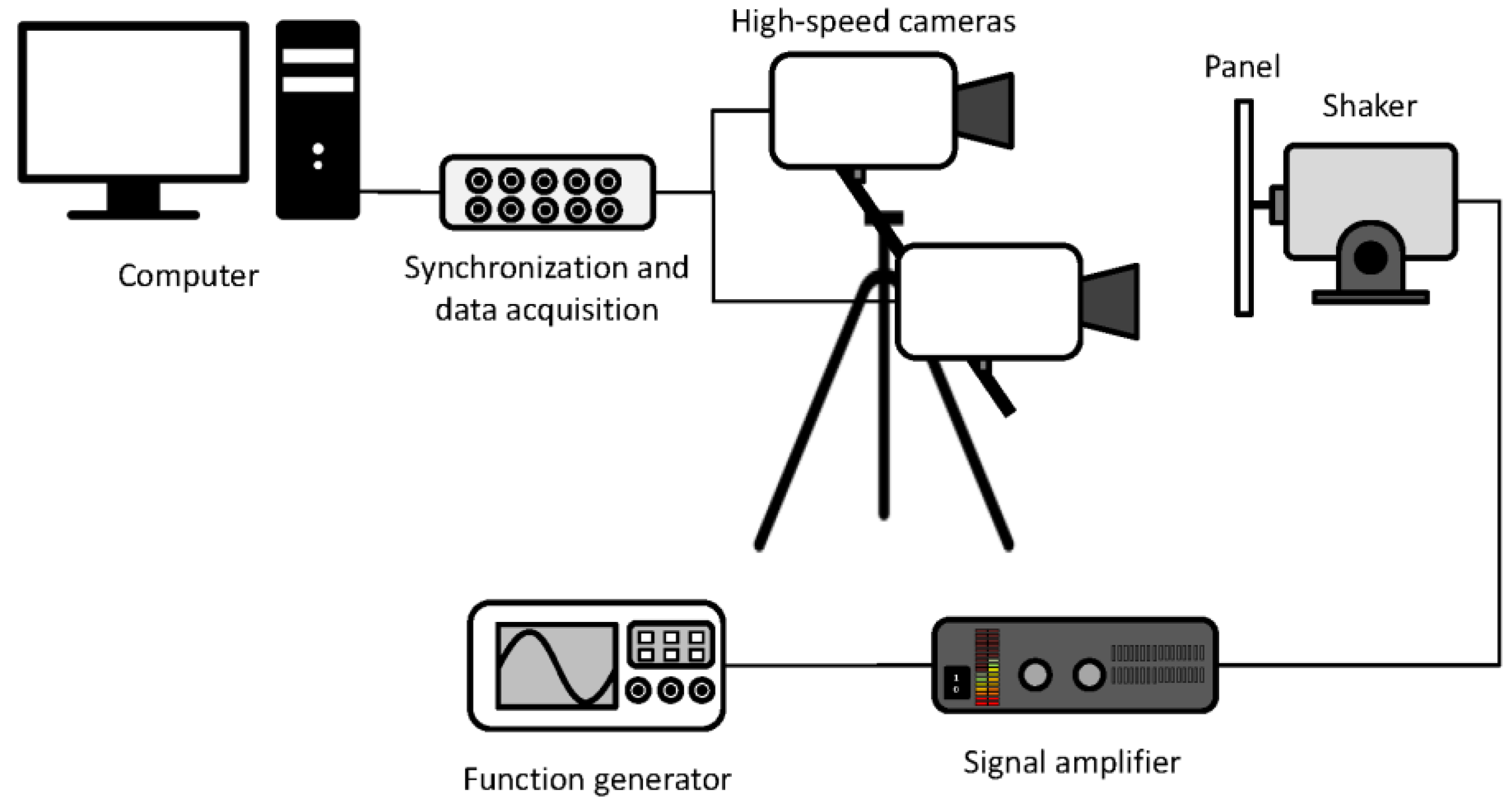
4.1. Experimental Measurements
- First, the panel is excited in different points by an impact hammer and the response is captured by a miniature accelerometer. The experimental data are processed to obtain the frequency response functions (FRFs) from which the natural frequencies are identified by peak-picking.
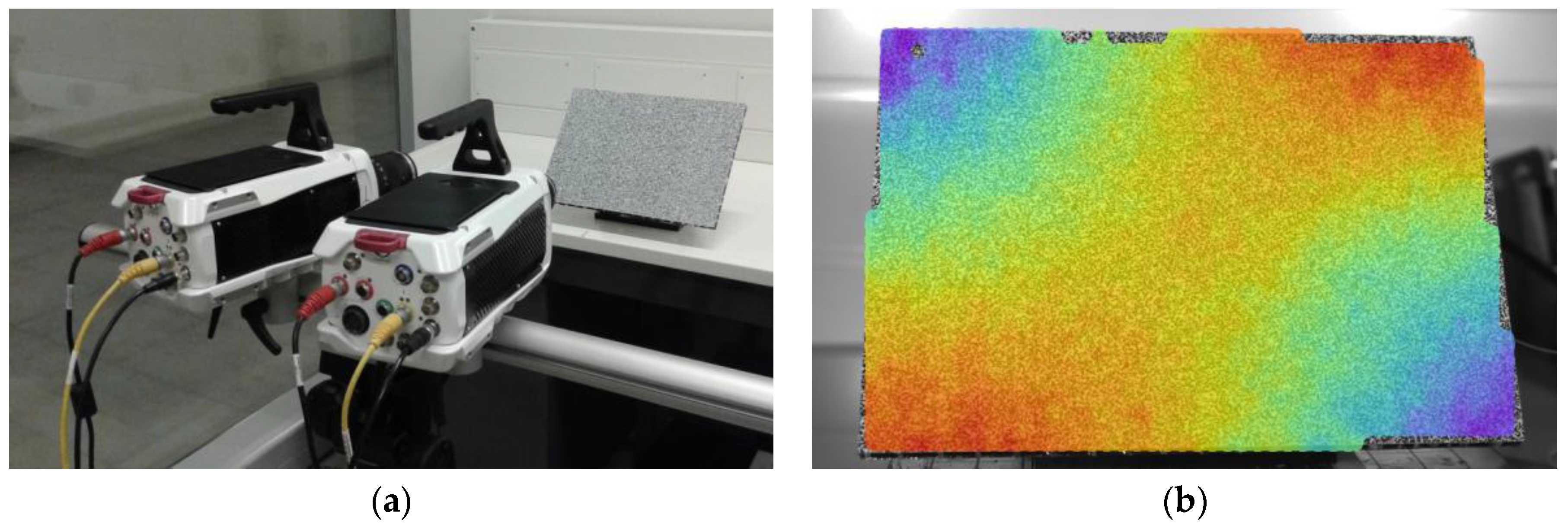
- A speckle pattern is added to the panel by means of an adhesive sheet. This pattern provided by Dantec Dynamics has been optimized for DIC measurements. The cameras are calibrated and the image correlation parameters are selected to minimize the experimental error, following the recommendations given by Siebert et al. [55].
- In the case of high-speed DIC measurements, single-frequency excitation has shown to be the best method to identify experimental mode shapes [48,56]. Therefore, to identify mode shapes the shaker excites the panel with a sinusoidal vibration tuned at a natural frequency, causing the panel to vibrate in resonance. Images are captured at a rate of 5 kHz with a resolution of 1024 × 1024 pixels. Figure 4 show the vibration measurements with the high-speed DIC system and a vibration mode shape at 444 Hz.
- The experimental displacements are exported in hdf5 files, which are imported into Matlab. The Fourier transform of the displacements is computed and then the amplitude at the resonance frequency is recorded at each point. With this information, the operational mode shape at the resonant frequency is reconstructed.
- Finally, the smoothing technique proposed by Garcia [21] is applied to reduce the experimental noise and to complete missing information in the mode shapes. Figure 5 and Figure 6 present the first six experimental model shapes for the undamaged and damaged panels. In both cases it is possible to see the effect of the shaker attachment in the middle of the panel. As expected, most of the natural frequencies of the damaged case are lower than the undamaged case. Regarding the mode shapes, the largest differences are found in the modes with higher frequencies.
4.2. Numerical Model
5. Results
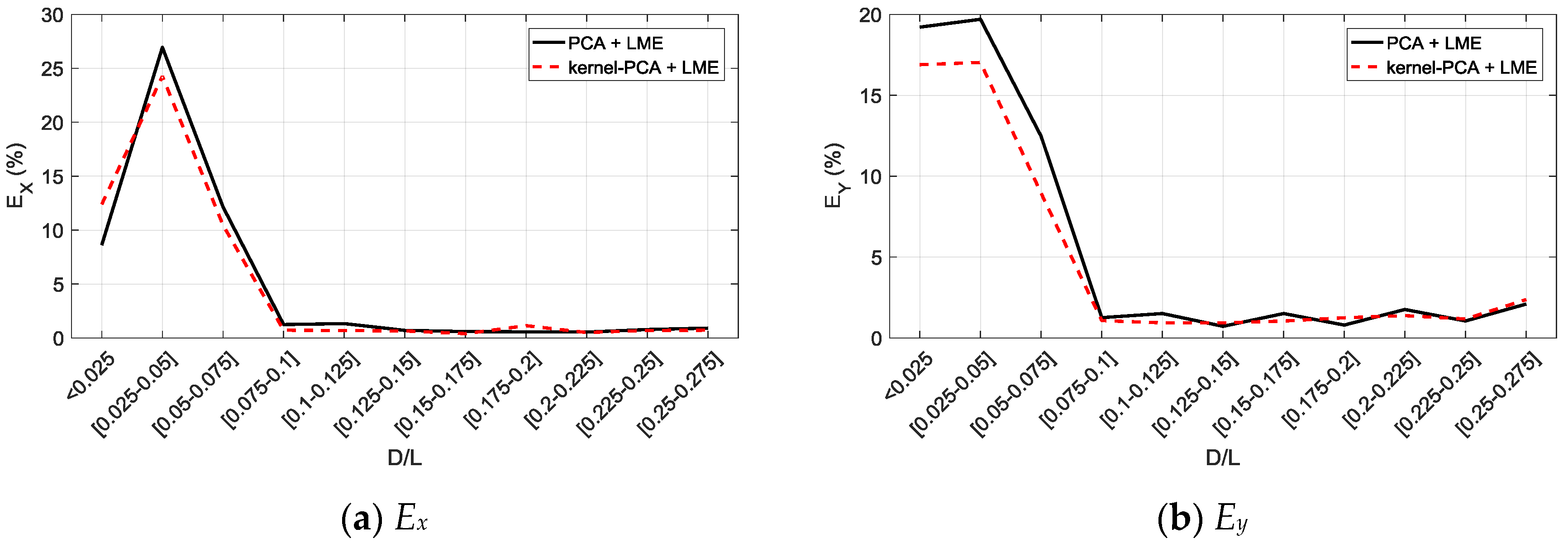
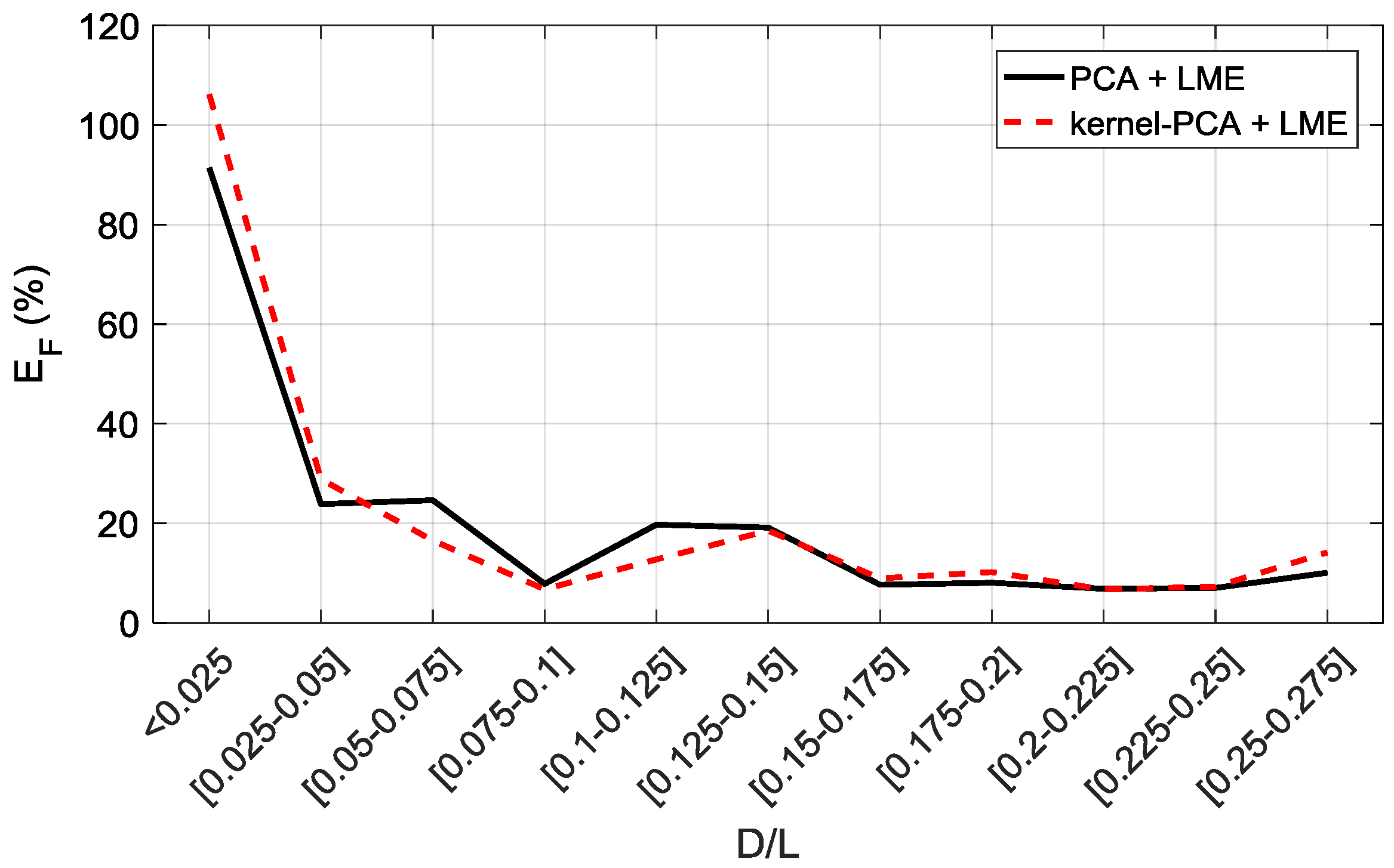
5.1. PCA + LME
5.2. Kernel-PCA + LME
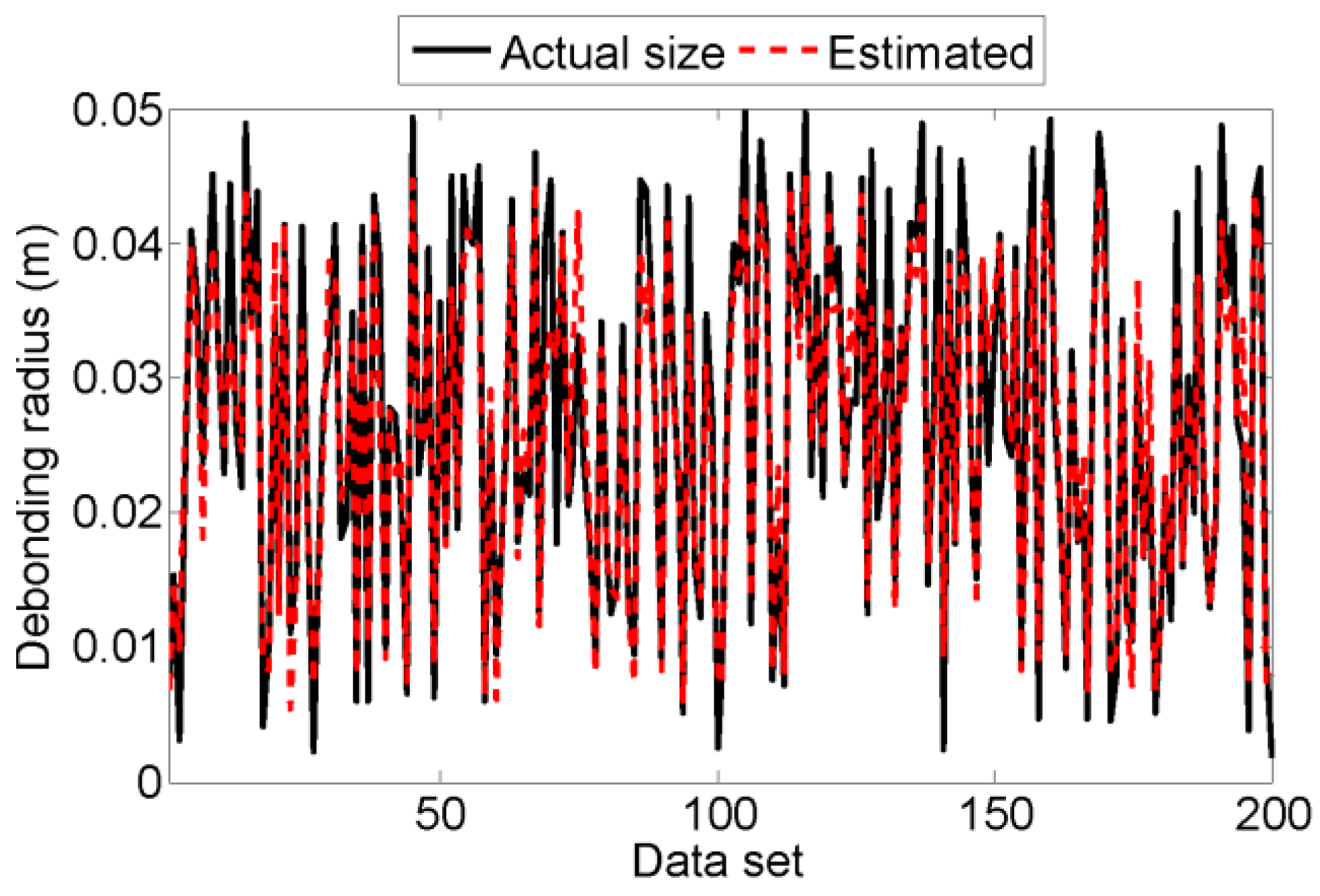
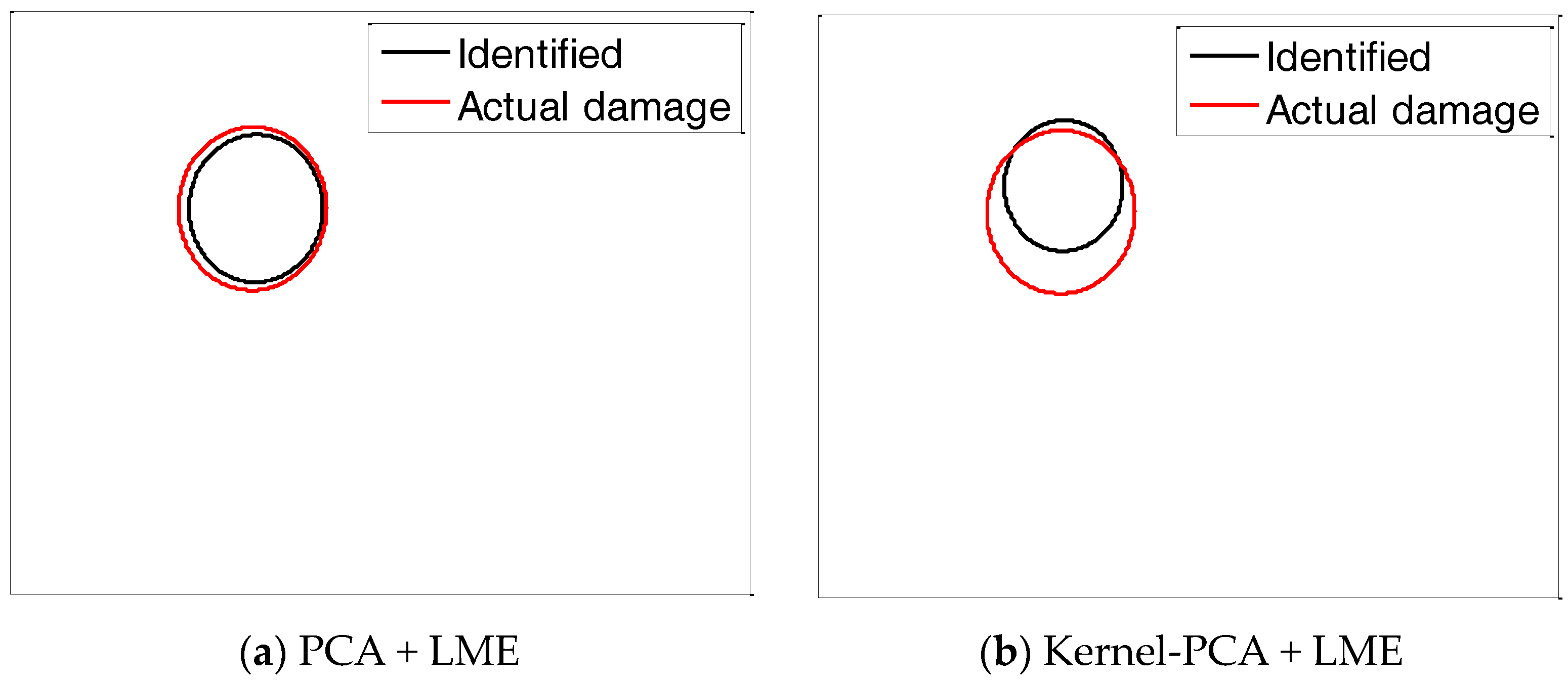
5.3. Damage Size
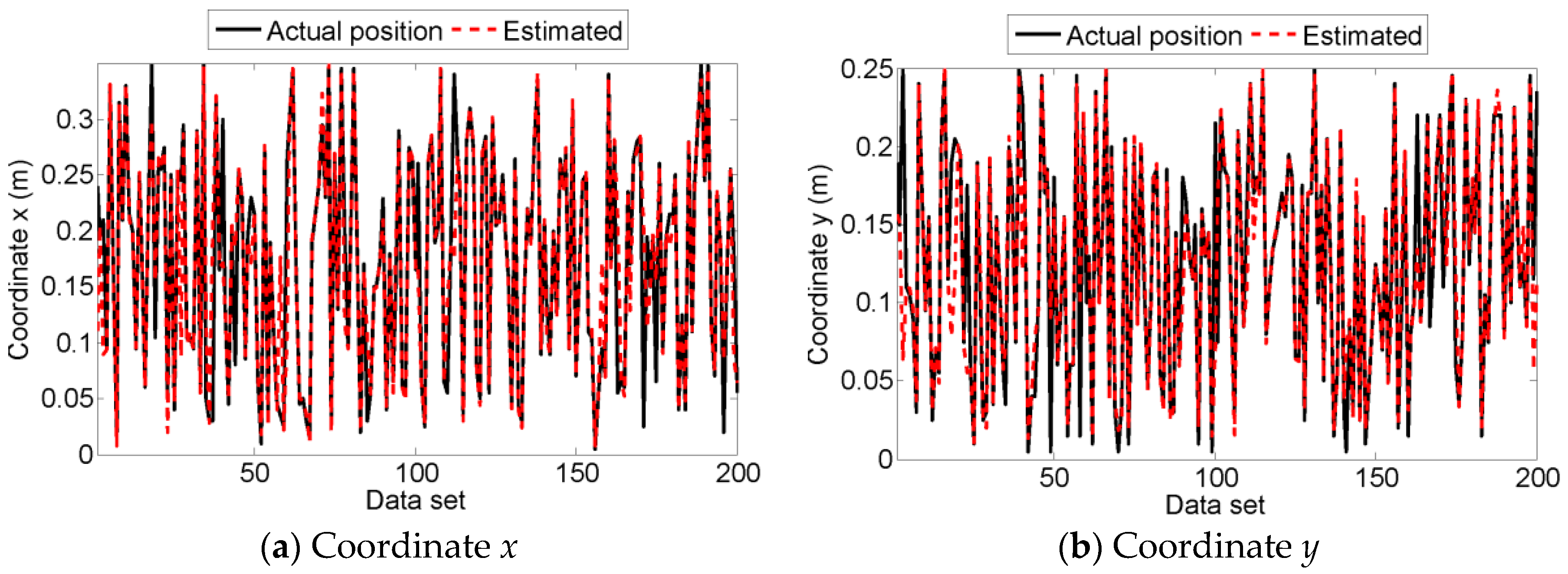
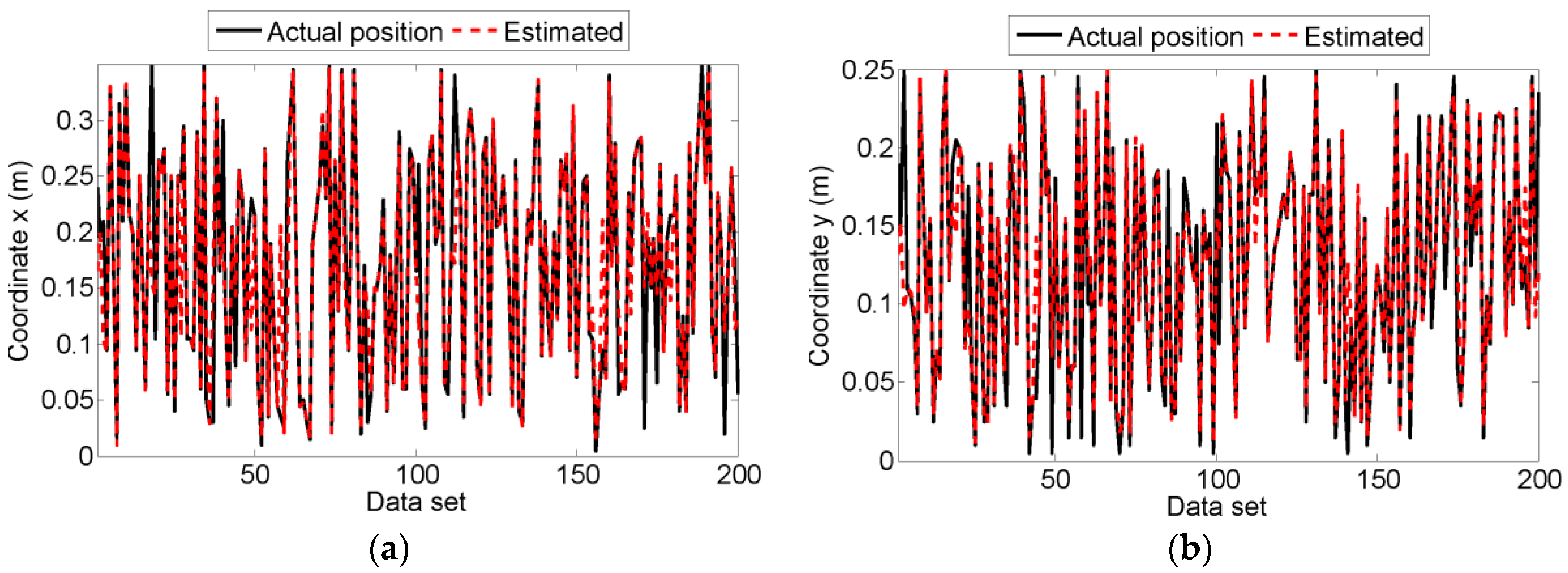
5.4. Experimental Results
6. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vinson, J.R. Sandwich structures: Past, present, and future. In Sandwich Structures 7: Advancing with Sandwich Structures and Materials; Springer: Dordrecht, The Netherlands, 2005; pp. 3–12. [Google Scholar]
- Herrmann, A.S.; Zahlen, P.C.; Zuardy, I. Sandwich Structures Technology in Commercail Aviation: Present Applications and Future Trends. In Sandwich Structures 7: Advancing with Sandwich Structures and Materials; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Carden, E.; Fanning, P. Vibration based condition monitoring: A review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Jiang, L.; Liew, K.; Lim, M.; Low, S. Vibratory behaviour of delaminated honeycomb structures: A 3-D finite element modelling. Comput. Struct. 1995, 55, 773–788. [Google Scholar] [CrossRef]
- Burlayenko, V.; Sadowski, T. Dynamic behaviour of sandwich plates containing single/multiple debonding. Comput. Mater. Sci. 2011, 50, 1263–1268. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Sadowski, T. Influence of skin/core debonding on free vibration behavior of foam and honeycomb cored sandwich plates. Int. J. Non-Linear Mech. 2010, 45, 959–968. [Google Scholar] [CrossRef]
- Kim, H.-Y.; Hwang, W. Effect of debonding on natural frequencies and frequency response functions of honeycomb sandwich beams. Compos. Struct. 2002, 55, 51–62. [Google Scholar] [CrossRef]
- Lou, J.; Wu, L.; Ma, L.; Xiong, J.; Wang, B. Effects of local damage on vibration characteristics of composite pyramidal truss core sandwich structure. Compos. Part B Eng. 2014, 62, 73–87. [Google Scholar] [CrossRef]
- Shahdin, A.; Morlier, J.; Gourinat, Y. Damage monitoring in sandwich beams by modal parameter shifts: A comparative study of burst random and sine dwell vibration testing. J. Sound Vib. 2010, 329, 566–584. [Google Scholar] [CrossRef] [Green Version]
- Farrar, C.R.; Lieven, N.A. Damage prognosis: The future of structural health monitoring. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 365, 623–632. [Google Scholar] [CrossRef] [PubMed]
- Meruane, V.; del Fierro, V. An inverse parallel genetic algorithm for the identification of skin/core debonding in honeycomb aluminium panels. Struct. Control Health Monit. 2015, 22, 1426–1439. [Google Scholar] [CrossRef]
- Islam, A.S.; Craig, K.C. Damage detection in composite structures using piezoelectric materials (and neural net). Smart Mater. Struct. 1994, 3, 318–328. [Google Scholar] [CrossRef]
- Okafor, A.C.; Chandrashekhara, K.; Jiang, Y. Delamination prediction in composite beams with built-in piezoelectric devices using modal analysis and neural network. Smart Mater. Struct. 1996, 5, 338–347. [Google Scholar] [CrossRef]
- Valoor, M.T.; Chandrashekhara, K. A thick composite-beam model for delamination prediction by the use of neural networks. Compos. Sci. Technol. 2000, 60, 1773–1779. [Google Scholar] [CrossRef]
- Ishak, S.; Liu, G.; Shang, H.; Lim, S. Locating and sizing of delamination in composite laminates using computational and experimental methods. Compos. Part B Eng. 2001, 32, 287–298. [Google Scholar] [CrossRef]
- Chakraborty, D. Artificial neural network based delamination prediction in laminated composites. Mater. Des. 2005, 26, 1–7. [Google Scholar] [CrossRef]
- Su, Z.; Ling, H.-Y.; Zhou, L.-M.; Lau, K.-T.; Ye, L. Efficiency of genetic algorithms and artificial neural networks for evaluating delamination in composite structures using fibre Bragg grating sensors. Smart Mater. Struct. 2005, 14, 1541–1553. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhan, C.; Shankar, K.; Morozov, E.V.; Singh, H.K.; Ray, T. Sensitivity analysis of inverse algorithms for damage detection in composites. Compos. Struct. 2017, 176, 844–859. [Google Scholar] [CrossRef]
- Zhang, Z.; Shankar, K.; Ray, T.; Morozov, E.V.; Tahtali, M. Vibration-based inverse algorithms for detection of delamination in composites. Compos. Struct. 2013, 102, 226–236. [Google Scholar] [CrossRef]
- Meruane, V.; Mahu, J. Real-time structural damage assessment using artificial neural networks and anti-resonant frequencies. Shock Vib. 2014, 2014, 653279. [Google Scholar]
- Meruane, V.; Ortiz-Bernardin, A. Structural damage assessment using linear approximation with maximum entropy and transmissibility dat. Mech. Syst. Signal Process. 2015, 54, 210–223. [Google Scholar] [CrossRef]
- Meruane, V.; del Fierro, V.; Ortiz-Bernardin, A. A Maximum Entropy Approach to Assess Debonding in Honeycomb Aluminum Plates. Entropy 2014, 16, 2869–2889. [Google Scholar] [CrossRef]
- Sanchez, N.; Meruane, V.; Ortiz-Bernardin, A. A novel impact identification algorithm based on a linear approximation with maximum entropy. Smart Mater. Struct. 2016, 25, 095050. [Google Scholar] [CrossRef]
- Meruane, V.; Véliz, P.; Droguett, E.L.; Ortiz-Bernardin, A. Impact Location and Quantification on an Aluminum Sandwich Panel Using Principal Component Analysis and Linear Approximation with Maximum Entropy. Entropy 2017, 19, 137. [Google Scholar] [CrossRef]
- Cawley, P.; Adams, R.D. The location of defects in structures from measurements of natural frequencies. J. Strain Anal. Eng. Des. 1979, 14, 49–57. [Google Scholar] [CrossRef]
- Lieven, N.A.J.; Ewins, D.J. Spatial correlation of mode shapes, the coordinate modal assurance criterion (COMAC). In Proceedings of the Sixth International Modal Analysis Conference, Orlando, FL, USA, 1–4 February 1988. [Google Scholar]
- Pandey, A.K.; Biswas, M.; Samman, M.M. Damage detection from changes in curvature mode shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Pandey, A.K.; Biswas, M. Damage detection in structures using changes in flexibility. J. Sound Vib. 1994, 169, 3–17. [Google Scholar] [CrossRef]
- Zhang, Z.; Aktan, A.E. Application of modal flexibility and its derivatives in structural identification. J. Res. Nondestruct. Eval. 1998, 10, 43–61. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Structural damage localization from modal strain energy change. J. Sound Vib. 1998, 218, 825–844. [Google Scholar] [CrossRef]
- Cornwell, P.; Doebling, S.W.; Farrar, C.R. Application of the strain energy damage detection method to plate-like structures. J. Sound Vib. 1999, 224, 359–374. [Google Scholar] [CrossRef]
- Li, Y.Y.; Cheng, L.; Yam, L.H.; Wong, W.O. Identification of damage locations for plate-like structures using damage sensitive indices: Strain modal approach. Comput. Struct. 2002, 80, 1881–1894. [Google Scholar] [CrossRef]
- Wu, D.; Law, S.S. Damage localization in plate structures from uniform load surface curvature. J. Sound Vib. 2004, 276, 227–244. [Google Scholar] [CrossRef]
- Wu, D.; Law, S.S. Sensitivity of uniform load surface curvature for damage identification in plate structures. Trans. ASME-J. Vib. Acoust. 2005, 127, 84–92. [Google Scholar] [CrossRef]
- Yoon, M.K.; Heider, D.; Gillespie, J.W.; Ratcliffe, C.P.; Crane, R.M. Local damage detection using the two-dimensional gapped smoothing method. J. Sound Vib. 2005, 279, 119–139. [Google Scholar] [CrossRef]
- Qiao, P.; Lu, K.; Lestari, W.; Wang, J. Curvature mode shape-based damage detection in composite laminated plates. Compos. Struct. 2007, 80, 409–428. [Google Scholar] [CrossRef]
- Moreno-García, P.; Lopes, H.; Santos, J.V.A.D.; Maia, N.M.M. Damage localisation in composite laminated plates using higher order spatial derivatives. In Proceedings of the Eleventh International Conference on Computational Structures Technology, Dubrovnik, Croatia, 4–7 September 2012. [Google Scholar]
- Chang, C.C.; Chen, L.W. Damage detection of a rectangular plate by spatial wavelet based approach. Appl. Acoust. 2004, 65, 819–832. [Google Scholar] [CrossRef]
- Douka, E.; Loutridis, S.; Trochidis, A. Crack identification in plates using wavelet analysis. J. Sound Vib. 2004, 270, 279–295. [Google Scholar] [CrossRef]
- Rucka, M.A.; Wilde, K.R. Application of continuous wavelet transform in vibration based damage detection method for beams and plates. J. Sound Vib. 2006, 297, 536–550. [Google Scholar] [CrossRef]
- Huang, Y.; Meyer, D.; Nemat-Nasser, S. Nemat-Nasser, Damage detection with spatially distributed 2D continuous wavelet transform. Mech. Mater. 2009, 41, 1096–1107. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. A 2-D continuous wavelet transform of mode shape data for damage detection of plate structures. Int. J. Solids Struct. 2009, 46, 4379–4395. [Google Scholar] [CrossRef]
- Yang, C.; Oyadiji, S.O. Delamination detection in composite laminate plates using 2D wavelet analysis of modal frequency surface. Comput. Struct. 2017, 179, 109–126. [Google Scholar] [CrossRef]
- Katunin, A. Damage identification in composite plates using two-dimensional B-spline wavelets. Mech. Syst. Signal Process. 2011, 25, 3153–3167. [Google Scholar] [CrossRef]
- Katunin, A. Stone impact damage identification in composite plates using modal data and quincunx wavelet analysis. Arch. Civ. Mech. Eng. 2015, 15, 251–261. [Google Scholar] [CrossRef]
- Katunin, A. Vibration-based spatial damage identification in honeycomb-core sandwich composite structures using wavelet analysis. Compos. Struct. 2014, 118, 385–391. [Google Scholar] [CrossRef]
- Seguel, F. Identificación de daño en Placas tipo Sándwich Usando un Sistema de Correlación de Imágenes Digital y la Curvatura de los Modos de Vibración. Master’s Thesis, Universidad de Chile, Santiago, Chile, 2016. (In Spanish). [Google Scholar]
- Helfrick, M.N.; Niezrecki, C.; Avitabile, P.; Schmidt, T. 3D digital image correlation methods for full-field vibration measurement. Mech. Syst. Signal Process. 2011, 25, 917–927. [Google Scholar] [CrossRef]
- Castellini, P.; Revel, G. An experimental technique for structural diagnostic based on laser vibrometry and neural networks. Shock Vib. 2000, 7, 381–397. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.R. Kernel principal component analysis. In International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Wang, Q. Kernel principal component analysis and its applications in face recognition and active shape model. arXiv, 2012; arXiv:1207.3538. [Google Scholar]
- Devroye, L.; Gyorfi, L.; Krzyzak, A.; Lugosi, G. On the strong universal consistency of nearest neighbor regression function estimates. Ann. Stat. 1994, 1994, 1371–1385. [Google Scholar] [CrossRef]
- Gupta, M.R.; Gray, R.M.; Olshen, R.A. Nonparametric supervised learning by linear. IEEE Trans. Pattern Anal. Mach. 2006, 28, 766–781. [Google Scholar] [CrossRef] [PubMed]
- Sukumar, N.; Wright, R. Overview and construction of meshfree basis functions: From moving least squares to entropy approximants. Int. J. Numer. Methods Eng. 2007, 70, 181–205. [Google Scholar] [CrossRef]
- Siebert, T.; Becker, T.; Spiltthof, K.; Neumann, I.; Krupka, R. High-speed digital image correlation: Error estimations and applications. Opt. Eng. 2007, 46, 051004. [Google Scholar] [CrossRef]
- Siebert, T.; Wood, R.; Splitthof, K. High speed image correlation for vibration analysis. J. Phys. Conf. Ser. 2009, 181, 012064. [Google Scholar] [CrossRef]
- Balmes, E.; Bianchi, J.P.; Leclère, J.M. Structural Dynamics Toolbox Users Guide; Version 6.1; Scientific Software Group: Paris, France, 2009. [Google Scholar]
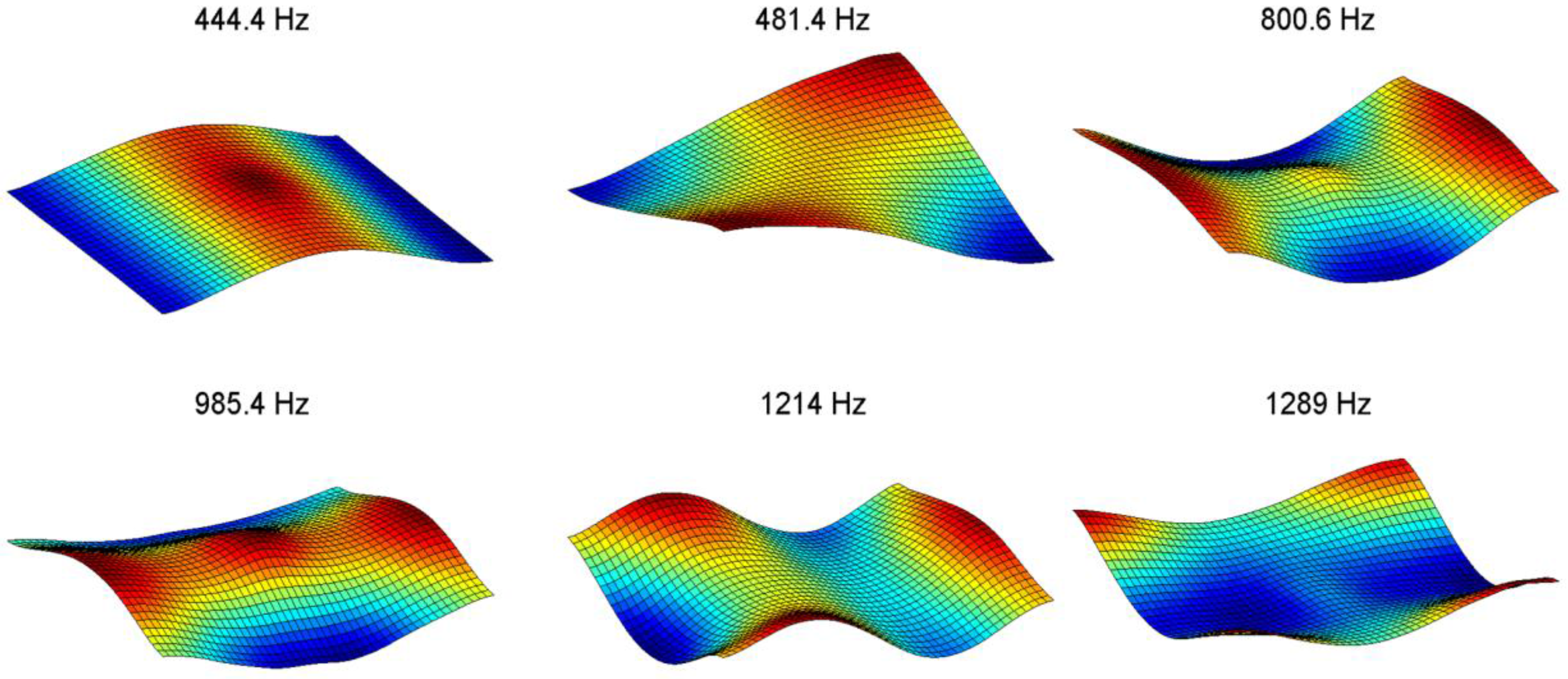
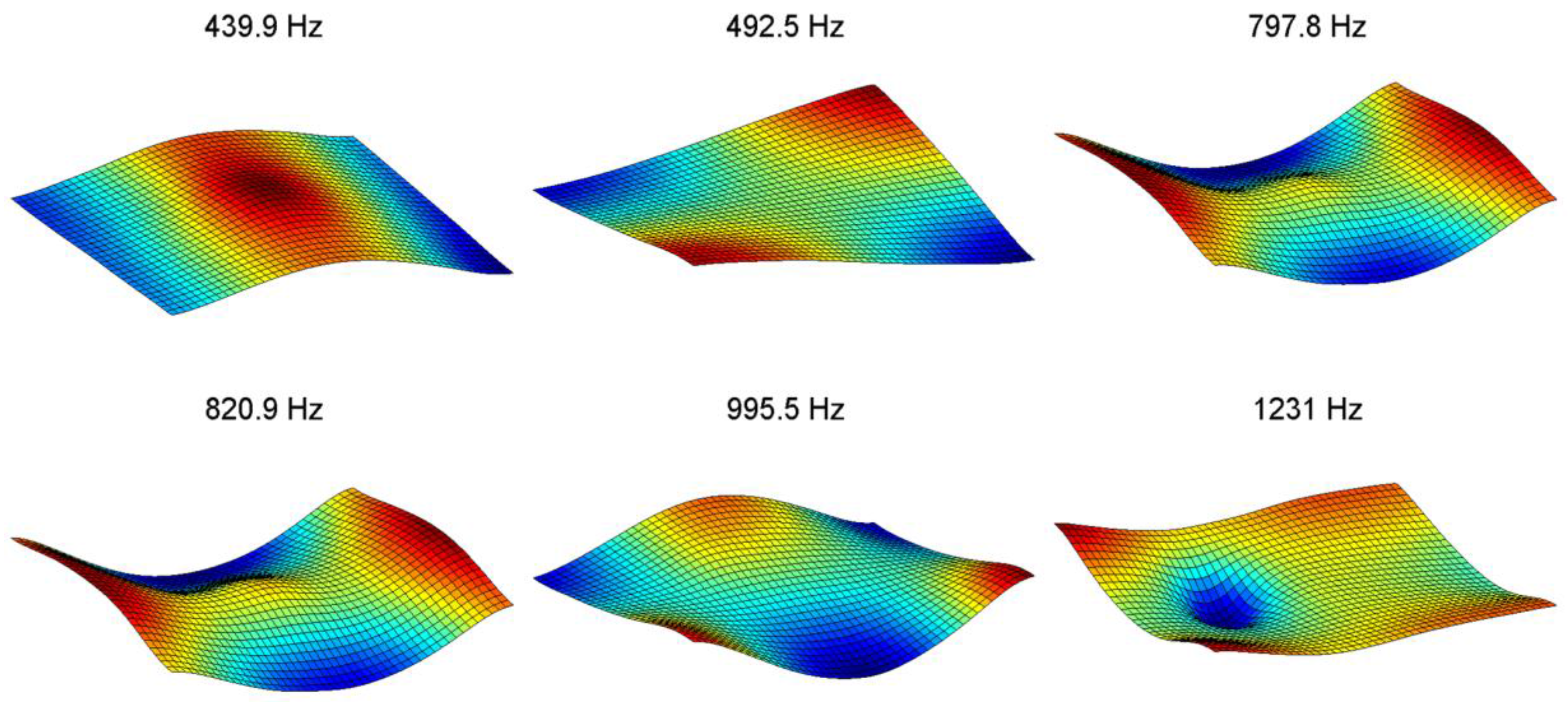




| Mode Shape Pair | (Hz) | (Hz) | (%) | MAC |
|---|---|---|---|---|
| 1 | 444 | 440 | –0.9 | 0.97 |
| 2 | 481 | 493 | 2.5 | 0.90 |
| 3 | 801 | 798 | –0.4 | 0.98 |
| 4 | 985 | 820 | –16.8 | 0.68 |
| 5 | 1290 | 1230 | –4.7 | 0.67 |
| PCA + LME | Kernel PCA + LME | |
|---|---|---|
| (%) | 0.46 | 0.36 |
| (%) | 0.03 | 4.43 |
| (%) | 9.59 | 19.90 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meruane, V.; Lasen, M.; López Droguett, E.; Ortiz-Bernardin, A. Modal Strain Energy-Based Debonding Assessment of Sandwich Panels Using a Linear Approximation with Maximum Entropy. Entropy 2017, 19, 619. https://doi.org/10.3390/e19110619
Meruane V, Lasen M, López Droguett E, Ortiz-Bernardin A. Modal Strain Energy-Based Debonding Assessment of Sandwich Panels Using a Linear Approximation with Maximum Entropy. Entropy. 2017; 19(11):619. https://doi.org/10.3390/e19110619
Chicago/Turabian StyleMeruane, Viviana, Matias Lasen, Enrique López Droguett, and Alejandro Ortiz-Bernardin. 2017. "Modal Strain Energy-Based Debonding Assessment of Sandwich Panels Using a Linear Approximation with Maximum Entropy" Entropy 19, no. 11: 619. https://doi.org/10.3390/e19110619





