Transport Coefficients from Large Deviation Functions
Abstract
1. Introduction
2. Theory and Methodology
2.1. Transport Coefficients from Large Deviation Functions
2.2. Calculation of Large Deviation Functions
3. Results and Discussion
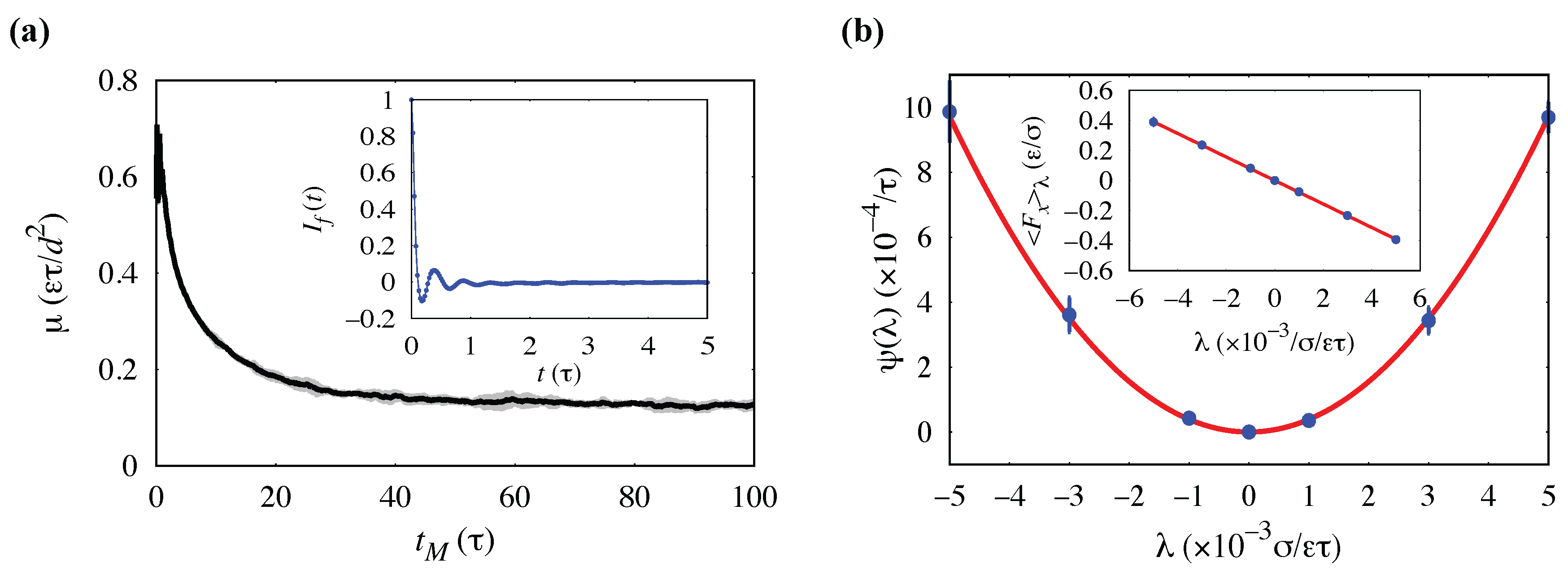
3.1. Validation of Methodology: Shear Viscosity
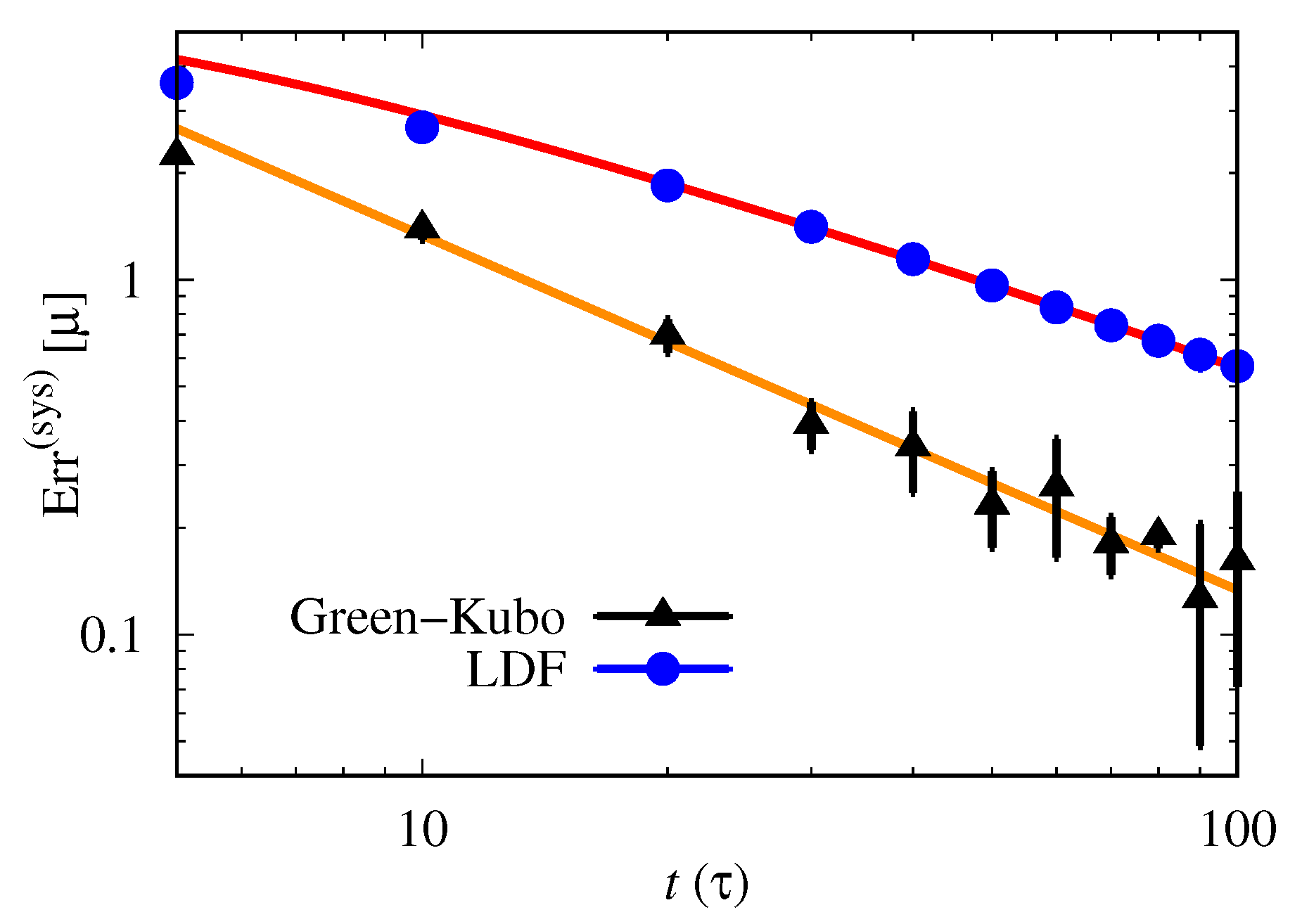
3.2. Analysis of Systematic Error: Interfacial Friction Coefficient
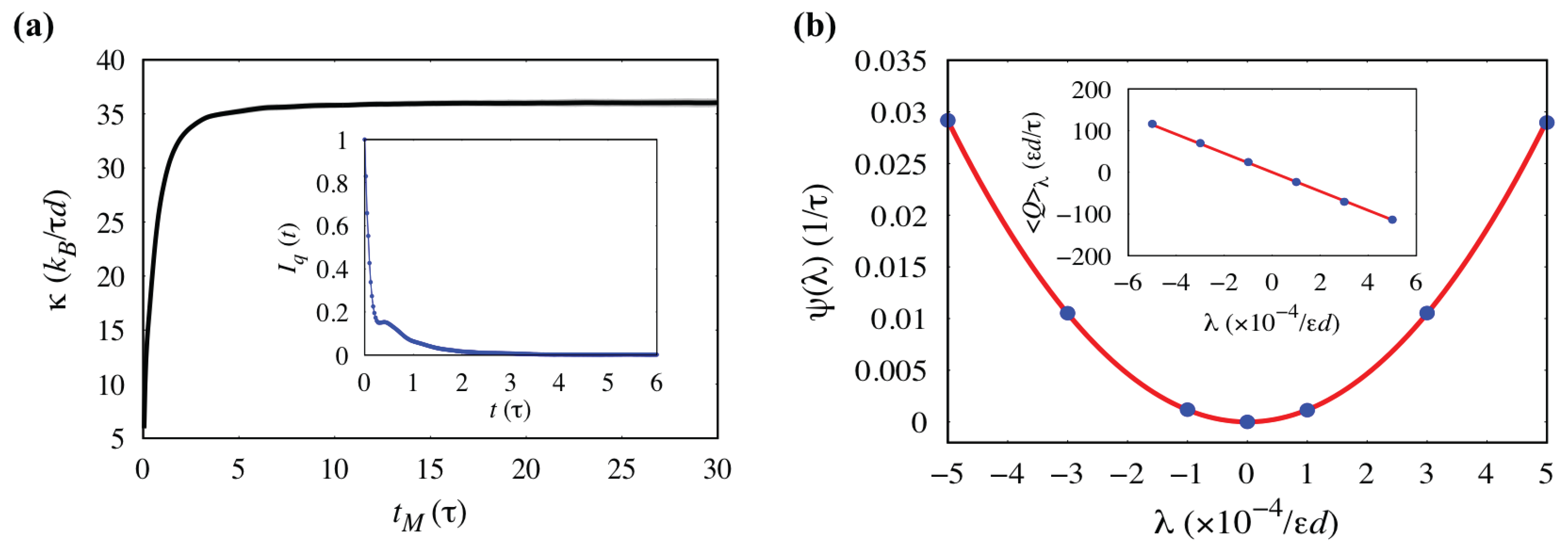
3.3. Analysis of Statistical Error: Thermal Conductivity
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Green, M.S. Markoff random processes and the statistical mechanics of time-dependent phenomena. II. Irreversible processes in fluids. J. Chem. Phys. 1954, 22, 398–413. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Levesque, D.; Verlet, L.; Kürkijarvi, J. Computer “experiments” on classical fluids. IV. Transport properties and time-correlation functions of the Lennard–Jones liquid near its triple point. Phys. Rev. A 1973, 7, 1690. [Google Scholar] [CrossRef]
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B 2002, 65, 144306. [Google Scholar] [CrossRef]
- Galamba, N.; de Nieto Castro, C.A.; Ely, J.F. Thermal conductivity of molten alkali halides from equilibrium molecular dynamics simulations. J. Chem. Phys. 2004, 120, 8676–8682. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.E.; Mandadapu, K.K. Adaptive Green–Kubo estimates of transport coefficients from molecular dynamics based on robust error analysis. J. Chem. Phys. 2012, 136, 154102. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.J.; Streett, W.B. Transport properties of homonuclear diatomics: II. Dense fluids. Mol. Phys. 1978, 36, 161–176. [Google Scholar] [CrossRef]
- Hess, B. Determining the shear viscosity of model liquids from molecular dynamics simulations. J. Chem. Phys. 2002, 116, 209–217. [Google Scholar] [CrossRef]
- Tenenbaum, A.; Ciccotti, G.; Gallico, R. Stationary nonequilibrium states by molecular dynamics. Fourier’s law. Phys. Rev. A 1982, 25, 2778. [Google Scholar] [CrossRef]
- Baranyai, A.; Cummings, P.T. Steady state simulation of planar elongation flow by nonequilibrium molecular dynamics. J. Chem. Phys. 1999, 110, 42–45. [Google Scholar] [CrossRef]
- Hoover, W.G.; Evans, D.J.; Hickman, R.B.; Ladd, A.J.C.; Ashurst, W.T.; Moran, B. Lennard–Jones triple-point bulk and shear viscosities. Green–Kubo theory, Hamiltonian mechanics, and nonequilibrium molecular dynamics. Phys. Rev. A 1980, 22, 1690. [Google Scholar] [CrossRef]
- Evans, D.J. Homogeneous NEMD algorithm for thermal conductivity—Application of non-canonical linear response theory. Phys. Lett. A 1982, 91, 457–460. [Google Scholar] [CrossRef]
- Mandadapu, K.K.; Jones, R.E.; Papadopoulos, P. A homogeneous nonequilibrium molecular dynamics method for calculating thermal conductivity with a three-body potential. J. Chem. Phys. 2009, 130, 204106. [Google Scholar] [CrossRef] [PubMed]
- Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar] [CrossRef]
- Zhou, X.W.; Aubry, S.; Jones, R.E.; Greenstein, A.; Schelling, P.K. Towards more accurate molecular dynamics calculation of thermal conductivity: Case study of GaN bulk crystals. Phys. Rev. B 2009, 79, 115201. [Google Scholar] [CrossRef]
- Tuckerman, M.E.; Mundy, C.J.; Balasubramanian, S.; Klein, M.L. Modified nonequilibrium molecular dynamics for fluid flows with energy conservation. J. Chem. Phys. 1997, 106, 5615–5621. [Google Scholar] [CrossRef]
- Tenney, C.M.; Maginn, E.J. Limitations and recommendations for the calculation of shear viscosity using reverse nonequilibrium molecular dynamics. J. Chem. Phys. 2010, 132, 014103. [Google Scholar] [CrossRef] [PubMed]
- Geissler, P.L.; Dellago, C. Equilibrium time correlation functions from irreversible transformations in trajectory space. J. Phys. Chem. B 2004, 108, 6667–6672. [Google Scholar] [CrossRef]
- Touchette, H. The large deviation approach to statistical mechanics. Phys. Rep. 2009, 478, 1–69. [Google Scholar] [CrossRef]
- Touchette, H. Introduction to dynamical large deviations of Markov processes. arXiv, 2017; arXiv:1705.06492. [Google Scholar]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar] [CrossRef]
- Barato, A.C.; Seifert, U. Thermodynamic uncertainty relation for biomolecular processes. Phys. Rev. Lett. 2015, 114, 158101. [Google Scholar] [CrossRef] [PubMed]
- Gingrich, T.R.; Horowitz, J.M.; Perunov, N.; England, J.L. Dissipation bounds all steady-state current fluctuations. Phys. Rev. Lett. 2016, 116, 120601. [Google Scholar] [CrossRef] [PubMed]
- Gaspard, P. Multivariate fluctuation relations for currents. New J. Phys. 2013, 15, 115014. [Google Scholar] [CrossRef]
- Andrieux, D.; Gaspard, P. Fluctuation theorem and Onsager reciprocity relations. J. Chem. Phys. 2004, 121, 6167–6174. [Google Scholar] [CrossRef] [PubMed]
- Andrieux, D.; Gaspard, P. A fluctuation theorem for currents and non-linear response coefficients. J. Stat. Mech. Theory Exp. 2007. [Google Scholar] [CrossRef]
- Dellago, C.; Bolhuis, P.G.; Csajka, F.S.; Chandler, D. Transition path sampling and the calculation of rate constants. J. Chem. Phys. 1998, 108, 1964–1977. [Google Scholar] [CrossRef]
- Geissler, P.L.; Dellago, C.; Chandler, D. Kinetic pathways of ion pair dissociation in water. J. Phys. Chem. B 1999, 103, 3706–3710. [Google Scholar] [CrossRef]
- Geissler, P.L.; Dellago, C.; Chandler, D.; Hutter, J.; Parrinello, M. Autoionization in liquid water. Science 2001, 291, 2121–2124. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Chandler, D.; Dellago, C.; Geissler, P.L. Transition path sampling: Throwing ropes over rough mountain passes, in the dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. [Google Scholar] [CrossRef] [PubMed]
- Radhakrishnan, R.; Schlick, T. Orchestration of cooperative events in DNA synthesis and repair mechanism unraveled by transition path sampling of DNA polymerase β’s closing. Proc. Natl. Acad. Sci. USA 2004, 101, 5970–5975. [Google Scholar] [CrossRef] [PubMed]
- Basner, J.E.; Schwartz, S.D. How enzyme dynamics helps catalyze a reaction in atomic detail: A transition path sampling study. J. Am. Chem. Soc. 2005, 127, 13822–13831. [Google Scholar] [CrossRef] [PubMed]
- Hagan, M.F.; Chandler, D. Dynamic pathways for viral capsid assembly. Biophys. J. 2006, 91, 42–54. [Google Scholar] [CrossRef] [PubMed]
- Peters, B. Recent advances in transition path sampling: Accurate reaction coordinates, likelihood maximisation and diffusive barrier-crossing dynamics. Mol. Simul. 2010, 36, 1265–1281. [Google Scholar] [CrossRef]
- Limmer, D.T.; Chandler, D. Theory of amorphous ices. Proc. Natl. Acad. Sci. USA 2014, 111, 9413–9418. [Google Scholar] [CrossRef] [PubMed]
- Giardina, C.; Kurchan, J.; Peliti, L. Direct evaluation of large-deviation functions. Phys. Rev. Lett. 2006, 96, 120603. [Google Scholar] [CrossRef] [PubMed]
- Giardina, C.; Kurchan, J.; Lecomte, V.; Tailleur, J. Simulating rare events in dynamical processes. J. Stat. Phys. 2011, 145, 787–811. [Google Scholar] [CrossRef]
- Nemoto, T.; Bouchet, F.; Jack, R.L.; Lecomte, V. Population-dynamics method with a multicanonical feedback control. Phys. Rev. E 2016, 93, 062123. [Google Scholar] [CrossRef] [PubMed]
- Klymko, K.; Geissler, P.L.; Garrahan, J.P.; Whitelam, S. Rare behavior of growth processes via umbrella sampling of trajectories. arXiv, 2017; arXiv:1707.00767. [Google Scholar]
- Ray, U.; Chan, G.K.-L.; Limmer, D.T. Exact fluctuations of nonequilibrium steady states from approximate auxiliary dynamics. arXiv, 2017; arXiv:1708.09482. [Google Scholar]
- Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
- Palmer, T.; Speck, T. Thermodynamic formalism for transport coefficients with an application to the shear modulus and shear viscosity. J. Chem. Phys. 2017, 146, 124130. [Google Scholar] [CrossRef] [PubMed]
- Abascal, J.L.F.; Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: London, UK, 1987. [Google Scholar]
- Morriss, G.P.; Evans, D.J. Statistical Mechanics of Nonequilbrium Liquids; ANU Press: Canberra, Australia, 2013. [Google Scholar]
- Lebowitz, J.L.; Spohn, H. A Gallavotti–Cohen-type symmetry in the large deviation functional for stochastic dynamics. J. Stat. Phys. 1999, 95, 333–365. [Google Scholar] [CrossRef]
- Helfand, E. Transport coefficients from dissipation in a canonical ensemble. Phys. Rev. 1960, 119, 1. [Google Scholar] [CrossRef]
- Foulkes, W.M.C.; Mitas, L.; Needs, R.J.; Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33. [Google Scholar] [CrossRef]
- Hurtado, P.I.; Garrido, P.L. Spontaneous symmetry breaking at the fluctuating level. Phys. Rev. Lett. 2011, 107, 180601. [Google Scholar] [CrossRef] [PubMed]
- Garrahan, J.P.; Jack, R.L.; Lecomte, V.; Pitard, E.; van Duijvendijk, K.; van Wijland, F. First-order dynamical phase transition in models of glasses: An approach based on ensembles of histories. J. Phys. A Math. Theor. 2009, 42, 075007. [Google Scholar] [CrossRef]
- Bodineau, T.; Lecomte, V.; Toninelli, C. Finite size scaling of the dynamical free-energy in a kinetically constrained model. J. Stat. Phys. 2012, 147, 1–17. [Google Scholar] [CrossRef]
- Allen, R.J.; Valeriani, C.; ten Wolde, P.R. Forward flux sampling for rare event simulations. J. Phys. Condens. Matter 2009, 21, 463102. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: San Diego, CA, USA, 2001; Volume 1. [Google Scholar]
- Nemoto, T.; Hidalgo, E.G.; Lecomte, V. Finite-time and finite-size scalings in the evaluation of large-deviation functions: Numerical approach in continuous time. Phys. Rev. E 2017, 95, 062134. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Ray, U.; Chan, G.K.-L.; Limmer, D.T. Importance sampling large deviations in nonequilibrium steady states: Part 1. arXiv, 2017; arXiv:1708.00459. [Google Scholar]
- González, M.A.; Abascal, J.L.F. The shear viscosity of rigid water models. J. Chem. Phys. 2010, 132, 096101. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Sendner, C.; Horinek, D.; Bocquet, L.; Netz, R.R. Interfacial water at hydrophobic and hydrophilic surfaces: Slip, viscosity, and diffusion. Langmuir 2009, 25, 10768–10781. [Google Scholar] [CrossRef] [PubMed]
- Petravic, J.; Harrowell, P. On the equilibrium calculation of the friction coefficient for liquid slip against a wall. J. Chem. Phys. 2007, 127. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Szlufarska, I. Green–Kubo relation for friction at liquid–solid interfaces. Phys. Rev. E 2014, 89, 032119. [Google Scholar] [CrossRef] [PubMed]
- Bocquet, L.; Barrat, J.L. On the Green–Kubo relationship for the liquid–solid friction coefficient. J. Chem. Phys. 2013, 139, 044704. [Google Scholar] [CrossRef] [PubMed]
- Alder, B.J.; Wainwright, T.E. Decay of the velocity autocorrelation function. Phys. Rev. A 1970, 1, 18–21. [Google Scholar] [CrossRef]
- Wainwright, T.; Alder, B.; Gass, D. Decay of time correlations in two dimensions. Phys. Rev. A 1971, 4, 233. [Google Scholar] [CrossRef]
- Isobe, M. Long-time tail of the velocity autocorrelation function in a two-dimensional moderately dense hard-disk fluid. Phys. Rev. E 2008, 77, 021201. [Google Scholar] [CrossRef] [PubMed]
- Che, J.; Cagin, T.; Goddard, W.A., III. Thermal conductivity of carbon nanotubes. Nanotechnology 2000, 11, 65–69. [Google Scholar] [CrossRef]


| Transport Coefficient | Green–Kubo Relation | Dynamical Observable |
|---|---|---|
| shear viscosity | ||
| interfacial friction coefficient | ||
| thermal conductivity |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.Y.; Limmer, D.T. Transport Coefficients from Large Deviation Functions. Entropy 2017, 19, 571. https://doi.org/10.3390/e19110571
Gao CY, Limmer DT. Transport Coefficients from Large Deviation Functions. Entropy. 2017; 19(11):571. https://doi.org/10.3390/e19110571
Chicago/Turabian StyleGao, Chloe Ya, and David T. Limmer. 2017. "Transport Coefficients from Large Deviation Functions" Entropy 19, no. 11: 571. https://doi.org/10.3390/e19110571
APA StyleGao, C. Y., & Limmer, D. T. (2017). Transport Coefficients from Large Deviation Functions. Entropy, 19(11), 571. https://doi.org/10.3390/e19110571




