Intermittent Motion, Nonlinear Diffusion Equation and Tsallis Formalism
Abstract
:1. Introduction
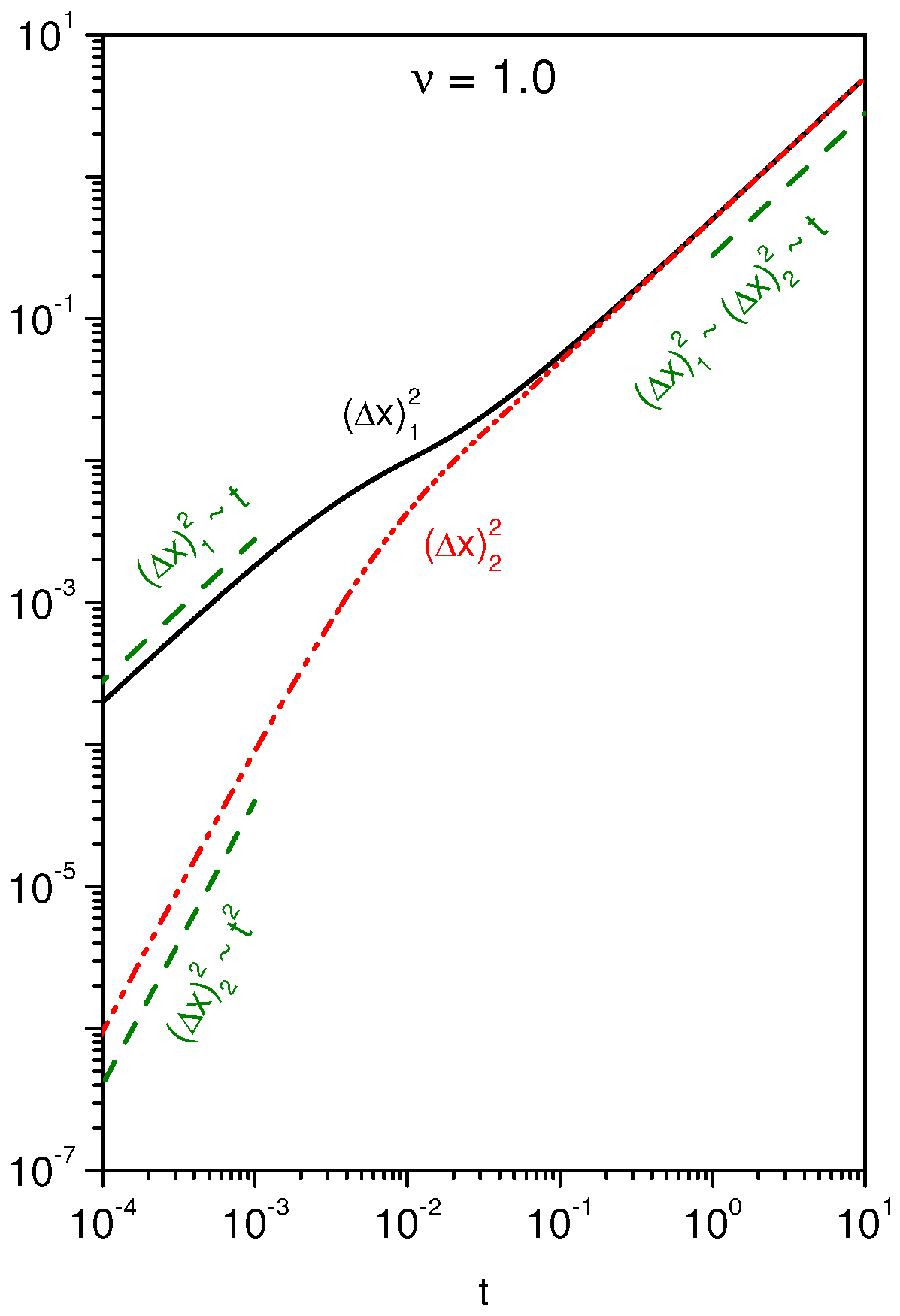
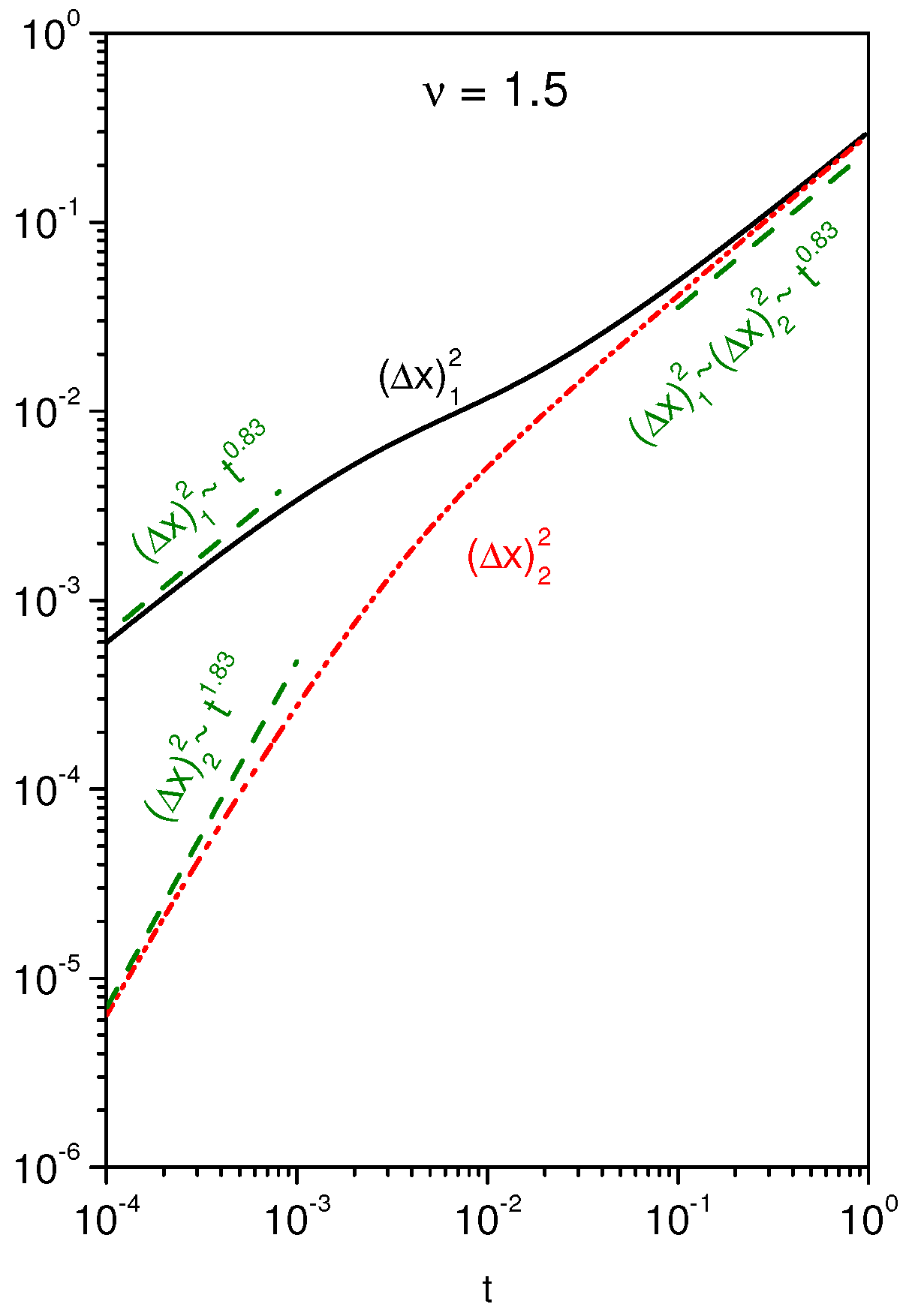
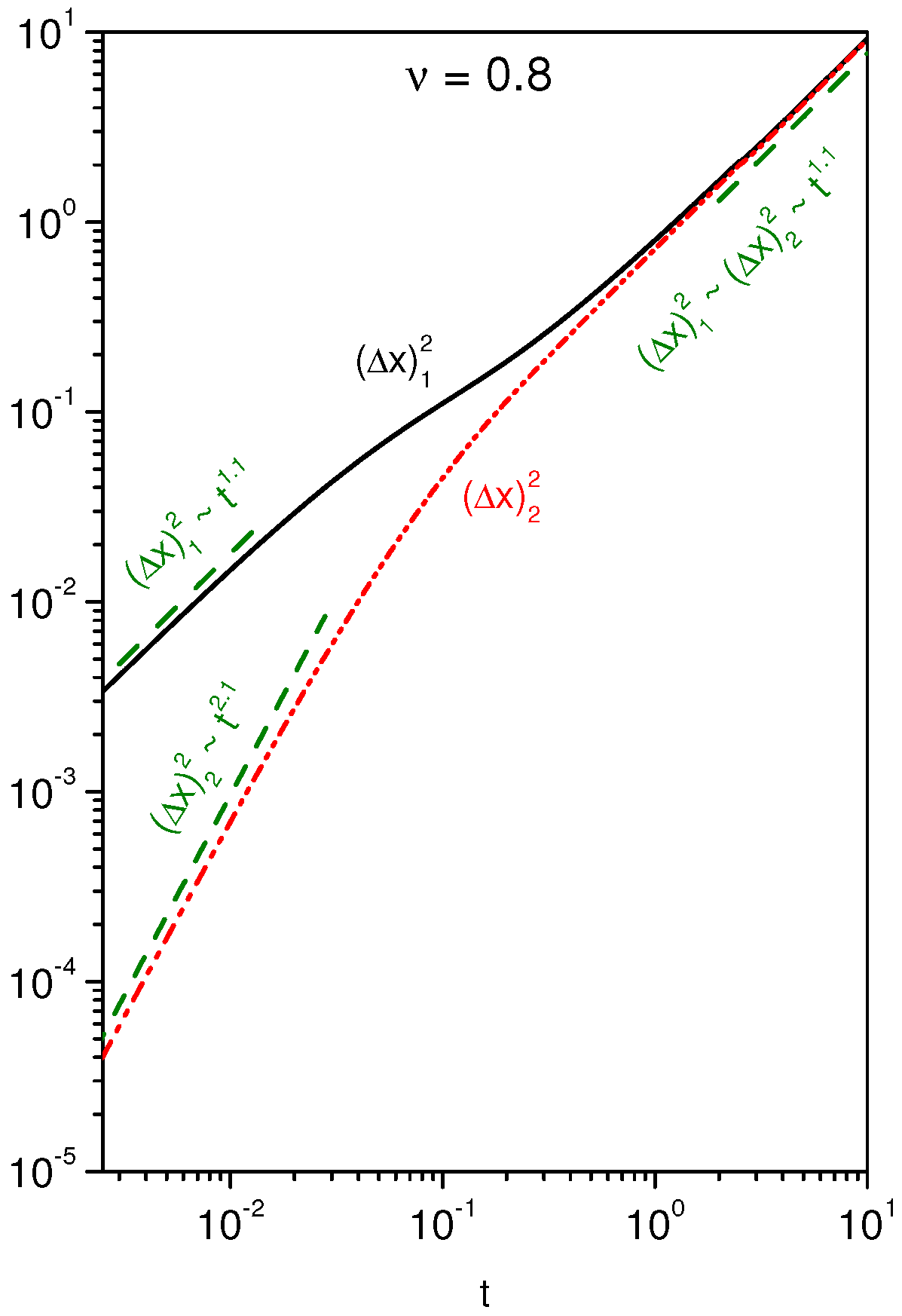
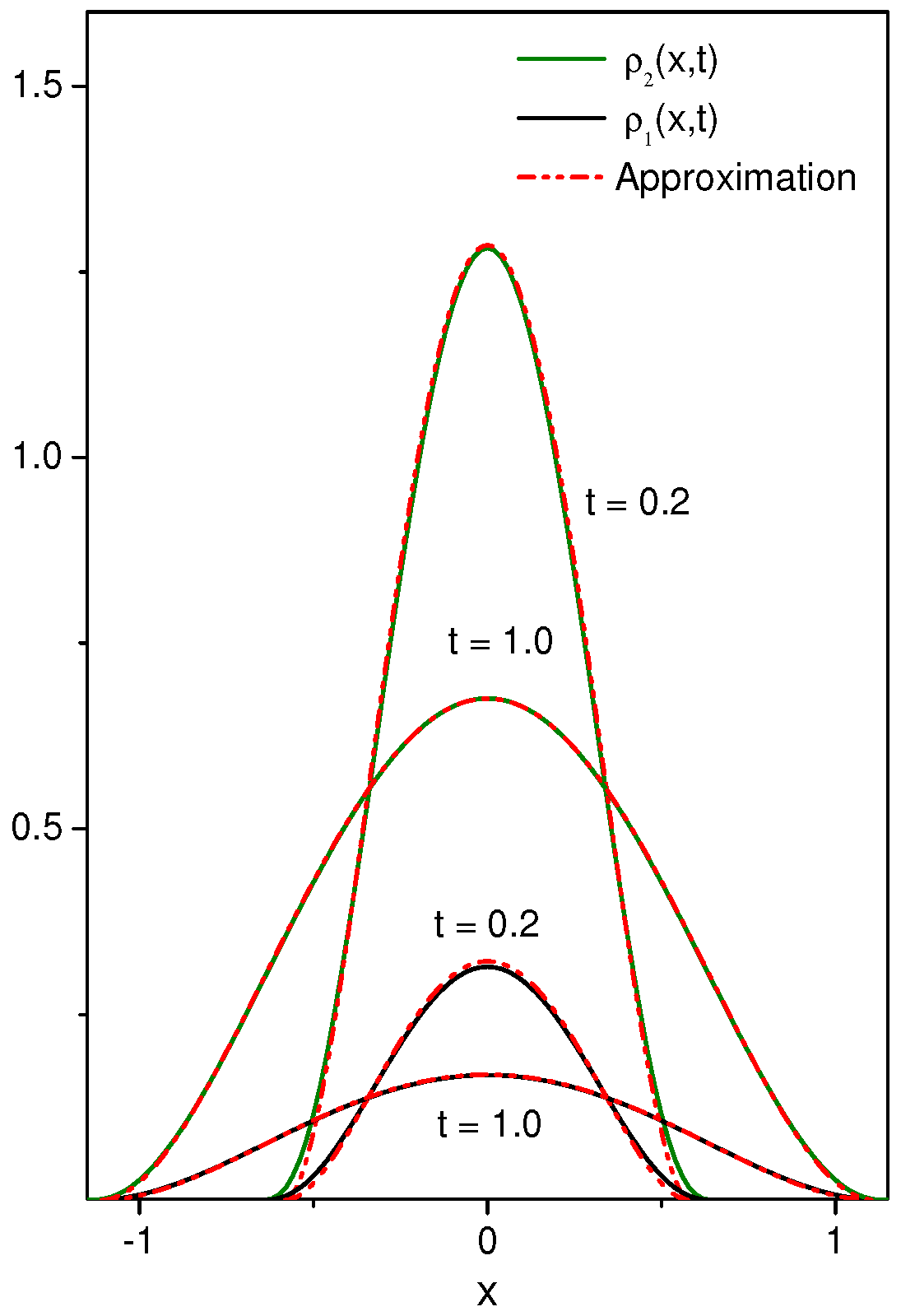
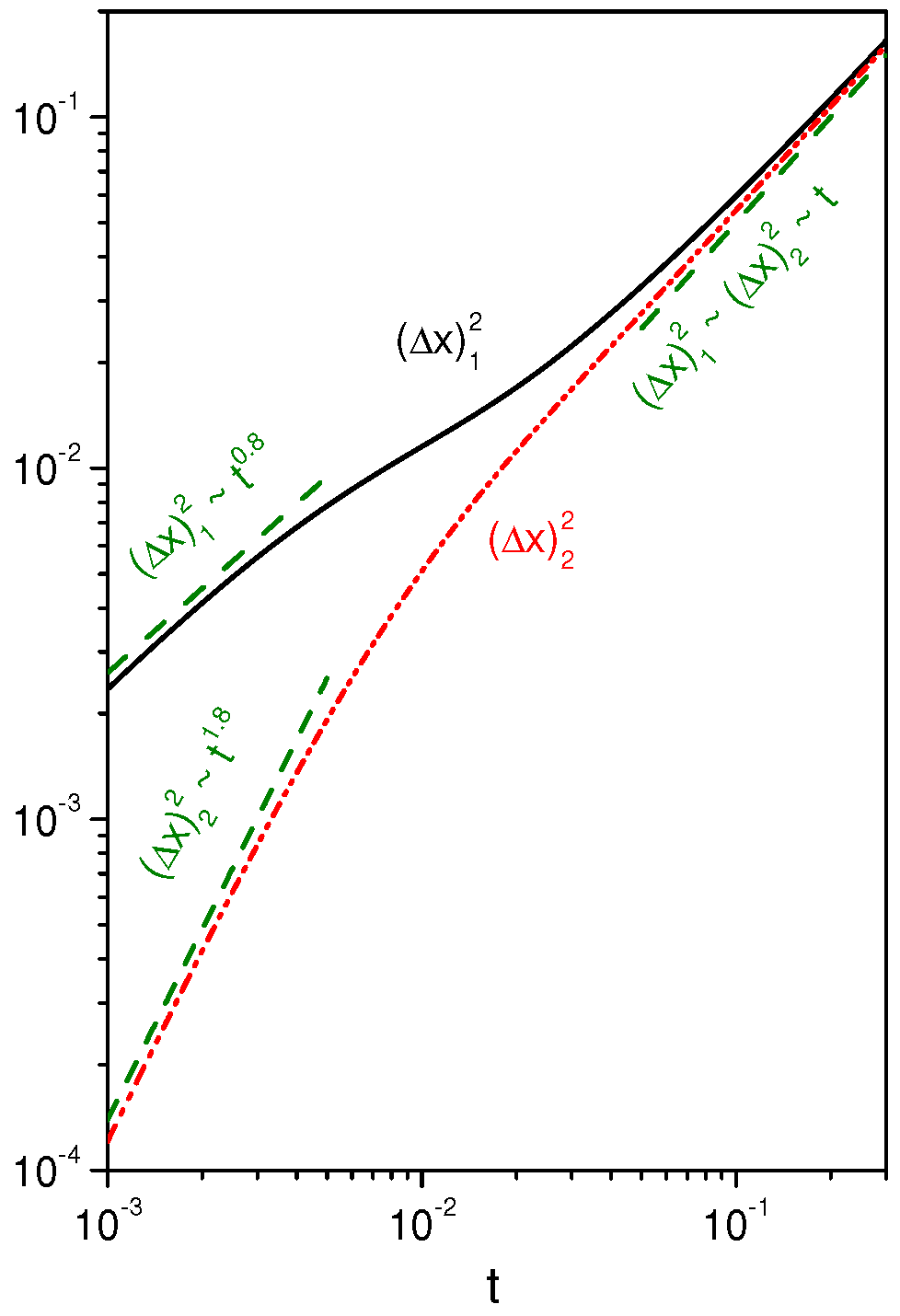
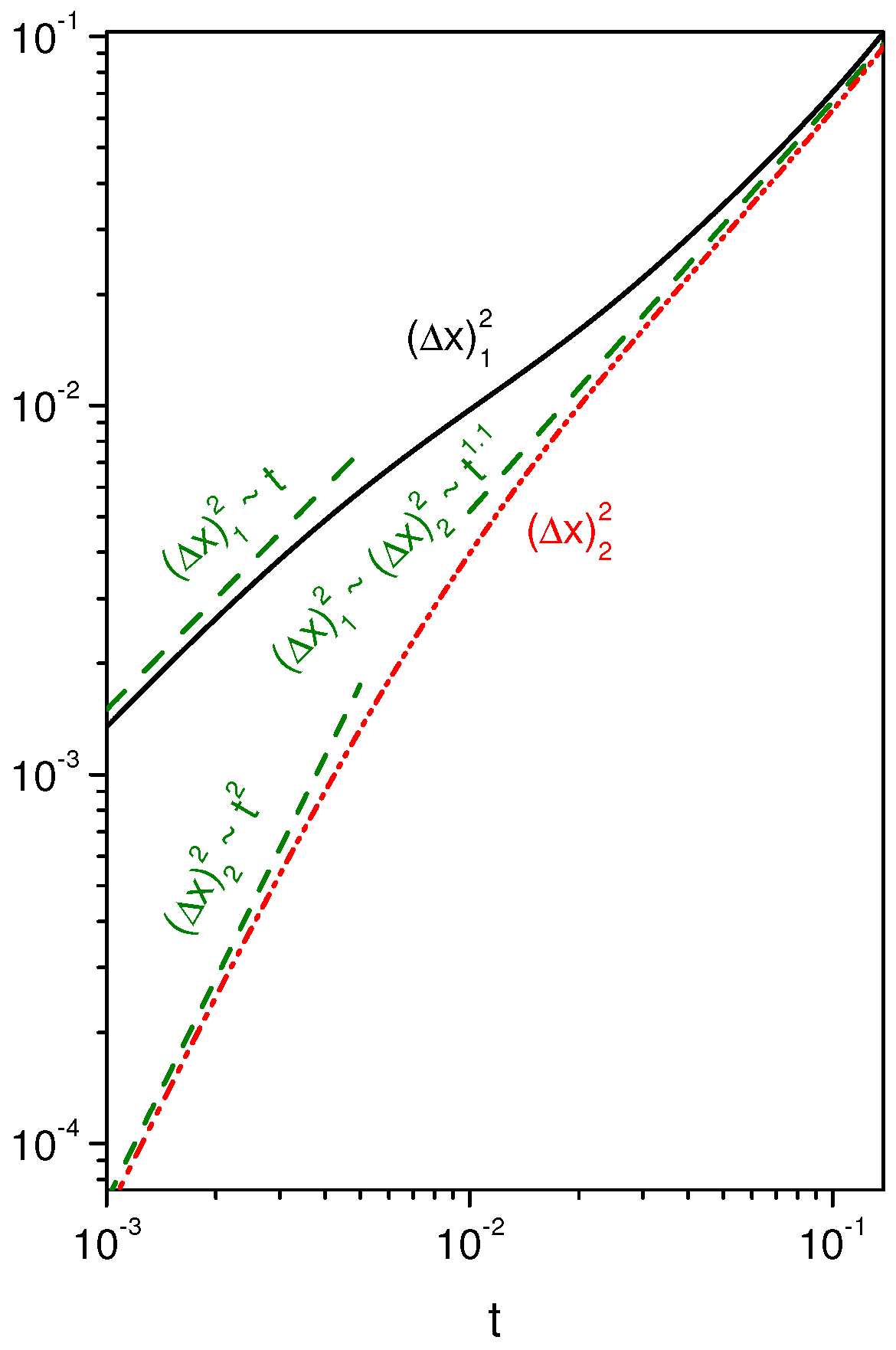
2. Diffusion and Pauses
3. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cherstvy, A.G.; Chechkin, A.V.; Metzler, R. 2014 Particle invasion, survival, and non-ergodicity in 2D diffusion processes with space-dependent diffusivity. Soft Matter 2014, 10, 1591–1601. [Google Scholar] [CrossRef] [PubMed]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [PubMed]
- Bressloff, P.C. Stochastic Processes in Cell Biology; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Snopok, B.A. Nonexponential Kinetics of Surface Chemical Reactions. Theor. Exp. Chem. 2014, 50, 67–95. [Google Scholar] [CrossRef]
- Strizhak, P.E. Macrokinetics of Chemical Processes on Porous Catalysts having regard to Anomalous Diffusion. Theor. Exp. Chem. 2004, 40, 203–208. [Google Scholar] [CrossRef]
- Avnir, D. The Fractal Approach to Heterogeneous Chemistry; Wiley-Interscience: New York, NY, USA, 1990. [Google Scholar]
- Ben-Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483–530. [Google Scholar] [CrossRef]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport: Foundations and Applications; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- McDowell-Boyer, L.M.; Hunt, J.M.; Sitar, N. Particle Transport Through Porous Media. Water Resour. Res. 1986, 22, 1901–1921. [Google Scholar] [CrossRef]
- De Smedt, F.; Wierenga, P.J. A generalized solution for solute flow in soils with mobile and immobile water. Water Resour. Res. 1979, 15, 1137–1141. [Google Scholar] [CrossRef]
- McGuffee, S.R.; Elcock, A.H. Diffusion, Crowding & Protein Stability in a Dynamic Molecular Model of the Bacterial Cytoplasm. PLoS Comput. Biol. 2010, 6, e1000694. [Google Scholar]
- Filipovitch, N.; Hill, K.M.; Longjas, A.; Voller, V.R. Infiltration experiments demonstrate an explicit connection between heterogeneity and anomalous diffusion behavior. Water Resour. Res. 2016, 52, 5167–5178. [Google Scholar] [CrossRef]
- Gmachowski, L. Fractal model of anomalous diffusion. Eur. Biophys. J. 2015, 44, 613–621. [Google Scholar] [CrossRef] [PubMed]
- Santoro, P.A.; de Paula, J.L.; Lenzi, E.K.; Evangelista, L.R. Anomalous diffusion governed by a fractional diffusion equation and the electrical response of an electrolytic cell. J. Chem. Phys. 2011, 135, 114704. [Google Scholar] [CrossRef] [PubMed]
- Lenzi, E.K.; Fernandes, P.R.G.; Petrucci, T.; Mukai, H.; Ribeiro, H.V. Anomalous-diffusion approach applied to the electrical response of water. Phys. Rev. E 2011, 84, 041128. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, I.M. Anomalous Diffusion on Fractal Networks. In Mathematics of Complexity and Dynamical Systems; Robert, A.M., Ed.; Springer: New York, NY, USA, 2011; pp. 13–25. [Google Scholar]
- Barkai, E. Fractional Fokker-Planck equation, solution, and application. Phys. Rev. E 2001, 63, 046118. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A Math. Gen. 2004, 37, R161. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Lenzi, M.K.; Zola, R.S.; Ribeiro, H.V.; Zola, F.C.; Evangelista, L.R.; Gonçalves, G. Reaction on a solid surface supplied by an anomalous mass transfer source. Physica A 2014, 410, 399–406. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.-H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [PubMed]
- Borland, L. Microscopic dynamics of the nonlinear Fokker-Planck equation: A phenomenological model. Phys. Rev. E 1998, 57, 6634–6642. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Lenzi, E.K.; da Silva, L.R.; Ribeiro, H.V.; Picoli, S., Jr.; Mendes, R.S. Different diffusive regimes, generalized Langevin and diffusion equations. Phys. Rev. E 2012, 85, 011147. [Google Scholar] [CrossRef] [PubMed]
- Kenkre, V.M.; Montroll, E.W.; Shlesinger, M.F. Generalized master equations for continuous-time random walks. J. Stat. Phys. 1973, 9, 45–50. [Google Scholar] [CrossRef]
- Pagnini, G.; Mura, A.; Mainardi, F. Generalized Fractional Master Equation for Self-Similar Stochastic Processes Modelling Anomalous Diffusion. Int. J. Stoch. Anal. 2012, 2012, 427383. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks: From Tools to Applications; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Silva, A.T.; Lenzi, E.K.; Evangelista, L.R.; Lenzi, M.K.; da Silva, L.R. Fractional nonlinear diffusion equation, solutions and anomalous diffusion. Physica A 2007, 375, 65–71. [Google Scholar] [CrossRef]
- Alibaud, N.; Cifani, S.; Jakobsen, E.R. Continuous dependence estimates for nonlinear fractional convection-diffusion equations. SIAM J. Math. Anal. 2012, 44, 603–632. [Google Scholar] [CrossRef] [Green Version]
- Pascal, H. A nonlinear model of heat conduction. J. Phys. A 1992, 25, 939–948. [Google Scholar] [CrossRef]
- Daly, E.; Porporato, A. Similarity solutions of nonlinear diffusion problems related to mathematical hydraulics and the Fokker-Planck equation. Phys. Rev. E 2004, 70, 056303. [Google Scholar] [CrossRef] [PubMed]
- Troncoso, P.; Fierro, O.; Curilef, S.; Plastino, A.R. A family of evolution equations with nonlinear diffusion, Verhulst growth, and global regulation: Exact time-dependent solutions. Physica A 2007, 375, 457–466. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Non-Extensive Statistical Mechanics and Generalized Fokker-Planck Equation. Physica A 1995, 222, 347–354. [Google Scholar] [CrossRef]
- Silva, P.C.; da Silva, L.R.; Lenzi, E.K.; Mendes, R.S.; Malacarne, L.C. Nonlinear diffusion equation, Tsallis formalism and exact solutions. Physica A 2004, 342, 16–19. [Google Scholar]
- Plastino, A.R.; Casas, M.; Plastino, A. A nonextensive maximum entropy approach to a family of nonlinear reaction-diffusion equations. Physica A 2000, 280, 289–303. [Google Scholar] [CrossRef]
- Wada, T.; Scarfone, A.M. On the non-linear Fokker-Planck equation associated with κ-entropy. AIP Conf. Proc. 2007, 965, 177–180. [Google Scholar]
- Wada, T.; Scarfone, A.M. Asymptotic solutions of a nonlinear diffusive equation in the framework of κ-generalized statistical mechanics. Eur. Phys. J. B 2009, 70, 65–71. [Google Scholar] [CrossRef]
- Frank, T.D. Nonlinear Fokker-Planck Equations; Springer-Verlag: Heidelberg, Germany, 2005. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer-Verlag: New York, NY, USA, 2009. [Google Scholar]
- Murray, J. Mathematical Biology; Springer: Berlin, Germany, 1989. [Google Scholar]
- Rigo, A.; Plastino, A.R.; Casas, M.; Plastino, A. Anomalous diffusion coupled with Verhulst-like growth dynamics: Exact time-dependent solutions. Phys. Lett. A 2000, 276, 97–102. [Google Scholar] [CrossRef]
- Mendez, V.; Campos, D.; Bartumeus, F. Stochastic Foundations in Movement Ecology; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-Mechanical Foundation of the Ubiquity of Lévy Distributions in Nature. Phys. Rev. Lett. 1995, 75, 3589–3593. [Google Scholar] [CrossRef] [PubMed]
- Muskat, M. The Flow of Homogeneous Fluids Through Porous Media; McGraw-Hill: New York, NY, USA, 1937. [Google Scholar]
- Polubarinova-Kochina, P.Y. Theory of Ground Water Movement; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Buckmaster, J. Viscous sheets advancing over dry beds. J. Fluid Mech. 1977, 81, 735–756. [Google Scholar] [CrossRef]
- Spohn, H. Surface dynamics below the roughening transition. J. Phys. France I 1993, 3, 69–81. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Menechini, N.R.; Tateishi, A.A.; Lenzi, M.K.; Ribeiro, H.V. Fractional diffusion equations coupled by reaction terms. Physica A 2016, 458, 9–16. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A. Numerical Recipes in Fortran: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Shigesada, N. Spatial Distribution of Dispersing Animals. J. Math. Biology 1980, 9, 85–96. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Mendes, R.S.; Tsallis, C. Crossover in diffusion equation: Anomalous and normal behaviors. Phys. Rev. E 2003, 67, 031104. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenzi, E.K.; Da Silva, L.R.; Lenzi, M.K.; Dos Santos, M.A.F.; Ribeiro, H.V.; Evangelista, L.R. Intermittent Motion, Nonlinear Diffusion Equation and Tsallis Formalism. Entropy 2017, 19, 42. https://doi.org/10.3390/e19010042
Lenzi EK, Da Silva LR, Lenzi MK, Dos Santos MAF, Ribeiro HV, Evangelista LR. Intermittent Motion, Nonlinear Diffusion Equation and Tsallis Formalism. Entropy. 2017; 19(1):42. https://doi.org/10.3390/e19010042
Chicago/Turabian StyleLenzi, Ervin K., Luciano R. Da Silva, Marcelo K. Lenzi, Maike A. F. Dos Santos, Haroldo V. Ribeiro, and Luiz R. Evangelista. 2017. "Intermittent Motion, Nonlinear Diffusion Equation and Tsallis Formalism" Entropy 19, no. 1: 42. https://doi.org/10.3390/e19010042








