Sparse Trajectory Prediction Based on Multiple Entropy Measures
Abstract
:1. Introduction
2. Trajectory Sequence with Time Based on Spatial Iterative Grid Partition
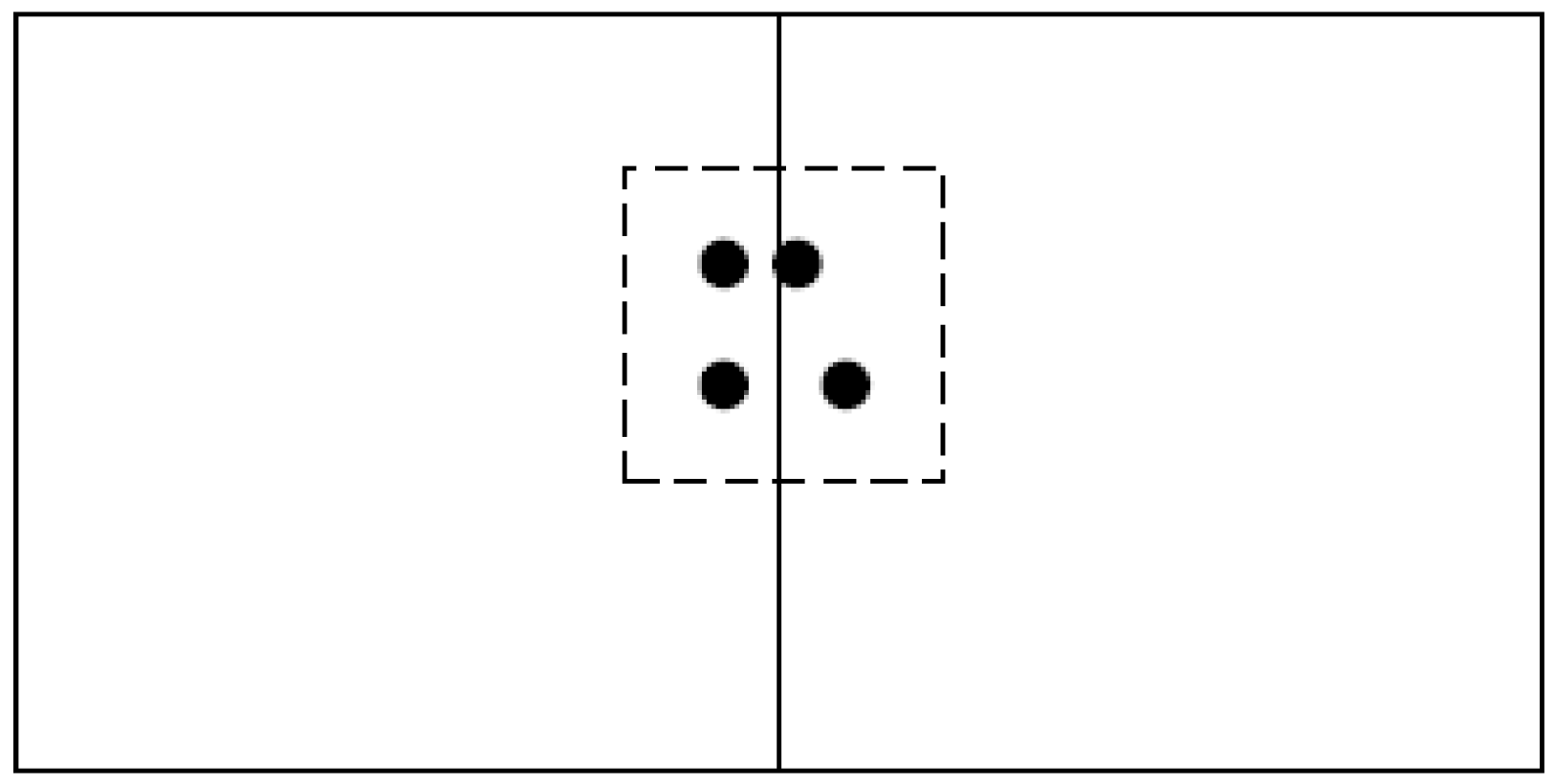
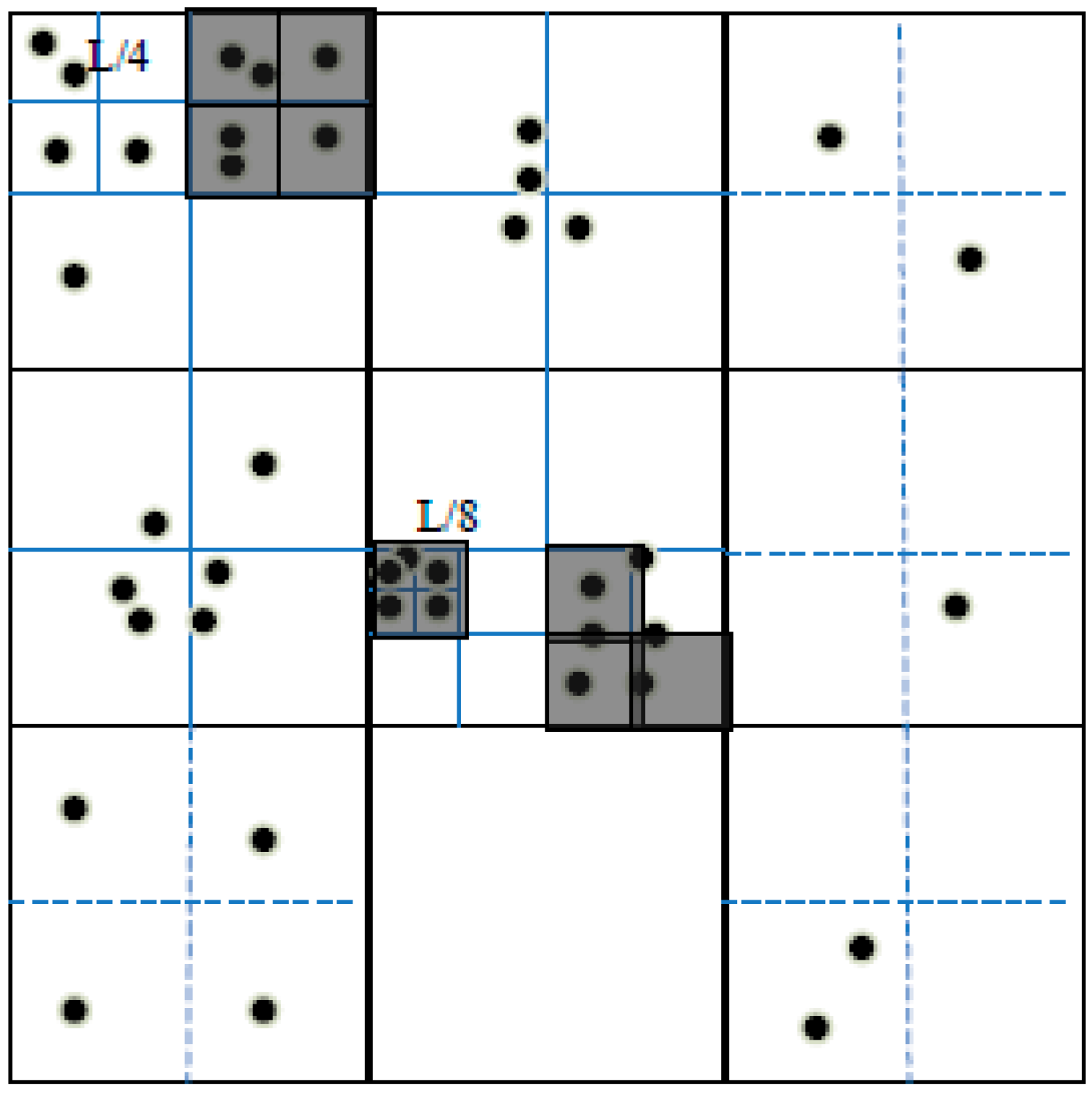
2.1. Spatial Iterative Grid Partition
| Algorithm 1. Spatial Iterative Grid Partition (SIGP) | |
| Input: D(GPS points dataset of historical trajectory), d (initial partition parameter), n(GPS point threshold of each grid) | |
| Output: G (iterative partition grid set) | |
| 1. | Partition the moving region to grid cells with the same size // Divide the initial space of moving object into grid cells |
| 2. | for each grid in |
| 3. | num = // Count the points located in each grid cell |
| 4. | if num n then // These grid cells need further dividing |
| 5. | Excecute // Call the iteration algorithm |
| 6. | else |
| 7. | G.push() //Put into the result set G |
| 8. | end |
| 9. | end |
| Algorithm 2. Iterate-Partition | |
| Input: (iterative partition grid set), (grid need to be divided); n(GPS point threshold of each grid) | |
| Output: (iterative partition grid set) | |
| 1. | Divide into four grid cells |
| 2. | Count the points in as |
| 3. | if then |
| 4. | |
| 5. | else |
| 6. | add into |
| 7. | return |
| 8. | end |
2.2. Trajectory Description Based on SIGP and Time
3. Trajectory Synthesis Based on L-Z Entropy Estimation
3.1. Trajectory Entropy
3.2. Trajectory Synthesis Based on Entropy Estimation
| Algorithm 3. Trajectory Synthesis Algorithm Based on Entropy Estimation (TS-EE) | |
| Input: (historical trajectory space), m(trajectory selection parameter) | |
| Output: (synthesized trajectory space) | |
| 1. | //Store sub_trajectories |
| 2. | foreach in |
| 3. | as |
| 4. | // Arrange by entropy |
| 5. | // Choose the minimum entropy of trajectories in |
| 6. | foreach in |
| 7. | foreach in |
| 8. | // Find all cross_nodes between and |
| 9. | // Divide and into sub_trajectories by cross_nodes |
| 10. | foreach in |
| 11. | // Compute entropy of |
| 12. | if // corresponds to sub_trajectories of has overlap |
| 13. | min{} // Keep sub_tra with minimum entropy |
| 14. | // Remove others from |
| 15. | // Replace sub_tras of with sub_tras in |
| 16. | // Add into |
| 17. | return |
4. Sparse Trajectory Prediction Based on Multiple Entropy Measures
4.1. Location Entropy
4.2. Time Entropy
4.3. Second-Order Markov Model for Trajectory Prediction
5. Experimental Evaluation and Analysis of the Results
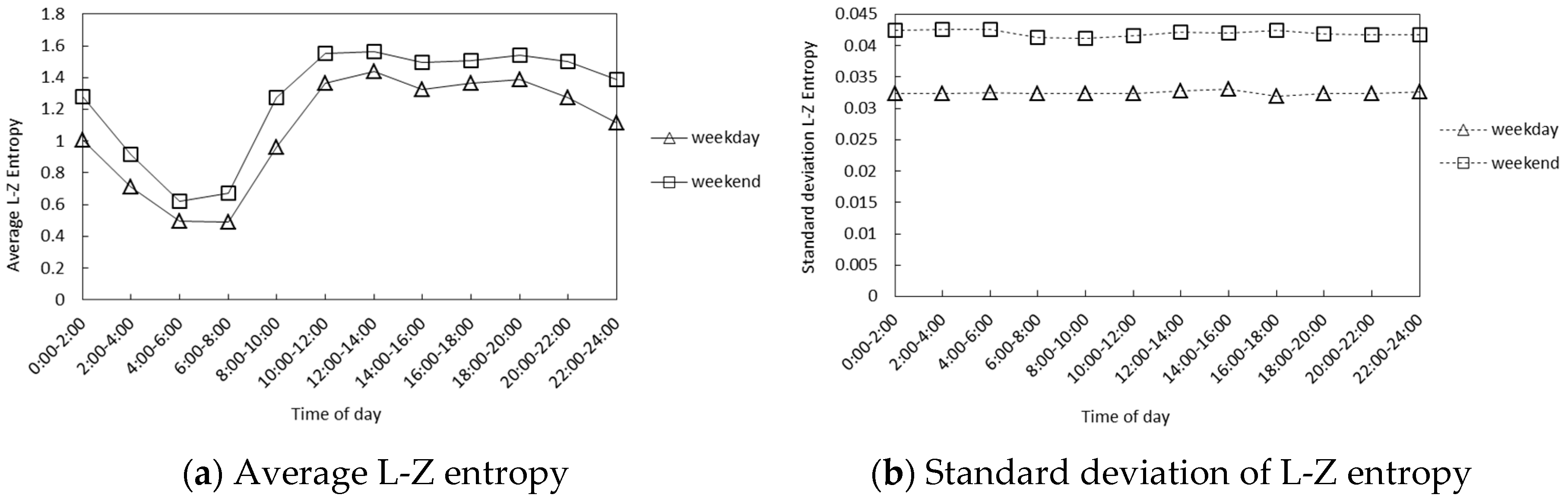
5.1. The Result of Trajectory L-Z Entropy
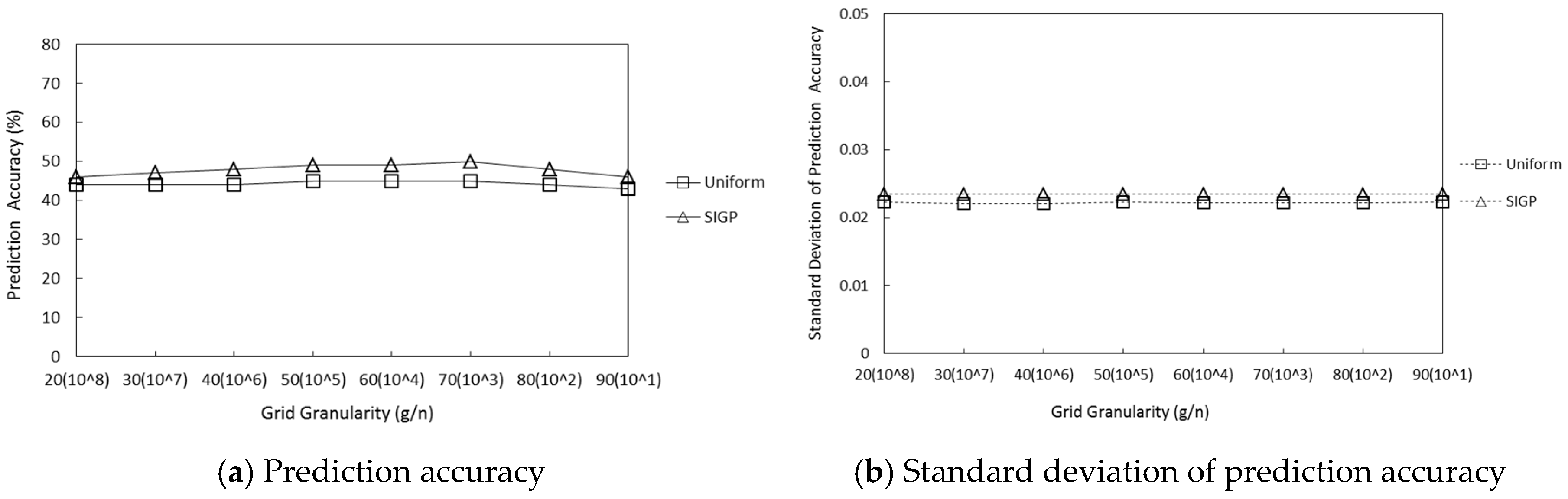
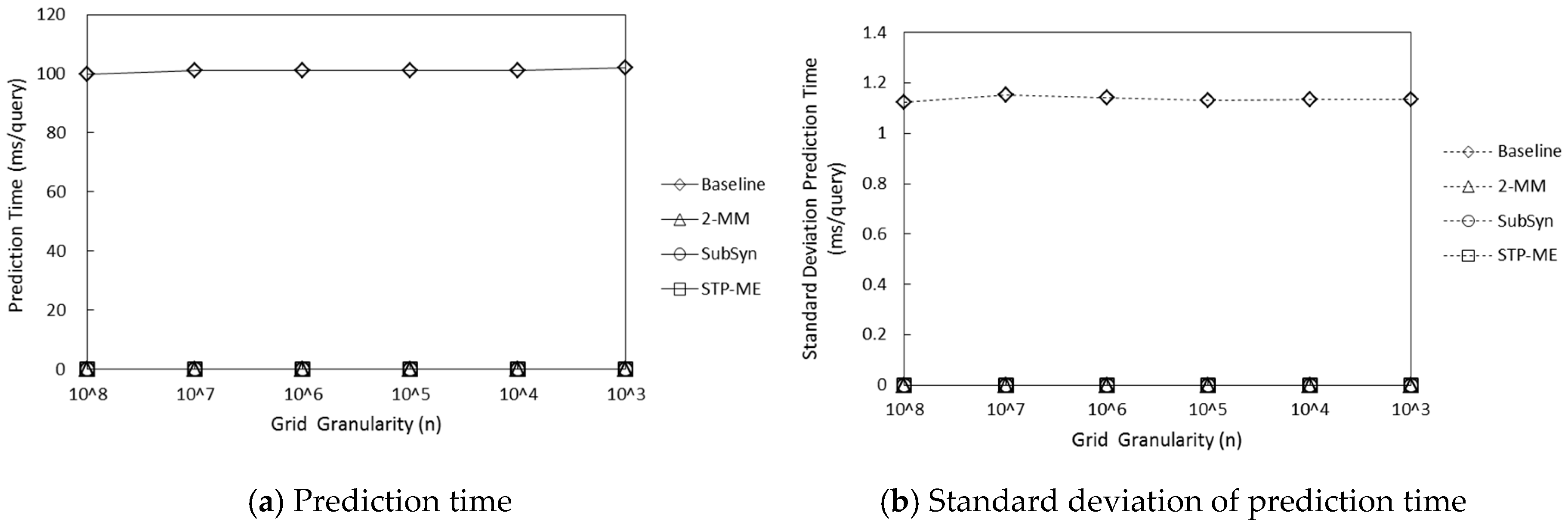
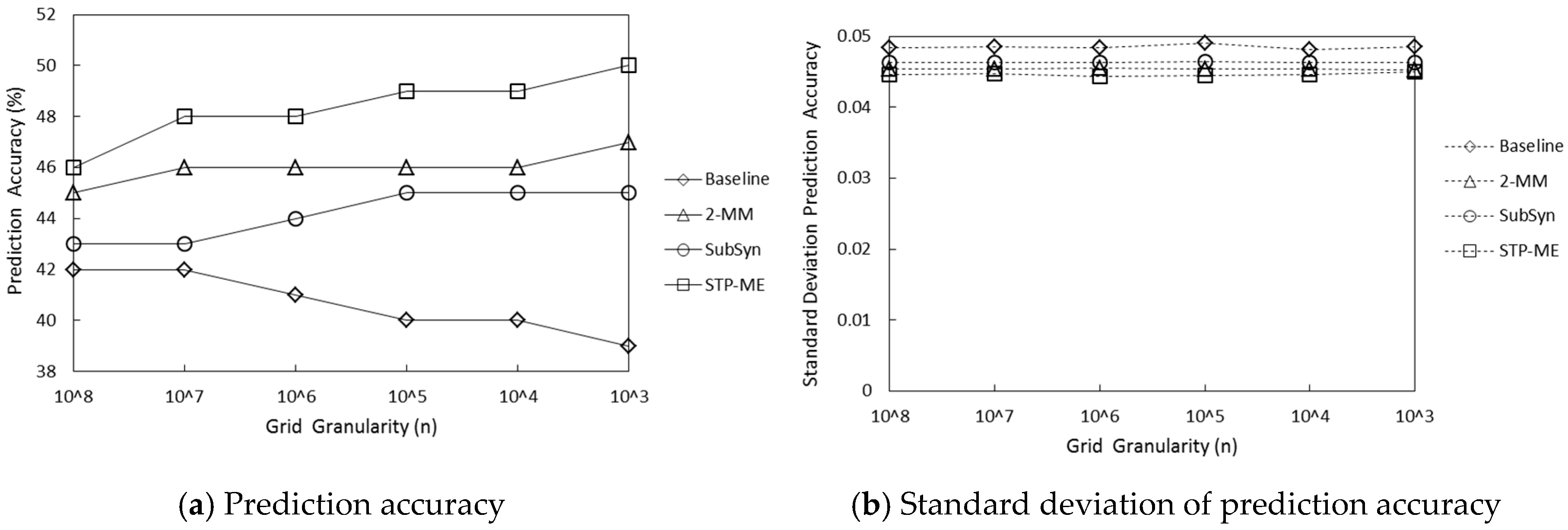
5.2. Comparison of Various Grid Partitioning Strategies
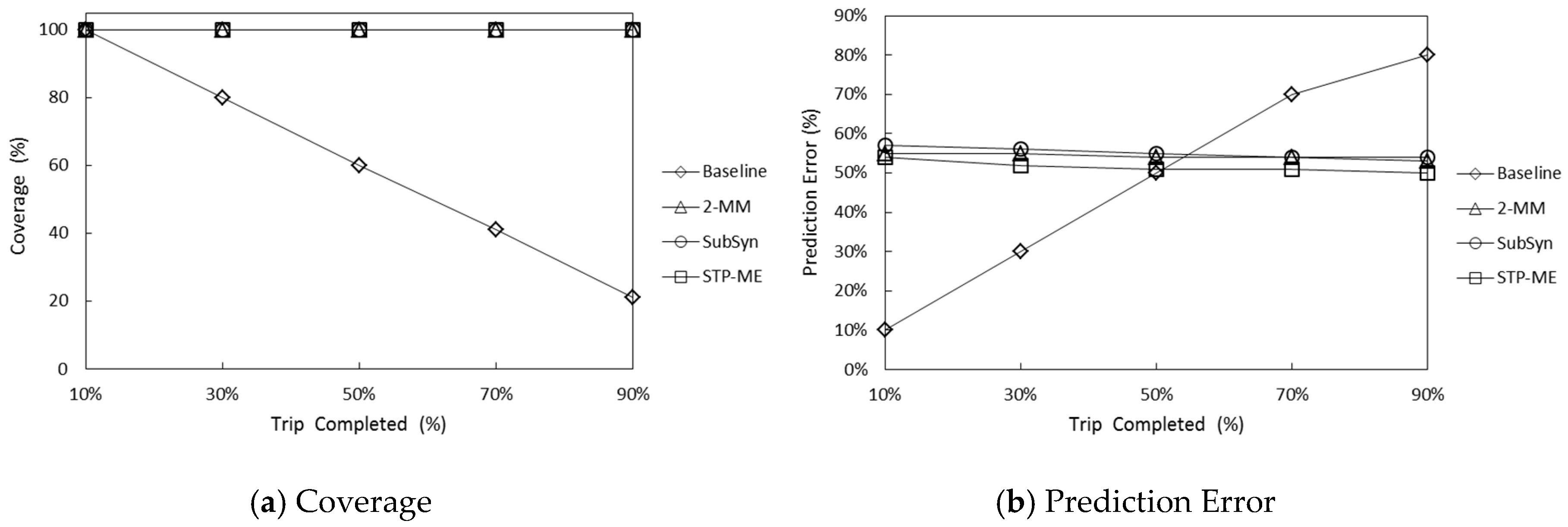
5.3. The Comparison of STP-ME Algorithm with Baseline, 2-MM, and SubSyn Algorithms
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.-L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Lian, D.; Xie, X.; Zheng, V.W.; Yuan, N.J.; Zhang, F.; Chen, E. CEPR: A collaborative exploration and periodically returning model for location prediction. ACM Trans. Intell. Syst. Technol. 2015, 6. [Google Scholar] [CrossRef]
- Yao, D.; Yu, C.; Jin, H.; Ding, Q. Human mobility synthesis using matrix and tensor factorizations. Inf. Fusion 2015, 23, 25–32. [Google Scholar] [CrossRef]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Li, F.-F.; Savarese, S. Social LSTM: Human Trajectory Prediction in Crowded Spaces. Available online: http://web.stanford.edu/~alahi/downloads/CVPR16_N_LSTM.pdf (accessed on 26 August 2016).
- Qiao, S.; Han, N.; Zhu, W.; Gutierrez, L.A. TraPlan: An Effective Three-in-One Trajectory-Prediction Model in Transportation Networks. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1188–1198. [Google Scholar] [CrossRef]
- Gambs, S.; Killijian, M.O.; Del Prado Cortez, M.N. Next place prediction using mobility Markov chains. In Proceedings of the First Workshop on Measurement, Privacy, and Mobility, Bern, Switzerland, 10–13 April 2012.
- Smith, G.; Wieser, R.; Goulding, J.; Barrack, D. A refined limit on the predictability of human mobility. In Proceedings of the 2014 IEEE International Conference on Pervasive Computing and Communications, Budapest, Hungary, 24–28 March 2014; pp. 88–94.
- Abdel-Fatao, H.; Li, J.; Liu, J. STMM: Semantic and Temporal-Aware Markov Chain Model for Mobility Prediction. In Data Science; Springer: Cham, Switzerland, 2015; pp. 103–111. [Google Scholar]
- Xue, A.Y.; Zhang, R.; Zheng, Y.; Xie, X.; Huang, J.; Xu, Z. Destination prediction by sub-trajectory synthesis and privacy protection against such prediction. In Proceedings of the IEEE 29th International Conference on Data Engineering (ICDE), Brisbane, Australia, 8–12 April 2013; pp. 254–265.
- Xue, A.Y.; Qi, J.; Xie, X.; Zhang, R.; Huang, J.; Li, Y. Solving the data sparsity problem in destination prediction. VLDB J. 2014, 24, 219–243. [Google Scholar] [CrossRef]
- Gao, Y.; Kontoyiannis, I.; Bienenstock, E. Estimating the entropy of binary time series: Methodology, some theory and a simulation study. Entropy 2008, 10, 71–99. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S.; Cheng, M.; Gao, X. Permutation Entropy for Random Binary Sequences. Entropy 2015, 17, 8207–8216. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Zhao, H.; Principe, J.C. Insights into Entropy as a Measure of Multivariate Variability. Entropy 2016, 18, 196. [Google Scholar] [CrossRef]
- Toffoli, T. Entropy? Honest! Entropy 2016, 18, 247. [Google Scholar] [CrossRef]
- Mclnerney, J.; Stein, S.; Rogers, A.; Jennings, N.R. Exploring Periods of Low Predictability in Daily Life Mobility. Available online: http://eprints.soton.ac.uk/339940/1/paper_extended_past2.pdf (accessed on 26 August 2016).
- Microsoft Research: T-Drive Trajectory Data Sample. Available online: https://www.microsoft.com/en-us/research/publication/t-drive-trajectory-data-sample/ (accessed on 26 August 2016).
- Ziebart, B.D.; Maas, A.L.; Dey, A.K.; Begnell, J.A. Navigate Like a Cabbie: Probabilistic Reasoning from Observed Context-Aware Behavior. Available online: http://www.cs.cmu.edu/~bziebart/publications/navigate-bziebart.pdf (accessed on 26 August 2016).

| Grid | … | ||||
|---|---|---|---|---|---|
| Frequency | 452 | 357 | 642 | … | 567 |
| Grid | … | |||||
|---|---|---|---|---|---|---|
| Frequency | 45 | 24 | 35 | 18 | ||
| 42 | 45 | 44 | 23 | |||
| 45 | 56 | 36 | 42 | |||
| … | ||||||
| 42 | 55 | 48 | 41 | |||
| Grid | … | |||||
|---|---|---|---|---|---|---|
| … | ||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Liu, L.; Xia, Z.; Li, W.; Fan, Q. Sparse Trajectory Prediction Based on Multiple Entropy Measures. Entropy 2016, 18, 327. https://doi.org/10.3390/e18090327
Zhang L, Liu L, Xia Z, Li W, Fan Q. Sparse Trajectory Prediction Based on Multiple Entropy Measures. Entropy. 2016; 18(9):327. https://doi.org/10.3390/e18090327
Chicago/Turabian StyleZhang, Lei, Leijun Liu, Zhanguo Xia, Wen Li, and Qingfu Fan. 2016. "Sparse Trajectory Prediction Based on Multiple Entropy Measures" Entropy 18, no. 9: 327. https://doi.org/10.3390/e18090327
APA StyleZhang, L., Liu, L., Xia, Z., Li, W., & Fan, Q. (2016). Sparse Trajectory Prediction Based on Multiple Entropy Measures. Entropy, 18(9), 327. https://doi.org/10.3390/e18090327






